T��de� absolventov matfyzu 2002

Abstrakty - Matematika

Model na predikciu �asov�ho r�du d�t - spotreby paliva energetickej spolo�nosti v z�vislosti od teploty
J�n B�be�a, Accenture Slovensko, Bratislava
Pondelok, 16. decembra 2002, 12:30-13:10 (Matematika I.)

Predpovedanie hodinovej spotreby paliva v z�vislosti od teploty sa pri ur�itej presnosti predikcie ukazuje ako ekonomicky u�ito�n� pre riadiace syst�my energetickej spolo�nosti. Model na predikciu mus� zoh�ad�ova� vplyv teploty, slene�n�ho svitu, hodinov� priebeh spotreby paliva po�as d�a, denn� priebeh po�as t��d�a a dlhodobej�ie peri�dy. Na zoh�adnenie v�etk�ch vplyvov bol pou�it� line�rny model a empirick� BLUP ako prediktor �asov�ho radu. Kv�li rozsahu d�t (8000 meran�) bol na v�po�et predikci� vyu�it� �tatistick� softv�r. Stanoven� model dostato�ne zoh�adnil dan� vplyvy a dosiahol stredn� relat�vnu chybu predikci� prijateln� pre zad�vate�a �lohy.

J�n B�be�a �tudoval na FMFI UK odbor pravdepodobnos� a �tatistika. Na �kole na�alej �tuduje ako extern� doktorand. Po skon�en� �t�dia pracoval na Ministerstve financi� (�tvar projektu �t�tnej pokladnice), kde sa podie�al na n�vrhu modelu pr�jmov a v�davkov �t�tnej pokladnice. V s��asnosti pracuje vo firme Accenture ako analytik, kde sa zaober� syst�movou integr�ciou bankov�ho softv�ru.

Obchodovanie na finan�n�ch trhoch
Du�an Svitek a �ubom�r Hlad�k, Slovensk� Sporite��a, Bratislava
Pondelok, 16. decembra 2002, 13:20-14:00 (Matematika I.)

V predn�ke najprv pop��eme situ�ciu na slovenskom finan�nom trhu, tzv. "Treasury". �alej rozoberieme princ�py oce�ovania Treasury produktov a rozdiely v ich oce�ovan� v te�rii a praxi.

Du�an Svitek ukon�il �t�dium na MFF UK v roku 1997 v odbore poistn� a finan�n� matematika a numerick� anal�za. Po skon�en� �t�dia p�sobil v Slovenskej sporite�ni na r�znych poz�ci�ch ako d�ler, ��f d�ler a napokon v s��astnosti p�sob� ako ved�ci odboru Trading and Sales. Z��astnil sa na viacer�ch zahrani�n�ch �tudijn�ch pobytoch. Vykon�va funkciu predsedu predstavenstva ACI Slovakia - Medzin�rodn� asoci�cia dealerov finan�n�ch trhov.

�ubom�r Hlad�k ukon�il �t�dium na MFF UK v roku 2001 v odbore ekonomick� a finan�n� matematika (�kolite� Doc. RNDr. Margar�ta Halick�, CSc.). Po skon�en� �t�dia p�sobil v ING Bank (1997-1999) a v Slovenskej sporite�ni (od 1999 doteraz).

Matematick� modely v riaden� akt�v a pas�v na finan�n�ch trhoch
Miroslav Morh��, Slovensk� Sporite��a, Bratislava
Pondelok, 16. decembra 2002, 14:00-14:40 (Matematika I.)

Predn�ka bude pozost�va� z troch �ast�: postavenie a �lohy ALM v r�mci banky, management �rokov�ho rizika, a management likviditn�ho rizika. V predn�ke pouk�em na vyu�itie matematick�ch modelov pri rie�en� probl�mov z uveden�ch oblast�. Podrobnej�ie bud� spomenut� anal�za �asov�ch radov (management lividitn�ho rizika) a Monte Carlo simul�cie (�rokov� riziko).

Miroslav Morh�� absolvoval MFF UK v roku 1997, odbor matematick� �tatistika a te�ria pravdepodobnosti, finan�n� a poistn� matematika (�kolite� diplomovej pr�ce doc. RNDr. Rastislav Potock�, CSc.). Po skon�en� p�sobil ako FX (foreign exchange) dealer v Slovenskej Sporite�ni (1996-1998), v Hypovereinsbank Slovakia (1998-2001) a v Hypovereinsbank Mn�chov (st� 2000-2001). Od roku 2001 pracuje v Slovenskej Sporite�ni, od roku 2002 ako ved�ci oddelenia riadenia likvidity.

Experiment�lna ekon�mia
Eugen Kov��, CERGE, Praha
Pondelok, 16. decembra 2002, 15:00-15:40 (Matematika II.)

Doteraj�ie modely spr�vania pri neur�itosti v mikroekon�mii boli zalo�en� hlavne na te�rii o�ak�van�ho ��itku a te�rii hier. Viacer� pr�pady z praxe potvrdzuj�, �e �udia sa nie v�dy spr�vaj� 'optim�lne', t.j. tak ako predpoved� te�ria. Preto sa v s��asnosti rob� mno�stvo experimentov, pomocou ktor�ch sa vedci-ekon�movia sna�ia vysvetli� odch�lky od 'optim�lneho' spr�vania (Nobelova cena za ekonomiu bola tohto roku udelen� D.Kahnemanovi, V.L. Smithovi pr�ve za experiment�lnu ekon�miu). Pr�spevok bude hovori� o princ�poch a cie�och v experiment�lnej ekon�mii ako aj o konkr�tnych experimentoch; jedn�m sa v s��asnosti zaober�m.

Eugen Kov�� ukon�il �t�dium na FMFI UK v roku 2001 v odbore matematika (matematick� anal�za, �kolite� prof. RNDr. Tibor �al�t, DrSc.). V s��asnosti p�sob� na CERGE-EI, Univerzita Karlova, Praha.

Met�dy symplektickej geometrie
Martin Niepel, Princeton University
Pondelok, 16. decembra 2002, 15:40-16:20 (Matematika II.)

Varieta M2n vybaven� nedegenerovanou uzavretou 2-formou omega sa naz�va symplektickou. Symplektick� �trukt�ry na varietach p�vodne pochadz�j� z klasickej mechaniky, kde symplektick� forma omega s�vis� s Hamiltoni�nom syst�mu.

V 80-tych a 90-tych rokoch zaznamenala n�zkorozmern� top�logia b�rliv� v�voj pr�ve v�aka objaveniu pomerne prekvapuj�cich vlastnost� 4-rozmern�ch symplektick�ch variet.

V pr�spevku budeme prezentova� s�vislosti medzi komplexn�mi a symplektick�mi varietami; prinesieme preh�ad techn�k, princ�pov a objektov, ktor� sa v tejto oblasti daj� pou�it - pseudoholomorfn� krivky, s�vislos� S-W a G-W invariantov v dimenzii 4, Floerove homol�gie. Na z�ver (v z�vislosti od �asu) spomenieme �pecifick� topologick� kon�trukciu, ktor� umo��uje 'zlepenie' dvoch 4-rozmern�ch symplektick�ch variet.

Martin Niepel �tudoval na MFF UK v rokoch 1994-1999 v odbore matematika, zamerania matematick� anal�za a algebra. �t�dium ukon�il diplomovou pr�cou "Vnorenia s��inov grafov a s��iny m�p" pod veden�m Doc. Martina �kovieru. Od roku 1999 je �tudentom doktorandsk�ho �t�dia na Princeton University. Oblas� jeho v�skumu je n�zkodimenzi�lna topol�gia a geometria a symplektick� a kontaktn� �trukt�ry.

Klasick� projekcie a klasick� limita kvantovej mechaniky
Marcel Polakovi�, FEI Slovensk� technick� univerzita, Bratislava
Pondelok, 16. decembra 2002, 16:20-17:00 (Matematika II.)

Vy�etruje sa klasick� limita kvantovej mechaniky v kontexte formalizmu tzv. klasick�ch projekci�, zaveden�ch P. B�nom. Prezentuj� sa v�sledky, kde (pre vhodn� triedy Hamiltoni�nov) Hamiltoni�n klasickej projekcie konverguje (pre h -> 0) k Hamiltoni�nu klasickej limity. Pre ist� triedy Hamiltoni�nov s� uveden� aj tvrdenia o konvergencii dynam�k.

Marcel Polakovi� �tudoval do roku 1992 na FMFI UK v odbore "Teoretick� kybernetika, matematick� informatika a te�ria syst�mov". �kolite�om jeho diplomovej pr�ce bol doc. RNDr. Peter Hor�k, CSc. Po skon�en� �t�dia p�sobil na fakulte ako doktorand v rokoch 1992-1996, odbor matematika, zameranie matematick� fyzika (�kolite� doc. Ing. Pavel B�na, CSc.) a od roku 1997 je odborn�m asistentom na Katedre matematiky FEI STU. V roku 2002 ukon�il PhD. v odbore aplikovan� matematika.

Suma�n� pravidl� pre Jakobiho matice a ortogon�lne polyn�my
Andrej Zlato�, California Institute of Technology, Pasadena
Streda, 18. decembra 2002, 15:00-15:40 (Matematika III.)

Jakobiho matica je diferen�n� oper�tor $ J$ druh�ho r�du

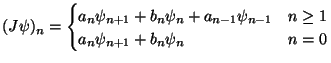
$\displaystyle (J\psi)_n = \begin{cases}a_{n}\psi_{n+1} + b_{n}\psi_{n} + a_{n-1}\psi _{n-1} & n\ge 1 \ a_{n}\psi_{n+1} + b_{n}\psi_{n} & n=0 \end{cases}$

($ a_n>0$ a $ b_n\in \mathbb{R}$) na Hilbertovom priestore $ \ell^2(\mathbb{Z}_0^+)$. Ako samoadjungovan� oper�tor m� spektr�lnu mieru $ \mu$, ktorej support je spektrom $ J$. Tento objekt je zauj�mav� v oblasti matematickej fyziky, preto�e je zov�eobecnen�m diskr�tnych Schr�dingerov�ch oper�torov, ako aj v oblasti ortogon�lnych polyn�mov, preto�e vlastn� funkcie $ u_n(x)$ (s $ x\in\mathbb{R}$) sp��aj�ce $ Ju=xu$ s� polyn�mami v $ x$, ktor� s� ortogon�lne vzh�adom na $ \mu$. V pr�spevku bud� prezentovan� vz�ahy medzi $ \mu$ a $ a_n,b_n$, naz�van� suma�n� pravidl�.

Andrej Zlato� ukon�il �t�dium na MFF UK v roku 1999 (odbor matematick� anal�za, �kolite� Doc. RNDr. Martin �koviera, PhD.). V s��asnosti je doktorandom na California Institute of Technology.

Maxim�lne rie�enia pre Yamabeho a pr�buzn� probl�my na oblastiach na Riemanov�ch variet�ch
Martin Dindo�, Cornell University, Ithaca
Streda, 18. decembra 2002, 15:40-16:20 (Matematika III.)

V pr�spevku budeme prezentova� kladn� rie�enia parci�lnej rovnice

\begin{displaymath}\Delta u+hu-k\psi(u)=-f \end{displaymath}

na oblasti $\Omega\subset M$, kde M je n-rozmern� kompaktn� Riemannova varieta. Rie�enie sp��aj�ce $u(x)\to\infty$ pre $x\to\partial\Omega$ budeme naz�va� maxim�lne rie�enie. Funkcia $\psi$ je kladn�, konvexn� a dostato�ne r�chlo rast�ca, typick�m pr�kladom je $\psi(u)=u^\alpha$ pre nejak� $\alpha>1$.

Rovnice tohto typu maj� ve�k� v�znam v differenci�lnej geometrii, konkr�tnym pr�kladom m��e by� Yamabeho rovnica ($n\ge 3$)

\begin{displaymath}\Delta u -\frac{n-2}{4(n-1)}Ru+\frac{n-2}{4(n-1)}R'u^{(n+2)/(n-2)}=0\end{displaymath}

Ak g je origin�lny metrick� tenzor M s krivos�ou R, potom g'=u4/(n-2) je nov� tenzor konform�lny s g a s krivos�ou R'. Hrani�n� podmienka $u(x)\to\infty$ (pokia� u rastie dostato�ne r�chlo) m� geometrick� v�znam, �e $(\Omega,g')$ je upln� priestor, teda ka�d� geodezick� krivka je �pln�.

Martin Dindo� ukon�il �t�dium na FMFI UK v roku 1995 (�kolite� doc. RNDr. Vladim�r Toma, PhD.). V rokoch 1995-2000 p�sobil ako doktorand na FMFI UK v odbore re�lna anal�za (prof. RNDr. Pavol Kostyrko, DrSc.) a v rokoch 1997-2001 na University of North Carolina, Chapel Hills (harmonick� anal�za, parci�lne diferenci�lne rovnice, �kolite� Michael Taylor). Obe �t�di� ukon�il z�skan�m titulu PhD. V roku 2001 p�sobil na Clay Mathematics Institute ako vedeck� pracovn�k a od roku 2001 je profesorom na Cornell University, Ithaca. Jeho v�skum sa s�stre�uje na parci�lne diferenci�lne rovnice a harmonick� a re�lnu anal�zu.

Topologicky netrivi�lne rie�enia neline�rnej Schr�dingerovej rovnice
Richard Koll�r, University of Maryland, College Park
Streda, 18. decembra 2002, 16:20-17:00 (Matematika III.)

Neline�rna Schr�dingerova rovnica modeluje mno�stvo r�znych fyzik�lnych dejov, napr�klad neline�rnu optiku, magnetiz�ciu, �i Bose-Einsteinove kondenz�ty. Pre v�etky tieto typy nelinear�t sk�mame existenciu a stabilitu z fyzik�lneho h�adiska zaujimav�ch topologicky netrivi�lnych (vortex) rie�en�.

Richard Koll�r ukon�il �t�dium na FMFI UK v roku 1997 v odbore matematick� anal�za (�kolite� doc. RNDr. Michal Fe�kan, DrSc.). V rokoch 1997-1998 p�sobil na �stave aplikovanej matematiky FMFI UK a od roku 1998 je PhD. �tudentom na University of Maryland, College Park (�kolite� Dr. Robert Pego a Dr. Jian-Guo Liu). Jeho v�skum je zameran� na parci�lne diferenci�lne rovnice - rovnice fyziky pr�denia tekut�n a neline�rne vlny.