1-BIN-301, 2-AIN-501 Methods in Bioinformatics

Website moved to https://fmfi-compbio.github.io/mbi/


MBI 2010/2011: Rozdiel medzi revíziami

Z MBI
Prejsť na: navigácia, hľadanie
(Created page with '=UCSC genome browser, cvičenia pre biológov= * Používajte čierne počítače, zvoľte v menu Bioinformatika, užívatel Bioinformatika * V programe Firefox choďte na strán…')
 
Riadok 1: Riadok 1:
 +
* [[Sekvenovanie genómov, cvičenia pre informatikov]]
 +
* [[Zarovnávanie sekvencií, cvičenia pre biológov]]
 +
* [[Zarovnávanie sekvencií 2, cvičenia pre biológov]]
 +
* [[Zarovnávanie sekvencií, cvičenia pre informatikov]]
 +
* [[Zarovnávanie sekvencií 2, cvičenia pre informatikov]]
 +
* [[Hľadanie génov a anotácia sekvencií, cvičenia pre biológov]]
 +
* [[Skryté Markovove modely, cvičenia pre informatikov]]
 +
* [[Evolúcia, cvičenia pre biológov]]
 +
* [[Evolúcia 2, cvičenia pre biológov]]
 +
* [[Evolúcia, cvičenia pre informatikov]]
 +
* [[Evolúcia 2, cvičenia pre informatikov]]
 +
* [[Proteíny, cvičenia pre biológov]]
 +
* [[Evolúcia 3 a proteíny, cvičenia pre informatikov]]
 +
* [[Proteíny, cvičenia pre informatikov]]
 +
* [[Expresia génov, cvičenia pre biológov]]
 +
* [[Proteíny 2, cvičenia pre informatikov]]
 +
* [[Hľadanie motívov, cvičenia pre informatikov]]
 +
* [[Hľadanie motívov a populačná genetika, cvičenia pre biológov]]
 +
* [[Populačná genetika, cvičenia pre informatikov]]
 +
 +
=Počítanie fylogenetických stromov, cvičenia pre informatikov=
 +
* Ako definujeme strom v teorii grafov? suvisly acyklicky neorientovany graf
 +
* Strom s n vrcholmi ma n-1 hran
 +
* Nezakoreneny binarny fylogeneticky strom: neorientovany suvisl acyklicky graf, v listoch sucasne druhy, vsetky vnutorne vrcholy stupna 3
 +
* Zakoreneny binarny fylogeneticky strom: vsetky hrany orientujeme od korena smerom k listom, kazdy vnutorny vrchol ma dve deti
 +
* Niekedy uvazujeme aj nebinarne stromy, v ktorych mame vnutorne vrcholy vyssieho stupna
 +
* Zakoreneny binarny strom s n listami ma n-1 vnutornch vrcholov, teda 2n-2 hran
 +
* Nezakoreneny binarny strom s n listami ma n-2 vnutornych vrcholov, teda 2n-3 hran
 +
* Pocet nezakorenenych fylogenetickych stromov s n listami:
 +
** a(3) = 1, a(4) = 3, a(n+1) = a(n) * (2n-3) a teda a(n) = 1 * 3 * 5 * ... * (2n-5) = (2n-5)!!
 +
* Pocet zakorenenych fylogenetickych stromov s n listami:
 +
** zakoren strom s n listami kazdy 2n-3 sposobmi, teda (2n-3)!!
 +
 
=UCSC genome browser, cvičenia pre biológov=
 
=UCSC genome browser, cvičenia pre biológov=
 
* Používajte čierne počítače, zvoľte v menu Bioinformatika, užívatel Bioinformatika
 
* Používajte čierne počítače, zvoľte v menu Bioinformatika, užívatel Bioinformatika
Riadok 148: Riadok 181:
 
* Realne pouzivana technologia, aj pre sekvenovanie novej generacie, napr. Zerbino and Birney 2008 program Velvet
 
* Realne pouzivana technologia, aj pre sekvenovanie novej generacie, napr. Zerbino and Birney 2008 program Velvet
  
−
=Počítanie fylogenetických stromov, cvičenia pre informatikov=
+
=Sekvenovanie genómov, cvičenia pre biológov=
−
* Ako definujeme strom v teorii grafov? suvisly acyklicky neorientovany graf
+
* Cvicenia pre biológov zo sekvenovania, pracovna verzia poznamok
−
* Strom s n vrcholmi ma n-1 hran
+
* Ospravedlnujem sa za chybajucu diakritiku
−
* Nezakoreneny binarny fylogeneticky strom: neorientovany suvisl acyklicky graf, v listoch sucasne druhy, vsetky vnutorne vrcholy stupna 3
+
* Pozrite tiez grafy k pravdepodobnosti: http://compbio.fmph.uniba.sk/vyuka/mbi/poznamky/cb02.pdf
−
* Zakoreneny binarny fylogeneticky strom: vsetky hrany orientujeme od korena smerom k listom, kazdy vnutorny vrchol ma dve deti
+
 
−
* Niekedy uvazujeme aj nebinarne stromy, v ktorych mame vnutorne vrcholy vyssieho stupna
+
===UCSC genome browser===
−
* Zakoreneny binarny strom s n listami ma n-1 vnutornch vrcholov, teda 2n-2 hran
+
* http://genome.ucsc.edu/
−
* Nezakoreneny binarny strom s n listami ma n-2 vnutornych vrcholov, teda 2n-3 hran
+
* Ukazali sme si niekolko trackov, ktore maju suvis so sekvenovanim a skladanim genomov, napr. gaps, quality score a pod. (v genomoch cloveka a macky)
−
* Pocet nezakorenenych fylogenetickych stromov s n listami:
+
 
−
** a(3) = 1, a(4) = 3, a(n+1) = a(n) * (2n-3) a teda a(n) = 1 * 3 * 5 * ... * (2n-5) = (2n-5)!!
+
===Pravdepodobnost===
−
* Pocet zakorenenych fylogenetickych stromov s n listami:  
+
 
−
** zakoren strom s n listami kazdy 2n-3 sposobmi, teda (2n-3)!!
+
* Nas problem: spocitanie pokrytia
 +
** G = dlzka genomu, napr. 1 000 000
 +
** N = pocet segmentov (readov), napr. 10 000
 +
** L = dlzka readu, napr. 1000
 +
** Celkova dlzka segmentov NL, pokrytie (coverage) NL/G, v nasom pripade 10x
 +
** V priemere kazda baza pokryta 10x
 +
** Niektore su ale pokryte viackrat, ine menej.
 +
** Zaujimaju nas otazky typu: kolko baz ocakavame, ze bude pokrytych menej ako 3x?
 +
** Dolezite pri planovani experimentov (aku velke pokrytie potrebujem na dosiahnutie urcitej kvality)
 +
 
 +
* Uvod do pravdepodobnosti
 +
** Myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealnou kockou/korunou
 +
** Vysledkom experimentu je nejaka hodnota (napr. cislo, alebo aj niekolko cisel, retazec)
 +
** Tuto neznamu hodnotu budeme volat nahodna premenna
 +
** Zaujima nas pravdepodobnost, s akou nahodna premenna nadobuda jednotlive mozne hodnoty
 +
** T.j. ak experiment opakujeme vela krat, ako casto uvidime nejaky vysledok
 +
** Priklad 1: hodime idealizovanou kockou, premenna X bude hodnota, ktoru dostaneme
 +
** Mozne hodnoty 1,2,..,6, kazda rovnako pravdepodobna
 +
** Piseme napr. Pr(X=2)=1/6
 +
** Priklad 2: hodime 2x kockou, nahodna premenna X bude sucet hodnot, ktore dostaneme
 +
** Mozne hodnoty: 2,3,...,12
 +
** Kazda dvojica hodnot na kocke rovnako pravdepodobna, t.j. pr. 1/36
 +
** Sucet 5 mozeme dostat 1+4,2+3,3+2,4+1 - t.j. P(X=5) = 4/36
 +
** Sucet 11 mozeme dostat 5+6 alebo 6+5, t.j. P(X=11) = 2/36
 +
** Rozdelenie pravdepodobnosti: 2: 1/36, 3:2/36, 4: 3/36, ... 7: 6/36, 8: 5/36 ... 12: 1/36
 +
** Overte, ze sucet je 1
 +
 
 +
* Pokrytie genomu: predpokladame, ze kazdy segment zacina na nahodnej pozicii zo vsetkych moznych G-L+1
 +
* Takze ak premenna Y_i bude zaciatok i-teho segmentu, jej rozdelenie bude rovnomerne
 +
** P(Y_i=1) = P(Y_i=2) = ... = P(Y_i=G-L+1) = 1/G-L+1
 +
* Uvazujme premennu X_j, ktora udava pocet segmentov pokryvajucich poziciu j
 +
** mozne hodnoty 0..N
 +
** i-ty segment pretina poziciu j s pravdepodobnostou L/(G-L+1), oznacme tuto hodnotu p
 +
** to iste ako keby sme N krat hodili mincou, na ktorej spadne hlava s pravd. p a znak 1-p a oznacili ako X_j pocet hlav
 +
** Priklad: majme mincu, ktora ma hlavu s pr. 1/4 a hodime je 3x.
 +
<pre>
 +
HHH 1/64
 +
HHT 3/64
 +
HTH 3/64
 +
HTT 9/64
 +
THH 3/64
 +
THT 9/64
 +
TTH 9/64
 +
TTT 27/64
 +
</pre>
 +
* P(X_j=3) = 1/64, P(X_j=2)=9/64, P(X_j=1)=27/64, P(X_j=0)=27/64
 +
** taketo rozdelenie pravdepodobnosti sa vola binomicke
 +
** P(X_j = k) = (N choose k) p^k (1-p)^(N-k), kde <math>{N \choose k} = \frac{N!}{k!(N-k)!}</math> a n! = 1*2*...*n
 +
** napr pre priklad s troma hodmi kockou P(X_j=2) = 3!/(2!*1!) * (1/4)^2 * (3/4)^1 = 9/64
 +
** Zle sa pocita pre velke N, preto sa niekedy pouziva aproximacia Poissonovym rozdelenim s parametrom lambda = Np, ktore ma <math>e^{-\lambda}\lambda^k / k!</math>
 +
** Spat k sekvenovaniu: vieme spocitat rozdelenie pravdepodobnosti a tiez napr. P(X_i<3) = P(X_i=0)+P(X_i=1)+P(X_i=2) = 0.000045+0.00045+0.0023=0.0028 (v priemere ocakavame 45 baz nepokrytych)
 +
** Takyto graf, odhad, vieme lahko spravit pre rozne pocty segmentov a tak naplanovat, kolko segmentov potrebujeme
 +
 
 +
* Chceme tiez odhadnut pocet kontigov (nebrali sme na cviceni, uvedene len pre zaujimavost)
 +
** Ak niekolko baz vobec nie je pokrytych segmentami, prerusi sa kontig
 +
** Vieme, kolko baz je v priemere nepokrytych, ale niektore mozu byt vedla seba
 +
** Novy kontig vznikne aj ak sa susedne segmenty malo prekryvaju
 +
** Predpokladajme, ze na spojenie dvoch segmentov potrebujeme prekryv aspon T
 +
** Lander a Waterman 1988 odhadli, ze dany segment ma pravdepodobnost zhruba exp(-N(L-T)/G), ze bude posledny v kontigu
 +
** Pre N segmentov dostaneme priemerny pocet kontigov 1+N*exp(-N(L-T)/G)
 +
** Ako keby sme dlzku segmentu skratili o dlzku prekryvu
 +
** Pre T=50 dostaneme priemerny pocet kontigov 1.75, ak znizime N na 5000 (5x pokrytie) dostaneme 44 kontigov
 +
 
 +
* Tento jednoduchy model nepokryva vsetky faktory:
 +
** Segmenty nemaju rovnaku dlzku
 +
** Problemy v zostavovani kvoli chybam, opkaovaniam a pod.
 +
** Segmenty nie su rozlozene rovnomerne (cloning bias a pod.)
 +
** Vplyv koncov chromozomov
 +
** Uzitocny ako hruby odhad
 +
** Na spresnenie mozeme skusat spravit zlozitejsie modely, alebo simulovat data
 +
 
 +
* Poznamka: pravdepodobnosti z binomickeho rozdelenia mozeme lahko spocitat napr. statistickym softverom R. Tu su prikazy, ktore sa na to hodia, pre pripad, ze by vas to zaujimalo:
 +
<pre>
 +
dbinom(10,1e4,0.001);  #(12.5% miest ma pokrytie presne 10)
 +
pbinom(10,1e4,0.001,lower.tail=TRUE); #(58% miest ma pokrytie najviac 10)
 +
dbinom(0:30,1e4,0.001); #tabulka pravdepodobnosti
 +
[1] 4.517335e-05 4.521856e-04 2.262965e-03 7.549258e-03 1.888637e-02
 +
[6] 3.779542e-02 6.302390e-02 9.007019e-02 1.126216e-01 1.251601e-01
 +
[11] 1.251726e-01 1.137933e-01 9.481826e-02 7.292252e-02 5.207187e-02
 +
[16] 3.470068e-02 2.167707e-02 1.274356e-02 7.074795e-03 3.720595e-03
 +
[21] 1.858621e-03 8.841718e-04 4.014538e-04 1.743354e-04 7.254524e-05
 +
[26] 2.897743e-05 1.112843e-05 4.115040e-06 1.467156e-06 5.050044e-07
 +
[31] 1.680146e-07
 +
</pre>
 +
 
 +
====Zhrnutie====
 +
* Pravdedpobnostny model: myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealizovanou kockou
 +
* Vysledok je hodnota, ktoru budeme volat nahodna premenna
 +
* Tabulka, ktora pre kazdu moznu hodnotu nahodnej premennej urci je pravdepodobnost sa vola rozdelenie pravdepodobnosti, sucet hodnot v tabulke je 1
 +
* Znacenie typu P(X=7)=0.1
 +
 
 +
* Priklad: mame genom dlzky G=1mil., nahodne umiestnime N=10000 segmentov dlzky L=1000
 +
* Nahodna premenna X_i je pocet segmentov pokryvajucich urcitu poziciu i
 +
* Podobne, ako keby sme N krat hodili kocku, ktora ma cca 1 promile sancu padnu ako hlava a 99.9% ako znak a pytame sa, kolko krat padne znak (1 promile sme dostali po zaukruhleni z L/(G-L+1))
 +
* Rozdelenie pravdepobnosti sa v tomto pripade vola binomicke a existuje vzorec, ako ho spocitat
 +
* Takyto model nam moze pomoct urcit, kolko segmentov potrebujeme osekvenovat, aby napr. aspon 95% pozicii bolo pokrytych aspon 4 segmentami
 +
 
 +
===Eulerovský ťah===
 +
* Nestihli sme na cviceniach, uvedene pre zaujimavost
 +
* Orientovany graf
 +
* Silne suvisly orientovany graf
 +
* Eulerovsky tah, uzatvoreny eulerovsky tah
 +
* Pouzitie v de Bruijnovom grafe na zostavovanie genomu
 +
* Silne súvislý orientovany graf ma uzatvoreny eulerovsky tah prave vtedy, ked v kazdom vrchole je rovnako vchadzajucich a vychadzajucich hran
 +
** ak ma tah, musi byt suvisly
 +
** ak ma tak, musia sediet pocty hran
 +
** ak je suvisly a sedia pocty hran:
 +
*** prechadzka po grafe, kym sa da pokracovat nepouzitou hranou
 +
*** musime skoncit, kde sme zacali (z ostatnych vrcholov vieme pokracovat)
 +
*** zvysok grafu stale splna podmienku s poctami hran
 +
*** najdi dalsi vrchol, ktory je na tahu a ma este nepouzite hrany
 +
*** musi taky existovat
 +
*** pokracuj v tom istom, az kym sa nevratime, kde sme zacali
 +
*** cele opakujeme, az kym sa neminu hrany
 +
* Poznamka: v neorientovanych grafoch musia byt stupne vsetkych vrcholov parne
 +
* Ak hladame otvoreny tah, spojime zaciatocny a koncovy vrchol hranou a najdeme uzatvoreny tah

Verzia zo dňa a času 20:23, 2. október 2011

Počítanie fylogenetických stromov, cvičenia pre informatikov

  • Ako definujeme strom v teorii grafov? suvisly acyklicky neorientovany graf
  • Strom s n vrcholmi ma n-1 hran
  • Nezakoreneny binarny fylogeneticky strom: neorientovany suvisl acyklicky graf, v listoch sucasne druhy, vsetky vnutorne vrcholy stupna 3
  • Zakoreneny binarny fylogeneticky strom: vsetky hrany orientujeme od korena smerom k listom, kazdy vnutorny vrchol ma dve deti
  • Niekedy uvazujeme aj nebinarne stromy, v ktorych mame vnutorne vrcholy vyssieho stupna
  • Zakoreneny binarny strom s n listami ma n-1 vnutornch vrcholov, teda 2n-2 hran
  • Nezakoreneny binarny strom s n listami ma n-2 vnutornych vrcholov, teda 2n-3 hran
  • Pocet nezakorenenych fylogenetickych stromov s n listami:
    • a(3) = 1, a(4) = 3, a(n+1) = a(n) * (2n-3) a teda a(n) = 1 * 3 * 5 * ... * (2n-5) = (2n-5)!!
  • Pocet zakorenenych fylogenetickych stromov s n listami:
    • zakoren strom s n listami kazdy 2n-3 sposobmi, teda (2n-3)!!

UCSC genome browser, cvičenia pre biológov

  • Používajte čierne počítače, zvoľte v menu Bioinformatika, užívatel Bioinformatika
  • V programe Firefox choďte na stránku UCSC genome browser http://genome.ucsc.edu
  • Hore v modrom menu zvoľte Genomes
  • Na ďalšej stránke zvoľte človeka a v menu Assembly zistite, kedy boli pridané posledné dve verzie ľudského genómu (hg18 a hg19)
  • Na tej istej stránke dole nájdete stručný popis zvolenej verzie genómu. Pre ktoré chromozómy máme viacero alternatívnych verzií?
  • Zadajte región chr21:31,200,000-31,400,000
  • Zapnite si track Mapability na "pack" a track RepeatMasker prepnite na "full"
  • Mapability: nakoľko sa daný úsek opakuje v genóme a či teda vieme jednoznačne jeho ready namapovať pri použití Next generation sequencing (detaily keď kliknete na linku "Mapability")
  • Približne v strede zobrazeného regiónu je pokles mapovateľnosti. Akému typu opakovania zodpovedá? (pozrite track RepeatMasker)
  • Zapnite si tracky "Assembly" a "Gaps" a pozrite si región chr2:110,000,000-110,300,000. Aká dlhá je neosekvenovaná medzera (gap) v strede tohto regiónu? Približnú veľkosť môžete odčítať z obrázku, presnejší údaj zistíte kliknutím na čierny obdĺžnik zodpovedajúci tejto medzere (úplne presnú dĺžku aj tak nepoznáme, nakoľko nie je osekvenovaná).
  • Prejdite na genóm Rhesus, región chr7:59,022,000-59,024,000, zapnite si tracky Contigs, Gaps, Quality scores
  • Aké typy problémov v kvalite sekvencie v tomto regióne vidíte?

Sekvenovanie genómov, cvičenia pre informatikov

Uvod do pravdepodobnosti, pocitanie pokrytia genomov

  • Nas problem: spocitanie pokrytia
    • G = dlzka genomu, napr. 1 000 000
    • N = pocet segmentov (readov), napr. 10 000
    • L = dlzka readu, napr. 1000
    • Celkova dlzka segmentov NL, pokrytie (coverage) NL/G, v nasom pripade 10x
    • V priemere kazda baza pokryta 10x
    • Niektore su ale pokryte viackrat, ine menej.
    • Zaujimaju nas otazky typu: kolko baz ocakavame, ze bude pokrytych menej ako 3x?
    • Dolezite pri planovani experimentov (aku velke pokrytie potrebujem na dosiahnutie urcitej kvality)
  • Uvod do pravdepodobnosti
    • Myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealnou kockou/korunou
    • Vysledkom experimentu je nejaka hodnota (napr. cislo, alebo aj niekolko cisel, retazec)
    • Tuto neznamu hodnotu budeme volat nahodna premenna
    • Zaujima nas pravdepodobnost, s akou nahodna premenna nadobuda jednotlive mozne hodnoty
    • T.j. ak experiment opakujeme vela krat, ako casto uvidime nejaky vysledok
    • Priklad 1: hodime idealizovanou kockou, premenna X bude hodnota, ktoru dostaneme
    • Mozne hodnoty 1,2,..,6, kazda rovnako pravdepodobna
    • Piseme napr. Pr(X=2)=1/6
    • Priklad 2: hodime 2x kockou, nahodna premenna X bude sucet hodnot, ktore dostaneme
    • Mozne hodnoty: 2,3,...,12
    • Kazda dvojica hodnot na kocke rovnako pravdepodobna, t.j. pr. 1/36
    • Sucet 5 mozeme dostat 1+4,2+3,3+2,4+1 - t.j. P(X=5) = 4/36
    • Sucet 11 mozeme dostat 5+6 alebo 6+5, t.j. P(X=11) = 2/36
    • Rozdelenie pravdepodobnosti: 2: 1/36, 3:2/36, 4: 3/36, ... 7: 6/36, 8: 5/36 ... 12: 1/36
    • Sucet tychot hodnot je 1
  • Pokrytie genomu: predpokladame, ze kazdy segment zacina na nahodnej pozicii zo vsetkych moznych G-L+1
  • Takze ak premenna Y_i bude zaciatok i-teho segmentu, jej rozdelenie bude rovnomerne
    • P(Y_i=1) = P(Y_i=2) = ... = P(Y_i=G-L+1) = 1/G-L+1
  • Uvazujme premennu X_j, ktora udava pocet segmentov pokryvajucich poziciu j
    • mozne hodnoty 0..N
    • i-ty segment pretina poziciu j s pravdepodobnostou L/(G-L+1), oznacme tuto hodnotu p
    • to iste ako keby sme N krat hodili mincou, na ktorej spadne hlava s pravd. p a znak 1-p a oznacili ako X_j pocet hlav
    • taketo rozdelenie pravdepodobnosti sa vola binomicke
    • P(X_j = k) = (N choose k) p^k (1-p)^(N-k)
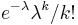
    • Zle sa pocita pre velke N, preto sa niekedy pouziva aproximacia Poissonovym rozdelenim s parametrom lambda = Np, ktore ma e^{{-\lambda }}\lambda ^{k}/k!
    • Spat k sekvenovaniu: vieme spocitat rozdelenie pravdepodobnosti a tiez napr. P(X_i<3) = P(X_i=0)+P(X_i=1)+P(X_i=2) = 0.000045+0.00045+0.0023=0.0028 (v priemere ocakavame 45 baz nepokrytych, 2800 s menej ako 3 segmentami)
    • Takyto graf, odhad, vieme lahko spravit pre rozne pocty segmentov a tak naplanovat, kolko segmentov potrebujeme
  • Chceme tiez odhadnut pocet kontigov (podla clanku Lander a Waterman 1988)
    • Ak niekolko baz vobec nie je pokrytych segmentami, prerusi sa kontig
    • Vieme, kolko baz je v priemere nepokrytych, ale niektore mozu byt vedla seba
    • Novy kontig vznikne aj ak sa susedne segmenty malo prekryvaju
    • Predpokladajme, ze na spojenie dvoch segmentov potrebujeme prekryv aspon T=50
    • Aka je pravdepodobnost, ze dany segment i bude posledny v kontigu?
    • Ziaden segment j!=i nesmie zacinat v prvych L-T bazach kontigu i
    • Kazdy segment tam zacina s pravdepodobnostou (L-T)/G, v priemere ich tam zacne N(L-T)/G
    • Pouzijeme Poissonovo rozdelenie pre 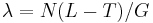\lambda =N(L-T)/G a k=0, t.j. pravdepodobnost, ze tam nezacne ziaden je zhruba exp(-N(L-T)/G)
    • Pre N segmentov dostaneme priemerny pocet kontigov N*exp(-N(L-T)/G)
    • Ako keby sme dlzku segmentu skratili o dlzku prekryvu
    • Pre T=50 dostaneme priemerny pocet kontigov 0.75 (v skutocnosti vzdy aspon 1, my sme vsak neuvazovali vplyv konca sekvencie). Ak znizime N na 5000 (5x pokrytie) dostaneme 43 kontigov
  • Tento jednoduchy model nepokryva vsetky faktory:
    • Segmenty nemaju rovnaku dlzku
    • Problemy v zostavovani kvoli chybam, opkaovaniam a pod.
    • Segmenty nie su rozlozene rovnomerne (cloning bias a pod.)
    • Vplyv koncov chromozomov
    • Uzitocny ako hruby odhad
    • Na spresnenie mozeme skusat spravit zlozitejsie modely, alebo simulovat data
  • Poznamka: pravdepodobnosti z binomickeho rozdelenia mozeme lahko spocitat napr. statistickym softverom R. Tu su prikazy, ktore sa na to hodia, pre pripad, ze by vas to zaujimalo: 
dbinom(10,1e4,0.001);  #(12.5% miest ma pokrytie presne 10)
pbinom(10,1e4,0.001,lower.tail=TRUE); #(58% miest ma pokrytie najviac 10)
dbinom(0:30,1e4,0.001); #tabulka pravdepodobnosti
 [1] 4.517335e-05 4.521856e-04 2.262965e-03 7.549258e-03 1.888637e-02
 [6] 3.779542e-02 6.302390e-02 9.007019e-02 1.126216e-01 1.251601e-01
[11] 1.251726e-01 1.137933e-01 9.481826e-02 7.292252e-02 5.207187e-02
[16] 3.470068e-02 2.167707e-02 1.274356e-02 7.074795e-03 3.720595e-03
[21] 1.858621e-03 8.841718e-04 4.014538e-04 1.743354e-04 7.254524e-05
[26] 2.897743e-05 1.112843e-05 4.115040e-06 1.467156e-06 5.050044e-07
[31] 1.680146e-07

Zhrnutie

  • Pravdedpobnostny model: myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealizovanou kockou
  • Vysledok je hodnota, ktoru budeme volat nahodna premenna
  • Tabulka, ktora pre kazdu moznu hodnotu nahodnej premennej urci je pravdepodobnost sa vola rozdelenie pravdepodobnosti, sucet hodnot v tabulke je 1
  • Znacenie typu P(X=7)=0.1
  • Priklad: mame genom dlzky G=1mil., nahodne umiestnime N=10000 segmentov dlzky L=1000
  • Nahodna premenna X_i je pocet segmentov pokryvajucich urcitu poziciu i
  • Podobne, ako keby sme N krat hodili kocku, ktora ma cca 1 promile sancu padnu ako hlava a 99.9% ako znak a pytame sa, kolko krat padne znak (1 promile sme dostali po zaukruhleni z L/(G-L+1))
  • Rozdelenie pravdepobnosti sa v tomto pripade vola binomicke a existuje vzorec, ako ho spocitat
  • Takyto model nam moze pomoct urcit, kolko segmentov potrebujeme osekvenovat, aby napr. aspon 95% pozicii bolo pokrytych aspon 4 segmentami

Zostavovanie genomu pomocou eulerovskych tahov

  • Opakovanie z teorie grafov:
    • Hamiltonovska kruznica: cyklus, ktory prechadza kazdym vrcholom prave raz
    • Eulerov tah: tah, ktory prechadza po kazdej hrane prave raz
    • Zistit, ci ma graf H.c. je NP-tazke
    • Problem obchodneho cestujuceho: najst najlacnejsiu H.c. je tiez NP-tazky
    • Zistit ci ma graf E.t. a najst ho je lahke
      • neorientovany graf na E.t. <=> je suvisly a vsetky vrcholy okrem najviac dvoch maju parny stupen
      • orientovany graf ma E.t. z u do v <=> po pridani hrany z v do u je silne suvisly a vsetky vrcholy maju rovnako vchadzajucich ako vychadzajucich hran
  • Najkratsie spolocne nadslovo: zjednodusena verzia problemu zostavovania genomov zo segmentov
  • Mame danu mnozinu retazcov, chceme zostavit najkratsi retazec, ktoremu su vsetky podslova
  • Priklad: GCCAAC,CCTGCC,ACCTTC zlozime v poradi 2,1,3: CCTGCCAACCTTC
  • Mozeme si predstavit problem ako obmenu problemu obchodneho cestujuceho:
    • retazcom priradim vrcholy
    • dlzka hrany z a do b je 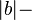|b|- prekryv medzi a a b
    • specialny zaciatocny vrchol, z ktoreho hrany do kazdeho a s cenou |a|
    • specialny koncovy vrchol, do ktoreho hrana z kazdeho a s cenou 0
    • hrana z koncoveho do zaciatocneho vrcholu na uzavretie cyklu
    • Hamiltonovske kruznice zodpovedaju nadslovam
    • Ak najdeme najlacnejsiu Hamiltonovsku kruznicu, mame najkratsie nadslovo
  • Ale vieme, ze problem obchodneho cestujuceho je NP-tazky
  • Je toto dokaz, ze aj najkratsie spolocne nadslovo je NP-tazke?
  • Pevzner, Tang and Waterman 2001 navrhuju namiesto Hamiltonovskej kruznice pouzit Eulerov tah (na inom grafe)
  • deBruijnov graf stupna k:
    • vrcholy: podretazce dlzky k vsetkych vstupnych retazcov
    • hrany: nadvazujuce k-tice v ramci kazdeho segmentu (s prekryvom k-1)
  • Priklad, k=2
  • Chceme prejst po vsetkych hranach, chceme chodit co najmenej, takze po kazdej len raz - Eulerov tah
  • V com je finta? Ako sme sa dostali od NP-tazkeho problemu k lahkemu?
  • Co ak deBruijnov graf nema Eulerovsky tah? Znasobime niektore hrany, tieto budu zodpovedat opakovaniam
  • Čo ak de Bruijnov graf má viacero Eulerovských ťahov?
    • Zoberieme taký ťah, ktorý obsahuje pôvodné segmenty ako podcesty
    • Zase ťažký problém, ale v praxi pomáhajú jednoduché pravidlá
  • Opatrné riešenie: Ak z vrcholu 2 cesty, rozdeľ na kontigy
  • Pouzitie sparovanych segmentov:
    • Nájdi vrcholy v grafe, ktoré im zodpovedajú
    • Ak je v grafe jediná cesta medzi týmito vrcholmi vhodnej dĺžky, premeň spárované segmenty na jeden veľký segment
  • Dalsie problemy, ktore treba riesit
    • sekvenovacie chyby: vytvaraju "bubliny" alebo slepe cesty
    • dve vlakna
  • Realne pouzivana technologia, aj pre sekvenovanie novej generacie, napr. Zerbino and Birney 2008 program Velvet

Sekvenovanie genómov, cvičenia pre biológov

UCSC genome browser

  • http://genome.ucsc.edu/
  • Ukazali sme si niekolko trackov, ktore maju suvis so sekvenovanim a skladanim genomov, napr. gaps, quality score a pod. (v genomoch cloveka a macky)

Pravdepodobnost

  • Nas problem: spocitanie pokrytia
    • G = dlzka genomu, napr. 1 000 000
    • N = pocet segmentov (readov), napr. 10 000
    • L = dlzka readu, napr. 1000
    • Celkova dlzka segmentov NL, pokrytie (coverage) NL/G, v nasom pripade 10x
    • V priemere kazda baza pokryta 10x
    • Niektore su ale pokryte viackrat, ine menej.
    • Zaujimaju nas otazky typu: kolko baz ocakavame, ze bude pokrytych menej ako 3x?
    • Dolezite pri planovani experimentov (aku velke pokrytie potrebujem na dosiahnutie urcitej kvality)
  • Uvod do pravdepodobnosti
    • Myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealnou kockou/korunou
    • Vysledkom experimentu je nejaka hodnota (napr. cislo, alebo aj niekolko cisel, retazec)
    • Tuto neznamu hodnotu budeme volat nahodna premenna
    • Zaujima nas pravdepodobnost, s akou nahodna premenna nadobuda jednotlive mozne hodnoty
    • T.j. ak experiment opakujeme vela krat, ako casto uvidime nejaky vysledok
    • Priklad 1: hodime idealizovanou kockou, premenna X bude hodnota, ktoru dostaneme
    • Mozne hodnoty 1,2,..,6, kazda rovnako pravdepodobna
    • Piseme napr. Pr(X=2)=1/6
    • Priklad 2: hodime 2x kockou, nahodna premenna X bude sucet hodnot, ktore dostaneme
    • Mozne hodnoty: 2,3,...,12
    • Kazda dvojica hodnot na kocke rovnako pravdepodobna, t.j. pr. 1/36
    • Sucet 5 mozeme dostat 1+4,2+3,3+2,4+1 - t.j. P(X=5) = 4/36
    • Sucet 11 mozeme dostat 5+6 alebo 6+5, t.j. P(X=11) = 2/36
    • Rozdelenie pravdepodobnosti: 2: 1/36, 3:2/36, 4: 3/36, ... 7: 6/36, 8: 5/36 ... 12: 1/36
    • Overte, ze sucet je 1
  • Pokrytie genomu: predpokladame, ze kazdy segment zacina na nahodnej pozicii zo vsetkych moznych G-L+1
  • Takze ak premenna Y_i bude zaciatok i-teho segmentu, jej rozdelenie bude rovnomerne
    • P(Y_i=1) = P(Y_i=2) = ... = P(Y_i=G-L+1) = 1/G-L+1
  • Uvazujme premennu X_j, ktora udava pocet segmentov pokryvajucich poziciu j
    • mozne hodnoty 0..N
    • i-ty segment pretina poziciu j s pravdepodobnostou L/(G-L+1), oznacme tuto hodnotu p
    • to iste ako keby sme N krat hodili mincou, na ktorej spadne hlava s pravd. p a znak 1-p a oznacili ako X_j pocet hlav
    • Priklad: majme mincu, ktora ma hlavu s pr. 1/4 a hodime je 3x. 
HHH 1/64
HHT 3/64
HTH 3/64
HTT 9/64
THH 3/64
THT 9/64
TTH 9/64
TTT 27/64
  • P(X_j=3) = 1/64, P(X_j=2)=9/64, P(X_j=1)=27/64, P(X_j=0)=27/64
    • taketo rozdelenie pravdepodobnosti sa vola binomicke
    • P(X_j = k) = (N choose k) p^k (1-p)^(N-k), kde 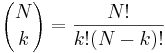{N \choose k}={\frac {N!}{k!(N-k)!}} a n! = 1*2*...*n
    • napr pre priklad s troma hodmi kockou P(X_j=2) = 3!/(2!*1!) * (1/4)^2 * (3/4)^1 = 9/64
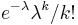
    • Zle sa pocita pre velke N, preto sa niekedy pouziva aproximacia Poissonovym rozdelenim s parametrom lambda = Np, ktore ma e^{{-\lambda }}\lambda ^{k}/k!
    • Spat k sekvenovaniu: vieme spocitat rozdelenie pravdepodobnosti a tiez napr. P(X_i<3) = P(X_i=0)+P(X_i=1)+P(X_i=2) = 0.000045+0.00045+0.0023=0.0028 (v priemere ocakavame 45 baz nepokrytych)
    • Takyto graf, odhad, vieme lahko spravit pre rozne pocty segmentov a tak naplanovat, kolko segmentov potrebujeme
  • Chceme tiez odhadnut pocet kontigov (nebrali sme na cviceni, uvedene len pre zaujimavost)
    • Ak niekolko baz vobec nie je pokrytych segmentami, prerusi sa kontig
    • Vieme, kolko baz je v priemere nepokrytych, ale niektore mozu byt vedla seba
    • Novy kontig vznikne aj ak sa susedne segmenty malo prekryvaju
    • Predpokladajme, ze na spojenie dvoch segmentov potrebujeme prekryv aspon T
    • Lander a Waterman 1988 odhadli, ze dany segment ma pravdepodobnost zhruba exp(-N(L-T)/G), ze bude posledny v kontigu
    • Pre N segmentov dostaneme priemerny pocet kontigov 1+N*exp(-N(L-T)/G)
    • Ako keby sme dlzku segmentu skratili o dlzku prekryvu
    • Pre T=50 dostaneme priemerny pocet kontigov 1.75, ak znizime N na 5000 (5x pokrytie) dostaneme 44 kontigov
  • Tento jednoduchy model nepokryva vsetky faktory:
    • Segmenty nemaju rovnaku dlzku
    • Problemy v zostavovani kvoli chybam, opkaovaniam a pod.
    • Segmenty nie su rozlozene rovnomerne (cloning bias a pod.)
    • Vplyv koncov chromozomov
    • Uzitocny ako hruby odhad
    • Na spresnenie mozeme skusat spravit zlozitejsie modely, alebo simulovat data
  • Poznamka: pravdepodobnosti z binomickeho rozdelenia mozeme lahko spocitat napr. statistickym softverom R. Tu su prikazy, ktore sa na to hodia, pre pripad, ze by vas to zaujimalo: 
dbinom(10,1e4,0.001);  #(12.5% miest ma pokrytie presne 10)
pbinom(10,1e4,0.001,lower.tail=TRUE); #(58% miest ma pokrytie najviac 10)
dbinom(0:30,1e4,0.001); #tabulka pravdepodobnosti
 [1] 4.517335e-05 4.521856e-04 2.262965e-03 7.549258e-03 1.888637e-02
 [6] 3.779542e-02 6.302390e-02 9.007019e-02 1.126216e-01 1.251601e-01
[11] 1.251726e-01 1.137933e-01 9.481826e-02 7.292252e-02 5.207187e-02
[16] 3.470068e-02 2.167707e-02 1.274356e-02 7.074795e-03 3.720595e-03
[21] 1.858621e-03 8.841718e-04 4.014538e-04 1.743354e-04 7.254524e-05
[26] 2.897743e-05 1.112843e-05 4.115040e-06 1.467156e-06 5.050044e-07
[31] 1.680146e-07

Zhrnutie

  • Pravdedpobnostny model: myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealizovanou kockou
  • Vysledok je hodnota, ktoru budeme volat nahodna premenna
  • Tabulka, ktora pre kazdu moznu hodnotu nahodnej premennej urci je pravdepodobnost sa vola rozdelenie pravdepodobnosti, sucet hodnot v tabulke je 1
  • Znacenie typu P(X=7)=0.1
  • Priklad: mame genom dlzky G=1mil., nahodne umiestnime N=10000 segmentov dlzky L=1000
  • Nahodna premenna X_i je pocet segmentov pokryvajucich urcitu poziciu i
  • Podobne, ako keby sme N krat hodili kocku, ktora ma cca 1 promile sancu padnu ako hlava a 99.9% ako znak a pytame sa, kolko krat padne znak (1 promile sme dostali po zaukruhleni z L/(G-L+1))
  • Rozdelenie pravdepobnosti sa v tomto pripade vola binomicke a existuje vzorec, ako ho spocitat
  • Takyto model nam moze pomoct urcit, kolko segmentov potrebujeme osekvenovat, aby napr. aspon 95% pozicii bolo pokrytych aspon 4 segmentami

Eulerovský ťah

  • Nestihli sme na cviceniach, uvedene pre zaujimavost
  • Orientovany graf
  • Silne suvisly orientovany graf
  • Eulerovsky tah, uzatvoreny eulerovsky tah
  • Pouzitie v de Bruijnovom grafe na zostavovanie genomu
  • Silne súvislý orientovany graf ma uzatvoreny eulerovsky tah prave vtedy, ked v kazdom vrchole je rovnako vchadzajucich a vychadzajucich hran
    • ak ma tah, musi byt suvisly
    • ak ma tak, musia sediet pocty hran
    • ak je suvisly a sedia pocty hran:
      • prechadzka po grafe, kym sa da pokracovat nepouzitou hranou
      • musime skoncit, kde sme zacali (z ostatnych vrcholov vieme pokracovat)
      • zvysok grafu stale splna podmienku s poctami hran
      • najdi dalsi vrchol, ktory je na tahu a ma este nepouzite hrany
      • musi taky existovat
      • pokracuj v tom istom, az kym sa nevratime, kde sme zacali
      • cele opakujeme, az kym sa neminu hrany
  • Poznamka: v neorientovanych grafoch musia byt stupne vsetkych vrcholov parne
  • Ak hladame otvoreny tah, spojime zaciatocny a koncovy vrchol hranou a najdeme uzatvoreny tah
Zdroj: „http://compbio.fmph.uniba.sk/vyuka/mbi/index.php?title=MBI_2010/2011&oldid=361“