1-BIN-301, 2-AIN-501 Methods in Bioinformatics

Website moved to https://fmfi-compbio.github.io/mbi/


CI04: Rozdiel medzi revíziami

Z MBI
Prejsť na: navigácia, hľadanie
(Vytvorená stránka „==Opakovanie dynamického programovania pre globálne zarovnanie== Uvažujme napríklad skórovanie zhoda +1, nezhoda -1, medzera -1 a vstupné sekvencie <math>X=x_1\d...“)
 
(→‎Opakovanie dynamického programovania pre globálne zarovnanie)
 
Riadok 3: Riadok 3:
 
Uvažujme napríklad skórovanie zhoda +1, nezhoda -1, medzera -1 a vstupné sekvencie <math>X=x_1\dots x_m</math> a <math>Y=y_1\dots y_n</math>. Nech s(x,y) je skóre písmen x a y, t.j. 1 ak sa zhodujú a -1 ak nie. Máme rekurenciu:
 
Uvažujme napríklad skórovanie zhoda +1, nezhoda -1, medzera -1 a vstupné sekvencie <math>X=x_1\dots x_m</math> a <math>Y=y_1\dots y_n</math>. Nech s(x,y) je skóre písmen x a y, t.j. 1 ak sa zhodujú a -1 ak nie. Máme rekurenciu:
  
−
:::<math>A[i,j]=\max\left\{A[i-1,j-1]+s(x_i,y_j), A[i-1,j]-1, A[i,j-1]\right\}</math>
+
:::<math>A[i,j]=\max\left\{A[i-1,j-1]+s(x_i,y_j), A[i-1,j]-1, A[i,j-1]-1\right\}</math>
  
 
* Ako presne by sme implementovali?
 
* Ako presne by sme implementovali?
−
* Ako spocitame maticu spatnych sipok B?
+
* Ako spočítame maticu spätných šípok B?
−
* Aka je casova a pamatova zlozitost?
+
* Aká je časová a pamäťová zložitosť?
  
 
==Reprezentácia pomocou grafu==
 
==Reprezentácia pomocou grafu==

Aktuálna revízia z 16:03, 2. november 2021

Opakovanie dynamického programovania pre globálne zarovnanie

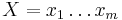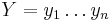Uvažujme napríklad skórovanie zhoda +1, nezhoda -1, medzera -1 a vstupné sekvencie X=x_{1}\dots x_{m} a Y=y_{1}\dots y_{n}. Nech s(x,y) je skóre písmen x a y, t.j. 1 ak sa zhodujú a -1 ak nie. Máme rekurenciu:

A[i,j]=\max \left\{A[i-1,j-1]+s(x_{i},y_{j}),A[i-1,j]-1,A[i,j-1]-1\right\}
  • Ako presne by sme implementovali?
  • Ako spočítame maticu spätných šípok B?
  • Aká je časová a pamäťová zložitosť?

Reprezentácia pomocou grafu

Takéto dynamické programovanie vieme reprezentovať vo forme acyklického orientovaného grafu:

  • vrchol (i,j) pre každé 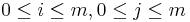0\leq i\leq m,0\leq j\leq m, t.j. pre každé políčko dyn. prog. tabuľky
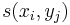
  • hrana z (i-1,j-1) do (i,j) s cenou s(x_{i},y_{j})
  • hrana z (i-1,j) do (i,j) s cenou -1
  • hrana z (i,j-1) do (i,j) s cenou -1
  • súčet súradníc na každej hrane rastie, graf teda nemôže obsahovať cyklus, je acyklický
  • každá cesta z (0,0) do (m,n) zodpovedá zarovnaniu, jej cena je cenou zarovnania (každá hrana jeden stĺpec)
  • optimálne zarovnanie teda zodpovedá ceste s maximálnou cenou

Krátka vsuvka o acyklických orientovaných grafoch

  • Mame dany acyklicky orientovany graf s ohodnotenymi hranami a startovaci vrchol s, koncovi vrchol t a chceme najst cestu s max. cenou z s do t.
  • Hladanie cesty s maximalnou cenou je vo vseobecnosti NP-tazke (podobne na Hamiltonovsku cestu)
  • V acyklickom grafe to vsak vieme riesit efektivne
  • Najskor si graf zotriedime topologicky, t.j. usporiadame vrcholy tak, aby kazda hrana isla z vrcholu z mensim cislom do vrcholu s vacsim cislom. To sa da modifikaciou prehladavania do hlbky v case O(|V|+|E|)
  • Potom pocitame dynamickym programovanim, kde A[u] je dlzka najdlhsej cesty z s do u: A[u]=\max _{{v:v\rightarrow u\in E}}A[v]+c(v\rightarrow u) pricom na zaciatku nastavime A[s]=0 a na konci mame cenu cesty v A[t].
  • Cas vypoctu je O(|V|+|E|)
  • Vsimnime si, ze tiez dostaneme najdlhsie cesty z s do vsetkych vrcholov.

Ak tento algoritmus nasadime na graf pre globalne zarovnanie, dostavame presne nasu rekurenciu (topologicke triedenie mozno vynechat - poradie zhora dole a zlava doprava je topologicky utriedene). Vyhoda je, ze mozeme modifikaciou grafu ziskavat riesenia roznych pribuznych problemov bez toho, aby sme vzdy vymyslali novu rekurenciu.

Lokálne zarovnanie

  • Zarovnanie moze zacat a skoncit hocikde v matici
  • Pridaj startovaci vrchol s, koncovy vrchol t
  • Pridaj hrany s->(i,j) a (i,j)->t s cenou 0 pre kazde (i,j)
  • Opat ekvivalentne s rekurenciou z prednasky

Variant: chceme zarovnat cely retazec X k nejakej casti retazca Y (napr. mapovanie sekvenovacich readov na genom)

  • Iba zmenime hrany z s a hrany do t (ako?)

Afínne skóre medzier

  • Napr. otvorenie medzery o=-3, pokracovanie medzery e=-1 
A  -  -  -  T  C  G
A  C  G  C  T  C  C
1 -3 -1 -1  1  1  -1


Nesprávne riešenie pomocou dynamického programovania

Pouzijeme bezne dynamicke programovanie pre globalne zarovnanie, ale v rekurencii zmenime vypocet penalty za medzeru:

A[i,j]=\max \left\{A[i-1,j-1]+s(x_{i},y_{j}),A[i-1,j]+c(i-1,j,hore),A[i,j-1]+c(i,j-1,vlavo)\right\}
  • c(i,j,s) = o, ak v policku A[i,j] mame sipku s
  • c(i,j,s) = e, ak v policku A[i,j] mame inu sipku

Preco toto riesenie nefunguje?

  • Co ak pre policko (i,j) je viac rovnako dobrych rieseni s roznymi sipkami?
  • Co ak pre policko (i,j) je najlepsie riesenie so sipkou napr. sikmo, ale druhe najlepsie je len 1 horsie a ma sipku hore?

Toto je obvykla chyba pri dynamickom programovani:

  • aby bolo dynamicke programovanie spravne, musi platit, ze optimalne riesenie vacsieho podproblemu musi obsahovat optimalne riesenie mensieho podproblemu

Správne riešenie pomocou dynamického programovanania

Riesenie 1:

  • Pridame hrany pre cele suvisle useky medzier so spravnou cenou
  • (i,j)->(i,k) s cenou o+(k-j)e
  • (i,j)->(k,j) s cenou o+(k-i)e
  • Cas O(mn(m+n)), t.j. kubicky
  • pozor, mame aj cesty, ktore nezopodvedaju ziadnemu spravnemu skore, napr. (i.j)->(i+1,j)->(i+2,j) ma cenou 2o, ale ma mat o+e. Nastastie hrana (i,j)->(i+2,j) ma vyssiu cenu, takze ta dlhsia cesta sa nepouzije.

Riesenie 2:

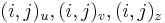
  • ztrojnasobime kazdy vrchol (i,j)_{u},(i,j)_{v},(i,j)_{z}
  • v indexe si pamatame, odkial sme do (i,j) prisli (u=uhlopriecne, v=vodorovne, z=zvislo)
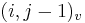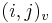  • ak ideme napr. z (i,j-1)_{v} do (i,j)_{v}, pokracujeme v uz existujucej medzere, takze skore je e
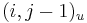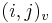  • ak ideme napr. z (i,j-1)_{u} do (i,j)_{v}, zaciname novu medzeru, takze skore je o
  • ake vsetky hrany teda mozeme mat? Kolko je spolu v grafe hran a vrcholov a aka je zlozitost algoritmu?

Lineárna pamäť: Hirshbergov algoritmus 1975

  • Klasicke dynamicke programovanie potrebuje cas O(nm)
  • Trivialna implementacia tiez pouzije pamat O(mn) - uklada si celu maticu A, pripadne maticu B so sipkami naspat
  • Na vypocet matice A nam z stacia dva riadky tejto matice: riadok i pocitam len pomocou riadku i-1, starsie viem zahodit
  • Ale ak chcem aj vy[isat zarovnanie, stale potrebujem pamat O(mn) na maticu sipok B
  • Hirschbergov algoritmus znizi pamat na O(m+n), zhruba zdvojnasobi cas (stale O(mn))
  • Prejdeme celú maticu a spočítame maticu A. Zapamätáme si, kde moja cesta prejde cez stredný riadok matice
    • Nech B_k[i,j] je najväčší index v riadku k, cez ktorý prechádza najkratšia cesta z (0,0) do (i,j)
  • Ako vieme B_k[i,j] spočítať?
    • ak A[i,j] = A[i-1,j-1]+w(S[i],T[j])$, potom B_k[i,j]=B_k[i-1,j-1].
    • ak A[i,j]=A[i-1,j]+1, potom B_k[i,j]=B_k[i-1,j].
    • ak A[i,j]=A[i,j-1]+1, potom B_k[i,j]=B_k[i,j-1]
    • Toto platí, ak i > k. Pre i=k nastavíme B_k[i,j]=j
  • Ak už poznáme A[i-1,*] a B_k[i-1,*], vieme spočítať A[i,*] a B_k[i,*].
    • Stacia nam teda iba dva riadky matice A a B_k
  • Nech k'=B_k[m,n]. Potom v optimálnom zarovnaní sa S[1..k] zarovná s T[1..k'] a S[k+1..m] s T[k'+1..n].
    • Toto použijeme na rekurzívny algoritmus na výpočet zarovnania: 
optA(l1, r1, l2, r2) { // align S[l1..r1] and T[l2..r2]
    if(r1-l1 <= 1 ||  r2-l2 <=1) 
        solve using dynamic programming
    else {
        k=(r-l+1)/2;
        for (i=0; i<=k; i++) 
           compute A[i,*] from A[i-1,*]
        for (i=k+1; i<=r-l+1; i++) 
           compute A[i,*], B_k[i,*] from A[i-1,*], B_k[i-1,*]
        k2=B_k[r1-l1-1,r2-l2-1];
        optA(l1, l1+k-1, l2, l2+k2-1); 
        optA(l1+k, r2, l2+k2, r2); 
    }
}

Casova zlozitost:

  • Označme si N=nm (súčin dĺžky dvoch daných reťazcov).
  • Na hornej úrovni rekurzie spúšťame dynamické programovanie pre celú maticu -- čas bude $cN$.
  • Na druhej urovni mame dva podproblemy, velkosti N1 a N2, pricom N1+N2<=0.5*N (z kazdeho stlpca matice A najviac polovica riadkov pocitana znova)
  • Na tretej urovni mame 4 podproblemy N11, N12, N21, N22, pricom N11+N12 <= 0.5*N1 a N21+N22 <= 0.5*N2 a teda celkovy sucet podproblemov na druhej urvni je najviac N/4.

Na stvrtej urovni je sucet podproblemov najviac N/8 atd, Dostavame geometricky rad cN+cn/2+cN/4+... ktoreho sucet je 2cN

Vypísanie všetkých najlepších riešení

  • Namiesto jednej spatnej sipky si pamatame vsetky, ktore v danom A[i,j] viedli k maximalnej cene
  • Potom mozeme rekurzivne prehladavat a vypisovat vsetky cesty z (m,n) do (0,0) ktore pozostavaju iba zo zapamatanych hran
  • Cas na vypisanie jednej cesty je polynomialny, ale ciest moze byt exponencialne vela!
  • Mozno namiesto toho chceme len pocet takych ciest, alebo vsetky dvojice pismen, ktore mozu byt spolu zarovnane v niektorom optimalnom zarovnani
Zdroj: „http://compbio.fmph.uniba.sk/vyuka/mbi/index.php?title=CI04&oldid=2661“