CI05: Rozdiel medzi revíziami
(Vytvorená stránka „== MinHash == Motivácia: Pri zostavovaní genómov pomocou overlap-layout-consensus frameworku na nájdenie prekryvov medzi čítaniami treba vykonať <math>O(N^2)</ma...“) |
|
(Žiaden rozdiel)
| |
Verzia zo dňa a času 11:56, 22. október 2020
Obsah
MinHash
Motivácia: Pri zostavovaní genómov pomocou overlap-layout-consensus frameworku na nájdenie prekryvov medzi čítaniami treba vykonať 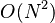 lokálnych zarovnaní medzi každou dvojicou čítaní (kde
lokálnych zarovnaní medzi každou dvojicou čítaní (kde 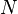 je počet čítaní), pričom každé zarovnanie trvá
je počet čítaní), pričom každé zarovnanie trvá 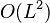 (kde
(kde 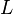 je dĺžka čítaní). Prirodzeným spôsobom zníženia časových nárokov je obmedzenie zarovnávaní iba medzi "sľubnými" dvojicami čítaní. Ako však také dvojice nájsť?
je dĺžka čítaní). Prirodzeným spôsobom zníženia časových nárokov je obmedzenie zarovnávaní iba medzi "sľubnými" dvojicami čítaní. Ako však také dvojice nájsť?
Odbočka do analýzy web-stránok: Podobnosť textov
Majme množinu webových stránok (webová stránka je postupnosť slov). Chceme nájsť medzi nimi dvojice podobných. Ako môžeme definovať podobnosť dvoch textov?
Jeden zo spôsobov ako to spraviť je pozrieť sa na množstvo slov, spoločných pre jednotlivé dvojice stránok. Očakávame, že čím viac spoločných slov majú, tým sú podobnejšie. Túto mieru podobnosti formalizuje matematický pojem Jaccardovej miery podobnosti.
Nech 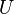 je univerzum slov a nech
je univerzum slov a nech 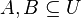 sú jeho podmnožinami (t.j. množiny slov dvoch textov). Potom Jaccardova miera podobnosti
sú jeho podmnožinami (t.j. množiny slov dvoch textov). Potom Jaccardova miera podobnosti 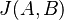 je definovaná nasledovne:
je definovaná nasledovne:
Táto miera nadobúda hodnotu 0 iba prípade, ak množiny sú disjunktné, a hodnotu 1 iba v prípade, že množiny sú totožné. Inak sa jej hodnota nachádza na otvorenom intervale 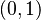 , a čím viac spoločných slov majú, tým je jej hodnota vyššia.
, a čím viac spoločných slov majú, tým je jej hodnota vyššia.
Potom otázku "Ktoré dvojice textov sú podobné?" môžeme preformulovať napríklad ako "Ktoré dvojice textov majú Jaccardovu mieru podobnosti vyššiu ako 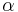 ?", kde
?", kde 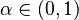 je nejaká prahová hodnota.
je nejaká prahová hodnota.
Exaktný výpočet Jaccardovej miery podobnosti nie je vždy dostatočne rýchly pre účely konkrétnej aplikácie, takže logickým riešením je pokúsiť sa jej hodnotu vypočítať iba približne (t.j. aproximovať).
Aproximácia Jaccardovej miery: MinHash
Nech je daná množina 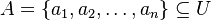 . Nech
. Nech 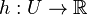 je injektívna náhodná hashovacia funkcia (t.j. bez kolízií). Potom minimálny hash množiny
je injektívna náhodná hashovacia funkcia (t.j. bez kolízií). Potom minimálny hash množiny 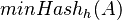 je definovaný nasledovne:
je definovaný nasledovne:
Keďže 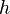 je náhodná hashovacia funkcia, tak sa na hodnotu
je náhodná hashovacia funkcia, tak sa na hodnotu 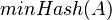 môžeme pozerať ako na náhodnú premennú, ktorá reprezentuje rovnomerne náhodný výber prvku z množiny
môžeme pozerať ako na náhodnú premennú, ktorá reprezentuje rovnomerne náhodný výber prvku z množiny 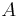 .
.
Nech 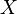 je náhodná premenná, ktorá nadobúda hodnotu 1, ak
je náhodná premenná, ktorá nadobúda hodnotu 1, ak 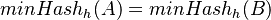 , a inak hodnotu 0. Potom
, a inak hodnotu 0. Potom ![Pr[X=1]=J(A,B)](/vyuka/mbi/images/math/f/8/2/f82bfce9ed488336b83d575fd8bad631.png)
Potom
![E(X)=0\cdot Pr[X=0]+1\cdot Pr[X=1]=Pr[X=1]=J(A,B)](/vyuka/mbi/images/math/4/1/a/41a82418582d44726d6ad464d66c68e5.png) .
.
Z toho vyplýva, že náhodná premenná 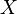 je nevychýleným odhadom Jaccardovej miery. Je to však veľmi nepohodlný odhad, lebo namiesto celej škály hodnôt od 0 po 1 vracia len dve možnosti.
je nevychýleným odhadom Jaccardovej miery. Je to však veľmi nepohodlný odhad, lebo namiesto celej škály hodnôt od 0 po 1 vracia len dve možnosti.
V štatistike základnou mierou kvality nevychýleného odhadu slúži jeho variancia 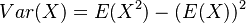 . Spočítajme si postupne obe hodnoty.
. Spočítajme si postupne obe hodnoty.
Čiže 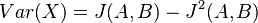 . Aká je maximálna možná hodnota variancie?
. Aká je maximálna možná hodnota variancie?
Táto otázka je ekvivalentná otázke "Aké je maximum funkcie 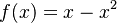 na intervale
na intervale ![[0,1]](/vyuka/mbi/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) ?". Pre určenie extrémov hladkých funkcií treba nájsť korene jej prvej derivácie. Derivácia tejto funkcie je
?". Pre určenie extrémov hladkých funkcií treba nájsť korene jej prvej derivácie. Derivácia tejto funkcie je 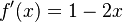 , jej koreň je hodnota
, jej koreň je hodnota 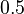 . Hodnota funkcie v tomto bode je rovná
. Hodnota funkcie v tomto bode je rovná 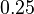 . Čiže
. Čiže 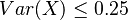 .
.
Ako môžeme tento odhad zlepšiť?
Jedna z možností je zobrať viacero nezávislých hashovacích funkcií 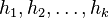 , a spočítať
, a spočítať 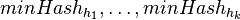 pre obidve množiny. Označme si príslušné náhodné premenné ako
pre obidve množiny. Označme si príslušné náhodné premenné ako 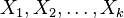 . Každá z nich má strednú hodnotu
. Každá z nich má strednú hodnotu 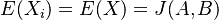 a rovnakú varianciu
a rovnakú varianciu 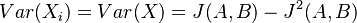 .
.
Nech náhodná premenná 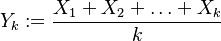 je ich priemer. Potom jej stredná hodnota je rovná
je ich priemer. Potom jej stredná hodnota je rovná ![E(Y_{k})=E\left({\frac {X_{1}+X_{2}+\ldots +X_{k}}{k}}\right)=k^{{-1}}E(X_{1}+X_{2}+\ldots +X_{k})=k^{{-1}}[E(X_{1})+E(X_{2})+\ldots +E(X_{k})]=k^{{-1}}kE(X)=E(X)=J(A,B)](/vyuka/mbi/images/math/a/2/b/a2bd44e6c33c42ef25db86efbbfe2d98.png) . Čiže aj
. Čiže aj 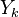 je nevychýleným odhadom Jaccardovej miery.
je nevychýleným odhadom Jaccardovej miery.
Pozrieme sa na jej varianciu: ![Var(Y_{k})=Var\left({\frac {X_{1}+X_{2}+\ldots +X_{k}}{k}}\right)={\dfrac {1}{k^{2}}}Var(X_{1}+X_{2}+\ldots +X_{k}){\overset {*}{=}}{\dfrac {1}{k^{2}}}[Var(X_{1})+\ldots Var(X_{k})]={\dfrac {1}{k^{2}}}k\cdot Var(X)={\dfrac {Var(X)}{k}}\leq {\dfrac {1}{4k}}](/vyuka/mbi/images/math/7/c/2/7c213a4c85784d2ff294349150587e79.png)
(*) tento prechod je možný len kvôli tomu, že premenné 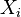 sú nezávislé.
sú nezávislé.
Vidíme teda, že varianciu (resp. kvalitu) môžeme potlačiť na ľubovoľne malú postupným zvýšením počtu hashov.
Všimnite si, že premenná 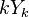 (t.j. nie priemer, ale súčet jednotlivých
(t.j. nie priemer, ale súčet jednotlivých 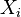 ) je súčtom nezávislých indikátorov s rovnakou distribúciou, a teda má binomické rozdelenie s parametrami
) je súčtom nezávislých indikátorov s rovnakou distribúciou, a teda má binomické rozdelenie s parametrami 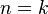 a
a 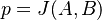 .
.
Druhá možnosť zlepšenia je nechať jednu hashovaciu funkciu, ale porovnávať nie 1, ale k najmenších hashov dvoch množín. Vedie to ku podobnému asymptotickému správaniu.
Návrat do porovnávania sekvencií
Ako "slová" použijeme všetky súvislé podreťazce fixnej dĺžky (dĺžka sa tradične označuje ako 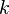 ) danej sekvencie. Tieto podreťazce sa tradične označujú ako
) danej sekvencie. Tieto podreťazce sa tradične označujú ako 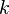 -mery.
Potom na hľadanie dvoch podobných čítaní z množiny čítaní môžeme použiť minhash.
-mery.
Potom na hľadanie dvoch podobných čítaní z množiny čítaní môžeme použiť minhash.
V prípade BLAST, t.j. lokálneho zarovnávania dvoch sekvencií sa ako texty berú okná (t.j. súvislé podreťazce väčšej dĺžky než 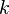 ). Potom dvojice podobných okien plnia tú istú funkciu ako jadrá zarovnávania v klasickom BLASTe.
). Potom dvojice podobných okien plnia tú istú funkciu ako jadrá zarovnávania v klasickom BLASTe.
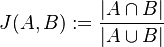
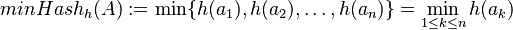
![E(X^{2})=0^{2}\cdot Pr[X=0]+1^{2}\cdot Pr[X=1]=Pr[X=1]=J(A,B)](/vyuka/mbi/images/math/0/1/2/012881361d10bcbd4d322794b819a493.png)