CI05
Obsah
Vzorec na výpočet senzitivity jadra
- Uvažujme jadro dĺžky w (ako v programe BLAST pre nukleotidy)
- Uvažujme pravdepodobnostný model zarovnania, v ktorom má každá pozícia pravdepodobnosť p, že bude zhoda a (1-p), ze bude nezhoda alebo medzera, zarovnanie ma dlzku L
- Nahodna premenna X_i = 1 ak na pozicii i je zhoda, 0 inak
- Nahodna premenna Y_i = 1 ak na pozicii i zacina jadro, t.j. ak
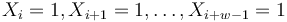
-
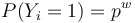 , nakolko X_i su navzajom nezavisle
, nakolko X_i su navzajom nezavisle
- Nech
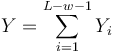
- Z linearity strednej hodnoty vieme lahko odhadnut
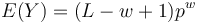
- Nas ale zaujima P(Y>0) = 1-P(Y=0)
- Ako by sme vedeli odhadnut simulaciou? My ale chceme rychlejsi sposob.
-
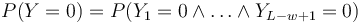
- Preco neplati,
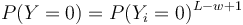 ?
?
- Jednotlive Y_i nie su nezavisle, napr.
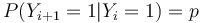
- V postupnosti Y_i sa jednotky maju tendenciu zhlukovat spolu
- Jednotlive Y_i nie su nezavisle, napr.
- Pravdepodobnost nepritomnosti jadra P(Y=0) ale vieme spocitat dynamickym programovanim
- Nech A[n] je pravdepodobnost nepritomnosti jadra v prvých n stlcoch zarovnania (0<=n<=L)
- Budeme rozlisovat pripady podla toho, kolko je na konci X_1..X_n jednotiek
- Tento pocet moze byt 0..w-1 (ak by bol >=w, mali by sme vyskyt jadra)
-
![A[n]=\left\{{\begin{array}{ll}1&{\mbox{ak }}n<w\\\sum _{{i=0}}^{{w-1}}p^{i}(1-p)A[n-i-1]&{\mbox{ak }}n\geq w\\\end{array}}\right.](/vyuka/mbi/images/math/7/2/9/729e56b2edc35e00cbaa9a0e01b5787f.png)
V druhom riadku 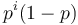 zodpoveda P(X_1...X_n konci presne i jednotkami).
zodpoveda P(X_1...X_n konci presne i jednotkami).
Minimizery: ako usetrit pamat
- k-merom nazveme k za sebou iducich pismen (nukleotidov DNA)
- Zakladne pouzite jadier: pri porovnavani dvoch sekvencii (alebo mnozin sekvencii) uloz vsetky k-mery jednej sekvencie do slovnika (napr. hash tabulky), potom prechadzaj vsetky k-mery druhej sekvencie a hladaj ich v slovniku
- Priklad k=5,
- DB vľavo, k-mery a ich pozície uložené do tabuľky,
- query vpravo, k-mery hľadané v tabuľke, šípkou vyznačené nájdené k-mery (jadrá)
AGTGGCTGCCAGGCTGG cGaGGCTGCCtGGtTGG
AGTGG,0 CGAGG
GTGGC,1 GAGGC
TGGCT,2 AGGCT <-
GGCTG,3 GGCTG <-
GCTGC,4 GCTGC <-
CTGCC,5 CTGCC <-
TGCCA,6 TGCCT
GCCAG,7 GCCTG
CCAGG,8 CCTGG
CAGGC,9 CTGGT
AGGCT,10 TGGTT
GGCTG,11 GGTTG
GCTGG,12 GTTGG
- Trik na znizenie potrebnej pamate (napr. program BLAT): ukladaj iba kazdy s-ty k-mer z prvej sekvencie, potom hladaj vsetky k-mery z druhej
- Trochu znizi aj senzitivitu, ale kedze jadra sa klastruju, mame sancu aspon jedno jadro z klastra najst
- Zarucene najdeme jadro, ak mame aspon s+k-1 zhod za sebou
- Mohli by sme v query tiež hľadať iba každý s-ty k-mer?
Priklad w=5, s=3, k-mery nalavo sa ulozia, k-mery napravo sa hladaju, najde sa jedno jadro
AGTGGCTGCCAGGCTGG cGaGGCTGCCtGGtTGG
AGTGG,0 CGAGG
GGCTG,3 GAGGC
TGCCA,6 AGGCT
CAGGC,9 GGCTG <-
GCTGG,12 GCTGC
CTGCC
TGCCT
GCCTG
CCTGG
CTGGT
TGGTT
GGTTG
GTTGG
- Prefikanejsia idea je minimizer: uvazuj vsetky skupiny s po sebe iducich k-merov (sliding window), v kazdej skupine najdi abecedne najmensi k-mer (minimizer) a uloz do slovnika
- Pri posune okna o jedno doprava casto najmensi k-mer zostava ten isty a netreba ho znovu ukladat, cim sa usetri pamat
- Rozdiel je pri hladani: v slovniku nehladame vsetky k-mery druhej sekvencie, ale tiez len minimizery, co moze usetrit cas
- Zarucene najdeme jadro, ak mame aspon s+k-1 zhod za sebou
- Priklad k=5, s=3, vlavo: do slovnika sa ulozia k-mery s cislom; vpravo: v slovniku sa hladaju k-mery s hviezdickou, najde sa jedna zhoda
AGTGGCTGCCAGGCTGG cGaGGCTGCCtGGtTGG
AGTGG,0 CGAGG
GTGGC GAGGC
TGGCT AGGCT*
GGCTG,3 GGCTG
GCTGC,4 GCTGC
CTGCC,5 CTGCC* <--
TGCCA TGCCT
GCCAG GCCTG
CCAGG,8 CCTGG*
CAGGC,9 CTGGT*
AGGCT,10 TGGTT
GGCTG GGTTG*
GCTGG GTTGG
- Obzvlast vyhodne ak prva a druha mnozina sekvencii su ta ista, napr. pri hladani prekryvov v citaniach pri skladani genomu. Kazde citanie ma mnozinu minimizerov, ktore sa pouziju ako kluce v slovniku, hodnoty su zoznamy citani. Dvojice citani zdielajuce nejaky minimizer (binning) sa dostanu do jedneho zoznamu a budu uvazovane pri vypocte vzajomneho prekryvu
- V praxi sa do slovnika neuklada lexikograficky najmensi k-mer, ale kazdy k-mer sa prehasuje nejakou funkciou f a zoberie sa ten s minimalnou hodnotou
- Dovod je, ze sa chceme vyhnut, aby minimizermi boli casto sekvencie typu AAAAA, ktore su v biologickych sekvenciach nadreprezentovane a casto nie su funkcne zaujimave
- Minimizery vyuziva napr. aj minimap2, velmi popularny nastroj na zarovnavanie citani navzajom a ku genomom
- na zarovnanie nanoporovych citani ku genomu pouziva k=15, s=10, prekryvy v nanoporovych citaniach k=15, s=5, porovnanie genomov s identitou nad 80% k=19, s=10
- Li, Heng. "Minimap and miniasm: fast mapping and de novo assembly for noisy long sequences." Bioinformatics 32.14 (2016): 2103-2110. [1]
- Roberts M, Hayes W, Hunt BR, Mount SM, Yorke JA. Reducing storage requirements for biological sequence comparison. Bioinformatics. 2004 Dec 12;20(18):3363-9. [2]
MinHash
Odbočka do analýzy web-stránok: Podobnosť textov
Majme množinu webových stránok (webová stránka je postupnosť slov). Chceme nájsť medzi nimi dvojice podobných. Ako môžeme definovať podobnosť dvoch textov?
Jeden zo spôsobov ako to spraviť je pozrieť sa na množstvo slov, spoločných pre jednotlivé dvojice stránok. Očakávame, že čím viac spoločných slov majú, tým sú podobnejšie. Túto mieru podobnosti formalizuje matematický pojem Jaccardovej miery podobnosti.
Nech 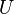 je univerzum slov a nech
je univerzum slov a nech 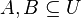 sú jeho podmnožinami (t.j. množiny slov dvoch textov). Potom Jaccardova miera podobnosti
sú jeho podmnožinami (t.j. množiny slov dvoch textov). Potom Jaccardova miera podobnosti 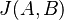 je definovaná nasledovne:
je definovaná nasledovne:
Táto miera nadobúda hodnotu 0 iba v prípade, ak množiny sú disjunktné, a hodnotu 1 iba v prípade, že množiny sú totožné. Inak sa jej hodnota nachádza na otvorenom intervale 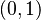 , a čím viac spoločných slov majú, tým je jej hodnota vyššia.
, a čím viac spoločných slov majú, tým je jej hodnota vyššia.
Potom otázku "Ktoré dvojice textov sú podobné?" môžeme preformulovať napríklad ako "Ktoré dvojice textov majú Jaccardovu mieru podobnosti vyššiu ako 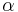 ?", kde
?", kde 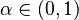 je nejaká prahová hodnota.
je nejaká prahová hodnota.
Exaktný výpočet Jaccardovej miery podobnosti nie je vždy dostatočne rýchly pre účely konkrétnej aplikácie, takže logickým riešením je pokúsiť sa jej hodnotu vypočítať iba približne (t.j. aproximovať).
Prvá idea: aproximácia vzorkovaním
- Ak by sme vedeli vzorkovať z
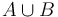 prvky u1, u2, ..., u_n (rovnomerne, nezavisle), a pre kazdy prvok u_i by sme vedeli rychlo zistit, ci patri do prieniku, mohli by sme odhadnut J(A, B) pomocou nahodnej premennej X
prvky u1, u2, ..., u_n (rovnomerne, nezavisle), a pre kazdy prvok u_i by sme vedeli rychlo zistit, ci patri do prieniku, mohli by sme odhadnut J(A, B) pomocou nahodnej premennej X
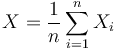 kde X_i=1 ak u_i patri do prieniku a nula inak
kde X_i=1 ak u_i patri do prieniku a nula inak
Pre kazde X_i
![E(X_{i})=0\cdot Pr[X_{i}=0]+1\cdot Pr[X_{i}=1]=Pr[X_{i}=1]=J(A,B)](/vyuka/mbi/images/math/4/7/b/47bdec1b5fa1ffbbfad85e347715b582.png) .
.
Z linearity strednej hodnoty
![E(X)=E({\frac {1}{n}}\sum _{{i=1}}^{n}X_{i})={\frac {1}{n}}\sum _{{i=1}}^{n}E[X_{i}]=J(A,B)](/vyuka/mbi/images/math/2/4/6/246ca646754ebd6dcf0b9d4bb9eea0b2.png) .
.
Z toho vyplýva, že náhodná premenná 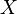 je nevychýleným odhadom Jaccardovej miery.
je nevychýleným odhadom Jaccardovej miery.
V štatistike základnou mierou kvality nevychýleného odhadu slúži jeho disperzia, odvodenie pozri nižšie
Pri zvyšujúcej veľkosti vzorky n teda klesá disperzia. Podobná situácia ako pri prieskumoch verenej mierky, kde pri väčšom súbore respondentov dosteneme lepšie výsledky.
Problémy:
- nie je ľahké rovnomerne vzorkovať z
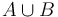
- na zisťovanie, či u_i je v prieniku potrebujeme mat reprezentaciu A a B v pamati
Aproximácia Jaccardovej miery: MinHash
Nech je daná množina 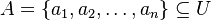 . Nech
. Nech 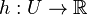 je injektívna náhodná hashovacia funkcia (t.j. bez kolízií). Potom minimálny hash množiny
je injektívna náhodná hashovacia funkcia (t.j. bez kolízií). Potom minimálny hash množiny 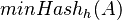 je definovaný nasledovne:
je definovaný nasledovne:
Keďže 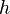 je náhodná hashovacia funkcia, tak sa na hodnotu
je náhodná hashovacia funkcia, tak sa na hodnotu 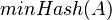 môžeme pozerať ako na náhodnú premennú, ktorá reprezentuje rovnomerne náhodný výber prvku z množiny
môžeme pozerať ako na náhodnú premennú, ktorá reprezentuje rovnomerne náhodný výber prvku z množiny 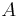 .
.
Nech 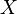 je náhodná premenná, ktorá nadobúda hodnotu 1, ak
je náhodná premenná, ktorá nadobúda hodnotu 1, ak 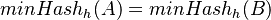 , a inak hodnotu 0. Potom
, a inak hodnotu 0. Potom ![Pr[X=1]=J(A,B)](/vyuka/mbi/images/math/f/8/2/f82bfce9ed488336b83d575fd8bad631.png)
Potom
![E(X)=0\cdot Pr[X=0]+1\cdot Pr[X=1]=Pr[X=1]=J(A,B)](/vyuka/mbi/images/math/4/1/a/41a82418582d44726d6ad464d66c68e5.png) .
.
Z toho vyplýva, že náhodná premenná 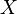 je nevychýleným odhadom Jaccardovej miery. Je to však veľmi nepohodlný odhad, lebo namiesto celej škály hodnôt od 0 po 1 vracia len dve možnosti.
je nevychýleným odhadom Jaccardovej miery. Je to však veľmi nepohodlný odhad, lebo namiesto celej škály hodnôt od 0 po 1 vracia len dve možnosti.
V štatistike základnou mierou kvality nevychýleného odhadu slúži jeho variancia 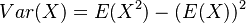 . Spočítajme si postupne obe hodnoty.
. Spočítajme si postupne obe hodnoty.
Čiže 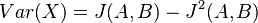 . Aká je maximálna možná hodnota variancie?
. Aká je maximálna možná hodnota variancie?
Táto otázka je ekvivalentná otázke "Aké je maximum funkcie 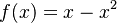 na intervale
na intervale ![[0,1]](/vyuka/mbi/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) ?". Pre určenie extrémov hladkých funkcií treba nájsť korene jej prvej derivácie. Derivácia tejto funkcie je
?". Pre určenie extrémov hladkých funkcií treba nájsť korene jej prvej derivácie. Derivácia tejto funkcie je 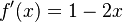 , jej koreň je hodnota
, jej koreň je hodnota 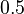 . Hodnota funkcie v tomto bode je rovná
. Hodnota funkcie v tomto bode je rovná 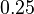 . Čiže
. Čiže 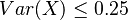 .
.
Ako môžeme tento odhad zlepšiť?
Jedna z možností je zobrať viacero nezávislých hashovacích funkcií 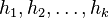 , a spočítať
, a spočítať 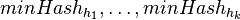 pre obidve množiny. Označme si príslušné náhodné premenné ako
pre obidve množiny. Označme si príslušné náhodné premenné ako 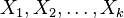 . Každá z nich má strednú hodnotu
. Každá z nich má strednú hodnotu 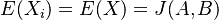 a rovnakú varianciu
a rovnakú varianciu 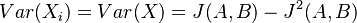 .
.
Nech náhodná premenná 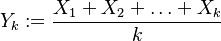 je ich priemer. Potom jej stredná hodnota je rovná
je ich priemer. Potom jej stredná hodnota je rovná ![E(Y_{k})=E\left({\frac {X_{1}+X_{2}+\ldots +X_{k}}{k}}\right)=k^{{-1}}E(X_{1}+X_{2}+\ldots +X_{k})=k^{{-1}}[E(X_{1})+E(X_{2})+\ldots +E(X_{k})]=k^{{-1}}kE(X)=E(X)=J(A,B)](/vyuka/mbi/images/math/a/2/b/a2bd44e6c33c42ef25db86efbbfe2d98.png) . Čiže aj
. Čiže aj 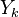 je nevychýleným odhadom Jaccardovej miery.
je nevychýleným odhadom Jaccardovej miery.
Pozrieme sa na jej varianciu: ![Var(Y_{k})=Var\left({\frac {X_{1}+X_{2}+\ldots +X_{k}}{k}}\right)={\dfrac {1}{k^{2}}}Var(X_{1}+X_{2}+\ldots +X_{k}){\overset {*}{=}}{\dfrac {1}{k^{2}}}[Var(X_{1})+\ldots Var(X_{k})]={\dfrac {1}{k^{2}}}k\cdot Var(X)={\dfrac {Var(X)}{k}}\leq {\dfrac {1}{4k}}](/vyuka/mbi/images/math/7/c/2/7c213a4c85784d2ff294349150587e79.png)
(*) tento prechod je možný len kvôli tomu, že premenné 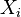 sú nezávislé.
sú nezávislé.
Vidíme teda, že varianciu (resp. kvalitu) môžeme potlačiť na ľubovoľne malú postupným zvýšením počtu hashov.
Všimnite si, že premenná 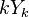 (t.j. nie priemer, ale súčet jednotlivých
(t.j. nie priemer, ale súčet jednotlivých 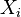 ) je súčtom nezávislých indikátorov s rovnakou distribúciou, a teda má binomické rozdelenie s parametrami
) je súčtom nezávislých indikátorov s rovnakou distribúciou, a teda má binomické rozdelenie s parametrami 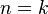 a
a 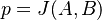 .
.
Druhá možnosť zlepšenia je nechať jednu hashovaciu funkciu, ale porovnávať nie 1, ale k najmenších hashov dvoch množín. Vedie to ku podobnému asymptotickému správaniu.
- Broder AZ. On the resemblance and containment of documents. InProceedings. Compression and Complexity of SEQUENCES 1997 (Cat. No. 97TB100171) 1997 Jun 13 (pp. 21-29). IEEE. [3]
Hľadanie podobných sekvencií
Ako "slová" použijeme všetky k-mery danej sekvencie. Potom na hľadanie dvoch podobných čítaní z množiny čítaní môžeme použiť minhash.
- Ondov BD, Treangen TJ, Melsted P, Mallonee AB, Bergman NH, Koren S, Phillippy AM. Mash: fast genome and metagenome distance estimation using MinHash. Genome biology. 2016 Dec;17(1):1-4. [4]
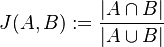
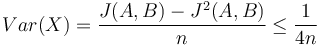
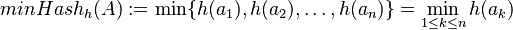
![E(X^{2})=0^{2}\cdot Pr[X=0]+1^{2}\cdot Pr[X=1]=Pr[X=1]=J(A,B)](/vyuka/mbi/images/math/0/1/2/012881361d10bcbd4d322794b819a493.png)