Exam

Exam rules

The exam is primarily written:

• You need at least 50% of points
• Time 3 hours
• About 50% of points for simple questions
  • examples on this page
  • in case of interest tutorial session before exam
• The rest of the questions mostly designing/modifying an algorithm or model
• You can use pen, simple calculator and a cheat sheet up to 2 A4 two-sided sheets

If you do not pass the first written exam, part of your exam may be oral on the second and third attempts.

Syllabus and examples of simple questions

Below we list the most important concepts that both biologists and computer scientists should know from this course.

We also list simple questions. Questions of this type will comprise approximately 50% of the exam. Not all of these questions will be used on the exam and particular string, numbers, grammars and sequences will differ.

Sequencing and genome assembly

Main concepts in English and Slovak

DNA sequencing and its use, sequencing read, paired reads, contigs, shortest common superstring problem, de Bruijn graphs

Sekvenovanie DNA a jeho využitie, čítanie (read), spárované čítania, kontig, problém najkratšieho spoločného nadslova, de Bruijnove grafy

Simple questions for the exam

• Find the shortest common superstring of strings GACAATAA, ATAACAC, GTATA, TAATTGTA.
• Find the de Bruijn graph for k=2 (nodes will be pairs of nucleotides) and reads CCTGCC, GCCAAC

Sequence alignment

Main concepts in English and Slovak

The problem of local and global alignment of two sequences, dynamic programming algorithms, scoring matrix and its probabilistic meaning, statistical significance (E-value, P-value), heuristic search of local alignments (BLAST), whole-genome and multiple alignments

Problém lokálneho a globálneho zarovnania dvoch sekvencií, jeho riešenie pomocou dynamického programovania, skórovacia matica a jej pravdepodobnostný význam, štatistická významnosť (E-value, P-value), heuristické hľadanie lokálnych zarovnaní (BLAST), celogenómové a viacnásobné zarovnania

Simple questions for the exam

• Fill in the dynamic programing matrices for local and global alignment of sequences TACGT and CAGGATT, where the match has score +3, mismatch -1, gap -2. Reconstruct also the optimal alignments found by the dynamic programming algorithm.

• Compute the score of the alignment shown below using the scoring matrix shown below, gap opening penalty -5, gap extension penalty -2 for each additional base. Find a global alignment with a higher score for these two sequences and compute its score. (It is not necessary to find the optimal alignment; you can use any method to arrive at the answer.)

Alignment:                             Matrix:
ATAGTTTAA                                 A   C   G   T
A-GGG--AA                             A   2  -2  -1  -2
                                      C  -2   1  -2  -1    
                                      G  -1  -2   1  -2
                                      T  -2  -1  -2   2

• Consider BLASTn algorithm starting from seeds of size w=3. How many seeds it finds while comparing sequences GATTACGGAT and CAGGATT? List all found seeds.

Gene finding

Main concepts in English and Slovak

Gene, exon, intron, mRNA, splicing and alternative splicing, genetic code, hidden Markov model (HMM), its states, transition and emission probabilities, use of HMMs in gene finding

Gén, exón, intrón, mRNA, zostrih a alternatívny zostrih, kodón, genetický kód, skrytý Markovov model (HMM), jeho stavy, pravdepodobnosti prechodu a emisie, použitie HMM na hľadanie génov

Simple questions for the exam

• What is the probability of generating sequence AGT using sequence of states 1,2,1 in the HMM below?

The HMM has three states 1, 2, 3. It always starts in state 1.
Transition probabilities:
From 1 to 1: 0.99
From 1 to 2: 0.01
From 2 to itself: 0.9
From 2 to 1: 0.05
From 2 to 3: 0.05
From 3 to itself: 0.99
From 3 to 2: 0.01
Emmision probabilities in state 1:
A 0.25, C 0.25, G 0.25, T 0.25
Emmision probabilities in state 2:
A 0.3, C 0.2, G 0.2, T 0.3
Emmision probabilities in state 3:
A 0.2, C 0.4, G 0.3, T 0.1

Evolution and comparative genomics

Main concepts in English and Slovak

Phylogenetic tree (rooted and unrooted), maximum parsimony method, neighbor joining method, maximum likelihood method, Jukes-Cantor substitution model and more complex substitution matrices, homolog, paralog, ortholog, detection of positive and negative selection, phylogenetic HMMs, likelihood ratio test

Fylogenetický strom (zakorenenený a nezakorenený), metóda maximálnej úspornosti (parsimony), metóda spájania susedov (neighbor joining), metóda maximálnej vierohodnosti (maximum likelihood), Jukes-Cantorov model substitúcií a zložitejšie substitučné matice, homológ, paralóg, ortológ, detekcia pozitívneho a negatívneho výberu, fylogenetické HMM, test pomerom vierohodností (likelihood ratio test)

Simple questions for the exam

• Find the most parsimonious assignment of bases at the ancestral nodes in the tree below given a column of alignment TTAAA (in the order gollum, hobbit, human, elf, orc). You can derive your answer using any method (but it has to be the most parsimonious assignment).

Gollum ----|
           |----|
Hobbit ----|    |----|
                |    |
Human  ---------|    |
                     |---
Elf --------|        |
            |--------|
Orc --------|

• Find the most parsimonious tree for the alignment given below. What is its cost (i.e. how many mutations are necessary to explain these sequences)? You can derive your answer using any method (but it has to be the most parsimonious tree).

whitebird ACAACGTCT
blackbird TCTGAATCA
graybird  TGTGAAAGA
blubird   ACTACGTCT
greenbird TGTGAAAGA

• Consider the tree for gollum, hobbit etc. given above, where each branch has the same length t. Let us assume that for any two different bases x and y, the probability of base x mutating to base y over time y is 0.1, and thus the probability of base x remaining the same after time t is 0.7. Probability of each base in the root is 0.25. Compute the probability that the tree will have base A in all internal nodes and in leaves bases TTAAA (from top to bottom). Find an assignment of bases in the ancestral nodes with a higher probability and compute this probability (you do not need to find the best possible assignment).

• Consider the distance matrix given below. Which pair of nodes will be connected as first by the neighbor joining method and what will be the new distance matrix after joining these two nodes?

                white   black    gray    blue
whitebird         0       5       7       4
blackbird         5       0       8       5
graybird          7       8       0       5
bluebird          4       5       5       0

Gene expression, regulation, motifs

Main concepts in English and Slovak

Measuring gene expressing using microarray or RNA-seq, hierarchical clustering, classification, representation of sequence motifs (transcription factor binding sites) as a consensus, regular expression and PSSM, finding new motifs in sequences, consensus pattern problem, finding motifs using probability models, EM algorithm

Určovanie génovej expresie pomocou microarray alebo sekvenovaním RNA-seq, hierarchické zhlukovanie, klasifikácia, reprezentácia sekvenčných motívov (väzobné miesta transkripčných faktorov) ako konsenzus, regulárny výraz a PSSM, hľadanie nových motívov v sekvenciách, consensus pattern problem, hľadanie motívu pomocou pravdepodobnostných modelov, algoritmus EM

Simple questions for the exam

• After a series of expression measurements for 5 genes, we have computed distances between pairs of expression profiles and obtained the distance table shown below. Find the hierarchical clustering of these genes, where the distance between two clusters is computed as the minimum of the closest genes in these clusters (single linkage clustering). Show the order in which you were creating individual clusters.

          A    B    C    D    E
gene A    0   0.6  0.1  0.3  0.7    
gene B   0.6   0   0.5  0.5  0.4
gene C   0.1  0.5   0   0.6  0.6
gene D   0.3  0.5  0.6   0   0.8
gene E   0.7  0.4  0.6  0.8   0

• Consider a motif represented by the PSSM shown below. Compute the score of string GGAG. Which sequences of length 4 will have the smallest and highest score in this PSSM?

A   -3    3   -2   -2
C   -2   -2    1   -2
G    0   -2   -1    3
T    1   -1    1   -2

• We are running the EM algorithm for finding matrix W of base frequencies at individual motif positions. Motif length is 3 and we have 2 sequences of length 5 each, so there are 3 positions where the motif can start in each sequence. For each of these positions, we calculated the probability that the motif starts there based on the previous version of matrix W. What will be the new matrix W? (We do not use pseudocounts here, so for example base G will have probability 0 everywhere.)

Sequence 1: AACAT, 
probabilities of motif starting at positions 0,1,2: 0.4, 0.2, 0.4

Sequence 2: AAAAT, 
probabilities of motif starting at positions 0,1,2: 0.2, 0.2, 0.6

• Find all occurrences of regular expression TA[CG][AT]AT in sequence GACGATATAGTATGTACAATATGC.

Proteins

Main concepts in English and Slovak

Primary, secondary and tertiary structure of a protein, protein domains and families, family representation by a profile (PSSM) and a profile HMM, protein threading, gene ontology.

Primárna, sekundárna a terciálna štruktúra proteínov, proteínové domény a rodiny, reprezentovanie rodiny pravdepodobnostným profilom a profilovým HMM, protein threading, gene ontology.

Simple questions for the exam

• Construct a profile (PSSM) for the sequence alignment shown below, assuming that amino acid A comprises 60% of all sequences in a database, G 40% and we do not consider other amino acids. Use natural logarithm (ln) and pseudocount 1.

AAGA
GAGA
GAAA
GGAG
GGAA

RNA

Main concepts in English and Slovak

Secondary structure of RNA, pseudoknot and well-parenthesized structures, Nussinov algorithm, energy minimization, stochastic context-free grammars, covariance models of RNA families

Sekundárna štruktúra RNA, pseudouzol a dobre uzátvorkovaná štruktúra, Nussinovovej algoritmus, minimalizácia energie, stochastické bezkontextové gramatiky, kovariančné modely rodín RNA.

Simple questions for the exam

• Fill in the missing values in the matrix of dynamic programming for Nussinov algorithm which finds the RNA secondary structure without pseudoknots with the highest number of paired bases in RNA sequence GAACUAUCUGA (we allow only complementary bases A-U, C-G) and show the secondary structure found by the algorithm.

 0 0 0 1 1 2 2 3 3 ? ?
   0 0 0 1 1 2 2 3 3 ?
     0 0 1 1 2 2 2 3 3
       0 0 1 1 1 1 2 3
         0 1 1 ? 1 2 3
           0 1 1 1 2 2
             0 0 0 1 2
               0 0 1 1
                 0 0 1
                   0 0
                     0

• Consider RNA sequence of length 27, which has secondary structure pairs on positions (2,23), (3,22), (4,21), (5,13), (6,12), (8,16), (9,15), (10,14), (18,26), (19,25). What is the smallest number of pairs that needs to be removed from this list to get a structure without pseudoknots? Which pairs will be removed?

• Consider RNA sequence ACUGAGUCCAAGG, which has secondary structure pairs on positions (1,7), (2,6), (3,5), (8,13) a (9,12). (Positions are numbered started from 1.) (This RNA is shown as an example in the lecture on RNA structure.) Show a derivation of this sequence using a grammar show below so that paired bases are always generated in the same step of the derivation.
  • Grammar 1: S->aSu|uSa|cSg|gSc|aS|cS|gS|uS|Sa|Sc|Sg|Su|SS|epsilon
  • Grammar 2: S->aSu|uSa|cSg|gSc|TS|ST|SS|epsilon; T->aT|cT|gT|tT|epsilon

Population genetics

Main concepts in English and Slovak

Polymorphism, SNP, allele, homozygote, heterozygote, recombination, allele frequency as a Markov chain, random genetic drift, linkage disequilibrium, association mapping, LD block, subpopulation.

Polymorfizmus, SNP, alela, homozygot, heterozygot, rekombinácia, frekvencia polymorfizmu ako markovovský reťazec, náhodný genetický drift, väzbová nerovnováha (linkage disequilibrium), mapovanie asociácií, LD blok, subpopulácia.

Simple questions for the exam

• For pairs of SNPs from the tables show below determine, if we can statistically reject the hypothesis that they are in linkage equilibrium (LE) at the significance level p=0.05, i.e. 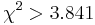$\chi ^{2}>3.841$. For each pair compute their 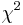$\chi ^{2}$ value.

    Q   q              Q  q             Q  q
P  100 200          P 10  20         P  1  2
p  300 200          p 30  20         p  3  2

Additional important concepts for computer scientists

• Advanced dynamic programming algorithms (protein MS/MS, variants of sequence alignment, variants of Nussinov algorithm)
• BLAST, MinHashing, minimizers
• Algorithms for HMM (Viterbi, forward)
• Felsenstein algorithm
• Integer linear programming
• EM algorithm for motif finding

Additional important concepts for biologists

• Dotplot interpretation
• Interpretation of phylogenetic trees, bootstrap, tree rooting
• Interpretation of UCSC genome browser visualizations
• Examples of various bioinformatics programs, interpretation of their settings and results using concepts from the lectures
• Enrichment analysis, multiple testing correction, K-means clustering