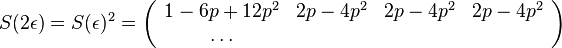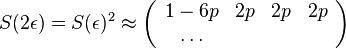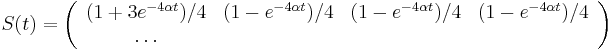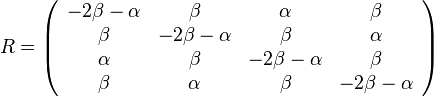MBI 2012/2013
Obsah
- 1 Úvod do dynamického programovania, cvičenia pre biológov
- 2 Sekvenovanie genómov, cvičenia pre informatikov
- 3 Zarovnávanie sekvencií, UCSC genome browser, cvičenia pre biológov
- 4 Zarovnávanie sekvencií, cvičenia pre informatikov
- 5 Zarovnávanie sekvencií 2, cvičenia pre biológov
- 6 Pravdepodobnosť, cvičenia pre biológov
- 7 Pravdepodobnosť, cvičenia pre informatikov
- 8 Fylogenetické stromy, cvičenia pre biológov
- 9 Evolúcia, cvičenia pre informatikov
- 10 Evolúcia, cvičenia pre biológov
- 11 HMM, cvičenia pre informatikov
- 12 Komparatívna genomika a HMM, cvičenia pre biológov
- 13 PhyloHMM a expresia génov, cvičenia pre informatikov
- 14 Expresia génov, cvičenia pre biológov
- 15 Proteíny, cvičenia pre informatikov
- 16 Proteíny, cvičenia pre biológov
- 17 Proteíny a RNA, cvičenia pre informatikov
- 18 RNA, cvičenia pre biológov
- 19 Hľadanie motívov, cvičenia pre informatikov
- 20 RNA a populačná genetika, cvičenia pre biológov
- 21 Články na journal club
- 22 Ukážkové príklady na skúšku
Úvod do dynamického programovania, cvičenia pre biológov
Dynamické programovanie
- Tuto techniku uvidime na dalsej prednaske na hladanie zarovnani (alignmentov)
- Uvazujme problem rozmienania minci
- Napr mame mince hodnoty 1,2,5 centov, z kazdej dostatok kusov
- Ako mozeme zaplatit urcitu sumu, napr. 13 centov, s co najmensim poctom minci?
- Ake je riesenie? 5+5+2+1 (4 mince)
- Vseobecna formulacia:
- Vstup: hodnoty k minci m_1,m_2,...,m_k a cielova suma X (vsetko kladne cele cisla)
- Vystup: najmensi pocet minci, ktore potrebujeme na zaplatenie X
- V nasom priklade k=3, m_1 = 1, m_2 = 2, m_3 = 5, X=13
- Jednoduchy sposob riesenia: pouzi najvacsiu mincu, ktora je najviac X, odcitaj od X, opakuj
- Priklad: najpr pouzijeme mincu 5, zostane name X=8, pouzijeme opat mincu 5, zostane X=3, pouzijeme mincu 2, zostane X=1, pouzijeme mincu 1.
- Nefunguje vzdy: zoberme mince hodnot 1,3,4. Pre X=6 najlepsie riesenie je 2 mince: 3+3, ale nas postup (algoritmus) najde 3 mince 4+1+1
- Ukazeme si algoritmus na zaklade dyn. programovania, ktory pre kazdy vstup najde najlepsie riesenie
- Zratame najlepsi pocet minci nielen pre X, ale pre vsetky mozne cielove sumy 1,2,3,...,X-1,X
- To zda byt ako tazsia uloha, ale ukaze sa, ze z riesenia pre mensie sumy vieme zostavit riesenie pre vacsie sumy, takze nam to vlastne pomoze
- Spravime si tabulku, kde si pre kazdu sumu i=0,1,2,...X pamatame A[i]=najmensi pocet minci, ktore treba na vyplatenie sumy i (ak je viac moznosti, zoberieme lubovolnu, napr. najvacsiu)
- Ukazme si to na priklade s mincami 1,3,4
i 0 1 2 3 4 5 6 7 8 9 A[i] 0 1 2 1 1 2 2 2 2 3
- Nevyplnali sme ju ziadnym konkretnym postupom, nejde o algoritmus
- Ale predstavme si, ze teraz chceme vyplnit A[10].
- V najlepsom rieseni je prva minca, ktoru pouzijeme 1,3, alebo 4
- ak je prva minca 1, zostane name zaplatit sumu 10-1=9, tu podla tabulky vieme najlepsie zaplatit na 3 mince, takze potrebujeme 4 mince na zaplatenie 10
- ak je prva minca 3, zostane nam zaplatit 10-3 = 7, na co potrebujeme podla tabulky 2 mince, takze spolu 3 mince na zaplatenie 10
- ak je prva minca 4, zostanem nam zaplatit 10-4 = 6, na co treba 2 mince, t.j. 3 mince na 10
- Nevieme, ktora z tychto moznosti je naozaj v najlepsom rieseni, ale pre druhe dva pripady dostaveme menej minci, takze vysledok bude 3 mince (napr. 3+3+4)
- Zovseobecnime: A[i] = 1+ min { A[i-1], A[i-3], A[i-4] }
- A[11] = 1 + min { 3, 2, 2} = 1 + 2 = 3
- Pre ine sustavy minci, napr. A[i] = 1+ min { A[i-1], A[i-2], A[i-5] }
- Vo vseobecnosti A[i] = 1+ min { A[i-m_1], A[i-m_2], ..., A[i-m_k] }
- Vzorec treba modifikovat pre male hodnoty i, ktore su mensie ako najvacsia minca, lebo A[-1] a pod. nie je definovane
- Zapisme algoritmus pre vseobecne mince
A[0] = 0;
pre kazde i od 1 po X
min = nekonecno
pre kazde j od 1 po k
ak i >= m_j a A[i-m_j] < min
min = A[i-m_j]
A[i] = 1 + min
vypis A[X]
- Ako najst, ktore mince pouzit?
- Pridame druhu tabulku B, kde v B[i] si pamatame, ktora bola najlepsia prva minca, ked sme pocitali A[i]
i 0 1 2 3 4 5 6 7 8 9 10 A[i] 0 1 2 1 1 2 2 2 2 3 3 B[i] - 1 1 3 4 4 3 4 4 4 4
- Potom ak chceme najst napr. mince pre 10, vidime, ze prva bola B[10]=4. Zvysok je 6 a prva minca na vyplatenie 6 je B[6]=3. Zostava nam 3 a B[3]=3. Potom nam uz zostava 0, takze sme hotovi. Takze najlepsie vyplatenie je 4+3+3
- Algoritmus:
Kym X>0 vypis B[X]; X = X-B[X];
- Dynamicke programovanie vo vseobecnosti
- Okrem riesenia celeho problemu, vyriesime aj spustu mensich podproblemov
- Riesenia podproblemov ukladame do tabulky
- Pri rieseni vacsieho podproblemu pouzivame uz vypocitane hodnoty pre mensie podproblemy
- Aka je casova zlozitost?
- Dva parametre: X a k.
- Tabulka velkost O(X), kazde policko cas O(k). Celkovo O(Xk).
Sekvenovanie genómov, cvičenia pre informatikov
Zostavovanie genomu pomocou eulerovskych tahov
- Opakovanie z teorie grafov:
- Hamiltonovska kruznica: cyklus, ktory prechadza kazdym vrcholom prave raz
- Eulerov tah: tah, ktory prechadza po kazdej hrane prave raz
- Zistit, ci ma graf H.c. je NP-tazke
- Problem obchodneho cestujuceho: najst najlacnejsiu H.c. je tiez NP-tazky
- Zistit ci ma graf E.t. a najst ho je lahke
- neorientovany graf na E.t. <=> je suvisly a vsetky vrcholy okrem najviac dvoch maju parny stupen
- orientovany graf ma E.t. z u do v <=> po pridani hrany z v do u je silne suvisly a vsetky vrcholy maju rovnako vchadzajucich ako vychadzajucich hran
- Najkratsie spolocne nadslovo: zjednodusena verzia problemu zostavovania genomov zo segmentov
- Mame danu mnozinu retazcov, chceme zostavit najkratsi retazec, ktoremu su vsetky podslova
- Priklad: GCCAAC,CCTGCC,ACCTTC zlozime v poradi 2,1,3: CCTGCCAACCTTC
- Mozeme si predstavit problem ako obmenu problemu obchodneho cestujuceho:
- retazcom priradim vrcholy
- dlzka hrany z a do b je
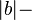 prekryv medzi a a b
prekryv medzi a a b
- specialny zaciatocny vrchol, z ktoreho hrany do kazdeho a s cenou |a|
- specialny koncovy vrchol, do ktoreho hrana z kazdeho a s cenou 0
- hrana z koncoveho do zaciatocneho vrcholu na uzavretie cyklu
- Hamiltonovske kruznice zodpovedaju nadslovam
- Ak najdeme najlacnejsiu Hamiltonovsku kruznicu, mame najkratsie nadslovo
- Ale vieme, ze problem obchodneho cestujuceho je NP-tazky
- Je toto dokaz, ze aj najkratsie spolocne nadslovo je NP-tazke?
- Pevzner, Tang and Waterman 2001 navrhuju namiesto Hamiltonovskej kruznice pouzit Eulerov tah (na inom grafe)
- deBruijnov graf stupna k:
- vrcholy: podretazce dlzky k vsetkych vstupnych retazcov
- hrany: nadvazujuce k-tice v ramci kazdeho segmentu (s prekryvom k-1)
- Priklad, k=2
- Chceme prejst po vsetkych hranach, chceme chodit co najmenej, takze po kazdej len raz - Eulerov tah
- V com je finta? Ako sme sa dostali od NP-tazkeho problemu k lahkemu?
- Co ak deBruijnov graf nema Eulerovsky tah? Znasobime niektore hrany, tieto budu zodpovedat opakovaniam
- Čo ak de Bruijnov graf má viacero Eulerovských ťahov?
- Zoberieme taký ťah, ktorý obsahuje pôvodné segmenty ako podcesty
- Zase ťažký problém, ale v praxi pomáhajú jednoduché pravidlá
- Opatrné riešenie: Ak z vrcholu 2 cesty, rozdeľ na kontigy
- Pouzitie sparovanych segmentov:
- Nájdi vrcholy v grafe, ktoré im zodpovedajú
- Ak je v grafe jediná cesta medzi týmito vrcholmi vhodnej dĺžky, premeň spárované segmenty na jeden veľký segment
- Dalsie problemy, ktore treba riesit
- sekvenovacie chyby: vytvaraju "bubliny" alebo slepe cesty
- dve vlakna
- Realne pouzivana technologia, aj pre sekvenovanie novej generacie, napr. Zerbino and Birney 2008 program Velvet
Uvod do pravdepodobnosti
- nedokoncili sme, pozri poznamky v casti Pravdepodobnosť,_cvičenia_pre_informatikov
Zarovnávanie sekvencií, UCSC genome browser, cvičenia pre biológov
Používanie počítačov na M218
- V textovom menu pri štarte zvoľte Bioinformatika, v grafickom prihasovacom menu nechajte užívatel User, heslo dostanete
- Na pravom okraji pracovnej plochy mate schovanu listu s casto pouzivanymi nastrojmi, napr. internetovy prehliadac firefox
- Vo firefoxe si otvorte stranku predmetu, cast Prednášky a poznámky, nalistujte materialy k dnesnemu cviceniu (poznamky a subory)
Príklad s mincami v Exceli
Práca so vzorcami v tabuľkovom procesore (Excel, OpenOffice, ...)
- Okrem konkrétnych hodnôt, napr. 0.3, môžu byť aj vzorce, ktoré začínajú =, napr =0.3*0.3 dá do políčka 0.09 (* znamená násobenie)
- Vo vzorcoch môžeme používať aj hodnoty z iných políčok, napr. =A2+B2 dáme do políčka C2, zobrazí sa tam súčet
- Ak políčko so vzorcom skopírujeme do iného políčka, Excel sa snaží uhádnuť, ako zmeniť vzorec
- Ak sme v C2 mali =A2+B2 a skopírovali sme to do C3, vzorec sa zmení na =A3+B3
- Ak niektoré adresy políčok majú zostávať rovnaké aj pri kopírovaní, dáme pred písmeno aj číslo $,
- Ak v C2 máme =A2+$B$2 a skopírujeme to do C3, dostaneme =A3+B2
- Dolár možeme dať aj pred iba jednu súradnicu (stĺpec alebo riadok), tá sa potom nebude pri kopírovaní meniť
Späť k minciam
- vratme sa k prikladu s rozmienanim minci a skusme si ho "naprogramovat" v Exceli, resp. spreadsheet aplikacii v OpenOffice
- Vseobecna formulacia:
- Vstup: hodnoty k minci m_1,m_2,...,m_k a cielova suma X (vsetko kladne cele cisla)
- Vystup: najmensi pocet minci, ktore potrebujeme na zaplatenie X
- My pouzijeme mince hodnot 1,3,4
- Spravime si tabulku, kde si pre kazdu sumu i=0,1,2,...X pamatame A[i]=najmensi pocet minci, ktore treba na vyplatenie sumy i (ak je viac moznosti, zoberieme lubovolnu, napr. najvacsiu)
i 0 1 2 3 4 5 6 7 8 9 A[i] 0 1 2 1 1 2 2 2 2 3
- vzorec A[i] = 1+ min { A[i-1], A[i-3], A[i-4] }
- aby sme nemuseli zvlast uvazovat hodnoty mensie ako 4, (kde sa neda A[i-4]), urcime si A[-1], A[-2] atd ako nejake velke cislo (napr 100), takze vzorec plati pre vsetky i>0
i -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 A[i] 100 100 100 100 0 1 2 1 1 2 2 2 2 3
- v exceli si najskor spravime horny riadok tabulky
- do nejakeho policka (napr, B4) zapiseme prvu hodnotu (-4)
- do susedneho C4 zapiseme vzorec =B4+1, dostaneme hodnotu -3
- vzorce zacinaju znamienkom =
- B4 je suradnica policka o jedno vlavo, k nedj pripocitame 1
- policko C4 nakopirujeme do riadku kolkokrat chceme, dostaneme hodnoty -2, -1, 0, 1,...
- kopirovat sa da tahanim laveho dolneho rohu okienka
- vzorec sa automaticky posuva na =C4+1, =D4+1, atd
- o riadok nizsie do B5..E5 napiseme hodnotu 100 (okienka A[-4]..A[-1])
- do F5 dame 0 (okienko A[0] nasej tabulky)
- do G5 napiseme vzorec =MIN(F5,D5,C5)+1 (t.j. A[1] = min(A[1-1],A[1-3],A[1-4])+1)
- tento vzorec potom nakopirujeme do riadku tabulky
- F5 sa bude posuvat na G5, H5,... a podobne ostatne dva cleny
- Ako by sme zmenili na inu mincovu sustavu, napr. 1,2,5?
Zarovnávanie sekvencií, opakovanie
- Uvazujme skorovanie zhoda +2, nezhoda -1, medzera -1
- Retazce TAACGG a CACACT
Globalne zarovnanie
- Rekurencia: A[i,j] = max {A[i-1,j]-1, A[i,j-1]-1, A[i-1,j-1]+c(p_i, q_j) }, pricom A[0,i]=-i, A[i,0]=-i
C A C A C T
0 -1 -2 -3 -4 -5 -6
T -1
A -2
A -3
C -4
G -5
G -6
Lokalne zarovnanie
- Rekurencia: A[i,j] = max {0, A[i-1,j]-1, A[i,j-1]-1, A[i-1,j-1]+c(p_i, q_j) }, pricom A[0,i]=0, A[i,0]=0
C A C A C T
0 0 0 0 0 0 0
T 0
A 0
A 0
C 0
G 0
G 0
Zarovnávanie sekvencií v Exceli
- skusme si aj dynamicke programovanie naprogramovat v Exceli
- budeme postupovat podobne, ale potrebujeme dve specialne funkcie: MID(text,od,dlzka) z textu vyberie urcitu cast. Pomocou toho si vstupny text rozdelime na jednotlive pismena, ktore si napiseme do zahlavia tabulky
- vsimnite si pouzivanie dolarov v nazvoch policok: ak je pred menom stlpca alebo riadku $, tento sa neposuva ked vzorec kopirujem do inych policok
- IF(podmienka,hodnota1,hodnota2) vyberie bud hodnotu 1 ak je podmienka splnena alebo hodnotu2 ak nie je. Napr IF(F$8=$B12 ,1,-1) zvoli skore +1 ak sa hodnota v F8 rovna hodnote v B12 a skore -1 ak sa nerovnaju.
Cvicenie: Zmente tabulku tak, aby skore pre zhody, nezhody a medzery bolo dane bunkami B1, B2 a B3 tabulky. Staci zmenit vzorce a policka D9, C10 a D10 a nakopriovat do zvysku tabulky. Ake bude skore najlepsieho zarovnania sekvencii AACGTA a ACACCTA ak skore nezhody je -2 a medzery -3?
UCSC genome browser
- V programe Firefox choďte na stránku UCSC genome browser http://genome.ucsc.edu/
- Hore v modrom menu zvoľte Genomes, potom zvoľte ľudský genóm. Do okienka search term zadajte HOXA2. Vo výsledkoch hľadania (UCSC genes) zvoľte gén homeobox A2. Koľko má exónov? Na ktorom chromozóme a pozícii je? Pozor, je na opačnom vlákne. Ako je táto skutočnosť naznačená na obrázku?
- V tracku UCSC Genes kliknite na gén, mali by ste sa dostať na stránku popisujúcu jeho rôzne vlastnosti. Čo ste sa dozvedeli o jeho funkcii?
- na tejto stránke nájdite linku na stiahnutie proteínovej sekvencie
Dotploty
- Dotplot je graf, ktory ma na kazdej osi jednu sekvenciu a ciarky zobrazuju lokalne zarovnania (cesty v matici)
- Na slidoch mame niekolko prikladov dotplotov porovnavajucich rozne mitochondrialne genomy
- Tieto boli vytvorene pomocou nastroja YASS http://bioinfo.lifl.fr/yass/yass.php
- Dalsi priklad je zarovnanie genu Oaz Drosophila zinc finger s genomickym usekom chr2R:10,346,241-10,352,965
- Trochu iny dotplot, ktory funguje pre proteiny a nerobi lokalne zarovnania, iba spocita skore bez medzier v kazdom okne danej vysky a nakresli ciaru ak pre kroci urcenu hodnotu
- http://emboss.bioinformatics.nl/cgi-bin/emboss/dotmatcher
- Vyskusame protein escargot voci sebe s hodnotami http://pfam.sanger.ac.uk/protein/ESCA_DROME window 8 threshold 24
- Pomocou YASSu vyskusame kluster zhlukov PRAME z ludskeho genomu
- Obrázky dotplotov na slidoch
Prakticke cvicenie: Yass a dotploty
- Na stranke UCSC genome browseru http://genome.ucsc.edu/ si zadajte ludsky genom, najnovsiu verziu (hg19)
- V druhom okne/tabe si otvorte YASS server na adrese http://bioinfo.lifl.fr/yass/yass.php
- V genome browseri zadajte region chr21:10,018,860-10,019,178
- tento región obsahuje Alu repeat. Tieto opakovania tvoria cca 10% ľudského genómu, viac ako milión kópií
- zobrazte si DNA sekvenciu tohto useku takto: na hornej modrej liste zvolte View, potom v podmenu DNA, na dalsej obrazovke tlacidlo get DNA
- DNA sekvenciu Alu opakovania chceme zarovnat samu k sebe programom YASS
- DNA sekvenciu Alu opakovania skopirujte do okienka "Paste your sequences" v stranke Yass-u a dvakrat stlacte tlacidlo Select vedla okienka
- Nizsie v casti "Selected DNA sequence(s)" by sa Vam malo v oboch riadkoch objavit "Pasted file 1"
- Nizsie v casti "Parameters" zvolte "E-value threshold" 0.01 a stlacte "Run YASS"
- Vo vysledkoch si pozrite Dotplot, co z neho viete usudit o podobnosti jednotlivych casti Alu opakovania?
- Vo vysledkoch si pozrite Raw: blast, ake su suradnice opakujucej sa casti a kolko zarovnanie obsahuje zhod/nezhod/medzier? (Pozor, prve zarovnanie je cela sekvencia sama k sebe, druhe je asi to, co chcete)
- V genome browseri zadajte poziciu chr21:9,440,000-9,450,000 (10kb sekvencie na chromozome 21, s niekolkymi vyskytmi Alu)
- Chceme teraz porovnat tento usek genomu so sekvenciou Alu pomocou YASSu
- Ako predtym si stiahnite DNA sekvenciu tohto useku
- V YASSe chodte sipkou spat na formular
- Skopirujte DNA sekvenciu do YASSoveho formulara, do okienka vpravo (vyznacit si ju mozete klavesovou kombinaciou Ctrl-A alebo Select All v menu Edit),
- V casti formulara Selected DNA sequence(s) stlacte Remove pri hornom riadku
- Pri pravom okienku, kam ste nakopirovali sekvenciu, stlacte Select
- Zase stlacte Run YASS
- Pozrite si vysledok ako Dotplot, kolko opakovani Alu ste nasli? Preco je jedno cervene?
- Pozrite si Raw: blast, na kolko percent sa podoba najpodobnejsia a na kolko druha najpodobnejsia kopia?
Sekvenovanie v UCSC genome browseri
- Vráťte sa na UCSC genome browser http://genome.ucsc.edu/
- Pozrieme si niekoľko vecí týkajúcich sa sekvenovania a skladania genómov
- Hore v modrom menu zvoľte Genomes
- Na ďalšej stránke zvoľte človeka a v menu Assembly zistite, kedy boli pridané posledné dve verzie ľudského genómu (hg18 a hg19)
- Na tej istej stránke dole nájdete stručný popis zvolenej verzie genómu. Pre ktoré oblasti genómu máme v hg19 viacero alternatívnych verzií?
- Zadajte región chr21:31,200,000-31,350,000
- Zapnite si tracky Mapability a RepeatMasker na "full"
- Mapability: nakoľko sa daný úsek opakuje v genóme a či teda vieme jednoznačne jeho ready namapovať pri použití Next generation sequencing
- Ako a prečo sa pri rôznych dĺžkach readov líšia? (Keď kliknete na linku "Mapability", môžete si prečítať bližšie detaily.)
- Približne v strede zobrazeného regiónu je pokles mapovateľnosti. Akému typu opakovania zodpovedá? (pozrite track RepeatMasker)
- Zapnite si tracky "Assembly" a "Gaps" a pozrite si región chr2:110,000,000-110,300,000. Aká dlhá je neosekvenovaná medzera (gap) v strede tohto regiónu? Približnú veľkosť môžete odčítať z obrázku, presnejší údaj zistíte kliknutím na čierny obdĺžnik zodpovedajúci tejto medzere (úplne presnú dĺžku aj tak nepoznáme, nakoľko nie je osekvenovaná).
- Prejdite na genóm Rhesus, región chr7:59,022,000-59,024,000, zapnite si tracky Contigs, Gaps, Quality scores
- Aké typy problémov v kvalite sekvencie v tomto regióne vidíte?
Zarovnávanie sekvencií, cvičenia pre informatikov
Opakovanie dynamického programovania pre globálne zarovnanie
Uvažujme napríklad skórovanie zhoda +1, nezhoda -1, medzera -1 a vstupné sekvencie 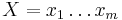 a
a 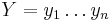 . Nech s(x,y) je skóre písmen x a y, t.j. 1 ak sa zhodujú a -1 ak nie. Máme rekurenciu:
. Nech s(x,y) je skóre písmen x a y, t.j. 1 ak sa zhodujú a -1 ak nie. Máme rekurenciu:
- Ako presne by sme implementovsali?
- Ako spocitame maticu spatnych sipok B?
- Akak je casova a pamatova zlozitost?
Reprezentácia pomocou grafu
Takéto dynamické programovanie vieme reprezentovať vo forme acyklického orientovaného grafu:
- vrchol (i,j) pre každé
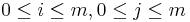 , t.j. pre každé políčko dyn. prog. tabuľky
, t.j. pre každé políčko dyn. prog. tabuľky
- hrana z (i-1,j-1) do (i,j) s cenou
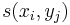
- hrana z (i-1,j) do (i,j) s cenou -1
- hrana z (i,j-1) do (i,j) s cenou -1
- súčet súradníc na každej hrane rastie, graf teda nemôže obsahovať cyklus, je acyklický
- každá cesta z (0,0) do (m,n) zodpovedá zarovnaniu, jej cena je cenou zarovnania (každá hrana jeden stĺpec)
- optimálne zarovnanie teda zodpovedá ceste s maximálnou cenou
Krátka vsuvka o acyklických orientovaných grafoch
- Mame dany acyklicky orientovany graf s ohodnotenymi hranami a startovaci vrchol s, koncovi vrchol t a chceme najst cestu s max. cenou z s do t.
- Hladanie cesty s maximalnou cenou je vo vseobecnosti NP-tazke (podobne na Hamiltonovsku cestu)
- V acyklickom grafe to vsak vieme riesit efektivne
- Najskor si graf zotriedime topologicky, t.j. usporiadame vrcholy tak, aby kazda hrana isla z vrcholu z mensim cislom do vrcholu s vacsim cislom. To sa da modifikaciou prehladavania do hlbky v case O(|V|+|E|)
- Potom pocitame dynamickym programovanim, kde A[u] je dlzka najdlhsej cesty z s do u:
![A[u]=\max _{{v:v\rightarrow u\in E}}A[v]+c(v\rightarrow u)](/vyuka/mbi/images/math/6/d/9/6d90a7118031848ff55c4204bc8b4552.png)
pricom na zaciatku nastavime A[s]=0 a na konci mame cenu cesty v A[t].
- Cas vypoctu je O(|V|+|E|)
- Vsimnime si, ze tiez dostaneme najdlhsie cesty z s do vsetkych vrcholov.
Ak tento algoritmus nasadime na graf pre globalne zarovnanie, dostavame presne nasu rekurenciu (topologicke triedenie mozno vynechat - poradie zhora dole a zlava doprava je topologicky utriedene). Vyhoda je, ze mozeme modifikaciou grafu ziskavat riesenia roznych pribuznych problemov bez toho, aby sme vzdy vymyslali novu rekurenciu.
Lokalne zarovnanie
- Zarovnanie moze zacat a skoncit hocikde v matici
- Pridaj startovaci vrchol s, koncovy vrchol t
- Pridaj hrany s->(i,j) a (i,j)->t s cenou 0 pre kazde (i,j)
- Opat ekvivalentne s rekurenciou z prednasky
Variant: chceme zarovnat cely retazec X k nejake casti retazca Y (napr. mapovanie sekvenovacich readov na genom)
- Iba zmenime hrany z s a hrany do t (ako?)
Afinne skore medzier
- Napr. otvorenie medzery -2, pokracovanie medzery -1
A - - - T C G A C G C T C C 1 -2 -1 -1 1 1 -1
Riesenie 1:
- Pridame hrany pre cele suvisle useky medzier so spravnou cenou
- (i,j)->(i,k) s cenou o+(k-j)e
- (i,j)->(k,j) s cenou o+(k-i)e
- Cas O(mn(m+n)), t.j. kubicky
- pozor, mame aj cesty, ktore nezopodvedaju ziadnemu spravnemu skore, napr. (i.j)->(i+1,j)->(i+2,j) ma cenou 2o, ale ma mat o+e. Nastastie hrana (i,j)->(i+2,j) ma vyssiu cenu, takze ta dlhsia cesta sa nepouzije.
Riesenie 2:
- ztrojnasobime kazdy vrchol
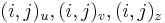
- v indexe si pamatame, odkial sme do (i,j) prisli (u=uhlopriecne, v=vodorovne, z=zvislo)
- ak ideme napr. z
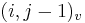 do
do 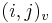 , pokracujeme v uz existujucej medzere, takze skore je e
, pokracujeme v uz existujucej medzere, takze skore je e
- ak ideme napr. z
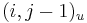 do
do 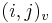 , zaciname novu medzeru, takze skore je o
, zaciname novu medzeru, takze skore je o
- ake vsetky hrany teda mozeme mat? Kolko je spolu v grafe hran a vrcholov a aka je zlozitost algoritmu?
Linearna pamat: Hirshbergov algoritmus 1975
- Klasicke dynamicke programovanie potrebuje cas O(nm)
- Trivialna implementacia tiez pouzije pamat O(mn) - uklada si celu maticu A, pripadne maticu B so sipkami naspat
- Na vypocet matice A nam z stacia dva riadky tejto matice: riadok i pocitam len pomocou riadku i-1, starsie viem zahodit
- Ale ak chcem aj vy[isat zarovnanie, stale potrebujem pamat O(mn) na maticu sipok B
- Hirschbergov algoritmus znizi pamat na O(m+n), zhruba zdvojnasobi cas (stale O(mn))
- Prejdeme celú maticu a spočítame maticu A. Zapamätáme si, kde moja cesta prejde cez stredný riadok matice
- Nech B_k[i,j] je najväčší index v riadku k, cez ktorý prechádza najkratšia cesta z (0,0) do (i,j)
- Ako vieme B_k[i,j] spočítať?
- ak A[i,j] = A[i-1,j-1]+w(S[i],T[j])$, potom B_k[i,j]=B_k[i-1,j-1].
- ak A[i,j]=A[i-1,j]+1, potom B_k[i,j]=B_k[i-1,j].
- ak A[i,j]=A[i,j-1]+1, potom B_k[i,j]=B_k[i,j-1]
- Toto platí, ak i > k. Pre i=k nastavíme B_k[i,j]=j
- Ak už poznáme A[i-1,*] a B_k[i-1,*], vieme spočítať A[i,*] a B_k[i,*].
- Stacia nam teda iba dva riadky matice A a B_k
- Nech k'=B_k[m,n]. Potom v optimálnom zarovnaní sa S[1..k] zarovná s T[1..k'] a S[k+1..m] s T[k'+1..n].
- Toto použijeme na rekurzívny algoritmus na výpočet zarovnania:
optA(l1, r1, l2, r2) { // align S[l1..r1] and T[l2..r2]
if(r1-l1 <= 1 || r2-l2 <=1)
solve using dynamic programming
else {
k=(r-l+1)/2;
for (i=0; i<=k; i++)
compute A[i,*] from A[i-1,*]
for (i=k+1; i<=r-l+1; i++)
compute A[i,*], B_k[i,*] from A[i-1,*], B_k[i-1,*]
k2=B_k[r1-l1-1,r2-l2-1];
optA(l1, l1+k-1, l2, l2+k2-1);
optA(l1+k, r2, l2+k2, r2);
}
}
Casova zlozitost:
- Označme si N=nm (súčin dĺžky dvoch daných reťazcov).
- Na hornej úrovni rekurzie spúšťame dynamické programovanie pre celú maticu -- čas bude $cN$.
- Na druhej urovni mame dva podproblemy, velkosti N1 a N2, pricom N1+N2<=0.5*N (z kazdeho stlpca matice A najviac polovica riadkov pocitana znova)
- Na tretej urovni mame 4 podproblemy N11, N12, N21, N22, pricom N11+N12 <= 0.5*N1 a N21+N22 <= 0.5*N2 a teda celkovy sucet podproblemov na druhej urvni je najviac N/4.
Na stvrtej urovni je sucet podproblemov najviac N/8 atd, Dostavame geometricky rad cN+cn/2+cN/4+... ktoreho sucet je 2cN
Vypisanie vsetkych najlepsich rieseni
- Namiesto jednej spatnej sipky si pamatame vsetky, ktore v danom A[i,j] viedli k maximalnej cene
- Potom mozeme rekurzivne prehladavat a vypisovat vsetky cesty z (m,n) do (0,0) ktore pozostavaju iba zo zapamatanych hran
- Cas na vypisanie jednej cesty je polynomialny, ale ciest moze byt exponencialne vela!
- Mozno namiesto toho chceme len pocet takych ciest, alebo vsetky dvojice pismen, ktore mozu byt spolu zarovnane v niektorom optimalnom zarovnani
Zarovnávanie sekvencií 2, cvičenia pre biológov
- Pozrime si spolu cvicenia o sekvenovani z minuleho tyzdna
Priklady praktickych programov
Pozrime sa na niekolko nastrojov, vsimnime si, ake poskytuju nastavenia a co vypisuju na vystupe, dajme to do suvisu s prednaskami
Plne dynamicke programovanie
- Balicek emboss, obsahuje programy na klasicke dynamicke programovanie (needle - globalne, water - lokalne), najdu sa na stranke EBI http://www.ebi.ac.uk/Tools/psa/
- su aj v online bioinf. portali http://mobyle.pasteur.fr/
- porovnanie lokalneho a globalneho zarovnania
- Dva proteiny s kinase doménou zarovnáme lokálne, globálne a globálne s tým, že neplatíme za medzery na koncoch
- Subor s datami a vysledkami
>sp|P50520|VPS34_SCHPO Phosphatidylinositol 3-kinase vps34 OS=Schizosaccharomyces pombe (strain 972 / ATCC 24843) GN=vps34 PE=2 SV=2 >tr|B1AKP8|B1AKP8_HUMAN FK506 binding protein 12-rapamycin associated protein 1 OS=Homo sapiens GN=FRAP1 PE=4 SV=1
NCBI Blast
- NCBI BLAST http://blast.ncbi.nlm.nih.gov/ vela roznych nastrojov (porovnavanie DNA vs proteiny, pripadne translacia DNA na protein v 6 ramcoch)
- Heuristicky algoritmus, moze niektore zarovnania vynechat
- rozne nastavenia, vystup E-value
Low complexity masking: nepouzivat pri hladani jadier zarovnania regiony v ktorych sa velakrat opakuje ta ista aminokyselina
- Priklad (z ucebnice Zvelebil and Baum):
>sp|P04156|PRIO_HUMAN Major prion protein OS=Homo sapiens GN=PRNP PE=1 SV=1 MANLGCWMLVLFVATWSDLGLCKKRPKPGGWNTGGSRYPGQGSPGGNRYPPQGGGGWGQP HGGGWGQPHGGGWGQPHGGGWGQPHGGGWGQGGGTHSQWNKPSKPKTNMKHMAGAAAAGA VVGGLGGYMLGSAMSRPIIHFGSDYEDRYYRENMHRYPNQVYYRPMDEYSNQNNFVHDCV NITIKQHTVTTTTKGENFTETDVKMMERVVEQMCITQYERESQAYYQRGSSMVLFSSPPV ILLISFLIFLIVG
Bez maskovania vypise najpr aj toto zarovnanie:
>ref|NP_065842.1| serine/threonine-protein kinase TAO1 isoform 1 [Homo sapiens]
Length=1001
Score = 45.1 bits (105), Expect = 1e-06, Method: Composition-based stats.
Identities = 26/61 (43%), Positives = 27/61 (44%), Gaps = 11/61 (18%)
Query 38 YPGQGSPGGNRYPPQGGGG--WGQPHGG---GWGQPHGGG---WGQPHGGGWGQPHGGGWG 90
YPG G + P GG G WG P GG WG P GG WG P G G P G G
Sbjct 904 YPGAS---GWSHNPTGGPGPHWGHPMGGPPQAWGHPMQGGPQPWGHPSGPMQGVPRGSSMG 961
Score = 40.0 bits (92), Expect = 4e-05, Method: Composition-based stats.
Identities = 25/62 (40%), Positives = 25/62 (40%), Gaps = 10/62 (16%)
Query 26 PKPGGW--NTGGSRYPGQGSPGGNRYPPQGGGGWGQPHGGG---WGQPHGGGWGQPHGGGWG 82
P GW N G P G P G PPQ WG P GG WG P G G P G
Sbjct 905 PGASGWSHNPTGGPGPHWGHPMGG--PPQA---WGHPMQGGPQPWGHPSGPMQGVPRGSSMG 961
Ak zapneme maskovanie, toto zarovnanie uz nenajde, v zarovnani sameho so sebou sa objavia male pismena alebo Xka:
>ref|NP_000302.1|major prion protein preproprotein [Homo sapiens]
Length=253
Score = 520 bits (1340), Expect = 0.0, Method: Compositional matrix adjust.
Identities = 253/253 (100%), Positives = 253/253 (100%), Gaps = 0/253 (0%)
Query 1 MANLGCWMLVLFVATWSDLGLCKKRPKPGGWNTGGSRYPGQGSPGGNRYppqggggwgqp 60
MANLGCWMLVLFVATWSDLGLCKKRPKPGGWNTGGSRYPGQGSPGGNRYPPQGGGGWGQP
Sbjct 1 MANLGCWMLVLFVATWSDLGLCKKRPKPGGWNTGGSRYPGQGSPGGNRYPPQGGGGWGQP 60
Query 61 hgggwgqphgggwgqphgggwgqphgggwgqgggTHSQWNKPSKPKTNMKHMagaaaaga 120
HGGGWGQPHGGGWGQPHGGGWGQPHGGGWGQGGGTHSQWNKPSKPKTNMKHMAGAAAAGA
Sbjct 61 HGGGWGQPHGGGWGQPHGGGWGQPHGGGWGQGGGTHSQWNKPSKPKTNMKHMAGAAAAGA 120
Query 121 vvgglggymlgsamsRPIIHFGSDYEDRYYRENMHRYPNQVYYRPMDEYSNQNNFVHDCV 180
VVGGLGGYMLGSAMSRPIIHFGSDYEDRYYRENMHRYPNQVYYRPMDEYSNQNNFVHDCV
Sbjct 121 VVGGLGGYMLGSAMSRPIIHFGSDYEDRYYRENMHRYPNQVYYRPMDEYSNQNNFVHDCV 180
Query 181 NITIKQHtvttttkgenftetDVKMMERVVEQMCITQYERESQAYYQRGSSMVLFSsppv 240
NITIKQHTVTTTTKGENFTETDVKMMERVVEQMCITQYERESQAYYQRGSSMVLFSSPPV
Sbjct 181 NITIKQHTVTTTTKGENFTETDVKMMERVVEQMCITQYERESQAYYQRGSSMVLFSSPPV 240
Query 241 illisfliflivG 253
ILLISFLIFLIVG
Sbjct 241 ILLISFLIFLIVG 253
BLAT, chains, nets v UCSC browseri
- Program BLAT v UCSC browseri http://genome.ucsc.edu/ rychlo vyhladava sekvencie v genome, ale nevie najst slabsie podobnosti
- Vhodne pouzitie: zarovnanie EST ku genomu, presne urcenie suradnic nejakej sekvencie, a pod.
- Net tracky v UCSC genome browseri nam umoznuju prechadzat medzi homologickymi oblastami roznych genomov
Prakticke cvicenie pri pocitaci: BLAT vs BLAST, nets v UCSC browseri
BLAT/BLAST
- Na stránke so súbormi otvorte subor rtpcr-seq.txt. Obsahuje sekvenciu, ktorá vznikla pomocou RT-PCR na ľudských cDNA knižniciach
- Choďte na UCSC genome browser http://genome.ucsc.edu/ , na modrej lište zvoľte BLAT, zadajte túto sekvenciu a hľadajte ju v ľudskom genóme. Akú podobnosť (IDENTITY) má najsilnejší nájdený výskyt? Aký dlhý úsek genómu zasahuje? (SPAN). Všimnite si, že ostatné výskyty sú oveľa kratšie.
- V stĺpci ACTIONS si pomocou Details môžete pozrieť detaily zarovnania a pomocou Browser si pozrieť príslušný úsek genómu.
- V tomto úseku genómu si zapnite track Vertebrate net na full a kliknutím na farebnú čiaru na obrázku pre tento track zistite, na ktorom chromozóme sliepky sa vyskytuje homologický úsek.
- Skusme tu istu sekvenciu namapovat do genomu sliepky: stlacte najprv na hornej modrej liste Genomes, zvolte Vertebrates a Chicken a potom na hornej liste BLAT. Do okienka zadajte tu istu sekvenciu. Akú podobnosť a dĺžku má najsilnejší nájdený výskyt teraz? Na ktorom je chromozóme?
- Skúsme to isté v NCBI blaste: Choďte na http://blast.ncbi.nlm.nih.gov/ zvoľte nucleotide blast, database others a z menu reference genomic sequence, organism chicken (taxid:9031), program blastn
- Aka je dlzka, identity a E-value najlepsieho zarovnania? Na ktorom je chromozome?
RT PCR sekvencia z cvičenia vyššie
AACCATGGGTATATACGACTCACTATAGGGGGATATCAGCTGGGATGGCAAATAATGATTTTATTTTGAC TGATAGTGACCTGTTCGTTGCAACAAATTGATAAGCAATGCTTTCTTATAATGCCAACTTTGTACAAGAA AGTTGGGCAGGTGTGTTTTTTGTCCTTCAGGTAGCCGAAGAGCATCTCCAGGCCCCCCTCCACCAGCTCC GGCAGAGGCTTGGATAAAGGGTTGTGGGAAATGTGGAGCCCTTTGTCCATGGGATTCCAGGCGATCCTCA CCAGTCTACACAGCAGGTGGAGTTCGCTCGGGAGGGTCTGGATGTCATTGTTGTTGAGGTTCAGCAGCTC CAGGCTGGTGACCAGGCAAAGCGACCTCGGGAAGGAGTGGATGTTGTTGCCCTCTGCGATGAAGATCTGC AGGCTGGCCAGGTGCTGGATGCTCTCAGCGATGTTTTCCAGGCGATTCGAGCCCACGTGCAAGAAAATCA GTTCCTTCAGGGAGAACACACACATGGGGATGTGCGCGAAGAAGTTGTTGCTGAGGTTTAGCTTCCTCAG TCTAGAGAGGTCGGCGAAGCATGCAGGGAGCTGGGACAGGCAGTTGTGCGACAAGCTCAGGACCTCCAGC TTTCGGCACAAGCTCAGCTCGGCCGGCACCTCTGTCAGGCAGTTCATGTTGACAAACAGGACCTTGAGGC ACTGTAGGAGGCTCACTTCTCTGGGCAGGCTCTTCAGGCGGTTCCCGCACAAGTTCAGGACCACGATCCG GGTCAGTTTCCCCACCTCGGGGAGGGAGAACCCCGGAGCTGGTTGTGAGACAAATTGAGTTTCTGGACCC CCGAAAAGCCCCCACAAAAAGCCG
Pravdepodobnosť, cvičenia pre biológov
Uvod do pravdepodobnosti
- Myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealnou kockou/korunou
- Vysledkom experimentu je nejaka hodnota (napr. cislo, alebo aj niekolko cisel, retazec)
- Tuto neznamu hodnotu budeme volat nahodna premenna
- Zaujima nas pravdepodobnost, s akou nahodna premenna nadobuda jednotlive mozne hodnoty
- T.j. ak experiment opakujeme vela krat, ako casto uvidime nejaky vysledok
- Priklad 1: hodime idealizovanou kockou, premenna X bude hodnota, ktoru dostaneme
- Mozne hodnoty 1,2,..,6, kazda rovnako pravdepodobna
- Piseme napr. Pr(X=2)=1/6
- Priklad 2: hodime 2x kockou, nahodna premenna X bude sucet hodnot, ktore dostaneme
- Mozne hodnoty: 2,3,...,12
- Kazda dvojica hodnot na kocke rovnako pravdepodobna, t.j. pr. 1/36
- Sucet 5 mozeme dostat 1+4,2+3,3+2,4+1 - t.j. P(X=5) = 4/36
- Sucet 11 mozeme dostat 5+6 alebo 6+5, t.j. P(X=11) = 2/36
- Rozdelenie pravdepodobnosti: (tabulka udavajuca pravdepodobnost pre kazdu moznu hodnotu)
hodnota i: 2 3 4 5 6 7 8 9 10 11 12 Pr(X=i): 1/36 2/36 3/36 4/36 5/36 6/36 5/36 5/36 6/36 5/36 1/36
- Overte, ze sucet pravdepodobnosti je 1
- Stredna hodnota E(X):
- priemer z moznych hodnot vahovanych ich pravdepodobnostami
- v nasom priklade
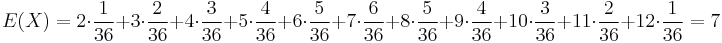
- Ak by sme experiment opakovali vela krat a zratali priemer hodnot X, ktore nam vysli, dostali by sme cislo blizke E(X)
- Iny vypocet strednej hodnoty:
- X=X1+X2, kde X1 je hodnota na prvej kocke a X2 je hodnota na druhej kocke
-
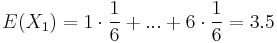 , podobne aj E(X2) = 3.5
, podobne aj E(X2) = 3.5
- Plati, ze E(X1+X2)=E(X1) + E(X2) a teda E(X) = 3.5 + 3.5 = 7
- Pozor, pre sucin a ine funkcie taketo vztahy platit nemusia, napr.
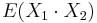 nie je vzdy
nie je vzdy 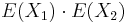
Pravdepodobnostny model nahodnej sekvencie
- Napriklad chceme modelovat nahodnu DNA sekvenciu dlzky n s obsahom GC 40%
- Mame vrece s gulockami oznacenyni A,C,G,T, pricom gulocok oznacenych A je 30%, C 20%, G 20% a T 30%.
- Vytiahneme gulicku, zapiseme si pismeno, hodime ju naspat, zamiesame a opakujeme s dalsim pismenom atd az kym nevygenerujeme n pismen
- Vytiahnime z mechu 2x gulicku. Prve pismeno ktore nam vyjde oznacme X1 a druhe X2
- Pr(X1=A) = 0.3, Pr(X2=C)=0.2
- Pr(X1=A a X2=C) = Pr(X1=A)*Pr(X2=C) = 0.3*0.2 = 0.06
- T.j. sanca ze dostaneme sekvenciu AC po dvoch tahaniach je 6%
- Ak ratame pravdepodobnost, ze sa dve nezavisle udalosti stanu, ich pravdepodobnosti nasobime. V tomto pripade to ci X1=A je nezavisle od toho, ci X2=C
- Pr(X1 je A alebo G) = Pr(X1=A)+Pr(X1=G) = 0.3+0.2 = 0.5
- Pravdepodobnost ze prve pismeno bude A alebo G je 50%
- Pravdepodobnosti navzajom sa vylucujucich udalosti (X1=A a X1=G) sa mozu scitat, cim dostaneme pravdepodobnost, ze aspon jedna z nich nastane
- Pr(X1 je A alebo X2 je G) nemozeme pocitat ako Pr(X1=A)+Pr(X2=G), lebo sa navzajom nevylucuju a pripad ze X1=A a X2=G by sme zapocitali dvakrat
- Spravne je Pr(v sekvencii je aspon jedno A) = Pr(X1=A) + Pr(X1 <> A a X2=G) = Pr(X1=A) + Pr(X1 <> A) * Pr(X2=G) 0.3+0.7*0.2 = 0.44
- Podobne napr Pr(v sekvencii je aspon jedno A) = Pr(X1=A alebo X2=A) = Pr(X1=A) + Pr(X1 <> A a X2=A) = Pr(X1=A) + Pr(X1 <> A) * Pr(X2=A) 0.3+0.7*0.3 = 0.51
- Pr(X1=X2) = Pr(X1=X2=A) + Pr(X1=X2=C) + Pr(X1=X2=G) + Pr(X1=X2=T) = 0.3*0.3+0.2*0.2+0.2*0.2+0.3*0.3 = 0.26.
- Ak u označíme pravdepodobnost u = Pr(X1=A)=Pr(X1=T)=Pr(X2=A)=Pr(X2=T) a v=Pr(X1=C)=Pr(X1=G)=Pr(X2=C)=Pr(X2=G), aky bude vzorec na Pr(X1=X2)?
E-hodnota (E-value) zarovnania
- Priklady k tejto casti v prezentacii [1]
- Mame dotaz dlzky m, databazu dlzky n, skore najlepsieho lok. zarovnania S
- E-value je ocakavany pocet zarovnani so skore aspon S ak dotaz aj databaza su nahodne
- Hrackarsky priklad: dotaz dlzky m=4, databaza dlzky n=200, S=4, t.j. presny vyskyt dotazu v databaze (pre presne vyskyty sa pravdepodobnosti pocitaju ovela lahsie ako ked dovolime nezhody a medzery)
- Zoberme nas nahodny model s obsahom GC 40%
- Mame vrece s gulockami oznacenyni A,C,G,T, pricom gulocok oznacenych A je 30%, C 20%, G 20% a T 30%.
- Vytiahneme gulicku, zapiseme si pismeno, hodime ju naspat, zamiesame a opakujeme s dalsim pismenom atd az kym nevygenerujeme m pismen pre dotaz a n pismen pre databazu
- Pre nase vygenerovane sekvencie spocitame, kolkokrat sa dotaz vyskytuje v databaze
- Cely experiment opakujeme vela krat a spocitame priemerny pocet vyskytov, co bude odhad E-value
- Vieme spocitat aj presne:
- Mame dotaz X1X2...Xm a databazu Y1Y2...Yn. Aka je sanca, ze X sa nachadza na zaciatku Y, t.j. ze X1=Y1, X2=2... Xm=Ym?
- Pripominame, ze pravdepodobnost zhody dvoch nukelotidov napr X1 a Y1 je Pr(X1=Y1) = Pr(X1=Y1=A) + Pr(X1=Y1=C) + Pr(X1=Y1=G) + Pr(X1=Y1=T) = 0.3*0.3+0.2*0.2+0.2*0.2+0.3*0.3 = 0.26.
- Pre rozne pozicie v X mame nezavisle udalosti, t.j. pravdepodobnost vyskytu X na prvej pozicii je Pr(X1=Y1)*Pr(X2=Y2)*...*Pr(Xm=Ym) = 0.26 * 0.26 * ... * 0.26 = 0.26^m (0.26 na m-tu)
- Tak isto nam vyjde aj pravdepodobnost vyskytu X na hociktorej inej pevnej pozicii v Y
- Pravdepodobnost, ze sa X nachadza na aspon jednej pozicii v Y je tazsie zratat - moze sa vyskytovat aj viackrat, udalosti ze sa nachadza na pozicii i sa navzajom nevylucuju
- Ale priemerny pocet vyskytov na pozicii i je 0.26^m, mame n-m+1 pozicii zaciatku, takze celkovy ocakavany pocet vyskytov je (n-m+1)0.26^m
- Toto je stredna hodnota nahodnej premennej C, ktora oznacuje pocet presnych vyskytov
- E(C) = E(C_1)+E(C_2)+...E(C_(n-m+1)), kde C_i je nahodna premenna, ktora je 1 ak sa X nachadza na pozicii i v Y
- E(C_i) = 0.26^m
- Ak je n velke v porovnani s m, clen -m+1 mozeme zanedbat, t.j. mame zhruba n*0.26^m
- Ako sa meni toto cislo s velkostou databazy n? linearne rastie (zdvojnasobime databazu, zdvojnasobi sa e-value)
- Ako sa meni s m? Exponencialne klesa, t.j. ak predlzime dotaz o 1, E-value klesne zhruba na stvrtinu
- Ako sa meni s GC obsahom? Zakodovane v cisle 0.26 - vyskusame si pri pocitaci v tabuľkovom procesore
Cvicenie pri pocitaci
- Stiahnite si subor [2], ulozte si ho a otvorte v openoffice
- Do zlteho policka vyplnte vzorec na vypocet pravdepodobnosti zhody medzi dvoma nahodne vygenerovanymi nukleotidmi v zacislosti od %GC v stlpci A.
- Vzorce v stlpcoch B-F nakopirujte do vsetkych riadkoch tabulky (napr dvojitym pokopanim na svtorcek v pravom dolnom roku okienka)
- Ako sa meni E-value v zavislosti od GC (hodnoty v modrom stlpci F)? Preco je to tak? Mozete si nakreslit aj graf.
- Potom skusajte menit hodnoty m a n a vsimnite si, ci maju taky vplyv na e-value, ako sme vraveli
Skorovacie matice
- Chceme urcit skorovaciu schemu pre zarovnavanie dvoch DNA sekvencii (bez medzier)
Mame dva modely, kazdy z nich vie vygenerovat 2 zarovnane skevencie dlzky n
Model R (random) reprezentuje nezavisle nahodne sekvencie
- Opat pouzijeme nase vrece s gulockami oznacenyni A,C,G,T, pricom gulocok oznacenych A je 30%, C 20%, G 20% a T 30%.
- Vytiahneme gulicku, zapiseme si pismeno, hodime ju naspat, zamiesame a opakujeme s dalsim pismenom atd az kym nevygenerujeme n pismen pre jednu sekvenciu a n pismen pre druhu
- Mame jednu sekvenciu ACT a druhu ACC. Aka je sanca, ze prave tieto sekvencie vygenerujeme v nasom modeli R?
- Nezavisle udalosti pre jednotlive pismena, t.j. Pr(X1=A)*Pr(X2=C)*Pr(X3=T)*Pr(Y1=A)*Pr(Y2=C)*Pr(Y3=C) = 0.3*0.2*0.3*0.3*0.2*0.2 = 0.000216
- Spolu mame v modeli 4 na 6 = 4096 moznosti ako vygenerovat 2 sekvencie dlzky 3
Pravdepodobnostny model H (homolog) vzajomne suvisiacich sekvencii
- mame mech, v ktorom je napr.
- po 21% guliciek oznacenych AA, TT
- po 14% oznacenych CC, GG
- po 2.4% oznacenych AC, AG, CA, CT, GA, GT, TC, TG
- po 3.6% oznacenych AT, TA
- po 1.6% oznacenych AG, GC.
Spolu mame 70% guliciek oznacenych rovnakymi pismenami, 30% roznymi
- n krat z neho vytiahneme gulicky a pismena piseme ako stlpce zarovnania.
- aka je pravdepodobnost, ze dostaneme ACT zarovnane s ACC?
- Pr(A1=AA)*Pr(A2=CC)*Pr(A3=TC) = 0.21*0.14*0.024 = 0.0007056
Cvicenie pri pocitaci
- Stiahnite si subor [3], ulozte si ho a otvorte v openoffice
- V zalozke Matica vyplnte do zltej oblasti vzorce na vypocet pravdepodobnosti kratkeho zarovnania, logaritmus pomeru pravdepodobnosti a sucet skore, pricom vo vzorcoch pouzijete odkazy na policka v riadkoch 11-15, stlpcoch B-E
- Sucet skore by mal zhruba rovny desatnasobku logaritmu pomeru - preco vidime rozdiely?
- Potom skusajte menit %GC a %identity v hornych riadkoch tabulky a pozrite sa, ako to ovplyvni skorovanie. Vysledne skore zo stlpca E rucne prepiste (bez formul) do tabulky v zalozke Vysledky. Preco nastavaju take zmeny ako vidite?
Pouzitie pravdepodobnosti na analyzu potrebneho pokrytia pri sekvenovani
Nerobili sme, uvedene pre zaujimavost
- Pozrite tiez grafy k pravdepodobnosti: http://compbio.fmph.uniba.sk/vyuka/mbi/poznamky/ci02.pdf
- Nas problem: spocitanie pokrytia
- G = dlzka genomu, napr. 1 000 000 (predpokladajme, že je cirkulárny)
- N = pocet segmentov (readov), napr. 10 000
- L = dlzka readu, napr. 1000
- Celkova dlzka segmentov NL, pokrytie (coverage) NL/G, v nasom pripade 10x
- V priemere kazda baza pokryta 10x
- Niektore su ale pokryte viackrat, ine menej.
- Zaujimaju nas otazky typu: kolko baz ocakavame, ze bude pokrytych menej ako 3x?
- Dolezite pri planovani experimentov (ake velke pokrytie potrebujem na dosiahnutie urcitej kvality)
- Pokrytie genomu: predpokladame, ze kazdy segment zacina na nahodnej pozicii zo vsetkych moznych G
- Takze ak premenna Y_i bude zaciatok i-teho segmentu, jej rozdelenie bude rovnomerne
- P(Y_i=1) = P(Y_i=2) = ... = P(Y_i=G) = 1/G
- Aka je pravdepodobnost ze nejaky konkretny i-ty segment pokryva konkretnu poziciu j?
- P(Y_i>=j-L+1 and Y_i<=j) = P(Y_i=j-L+1)+...+P(Y_i=j) = L/G, oznacme tuto hodnotu p, nasom priklade p=0.001 (1 promile)
- Uvazujme premennu X_j, ktora udava pocet segmentov pokryvajucich poziciu j
- mozne hodnoty 0..N
- i-ty segment pretina poziciu j s pravdepodobnostou p=L/G
- to iste ako keby sme N krat hodili mincou, na ktorej spadne hlava s pravd. p a znak 1-p a oznacili ako X_j pocet hlav
- Priklad: majme mincu, ktora ma hlavu s pr. 1/4 a hodime je 3x.
HHH 1/64 HHT 3/64 HTH 3/64 HTT 9/64 THH 3/64 THT 9/64 TTH 9/64 TTT 27/64
- P(X_j=3) = 1/64, P(X_j=2)=9/64, P(X_j=1)=27/64, P(X_j=0)=27/64
- taketo rozdelenie pravdepodobnosti sa vola binomicke
- P(X_j = k) = (N choose k) p^k (1-p)^(N-k), kde
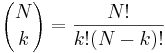 a n! = 1*2*...*n
a n! = 1*2*...*n
- napr pre priklad s troma hodmi kockou P(X_j=2) = 3!/(2!*1!) * (1/4)^2 * (3/4)^1 = 9/64
- Zle sa pocita pre velke N, preto sa niekedy pouziva aproximacia Poissonovym rozdelenim s parametrom lambda = Np, ktore ma
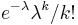
- Spat k sekvenovaniu: vieme spocitat rozdelenie pravdepodobnosti a tiez napr. P(X_i<3) = P(X_i=0)+P(X_i=1)+P(X_i=2) = 0.000045+0.00045+0.0023=0.0028 (v priemere ocakavame 45 baz nepokrytych, 2800 pokrytých menej ako 3 krát)
- Takyto graf, odhad, vieme lahko spravit pre rozne pocty segmentov a tak naplanovat, kolko segmentov potrebujeme
- Chceme tiez odhadnut pocet kontigov (nebrali sme na cviceni, uvedene len pre zaujimavost)
- Ak niekolko baz vobec nie je pokrytych segmentami, prerusi sa kontig
- Vieme, kolko baz je v priemere nepokrytych, ale niektore mozu byt vedla seba
- Novy kontig vznikne aj ak sa susedne segmenty malo prekryvaju
- Predpokladajme, ze na spojenie dvoch segmentov potrebujeme prekryv aspon T
- Lander a Waterman 1988 odhadli, ze dany segment ma pravdepodobnost zhruba exp(-N(L-T)/G), ze bude posledny v kontigu
- Pre N segmentov dostaneme priemerny pocet kontigov N*exp(-N(L-T)/G)
- Ako keby sme dlzku segmentu skratili o dlzku prekryvu
- Pre T=50 dostaneme priemerny pocet kontigov 0.75 (v skutocnosti ide skor o pocet koncov kontigov - ak dostaneme cely kruh, tento pocet je 0, preto dostavame priemer nizsi ako 1)
- ak znizime N na 5000 (5x pokrytie) dostaneme 44 kontigov
- Tento jednoduchy model nepokryva vsetky faktory:
- Segmenty nemaju rovnaku dlzku
- Problemy v zostavovani kvoli chybam, opakovaniam a pod.
- Segmenty nie su rozlozene rovnomerne (cloning bias a pod.)
- Vplyv koncov chromozomov pri linearnych chromozomoch
- Uzitocny ako hruby odhad
- Na spresnenie mozeme skusat spravit zlozitejsie modely, alebo simulovat data
- Poznamka: pravdepodobnosti z binomickeho rozdelenia mozeme lahko spocitat napr. statistickym softverom R. Tu su prikazy, ktore sa na to hodia, pre pripad, ze by vas to zaujimalo:
dbinom(10,1e4,0.001); #(12.5% miest ma pokrytie presne 10) pbinom(10,1e4,0.001,lower.tail=TRUE); #(58% miest ma pokrytie najviac 10) dbinom(0:30,1e4,0.001); #tabulka pravdepodobnosti [1] 4.517335e-05 4.521856e-04 2.262965e-03 7.549258e-03 1.888637e-02 [6] 3.779542e-02 6.302390e-02 9.007019e-02 1.126216e-01 1.251601e-01 [11] 1.251726e-01 1.137933e-01 9.481826e-02 7.292252e-02 5.207187e-02 [16] 3.470068e-02 2.167707e-02 1.274356e-02 7.074795e-03 3.720595e-03 [21] 1.858621e-03 8.841718e-04 4.014538e-04 1.743354e-04 7.254524e-05 [26] 2.897743e-05 1.112843e-05 4.115040e-06 1.467156e-06 5.050044e-07 [31] 1.680146e-07
Zhrnutie
- Pravdedpobnostny model: myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealizovanou kockou
- Vysledok je hodnota, ktoru budeme volat nahodna premenna
- Tabulka, ktora pre kazdu moznu hodnotu nahodnej premennej urci je pravdepodobnost sa vola rozdelenie pravdepodobnosti, sucet hodnot v tabulke je 1
- Znacenie typu P(X=7)=0.1
- Priklad: mame genom dlzky G=1mil., nahodne umiestnime N=10000 segmentov dlzky L=1000
- Nahodna premenna X_i je pocet segmentov pokryvajucich urcitu poziciu i
- Podobne, ako keby sme N krat hodili kocku, ktora ma cca 1 promile sancu padnu ako hlava a 99.9% ako znak a pytame sa, kolko krat padne znak (1 promile sme dostali po zaukruhleni z L/(G-L+1))
- Rozdelenie pravdepobnosti sa v tomto pripade vola binomicke a existuje vzorec, ako ho spocitat
- Takyto model nam moze pomoct urcit, kolko segmentov potrebujeme osekvenovat, aby napr. aspon 95% pozicii bolo pokrytych aspon 4 segmentami
Pravdepodobnosť, cvičenia pre informatikov
Počítanie fylogenetických stromov, cvičenia pre informatikov
- Ako definujeme strom v teorii grafov? suvisly acyklicky neorientovany graf
- Strom s n vrcholmi ma n-1 hran
- Nezakoreneny binarny fylogeneticky strom: neorientovany suvisly acyklicky graf, v listoch sucasne druhy, vsetky vnutorne vrcholy stupna 3
- Zakoreneny binarny fylogeneticky strom: vsetky hrany orientujeme od korena smerom k listom, kazdy vnutorny vrchol ma dve deti
- Niekedy uvazujeme aj nebinarne stromy, v ktorych mame vnutorne vrcholy vyssieho stupna
- Zakoreneny binarny strom s n listami ma n-1 vnutornych vrcholov, teda 2n-2 hran
- Nezakoreneny binarny strom s n listami ma n-2 vnutornych vrcholov, teda 2n-3 hran
- Pocet nezakorenenych fylogenetickych stromov s n listami:
- a(3) = 1, a(4) = 3, a(n+1) = a(n) * (2n-3) a teda a(n) = 1 * 3 * 5 * ... * (2n-5) = (2n-5)!!
- Pocet zakorenenych fylogenetickych stromov s n listami:
- zakoren strom s n listami kazdy 2n-3 sposobmi, teda (2n-3)!!
Uvod do pravdepodobnosti
- Myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealnou kockou/korunou
- Vysledkom experimentu je nejaka hodnota (napr. cislo, alebo aj niekolko cisel, retazec)
- Tuto neznamu hodnotu budeme volat nahodna premenna
- Zaujima nas pravdepodobnost, s akou nahodna premenna nadobuda jednotlive mozne hodnoty
- T.j. ak experiment opakujeme vela krat, ako casto uvidime nejaky vysledok
- Priklad 1: hodime idealizovanou kockou, premenna X bude hodnota, ktoru dostaneme
- Mozne hodnoty 1,2,..,6, kazda rovnako pravdepodobna
- Piseme napr. Pr(X=2)=1/6
- Priklad 2: hodime 2x kockou, nahodna premenna X bude sucet hodnot, ktore dostaneme
- Mozne hodnoty: 2,3,...,12
- Kazda dvojica hodnot na kocke rovnako pravdepodobna, t.j. pr. 1/36
- Sucet 5 mozeme dostat 1+4,2+3,3+2,4+1 - t.j. P(X=5) = 4/36
- Sucet 11 mozeme dostat 5+6 alebo 6+5, t.j. P(X=11) = 2/36
- Rozdelenie pravdepodobnosti: (tabulka udavajuca pravdepodobnost pre kazdu moznu hodnotu)
hodnota i: 2 3 4 5 6 7 8 9 10 11 12 Pr(X=i): 1/36 2/36 3/36 4/36 5/36 6/36 5/36 5/36 6/36 5/36 1/36
- Overte, ze sucet pravdepodobnosti je 1
- Stredna hodnota E(X):
- priemer z moznych hodnot vahovanych ich pravdepodobnostami
- v nasom priklade
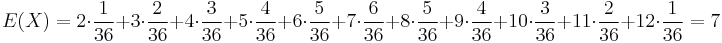
- Ak by sme experiment opakovali vela krat a zratali priemer hodnot X, ktore nam vysli, dostali by sme cislo blizke E(X)
- Iny vypocet strednej hodnoty:
- X=X1+X2, kde X1 je hodnota na prvej kocke a X2 je hodnota na druhej kocke
-
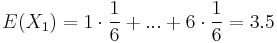 , podobne aj E(X2) = 3.5
, podobne aj E(X2) = 3.5
- Plati, ze E(X1+X2)=E(X1) + E(X2) a teda E(X) = 3.5 + 3.5 = 7
- Pozor, pre sucin a ine funkcie taketo vztahy platit nemusia, napr.
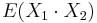 nie je vzdy
nie je vzdy 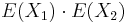
Pravdepodobnostny model nahodnej sekvencie
- Napriklad chceme modelovat nahodnu DNA sekvenciu dlzky n s obsahom GC 40%
- Mame vrece s gulockami oznacenyni A,C,G,T, pricom gulocok oznacenych A je 30%, C 20%, G 20% a T 30%.
- Vytiahneme gulicku, zapiseme si pismeno, hodime ju naspat, zamiesame a opakujeme s dalsim pismenom atd az kym nevygenerujeme n pismen
- Vytiahnime z mechu 2x gulicku. Prve pismeno ktore nam vyjde oznacme X1 a druhe X2
- Pr(X1=A) = 0.3, Pr(X2=C)=0.2
- Pr(X1=A a X2=C) = Pr(X1=A)*Pr(X2=C) = 0.3*0.2 = 0.06
- T.j. sanca ze dostaneme sekvenciu AC po dvoch tahaniach je 6%
- Ak ratame pravdepodobnost, ze sa dve nezavisle udalosti stanu, ich pravdepodobnosti nasobime. V tomto pripade to ci X1=A je nezavisle od toho, ci X2=C
- Pr(X1 je A alebo G) = Pr(X1=A)+Pr(X1=G) = 0.3+0.2 = 0.5
- Pravdepodobnost ze prve pismeno bude A alebo G je 50%
- Pravdepodobnosti navzajom sa vylucujucich udalosti (X1=A a X1=G) sa mozu scitat, cim dostaneme pravdepodobnost, ze aspon jedna z nich nastane
- Pr(X1 je A alebo X2 je G) nemozeme pocitat ako Pr(X1=A)+Pr(X2=G), lebo sa navzajom nevylucuju a pripad ze X1=A a X2=G by sme zapocitali dvakrat
- Spravne je Pr(v sekvencii je aspon jedno A) = Pr(X1=A) + Pr(X1 <> A a X2=G) = Pr(X1=A) + Pr(X1 <> A) * Pr(X2=G) 0.3+0.7*0.2 = 0.44
- Podobne napr Pr(v sekvencii je aspon jedno A) = Pr(X1=A alebo X2=A) = Pr(X1=A) + Pr(X1 <> A a X2=A) = Pr(X1=A) + Pr(X1 <> A) * Pr(X2=A) 0.3+0.7*0.3 = 0.51
- Pr(X1=X2) = Pr(X1=X2=A) + Pr(X1=X2=C) + Pr(X1=X2=G) + Pr(X1=X2=T) = 0.3*0.3+0.2*0.2+0.2*0.2+0.3*0.3 = 0.26.
- Ak u označíme pravdepodobnost u = Pr(X1=A)=Pr(X1=T)=Pr(X2=A)=Pr(X2=T) a v=Pr(X1=C)=Pr(X1=G)=Pr(X2=C)=Pr(X2=G), aky bude vzorec na Pr(X1=X2)?
E-hodnota (E-value) zarovnania
- Priklady k tejto casti v prezentacii [4]
- Mame dotaz dlzky m, databazu dlzky n, skore najlepsieho lok. zarovnania S
- E-value je ocakavany pocet zarovnani so skore aspon S ak dotaz aj databaza su nahodne
- Hrackarsky priklad: dotaz dlzky m=4, databaza dlzky n=200, S=4, t.j. presny vyskyt dotazu v databaze (pre presne vyskyty sa pravdepodobnosti pocitaju ovela lahsie ako ked dovolime nezhody a medzery)
- Zoberme nas nahodny model s obsahom GC 40%
- Mame vrece s gulockami oznacenyni A,C,G,T, pricom gulocok oznacenych A je 30%, C 20%, G 20% a T 30%.
- Vytiahneme gulicku, zapiseme si pismeno, hodime ju naspat, zamiesame a opakujeme s dalsim pismenom atd az kym nevygenerujeme m pismen pre dotaz a n pismen pre databazu
- Pre nase vygenerovane sekvencie spocitame, kolkokrat sa dotaz vyskytuje v databaze
- Cely experiment opakujeme vela krat a spocitame priemerny pocet vyskytov, co bude odhad E-value
- Vieme spocitat aj presne:
- Mame dotaz X1X2...Xm a databazu Y1Y2...Yn. Aka je sanca, ze X sa nachadza na zaciatku Y, t.j. ze X1=Y1, X2=2... Xm=Ym?
- Pripominame, ze pravdepodobnost zhody dvoch nukelotidov napr X1 a Y1 je Pr(X1=Y1) = Pr(X1=Y1=A) + Pr(X1=Y1=C) + Pr(X1=Y1=G) + Pr(X1=Y1=T) = 0.3*0.3+0.2*0.2+0.2*0.2+0.3*0.3 = 0.26.
- Pre rozne pozicie v X mame nezavisle udalosti, t.j. pravdepodobnost vyskytu X na prvej pozicii je Pr(X1=Y1)*Pr(X2=Y2)*...*Pr(Xm=Ym) = 0.26 * 0.26 * ... * 0.26 = 0.26^m (0.26 na m-tu)
- Tak isto nam vyjde aj pravdepodobnost vyskytu X na hociktorej inej pevnej pozicii v Y
- Pravdepodobnost, ze sa X nachadza na aspon jednej pozicii v Y je tazsie zratat - moze sa vyskytovat aj viackrat, udalosti ze sa nachadza na pozicii i sa navzajom nevylucuju
- Ale priemerny pocet vyskytov na pozicii i je 0.26^m, mame n-m+1 pozicii zaciatku, takze celkovy ocakavany pocet vyskytov je (n-m+1)0.26^m
- Toto je stredna hodnota nahodnej premennej C, ktora oznacuje pocet presnych vyskytov
- E(C) = E(C_1)+E(C_2)+...E(C_(n-m+1)), kde C_i je nahodna premenna, ktora je 1 ak sa X nachadza na pozicii i v Y
- E(C_i) = 0.26^m
- Ak je n velke v porovnani s m, clen -m+1 mozeme zanedbat, t.j. mame zhruba n*0.26^m
- Ako sa meni toto cislo s velkostou databazy n? linearne rastie (zdvojnasobime databazu, zdvojnasobi sa e-value)
- Ako sa meni s m? Exponencialne klesa, t.j. ak predlzime dotaz o 1, E-value klesne zhruba na stvrtinu
- Ako sa meni s GC obsahom? Zakodovane v cisle 0.26 - mozete si vyskusat v tabuľkovom procesore (nerobili sme)
- Stiahnite si subor [5], ulozte si ho a otvorte v openoffice
- Do zlteho policka vyplnte vzorec na vypocet pravdepodobnosti zhody medzi dvoma nahodne vygenerovanymi nukleotidmi v zacislosti od %GC v stlpci A.
- Vzorce v stlpcoch B-F nakopirujte do vsetkych riadkoch tabulky (napr dvojitym pokopanim na svtorcek v pravom dolnom roku okienka)
- Ako sa meni E-value v zavislosti od GC (hodnoty v modrom stlpci F)? Preco je to tak? Mozete si nakreslit aj graf.
- Potom skusajte menit hodnoty m a n a vsimnite si, ci maju taky vplyv na e-value, ako sme vraveli
Pouzitie pravdepodobnosti na analyzu potrebneho pokrytia pri sekvenovani
- Pozrite tiez grafy k pravdepodobnosti: http://compbio.fmph.uniba.sk/vyuka/mbi/poznamky/ci02.pdf
- Nas problem: spocitanie pokrytia
- G = dlzka genomu, napr. 1 000 000 (predpokladajme, že je cirkulárny)
- N = pocet segmentov (readov), napr. 10 000
- L = dlzka readu, napr. 1000
- Celkova dlzka segmentov NL, pokrytie (coverage) NL/G, v nasom pripade 10x
- V priemere kazda baza pokryta 10x
- Niektore su ale pokryte viackrat, ine menej.
- Zaujimaju nas otazky typu: kolko baz ocakavame, ze bude pokrytych menej ako 3x?
- Dolezite pri planovani experimentov (ake velke pokrytie potrebujem na dosiahnutie urcitej kvality)
- Pokrytie genomu: predpokladame, ze kazdy segment zacina na nahodnej pozicii zo vsetkych moznych G
- Takze ak premenna Y_i bude zaciatok i-teho segmentu, jej rozdelenie bude rovnomerne
- P(Y_i=1) = P(Y_i=2) = ... = P(Y_i=G) = 1/G
- Aka je pravdepodobnost ze nejaky konkretny i-ty segment pokryva konkretnu poziciu j?
- P(Y_i>=j-L+1 and Y_i<=j) = P(Y_i=j-L+1)+...+P(Y_i=j) = L/G, oznacme tuto hodnotu p, nasom priklade p=0.001 (1 promile)
- Uvazujme premennu X_j, ktora udava pocet segmentov pokryvajucich poziciu j
- mozne hodnoty 0..N
- i-ty segment pretina poziciu j s pravdepodobnostou p=L/G
- to iste ako keby sme N krat hodili mincou, na ktorej spadne hlava s pravd. p a znak 1-p a oznacili ako X_j pocet hlav
- Priklad: majme mincu, ktora ma hlavu s pr. 1/4 a hodime je 3x.
HHH 1/64 HHT 3/64 HTH 3/64 HTT 9/64 THH 3/64 THT 9/64 TTH 9/64 TTT 27/64
- P(X_j=3) = 1/64, P(X_j=2)=9/64, P(X_j=1)=27/64, P(X_j=0)=27/64
- taketo rozdelenie pravdepodobnosti sa vola binomicke
- P(X_j = k) = (N choose k) p^k (1-p)^(N-k), kde
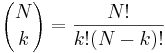 a n! = 1*2*...*n
a n! = 1*2*...*n
- napr pre priklad s troma hodmi kockou P(X_j=2) = 3!/(2!*1!) * (1/4)^2 * (3/4)^1 = 9/64
- Zle sa pocita pre velke N, preto sa niekedy pouziva aproximacia Poissonovym rozdelenim s parametrom lambda = Np, ktore ma
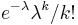
- Spat k sekvenovaniu: vieme spocitat rozdelenie pravdepodobnosti a tiez napr. P(X_i<3) = P(X_i=0)+P(X_i=1)+P(X_i=2) = 0.000045+0.00045+0.0023=0.0028 (v priemere ocakavame 45 baz nepokrytych, 2800 pokrytých menej ako 3 krát)
- Takyto graf, odhad, vieme lahko spravit pre rozne pocty segmentov a tak naplanovat, kolko segmentov potrebujeme
- Chceme tiez odhadnut pocet kontigov (podla clanku Lander a Waterman 1988) (nerobili sme)
- Ak niekolko baz vobec nie je pokrytych segmentami, prerusi sa kontig
- Vieme, kolko baz je v priemere nepokrytych, ale niektore mozu byt vedla seba
- Novy kontig vznikne aj ak sa susedne segmenty malo prekryvaju
- Predpokladajme, ze na spojenie dvoch segmentov potrebujeme prekryv aspon T=50
- Aka je pravdepodobnost, ze dany segment i bude posledny v kontigu?
- Ziaden segment j!=i nesmie zacinat v prvych L-T bazach kontigu i
- Kazdy segment tam zacina s pravdepodobnostou (L-T)/G, v priemere ich tam zacne N(L-T)/G
- Pouzijeme Poissonovo rozdelenie pre
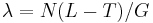 a k=0, t.j. pravdepodobnost, ze tam nezacne ziaden je zhruba exp(-N(L-T)/G)
a k=0, t.j. pravdepodobnost, ze tam nezacne ziaden je zhruba exp(-N(L-T)/G)
- Pre N segmentov dostaneme priemerny pocet kontigov N*exp(-N(L-T)/G)
- Ako keby sme dlzku segmentu skratili o dlzku prekryvu
- Pre T=50 dostaneme priemerny pocet koncov kontigov 0.75 (ak pokryjeme cely kruh, mame nula koncov, preto je hodnota mensia ako 1). Ak znizime N na 5000 (5x pokrytie) dostaneme 43 kontigov
- Moze sa zdat zvlastne, ze pri priemernom pocte nepokrytych baz 45 mame pocet koncov v priemere menej ako jedna. Situacia je vsak taka, ze pri opakovaniach tohto experimentu casto dostavame jeden suvisly kontig, ale ak je uz aspon jeden koniec kontigu, byva tam pomerne velka medzera. Tu je napriklad 50 opakovani expertimentu s T=0, priemerny pocet koncov je 0.55, priemerny pocet nepokrytych baz je 49.
empty: 0 last: 0 empty: 0 last: 0 empty: 0 last: 0 empty: 274 last: 2 empty: 282 last: 1 empty: 0 last: 0 empty: 0 last: 0 empty: 0 last: 0 empty: 8 last: 1 empty: 0 last: 0 empty: 12 last: 1 empty: 0 last: 0 empty: 122 last: 1 empty: 135 last: 1 empty: 111 last: 1 empty: 13 last: 1 empty: 1 last: 1 empty: 56 last: 1 empty: 265 last: 1 empty: 0 last: 0 empty: 10 last: 1 empty: 0 last: 0 empty: 0 last: 0 empty: 130 last: 1 empty: 217 last: 1 empty: 3 last: 1 empty: 0 last: 0 empty: 0 last: 0 empty: 0 last: 0 empty: 86 last: 1 empty: 139 last: 2 empty: 0 last: 0 empty: 0 last: 0 empty: 76 last: 1 empty: 221 last: 1 empty: 26 last: 1 empty: 0 last: 0 empty: 1 last: 1 empty: 0 last: 0 empty: 0 last: 0 empty: 0 last: 0 empty: 0 last: 0 empty: 0 last: 0 empty: 0 last: 0 empty: 12 last: 1 empty: 103 last: 2 empty: 0 last: 0 empty: 71 last: 1 empty: 69 last: 1 empty: 0 last: 0
- Tento jednoduchy model nepokryva vsetky faktory:
- Segmenty nemaju rovnaku dlzku
- Problemy v zostavovani kvoli chybam, opakovaniam a pod.
- Segmenty nie su rozlozene rovnomerne (cloning bias a pod.)
- Vplyv koncov chromozomov pri linearnych chromozomoch
- Uzitocny ako hruby odhad
- Na spresnenie mozeme skusat spravit zlozitejsie modely, alebo simulovat data
- Poznamka: pravdepodobnosti z binomickeho rozdelenia mozeme lahko spocitat napr. statistickym softverom R. Tu su prikazy, ktore sa na to hodia, pre pripad, ze by vas to zaujimalo:
dbinom(10,1e4,0.001); #(12.5% miest ma pokrytie presne 10) pbinom(10,1e4,0.001,lower.tail=TRUE); #(58% miest ma pokrytie najviac 10) dbinom(0:30,1e4,0.001); #tabulka pravdepodobnosti [1] 4.517335e-05 4.521856e-04 2.262965e-03 7.549258e-03 1.888637e-02 [6] 3.779542e-02 6.302390e-02 9.007019e-02 1.126216e-01 1.251601e-01 [11] 1.251726e-01 1.137933e-01 9.481826e-02 7.292252e-02 5.207187e-02 [16] 3.470068e-02 2.167707e-02 1.274356e-02 7.074795e-03 3.720595e-03 [21] 1.858621e-03 8.841718e-04 4.014538e-04 1.743354e-04 7.254524e-05 [26] 2.897743e-05 1.112843e-05 4.115040e-06 1.467156e-06 5.050044e-07 [31] 1.680146e-07
Zhrnutie
- Pravdedpobnostny model: myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealizovanou kockou
- Vysledok je hodnota, ktoru budeme volat nahodna premenna
- Tabulka, ktora pre kazdu moznu hodnotu nahodnej premennej urci je pravdepodobnost sa vola rozdelenie pravdepodobnosti, sucet hodnot v tabulke je 1
- Znacenie typu P(X=7)=0.1
- Priklad: mame genom dlzky G=1mil., nahodne umiestnime N=10000 segmentov dlzky L=1000
- Nahodna premenna X_i je pocet segmentov pokryvajucich urcitu poziciu i
- Podobne, ako keby sme N krat hodili kocku, ktora ma cca 1 promile sancu padnu ako hlava a 99.9% ako znak a pytame sa, kolko krat padne znak (1 promile sme dostali po zaukruhleni z L/(G-L+1))
- Rozdelenie pravdepobnosti sa v tomto pripade vola binomicke a existuje vzorec, ako ho spocitat
- Takyto model nam moze pomoct urcit, kolko segmentov potrebujeme osekvenovat, aby napr. aspon 95% pozicii bolo pokrytych aspon 4 segmentami
Fylogenetické stromy, cvičenia pre biológov
Fylogeneticke stromy
- Terminologia: zakoreneny/nezakoreneny strom, hrana, vrchol, list, vnutorny vrchol, koren
- Ak mame zakoreneny strom s n listami a kazdy vnutorny vrchol ma 2 deti, bude mat n-1 vnutornych vrcholov (preco?)
- V nezakorenenom strome s n listami, ak ma kazdy vrchol 3 susedov, bude mat n-2 vnutornych vrcholov
- Kolkymi sposobmi mozeme zakorenit nezakoreneny strom?
- Ak nakreslime zakoreneny strom obvyklym sposobom, listy su usporiadane zhora nadol. Kolko roznych poradi listov vieme dostat roznym zakreslovanim toho isteho stromu? Kolko je vobec roznych poradi listov, ak neberieme do uvahy strom?
- Co vieme zistit o pribuznosti organizmov z nezakoreneneho stromu (napr. kvartet 4 organizmov)?
- Ine pouzitie stromov v informatike: uvidime hierarchicke clustrovanie, bayesovske siete, ale tiez efektivne datove struktury
Bootstrap
- Nahodne vyberieme niektore stlpce zarovnania, zostrojime strom vybranou metodou
- Cele to opakujeme vela krat
- Znacime si, kolkokrat sa ktora vetva opakuje v stromoch, ktore dostavame
- Pri nezakoreneneych stromoch je vetva rozdelenie listov na dve skupiny
- Nakoniec zostavime strom z celych dat a pozrieme sa ako casto sa ktora jeho vetva vyskytovala
- Mozeme zostavit aj strom casto sa vyskytujucich hran (napr tych, ktore su vo viac ako 50% stromov)
- Bootstrap hodnoty nam daju urcity odhad spolahlivosti, hlavne ak mame celkovo malo dat (kratke zarovnanie)
- Ak vsak data velmi dobre nezodpovedaju vybranej metode tak aj pre zly strom mozeme dostat vysoky bootstrap
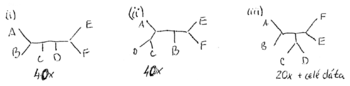
Priklad
- Robili sme 100x bootstrap, 40x sme dostali strom (i) na obrazku, 40x sme dostali strom (ii) a 20x sme dostali strom (iii)
- Strom (iii) sme dostali aj spustenim metody na celych datach
- Zistite uroven bootstrap podpory pre jednotlive vetvy stromu (iii)
- Ktore dalsie biparticie maju podporu aspon 20%?
- Aky strom by sme dostali, ak by sme chceli nechat iba vetvy s podporou aspon 80%?
Prakticka ukazka tvorby stromov
- V UCSC browseri mozeme ziskavat viacnasobne zarovnania jednotlivych genov (nukleotidy alebo proteiny). Nasledujuci postup nemusite robit, subor si stiahnite tu: http://compbio.fmph.uniba.sk/vyuka/mbi/poznamky/cb06/cb06-aln.fa
- UCSC browseri si pozrieme usek ludskeho genomu chr6:136,214,527-136,558,402 s genom PDE7B (phosphodiesterase 7B)
- Na modrej liste zvolime Tools, Table browser. V nastaveniach tabuliek Track: RefSeq genes, zaklikneme Region: position, a Output fomat: CDS FASTA alignment a stlacime Get output
- Na dalsej obrazovke zaklikneme show nucleotides. Z primatov zvolime chimp, rhesus, tarsier, z inych cicavcov mouse, rat, dog, elephant a z dalsich organizmov opposum, platypus, chicken, lizard, stlacime Get output.
- Vystup ulozime do suboru, nechame si iba prvu formu genu, z mien sekvencii zmazeme spolocny prefix NM_018945_, pripadne celkovo prepiseme mena na anglicke nazvy,
- Skusme zostavit strom na stranke http://mobyle.pasteur.fr/cgi-bin/portal.py
- Pouzijeme program quicktree, metodu neighbor joining, bootstrap 100
- Na zobrazenie stromu vysledok dalej prezenieme cez zobrazovacie programy drawtree alebo newicktops (zvolit v menu pri tlacidle further analysis)
- Vysledok z drawtree, nezakoreneny, nezobrazuje bootstrap hodnoty
- Vysledok z newicktops, zakoreneny na nahodnom mieste (nie spravne) zobrazuje bootstrap hodnoty
- v drawtree sme nastavili sme formát výstupu MS-Windows Bitmap a X,Y resolution aspoň 1000, v newicktops sme nastavili show bootstrap values
- "Spravny strom" [6] v nastaveniach Conservation track-u v UCSC browseri (podla clanku Murphy WJ, Eizirik E, O'Brien SJ, Madsen O, Scally M, Douady CJ, Teeling E, Ryder OA, Stanhope MJ, de Jong WW, Springer MS. Resolution of the early placental mammal radiation using Bayesian phylogenetics. Science. 2001 Dec 14;294(5550):2348-51.)
- Nas strom ma long branch attraction (zle postavenie hlodavcov, ktori maju dlhu vetvu aj slona, co moze byt zapricene sekvenovacimi chybami).
- Ine programy, ktore mozete skusit na mobyle
- phyml: metoda maximalnej vierohodnosti (daju sa nastavit detaily modelu, bootstraps, ktory ale moze dost dlho trvat, typy operacii na strome pri heuristickom hladani najlepsieho stromu)
- dnapars alebo protpars na parsimony
- viacnasobne zarovnanie pomocou clustalw alebo modernejsou alternativou muscle
- Ak chcete skusat zarovnania, zacnite z nezarovnanych sekvencii: http://compbio.fmph.uniba.sk/vyuka/mbi/poznamky/cb06/cb06-seq.fa
Evolúcia, cvičenia pre informatikov
Felsensteinov algoritmus 1981
- Mame dany strom T s dlzkami hran a bazy v listoch (jeden stlpec zarovnania) a maticu rychlosti R. Spocitajme pravdepodobnost, ze z modelu dostaneme prave tuto kombinaciu baz v listoch.
- Nech X_v je premenna reprezentujuca bazu vo vrchole v a nech x_v je konkretna baza v liste v. Nech listy su 1..n a vnut. vrcholy n+1..2n-1. Nech dlzka hrany z v do rodica je t_v. Nech P(a|b,t) je pravdepodobnost, ze b sa zmeni na a za cas t (spocitame z matice R, uvidime neskor ako). Nech q_a je pravdepodobnost bazy a v koreni (ekvilibrium matice R)
- Napr. v Jukes-Cantorovom modeli
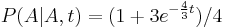 ,
, 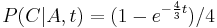
- Chceme pravdepodobnost
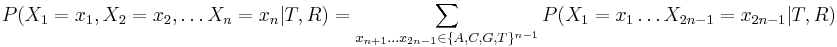
- Spocitame rychlejsie dynamickym programovanim.
- Nech A[v,a] je pravdepodobnost dat v podstrome s vrcholom v ak X_v=a
- A[v,a] pocitame od listov ku korenu
- v liste A[v,a] = [a=x_v]
- Vo vnut. vrchole s detmi x a y mame
![A[v,a]=\sum _{{b,c}}A[x,b]A[y,c]P(b|a,t_{x})P(c|a,t_{y})](/vyuka/mbi/images/math/3/9/4/39459db83d38746a33e427169d62d215.png)
- Celkova pravdepodobnost je
![P(X_{1}=x_{1},X_{2}=x_{2},\dots X_{n}=x_{n}|T,R)=\sum _{a}A[r,a]q_{a}](/vyuka/mbi/images/math/3/0/d/30d167737e880c69f2a1cd08a5dfc5a5.png) pre koren r.
pre koren r.
Zlozitost, zlepsenie
- Zlozitost
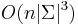
- Pre nebinarne stromy exponencialne
- Zlepsenie
![A[v,a]=(\sum _{{b}}A[x,b]P(b|a,t_{x}))(\sum _{c}A[y,c](c|a,t_{y}))](/vyuka/mbi/images/math/9/3/a/93a8ecffd2e352290f8d57ddc469bb66.png)
- Zlozitost
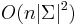 aj pre nebinarne stromy
aj pre nebinarne stromy
Chybajuce data
- Ak v niektorom liste mame neznamu bazu N, nastavime A[v,a]=1
- Podobne sa spracovavaju medzery v zarovnani, aj ked mohli by sme mat aj model explicitne ich modelujuci
Aposteriorna pravdepodobnost
- Co ak chceme spocitat pravdepodobnost P(X_v=a|X_1=x_1, X_2=x_2,\dots X_n=x_n,T,R)? Zaujimaju nas teda sekvencie genomov predkov.
- Potrebujeme B[v,a]=pravdpodobnost dat ak podstrom v nahradim listom s bazou a.
- B[v,a] pocitame od korena k listom
- V koreni B[v,a] = q_a
- Vo vrchole v s rodicom u a surodencom x mame
![B[v,a]=\sum _{{b,c}}B[u,b]A[x,c]P(a|b,t_{v})P(c|b,t_{v})](/vyuka/mbi/images/math/0/4/c/04cc0bf38cc6bbf3b4ddf7ce0e346560.png)
- Ziadana pravdepodobnost je
![B[v,a]A[v,a]/P(X_{1}=x_{1},X_{2}=x_{2},\dots X_{n}=x_{n}|T,R)](/vyuka/mbi/images/math/c/c/2/cc2c38f95bb6131cc0a4edfdc7db8bdb.png)
Substitucne modely - odvodenie
- Nech
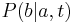 je pravdepodobnost, ze ak zacneme s bazou a, tak po case t budeme mat bazu b.
je pravdepodobnost, ze ak zacneme s bazou a, tak po case t budeme mat bazu b.
- Pre dane t mozeme take pravdepodobnosti usporiadat do matice 4x4 (ak studujeme DNA), kde
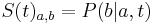
- Intuitivne cim vacsie t, tym vacsia pravdepodobnost zmeny;
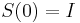 (jednotkova matica),
(jednotkova matica), 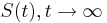 ma vsetky riadky rovnake, napr. 1/4, 1/4, 1/4, 1/4
ma vsetky riadky rovnake, napr. 1/4, 1/4, 1/4, 1/4
- Ak mame matice pre casy
 a
a  , vieme spocitat maticu pre cas
, vieme spocitat maticu pre cas  :
:  a teda v maticovej notacii
a teda v maticovej notacii 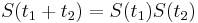 . Takyto model nazyvame multiplikativny a predpoklada, ze pravdepodobnost mutacie zavisi len od aktualnej bazy, nie od minulych stavov.
. Takyto model nazyvame multiplikativny a predpoklada, ze pravdepodobnost mutacie zavisi len od aktualnej bazy, nie od minulych stavov.
- Ak by sme uvazovali iba diskretne (celocislene) casy, stacilo by nam urcit iba
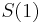 a vsetky ostatne casy dostaneme umocnenim tejto matice. Je vsak elegantnejsie mat
a vsetky ostatne casy dostaneme umocnenim tejto matice. Je vsak elegantnejsie mat 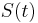 definovane aj pre realne t.
definovane aj pre realne t.
- Jukes-Cantor-ov model evolucie predpoklada, ze vsetky substitucie su rovnako pravdepodobne.
- Pre velmi maly cas mame maticu
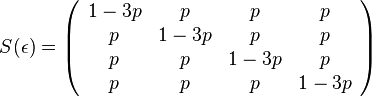
- kde
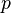 je tiez velmi male cislo.
je tiez velmi male cislo.
- Pre cas
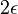 dostavame maticu
dostavame maticu
- Ale cleny s
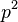 su ovela mensie ako cleny s
su ovela mensie ako cleny s 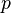 , takze tato matica je priblizne
, takze tato matica je priblizne
- Vytvorme si teraz maticu rychlosti (rate matrix), kde
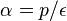
- Dostavame, ze pre velmi male casy plati
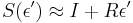 (skusme dosadit
(skusme dosadit 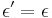 ,
, 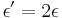 ...)
...)
-
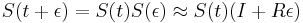 a teda
a teda 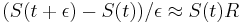 a v limite pre
a v limite pre 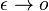 dostavame
dostavame 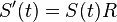 (diferencialne rovnice, pociatocny stav
(diferencialne rovnice, pociatocny stav 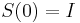 ).
).
- Ak diagonalne prvky
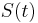 oznacime
oznacime 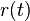 a nediagonalne
a nediagonalne 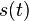 , nasobenim matic S(t)R dostavame, ze diagonalny prvok
, nasobenim matic S(t)R dostavame, ze diagonalny prvok 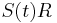 je
je 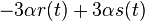 a nediagonalny
a nediagonalny 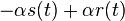 . Takze dostavame diferencialne rovnice
. Takze dostavame diferencialne rovnice 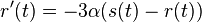 a
a 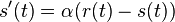 .
.
-
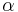 je teda pravdepodobnost zmeny za jednotku casu, ak uvazujeme velmi kratke casy alebo derivacia prvku S(t) vzhladom na t v bode 0
je teda pravdepodobnost zmeny za jednotku casu, ak uvazujeme velmi kratke casy alebo derivacia prvku S(t) vzhladom na t v bode 0
- Overme, ze riesenim tejto rovnice je
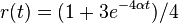 a
a 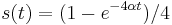 :
:
- Zderivujeme
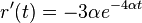 a
a 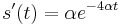 , dosadime do rovnic.
, dosadime do rovnic.
- Zderivujeme
- Takze mame maticu:
- Ked
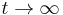 , dostavame 1/4.
, dostavame 1/4.
- V case
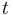 je pravdepodobnost, ze uvidime zmenenu bazu
je pravdepodobnost, ze uvidime zmenenu bazu 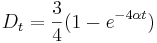 a teda ak v skutocnosti vidime
a teda ak v skutocnosti vidime 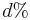 zmenenych baz, vieme spatne zratat t, ktore by hodnote
zmenenych baz, vieme spatne zratat t, ktore by hodnote 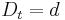 prinalezalo.
prinalezalo.
- Aby sme nemali naraz aj
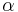 aj
aj 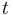 , zvykneme maticu R normalizovat tak, aby priemerny pocet substitucii za jednotku casu bol 1. V pripade Jukes-Cantorovho modelu je to ked
, zvykneme maticu R normalizovat tak, aby priemerny pocet substitucii za jednotku casu bol 1. V pripade Jukes-Cantorovho modelu je to ked 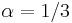 .
.
- Dostavame teda vzorec pre vzdialenost, ktory sme videli na prednaske
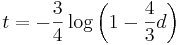
- Ak
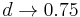 , dostavame
, dostavame 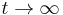
- Preco sme ten vzorec odvodili takto? V skutocnosti chceme najst najvierohodnejsiu hodnotu t, t.j. taku, pre ktore hodnota P(data|t) bude najvacsia. Zhodou okolnosti vyjde takto.
Zlozitejsie modely
- V praxi sa pouzivaju komplikovanejsie substitucne modely, ktore maju vseobecnejsiu maticu rychlosti R
-
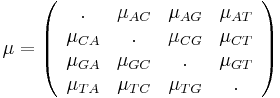
Hodnoty na diagonále matice sa dopočítavajú aby sucet kazdeho riadku bol 0.
- Hodnota
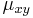 v tejto matici vyjadruje rýchlosť, akou sa určitá báza x mení na inú bázu y.
v tejto matici vyjadruje rýchlosť, akou sa určitá báza x mení na inú bázu y.
- Presnejsie
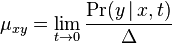 .
.
- Kimurov model napr. zachytava, ze puriny sa castejsie menia na ine puriny (A a G) a pyrimidiny na ine pyrimidiny (C a T) ma dva parametre:
- rychlost tranzicii beta, tranzverii alfa
- HKY model (Hasegawa, Kishino & Yano) tiez umoznuje rozne pravdepodobnosti A, C, G a T v ekvilibriu.
- Parameter kapa: pomer tranzicii a transverzii (beta/alfa)
- Ak nastavíme čas v evolučnom modeli na nekonečno, nezáleží na tom, zktorej bázy sme začali, Frekvencia výskytu jednotlivých báz sa ustáli v tzv. ekvilibriu.
- V Jukes-Cantorovom modeli je pravdepodobnosť ľubovoľnej bázy v ekvilibriu 1/4.
- V HKY si zvolime aj frekvencie jednotlivých nukleotidov v ekvilibriu
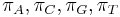 so suctom 1
so suctom 1
- Matica rychlosti:
-
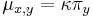 ak ak mutácia x->y je tranzícia,
ak ak mutácia x->y je tranzícia,
-
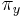 ak mutácia x->y je transverzia
ak mutácia x->y je transverzia
-
- Vo vseobecnosti pre maticu rychlosti
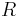 dostavame
dostavame 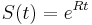 . Ak R diagonalizujeme (urcite sa da pre symetricke R)
. Ak R diagonalizujeme (urcite sa da pre symetricke R) 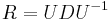 , kde D je diagonalna matica (na jej diagonale budu vlastne hodnoty R), tak
, kde D je diagonalna matica (na jej diagonale budu vlastne hodnoty R), tak 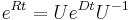 , t.j. exponencialnu funkciu uplatnime iba na prvky na uhlopriecke matice D.
, t.j. exponencialnu funkciu uplatnime iba na prvky na uhlopriecke matice D.
Evolúcia, cvičenia pre biológov
Fitchov algoritmus
- Parsimony/uspornost
- Vstup: fylogeneticky strom, 1 stlpec zarovnania (jedna baza v kazdom liste stromu)
- Vystup: priradenie baz predkom minimalizujuce pocet substitucii
- Priklad - obr 1
- Uvazujme, co vieme povedat o strome s dvoma susednymi listami vo vacsom strome (oznacenie: obr. 2, listy v1 a v2, hrany do listov e1, e2, ich predok v3, hrana z v3 vyssie e3).
- Ak oba listy maju bazu rovanku bazu, napr. A, predok v3 v optimalnom rieseni bude urcite mat bazu A
- Dokaz sporom: nech to tak nie je, nech optimalne riesenie ma nejaku inu bazu, napr. C. Vymenme v tomto rieseni toto C za A. Moze nam pribudnut jedna mutacia na hrane e3, ale ubudnu dve na hranach e1 a e2. Tym celkova cena riesenia klesne o 1, takze nebolo optimalne.
- Ak tieto dva listy maju rozne bazy, napr. A a C, tak existuje optimalne riesenie, ktore ma v predkovi v3 bazu A alebo C.
- Dokaz: vezmime optimalne riesenie. Ak ma v3 bazu A alebo C, tvrdenie plati. Ak ma v3 nejaku inu bazu, napr T, mozeme ju vymenit napr. za A, ci mozno pribudne jedna mutacia na e3 ale urcite ubudne mutacia na e1. Teda celkovy pocet mutacii sa nezvysi a nase nove riesenie je stale optimalne. Pozor, vo vseobecnosti nevieme povedat, ci ma v3 mat bazu A alebo C. V niektorych pripadoch su optimalne obe, v niektorych len jedna z nich.
- Fitchov algoritmus 1971
- Kazdemu vrcholu v priradime mnozinu baz M(v)
- M(v) pocitame od listov smerom ku korenu
- Pre list v bude M(v) obsahovat bazu v tomto liste
- Uvazujme vnutorny vrchol v s detmi x a y. Mame uz spocitane M(x) a M(y), chceme M(v)
- Ak M(x) a M(y) maju nejake spolocne bazy, vsetky tieto spolocne bazy dame do M(v), t.j.
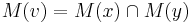
- Ak M(x) a M(y) nemaju spolocne bazy, do M(v) dame vsetky bazy z M(x) aj M(v), t.j.
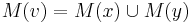
- V tomto pripade pocet mutacii vzrastie o jedna
- Ked mame M(v) spocitane pre vsetky vrcholy, ideme od korena smerom k listom a vyberieme vzdy jednu bazu z M(v).
- Ak sme vybrali pre rodica bazu x a x je v M(v), zvolime x aj pre v, inak zvolime lubovolnu bazu z M(v).
- Priklad algoritmu na obr 3
Opakovanie pravdepodobnostnych modelov
Ake sme doteraz videli modely
- E-value v BLASTe: nahodne vygenerujeme databazu a dotaz (query), kolko bude v priemere medzi nimi lokalnych zarovnani so skore aspon T?
- Hladanie genov: model generujuci sekvenciu+anotaciu naraz (parametre nastavene na znamych genoch). Pre danu sekvenciu, ktora pravdedpodobnost je najpravdepodobnejsia?
- Evolucia, Jukes-Cantorov model: model generujuci stlpec zarovnania. Nezname parametre: strom, dlzky hran. Pre danu sadu stlpcov zarovnania, ktore parametre povedu k najvacsej pravdepodobnosti?
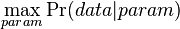
- Trochu detailov: pravdepodobnost zmeny/nezmeny na hrane dlzky t:
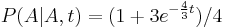 ,
, 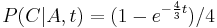
- Ak pozname ancestralne sekvencie, vieme spocitat pravdepodobnost dat
- Ancestralne sekvencie su nahodne premenne, ktore nas nezaujimaju: marginalizujeme ich (uvazujeme vsetky ich mozne hodnoty)
Zlozitejsie evolucne modely
- Jukes-Cantorov model uvazuje len dlzku hrany udanu v priemernom pocte substitucii (vratane tych, ktore nevidime, kvoli tomu, ze su dve na tom istom mieste)
- Nie vsetky substitucie sa deju rovnako casto: tranzicie (v ramci pyrimidinov T<->C, v ramci purinov A<->G) su pravdepodobnjesie ako transverzie (A,G)<->(C,T)
- Nie vsekty nukleotidy sa v danom genome objavuju rovnako casto (napr. mitochondrialne genomy velmi male C,G)
- Tieto javy zachytava HKY model (Hasegawa, Kishino & Yano)
- Matica rychlosti
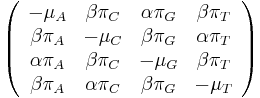
-
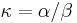 je pomer rychlosti, ktorymi sa deju tranzicie vs. transverzie
je pomer rychlosti, ktorymi sa deju tranzicie vs. transverzie
-
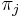 je frekvencia bazy
je frekvencia bazy 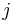 v sekvencii
v sekvencii
- Rychlost, ako sa deje substitucia z X do Y je sucin pravdepodobnosti Y a faktoru, ktory zavisi od toho, ci ide o tranziciu alebo transverziu
- Sucet kazdeho stlpca matice ma byt 0, t.j.
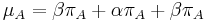
- Matica sa znormalizuje tak, aby priemerny pocet substitucii za jednotku casu bol 1
- Matica ma styri parametre:
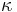 a tri frekvencie (stvrta musi doplnit do 1) plus dlzka hrany
a tri frekvencie (stvrta musi doplnit do 1) plus dlzka hrany
- Zlozitejsi model lepsie zodpoveda skutocnym procesom, ale na odhad viac parametrov potrebujeme viacej dat.
- Existuju metody, ktore pre dany cas t z matice spocitaju pravdepodobnost, ze baza X zmutuje na bazu Y Pr(Y|X,t)
- Napr. pre velmi velmi maly cas
 mame
mame  je zhruba
je zhruba 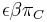
- Pre rozumne dlhe casy toto neplati, preto sa pouzivaju algebraicke metody, ktore beru do uvahy moznost viacerych substitucii na tom istom mieste
- Je aj vela inych modelov s mensim alebo vacsim poctom parametrov
HMM, cvičenia pre informatikov
Opakovanie
Parametre HMM:
-
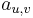 : prechodová pravdepodobnosť zo stavu
: prechodová pravdepodobnosť zo stavu  do stavu
do stavu 
-
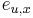 : pravdepodobnosť emisie
: pravdepodobnosť emisie 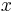 v stave
v stave 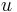
-
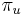 : pravdepodobnosť, že začneme v stave
: pravdepodobnosť, že začneme v stave 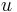
- Sekvencia
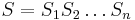
- Anotácia
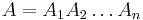
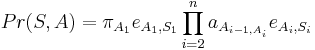
Trénovanie
- Proces, pri ktorom sa snažíme čo najlepšie odhadnúť pravdepodobnosti
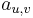 a
a 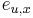 v modeli podľa trénovacích dát
v modeli podľa trénovacích dát
Usudzovanie (inferencia)
- Proces, pri ktorom sa snažíme pre sekvenciu
 nájsť anotáciu
nájsť anotáciu  , ktorá sekvenciu
, ktorá sekvenciu 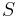 emituje s veľkou pravdepodobnosťou.
emituje s veľkou pravdepodobnosťou.
Inferencia pomocou najpravdepodobnejšej cesty, Viterbiho algoritmus
Hľadáme najpravdepodobnejšiu postupnosť stavov 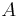 , teda
, teda 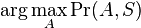 . Úlohu budeme riešiť dynamickým programovaním.
. Úlohu budeme riešiť dynamickým programovaním.
- Podproblém
![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) : Pravdepodobnosť najpravdepodobnejšej cesty končiacej po
: Pravdepodobnosť najpravdepodobnejšej cesty končiacej po 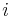 krokoch v stave
krokoch v stave 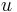 , pričom vygeneruje
, pričom vygeneruje 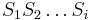 .
.
- Rekurencia:
-
![V[1,u]=\pi _{u}e_{{u,s_{1}}}](/vyuka/mbi/images/math/0/6/4/064578ee79b46dd2e01d1137e1c437c3.png) (*)
(*)
-
![V[i,u]=\max _{w}V[i-1,w]a_{{w,u}}e_{{u,x_{i}}}](/vyuka/mbi/images/math/0/8/3/083b392b95a92c1085c10159d0c12236.png) (**)
(**)
-
Algoritmus:
- Nainicializuj
![V[1,*]](/vyuka/mbi/images/math/5/d/9/5d9f1d4ebd3080a0804a6501977b5dae.png) podľa (*)
podľa (*)
- for i=2 to n=dĺžka reťazca
- for u=1 to m=počet stavov
- vypočítaj
![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) pomocou (**)
pomocou (**)
- vypočítaj
- for u=1 to m=počet stavov
- Maximálne
![V[n,j]](/vyuka/mbi/images/math/1/2/9/12924883f1d662364326a1d3f0fed497.png) je pravdepodobnosť najpravdepodobnejšej cesty
je pravdepodobnosť najpravdepodobnejšej cesty
Aby sme vypísali anotáciu, pamätáme si pre každé ![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) stav
stav 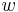 , ktorý viedol k maximálnej hodnote vo vzorci (**).
, ktorý viedol k maximálnej hodnote vo vzorci (**).
Zložitosť: 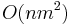
Poznámka: pre dlhé sekvencie budú čísla ![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) veľmi malé a môže dôjsť k podtečeniu. V praxi teda používame zlogarimované hodnoty, namiesto násobenia súčet.
veľmi malé a môže dôjsť k podtečeniu. V praxi teda používame zlogarimované hodnoty, namiesto násobenia súčet.
Inferencia - dopredný algoritmus
Aká je celková pravdepodobnosť, že vygenerujeme sekvenciu 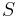 , t.j.
, t.j. 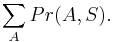 Podobný algoritmus ako Viterbiho.
Podobný algoritmus ako Viterbiho.
Podproblém 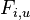 : pravdepodobnosť, že po
: pravdepodobnosť, že po 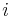 krokoch vygenerujeme
krokoch vygenerujeme 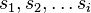 a dostaneme sa do stavu
a dostaneme sa do stavu 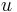 .
.
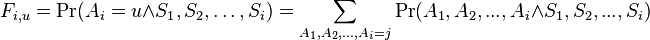
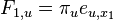
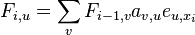
Celková pravdepodobnosť 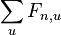
Inferencia - posterior decoding
Aposteriórna pravdepodobnosť stavu u na pozícii i: 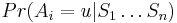
Pre každý index i chceme nájsť stav u s najväčšiou aposteriórnou pravdepodobnosťou, dostaneme tak inú možnú anotáciu.
Spustíme dopredný algoritmus a jeho symetrickú verziu, spätný algoritmus, ktorý počíta hodnoty
![B[i,u]=\Pr(A_{i}=u\wedge S_{{i+1}}\dots S_{n})](/vyuka/mbi/images/math/6/e/8/6e82648bde89df23b004629c06c05c23.png)
Aposteriórna pravdepodobnosť stavu u na pozícii i: ![Pr(A_{i}=u|S_{1}\dots S_{n})=F[i,u]B[i,u]/\sum _{u}F_{{n,u}}.](/vyuka/mbi/images/math/1/1/d/11de5bc85e3e6b3b8329d6b9686e7121.png)
Posterior decoding uvažuje všetky anotácie, nielen jednu s najvyššou pravdepodobnosťou. Môže však vypísať anotáciu, ktorá má sama o sebe nulovú pravdepodobnosť (napr. počet kódujúcich báz v géne nie je deliteľný 3).
Trénovanie HMM
- Stavový priestor + povolené prechody väčšinou ručne
- Parametre (pravdepodobnosti prechodu, emisie a počiatočné) automaticky z trénovacích sekvencií
- Ak máme anotované trénovacie sekvencie, jednoducho počítame frekvencie
- Ak máme iba neanotované sekvencie, snažíme sa maximalizovať vierohodnosť trénovacích dát v modeli. Používajú sa heuristické iteratívne algoritmy, napr. Baum-Welchov, ktorý je verziou všeobecnejšieho algoritmu EM (expectation maximization).
- Čím zložitejší model a viac parametrov máme, tým potrebujeme viac trénovacích dát, aby nedošlo k preučeniu, t.j. k situácii, keď model dobre zodpvedá nejakým zvláštnostiam trénovacích dát, nie však ďalším dátam.
- Presnosť modelu testujeme na zvláštnych testovacích dátach, ktoré sme nepoužili na trénovanie.
Tvorba stavového priestoru modelu
- Promótor + niekoľko eukaryotických génov
- Repeaty v intrónoch: multiple path problem
- Intrón má dĺžku aspoň 10
Zovšeobecnené HMM
- Problém s modelovaním rozdelenia dĺžok - v základnom modeli je geometrické
- Zovseobecnene HMM v jednom stave vygenerujú viac znakov
- Viterbi alg. a spol budú pomalšie (kvadratické od dĺžky sekvencie)
Komparatívna genomika a HMM, cvičenia pre biológov
- Pozri slidy [7]
Príklady stavových automatov pre HMM
Uvazujme HMM so specialnym zaciatocnym stavom b a koncovym stavom e, ktore nic negeneruju.
- Nakreslite HMM (stavovy diagram), ktory generuje sekvencie, ktore zacinaju niekolkymi cervenymi pismenami a potom obsahuju niekolko modrych
- Ako treba zmenit HMM, aby dovoloval ako "niekolko" aj nula?
- Ako treba zmenit HMM, aby pocet cervenych aj modrych bol vzdy parne cislo?
- Ako zmenit HMM, aby sa striedali cervene a modre kusy parnej dlzky?
V dalsich prikladoch uvazujeme aj to, ktore pismena su v ktorom stave povolene (pravdepodobnost emisie > 0) a ktore su zakazane
- cervena sekvencia dlzky dva, ktora zacina na A
- cervena sekvencia dlzky dva, ktora je hocico okrem AA
- toto sa da rozsirit na HMM, ktory reprezentuje ORF, teda nieco, co zacina start kodonom, potom niekolko beznych kodonov, ktore nie su stop kodonom a na koniec stop kodon
Dalsi biologicky priklad HMM: topologia transmembranovych proteinov.
Hľadanie génov v prokaryotických genómoch
- ORF: open reading frame, jednoduche hladanie
- ako najst zaciatok, ako rozlisit psedogeny a nahodne ORF-y
- samotrenujuce sa HMM, codon bias, GC%
E. coli http://nar.oxfordjournals.org/content/34/1/1.full
- Prvykrat sekvenovana a anotovana 1997
- Porovnanie s verziou 2005 (oprava sekvenovacích chýb aj chýb v anotácii)
- 682 zmien v start kodone
- 31 génov zrušených
- 48 nových génov
- Celkovo asi 4464 génov
Programy na anotovanie prokaryotických genómov
Histónové modifikácie
- A. Barski, S. Cuddapah, K. Cui, T. Roh, D. Schones, Z. Wang, G. Wei, I. Chepelev, K. Zhao (2007) High-Resolution Profiling of Histone Methylations in the Human Genome Cell, Volume 129, Issue 4, Pages 823-837 pdf
Gény v ľudskom genóme
- What is a gene, post-ENCODE? History and updated definition. Gerstein MB, Bruce C, Rozowsky JS, Zheng D, Du J, Korbel JO, Emanuelsson O, Zhang ZD, Weissman S, Snyder M.
- Most "dark matter" transcripts are associated with known genes. H Van Bakel, C Nislow, BJ Blencowe, TR Hughes - PLoS Biol, 2010
- Transcribed dark matter: meaning or myth? CP Ponting, TG Belgard - Human molecular genetics, 2010
- Landscape of transcription in human cells. Djebali et al (ENCODE), Nature 2012
Geny, evolucia a komparativna genomika v UCSC genome browseri
- Chodte na stranku http://genome.ucsc.edu/
- Zvolte starsiu verziu ludskeho genomu hg18, ktora ma viac informacii
- Do okienka position zadajte gen MAGEA2B a potom zvolte vyskyt na pozicii cca chrX:151636040-151637735 (ma dva vyskyty)
- Dostanete sa tam aj touto linkou: [12]
- Ak date 3x zoom out, mozete si vsimnut, ze tento gen ma viacero foriem zostrihu, ktore sa ale lisia iba v 5' UTR
- Vsimnite si ENCODE Regulation Super-track, ktory zobrazuje ChIP data pre niektore histonove modifikacie
- Vela veci sa mozete dozvediet klikanim na rozne casti broswera: napr, kliknutim na gen si mozete precitat o jeho funkcii, kliknutim na listu ku tracku (lavy okraj obazku) sa dozviete viac o tracku a mozete nastavovat parametre zobrazenia
- V casti Genes and Gene Prediction Tracks zapnite track Pos Sel Genes, ktory obsahuje geny s pozitivnym vyberom (cervenou, pripadne slabsie fialovou a modrou)
- Ked kliknete na cerveny obdlznik pre tento gen, uvidite, v ktorych castiach fylogenetickeho stromu bol detekovany pozitivny vyber
- V casti multiz alignments tracku Conservation vidite zarovnania k roznym inym genomom (da sa zapinat, ze ku ktorym). Mozete si pozriet, ako sa uroven zarovnania zmeni ked sa priblizujeme a vzdalujeme (zoom in/zoom out).
- Ked sa priblizite spat na gen MAGEA2B a potom tak, aby ste boli na urovni "base", t.j. zobrazenych cca 100bp, v obdlzniku multiz alignment uvidite zarovnanie s homologickym usekom v inych genomoch. Konkretne v MAGEA2B vidime pomerne dost rozdielov v proteine medzi clovekom a makakom rezus, vdaka ktorym bol zrejme klasifikovany ako pod pozitivnym vyberom.
- V casti conservation by PhyloP vidime graf toho, ako silne su zachovane jednotlive stlpce zarovnania
- Da sa zapnut aj track 28-Way Most Cons, ktory zobrazuje konkretne useky, ktore su najvac konzervovane
- Ak chceme zistit, kolko percent genomu tieto useky pokryvaju, ideme na modrej liste do casti Tools->Table browser, zvolime group Comparative genomics, track 28-way most cons, table Mammal alebo Vertebrate, region zvolime genome (v celom genome) a stlacime tlacidlo Summary/statistics
Objavenie génu HAR1 pomocou komparatívnej genomiky
- Pollard KS, Salama SR, Lambert N, et al. (September 2006). "An RNA gene expressed during cortical development evolved rapidly in humans". Nature 443 (7108): 167–72. doi:10.1038/nature05113. PMID 16915236. pdf
- Zobrali všetky regióny dĺžky aspoň 100bp s > 96% podobnosťou medzi šimpanzom a myšou/potkanom (35,000)
- Porovnali s ostatnými cicavcami, zistili, ktoré majú veľa mutáci v človeku, ale málo inde (pravdepodobnostný model)
- 49 štatisticky významných regiónov, 96% nekódujúcich oblastiach
- Najvýznamnejší HAR1: 118nt, 18 substitúcii u človeka, očakávali by sme 0.27. Iba 2 zmeny medzi šimpanzom a sliepkou (310 miliónov rokov), ale nebol nájdený v rybách a žabe.
- Nezdá sa byť polymorfný u človeka
- Prekrývajúce sa RNA gény HAR1R a HAR1F
- HAR1F je exprimovaný v neokortexe u 7 a 9 týždenných embrií, neskôr aj v iných častiach mozgu (u človeka aj iných primátov)
- Všetky substitúcie v človeku A/T->C/G, stabilnejšia RNA štruktúra (ale tiež sú blízko k telomére, kde je viacej takýchto mutácii kvôli rekombinácii a biased gene conversion)
- Môžete si pozrieť tento region v browseri: chr20:61,203,911-61,204,071 (hg18), pricom ak sa este priblizite, uvidite zarovnanie aj s bazami a mozete vidiet, ze vela zmien je specifickych pre cloveka
- Vynimkou je slon, niektore zmeny v slonovi su sposobene nizkou kvalitou sekvencie. Ked pomocou nastroja Convert na hornej liste premapujete do najnovsej verzie ludskeho genomu (hg19), uvidite, ze aj v najnovsej verzii genomu slona su mnohe zmeny, nechyba tam uz vsak cast sekvencie, ako vo verzii pouzitej v hg18.
PhyloHMM a expresia génov, cvičenia pre informatikov
Vzorové riešenia DÚ1
Fylogeneticke HMM
- Spojenie HMM a fylogenetickeho stromu
- Konecne mnozina stavov
-
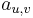 : prechodová pravdepodobnosť zo stavu
: prechodová pravdepodobnosť zo stavu 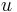 do stavu
do stavu 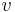
-
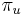 : pravdepodobnosť, že začneme v stave
: pravdepodobnosť, že začneme v stave 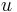
- Namiesto emisnej pravdepodobnosti mame pre kazdy stav dlzky hran, maticu rychlosti R
Priklad:
- PhastCons: 2 stavy: zachovana a nezachovana sekvencia
- Komparativne hladanie genov
Opakovanie: Viterbiho algoritmus pre HMM
- Podproblém
![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) : Pravdepodobnosť najpravdepodobnejšej cesty končiacej po
: Pravdepodobnosť najpravdepodobnejšej cesty končiacej po 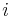 krokoch v stave
krokoch v stave 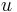 , pričom vygeneruje
, pričom vygeneruje 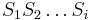 .
.
-
![V[i,u]=\max _{v}V[i-1,v]a_{{v,u}}e_{{u,x_{i}}}](/vyuka/mbi/images/math/d/f/4/df4cfd46959f058d7469666b7e588fb6.png)
Modifikacia pre fylogeneticke HMM:
- Pre kazdy stlpec zarovnania i a stav u spustime Felsensteinov algoritmus
- Vyslednu pravdepodobnost pouzijeme namiesto
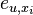
- Zlozitost pre k stavov, dlzku zarovnania n, pocet organizmov m: O(nmk + nk^2)
Uvod do expresie genov, regulacie, microarrays
- pozri prezentaciu z prednasky
Zhlukovanie (clustering)
Využitie:
- taggovanie nových príspevkov na blogu pomocou taggov príspektov, s ktorými je nový príspevok v zhluku
- news.google.com - zhlukovanie správ podľa spoločnej témy
- počítačová grafika
- segmentácia obrázkov - rozdelenie obrázka na "rozumné" časti
- zníženie počet farieb
- výpočtová biológia - funkčné skupiny génov
- detekcia anomálií - napr. testovanie motorov do lietadiel (predpokladám, že väčšina vyrobených motorov je dobrá, na základe meraní motory pozhlukujem a tie mimo hlavného vyhlásim za potencionálne závadné)
K-Means
- Vstup: Body
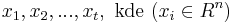 a počet zhlukov k
a počet zhlukov k
- Výstup: Rozdelenie do k zhlukov takéto:
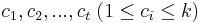 - priradenie bodu k zhluku
- priradenie bodu k zhluku
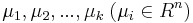 - centrá každého zhluku centroidy
- centrá každého zhluku centroidy
- Úloha: minimalizovať chybovú funkciu
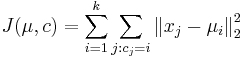 (inými slovami, počítam ako ďaleko (Euklidovská vzdialenosť) je každý bod od svojho centroidu?)
(inými slovami, počítam ako ďaleko (Euklidovská vzdialenosť) je každý bod od svojho centroidu?)
Algoritmus
- inicializácia: náhodne vyber k centroidov
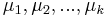
- opakuj až do konvergencie:
- priraď každý bod najbližšiemu centroidu:
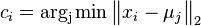
- vypočítaj nové centroidy:
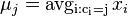 (spriemerujem všetky body v jednom zhluku)
(spriemerujem všetky body v jednom zhluku)
- priraď každý bod najbližšiemu centroidu:
Expresia génov, cvičenia pre biológov
Na týchto cvičeniach sa budeme venovat dvom statistickym temam suvisiacim s komparativnou genomikou a s analyzou expresie genov. Tieto techniky sa vsak vyuzivaju aj v inych oblastiach a mozete sa s nimi casto stretnut v genomickych clankoch.
Nadreprezentacia, obohatenie (enrichment)
- Mnohe celogenomove analyzy nam daju zoznam genov, ktore sa v nejakom ukazovateli vyrazne lisia od priemeru.
- Napriklad geny s pozitivnym vyberom v komparativnej genomike, geny vyrazne nadexprimovane alebo podexprimovane v microrarray experimentoch, geny regulovane urcitym transkripcnym faktorom a pod.
- Niektore z nich budu preskumanejsie (znama funkcia a pod.), niektore mozu mat nejake udaje o funkcii prenesene z homologov a dalsie mozu byt uplne nezname
- Co s takym zoznamom "zaujimavych genov"?
- moznost 1: vybrat si z neho niekolko malo zaujimavych kandidatov a preskumat ich podrobnejsie (experimentalne alebo informaticky)
- moznost 2: zistit, ci tato cela skupina je obohatena o geny urcitych skupin
- napr. v pripade pozitivneho vyberu nam casto vychadzaju geny suvisiace s imunitou, lebo su pod velkym evolucnym tlakom od patogenov
- takato analyza nam teda da informaciu o suvislostiach medzi roznymi procesmi
- Priklad (Kosiol et al)
- 16529 genov celkovo, 70 genov v GO kategorii innate immune response (0.4% zo vsetkych genov)
- 400 genov s pozivnym vyberom, mame 8 genov s innate immune response (2% zo vsetky genov s poz. vyb.)
- Celkovy pocet genov n, imunitnych ni, pozitivny vyber np, imunitnych s poz. vyb. nip.
- Kontingencna tabulka
| Pozitivny vyber | Bez poz. vyberu | Sucet | |
|---|---|---|---|
| Imunitne | 8 (nip) | 62 | 70 (ni) |
| Ostatne | 392 | 16067 | 16459 |
| Sucet | 400 (np) | 16129 | 16529 (n) |
- Nulova hypoteza: geny v nasom zozname boli nahodne vybrane z celeho genomu, t.j. ak v celom genome je frekvencia imunitnych genov ni/n, vo vzorke velkosti np (geny s pozitivnym vyberom) ocakavame cca np * ni / n imunitnych genov.
- aj v nulovej hypoteze vsak vzorka velkosti ni cisto nahodou moze obsahovat viac alebo menej takych genov.
- presnejsie mame urnu so ni (70) bielymi a n-ni (16459) ciernymi gulickami, vytiahneme nahodne np (400) guliciek, kolko budem medzi nimi bielych, azvime tuto nahodnu premennu xip
- v nasom priklade by sme ocakavali 1.7 genu s innate immune response, ale mame 8 (4.7xviac)
- Rozdelenie pravdepodobnosti nip je hypergeometricke, t.j. pravdepodobnost ze xip = nip je
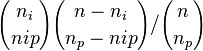
- Aka je pravdepodobnost, ze v nulovej hypoteze bude xip tolko, kolko sme namerali alebo viac? (Chvost rozdelenia). V nasom pripade p-value 2.8e-4.
- Hypergeometric or Fisher's exact test, pripadne ich aproximacie pre velke hodnoty v tabulke (chi^2 test) zisti, ci sa nasa tabulka velmi lisi od toho, co by sme ocakavali v nulovej hypoteze
- Suvisiace clanky
- Rivals I, Personnaz L, Taing L, Potier MC (February 2007). "Enrichment or depletion of a GO category within a class of genes: which test?". Bioinformatics (Oxford, England) 23 (4): 401–7. doi:10.1093/bioinformatics/btl633. PMID 17182697.
- Huang da W, Sherman BT, Lempicki RA (January 2009). "Bioinformatics enrichment tools: paths toward the comprehensive functional analysis of large gene lists". Nucleic Acids Research 37 (1): 1–13. doi:10.1093/nar/gkn923. PMID 19033363.
- Existuju web servery, napr. GOrilla pre ludske geny: http://cbl-gorilla.cs.technion.ac.il/, DAVID (http://david.niaid.nih.gov), g:Profiler http://biit.cs.ut.ee/gprofiler/
- Treba dat pozor, ci pocitaju to co chceme
- Kod v statistickom systeme R na pocitanie hypergeometrickeho rozdelenia
> dhyper(0:70, 70, 16529-70, 400); [1] 1.793421e-01 3.126761e-01 2.679872e-01 1.505169e-01 6.231088e-02 [6] 2.027586e-02 5.400796e-03 1.210955e-03 2.332580e-04 3.920215e-05 [11] 5.818723e-06 7.702558e-07 9.166688e-08 9.873221e-09 9.678760e-10 [16] 8.677204e-11 7.143849e-12 5.420388e-13 3.802134e-14 2.472342e-15 [21] 1.493876e-16 8.405488e-18 4.412274e-19 2.164351e-20 9.935473e-22 [26] 4.273662e-23 1.724446e-24 6.533742e-26 2.326517e-27 7.791092e-29 [31] 2.455307e-30 7.285339e-32 2.036140e-33 5.361856e-35 1.330660e-36 [36] 3.112566e-38 6.862558e-40 1.426089e-41 2.792792e-43 5.153006e-45 [41] 8.955105e-47 1.465159e-48 2.255667e-50 3.265636e-52 4.442631e-54 [46] 5.674366e-56 6.797781e-58 7.629501e-60 8.012033e-62 7.860866e-64 [51] 7.193798e-66 6.129013e-68 4.851139e-70 3.558526e-72 2.412561e-74 [56] 1.506983e-76 8.641725e-79 4.530590e-81 2.161126e-83 9.326620e-86 [61] 3.617279e-88 1.250737e-90 3.817900e-93 1.016417e-95 2.323667e-98 [66] 4.469699e-101 7.034762e-104 8.698702e-107 7.924236e-110 4.728201e-113 [71] 1.386176e-116 phyper(7, 70, 16529-70, 400, lower.tail=FALSE); # pr pocet bielych>7 (t.j. >=8) ak taham 400 z vreca so 70 bielymi a 16529-70 ciernymi # sucet cisiel z tabulky od 2.332580e-04 az po koniec
Multiple testing correction
- V mnohych situaciach robime vela testov toho isteho typu, kazdy ma urcitu p-value
- Napr. testujeme 1000 genov v genome na pozitivny vyber, zvolime tie, kde p-value <= 0.05
- Alebo testujeme obohatenie 1000 funkcnych kategorii v nejakej vzorke genov, zvolime tie, kde p-value <= 0.05
- Problem: ak kazda z 1000 kategorii ma 5% sancu tam byt len nahodou, ocakavali by sme 50 cisto nahodnych pozitivnych vysledkov. Ak sme napr. nasli 100 pozitivnych vysledkov (obohatenych kategorii), cca polovica z nich je zle
- Preto potrebujeme pri velkom mnozstve testov umelo znizit prah na p-value tak, aby nahodny sum netvoril velke percento nasich vysledkov
- Toto sa vola multiple testing correction, je viac technik, napr. FDR (false discovery rate)
Zhlukovanie
- Máme vstupné dáta, väčšinou ako vektory dľžky n
- Snažíme sa ich rozdeliť do skupín tak, aby dáta v rámci skupiny boli podobné a medzi skupinami rôzne
Využitie:
- hľadanie génov s podobným profilom expresie
- hľadanie skupín pacientov s podobným profilom expresie génov (objavovanie podtypov nejakej choroby)
- hľadanie rodín podobných proteínov
- automatická segmentácia obrázkov (napríklad rozlíšiť jednotlivé políčka microarraz alebo gelu od pozadia)
K-Means
- Vstup: n-rozmerné vektory
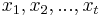 a počet zhlukov k
a počet zhlukov k
- Výstup: Rozdelenie vektorov do k zhlukov takéto:
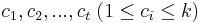 - priradenie vektoru k zhluku
- priradenie vektoru k zhluku
- n-rozmerné vektory
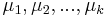 - centrá každého zhluku
- centrá každého zhluku
- Úloha: minimalizovať súčet vzdialeností od každého vektoru k centru jeho zhluku:
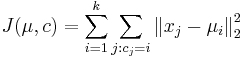 (inými slovami, počítam ako ďaleko (Euklidovská vzdialenosť) je každý bod od svojho centroidu?)
(inými slovami, počítam ako ďaleko (Euklidovská vzdialenosť) je každý bod od svojho centroidu?)
Algoritmus
- inicializácia: náhodne vyber k centier
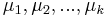
- opakuj až do konvergencie:
- priraď každý bod najbližšiemu centru:
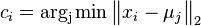
- vypočítaj nové centroidy:
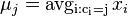 (spriemerujeme všetky body v jednom zhluku)
(spriemerujeme všetky body v jednom zhluku)
- priraď každý bod najbližšiemu centru:
Prakticke cvicenie
Data o expresii ludskych genov v roznych tkanivach a podobne v UCSC genome browseri
- Chodte na stranku http://genome.ucsc.edu/, najdite PTPRZ1 gen v ludskom genome
- Zvolte Tools->Gene Sorter, sort by nechajme Expression (GNF Atlas 2), search PTPRZ1
- Dostane tabulku genov s podobny profilom expresie ako PTPRZ1
- Teraz chceme dostat iba zoznam podobnych genov bez dalsich udajov:
- Stlac configure, tlacidlom hide all zrusite vsetky zaskrtnute typy informacie a zakrtnite iba Gene name, date submit
- Potom stalte tlaidlo text a dostanete cislo zoznam mien genov v textovom formate
- V prípade problémov ho najdete ho aj tu
- http://biit.cs.ut.ee/gprofiler/ mena genov skopirujme do policka Query, stlacte g:Profile!
- Vo vyslednej tabulke je kazdy riadok jedna funkcna kategoira, v ktorej su geny s tymto profilom expresie nadreprezentovane, kazdy stlpec jeden gen. mena kategorii su uplne vpravo.
- Co by sme na zaklade nadreprezentovanych kategorii usudzovali o tomto gene?
- Najdite tento gen v Uniprote (http://www.uniprot.org/), potvrdzuje nase domnienky?
- Vratme sa do genome browsera, najdime si PTPRZ1 gen v genome
- V browseri su rozne tracky tykajuce sa expresie, napr. GNF Atlas 2. Precitajte si, co je v tomto tracku zobrazene, zapnite si ho a pozrite si expresiu okolitych genov okolo PTPRZ1
- Kliknite na gen v tracku UCSC known genes. V tabulke uvidite zase prehlad expresie v roznych tkanivach (podla GNF Atlasu), linku na Visigene.
NCBI Gene Expression Omnibus http://www.ncbi.nlm.nih.gov/geo/
- Databaza gene expression dat na NCBI
- Do okienka Data sets zadajme GDS2925
- Mali by sme dostat Various weak organic acids effect on anaerobic yeast chemostat cultures
- Mozeme si pozriet zakladne udaje, napr. citation, platform
- Link expression profiles nam zobrazi grafy pre rozne geny
- Pri kazdom profile mozeme kliknut na profile neighbors, aby sme videli geny s podobnym profilom
- Data analysis tools, cast Cluster heatmaps, K-means, skuste rozne pocty clustrov
Proteíny, cvičenia pre informatikov
Uvod do proteomiky
- Viac informacii: [13], Bafna, Reinert 2004
Gélová elektroforéza (gel electrophoresis)
- Izolovanie jednotlivých proteínov, porovnávanie ich množstva.
- Negatívne nabité proteíny migrujú v géli v elektrickom poli. Väčšie proteíny migrujú pomalšie, dochádza v oddeleniu do pruhov. Táto metóda sa používa aj na DNA a RNA. Pre proteíny možno tiež robiť 2D gél (podľa hmotnosti a náboja).
- Bioinformatický problém: zisti, ktoré fliačiky na dvoch 2D géloch zodpovedajú tým istým proteínom.
- Automatizovanejšia technológia: kvapalinová chromatografia (liquid chromatography) - separácia proteínov v tenkom stĺpci
Hmotnostná spektrometria (mass spectrometry)
- Hmotnostná spektrometria meria pomer hmostnosť/náboj molekúl vo vzorke.
- Používa sa na identifikáciu proteínov, napr. z 2D gélu.
- Proteín nasekáme enzýmom trypsín (seká na [KR]{P}) na peptidy
- Meriame hmostnosť kúskov, porovnáme s databázou proteínov.
- Tandemová hmotnostná spektrometria (MS/MS) ďalej fragmentuje každý kúsok a dosiahne podrobnejšie spektrum, ktoré obsahuje viac informácie
Sekvenovanie proteinov pomocou MS/MS
Berme do uvahy len b-iony, ktore zodpovedaju hmotnosti prefixu
- Vsetky hmotnosti budu cele cisla, pozname celkovu hmotnost peptidu M a hmotnosti aminokyselin

- Mame skorovaciu funkciu/tabulku f(m), ktora pre prefix peptidu s hmotnostou m urci skore, ako dobre sedi so spektrom
- Chceme najst peptid, ktory maximalizuje sucet skore svojich prefixov
- Dynamicke programovanie s podproblemom A[m] je skore najlepsieho prefixu s hmotnostou m
- Rekurencia? Zlozitost? Je to polynomialny algoritmus? (Co je vlastne vstup?)
Co ak berieme do uvahy aj y-iony, ktore meraju hmotnost sufixu?
- Idea 1: upravme skorovaciu funkciou f(m): skontroluje signal na pozicii m aj M-m
- Problem: jeden signal sa moze ratat dvakrat, raz ako b-ion, raz ako y-ion, algoritmus ma tendenciu pridavat taketo artefakty
- Nove skorovanie: ak hmotnost nejakeho prefixu a nejakeho sufixu su rovnake, zarataj ich skore iba raz (skore peptidu je skore mnoziny hmotnosti jeho prefixov a sufixov)
- Definuj novy podproblem: A[p,s] je najlepsie skore, ktore moze dosiahnut prefix s hmotnostou p a sufix s hmotnostou s
- Budeme uvazovat p,s<M/2, pricom f(m) stale skontroluje signal na pozicii m aj M-m
![A[p,s]=\left\{{\begin{array}{ll}\max _{{i=1\dots 20}}A[p,s-a_{i}]+f(s)&{\mbox{ak }}p<s\\\max _{{i=1\dots 20}}A[p-a_{i},s]+f(p)&{\mbox{ak }}p>s\\\max _{{i=1\dots 20}}A[p-a_{i},s]&{\mbox{ak }}p=s\\\end{array}}\right.](/vyuka/mbi/images/math/4/1/1/4116ee1f8978b2d5beb1adbcf2ea3540.png)
- Ako ukoncime dynamicke programovanie? Zlozitost?
- Zrychlenie: staci uvazovat s od p-w po p+w kde w je maximalna hmotnost aminokyseliny
Detekcia znamych proteinov pomocou MS
- Predikcia spektra pre dany peptid, porovnanie s realnym spektrom, zlozite skorovacie schemy
- Filtrovanie kandidatov na proteiny, ktore obsahuju peptidy s pozorovanou hmotnostou
- Problem: mame danu databazu proteinov a cielovu hmotnost peptidu M, pozname hmotnost kazdej aminokyseliny. Najdite vsetky podretazce s hmotnostou M.
- Databazu proteinov si vieme predstavit aj ako postupnost cisel - hmotnosti aminokyselin, hladame intervaly so suctom M.
- Trivialny algoritmus: zacni na kazdej pozicii, pricitavaj kym nedosiahnes hmotnost>=M. Zlozitost? Vieme zlepsit?
- Predspracovanie: pocitajme hmotnosti vsetkych podretazcov, potom vyhladajme binarne. Zlozitost?
- Zlozitejsi alg. s predspracovanim pomocou FFT (Fast Fourier Transform) Bansal, Cieliebak, Liptak 2004
Proteíny, cvičenia pre biológov
Proteíny
- Toto cvičenie je z časti inšpirované stránkou [14]
- Pozrieme sa na enzým Bis(5'-adenosyl)-triphosphatase
- Nájdime ho na stránke http://www.uniprot.org/ pod názvom FHIT_HUMAN
- O mnohých údajoch na stránke sme sa rozprávali na prednáške (GO kategórie, domény, sekundárna a 3D štruktúra)
- Všimnime si Pfam doménu a pozrime si jej stránku, do akej super-rodiny (klanu) patrí?
- Tento enzým je vzdialene podobný na enzým galactose-1-phosphate uridylyltransferase (GALT/GAL7)
- Skúsme nájsť túto podobnosť v BLASTe: http://blast.ncbi.nlm.nih.gov/ v časti proteíny, zvoľme databázu Swissport, ako Query zadajme Accesion nášho proteínu P49789
- GAL gén (konkrétne GAL7_HAEIN) sa nachádza medzi výsledkami, ale s vysokou E-value
- Odložme si tieto výsledky a v novom okne spustíme PSI-BLAST, dve iterácie
- Aká je E-value teraz? V čom sa líšia zarovnania?
- Nájdime v Uniprote proteín GAL7_HAEIN.
- Ak sa pozrieme na jeho Pfam domény, v akom sú klane?
Sekvenčné motívy
MEME
- Vazobne miesta transkripcnych faktorov sa casto reprezentuju ako sekvencne motivy
- Ak mame skupinu sekvencii, mozeme hladat motiv, ktory maju spolocny
- Znamy program na tento problem je MEME
- Chodte na stranku http://meme.nbcr.net/
- Zvolte nastroj MEME a do okienka "actual sequences" zadajte tieto sekvencie
- Pozrite si ostatne nastavenia. Co asi robia?
- Ak server pocita dlho, mozete si pozriet vysledky tu
Proteíny a RNA, cvičenia pre informatikov
- Obcas chceme najst optimalne riesenie nejakeho NP-tazkeho problemu
- Jedna moznost je previest na iny NP tazky problem, pre ktory existuju pomerne dobre prakticke programy, napriklad integer linear programming (ILP)
Prakticke programy na NP tazke problemy
- najdu optimalne riesenie, mnohe instancie zrataju v rozumnom case, ale mozu bezat aj velmi dlho
- CPLEX [15] a Gurobi [16] komercne baliky na ILP, akademicka licencia zadarmo
- SYMPHONY v projekte COIN-OR [17] open source
- Minisat [18] open source SAT solver
- Concorde TSP solver [19] - riesi problem obchodneho cestujuceho so symetrickymi vzdialenostami, zadarmo na akademicke ucely
- Pre zaujimavost: TSP art [20]
ILP
Linearny program:
- Mame realne premenne x_1...x_n, minimalizujeme nejaku ich linearnu kombinaciu
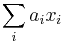 kde a_i su dane vahy.
kde a_i su dane vahy.
- Mame tiez niekolko podmienok v tvare linearnych rovnosti alebo nerovnosti, napr.
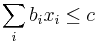
- Hladame teda hodnoty premennych, ktore minimalizuju cielovu sumu, ale pre ktore platia vsetky podmienky
- Da sa riesit v polynomialnom case
Integer linear program
- Program, v ktorom vsetky premenne musia mat celociselne hodnoty, alebo dokonca povolime oba hodnoty 0 a 1.
- NP uplny problem
Ako zapisat (NP-tazke) problemy ako ILP
Knapsack
- Problem: mame dane predmety s hmotnostami w_1..w_n a cenami c_1..c_n, ktore z nich vybrat, aby celkova hmotnost bola najviac T a cena bola co najvyssia?
- Pouzijeme binarne premenne x_1..x_n, kde x_i = 1 prave vtedy ked sme zobrali i-ty predmet.
- Chceme maximalizovat
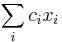
- za podmienky ze
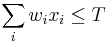
Set cover:
- Mame n mnozin S_1...S_n nad mnozinou {1...m}. Chceme vybrat co najmensiu pomnozinu A tak, aby kazde S_i obsahovalo aspon jeden prvok z A
- Binarne premenne x_i=1 ak vyberieme i-ty prvok
- Chceme minimalizovat
- za podmienky, ze pre kazde i plati
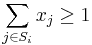
Protein threading
- Ciel: protein A ma znamu sekvenciu aj strukturu, protein B iba sekvenciu. Chceme zarovnat proteiny A a B, pricom budeme brat do uvahy znamu strukturu, t.j. ak su dve amino kyseliny blizko v A tak ich ekvivalenty v B by mali byt "kompatibilne".
- Tento problem chceme riesit tak, ze v strukture A urcime nejake jadra, ktore by v evolucii mali zostat zachovane bez inzercii a delecii a v rovnakom poradi. Tieto jadra su oddelene sluckami, ktorych dlzka sa moze lubovolne menit a ktorych zarovnania nebudeme skorovat.
- Formulacia problemu: Mame danu sekvenciu B=b1..bn, dlzky m jadier c_1...c_m a skorovacie tabulky E_ij, ktora vyjadruje, ako dobre bj..b_{j+c_i-1} sedi do sekvencie jadra i a E_ijkl ktora vyjadruje, ako dobre by jadra i a k interagovali, keby mali sekvencie zacinajuce v B na poziciach j a l. Uloha je zvolit polohy jadier x_1<x_2<...<x_m tak, aby sa ziadne dve jadra neprekryvali a aby sme dosiahli najvyssie skore.
- Poznamka: nevraveli sme, ako konkretne zvoli jadra a skorovacie tabulky, co je modelovaci, nie algoritmicky problem (mozeme skusit napr. nejake pravdepodonostne modely)
Protein threading ako ILP
- Premenne v programe:
- x_ij=1 ak je zaciatok i-teho jadra zarovnane s b_j
- y_ijkl=1 ak je zaciatok i-teho jadra na b_j a zaciatok k-teho na b_l (i<k, j<l)
- Chceme maximalizovat
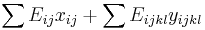
- Podmienky:
-
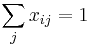 pre kazde i
pre kazde i
-
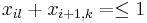 pre vsetky i,k,l, kde k<l+c_i
pre vsetky i,k,l, kde k<l+c_i
-
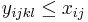 pre vsetky i,j,k,l, kde i<k, j<l
pre vsetky i,j,k,l, kde i<k, j<l
-
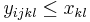 pre vsetky i,j,k,l, kde i<k, j<l
pre vsetky i,j,k,l, kde i<k, j<l
-
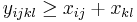 pre vsetky i,j,k,l, kde i<k, j<l
pre vsetky i,j,k,l, kde i<k, j<l
-
Na zamyslenie:
- Aka bude velkost programu ako funkcia n a m?
- Co ak nie vsetky jadra navzajom interaguju? Mozeme na velkosti programu usetrit?
- Preco asi vobec autori zaviedli jadra a ako by sme zmenili program, ak by sme chceli uvazovat kazdu aminokyselinu zvlast?
Bezkontextove gramatiky
RNA, cvičenia pre biológov
Nussinovov algoritmus
Z cvičných príkladov na skúšku
- Vyplnte maticu dynamického programovania (Nussinovov algoritmus) pre nájdenie najväčšieho počtu dobre uzátvorkovaných spárovaných báz v RNA sekvencii GAACUUCACUGA (dovoľujeme len komplementárne páry A-U, C-G) a nakreslite sekundárnu štruktúru, ktorú algoritmus našiel.
G A A C U U C A C U G A
0 0 0 1 1 2 3 3 3 4 4 4 G
0 0 0 1 2 2 2 2 3 4 4 A
0 0 1 1 1 2 2 2 3 4 A
0 0 0 0 1 1 1 2 3 C
0 0 0 1 1 1 2 3 U
0 0 1 1 1 2 3 U
0 0 0 1 2 2 C
0 0 1 1 1 A
0 0 1 1 C
0 0 1 U
0 0 G
0 A
Bezkontextove gramatiky
- Na modelovanie struktury RNA sa pouzivaju stochasticke bezkontextove gramatiky
- My si teraz ukazeme bezkontextove gramatiky, ktore nemaju pravdepodobnosti
- Zaviedol Noam Chomsky v lingvistike 50-te roky 20. storocia, tiez dolezite v informatike
- Gramatika
- Dva typy symbolov: terminaly (male pismena), neterminaly (velke pismena)
- Pravidla prepisujuce neterminal na retazec terminalov a neterminalov (moze byt aj prazdny retazec, ktory oznacujeme epsilon)
- Neterminal S je "startovaci"
- Priklad: S->aSb, S->epsilon (piseme aj skratene S->aSb|epsilon)
- Pouzitie gramatiky na generovanie retazcov
- Zacneme so startovacim neterminalom S
- V kazdom kroku prepiseme najlavejsi neterminal podla niektoreho pravidla
- Skoncime, ked nezostanu ziadne neterminaly
- Priklad: S->aSb->aaSbb->aaaSbbb->epsilon
- Ake vsetky slova vie tato gramatika generovat?
- V tvare aa...abb...b s rovnakym poctom acok a bciek (informatici pisu a^kb^k)
- Zostavte gramatiku na slova typu aa..abb..b kde acok je rovnako alebo viac ako bcok
- S->aSb|aS|epsilon
- zostavte gramatiku pre slova toho isteho typu, kde acok je viac ako bcok
- S->aSb|aT T->aT|epsilon (alebo S->aSb|aS|a)
- uvazujme dobre uzatvorkovane vyrazy zo zatvoriek (,),[,] napr. [()()([])] je dobre uzatvorkovany, ale [(]) nie je.
- S->SS|(S)|[S]|epsilon
- S->[S]->[SS]->[SSS]->[(S)SS]->[()SS]->[()(S)S]->[()()S]->[()()(S)]->[()()([S])]->[()()([])]
- Parsovanie retazca pomocou gramatiky: urcit, ako mohol byt retazec vygenerovany pomocou pravidiel
- Tato gramatika nam pomoze urcit, ktora zatvorka patri ku ktorej: tie, ktore boli vygenerovane v jednom kroku
- Zostavte gramatiku na DNA palindromy, t.j. sekvencie, ktore zozadu po skomplementovani baz daju to iste, ako napr. GATC
- S->gSc|cSg|aSt|tSa|epsilon
- Zostavte gramatiku na slova s rovnakym poctom acok a bcok v lubovolnom poradi
- S->epsilon|aSbS|bSaS
- preco vie vygenerovat vsetky take retazce?
Hľadanie motívov, cvičenia pre informatikov
- Prehlad semestra: pozri prezentacia
Hladanie motivov zadefinovanych pravdepodobnostnou maticou
- Mame danych n sekvencii S=(S1..Sn), kazda dlzky m, dlzku motivu L, nulova hypoteza q (rozdelenie nukleotidov)
- Hladame motiv vo forme pravdepodobnostneho profilu dlzky L a jeho vyskyt v kazdej sekvencii
- Nech
 je pravdepodobnost, ze na pozicii i motivu bude baza a, W cela matica
je pravdepodobnost, ze na pozicii i motivu bude baza a, W cela matica
- o_i je pozicia vyskytu v sekvencii S_i, O=(o_1...o_n) su vsetky vyskyty dokopy
- Pr(S|W.O) je jednoduchy sucin, kde pre pozicie v oknach pouzijeme pravdepodobnosti z W, pre pozicie mimo okna pouzijeme q
- Hladame W,O, ktore maximalizuju tuto pravdepodobnost (najvierhododnejsie)
- Nepozname efektivny algoritmus, ktory by to vedel vzdy najst maximum
- Dali by sa skusat vsetky moznosti O, pre dane O je najlepsie W frekvencie z dat
- Naopak ak pozname W, vieme najst najlepsie O
- EM algoritmus: iterativne zlepsuje W, pricom berie Vsetky O vahovane podla ich pravdepodohnosti vzhladom na W z minuleho kola
- Casto sa v zlozitych pravdepdobnostnych modeloch pouziva namiesto optimalizacie parametrov vzorkovanie (sampling)
- Rozsirime model, aby aj O a W boli nahodne premenne, takze mame rozdelenie Pr(S,W,O)
- Vzorkujeme z Pr(O|S)
- Mozeme pre kazdu vzorku spocitat Pr(S|W,O) a zobrat najlepsiu
- Alebo si mozeme si pamatat, ktore okno ako casto vnutri motivu, robit priemery roznych velicin, skumat tvar rozdelenia
- My pouzijeme metodu Markov chain Monte Carlo (MCMC) a konkretne jej variant Gibbsovo vzorkovanie (Gibbs sampling)
Hladanie motivov pomocou Gibbsovho vzorkovania
Zadefinujeme cele ako velky pravdepodobnostny model:
- vygeneruje sa nahodne matica pravdepodobnosti W (napr z roznomernej distribucie cez vsetky matice)
- v kazdej sekvencii i sa zvoli okno
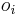 dlzky L (rovnomerne z m-L+1 moznosti)
dlzky L (rovnomerne z m-L+1 moznosti)
- V okne sa generuje sekvencia podla profilu W
- mimo okna sa generuje sekvencia z nulovej hypotezy (nezavisle bazy)
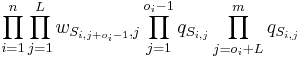
Gibbsovo vzorkovanie:
- Mame dane S, vzorkujeme O (
 ) (ak treba, z
) (ak treba, z  mozeme zostavit maticu
mozeme zostavit maticu 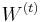 )
)
- zacni s nahodnymi oknami
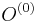
- v kroku t+1 zvol jednu sekvenciu i a pre vsetky pozicie
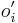 spocitaj
spocitaj 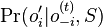 (kde
(kde 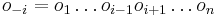 , t.j. všetky pozície výskytov okrem i-tej).
, t.j. všetky pozície výskytov okrem i-tej).
- nahodne zvol jedno
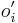 umerne k tymto pravdepodobnostiam
umerne k tymto pravdepodobnostiam
-
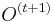 dostaneme z
dostaneme z 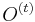 vymenou pozicie v sekvencii i za prave zvolenu
vymenou pozicie v sekvencii i za prave zvolenu
- opakuj vela krat
- zacni s nahodnymi oknami
- Konverguje k cielovemu rozdeleniu
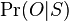 , ale vzorky nie su nezavisle
, ale vzorky nie su nezavisle
- Dalsie mozne kroky vo vzorkovani: posun vsetky okna o konstantu vlavo alebo vpravo
- Dalsie moznosti rozsirenia modelu/algoritmu: pridaj rozdelenie cez L a nahodne zvacsuj/zmensuj L, dovol vynechat motiv v niektorych sekvenciach, hladaj viac motivov naraz,...
Ako spocitat 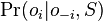 ? (nezaujimaju nas normalizacne konstanty, lahko znormalizujeme scitanim cez vsetky
? (nezaujimaju nas normalizacne konstanty, lahko znormalizujeme scitanim cez vsetky  )
)
-
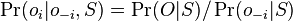 , ale menovatel konstanta
, ale menovatel konstanta
-
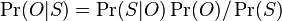 , kde
, kde 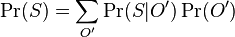
- Menovatel nas nezaujima (normalizacna konstanta)
-
 je tiez konstanta (rovnomerne rozdelenie pozicii okien)
je tiez konstanta (rovnomerne rozdelenie pozicii okien)
- Teda mame
 je umerne
je umerne 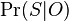
- Lahko vieme spocitat
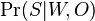 , potrebujeme "zrusit" W, da sa spocitat vzorec...
, potrebujeme "zrusit" W, da sa spocitat vzorec...
- Skusame vsetky mozne hodnoty
 , pocitame pravdepodobnost
, pocitame pravdepodobnost 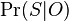 , vzorkujeme umerne k tomu
, vzorkujeme umerne k tomu
Dalsie detaily vypoctu 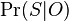 :
:
- Nech
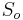 su len sekvencie v oknach a
su len sekvencie v oknach a 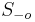 mimo okien. Mame
mimo okien. Mame 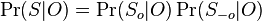
-
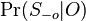 lahko spocitame (nezavisi od W)
lahko spocitame (nezavisi od W)
-
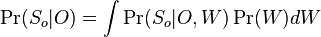 kde integral ide cez hodnoty, kde
kde integral ide cez hodnoty, kde 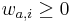 a
a 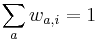
-
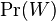 je konstanta (rovnomerne rozdelenie; nejde o pravdepodobnost ale hustotu),
je konstanta (rovnomerne rozdelenie; nejde o pravdepodobnost ale hustotu), 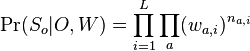 , kde
, kde  je pocet vyskytov bazy a na pozicii i v oknach
je pocet vyskytov bazy a na pozicii i v oknach 
-
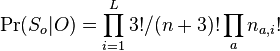 (bez dokazu)
(bez dokazu)
Siddharthan R, Siggia ED, van Nimwegen E (December 2005). "PhyloGibbs: a Gibbs sampling motif finder that incorporates phylogeny". PLoS Comput. Biol. 1 (7): e67. doi:10.1371/journal.pcbi.0010067. PMID 16477324.
Gibbs sampling, Gibbsovo vzorkovanie vseobecne
- Cielove rozdelenie ma n premennych
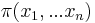
- V kazdom kroku vzorkujeme jednu premennu z podmienenej pravdepodobnosti
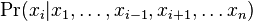
- Ostatne hodnoty nechame rovnake ako v predchadzajucom kroku
- Premennu
 zvolime nahodne alebo periodicky
zvolime nahodne alebo periodicky 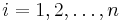
- Vzorky nie su nezavisle, no vieme dokazat nieco o konvergencii k
 (pozri nizsie)
(pozri nizsie)
Markovove reťazce
- Markovov reťazec je postupnosť náhodných premenných
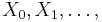 taká, že
taká, že 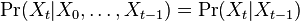 , t..j. hodnota v čase
, t..j. hodnota v čase  závisí len od hodnoty v čase
závisí len od hodnoty v čase  a nie ďalších predchádzajúcich hodnôt.
a nie ďalších predchádzajúcich hodnôt.
- Nás budú zaujímať homogénne Markovove reťazce, v ktorých
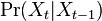 nezávisí od
nezávisí od  .
.
- Tiez nas zaujimaju len retazce v ktorych je
 z konecnej abecedy (mozne hodnoty
z konecnej abecedy (mozne hodnoty  nazyvame stavy)
nazyvame stavy)
- Napriklad stavy A,C,G,T
- V nasom Gibbsovom vzorkovani bude stav konfiguracia premennych O (.t.j mame (m-L+1)^n stavov)
- Vzorka v kroku t zavisi od vzorky v kroku t-1 (a lisi sa len v hodnote jedneho o_i)
- Pravdepodobnosti prechodu medzi stavmi za jeden krok mozeme vyjadrit maticou pravdepodobnosti P, ktorej prvok
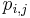 oznacuje pravdepodobnost prechodu zo stavu i do stavu j
oznacuje pravdepodobnost prechodu zo stavu i do stavu j 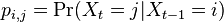
- Sucet kazdeho riadku je 1, cisla nezaporne
- Ako
 budeme oznacovat
budeme oznacovat 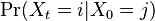 , tieto hodnoty dostaneme umocnenim matice P na t
, tieto hodnoty dostaneme umocnenim matice P na t
- Vravime ze matica je ergodicka (niekedy volane regularna), ak
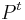 pre nejake t>0 ma vsetky polozky nenulove
pre nejake t>0 ma vsetky polozky nenulove
- Priklady neergodickych matic
1 0 0.5 0.5 0 1 0.5 0.5 0 1 0 1 1 0 1 0 nesuvisla slabo suvisla periodicka ergodicka
- Rozdelenie
 na mnozine stavov sa nazyva stacionarne pre Markovov retazec
na mnozine stavov sa nazyva stacionarne pre Markovov retazec 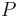 , ak pre kazde j plati
, ak pre kazde j plati 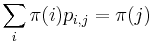 (alebo v maticovej notacii
(alebo v maticovej notacii 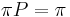 )
)
- Pre ergodicke matice existuje prave jedno stacionarne rozdelenie, pre ktore navyse plati, ze pre kazde i a j plati
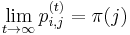
- V HMM stavy tvoria Markovov retazec; hladanie genov ergodicky stavovy priestor, profilove HMM nie
- Ine varianty: nekonecne stavove priestory (zlozitejsia teoria), spojity cas (videli sme pri evolucnych modeloch), retazce vyssieho radu, kde urcujeme
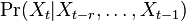 a pod.
a pod.
- Pouzitie v bioinformatike: charakterizacia nahodnych sekvencii (nulova hypoteza), pre DNA sa pouzivaju rady az do 5, lepsie ako nezavisle premenne
Markov chain Monte Carlo MCMC
- Chceme generovať náhodné vzorky z nejakeho cieloveho rozdelenia
 , ale toto rozdelenie prilis zlozite.
, ale toto rozdelenie prilis zlozite.
- Zostavime ergodicky Markovov retazec, ktoreho stacionarne rozdelenie je rozdelenie
 , tak aby sme efektivne vedeli vzorkovat
, tak aby sme efektivne vedeli vzorkovat 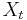 ak vieme
ak vieme 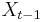 .
.
- Ak zacneme z lubovolneho bodu, po urcitom case t rozdelenie
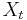 priblizne
priblizne 
- Ale za sebou iduce vzorky nie su nezavisle!
- Vieme vsak odhadovat ocakavane hodnoty roznych velicin
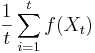 konverguje k
konverguje k ![E_{\pi }[f(X)]](/vyuka/mbi/images/math/a/a/4/aa4ecd5f5f91f0aaf04047c7435e1922.png)
Dokaz spravnosti Gibbsovo vzorkovania
- Pozor! Gibbsovo vzorkovanie nie je vzdy ergodicke, ak niektore kombinacie hodnot maju nulovu pravdepodobnost!
- Treba dokazat, ze ak je ergodicky, tak ma ako stacionarnu distribuciu nase zvolene

- Dokazeme tzv. detailed balance, ze pre kazde dva vektory hodnot x a x' mame
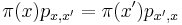
- ak pre nejaky retazec a nejaku distribuciu
 plati detailed balance,
plati detailed balance,  je stacionarna distribucia:
je stacionarna distribucia: 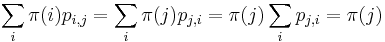
- Pre nas retazec plati detailed balance: uvazujme dva za sebou iduce vektory hodnot x a x', ktore sa lisia v i-tej suradnici. Nech
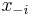 su hodnoty vsetkych ostatnych premennych okrem
su hodnoty vsetkych ostatnych premennych okrem 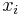
-
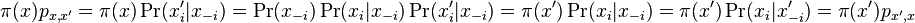
- Dokazeme tzv. detailed balance, ze pre kazde dva vektory hodnot x a x' mame
RNA a populačná genetika, cvičenia pre biológov
- zhrnutie semestra
- vynechane casti prednasok o RNA a populacnej genomike
Prakticke cvicenie
RNA
- Znama databaza rodin RNA genov je Rfam
- Najdite si v nej rodinu RF00015 (U4 spliceosomal RNA)
- V casti Secondary structure si mozete pozriet obrazky farebne kodovane podla roznych kriterii
- Skuste pochopit, co jednotlive obrazky a ich farby znamenaju
- Jedna z mnohych ludskych kopii je tato:
AGCTTTGCGCAGTGGCAGTATCGTAGCCAATGAGGTTTATCCGAGGCGCG ATTATTGCTAATTGAAAACTTTTCCCAATACCCCGCCATGACGACTTGAA ATATAGTCGGCATTGGCAATTTTTGACAGTCTCTACGGAGA
- Skuste ju najst v ludskom genome nastrojom BLAT v UCSC genome browseri
- Pozrite si tracky Mapability, Ensembl genes, conservation, Repeats v jej okoli
- Pozrite si track "CSHL Sm RNA-seq" ktory obsahuje RNASeq kratkych RNA z roznych casti buniek, zapnite si v jeho nastaveniach aj zobrazenie RNA z jadra (nucleus)
- Zadajte sekvenciu na RNAfold serveri [21]
- Ak vypocet dlho trva, pozrite si vysledok tu
- Podoba sa na strukturu zobrazenu v Rfame? v com sa lisi?
Populacna genomika v UCSC genome browseri
- Verzia hg18 na UCSC genome browseri ma viacero trackov tykajucich sa populacnej genomiky a polymorfizmov
- V casti Phenotype and Disease Associations si zapnite GAD view
- V casti Variation and Repeats si zapnite
- HGDP Allele Freq na Pack (po kliknuti na SNP zobrazi mapu sveta s distribuciou alel)
- "HapMap LD Phased" na Full
- "DGV Struct Var" na Pack
- Pozrite si napriklad region chr2:164,862-426,468
- Track Genome Variants obsahuje genomy niekolkych ludi, napr Jim Watsona
- Takisto sa da pozriet genom ludi z jaskyne Denisova a Neandertalcov
- Browser diverzity u S.cerevisae: [22]
Články na journal club
Zadelenie študentov do skupín:
3. Kent WJ, Baertsch R, Hinrichs A, Miller W, Haussler D (2003). "Evolution's cauldron: duplication, deletion, and rearrangement in the mouse and human genomes.". Proc Natl Acad Sci U S A 100 (20): 11484-9. doi:10.1073/pnas.1932072100. PMID 14500911. Čítajú Herencsár, B.Ivan, Šuníková, F.Marek, Gergeľ, Gibaštíková, Mizerák
4. Siepel A, Bejerano G, Pedersen JS, Hinrichs AS, Hou M, Rosenbloom K et al. (2005). "Evolutionarily conserved elements in vertebrate, insect, worm, and yeast genomes". Genome Res 15 (8): 1034-50. doi:10.1101/gr.3715005. PMID 16024819. Čítajú Račko, Repka, Racik, Šušuková, Lacko, Štibraný, Hlavenková
7. Eisen MB, Spellman PT, Brown PO, Botstein D (1998). "Cluster analysis and display of genome-wide expression patterns.". Proc Natl Acad Sci U S A 95 (25): 14863-8. PMID 9843981. Čítajú Sternmüller, Pukancová, Kotrlová, Chripko, Jusko, Filipčík, Bohunský
10. Sharan R, Suthram S, Kelley RM, Kuhn T, McCuine S, Uetz P et al. (2005). "Conserved patterns of protein interaction in multiple species.". Proc Natl Acad Sci U S A 102 (6): 1974-9. doi:10.1073/pnas.0409522102. PMID 15687504. Čítajú Rapčík, Miniariková, Bielik, Byrtus, Fečík, Baláž, Zamba
11. Andronescu M, Fejes AP, Hutter F, Hoos HH, Condon A (2004). "A new algorithm for RNA secondary structure design.". J Mol Biol 336 (3): 607-24. doi:10.1016/j.jmb.2003.12.041. PMID 15095976. Čítajú Benko, Simanová, Zezulová, Fulla, Kováč, Pánis, Kempa, Ondruš
Nevybrané články
1. Zerbino DR, Birney E (2008). "Velvet: algorithms for de novo short read assembly using de Bruijn graphs.". Genome Res 18 (5): 821-0. doi:10.1101/gr.074492.107. PMID 18349386.
2. Lunter G (2007). "Probabilistic whole-genome alignments reveal high indel rates in the human and mouse genomes.". Bioinformatics 23 (13): i289-96. doi:10.1093/bioinformatics/btm185. PMID 17646308.
5. Wapinski I, Pfeffer A, Friedman N, Regev A (2007). "Natural history and evolutionary principles of gene duplication in fungi". Nature 449 (7158): 54-61. doi:10.1038/nature06107. PMID 17805289.
6. Clamp M, Fry B, Kamal M, Xie X, Cuff J, Lin MF et al. (2007). "Distinguishing protein-coding and noncoding genes in the human genome.". Proc Natl Acad Sci U S A 104 (49): 19428-33. doi:10.1073/pnas.0709013104. PMID 18040051.
8. Harbison CT, Gordon DB, Lee TI, Rinaldi NJ, Macisaac KD, Danford TW et al. (2004). "Transcriptional regulatory code of a eukaryotic genome.". Nature 431 (7004): 99-104. doi:10.1038/nature02800. PMID 15343339.
9. Bystroff C, Thorsson V, Baker D (August 2000). "HMMSTR: a hidden Markov model for local sequence-structure correlations in proteins". J. Mol. Biol. 301 (1): 173–90. doi:10.1006/jmbi.2000.3837. PMID 10926500.
12. Hernandez RD, Hubisz MJ, Wheeler DA, Smith DG, Ferguson B, Rogers J et al. (2007). "Demographic histories and patterns of linkage disequilibrium in Chinese and Indian rhesus macaques.". Science 316 (5822): 240-3. doi:10.1126/science.1140462. PMID 17431170.
Ukážkové príklady na skúšku
Určitú časť bodov na skúške bude možné pre biológov aj informatikov možné získať z príkladov typu uvedeného nižšie. Samozrejme, na skúške nepoužijeme všetky tieto príklady a konkrétne reťazce, čísla, stromy a pod. budú iné. Na skúške máte dovolené používať kalkulačku s bežnými matematickými funkciami (nie však zložitejšie výpočtové zariadenia) a ťahák na dvoch listoch formátu A4, ktoré môžu byť z oboch strán popísané alebo potlačené ľubovoľným obsahom. Ostatné príklady na skúške budú prekvapením.
- Nájdite najkratšie spoločné nadslovo reťazcov GACAATAA, ATAACAC, GTATA, TAATTGTA.
- Vyplňte maticu dynamického programovania pre lokálne (resp. globálne) zarovnanie reťazcov TACGT a CAGGATT, pričom zhodu skórujeme ako +3, nezhodu -1, medzeru -2. Napíšte aj optimálne zarovnanie, ktoré ste takto našli.
- Spočítaje skóre nižšieuvedeného zarovnania, pričom použijete skórovaciu maticu uvedenú nižšie, začatie medzery -5, rozšírenie medzery o jednu ďalšiu bázu -2. Nájdite globálne zarovnanie s vyšším skóre pre tieto dve sekvencie (netreba nájsť optimálne zarovnanie; pri hľadaní môžete použiť ľubovoľný postup alebo úvahu) a spočítajte aj skóre vášho nového zarovnania.
Zarovnanie: Matica:
ATAGTTTAA A C G T
A-GGG--AA A 2 -2 -1 -2
C -2 1 -2 -1
G -1 -2 1 -2
T -2 -1 -2 2
- Uvažujme BLASTn, ktorý začína z jadier veľkosti w=3. Koľko jadier nájde pri porovnávaní sekvencií GATTACGGAT a CAGGATT? Ktoré to budú?
- Pre model na strane 16 prednášky o hľadaní génov (bol by v zadaní) spočítajte pravdepodobnosť vygenerovania báz AGT a stavov modrý,červený,modrý.
- Na strome na strane 6 v prednáške o evolúcii (bol by v zadaní) nájdite najúspornejšie ancestrálne znaky pre stĺpec zarovnania TTAAA (v poradí glum, hobit, človek, elf, ork). Nemusíte použiť algoritmy z prednášky resp. cvičení.
- Nájdite najúspornejší strom pre zarovnanie uvedené nižšie. Aká je jeho cena (koľko mutácií je nutných na vysvetlenie týchto sekvencií)? Odpoveď môžete spočítať ľubovoľným spôsobom.
vtáčik biely ACAACGTCT vtáčik čierny TCTGAATCA vtáčik sivý TGTGAAAGA vtáčik modrý ACTACGTCT vtáčik zelený TGTGAAAGA
- Uvažujme maticu vzdialeností uvedenú nižšie. Ktorú dvojicu vrcholov spojí metóda spájania susedov ako prvú a aká bude nová matica po spojení?
biely čierny sivý modrý
vtáčik biely 0 5 7 4
vtáčik čierny 5 0 8 5
vtáčik sivý 7 8 0 5
vtáčik modrý 4 5 5 0
- Uvažujme strom ako na strane 6 v prednáške o evolúcii (bol by v zadaní), pričom každá hrana má rovnakú dĺžku a pravdepodobnosť každej mutácie na jednej hrane je 0.1 (t.j. napr. Pr(C|A,t)=0.1) a teda pravdepodobnosť zachovania tej istej bázy je 0.7, pravdepodobnosť každej bázy v koreni je 0.25. Aká je pravdepodobnosť, že v listoch dostaneme TTAAA a vo vnútorných vrcholoch samé Áčka? Nájdite priradenie ancestrálnych báz vo vnútorných vrcholoch, ktoré má väčšiu pravdepodobnosť a spočítajte, aká tá pravdepodobnosť je (nemusíte nájsť najlepšie možné priradenie).
- Zostavte profil (PSSM) pre zarovnanie sekvencií uvedené nižšie, pričom predpokladáme, že v celej databáze A tvorí 60% a T 40% všetkých sekvencií (iné bázy neuvažujeme). Použite prirodzený logaritmus (ln) a pseudocount 1.
AATA TATA TAAA TTAT TTAA
- Uvažujme microarray experimenty pre 5 génov. Medzi každými dvomi génmi sme spočítali vzdialenosť ich profilov expresie a dostali sme tabuľku vzdialeností uvedenú nižšie. Nájdite hierarchické zhlukovanie týchto génov, pričom vzdialenosť medzi dvoma zhlukmi (clustrami) bude vzdialenosť najbližších génov v nich.
A B C D E
gén A 0 0.6 0.1 0.3 0.7
gén B 0.6 0 0.5 0.5 0.4
gén C 0.1 0.5 0 0.6 0.6
gén D 0.3 0.5 0.6 0 0.8
gén E 0.7 0.4 0.6 0.8 0
- Uvažujte motív reprezentovaný profilom (skórovaciou maticou, PSSM) uvedenou nižšie. Spočítajte skóre reťazca GGAG. Ktorá sekvencia dĺžky 4 bude mať najmenšie a ktorá najväčšie skóre?
A -3 3 -2 -2 C -2 -2 1 -2 G 0 -2 -1 3 T 1 -1 1 -2
- Nájdite všetky výskyty regulárneho výrazu TA[CG][AT]AT v sekvencii GACGATATAGTATGTACAATATGC.
- Doplňte chýbajúce hodnoty za otázniky v matici dynamického programovania (Nussinovov algoritmus) pre nájdenie najväčšieho počtu dobre uzátvorkovaných spárovaných báz v RNA sekvencii GAACUAUCUGA (dovoľujeme len komplementárne páry A-U, C-G) a nakreslite sekundárnu štruktúru, ktorú algoritmus našiel.
0 0 0 1 1 2 2 3 3 ? ?
0 0 0 1 1 2 2 3 3 ?
0 0 1 1 2 2 2 3 3
0 0 1 1 1 1 2 3
0 1 1 ? 1 2 3
0 1 1 1 2 2
0 0 0 1 2
0 0 1 1
0 0 1
0 0
0
- Pre dvojice SNPov, ktorých tabuľky sú uvedené nižšie, určite, či môžeme štatisticky vylúčiť hypotézu, že sú v stave LE (linkage equilibrium) pri hladine významnosti p=0.05, resp.
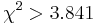 . Pre každú dvojicu spočítajte veličinu
. Pre každú dvojicu spočítajte veličinu  .
.
Q q Q q Q q
P 100 200 P 10 20 P 1 2
p 300 200 p 30 20 p 3 2
![A[i,j]=\max \left\{A[i-1,j-1]+s(x_{i},y_{j}),A[i-1,j]-1,A[i,j-1]\right\}](/vyuka/mbi/images/math/1/6/f/16f1ddd6bdc5d2a31e14184fdad3cf04.png)