1-BIN-301, 2-AIN-501 Methods in Bioinformatics, 2023/24
Exam
Obsah
- 1 Exam rules
- 2 Sylabus and examples of problem
- 2.1 Sequencing and genome assembly
- 2.2 Sequence alignment
- 2.3 Gene finding
- 2.4 Evolution and comparative genomics
- 2.5 Expresia génov, regulácia, motívy
- 2.6 Proteíny
- 2.7 RNA
- 2.8 Populačná genetika
- 2.9 Ďalšie dôležité znalosti z cvičení pre informatikov
- 2.10 Ďalšie dôležité znalosti z cvičení pre biológov
Exam rules
The main part is written:
- You need at least 50% of points
- Time 3 hours
- About 50% of points for simple questions,
- examples on this page
- in case of interest tutorial session before exam
- The rest of the questions mostly designing/modifying an algorithm or model
- Online or in person, depending on circumstances
- You can use pen, simple calculator and a cheat sheet up to 2 A4 two-sided sheets
Written exam, online version
- Exam questions and submission in Moodle (e-mail for guests)
- MS teams: annoucements, questions
- Write in an editor, create pdf or write on paper, scan/photo, convert to pdf
- Allowed aids:
- Same as in person (incl. cheat sheet)
- Plus: Text and image editors, software for digitization of handwritten pages, MS Teams to communicate with instructors Moodle for getting and submitting exam
- Not allowed:
- Communication with other persons except instructors
- Other webpages
- Other software (e.g. specialized bioinformatics programs, compilers)
Oral exam
- Only for online exam
- Videocall in MS Teams
- After written exam, time slots over several days
- We will discuss your exam
- You should be able to explain your answers in detail
- Oral exam influences exam grade
- If you are unable to explain your answers, you will get Fx
“Second chance” exam
- The same for as the first or oral-only
- The dates arranged with those who need them
Sylabus and examples of problem
Below we list the most important concepts that both biologists and computer scientists should know form this course.
We also list simple questions. Questions of this type will comprise approximately 50% of the exam. Not all of these questions will be used on the exam and particular string, numbers and sequences will differ.
Sequencing and genome assembly
DNA sequencing and its use, sequencing read, paired reads, contigs, shortest common superstring problem, de Bruijn graphs
Sekvenovanie DNA a jeho využitie, čítanie (read), spárované čítania, kontig, problém najkratšieho spoločného nadslova, de Bruijnove grafy
- Find the shortest common superstring of strings GACAATAA, ATAACAC, GTATA, TAATTGTA.
- Find the de Bruijn graph for k=2 (nodes will be pairs of nucleotides) and reads CCTGCC, GCCAAC
Sequence alignment
The problem of local and global alignment of two sequences, dynamic programming algorithms, scoring matrix and its probabilistic meaning, statistical significance (E-value, P-value), heuristic search of local alignments (BLAST), whole-genome and multiple alignments
Problém lokálneho a globálneho zarovnania dvoch sekvencií, jeho riešenie pomocou dynamického programovania, skórovacia matica a jej pravdepodobnostný význam, štatistická významnosť (E-value, P-value), heuristické hľadanie lokálnych zarovnaní (BLAST), celogenómové a viacnásobné zarovnania
- Fill in the dynamic programing matrices for local and global alignment of sequences TACGT a CAGGATT, where the match has score +3, mismatch -1, gap -2. Reconstruct also the optimal alignments found by the dynamic programming algorithm
- Compute the score of the alignment shown below using the scoring matrix shown below, gap opening penalty -5, gap extension penalty -2 for each additional base. Find a global alignment with a higher score for these two sequences and compute its score. (It is not necessary to find the optimal alignment; you can use any method to arrive at the answer.)
Alignment: Matrix:
ATAGTTTAA A C G T
A-GGG--AA A 2 -2 -1 -2
C -2 1 -2 -1
G -1 -2 1 -2
T -2 -1 -2 2
- Consider BLASTn algorithm starting from seeds of size w=3. How many seeds it finds while comparing sequences GATTACGGAT and CAGGATT? List all found seeds.
Gene finding
Gene, exon, intron, mRNA, splicing and alternative splicing, genetic code, hidden markov model (HMM), its states, transition and emission probabilities, use of HMMs in gene finding
Gén, exón, intrón, mRNA, zostrih a alternatívny zostrih, kodón, genetický kód, skrytý Markovov model (HMM), jeho stavy, pravdepodobnosti prechodu a emisie, použitie HMM na hľadanie génov
- What is the probablity of generating sequence AGT using sequence of states 1,2,1 in the HMM below?
The HMM has three states 1, 2, 3. It always starts in state 1. Transition probabilities: From 1 to 1: 0.99 From 1 to 2: 0.01 From 2 to itself: 0.9 From 2 to 1: 0.05 From 2 to 3: 0.05 From 3 to itself: 0.99 From 3 to 2: 0.01 Emmision probabilities in state 1: A 0.25, C 0.25, G 0.25, T 0.25 Emmision probabilities in state 2: A 0.3, C 0.2, G 0.2, T 0.3 Emmision probabilities in state 3: A 0.2, C 0.4, G 0.3, T 0.1
Evolution and comparative genomics
Phylogenetic tree (rooted and unrooted), maximum parsimony method, neighbor joining method, maximum likelihood method, Jukes-Cantor substitution model and more complex substitution matrices, homolog, paralog, ortholog, positive and negative selection detection, phylogenetic HMMs, likelihood ratio test
Fylogenetický strom (zakorenenený a nezakorenený), metóda maximálnej úspornosti (parsimony), metóda spájania susedov (neighbor joining), metóda maximálnej vierohodnosti (maximum likelihood), Jukes-Cantorov model substitúcií a zložitejšie substitučné matice, homológ, paralóg, ortológ, detekcia pozitívneho a negatívneho výberu, fylogenetické HMM, test pomerom vierohodností (likelihood ratio test)
- Find the most parsimonious assignment of bases at the ancestral nodes in the tree below given a column of alignment TTAAA (in the order gollum, hobbit, human, elf, orc). You can derive your answer using any method.
Gollum ----|
|----|
Hobbit ----| |----|
| |
Human ---------| |
|---
Elf --------| |
|--------|
Orc --------|
- Find the most parsimonious tree for the alignment given below. What is its cost (i.e. how many mutations are necessary to explain these sequences)? You can derive your answer using
any method.
whitebird ACAACGTCT blackbird TCTGAATCA graybird TGTGAAAGA blubird ACTACGTCT greenbird TGTGAAAGA
- Consider the tree for gollum, hobbit etc. given above, where each branch has the same length t. Let us assume that for any two different bases x and y, the probability of base x mutating to base y over time y is 0.1, and thus the probability of base x remaining the same after time t is 0.7. Probability of each base in the root is 0.25. Compute the probability that the tree will have base A in all internal nodes and in leaves bases TTAAA (from top to bottom). Find an asignment of bases in the ancestral nodes with a higher probablity and compute this probability (you do not need to find the best possible assignment).
- Consider the distance matrix given below. Which pair of nodes will be connected as first by the neighbor joining method and what will be the new distance matrix after joining these two nodes?
white black gray blue
whitebird 0 5 7 4
blackbird 5 0 8 5
graybird 7 8 0 5
bluebird 4 5 5 0
Expresia génov, regulácia, motívy
Measuring gene expressing using microarray or RNA-seq, hierarchical clustering, classification, representation of sequence motifs (transcription factor binding sites) as a consensus, regular expression and PSSM, finding new motifs in sequences, consensus pattern problem, finding motifs using probability models (EM algorithm)
Určovanie génovej expresie pomocou microarray alebo sekvenovaním RNA-seq, hierarchické zhlukovanie, klasifikácia, reprezentácia sekvenčných motívov (väzobné miesta transkripčných faktorov) ako konsenzus, regulárny výraz a PSSM, hľadanie nových motívov v sekvenciách, consensus pattern problem, hľadanie motívu pomocou pravdepodobnostných modelov (EM algoritmus)
- After a series of expression measurements for 5 genes, we have computed distances between pairs of expression profiles and obtained the distance table shown below. Find the hierarchical clustering of these genes, where the distance between two clusters is computed as the minimum of the closest genes in these clusters (single linkage clustering). Show the order in which you were creating individual clusters.
A B C D E
gene A 0 0.6 0.1 0.3 0.7
gene B 0.6 0 0.5 0.5 0.4
gene C 0.1 0.5 0 0.6 0.6
gene D 0.3 0.5 0.6 0 0.8
gene E 0.7 0.4 0.6 0.8 0
- Consider a motif represented by a PSSM shown below. Compute the score of string GGAG. Which sequence of length 4 will have the smallest and highest score?
A -3 3 -2 -2 C -2 -2 1 -2 G 0 -2 -1 3 T 1 -1 1 -2
- Find all occurrences of regular expression TA[CG][AT]AT in sequence GACGATATAGTATGTACAATATGC.
Proteíny
Primárna, sekundárna a terciálna štruktúra proteínov, proteínové domény a rodiny, reprezentovanie rodiny pravdepodobnostným profilom a profilovým HMM, protein threading, gene ontology.
- Zostavte profil (PSSM) pre zarovnanie sekvencií uvedené nižšie, pričom predpokladáme, že v celej databáze A tvorí 60% a G 40% všetkých sekvencií (iné aminokyseliny neuvažujeme). Použite prirodzený logaritmus (ln) a pseudocount 1.
AAGA GAGA GAAA GGAG GGAA
RNA
Sekundárna štruktúra RNA, pseudouzol a dobre uzátvorkovaná štruktúra, Nussinovovej algoritmus, minimalizácia energie, stochastické bezkontextové gramatiky, kovariančné modely.
- Doplňte chýbajúce hodnoty za otázniky v matici dynamického programovania (Nussinovovej algoritmus) pre nájdenie najväčšieho počtu dobre uzátvorkovaných spárovaných báz v RNA sekvencii GAACUAUCUGA (dovoľujeme len komplementárne páry A-U, C-G) a nakreslite sekundárnu štruktúru, ktorú algoritmus našiel.
0 0 0 1 1 2 2 3 3 ? ?
0 0 0 1 1 2 2 3 3 ?
0 0 1 1 2 2 2 3 3
0 0 1 1 1 1 2 3
0 1 1 ? 1 2 3
0 1 1 1 2 2
0 0 0 1 2
0 0 1 1
0 0 1
0 0
0
- Uvažujme RNA sekvenciu dĺžky 27, ktorá má v sekundárnej štruktúre spárované komplementárne bázy na pozíciách: (2,23), (3,22), (4,21), (5,13), (6,12), (8,16), (9,15), (10,14), (18,26) a (19,25). Koľko najmenej párov z tohto zoznamu musíme odstrániť, aby sme dostali štruktúru bez pseudouzlov? Ktoré páry to budú?
- Uvažujme sekvenciu RNA ACUGAGUCCAAGG, ktorá má v sekundárnej štruktúre spárované bázy na pozíciách (1,7), (2,6), (3,5), (8,13) a (9,12). (Pozície číslujeme od 1.) (Táto RNA je uvedená ako príklad na strane 12 prednášky o RNA.) Ukážte akou postupnosťou pravidiel by sme ju mohli odvodiť v gramatike uvedenej nižšie tak, aby spárované bázy boli vždy vytvorené v jednom kroku odvodenia.
- Gramatika: S->aSu|uSa|cSg|gSc|aS|cS|gS|uS|Sa|Sc|Sg|Su|SS|epsilon
- Iný príklad gramatiky: S->aSu|uSa|cSg|gSc|TS|ST|SS|epsilon; T->aT|cT|gT|tT|epsilon
Populačná genetika
Polymorfizmus, SNP, alela, homozygot, heterozygot, rekombinácia, frekvencia polymorfizmu ako markovovský reťazec, náhodný genetický drift, väzbová nerovnováha (linkage disequilibrium), mapovanie asociácií, LD blok, subpopulácia.
- Pre dvojice SNPov, ktorých tabuľky sú uvedené nižšie, určite, či môžeme štatisticky vylúčiť hypotézu, že sú v stave väzbovej rovnováhy (LE, linkage equilibrium) pri hladine významnosti p=0.05, resp.
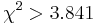 . Pre každú dvojicu spočítajte veličinu
. Pre každú dvojicu spočítajte veličinu 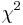 .
.
Q q Q q Q q
P 100 200 P 10 20 P 1 2
p 300 200 p 30 20 p 3 2
Ďalšie dôležité znalosti z cvičení pre informatikov
(iba informatická časť skúšky)
- Pokročilejšie ukážky dynamického programovania (proteíny MS/MS, varianty zarovnávania sekvencií, varianty Nussinovovej algoritmu)
- BLAST, MinHashing
- Algoritmy pre použitie HMM (Viterbiho, dopredný)
- Felsensteinov algoritmus
- Celočíselné lineárne programovanie
- EM algoritmus na hľadanie motívov
Ďalšie dôležité znalosti z cvičení pre biológov
(iba biologická časť skúšky)
- Interpretácia dotplotov
- Interpretácia fylogenetických stromov, bootstrap, zakorenenie
- Interpretácia vizualizácií z UCSC genome browsera
- Ukážky rôznych bioinformatických programov, súvis ich nastavení a výsledkov s pojmami z prednášky
- Analýza nadreprezentácie, multiple testing correction, K-means clustering