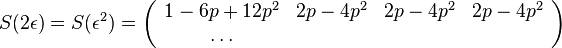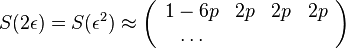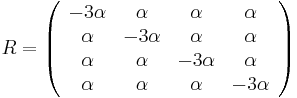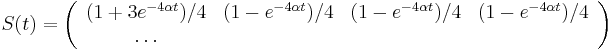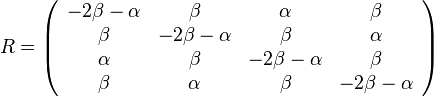1-BIN-301, 2-AIN-501 Methods in Bioinformatics, 2023/24
MBI 2009/2010: Rozdiel medzi revíziami
(Created page with ''''Metódy v bioinformatike, školský rok 2009/2010''' Táto wiki obsahuje rôzne poznámky k predmetu [http://compbio.fmph.uniba.sk/vyuka/mbi/ Metódy v bioinformatike] (2-AIN…') |
(→Typy projektov) |
||
| Riadok 950: | Riadok 950: | ||
Toto su typicke druhy projektov, mozete sa vsak pokusit aj o projekt ineho typu, alebo skombinovat niekolko typov. | Toto su typicke druhy projektov, mozete sa vsak pokusit aj o projekt ineho typu, alebo skombinovat niekolko typov. | ||
* '''Prehladove''': prestudujte niekolko suvisiach clankov (cca 3 ale moze byt aj viac) a spiste prehlad ich vysledkov. | * '''Prehladove''': prestudujte niekolko suvisiach clankov (cca 3 ale moze byt aj viac) a spiste prehlad ich vysledkov. | ||
| − | * '''Aplikacne''': pouzite existujuce programy na nove data (data mozu byt nahodne generovane, stiahnute z databaz na internete, alebo z vasho vlastneho vyskumu). Mali by ste rozumiet, aky problem presne pouzite programy riesia a aky je vyznam ich parametrov. Ak pouzivate len jeden program, skuste aspon menit nastavenia parametrov | + | * '''Aplikacne''': pouzite existujuce programy na nove data (data mozu byt nahodne generovane, stiahnute z databaz na internete, alebo z vasho vlastneho vyskumu). Mali by ste rozumiet, aky problem presne pouzite programy riesia a aky je vyznam ich parametrov. Ak pouzivate len jeden program, skuste aspon menit nastavenia parametrov a vsimat si ich vplyv na vysledok. Druha moznost je porovnat vysledky roznych programov alebo urobit zlozitejsiu analyzu pomocou viacerych programov, ktore na seba nadvazuju. V kazdom pripade by sme mali nejako (aspon nepriamo) vyhodnotit, ci program dava rozumne vysledky. |
* '''Implementacne''': implementujte zlozitejsi algoritmus z nejakeho clanku (pripadne aj z prednasky) a otestujte ho na datach. Okrem testov na odstranenie chyb v kode, ktore by mali byt samozrejmostou, treba spravit aj testy, ktore vyhodnocuju rychlost algoritmu alebo presnost jeho vysledkov, najlepsie v porovnani s inymi algoritmami/implementaciami alebo v zavislosti od nejakych parametrov. | * '''Implementacne''': implementujte zlozitejsi algoritmus z nejakeho clanku (pripadne aj z prednasky) a otestujte ho na datach. Okrem testov na odstranenie chyb v kode, ktore by mali byt samozrejmostou, treba spravit aj testy, ktore vyhodnocuju rychlost algoritmu alebo presnost jeho vysledkov, najlepsie v porovnani s inymi algoritmami/implementaciami alebo v zavislosti od nejakych parametrov. | ||
* '''Vymyslacie''': vymyslite novy algoritmus alebo pravdepodobnostny model, analyzujte existujuci algoritmus a podobne. Pripadne potom mozete svoje napady skusit aj implementovat a testovat. | * '''Vymyslacie''': vymyslite novy algoritmus alebo pravdepodobnostny model, analyzujte existujuci algoritmus a podobne. Pripadne potom mozete svoje napady skusit aj implementovat a testovat. | ||
Verzia zo dňa a času 20:54, 3. október 2010
Metódy v bioinformatike, školský rok 2009/2010
Táto wiki obsahuje rôzne poznámky k predmetu Metódy v bioinformatike (2-AIN-501).
Obsah
- 1 Sekvenovanie genómov, cvičenia pre biológov
- 2 Úvod do dynamického programovania, cvičenia pre biológov
- 3 Zarovnávanie sekvencií, cvičenia pre biológov
- 4 Evolúcia, cvičenia pre biológov
- 5 Evolúcia, cvičenia pre informatikov
- 6 Expresia génov, cvičenia pre biológov
- 7 Hľadanie motívov, cvičenia pre biológov
- 8 Hľadanie motívov, cvičenia pre informatikov
- 9 Články na journal club
- 10 Ukážkové príklady na skúšku
- 11 Pokyny k projektom
Sekvenovanie genómov, cvičenia pre biológov
- Cvicenia pre biológov zo sekvenovania, pracovna verzia poznamok
- Ospravedlnujem sa za chybajucu diakritiku
- Pozrite tiez grafy k pravdepodobnosti: http://compbio.fmph.uniba.sk/vyuka/mbi/poznamky/cb02.pdf
UCSC genome browser
- http://genome.ucsc.edu/
- Ukazali sme si niekolko trackov, ktore maju suvis so sekvenovanim a skladanim genomov, napr. gaps, quality score a pod. (v genomoch cloveka a macky)
Pravdepodobnost
- Nas problem: spocitanie pokrytia
- G = dlzka genomu, napr. 1 000 000
- N = pocet segmentov (readov), napr. 10 000
- L = dlzka readu, napr. 1000
- Celkova dlzka segmentov NL, pokrytie (coverage) NL/G, v nasom pripade 10x
- V priemere kazda baza pokryta 10x
- Niektore su ale pokryte viackrat, ine menej.
- Zaujimaju nas otazky typu: kolko baz ocakavame, ze bude pokrytych menej ako 3x?
- Dolezite pri planovani experimentov (aku velke pokrytie potrebujem na dosiahnutie urcitej kvality)
- Uvod do pravdepodobnosti
- Myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealnou kockou/korunou
- Vysledkom experimentu je nejaka hodnota (napr. cislo, alebo aj niekolko cisel, retazec)
- Tuto neznamu hodnotu budeme volat nahodna premenna
- Zaujima nas pravdepodobnost, s akou nahodna premenna nadobuda jednotlive mozne hodnoty
- T.j. ak experiment opakujeme vela krat, ako casto uvidime nejaky vysledok
- Priklad 1: hodime idealizovanou kockou, premenna X bude hodnota, ktoru dostaneme
- Mozne hodnoty 1,2,..,6, kazda rovnako pravdepodobna
- Piseme napr. Pr(X=2)=1/6
- Priklad 2: hodime 2x kockou, nahodna premenna X bude sucet hodnot, ktore dostaneme
- Mozne hodnoty: 2,3,...,12
- Kazda dvojica hodnot na kocke rovnako pravdepodobna, t.j. pr. 1/36
- Sucet 5 mozeme dostat 1+4,2+3,3+2,4+1 - t.j. P(X=5) = 4/36
- Sucet 11 mozeme dostat 5+6 alebo 6+5, t.j. P(X=11) = 2/36
- Rozdelenie pravdepodobnosti: 2: 1/36, 3:2/36, 4: 3/36, ... 7: 6/36, 8: 5/36 ... 12: 1/36
- Overte, ze sucet je 1
- Pokrytie genomu: predpokladame, ze kazdy segment zacina na nahodnej pozicii zo vsetkych moznych G-L+1
- Takze ak premenna Y_i bude zaciatok i-teho segmentu, jej rozdelenie bude rovnomerne
- P(Y_i=1) = P(Y_i=2) = ... = P(Y_i=G-L+1) = 1/G-L+1
- Uvazujme premennu X_j, ktora udava pocet segmentov pokryvajucich poziciu j
- mozne hodnoty 0..N
- i-ty segment pretina poziciu j s pravdepodobnostou L/(G-L+1), oznacme tuto hodnotu p
- to iste ako keby sme N krat hodili mincou, na ktorej spadne hlava s pravd. p a znak 1-p a oznacili ako X_j pocet hlav
- Priklad: majme mincu, ktora ma hlavu s pr. 1/4 a hodime je 3x.
HHH 1/64 HHT 3/64 HTH 3/64 HTT 9/64 THH 3/64 THT 9/64 TTH 9/64 TTT 27/64
- P(X_j=3) = 1/64, P(X_j=2)=9/64, P(X_j=1)=27/64, P(X_j=0)=27/64
- taketo rozdelenie pravdepodobnosti sa vola binomicke
- P(X_j = k) = (N choose k) p^k (1-p)^(N-k), kde
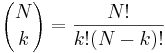 a n! = 1*2*...*n
a n! = 1*2*...*n
- napr pre priklad s troma hodmi kockou P(X_j=2) = 3!/(2!*1!) * (1/4)^2 * (3/4)^1 = 9/64
- Zle sa pocita pre velke N, preto sa niekedy pouziva aproximacia Poissonovym rozdelenim s parametrom lambda = Np, ktore ma
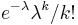
- Spat k sekvenovaniu: vieme spocitat rozdelenie pravdepodobnosti a tiez napr. P(X_i<3) = P(X_i=0)+P(X_i=1)+P(X_i=2) = 0.000045+0.00045+0.0023=0.0028 (v priemere ocakavame 45 baz nepokrytych)
- Takyto graf, odhad, vieme lahko spravit pre rozne pocty segmentov a tak naplanovat, kolko segmentov potrebujeme
- Chceme tiez odhadnut pocet kontigov (nebrali sme na cviceni, uvedene len pre zaujimavost)
- Ak niekolko baz vobec nie je pokrytych segmentami, prerusi sa kontig
- Vieme, kolko baz je v priemere nepokrytych, ale niektore mozu byt vedla seba
- Novy kontig vznikne aj ak sa susedne segmenty malo prekryvaju
- Predpokladajme, ze na spojenie dvoch segmentov potrebujeme prekryv aspon T
- Lander a Waterman 1988 odhadli, ze dany segment ma pravdepodobnost zhruba exp(-N(L-T)/G), ze bude posledny v kontigu
- Pre N segmentov dostaneme priemerny pocet kontigov 1+N*exp(-N(L-T)/G)
- Ako keby sme dlzku segmentu skratili o dlzku prekryvu
- Pre T=50 dostaneme priemerny pocet kontigov 1.75, ak znizime N na 5000 (5x pokrytie) dostaneme 44 kontigov
- Tento jednoduchy model nepokryva vsetky faktory:
- Segmenty nemaju rovnaku dlzku
- Problemy v zostavovani kvoli chybam, opkaovaniam a pod.
- Segmenty nie su rozlozene rovnomerne (cloning bias a pod.)
- Vplyv koncov chromozomov
- Uzitocny ako hruby odhad
- Na spresnenie mozeme skusat spravit zlozitejsie modely, alebo simulovat data
- Poznamka: pravdepodobnosti z binomickeho rozdelenia mozeme lahko spocitat napr. statistickym softverom R. Tu su prikazy, ktore sa na to hodia, pre pripad, ze by vas to zaujimalo:
dbinom(10,1e4,0.001); #(12.5% miest ma pokrytie presne 10) pbinom(10,1e4,0.001,lower.tail=TRUE); #(58% miest ma pokrytie najviac 10) dbinom(0:30,1e4,0.001); #tabulka pravdepodobnosti [1] 4.517335e-05 4.521856e-04 2.262965e-03 7.549258e-03 1.888637e-02 [6] 3.779542e-02 6.302390e-02 9.007019e-02 1.126216e-01 1.251601e-01 [11] 1.251726e-01 1.137933e-01 9.481826e-02 7.292252e-02 5.207187e-02 [16] 3.470068e-02 2.167707e-02 1.274356e-02 7.074795e-03 3.720595e-03 [21] 1.858621e-03 8.841718e-04 4.014538e-04 1.743354e-04 7.254524e-05 [26] 2.897743e-05 1.112843e-05 4.115040e-06 1.467156e-06 5.050044e-07 [31] 1.680146e-07
Zhrnutie
- Pravdedpobnostny model: myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealizovanou kockou
- Vysledok je hodnota, ktoru budeme volat nahodna premenna
- Tabulka, ktora pre kazdu moznu hodnotu nahodnej premennej urci je pravdepodobnost sa vola rozdelenie pravdepodobnosti, sucet hodnot v tabulke je 1
- Znacenie typu P(X=7)=0.1
- Priklad: mame genom dlzky G=1mil., nahodne umiestnime N=10000 segmentov dlzky L=1000
- Nahodna premenna X_i je pocet segmentov pokryvajucich urcitu poziciu i
- Podobne, ako keby sme N krat hodili kocku, ktora ma cca 1 promile sancu padnu ako hlava a 99.9% ako znak a pytame sa, kolko krat padne znak (1 promile sme dostali po zaukruhleni z L/(G-L+1))
- Rozdelenie pravdepobnosti sa v tomto pripade vola binomicke a existuje vzorec, ako ho spocitat
- Takyto model nam moze pomoct urcit, kolko segmentov potrebujeme osekvenovat, aby napr. aspon 95% pozicii bolo pokrytych aspon 4 segmentami
Eulerovský ťah
- Nestihli sme na cviceniach, uvedene pre zaujimavost
- Orientovany graf
- Silne suvisly orientovany graf
- Eulerovsky tah, uzatvoreny eulerovsky tah
- Pouzitie v de Bruijnovom grafe na zostavovanie genomu
- Silne súvislý orientovany graf ma uzatvoreny eulerovsky tah prave vtedy, ked v kazdom vrchole je rovnako vchadzajucich a vychadzajucich hran
- ak ma tah, musi byt suvisly
- ak ma tak, musia sediet pocty hran
- ak je suvisly a sedia pocty hran:
- prechadzka po grafe, kym sa da pokracovat nepouzitou hranou
- musime skoncit, kde sme zacali (z ostatnych vrcholov vieme pokracovat)
- zvysok grafu stale splna podmienku s poctami hran
- najdi dalsi vrchol, ktory je na tahu a ma este nepouzite hrany
- musi taky existovat
- pokracuj v tom istom, az kym sa nevratime, kde sme zacali
- cele opakujeme, az kym sa neminu hrany
- Poznamka: v neorientovanych grafoch musia byt stupne vsetkych vrcholov parne
- Ak hladame otvoreny tah, spojime zaciatocny a koncovy vrchol hranou a najdeme uzatvoreny tah
Úvod do dynamického programovania, cvičenia pre biológov
- Cvicenia pre biológov z dynamickeho programovania, pracovna verzia poznamok
- Ospravedlnujem sa za chybajucu diakritiku
Dynamické programovanie
- Tuto techniku uvidime dnes na prednaske na hladanie zarovnani (alignmentov)
- Uvazujme problem rozmienania minci
- Napr mame mince hodnoty 1,2,5 centov, z kazdej dostatok kusov
- Ako mozeme zaplatit urcitu sumu, napr. 13 centov, s co najmensim poctom minci?
- Ake je riesenie? 5+5+2+1 (4 mince)
- Vseobecna formulacia:
- Vstup: hodnoty k minci m_1,m_2,...,m_k a cielova suma X (vsetko kladne cele cisla)
- Vystup: najmensi pocet minci, ktore potrebujeme na zaplatenie X
- V nasom priklade k=3, m_1 = 1, m_2 = 2, m_3 = 5, X=13
- Jednoduchy sposob riesenia: pouzi najvacsiu mincu, ktora je najviac X, odcitaj od X, opakuj
- Priklad: najpr pouzijeme mincu 5, zostane name X=8, pouzijeme opat mincu 5, zostane X=3, pouzijeme mincu 2, zostane X=1, pouzijeme mincu 1.
- Nefunguje vzdy: zoberme mince hodnot 1,3,4. Pre X=6 najlepsie riesenie je 2 mince: 3+3, ale nas postup (algoritmus) najde 3 mince 4+1+1
- Ukazeme si algoritmus na zaklade dyn. programovania, ktory pre kazdy vstup najde najlepsie riesenie
- Zratame najlepsi pocet minci nielen pre X, ale pre vsetky mozne cielove sumy 1,2,3,...,X-1,X
- To zda byt ako tazsia uloha, ale ukaze sa, ze z riesenia pre mensie sumy vieme zostavit riesenie pre vacsie sumy, takze nam to vlastne pomoze
- Spravime si tabulku, kde si pre kazdu sumu i=0,1,2,...X pamatame A[i]=najmensi pocet minci, ktore treba na vyplatenie sumy i (ak je viac moznosti, zoberieme lubovolnu, napr. najvacsiu)
- Ukazme si to na priklade s mincami 1,3,4
i 0 1 2 3 4 5 6 7 8 9 A[i] 0 1 2 1 1 2 2 2 2 3
- Nevyplnali sme ju ziadnym konkretnym postupom, nejde o algoritmus
- Ale predstavme si, ze teraz chceme vyplnit A[10].
- V najlepsom rieseni je prva minca, ktoru pouzijeme 1,3, alebo 4
- ak je prva minca 1, zostane name zaplatit sumu 10-1=9, tu podla tabulky vieme najlepsie zaplatit na 3 mince, takze potrebujeme 4 mince na zaplatenie 10
- ak je prva minca 3, zostane nam zaplatit 10-3 = 7, na co potrebujeme podla tabulky 2 mince, takze spolu 3 mince na zaplatenie 10
- ak je prva minca 4, zostanem nam zaplatit 10-4 = 6, na co treba 2 mince, t.j. 3 mince na 10
- Nevieme, ktora z tychto moznosti je naozaj v najlepsom rieseni, ale pre druhe dva pripady dostaveme menej minci, takze vysledok bude 3 mince (napr. 3+3+4)
- Zovseobecnime: A[i] = 1+ min { A[i-1], A[i-3], A[i-4] }
- A[11] = 1 + min { 3, 2, 2} = 1 + 2 = 3
- Pre ine sustavy minci, napr. A[i] = 1+ min { A[i-1], A[i-2], A[i-5] }
- Vo vseobecnosti A[i] = 1+ min { A[i-m_1], A[i-m_2], ..., A[i-m_k] }
- Vzorec treba modifikovat pre male hodnoty i, ktore su mensie ako najvacsia minca, lebo A[-1] a pod. nie je definovane
- Zapisme algoritmus pre vseobecne mince
A[0] = 0;
pre kazde i od 1 po X
min = nekonecno
pre kazde j od 1 po k
ak i >= m_j a A[i-m_j] < min
min = A[i-m_j]
A[i] = 1 + min
vypis A[X]
- Ako najst, ktore mince pouzit?
- Pridame druhu tabulku B, kde v B[i] si pamatame, ktora bola najlepsia prva minca, ked sme pocitali A[i]
i 0 1 2 3 4 5 6 7 8 9 10 A[i] 0 1 2 1 1 2 2 2 2 3 3 B[i] - 1 1 3 4 4 3 4 4 4 4
- Potom ak chceme najst napr. mince pre 10, vidime, ze prva bola B[10]=4. Zvysok je 6 a prva minca na vyplatenie 6 je B[6]=3. Zostava nam 3 a B[3]=3. Potom nam uz zostava 0, takze sme hotovi. Takze najlepsie vyplatenie je 4+3+3
- Algoritmus:
Kym X>0 vypis B[X]; X = X-B[X];
- Dynamicke programovanie vo vseobecnosti
- Okrem riesenia celeho problemu, vyriesime aj spustu mensich podproblemov
- Riesenia podproblemov ukladame do tabulky
- Pri rieseni vacsieho podproblemu pouzivame uz vypocitane hodnoty pre mensie podproblemy
- Aka je casova zlozitost?
- Dva parametre: X a k.
- Tabulka velkost O(X), kazde policko cas O(k). Celkovo O(Xk).
Genome browser ešte raz
- Pozreli sme si mappability track v ludskom genome v UCSC genome browseri
- Nasledujuca sekvencia je vysledok RT-PCR na ludskych cDNA knizniciach:
AACCATGGGTATATACGACTCACTATAGGGGGATATCAGCTGGGATGGCAAATAATGATTTTATTTTGAC TGATAGTGACCTGTTCGTTGCAACAAATTGATAAGCAATGCTTTCTTATAATGCCAACTTTGTACAAGAA AGTTGGGCAGGTGTGTTTTTTGTCCTTCAGGTAGCCGAAGAGCATCTCCAGGCCCCCCTCCACCAGCTCC GGCAGAGGCTTGGATAAAGGGTTGTGGGAAATGTGGAGCCCTTTGTCCATGGGATTCCAGGCGATCCTCA CCAGTCTACACAGCAGGTGGAGTTCGCTCGGGAGGGTCTGGATGTCATTGTTGTTGAGGTTCAGCAGCTC CAGGCTGGTGACCAGGCAAAGCGACCTCGGGAAGGAGTGGATGTTGTTGCCCTCTGCGATGAAGATCTGC AGGCTGGCCAGGTGCTGGATGCTCTCAGCGATGTTTTCCAGGCGATTCGAGCCCACGTGCAAGAAAATCA GTTCCTTCAGGGAGAACACACACATGGGGATGTGCGCGAAGAAGTTGTTGCTGAGGTTTAGCTTCCTCAG TCTAGAGAGGTCGGCGAAGCATGCAGGGAGCTGGGACAGGCAGTTGTGCGACAAGCTCAGGACCTCCAGC TTTCGGCACAAGCTCAGCTCGGCCGGCACCTCTGTCAGGCAGTTCATGTTGACAAACAGGACCTTGAGGC ACTGTAGGAGGCTCACTTCTCTGGGCAGGCTCTTCAGGCGGTTCCCGCACAAGTTCAGGACCACGATCCG GGTCAGTTTCCCCACCTCGGGGAGGGAGAACCCCGGAGCTGGTTGTGAGACAAATTGAGTTTCTGGACCC CCGAAAAGCCCCCACAAAAAGCCG
- Skusme ju namapovat na genom programom blat na genome.ucsc.edu
- Dostavame jeden velmi dobry vyskyt na chr18, dalsie su len kratke
- Skusme tu istu sekvenciu namapovat do genomu sliepky -najde nieco a zda sa, ze je to aj v zodpovedajucom regione
- Ale zarovnal sa len maly kusok query
- Skusme to iste v ncbi blaste: http://blast.ncbi.nlm.nih.gov/Blast.cgi
- Zvolime nucleotide blast, reference genomic sequences, organism chicken (taxid:9031), program blastn
- Dostavame ovela vacsie zarovnanie
Zarovnávanie sekvencií, cvičenia pre biológov
- Cvicenia pre biológov z dynamickeho programovania, pracovna verzia poznamok
- Ospravedlnujem sa za chybajucu diakritiku
Opakovanie dynamickeho programovania
- Uvazujme skorovanie zhoda +2, nezhoda -1, medzera -1
- Skusime si dynamicke programovanie pre lokalne zarovnanie retazcov TAACGG a CACACT
- Rekurencia: A[i,j] = min {0, A[i-1,j]-1, A[i,j-1]-1, A[i-1,j-1]+c(p_i, q_j) }, pricom A[0,i]=-i, A[i,0]=-i
- Vyplnme maticu
C A C A C T
0 0 0 0 0 0 0
T 0 0 0 0 0 0 2
A 0 0 2 1 2 1 1
A 0 0 2 1 3 2 1
C 0 2 1 4 3 5 4
G 0 1 1 3 3 4 4
G 0 0 0 2 2 3 3
ACAC
A-AC
Dotplot
- Dotplot je graf, ktory ma na kazdej osi jednu sekvenciu a ciarky zobrazuju lokalne zarovnania (cesty v matici)
- Na slidoch mame niekolko prikladov dotplotov porovnavajucich rozne mitochondrialne genomy
- Tieto boli vytvorene pomocou nastroja YASS http://bioinfo.lifl.fr/yass/yass.php
- Dalsi priklad je zarovnanie genu Oaz Drosophila zinc finger s genomickym usekom chr2R:10,346,241-10,352,965
- Ako by sme to vedeli tieto data ziskat na UCSC genome browseri? http://genome.ucsc.edu
- Trochu iny dotplot, ktory funguje pre proteiny a nerobi lokalne zarovnania, iba spocita skore bez medzier v kazdom okne danej vysky a nakresli ciaru ak pre kroci urcenu hodnotu
- http://emboss.bioinformatics.nl/cgi-bin/emboss/dotmatcher
- Vyskusame protein escargot voci sebe s hodnotami http://pfam.sanger.ac.uk/protein/ESCA_DROME window 8 threshold 24
- Pomocou YASSu vyskusame kluster zhlukov PRAME z ludskeho genomu
- Obrázky dotplotov na slidoch
Opakovanie dotplotov
- Pomocou YASSu vyskusame kluster zhlukov AMY z ludskeho genomu na suradniciach chr1:103,890,000-104,120,000 voci sebe
- Pozrime si tento usek genomu v UCSC browseri http://genome.ucsc.edu/
- Zapnime si track segmental duplications
- Vyrobme dotplot pomocou nastroja YASS http://bioinfo.lifl.fr/yass/yass.php
- Najdime si transkript genu AMY2A, nablatujme ho na genom, pozrime si niektore slabsie vyskyty
Ako sa pohybovať medzi genómami
- Na http://genome.ucsc.edu/ si pozrime región AMY chr1:103,890,000-104,120,000
- Pomocou "dog net" premapujme do genómu psa
Zarovnanie
- Stiahnime si gen RAP1 z kvasinky Saccharomyces cerevisiae http://www.yeastgenome.org/cgi-bin/locus.fpl?locus=S000005160
- Pouzime NCBI BLAST http://www.ncbi.nlm.nih.gov/BLAST/
- Hladajme v Canadida albicans
- Provnajme maticu BLOSUM62 a BLOSUM45
BLOSUM45 ref|XP_714418.1| hypothetical protein CaO19.1773 [Candida alb... 91.0 9e-19 ref|XP_714378.1| hypothetical protein CaO19.9342 [Candida alb... 90.7 1e-18 ref|XP_715339.1| dsDNA break repair ligase [Candida albicans ... 47.7 1e-05 BLOSUM62 ref|XP_714378.1| hypothetical protein CaO19.9342 [Candida alb... 94.0 1e-19 ref|XP_714418.1| hypothetical protein CaO19.1773 [Candida alb... 92.0 4e-19
- Jeden protein vobec nebol najdeny pomocou BLOSUM62, len BLOSUM45
>ref|XP_715339.1| Gene info dsDNA break repair ligase [Candida albicans SC5314]
ref|XP_715274.1| Gene info dsDNA break repair ligase [Candida albicans SC5314]
Length=928
GENE ID: 3642986 LIG4 | ATP-dependent DNA ligase implicated in dsDNA break
repair via nonhomologous end-joining [Candida albicans SC5314]
(10 or fewer PubMed links)
Score = 47.7 bits (147), Expect = 1e-05, Method: Compositional matrix adjust.
Identities = 45/201 (22%), Positives = 86/201 (42%), Gaps = 16/201 (7%)
Query 35 PSDSAA-EVKANQNEENTGATAAETSEKVDQTEVEKKDDDDTTE-VGVTTTTPSIADTAA 92
PSDS E++A + G + A S + + ++D E V + T A+
Sbjct 584 PSDSLVLEIRARSIDTRAGTSYAVGSTLHNNHCRKIREDKSIDECVTLQEYTHIKANYIN 643
Query 93 TANIASTSGASVTEPT-TDDTAADEKKEQVSGPPLSNMKFYLNRDA-DAHDSLNDIDQLA 150
N A T+ EP + D + KK +V S ++F + D +A + I+++
Sbjct 644 DLNKAQTALGKKREPVYSLDNESKLKKVKVESDLFSGIEFLIMSDKREADGEVTTIEEMK 703
Query 151 RLIRANGGEVLDSKPRESKENVFIV--------SPYNHTNLPTVTPTYIKACCQSNSLLN 202
+++ GG++++S + + ++ S Y + V P +I C + +L
Sbjct 704 AMVKQYGGKIVNSVDLATNYQIMVITERELPVSSQYLSKGIDLVKPIWIYECIKRGCVLQ 763
Query 203 MENYLVP----YDNFREVVDS 219
+E Y + +DNF +VD
Sbjct 764 LEPYFIFASKNWDNFNHMVDQ 784
- Stiahnime si aj nukleotidovu sekvenciu a hladajme ju v genome Candida albicans
- Translated search
=Jadrá s medzerami, cvičenia pre informatikov
- Cvicenia pre informatikov z jadier s medzerami (spaced seeds)
- Ospravedlnujem sa za chybajucu diakritiku
- Prva cast na slidoch
Vzorec na vypocet senzitivity jadra bez medzier
- Uvazujme jadro bez medzier dlzky w (ako v programe BLAST pre nukleotidy)
- Uvazujme pravdepodobnostny model zarovnania, v ktorom ma kazda pozicia pravdepodobnost p, ze bude zhoda a (1-p), ze bude nezhoda, medzery neuvazujeme.
- Nech f(L) je pravdepodobnost vyskytu jadra v zarovnani dlzky L, t.j. pravdepodobnost w za sebou iducich zhod.
-
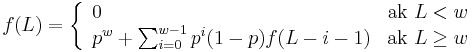
Jadra s medzerami
- Da sa tento rekurentny vzorec rozsirit na jadro s medzerami?
-
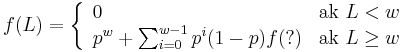
- Co by sme pouzili namiesto otaznika?
- Napr pre jadro 1011 a zaciatok zarovnania 1?10 moze byt vyskyt na pozicii 3, ale jeho pravdepodobnost nie je f(L-2), lebo mame dane prve dva znaky
Vseobecny algoritmus pre vektorove jadra
- Zial vo vseobecnosti exponencialny od dlzky jadra, ale pre male jadra sa da zbehnut v rozumnom case
- Jadro (Q,T), kde Q je vektor realnych cisel dlzky k a T je realne cislo, mnozina skor D, q_d je pravdepodobnost skore d v zarovnani
- H nech je mnozina vyskytov jadra Q (t.j. mnozina vektorov x dlzky k nad mnozinou D, ktore splnaju podmienku
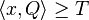 )
)
- Nech H_p je mnozina prefixov retazcov z H (mozne vyskyty) a H_g je mnozina prefixov retazcov z H, ktorych kazde rozsirenie na dlzku k je vyskyt (garantovane vyskyty)
-
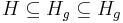
- Nech f(L,x) je pravdepodobnost vyskytu jadra v zarovnani dlzky L, ktore zacina na retazec x.
-
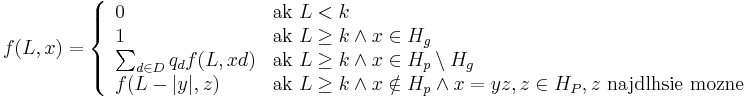
- f(L,x) budeme pocitat pre rastuce L a pre kazde L od najdlhsich x. Staci uvazovat x z H_p alebo x, ktore dostaneme pridanim jedneho znaku k slovu z H_p.
- vysledok je
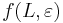
Evolúcia, cvičenia pre biológov
Hladanie genov
- Histonove modifikacie
- A. Barski, S. Cuddapah, K. Cui, T. Roh, D. Schones, Z. Wang, G. Wei, I. Chepelev, K. Zhao (2007) High-Resolution Profiling of Histone Methylations in the Human Genome Cell, Volume 129, Issue 4, Pages 823-837 pdf
- Prekryvajuce sa transkripty
- What is a gene, post-ENCODE? History and updated definition. Gerstein MB, Bruce C, Rozowsky JS, Zheng D, Du J, Korbel JO, Emanuelsson O, Zhang ZD, Weissman S, Snyder M.
- Priklady gene finderov v UCSC browseri, ludsky genom
- chr2:149,242,117-149,247,381 kusok genu
- chr2:149,118,916-149,120,420 zaciatok genu
- chr2:149,115,905-149,266,404 cely gen
- chr21:33,860,819-34,247,408 priklad z encode
- Pozri slidy [1]
Fitchov algoritmus
- Parsimony/uspornost
- Vstup: fylogeneticky strom, 1 stlpec zarovnania (jedna baza v kazdom liste stromu)
- Vystup: priradenie baz predkom minimalizujuce pocet substitucii
- Priklad - obr 1
- Terminologia: strom, hrana, vrchol, list, vnuturny vrchol, koren
- stromy su suvisle grafy bez cyklov
- Uvazujme, co vieme povedat o strome s dvoma susednymi listami vo vacsom strome (oznacenie: obr. 2, listy v1 a v2, hrany do listov e1, e2, ich predok v3, hrana z v3 vyssie e3).
- Ak oba listy maju bazu rovanku bazu, napr. A, predok v3 v optimalnom rieseni bude urcite mat bazu A
- Dokaz sporom: nech to tak nie je, nech optimalne riesenie ma nejaku inu bazu, napr. C. Vymenme v tomto rieseni toto C za A. Moze nam pribudnut jedna mutacia na hrane e3, ale ubudnu dve na hranach e1 a e2. Tym celkova cena riesenia klesne o 1, takze nebolo optimalne.
- Ak tieto dva listy maju rozne bazy, napr. A a C, tak existuje optimalne riesenie, ktore ma v predkovi v3 bazu A alebo C.
- Dokaz: vezmime optimalne riesenie. Ak ma v3 bazu A alebo C, tvrdenie plati. Ak ma v3 nejaku inu bazu, napr T, mozeme ju vymenit napr. za A, ci mozno pribuden jedna muracia na e3 ale urcite ubudne mutaci na e1. Teda celkovy pocet mutacii sa nezvyi a nase nove riesenie je stale optimalne. Pozor, vo vseobecnosti nevieme povedat, ci ma mat v3 bazu A alebo C. V niektorych pripadoch su optimalne obe, v niektorych len jedna.
- Fitchov algoritmus 1971
- Kazdemu vrcholu v priradime mnozinu baz M(v)
- M(v) pocitame od listov smerom ku korenu
- Pre list v bude M(v) obsahovat bazu v tomto liste
- Uvazujme vnutorny vrchol v s detmi x a y. Mame uz spocitane M(x) a M(y), chceme M(v)
- Ak M(x) a M(y) maju nejake spolocne bazy, vsetky tieto spolocne bazy dame do M(v), t.j.
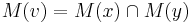
- Ak M(x) a M(y) nemaju spolocne bazy, do M(v) dame vsetky bazy z M(x) aj M(v), t.j.
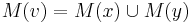
- V tomto pripade pocet mutacii vzrastie o jedna
- Ked mame M(v) spocitane pre vsetky vrcholy, ideme od korena smerom k listom a vyberieme vzdy jednu bazu z M(v).
- Ak sme vybrali pre rodica bazu x a x je v M(v), zvolime x aj pre v, inak zvolime lubovolnu bazu z M(v).
- Priklad algoritmu na obr 3
Opakovanie pravdepodobnostnych modelov
Ake sme doteraz videli modely
- Zostavovanie genomov, planovanie pokrytia: N readov nahodne rozhodenych po genome, kolko miest v priemere zostava nepokrytych?
- E-value v BLASTe: nahodne vygenerujeme databazu a dotaz (query), kolko bude v priemere medzi nimi lokalnych zarovnani so skore aspon T?
- Hladanie genov: model generujuci sekvenciu+anotaciu naraz (parametre nastavene na znamych genoch). Pre danu sekvenciu, ktora pravdedpodobnost je najpravdepodobnejsia?
- Evolucia, Jukes-Cantorov model: model generujuci stlpec zarovnania. Nezmame parametre: strom, dlzky hran. Pre danu sadu stlpcov zarovnania, ktore parametre povedu k najvacsej pravdepodobnosti?
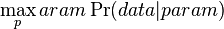
- Trochu detailov: pravdepodobnost zmeny/nezmeny na hrane dlzky t:
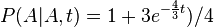 ,
, 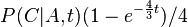
- Ak pozname ancestralne sekvencie, vieme spocitat pravdepodobnost dat
- Ancestralne sekvencie su nahodne premenne, ktore nas nezaujimaju: marginalizujeme ich (uvazujeme vsetky ich mozne hodnoty)
Zlozitejsie evolucne modely
- Jukes-Cantorov model uvazuje len dlzku hrany udanu v priemernom pocte substitucii (vratane tych, ktore nevidime, kvoli tomu, ze su dve na tom istom mieste)
- Nie vsetky substitucie sa deju rovnako casto: tranzicie (v ramci pyrimidonov T<->C, v ramci purinov A<->G) su pravdepodobnjesie ako transverzie (A,G)<->(C,T)
- Nie vsekty nukleotidy sa v danom genome objavuju rovnako casto (napr. mitochondrialne genomy velmi male C,G)
- Tieto javy zachytava HKY model
- Matica rychlosti
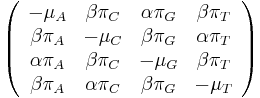
-
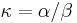 je pomer rychlosti, ktorymi sa deju tranzicie vs. transverzie
je pomer rychlosti, ktorymi sa deju tranzicie vs. transverzie
-
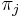 je frekvencia bazy
je frekvencia bazy 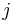 v sekvencii
v sekvencii
- Rychlost, ako sa deje substitucia z X do Y je sucin pravdepodobnosti Y a faktoru, ktory zavisi od toho, ci ide o tranziciu alebo transverziu
- Sucet kazdeho stlpca matice ma byt 0, t.j.
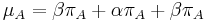
- Matica sa znormalizuje tak, aby priemerny pocet substitucii za jednotku casu bol 1
- Matica ma styri parametre:
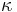 a tri frekvencie (svrta musi doplnit do 1) plus dlzka hrany
a tri frekvencie (svrta musi doplnit do 1) plus dlzka hrany
- Zlozitejsi model lepsie zodpoveda skutocnym procesom, ale na odhad viac parametrov potrebujeme viacej dat.
- Existuju metody, ktore pre dany cas t z matice spocitaju pravdepodobnost, ze baza X zmutuje na bazu Y Pr(Y|X,t)
- Napr. pre velmi velmi maly cas
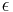 mame
mame 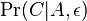 je zhruba
je zhruba 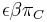
- Pre rozumne dlhe casy toto neplati, preto sa pouzvaju algebraicke metody, ktore beru do uvahy moznost viacerych substitucii na tom istom mieste
- Je aj vela inych modelov s mensim alebo vacsim poctom parametrov
Prakticka ukazka tvorby stromov
- UCSC browseri si pozrieme usek ludskeho genomu chr6:136,214,527-136,558,402 s genom PDE7B (phosphodiesterase 7B)
- Na modrej liste zvolime Tables, v nej RefSeq genes, zaklikneme Region: position, a Output fomat: CDS FASTA alignment a stlacime Get output
- Na dalsej obazovke zaklikneme show nucleotides. Z primatov zvolime chimp, rhesus, tarsier, z inych cicavcov mouse, rat, dog, elephant a z dalsich organizmov opposum, platypus, chicken, lizard, stalcime Get output.
- Vystup ulozime do suboru, z mien sekvencii zmazeme spolocny prefix NM_018945_, pripadne celkovo prepiseme mena na anglicke nazvy
- Tento subor mozete najst tu
- Skusme zostavit strom na stranke http://mobyle.pasteur.fr/cgi-bin/portal.py
- Pozuijeme program quicktree, metodu neighbor joining, bootstrap 100
- Na zobrazenie stromu vysledok dalej prezenieme cez zobrazovacie programy drawtree alebo newicktops
- Vysledok z drawtree, nezakoreneny, nezobrazuje bootstrap hodnoty
- Vysledok z newicktops, zakoreneny na nahodnom mieste (nie spravne), zobrazuje bootstrap hodnoty
- "Spravny strom [2] v nastaveniach Conservation track-u v UCSC browseri (podla clanku Murphy WJ, Eizirik E, O'Brien SJ, Madsen O, Scally M, Douady CJ, Teeling E, Ryder OA, Stanhope MJ, de Jong WW, Springer MS. Resolution of the early placental mammal radiation using Bayesian phylogenetics. Science. 2001 Dec 14;294(5550):2348-51.)
- Nas strom ma long branch attraction (zle postavenie hlodavcov, ktori maju dlhu vetvu).
Bootstrap
- Zostrojime strom T vybranou metodou
- Nahodne vyberieme niektore stlpce zarovnania, zostrojime dalsi strom
- Cele to opakujeme vela krat
- Pri strome T si znacime, kolkorat sa ktora hrana opakuje
- To nam da urcity odhad spolahlivosti, hlavne ak mame clekovo malo dat (kratke zarovnanie)
- Ak vsak data velmi dobre nezodpovdedaju vybranej metode tak aj pre zly strom mozeme dostat vysoky bootstrap
Komparativna genomika v UCSC genome browseri
- phastcons, most conserved
- pozitivny vyber, napr. gen MAGEA2B
Objavenie genu HAR1 pomocou komparativnej genomiky
- Nerobili sme na cviceniach, len pre zaujimavost
- Pollard et al Nature 2006
- zobrali vsetky regiony dlzky aspon 100 s > 96% podobnostou medzi simpanzom mysou/potkanom (35,000)
- porovnaj s ostatnymi cicavcami, zisti, ktore maju vela mutaci v cloveku ale malo inde (pravdepodobnostny model)
- 49 statisticky signifikantych regionov, 96% nekoduje oblasti
- najvyznamnejsi HAR1: 118nt, 18 substitucii u cloveka, ocakavali by sme 0.27. Iba 2 zmeny medzi simpanzom a sliepkou (310 milionov rokov), ale nebol najdeny v rybach a zabe.
- nezda sa byt polymorfny u cloveka
- Prekryvajuce sa RNA geny HAR1R a HAR1F
- HAR1F je exprimovany v neokortexe u 7 a 9 tyzdennych embrii, neskor aj v inych castiach mozgu (u cloveka aj inych primatov)
- vsetky substitucie v cloveku A/T->C/G, stabilnejsia RNA struktura (ale tiez su blizko k telomere, kde je viacej takychto mutacii kvoli rekombinacii a biased gene conversion)
Evolúcia, cvičenia pre informatikov
Cvicenie informatici
RT-PCR
- Pozri slidy [3]
Substitucne modely - odvodenie
- Nech
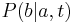 je pravdepodobnost, ze ak sme zacneme s bazou a, tak po case t budeme mat bazu b.
je pravdepodobnost, ze ak sme zacneme s bazou a, tak po case t budeme mat bazu b.
- Pre dane t mozeme take pravdepodobnosti usporiadat do matice 4x4 (ak studujeme DNA), kde
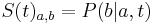
- Intuitivne cim vacsie t, tym vacsia pravdepodobnost zmeny;
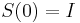 (jednotkova matica),
(jednotkova matica), 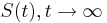 ma vsetky riadky rovnake, napr. 1/4, 1/4, 1/4, 1/4
ma vsetky riadky rovnake, napr. 1/4, 1/4, 1/4, 1/4
- Ak mame matice pre casy
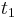 a
a 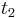 , vieme spocitat maticu pre cas
, vieme spocitat maticu pre cas 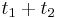 :
: 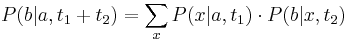 a teda v maticovej notacii
a teda v maticovej notacii 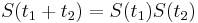 . Takyto model nazyvame multiplikativny a predpoklada, ze pravdepodobnost mutacie zavisi len od aktualne bazy, nie od minulych stavov.
. Takyto model nazyvame multiplikativny a predpoklada, ze pravdepodobnost mutacie zavisi len od aktualne bazy, nie od minulych stavov.
- Ak by sme uvazovali iba diskretne (celocislene) casy, stacilo by nam urcit iba
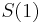 a vsetky ostatne casy dostaneme umocnenim tejto matice. Je vsak elegantnejsie mat
a vsetky ostatne casy dostaneme umocnenim tejto matice. Je vsak elegantnejsie mat 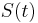 definovane aj pre realne t.
definovane aj pre realne t.
- Jukes-Cantor-ov model evolucie predpoklada, ze vsetky substitucie su rovnako pravdepodobne.
- Pre velmi maly cas mame maticu
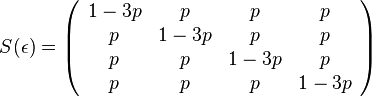
- kde
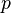 je tiez velmi male cislo.
je tiez velmi male cislo.
- Pre cas
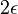 dostavame maticu
dostavame maticu
- Ale cleny s
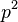 su ovela mensie ako cleny s
su ovela mensie ako cleny s 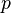 , takze tato matica je priblizne
, takze tato matica je priblizne
- Vytvorme si teraz maticu rychlosti (rate matrix)
- Dostavame, ze pre velmi male casy plati
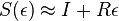 (
(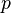 pouzivane vyssie by malo hodnotu
pouzivane vyssie by malo hodnotu 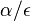 ).
).
-
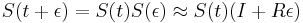 a teda
a teda 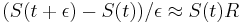 a v limite pre
a v limite pre 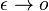 dostavame
dostavame 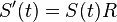 (diferencialne rovnice, pociatocny stav
(diferencialne rovnice, pociatocny stav 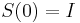 ).
).
- Ak diagonalne prvky
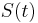 oznacime
oznacime 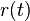 a nediagnoalne
a nediagnoalne 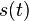 , dostavame, ze diagonalny prvok
, dostavame, ze diagonalny prvok 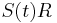 je
je 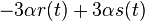 a nediagonalny
a nediagonalny 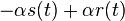 . Takze dostavame diferencialne rovnice
. Takze dostavame diferencialne rovnice 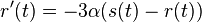 a
a 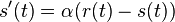 .
.
- Overme, ze riesenim tejto rovnice je
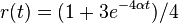 a
a 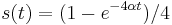 :
:
- Zderivujeme
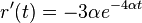 a
a 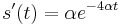 , dosadime do rovnic.
, dosadime do rovnic.
- Zderivujeme
- Takze mame maticu:
- V case
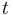 je pravdepodobnost, ze uvidime zmenenu bazu
je pravdepodobnost, ze uvidime zmenenu bazu 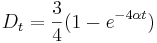 a teda ak v skutocnosti vidime
a teda ak v skutocnosti vidime 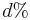 zmenenych baz, vieme spatne zratat t, ktore by hodnote
zmenenych baz, vieme spatne zratat t, ktore by hodnote 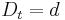 prinalezalo.
prinalezalo.
- Aby sme nemali naraz aj
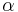 aj
aj 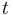 , zvykneme maticu R normalizovat tak, aby priemerny pocet substitucii za jednotku casu bol 1. V pripade Jukes-Cantorovho modelu je to ked
, zvykneme maticu R normalizovat tak, aby priemerny pocet substitucii za jednotku casu bol 1. V pripade Jukes-Cantorovho modelu je to ked 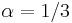 .
.
- Dostavame teda vzorec pre vzdialenost, ktory sme videli na prednaske
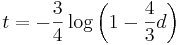
- Preco sme ten vzorec odvodili takto? V skutocnosti chceme najst najvierohodnejsiu hodnotu t, t.j. taku, pre ktore hodnota P(data|t) bude najvacsia. Zhodou okolnosti vyjde takto.
- V praxi sa pouzivaju komplikovanejsie substitucne modely, ktore maju vseobecnejsiu maticu rychlosti R
- Kimurov model napr. zachytava, ze puriny sa castejsie menia na ine puriny (A a G) a pyrimidiny na ine pyrimidiny (C a T) ma dva parametre:
- HKY model (Hasegawa, Kishino & Yano) tiez umoznuje rozne pravdepodobnosti A, C, G a T v ekvilibriu.
- Vo vseobecnosti pre rate matrix
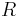 dostavame
dostavame 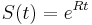 . Ak R diagonalizujeme (urcite sa da pre symetricke R)
. Ak R diagonalizujeme (urcite sa da pre symetricke R) 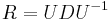 , kde D je diagonalna matica (na jej diagonale budu vlastne hodnoty R), tak
, kde D je diagonalna matica (na jej diagonale budu vlastne hodnoty R), tak 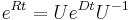 , t.j. exponencialnu funkciu uplatnime iba na prvky na uhlopriecke matice D.
, t.j. exponencialnu funkciu uplatnime iba na prvky na uhlopriecke matice D.
Felsensteinov algoritmus 1981
- Mame dany strom T s dlzkami hran a bazy v listoch (jeden stlpec zarovnania) a maticu rychlosti R. Spocitajme pravdepodobnost, ze z modelu dostaneme prave tuto kombinaciu baz v listoch.
- Nech X_v je premenna reprezentujuca bazu vo vrchole v a nech x_v je konkretna baza v liste v. Nech listy su 1..n a vnut. vrcholy n+1..2n-1. Nech dlzka hrany z v do rodica je t_v. Nech P(a|b,t) je pravdepodobnost, ze b sa zmeni na a za cas t (z matice R). Nech q_a je pravdepodobnost bazy a v koreni (ekvilibrium matice R)
- Chceme pravdepodobnost
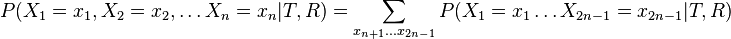
- Spocitame rychlejsie dynamickym programovanim.
- Nech A[v,a] je pravdedpodobnost dat v podstrome s vrcholom v ak X_v=a
- A[v,a] pocitame od listov ku korenu
- v liste A[v,a] = [a=x_v]
- Vo vnut. vrchole s detmi x a y mame
![A[v,a]=\sum _{{b,c}}A[x,b]A[y,c]P(b|a,t_{x})P(c|a,t_{y})](/vyuka/mbi/images/math/3/9/4/39459db83d38746a33e427169d62d215.png)
- Celkova pravdepodobnost je
![P(X_{1}=x_{1},X_{2}=x_{2},\dots X_{n}=x_{n}|T,R)=\sum _{a}A[r,a]q_{a}](/vyuka/mbi/images/math/3/0/d/30d167737e880c69f2a1cd08a5dfc5a5.png) pre koren r.
pre koren r.
- Zlozitost
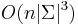
- Pre nebinarne stromy exponencialne
- Zlepsenie
![A[v,a]=(\sum _{{b}}A[x,b]P(b|a,t_{x}))(\sum _{c}A[y,c](c|a,t_{y}))](/vyuka/mbi/images/math/9/3/a/93a8ecffd2e352290f8d57ddc469bb66.png)
- Zlozitost
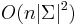 aj pre nebinarne stromy
aj pre nebinarne stromy
- Co ak chceme spocitat pravdepodobnost P(X_v=a|X_1=x_1, X_2=x_2,\dots X_n=x_n,T,R)?
- Potrebujeme B[v,a]=pravdpodobnost dat ak podstrom v nahradim listom s bazou a.
- B[v,a] pocitame od korena k listom
- V koreni B[v,a] = q_a
- Vo vrchole v s rodicom u a surodencom x mame
![B[v,a]=\sum _{{b,c}}B[u,b]A[x,c]P(a|b,t_{v})P(c|b,t_{v})](/vyuka/mbi/images/math/0/4/c/04cc0bf38cc6bbf3b4ddf7ce0e346560.png)
- Ziadana pravdedpodobnost je
![B[v,a]A[v,a]/P(X_{1}=x_{1},X_{2}=x_{2},\dots X_{n}=x_{n}|T,R)](/vyuka/mbi/images/math/c/c/2/cc2c38f95bb6131cc0a4edfdc7db8bdb.png)
Expresia génov, cvičenia pre biológov
Data o expresii ludskych genov v roznych tkanivach a podobne v UCSC genome browseri
- V browseri su rozne tracky, napr. Affy Exon Tissues, Affy RNA Loc (signal), GNF Atlas 2 a dalsie
- UCSC genes obsahuju prehlad ich expresie v roznych tkanivach
- UCSC gene sorter, Visigene su dalsie sposoby ako porovnavat expresiu genov
NCBI Gene Expression Omnibus http://www.ncbi.nlm.nih.gov/geo/
- Databaza gene expression dat na NCBI
- Browse -> Data sets -> Advanced search dostaneme zoznam najcastejsich organizmov
- Zvolme Saccharomyces cerevisiae
- Zvolme druhy v poradi [4] (Various weak organic acids effect on anaerobic yeast chemostat cultures)
- Mozeme si pozriet citation, platform, expression profiles and similarities, data analysis tools
Normalizacia dat (nepreberané na cvičeniach, uvádzané pre zaujímavosť)
Nadreprezentacia, obohatenie (enrichment)
- Mnohe celogenomove analyzy nam daju zoznam genov, ktore sa v nejakom ukazovateli vyrazne lisia od priemeru.
- Napriklad geny s pozitivnym vyberom v komparativnej genomike, geny vyrazne nadexprimovane alebo podexprimovane v microrarray experimentoch, geny regulovane urcitym transkripcnym faktorom a pod.
- Niektore z nich budu preskumanejsie (znama funkcia a pod.), niektore mozu mat nejake udaje o funkcii prenesene z homologov a dalsie mozu byt uplne nezname
- Co s takym zoznamom "zaujimavych genov"?
- moznost 1: vybrat si z neho niekolko malo zaujimavych kandidatov a preskumat ich podrobnejsie (experimentalne alebo informaticky)
- moznost 2: zistit, ci tato cela skupina je obohatena o geny urcitych skupin
- napr. v pripade pozitivneho vyberu nam casto vychadzaju geny suvisiace s imunitou, lebo su pod velkym evolucnym tlakom od patogenov
- takato analyza nam teda da informaciu o suvislostiach medzi roznymi procesmi
- Priklad (Kosiol et al)
- 16529 genov celkovo, 70 genov v GO kategorii innate immune response (0.4% zo vsetkych genov)
- 400 genov s pozivnym vyberom, mame 8 genov s innate immune response (2% zo vsetky genov s poz. vyb.)
- Celkovy pocet genov n, imonitnych ni, pozitvny vyber np, imunotnych s poz. vyb. nip.
- Nulova hypoteza: geny v nasom zozname boli nahodne vybrane z celeho genomu, t.j. ak v celom genome je frekvencia imunitnych genov ni/n, vo vzorke velkosti np (geny s pozitivnym vyberom) ocakavame cca np * ni / n imunitnych genov.
- v nasom priklade by sme ocakavali 1.7 genu s innate immune response, ale mame 8 (4.7xviac)
- Aj v nulovej hypoteze vsak vzorka velkosti ni cisto nahodou moze obsahovat viac alebo menej takych genov.
- Rozdelenie pravdedpodbnosti nip je hypergeometricke, t.j. pravdedpodobnost ze nip=x je <tex>{n_i \choose x}{n-n_i\choose n_i-x}/{n\choose n_p}</tex>
- Aka je pravdepodobnost, ze v nulovej hypoteze bude nip tolko, kolko sme namerali alebo viac? (Chvost rozdelenia). V nasom pripade p-value 2.8e-4.
- hypergeometric or Fisher's exact test, pripadne ich aproximacie pre velke hodnoty v tabulke (chi^2 test) zisti, ci sa nasa tabulka velmi lisi od toho, co by sme ocakavali v nulovej hypoteze
- Ak skusame vela (vsetky) GO kategorie, musime uplatnit "multiple testing correction": napr. skusame 1000 kategorii, ocakavali by sme cisto nahodou 50 kategorii, ktore budu vyznamne pre p<=0.05. Ak najdeme takych 100, tak cca polovica z nasich vysledkov su falosne, cisto nahodne asociacie. Takze chceme znizit p-value tak, aby ocakavane nahodne asociacie netvorili vyznamnu cast vysledkov.
- Suvisiace clanky 17182697, 19033363
- Rivals I, Personnaz L, Taing L, Potier MC (February 2007). "Enrichment or depletion of a GO category within a class of genes: which test?". Bioinformatics (Oxford, England) 23 (4): 401–7. doi:10.1093/bioinformatics/btl633. PMID 17182697.
- Huang da W, Sherman BT, Lempicki RA (January 2009). "Bioinformatics enrichment tools: paths toward the comprehensive functional analysis of large gene lists". Nucleic Acids Research 37 (1): 1–13. doi:10.1093/nar/gkn923. PMID 19033363.
- Existuju web servery, napr. GOrilla pre ludske geny: http://cbl-gorilla.cs.technion.ac.il/, DAVID (http://david.niaid.nih.gov)
- Treba dat pozor, ci pocitaju to co chceme
- Kod v statistickom systeme R na pocitanie hypergeometrickeho rozdelenia
> dhyper(0:70, 70, 16529-70, 400); [1] 1.793421e-01 3.126761e-01 2.679872e-01 1.505169e-01 6.231088e-02 [6] 2.027586e-02 5.400796e-03 1.210955e-03 2.332580e-04 3.920215e-05 [11] 5.818723e-06 7.702558e-07 9.166688e-08 9.873221e-09 9.678760e-10 [16] 8.677204e-11 7.143849e-12 5.420388e-13 3.802134e-14 2.472342e-15 [21] 1.493876e-16 8.405488e-18 4.412274e-19 2.164351e-20 9.935473e-22 [26] 4.273662e-23 1.724446e-24 6.533742e-26 2.326517e-27 7.791092e-29 [31] 2.455307e-30 7.285339e-32 2.036140e-33 5.361856e-35 1.330660e-36 [36] 3.112566e-38 6.862558e-40 1.426089e-41 2.792792e-43 5.153006e-45 [41] 8.955105e-47 1.465159e-48 2.255667e-50 3.265636e-52 4.442631e-54 [46] 5.674366e-56 6.797781e-58 7.629501e-60 8.012033e-62 7.860866e-64 [51] 7.193798e-66 6.129013e-68 4.851139e-70 3.558526e-72 2.412561e-74 [56] 1.506983e-76 8.641725e-79 4.530590e-81 2.161126e-83 9.326620e-86 [61] 3.617279e-88 1.250737e-90 3.817900e-93 1.016417e-95 2.323667e-98 [66] 4.469699e-101 7.034762e-104 8.698702e-107 7.924236e-110 4.728201e-113 [71] 1.386176e-116 phyper(7, 70, 16529-70, 400, lower.tail=FALSE);
Hľadanie motívov, cvičenia pre biológov
Opakovanie z prednasky
- Hladame vazobne miesta TF
- Reprezentujeme ako sekvencne motivy (vo forme konsenzus retazcov, regularnych vyrazov alebo PSSM)
- Dva bioinformaticke problemy:
- Hladanie novych motivov
- hladame motiv, ktory sa opakuje vo vstupnych sekvenciach
- sekvencie ziskame pomocou ChIP, alebo ako promotery koregulovanych genov
- vypoctovo narocny problem
- nasli sme to, co sme chceli?
- Hladanie novych vyskytov znameho motivu
- vypoctovo jednoduchy problem
- zvycajne najdeme vela vyskytov, nie vsetky biologicky relevantne
Programy na pracu s motivmi: Mobyle
- Nejake programy na pracu s motivmi najdete na stranke http://mobyle.pasteur.fr/
- Hladanie vyskytov znamych motivov
- iANTPatScan
- pftools, sig
- scan_for_matches
- prophet, profit (matice)
- jaspscan (jaspar db), tfscan (old version of transfac)
- Hladanie novych motivov
- SMILE
- CONSENSUS
- prophecy (matrix from alignment)
- Programy roznej kvality, treba skontrolovat, ci robia to, co chcete
MEME
- Znamy program na hladanie novych motivov
- Webserver MEME http://meme.nbcr.net/
Komparativne hladanie motivov
- Z vela vyskytov motivu chceme najst tie skutocne funkcne
- Purifikacny vyber: funkcne sekvencie sa menia pomalsie ako zvysok genomu
- Toto by malo platit aj pre vazobne miesta TF
- Chceme teda najst vyskyty motivu zachovane aj v pribuznych organizmoch
- Mala fylogeneticka vzdialenost (napr. clovek-simpanz): mala sanca, ze bude mutacia v kratkom okne, nie je mozne statisticky rozpoznat "zachovane" sekvencie pre kratke motivy
- Velka fylogeneticka vzdialenost: nekodujuce oblasti tazko zarovnatelne, takze aj homologicke vyskyty motivu nebudu zarovnane (lebo su kratke)
- Ako zostavujeme celogenomove zarovnania:
- najdeme signifikantne lokalne zarovnania (mama e-value)
- tie spajame dokopy do retazi a sieti
- ak je jeden kratky motiv uprostred neutralne sa vyvijajucej DNA, nebude mat signifikantne lokalne zarovnanie
- Mnohe programy dovoluju posun motivu v urcitom okne zarovnania
- Priklad: Kheradpour P, Stark A, Roy S, Kellis M (December 2007). "Reliable prediction of regulator targets using 12 Drosophila genomes". Genome Res. 17 (12): 1919–31. doi:10.1101/gr.7090407. PMID 17989251.
- Drosophila melanogaster ako referencny genom
- pre kazdy vyskyt motivu hladaj v ostatnych genomoch v urcitom okne
- spocitaj v akom percente stromu najdene vyskyty
- spocitaj p-value pomocou motivov s nahodne poprehadzovanymi stlpcami
Bezkontextove gramatiky
- Dakedy sme mali konecne automaty ako uvod do HMM
- Bezkontextove gramatiky ako uvod do stochastickych bezkontextovych gramatik, ktore budeme pouzivat na prednaske na modelovanie struktury RNA
- Zaviedol Noam Chomsky v lingvistike 50-te roky 20. storocia, tiez dolezite v informatike
- Gramatika
- Dva typy symbolov: terminaly (male pismena), neterminaly (velke pismena)
- Pravidla prepisujuce neterminal na retazec terminalov a neterminalov (moze byt aj prazdny retazec, ktory oznacujeme epsilon)
- Neterminal S je "startovaci"
- Priklad: S->aSb, S->epsilon (piseme aj skratene S->aSB|epsilon)
- Pouzitie gramatiky na generovanie retazcov
- Zacneme so startovacim neterminalom S
- V kazdom kroku prepiseme najlavejsi neterminal podla niektoreho pravidla
- Skoncime, ked nezostanu ziadne neterminaly
- Priklad: S->aSb->aaSbb->aaaSbbb->epsilon
- Ake vsetky slova vie tato gramatika generovat?
- V tvare aa...abb...b s rovnakym poctom acok a bciek (informatici pisu a^kb^k)
- taketo slova nevieme rozpoznavat konecnym automatom (konecny pocet stavov, nevieme si zapamatat kolko bolo acok, ale toto nie je celkom dokaz...)
- Zostavte gramatiku na slova typu aa..abb..b kde acok je rovnako alebo viac ako bcok
- S->aSb|aS|epsilon
- zostavte gramatiku pre slova toho isteho typu, kde acok je viac ako bcok
- S->aSb|aT T->aT|epsilon
- uvazujme dobre uzatvorkovane vyrazy zo zatvoriek (,),[,] napr. [()()([])] je dobre uzatvorkovany, ale [(]) nie je.
- S->SS|(S)|[S]|epsilon
- S->[S]->[SS]->[SSS]->[(S)SS]->[()SS]->[()(S)S]->[()()S]->[()()(S)]->[()()([S])]->[()()([])]
- Parsovanie retazca pomocou gramatiky: urcit, ako mohol byt retazec vygenerovany pomocou pravidiel
- Tato gramatika nam pomoze urcit, ktora zatvorka patri ku ktorej: tie, ktore boli vygenerovane v jednom kroku
- Zostavte gramatiku na DNA palindromy, t.j. sekvencie, ktore zozadu po skomplementovani baz daju to iste, ako napr. GATC
- S->GSC|CSG|AST|TSA|epsilon
- Zostavte gramatiku na slova s rovnakym poctom acok a bcok v lubovolnom poradi
- S->epsilon|aSbS|bSaS
- preco vie vygenerovat vsetky take retazce?
Hľadanie motívov, cvičenia pre informatikov
Markovove reťazce
- Markovov reťazec je postupnosť náhodných premenných
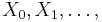 taká, že
taká, že 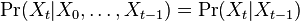 , t..j. hodnota v čase
, t..j. hodnota v čase 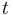 závisí len od hodnoty v čase
závisí len od hodnoty v čase 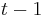 a nie ďalších predchádzajúcich hodnôt.
a nie ďalších predchádzajúcich hodnôt.
- Nás budú zaujímať homogénne Markovove reťazce, v ktorých
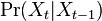 nezávisí od
nezávisí od 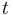 .
.
- Tiez nas zaujimaju len retazce v ktorych je
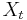 z konecnej abecedy (mozne hodnoty
z konecnej abecedy (mozne hodnoty 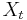 nazyvame stavy)
nazyvame stavy)
- Napriklad stavy A,C,G,T
- Teda pravdepodobnosti prechodu medzi stavmi za jeden krok mozeme vyjadrit maticou pravdepodobnosti P, ktorej prvok
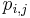 oznacuje pravdepodobnost prechodu zo stavu i do stavu j
oznacuje pravdepodobnost prechodu zo stavu i do stavu j 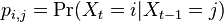
- Sucet kazdeho riadku je 1, cisla nezaporne
- Ako
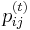 budeme oznacovat
budeme oznacovat 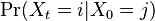 , tieto hodnoty dostaneme umocnenim matice P na t
, tieto hodnoty dostaneme umocnenim matice P na t
- matica je ergodicka (niekedy volane regularna), ak
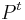 pre nejake t>0 ma vsetky polozky nenulove
pre nejake t>0 ma vsetky polozky nenulove
- priklady neergodickych matic
1 0 0.5 0.5 0 1 0.5 0.5 0 1 0 1 1 0 1 0 nesuvisla slabo suvisla periodicka ergodicka
- Rozdelenie
 na mnozine stavov sa nazyva stacionarne pre Markovov retazec
na mnozine stavov sa nazyva stacionarne pre Markovov retazec 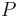 , ak pre kazde j plati
, ak pre kazde j plati 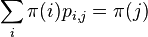 (alebo v maticovej notacii
(alebo v maticovej notacii 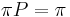 )
)
- Pre ergodicke matice jedine stacionarne rozdelenie, pre ktore navyse plati , ze pre kazde i a j plati
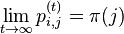
- v HMM stavy tvoria Markovov retazec; hladanie genov ergodicky stavovy priestor, profilove HMM nie
- ine varianty: nekonecne stavove priestory (zlozitejsia teoria), spojity cas (videli sme pri evolucnych modeloch), retazce vyssieho radu, kde urcujeme
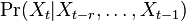 a pod
a pod
- pouzitie v bioinformatike: charakterizacia nahodnych sekvencii (nulova hypoteza), pre DNA sa pouzivaju rady az do 5, lepsie ako nezavisle premenne
Markov chain Monte Carlo MCMC
- Chceme generovať náhodné vzorky z nejakeho cieloveho rozdelenia
 , ale toto rozdelenie prilis zlozite.
, ale toto rozdelenie prilis zlozite.
- Naco je vobec dobre vzorkovanie?
- Namiesto optimalizacie pravdepodobnosti
- Na vypocet roznych hodnot z celej distribucie
- Priklad: fylogeneticke stromy
- Zostavime ergodicky Markovov retazec, ktoreho stacionarne rozdelenie je rozdelenie
 , tak aby sme efektivne vedeli vzorkovat
, tak aby sme efektivne vedeli vzorkovat 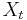 ak vieme
ak vieme 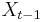 .
.
- Ak zacneme z lubovolneho bodu, po urcitom case t rozdelenie
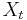 priblizne
priblizne 
- Ale za sebou iduce vzorky nie su nezavisle!
- Vieme vsak odhadovat ocakavane hodnoty roznych velicin
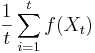 konverguje k
konverguje k ![E_{\pi }[f(X)]](/vyuka/mbi/images/math/a/a/4/aa4ecd5f5f91f0aaf04047c7435e1922.png)
Gibbs sampling, Gibbsovo vzorkovanie
- Specialny pripad MCMC
- Cielove rozdelenie ma n premennych
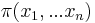
- V kazdom kroku vzorkujeme jednu premennu z podmienenej pravdepodobnosti
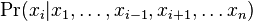
- Ostatne hodnoty nechame rovnake ako v predchadzajucom kroku
- Premennu
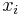 zvolime nahodne alebo periodicky
zvolime nahodne alebo periodicky 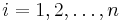
- Pozor! Nie vzdy ergodicke, ak niektore kombinacie hodnot maju nulovu pravdepodobnost!
- Treba dokazat, ze ak je ergodicky, ma stacionarnu distribuciu

- Dokazeme tzv. detailed balance, ze pre kazde dva vektory hodnot x a x' mame
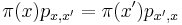
- ak pre nejaky retazec a nejaku distribuciu
 plati detailed balance,
plati detailed balance,  je stacionarna distribucia:
je stacionarna distribucia: 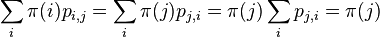
- Pre nas retazec plati detailed balance: uvazujme dva za sebou iduce vektory hodnot x a x', ktore sa lisia v i-tej suradnici. Nech
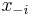 su hodnoty vsetkych ostatnych premennych okrem
su hodnoty vsetkych ostatnych premennych okrem 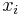
-
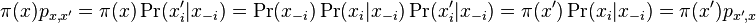
- Dokazeme tzv. detailed balance, ze pre kazde dva vektory hodnot x a x' mame
Hladanie motivov pomocou Gibbsovho vzorkovania
- Danych n sekvencii kazda dlzky m, dlzka motivu L
- Hladame motiv vo forme pravdepodobnostneho profilu dlzky L a jeho vyskyt v kazdej sekvencii
- Nech
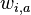 je pravdepodobnost, ze na pozicii i motivu bude baza a
je pravdepodobnost, ze na pozicii i motivu bude baza a
- Zadefinujeme cele ako velky pravdepodobnostny model:
- dane L, nulova hypoteza q (distribucia nukleotidov)
- vygeneruje sa nahodny profil w (napr z roznomernej distribucie cez vsetky profily)
- v kazdej sekvencii i sa zvoli okno
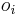 dlzky L (rovnomerne z m-L+1 moznosti)
dlzky L (rovnomerne z m-L+1 moznosti)
- V okne sa nageneruje sekvencia podla profilu w
- mimo okna sa nageneruje sekvencia z nulovej hypotezy (nezavisle bazy)
- celkove sekvencie oznacime S
-
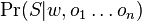 je jednoduchy sucin, kde pre pozicie v oknach pouzijeme pravdepodobnosti z w, pre pozicie mimo okna pouzijeme q
je jednoduchy sucin, kde pre pozicie v oknach pouzijeme pravdepodobnosti z w, pre pozicie mimo okna pouzijeme q
- Gibbsovo vzorkovanie:
- Mame dane S, chceme najst okna (vyskyty motivu), z nich uz lahko zostavime maticu
- zacni s nahodnymi oknami

- v kazdom kroku zvol jednu sekvenciu i a pre vsetky pozicie
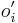 spocitaj
spocitaj 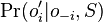
- nahodne zvol jedno
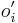 umerne k tymto pravdepodobnostiam
umerne k tymto pravdepodobnostiam
- opakuj vela krat, konverguje k cielovemu rozdeleniu
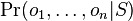
- mozeme si pamatat, ktore okno ako casto vnutri motivu alebo konfiguraciu s najvacsou pravdepodobnostou, aku sme stretli pocas vzorkovania
- dalsie mozne kroky vo vzorkovani: posun vsetky okna o konstantu vlavo alebo vpravo
- dalsie moznosti rozsirenia modelu/algoritmu: pridaj rozdelenie cez L a nahodne zvacsuj/zmensuj L, dovol vynechat motiv v niektorych sekvenciach, hladaj viac motivov naraz,...
- Ako spocitat
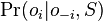 ? (nezaujimaju nas normalizacne konstanty, lahko znormalizujeme scitanim cez vsetky
? (nezaujimaju nas normalizacne konstanty, lahko znormalizujeme scitanim cez vsetky 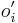 )
)
-
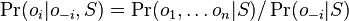 , ale menovatel konstanta
, ale menovatel konstanta
-
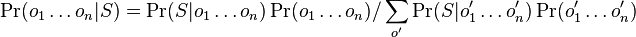
- Citatel nas nezaujima (normalizacna konstanta)
-
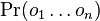 je konstanta (rovnomerne rozdelenie pozicii okien)
je konstanta (rovnomerne rozdelenie pozicii okien)
- Nech
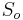 su len sekvencie v oknach, mame
su len sekvencie v oknach, mame 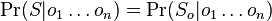 * pravdepodobnosti z nulovej hypotezy pre miesta mimo okien
* pravdepodobnosti z nulovej hypotezy pre miesta mimo okien
-
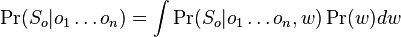 kde integral ide cez hodnoty, kde
kde integral ide cez hodnoty, kde 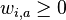 a
a 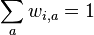
-
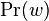 je konstanta (rovnomerne rozdelenie),
je konstanta (rovnomerne rozdelenie), 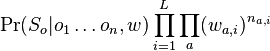 , kde
, kde 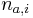 je pocet vyskytov bazy a na pozicii i v oknach
je pocet vyskytov bazy a na pozicii i v oknach 
-
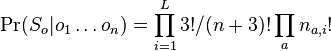 (bez dokazu)
(bez dokazu)
-
- Celkovy trik: vieme lahko spocitat pravdepodobnost dat ak vieme vsetky parametre
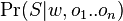
- Pomocou integralu vieme tiez odmarginalizovat w, t.j. spocitat
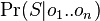
- Skusame vsetky mozne hodnoty
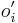 , pocitame pravdepodobnost dat, vzorkujeme umerne k tomu
, pocitame pravdepodobnost dat, vzorkujeme umerne k tomu
Siddharthan R, Siggia ED, van Nimwegen E (December 2005). "PhyloGibbs: a Gibbs sampling motif finder that incorporates phylogeny". PLoS Comput. Biol. 1 (7): e67. doi:10.1371/journal.pcbi.0010067. PMID 16477324.
Články na journal club
Podľa vašich preferencií sme Vás zadelili ku článkom (v prípade, že o vaše vybrané články bol velký záujem, snažili sme sa dať prednosť študentom, ktorí svoje preferencie odvzdali skôr).
1. Do CB, Mahabhashyam MS, Brudno M, Batzoglou S (2005). "ProbCons: Probabilistic consistency-based multiple sequence alignment.". Genome Res 15 (2): 330-40. PMID 15687296.
2. Lunter G (2007). "Probabilistic whole-genome alignments reveal high indel rates in the human and mouse genomes.". Bioinformatics 23 (13): i289-96. doi:10.1093/bioinformatics/btm185. PMID 17646308.
3. Kent WJ, Baertsch R, Hinrichs A, Miller W, Haussler D (2003). "Evolution's cauldron: duplication, deletion, and rearrangement in the mouse and human genomes.". Proc Natl Acad Sci U S A 100 (20): 11484-9. doi:10.1073/pnas.1932072100. PMID 14500911.
- Čítajú Michal Burger, Peter Galiovský, Peter Jurčo, Marcel Kucharík, Bianka Mateášiková
4. Siepel A, Bejerano G, Pedersen JS, Hinrichs AS, Hou M, Rosenbloom K et al. (2005). "Evolutionarily conserved elements in vertebrate, insect, worm, and yeast genomes". Genome Res 15 (8): 1034-50. doi:10.1101/gr.3715005. PMID 16024819.
- Čítajú Tomáš Eichler, Martin Gallus, Martin Sárközi, Martina Višňovská, Matej Vitko
5. Wapinski I, Pfeffer A, Friedman N, Regev A (2007). "Natural history and evolutionary principles of gene duplication in fungi". Nature 449 (7158): 54-61. doi:10.1038/nature06107. PMID 17805289.
- Čítajú Barbora Candráková, Jakub Kováč, Michal Kožuch, Ján Kriška, Milan Uherčík
6. Clamp M, Fry B, Kamal M, Xie X, Cuff J, Lin MF et al. (2007). "Distinguishing protein-coding and noncoding genes in the human genome.". Proc Natl Acad Sci U S A 104 (49): 19428-33. doi:10.1073/pnas.0709013104. PMID 18040051.
- Čítajú Michal Antonič, Matej Darebník, Juraj Mešťánek, Pavol Panák, Tomáš Paulenda
7. Eisen MB, Spellman PT, Brown PO, Botstein D (1998). "Cluster analysis and display of genome-wide expression patterns.". Proc Natl Acad Sci U S A 95 (25): 14863-8. PMID 9843981.
8. Harbison CT, Gordon DB, Lee TI, Rinaldi NJ, Macisaac KD, Danford TW et al. (2004). "Transcriptional regulatory code of a eukaryotic genome.". Nature 431 (7004): 99-104. doi:10.1038/nature02800. PMID 15343339.
- Čítajú Ladislav Benc, Maroš Gálik, Jana Konkoľová, Martin Kravec, Michaela Libiaková
9. Bystroff C, Baker D (1998). "Prediction of local structure in proteins using a library of sequence-structure motifs.". J Mol Biol 281 (3): 565-77. doi:10.1006/jmbi.1998.1943. PMID 9698570.
- Čítajú Matúš Fedák, Jana Hlavačiková, Adam Ješko, Lenka Kyjacová, Michal Nánási
10. Sharan R, Suthram S, Kelley RM, Kuhn T, McCuine S, Uetz P et al. (2005). "Conserved patterns of protein interaction in multiple species.". Proc Natl Acad Sci U S A 102 (6): 1974-9. doi:10.1073/pnas.0409522102. PMID 15687504.
- Čítajú Stanislav Hreha, Martin Králik, Martin Macko, Miroslav Nadhajský, Martina Petrušová
11. Andronescu M, Fejes AP, Hutter F, Hoos HH, Condon A (2004). "A new algorithm for RNA secondary structure design.". J Mol Biol 336 (3): 607-24. doi:10.1016/j.jmb.2003.12.041. PMID 15095976.
- Čítajú Peter Herman, Jakub Kollár, Peter Kováč, Peter Perešíni, Ladislav Rampášek, Jozef Vavro
12. Hernandez RD, Hubisz MJ, Wheeler DA, Smith DG, Ferguson B, Rogers J et al. (2007). "Demographic histories and patterns of linkage disequilibrium in Chinese and Indian rhesus macaques.". Science 316 (5822): 240-3. doi:10.1126/science.1140462. PMID 17431170.
Ukážkové príklady na skúšku
Aspoň polovicu bodov na skúške bude možné pre biológov aj informatikov možné získať z príkladov typu uvedeného nižšie. Samozrejme, na skúške nepoužijeme všetky tieto príklady a konkrétne reťazce, čísla, stromy a pod. budú iné. Na skúške máte dovolené používať kalkulačku s bežnými matematickými funkciami (nie však zložitejšie výpočtové zariadenia) a ťahák na dvoch listoch formátu A4, ktoré môžu byť z oboch strán popísané alebo potlačené ľubovoľným obsahom. Ostatné príklady na skúške budú prekvapením.
- Nájdite najkratšie spoločné nadslovo reťazcov GACAATAA, ATAACAC, GTATA, TAATTGTA.
- Zostavte deBruijnov graf stupňa k=3 pre reťazce GACAATAA, ATAACAC, GTATA, TAATTGTA a zistite, či má Eulerov ťah. Ak áno, akému reťazcu zodpovedá? Ak nie, prečo?
- Vyplňte maticu dynamického programovania pre lokálne (resp. globálne) zarovnanie reťazcov TACGT a CAGGATT, pričom zhodu skórujeme ako +3, nezhodu -1, medzeru -2. Napíšte aj optimálne zarovnanie, ktoré ste takto našli.
- Spočítaje skóre nižšieuvedeného zarovnania, pričom použijete skórovaciu maticu uvedenú nižšie, začatie medzery -5, rozšírenie medzery o jednu ďalšiu bázu -2. Nájdite globálne zarovnanie s vyšším skóre pre tieto dve sekvencie (netreba nájsť optimálne zarovnanie; pri hľadaní môžete použiť ľubovoľný postup alebo úvahu) a spočítajte aj skóre vášho nového zarovnania.
Zarovnanie: Matica:
ATAGTTTAA A C G T
A-GGG--AA A 2 -2 -1 -2
C -2 1 -2 -1
G -1 -2 1 -2
T -2 -1 -2 2
- Uvažujme BLASTn, ktorý začína z jadier veľkosti w=3. Koľko jadier nájde pri porovnávaní sekvencií GATTACGGAT a CAGGATT? Ktoré to budú?
- Pre model na strane 16 prednášky o hľadaní génov (bol by v zadaní) spočítajte pravdepodobnosť vygenerovania báz AGT a stavov modrý,červený,modrý.
- Na strome na strane 6 v prednáške o evolúcii (bol by v zadaní) nájdite najúspornejšie ancestrálne znaky pre stĺpec zarovnania TTAAA (v poradí glum, hobit, človek, elf, ork). Nemusíte použiť algoritmy z prednášky resp. cvičení.
- Nájdite najúspornejší strom pre zarovnanie uvedené nižšie. Aká je jeho cena (koľko mutácií je nutných na vysvetlenie týchto sekvencií)? Odpoveď môžete spočítať ľubovoľným spôsobom.
vtáčik biely ACAACGTCT vtáčik čierny TCTGAATCA vtáčik sivý TGTGAAAGA vtáčik modrý ACTACGTCT vtáčik zelený TGTGAAAGA
- Uvažujme maticu vzdialeností uvedenú nižšie. Ktorú dvojicu vrcholov spojí metóda spájania susedov ako prvú a aká bude nová matica po spojení?
biely čierny sivý modrý
vtáčik biely 0 5 7 4
vtáčik čierny 5 0 8 5
vtáčik sivý 7 8 0 5
vtáčik modrý 4 5 5 0
- Uvažujme strom ako na strane 6 v prednáške o evolúcii (bol by v zadaní), pričom každá hrana má rovnakú dĺžku a pravdepodobnosť každej mutácie na jednej hrane je 0.1 (t.j. napr. Pr(C|A,t)=0.1) a teda pravdepodobnosť zachovania tej istej bázy je 0.7, pravdepodobnosť každej bázy v koreni je 0.25. Aká je pravdepodobnosť, že v listoch dostaneme TTAAA a vo vnútorných vrcholoch samé Áčka? Nájdite priradenie ancestrálnych báz vo vnútorných vrcholoch, ktoré má väčšiu pravdepodobnosť a spočítajte, aká tá pravdepodobnosť je (nemusíte nájsť najlepšie možné priradenie).
- Zostavte profil (PSSM) pre zarovnanie sekvencií uvedené nižšie, pričom predpokladáme, že v celej databáze A tvorí 60% a T 40% všetkých sekvencií (iné bázy neuvažujeme). Použite prirodzený logaritmus (ln) a nepoužívajte pseudocounty.
AATA TATA TAAA TTAT TTAA
- Uvažujme microarray experimenty pre 5 génov. Medzi každými dvomi profilmi sme spočítali vzdialenosť (napr. pomocou Pearsonovho korelačného koeficientu) a dostali sme tabuľku vzdialeností uvedenú nižšie. Nájdite hierarchické zhlukovanie týchto génov, pričom vzdialenosť medzi dvoma zhlukmi (clustrami) bude vzdialenosť najbližších génov v nich.
A B C D E
gén A 0 0.6 0.1 0.3 0.7
gén B 0.6 0 0.5 0.5 0.4
gén C 0.1 0.5 0 0.6 0.6
gén D 0.3 0.5 0.6 0 0.8
gén E 0.7 0.4 0.6 0.8 0
- Uvažujte motív reprezentovaný profilom (skórovaciou maticou, PSSM) uvedenou nižšie. Spočítajte skóre reťazca GGAG. Ktorá sekvencia dĺžky 4 bude mať najmenšie a ktorá najväčšie skóre?
A -3 3 -2 -2 C -2 -2 1 -2 G 0 -2 -1 3 T 1 -1 1 -2
- Nájdite všetky výskyty regulárneho výrazu TA[CG][AT]AT v sekvencii GACGATATAGTATGTACAATATGC.
- Doplňte chýbajúce hodnoty za otázniky v matici dynamického programovania (Nussinovov algoritmus) pre nájdenie najväčšieho počtu dobre uzátvorkovaných spárovaných báz v RNA sekvencii GAACUAUCUGA (dovoľujeme len komplementárne páry A-U, C-G) a nakreslite sekundárnu štruktúru, ktorú algoritmus našiel.
0 0 0 1 1 2 2 3 3 ? ?
0 0 0 1 1 2 2 3 3 ?
0 0 1 1 2 2 2 3 3
0 0 1 1 1 1 2 3
0 1 1 ? 1 2 3
0 1 1 1 2 2
0 0 0 1 2
0 0 1 1
0 0 1
0 0
0
- Pre dvojice SNPov, ktorých tabuľky sú uvedené nižšie, určite, či môžeme štatisticky vylúčiť hypotézu, že sú v stave LE (linkage equilibrium) pri hladine významnosti p=0.05, resp.
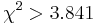 . Pre každú dvojicu spočítajte veličinu
. Pre každú dvojicu spočítajte veličinu 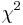 .
.
Q q Q q Q q
P 100 200 P 10 20 P 1 2
p 300 200 p 30 20 p 3 2
Pokyny k projektom
- Navrhom projektu sa zavazne prihlasite, ze chcete robit projekt a nie skusku. Vyzadujeme ho aj od tych, co sa uz s nami o projekte rozpravali.
- Navrh posielajte e-mailom na adresu B. Brejovej (uvedena na stranke predmetu) do 18.12.2009
- Uvedte meno a e-mailovu adresu a hlavny ciel projektu
- Uvedte aj nejake detaily planovanej prace (podla typu projektu), napriklad:
- Ake data alebo programy chcete pouzit
- Co chcete implementovat
- Ako vyhodnotite uspesnost pouzitych metod
- Ake clanky chcete studovat (najma pre prehladove projekty)
- Popis projektu nemusi byt dlhy, staci zopar viet.
- Pre skupinove projekty staci poslat jeden e-mail za celu skupinu, kde vymenujete mena a emaily vsetky clenov.
- Plan nemusite dodrzat, ak okolnosti ukazu, ze by sa viac hodilo postupovat inak.
- Pokusime sa vam k planu poslat nase komentare.
- Aj pocas prace na projekte nas nevahajte kontaktovat (e-mailom alebo osobne), ak mate nejake otazky alebo problemy. Nenechavajte si vsak vsetko na poslednu chvilu, lebo moze nejaky cas trvat, kym vam odpovieme.
Typy projektov
Toto su typicke druhy projektov, mozete sa vsak pokusit aj o projekt ineho typu, alebo skombinovat niekolko typov.
- Prehladove: prestudujte niekolko suvisiach clankov (cca 3 ale moze byt aj viac) a spiste prehlad ich vysledkov.
- Aplikacne: pouzite existujuce programy na nove data (data mozu byt nahodne generovane, stiahnute z databaz na internete, alebo z vasho vlastneho vyskumu). Mali by ste rozumiet, aky problem presne pouzite programy riesia a aky je vyznam ich parametrov. Ak pouzivate len jeden program, skuste aspon menit nastavenia parametrov a vsimat si ich vplyv na vysledok. Druha moznost je porovnat vysledky roznych programov alebo urobit zlozitejsiu analyzu pomocou viacerych programov, ktore na seba nadvazuju. V kazdom pripade by sme mali nejako (aspon nepriamo) vyhodnotit, ci program dava rozumne vysledky.
- Implementacne: implementujte zlozitejsi algoritmus z nejakeho clanku (pripadne aj z prednasky) a otestujte ho na datach. Okrem testov na odstranenie chyb v kode, ktore by mali byt samozrejmostou, treba spravit aj testy, ktore vyhodnocuju rychlost algoritmu alebo presnost jeho vysledkov, najlepsie v porovnani s inymi algoritmami/implementaciami alebo v zavislosti od nejakych parametrov.
- Vymyslacie: vymyslite novy algoritmus alebo pravdepodobnostny model, analyzujte existujuci algoritmus a podobne. Pripadne potom mozete svoje napady skusit aj implementovat a testovat.
Sprava k projektu
- Zakladom hodnotenia vasho projektu bude sprava, ktoru o projekte napisete.
- Dolezity v sprave je uvod, v ktorom popisete celkovu motivaciu a ciele projektu a zavediete potrebne pojmy a zaver, v ktorom interpretujete a zhodnotite ziskane vysledky a popisete problemy, ktore ste nevedeli v projekte vyriesit ci navrhnete moznosti dalsej prace v tejto oblasti.
- V hlavnej casti spravy uvedte detaily vasej prace. Napriklad, pri implementacnych projektoch strucne popiste implementovany algoritmus a uvedte zaujimavejsie podrobnosti svojej implementacie (ked ste sa museli napr. rozhodnut, aku datovu strukturu pouzit a podobne). Ak ste robili nejake vypoctove experimenty s datami, popiste, ake data ste pouzili (akeho su typu, kde ste ich vzali, ake su velke a pod.), ake programy ste pouzili (kde ste ich nasli, co robia), ake ste pouzili nastavenia a ake ste dostali vysledky.
- Pri prehladovych projektoch sa pokuste podrobne vysvetlit aspon jednu metodu alebo jej ucelenu cast a tiez strucne zhrnte a porovnajte ostatne metody alebo biologicke vysledky z clankov. Pokuste sa tiez vyjadrit svoj nazor na to, co su ich silnejsie a slabsie stranky.
- Sprava moze byt po slovensky alebo po anglicky. Neopisovat (pozrite pravidla a pokyny na stranke predmetu).
Odovzdanie a ustna skuska
- Spravu k projektu odovzdajte v papierovej forme do 11.1. na M163. Data, vase programy a ine subory suvisiace s projektom odovzdajte e-mailom B.Brejovej do toho isteho datumu. Ak su data velmi velke alebo su nepublikovane a preto ich kvoli ochrane nechcete posielat, doneste ich so sebou na USB kluciku na ustnu skusku, pre pripad, ze by sme sa na nieco chceli pozriet.
- Na ustnej skuske sa budeme sa snazit zistit, ci naozaj rozumiete problematike, ktoru v projekte riesite. Budeme diskutovat o detailoch vasho projektu, najma ak neboli uplne jasne zo spravy, o jeho moznych rozsireniach, o problemoch, na ktore ste narazili a podobne.
- Ustne skusky sa budu konat v tyzdni 18.-22.1.2009, terminy este oznamime. Ak by vam tento termin sposoboval problemy, dajte nam vediet.