Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
Burrowsova–Wheelerova transformácia: Rozdiel medzi revíziami
Z VPDS
(Vytvorená stránka „==FM index== * Ferragina and Manzini 2000 [http://ilex.iit.cnr.it/manzini/papers/focs00draft.pdf] * hladanie vyskytov P v T pomocou BWT a ranku * T dlzky n, pripojime $ ...“) |
(→FM index) |
||
| Riadok 3: | Riadok 3: | ||
* hladanie vyskytov P v T pomocou BWT a ranku | * hladanie vyskytov P v T pomocou BWT a ranku | ||
* T dlzky n, pripojime $ na poziciu T[n] | * T dlzky n, pripojime $ na poziciu T[n] | ||
| − | * zostrojime sufixove pole SA pre T a < | + | * zostrojime sufixove pole SA pre T a <math>L = BWT(T)</math> |
* spocitame si rank[a,i] v L, co je pocet vyskytov znaku a v L[0..i] | * spocitame si rank[a,i] v L, co je pocet vyskytov znaku a v L[0..i] | ||
| − | * spocitame < | + | * spocitame <math>C[a]=\sum_{b\in\Sigma,b<a}</math> pocet vyskytov b v T (resp. v L) |
* nech l(S) = najmensi index i t.z. S je prefix T[SA[i]..n] | * nech l(S) = najmensi index i t.z. S je prefix T[SA[i]..n] | ||
* nech r(S) = najvacsi index ... | * nech r(S) = najvacsi index ... | ||
Verzia zo dňa a času 19:20, 24. jún 2014
FM index
- Ferragina and Manzini 2000 [1]
- hladanie vyskytov P v T pomocou BWT a ranku
- T dlzky n, pripojime $ na poziciu T[n]
- zostrojime sufixove pole SA pre T a
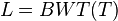
- spocitame si rank[a,i] v L, co je pocet vyskytov znaku a v L[0..i]
- spocitame
![C[a]=\sum _{{b\in \Sigma ,b<a}}](/vyuka/vpds/images/math/a/b/2/ab212f62c135d61b999a718b864f34a1.png) pocet vyskytov b v T (resp. v L)
pocet vyskytov b v T (resp. v L)
- nech l(S) = najmensi index i t.z. S je prefix T[SA[i]..n]
- nech r(S) = najvacsi index ...
- pre S = epsilon, mame l(S)=0, r(S)=n
- ak aS je podslovo T, l(aS) = C[a]+rank[a,l(S)-1]
- ak aS je podslovo T, r(aS) = C[a]+rank[a,r(S)]-1
- navyse ak S je podslovo T, tak aS je podslovo T prave vtedy ak l(aS)<=r(aS)
- Opakujeme pre stale dlhsie sufixy P, nakoniec dostaneme interval SA, kde sa nachadzaju vyskyty - spatne hladanie
Priklad
hladam .ama l(epsilon) = 0 r(epsilon) = 23 l(a) = C(a) + rank[a,L(epsilon)-1] = 6 + rank[a,-1] = 6 r(a) = C(a) + rank[a,R(epsilon)]-1 = 6 + rank[a,23]-1 = 11 l(ma) = C(m) + rank[m,L(a)-1] = 14 + rank[m,5] = 14 r(ma) = C(m) + rank[m,R(a)]-1 = 14 + rank[m,11] - 1 = 19 l(ama) = C(a) + ra(L(ma)-1) = 6 + ra(13) = 10 r(ama) = C(a) + ra(R(ma))-1 = 6 + ra(19) - 1 = 10 l(.ama) = C(.) + r.(L(ama)-1) = 1 + r.(9) = 1 r(.ama) = C(.) + r.(R(ama))-1 = 1 + r.(10)-1 = 0
Analyza
- zistovanie vyskytu, ratanie ich poctu potrebuje len polia rank a C
- na vypisanie pozicii potrebujeme aj SA
- pamat O(n sigma) cisel, hladanie v O(m)
- zlepsenie pamate pre rank:
- jednoducha finta: ulozime si rank len pre niektore i, zvysne dopocitame na zaklade pocitania vyskytov v L (vydelime pamat k, vynasobime cas k)
- na dalsich prednaskach si ukazeme wavelet tree: ako ulozit L + rank polia v n log sigma + o(n log sigma) bitoch, hladanie vyskytov sa spomali na O(m log sigma)
- ako kompaktnejsie ulozit SA
- trochu ina reverzna transformacia:
- predtym: najdi riadok j, v ktorom L[j] zodpoveda danemu F[i]
- teraz: najdi riadok j, v ktorom F[j] zopoveda danemu L[i] (toto j oznacime LF[i])
- LF[i] = C[L[i]]+ rank[L[i], i-1]
- ak riadok i zodpoveda sufixu T[k..n], tak riadok LF[i] zodpoveda sufixu T[k-1..n]
- T[n] = $, s = 0, i = n-1; while(i>=0) { T[i] = L[s]; s = LF[s]; i--; }
- pomocou tejto transformacie mozeme ulozit SA len pre niektore riadky, pre ine sa pomocou LF transformacie dostaneme k najblizsiemu riadku pre ktory mame SA
- ako presne ulozit "niektore riadky" ked su nerovnomerne rozmiestnene v SA (rovnomerne v T)?
- samotne L mozeme ulozit aj komprimovanie s vhodnymi indexami, vid. clanok od F a M alebo ho mame reprezentovane implicitne vo wavelet tree