1-BIN-301, 2-AIN-501 Methods in Bioinformatics

Website moved to https://fmfi-compbio.github.io/mbi/


CI12: Rozdiel medzi revíziami

Z MBI
Prejsť na: navigácia, hľadanie
(→‎Prakticke programy na NP tazke problemy)
 
(2 intermediate revisions by the same user not shown)
Riadok 13: Riadok 13:
  
 
===ILP===
 
===ILP===
−
'''Linearny program:'''  
+
'''Lineárny program:'''  
−
* Mame realne premenne x_1...x_n, minimalizujeme nejaku ich linearnu kombinaciu <math>\sum_i a_i x_i\,</math> kde a_i su dane vahy.
+
* Mame reálne premenné x_1...x_n, minimalizujeme nejaku ich linearnu kombinaciu <math>\sum_i a_i x_i\,</math> kde a_i su dane vahy.
 
* Mame tiez niekolko podmienok v tvare linearnych rovnosti alebo nerovnosti, napr. <math>\sum_i b_i x_i \le c</math>
 
* Mame tiez niekolko podmienok v tvare linearnych rovnosti alebo nerovnosti, napr. <math>\sum_i b_i x_i \le c</math>
 
* Hladame teda hodnoty premennych, ktore minimalizuju cielovu sumu, ale pre ktore platia vsetky podmienky
 
* Hladame teda hodnoty premennych, ktore minimalizuju cielovu sumu, ale pre ktore platia vsetky podmienky
Riadok 34: Riadok 34:
 
* Chceme minimalizovat <math>\sum_{i=1}^n x_i\,</math>
 
* Chceme minimalizovat <math>\sum_{i=1}^n x_i\,</math>
 
* za podmienky, ze pre kazde j z {1..m} plati <math>\sum_{i:j\in S_i} x_j \ge 1</math>
 
* za podmienky, ze pre kazde j z {1..m} plati <math>\sum_{i:j\in S_i} x_j \ge 1</math>
 +
  
 
===Protein threading===
 
===Protein threading===
Riadok 60: Riadok 61:
 
Zdroj:
 
Zdroj:
 
* Jinbo Xu, Ming Li, Dongsup Kim, and Ying Xu. "RAPTOR: optimal protein threading by linear programming." Journal of bioinformatics and computational biology 1, no. 01 (2003): 95-117. [http://ttic.uchicago.edu/~jinbo/SelectedPubs/RAPTOR.pdf]
 
* Jinbo Xu, Ming Li, Dongsup Kim, and Ying Xu. "RAPTOR: optimal protein threading by linear programming." Journal of bioinformatics and computational biology 1, no. 01 (2003): 95-117. [http://ttic.uchicago.edu/~jinbo/SelectedPubs/RAPTOR.pdf]
 +
 +
===Iný príklad: Zarovnanie sekvencií RNA so štruktúrou===
 +
 +
Máme dané dve sekvencie RNA a pre každú z nich máme daný zoznam párov báz (pozícií v rámci sekvencie), ktoré by mohli byť prítomné v sekundárnej štruktúre.
 +
* Zoznam párov môže byť konkrétna známa sekundárna štruktúra danej sekvencie alebo väčšia množina párov, ktoré by sa v štruktúre mohli vyskytovať, napríklad dvojice, ktoré majú pomerne veľkú pravdepodobnosť byť spárené v SCFG modeli alebo dokonca všetky dvojice komplementárnych báz.
 +
 +
Cieľom je nájsť optimálne zarovnanie týchto dvoch sekvencií, v ktorom použijeme obvyklé skórovanie zhôd, nezhôd a medzier, ale navyše pridáme nejaké skóre za zhody v štruktúre. Dva potenciálne páry, každý z jednej sekvencie, považujeme za zarovnané, ak sú navzájom zarovnané bázy na ich obidvoch koncoch. Do skórovania vyberieme podmnožinu zarovnaných párov tak, aby každá báza bola v najviac jednom páre a každému takému páru priradíme nejaké kladné skóre.
 +
 +
Detaily:
 +
https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-8-271

Aktuálna revízia z 09:03, 14. december 2023

Protein threading

Praktické programy na NP ťažké problémy

  • Obcas chceme najst optimalne riesenie nejakeho NP-tazkeho problemu
  • Jedna moznost je previest na iny NP tazky problem, pre ktory existuju pomerne dobre prakticke programy, napriklad integer linear programming (ILP)
  • najdu optimalne riesenie, mnohe instancie zrataju v rozumnom case, ale mozu bezat aj velmi dlho
  • CPLEX [1] a Gurobi [2] komercne baliky na ILP, akademicka licencia zadarmo
  • SCIP [3] nekomercny program pre ILP
  • SYMPHONY v projekte COIN-OR [4]
  • Minisat [5] open source SAT solver, tiež Lingeling, glucose, CryptoMiniSat, painless
  • Concorde TSP solver [6] - riesi problem obchodneho cestujuceho so symetrickymi vzdialenostami, zadarmo na akademicke ucely
    • Pre zaujimavost: TSP art [7]

ILP

Lineárny program:

  • Mame reálne premenné x_1...x_n, minimalizujeme nejaku ich linearnu kombinaciu 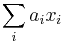\sum _{i}a_{i}x_{i}\, kde a_i su dane vahy.
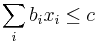
  • Mame tiez niekolko podmienok v tvare linearnych rovnosti alebo nerovnosti, napr. \sum _{i}b_{i}x_{i}\leq c
  • Hladame teda hodnoty premennych, ktore minimalizuju cielovu sumu, ale pre ktore platia vsetky podmienky
  • Da sa riesit v polynomialnom case

Integer linear program

  • Program, v ktorom vsetky/vybrane premenne musia mat celociselne hodnoty, alebo dokonca povolime iba hodnoty 0 a 1.
  • NP uplny problem

Ako zapisat (NP-tazke) problemy ako ILP

Knapsack

  • Problem: mame dane predmety s hmotnostami w_1..w_n a cenami c_1..c_n, ktore z nich vybrat, aby celkova hmotnost bola najviac T a cena bola co najvyssia?
  • Pouzijeme binarne premenne x_1..x_n, kde x_i = 1 prave vtedy ked sme zobrali i-ty predmet.
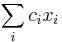
  • Chceme maximalizovat \sum _{i}c_{i}x_{i}\,
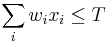
  • za podmienky ze \sum _{i}w_{i}x_{i}\leq T

Set cover:

  • Mame n mnozin S_1...S_n nad mnozinou {1...m}. Chceme vybrat co najmensi pocet zo vstupnych mnozin tak, aby ich zjednotenie bola cela mnozina {1..m}
  • Binarne premenne x_i=1 ak vyberieme i-tu mnozinu
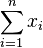
  • Chceme minimalizovat \sum _{{i=1}}^{n}x_{i}\,
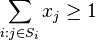
  • za podmienky, ze pre kazde j z {1..m} plati \sum _{{i:j\in S_{i}}}x_{j}\geq 1


Protein threading

  • Ciel: protein A ma znamu sekvenciu aj strukturu, protein B iba sekvenciu. Chceme zarovnat proteiny A a B, pricom budeme brat do uvahy znamu strukturu, t.j. ak su dve amino kyseliny blizko v A tak ich ekvivalenty v B by mali byt "kompatibilne".
  • Tento problem chceme riesit tak, ze v strukture A urcime nejake jadra, ktore by v evolucii mali zostat zachovane bez inzercii a delecii a v rovnakom poradi. Tieto jadra su oddelene sluckami, ktorych dlzka sa moze lubovolne menit a ktorych zarovnania nebudeme skorovat.
  • Formulacia problemu: Mame danu sekvenciu B=b1..bn, dlzky m jadier c_1...c_m a skorovacie tabulky E_ij, ktora vyjadruje, ako dobre bj..b_{j+c_i-1} sedi do sekvencie jadra i a E_ijkl ktora vyjadruje, ako dobre by jadra i a k interagovali, keby mali sekvencie zacinajuce v B na poziciach j a l. Uloha je zvolit polohy jadier x_1<x_2<...<x_m tak, aby sa ziadne dve jadra neprekryvali a aby sme dosiahli najvyssie skore.
  • Poznamka: nevraveli sme, ako konkretne zvolit jadra a skorovacie tabulky, co je modelovaci, nie algoritmicky problem (mozeme skusit napr. nejake pravdepodobnostne modely)

Protein threading ako ILP

  • Premenne v programe:
    • x_ij=1 ak je zaciatok i-teho jadra zarovnane s b_j
    • y_ijkl=1 ak je zaciatok i-teho jadra na b_j a zaciatok k-teho na b_l (i<k, j<l)
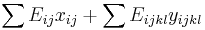
  • Chceme maximalizovat \sum E_{{ij}}x_{{ij}}+\sum E_{{ijkl}}y_{{ijkl}}
  • Podmienky:
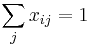    • \sum _{j}x_{{ij}}=1\, pre kazde i
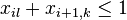    • x_{{il}}+x_{{i+1,k}}\leq 1 pre vsetky i,k,l, kde k<l+c_i
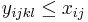    • y_{{ijkl}}\leq x_{{ij}} pre vsetky i,j,k,l, kde i<k, j<l
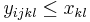    • y_{{ijkl}}\leq x_{{kl}} pre vsetky i,j,k,l, kde i<k, j<l
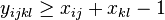    • y_{{ijkl}}\geq x_{{ij}}+x_{{kl}}-1 pre vsetky i,j,k,l, kde i<k, j<l

Na zamyslenie:

  • Aka bude velkost programu ako funkcia n a m?
  • Co ak nie vsetky jadra navzajom interaguju? Mozeme na velkosti programu usetrit?
  • Preco asi vobec autori zaviedli jadra a ako by sme zmenili program, ak by sme chceli uvazovat kazdu aminokyselinu zvlast?

Zdroj:

  • Jinbo Xu, Ming Li, Dongsup Kim, and Ying Xu. "RAPTOR: optimal protein threading by linear programming." Journal of bioinformatics and computational biology 1, no. 01 (2003): 95-117. [8]

Iný príklad: Zarovnanie sekvencií RNA so štruktúrou

Máme dané dve sekvencie RNA a pre každú z nich máme daný zoznam párov báz (pozícií v rámci sekvencie), ktoré by mohli byť prítomné v sekundárnej štruktúre.

  • Zoznam párov môže byť konkrétna známa sekundárna štruktúra danej sekvencie alebo väčšia množina párov, ktoré by sa v štruktúre mohli vyskytovať, napríklad dvojice, ktoré majú pomerne veľkú pravdepodobnosť byť spárené v SCFG modeli alebo dokonca všetky dvojice komplementárnych báz.

Cieľom je nájsť optimálne zarovnanie týchto dvoch sekvencií, v ktorom použijeme obvyklé skórovanie zhôd, nezhôd a medzier, ale navyše pridáme nejaké skóre za zhody v štruktúre. Dva potenciálne páry, každý z jednej sekvencie, považujeme za zarovnané, ak sú navzájom zarovnané bázy na ich obidvoch koncoch. Do skórovania vyberieme podmnožinu zarovnaných párov tak, aby každá báza bola v najviac jednom páre a každému takému páru priradíme nejaké kladné skóre.

Detaily: https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-8-271

Zdroj: „https://compbio.fmph.uniba.sk/vyuka/mbi/index.php?title=CI12&oldid=3060“