CB06: Rozdiel medzi revíziami
Z MBI
(→Bootstrap) |
(→Zložitejšie evolučné modely) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Riadok 52: | Riadok 52: | ||
Aké sme doteraz videli modely | Aké sme doteraz videli modely | ||
| − | * Skórovacie matice: | + | * Skórovacie matice: porovnávame model náhodných sekvencií a model náhodných zarovnaní |
| − | * E-value v BLASTe: | + | * E-value v BLASTe: náhodne vygenerujeme databázu a dotaz (query), koľko bude v priemere medzi nimi lokálnych zarovnaní so skóre aspoň S? |
| − | * | + | * Hľadanie génov: model generujúci sekvenciu+anotáciu naraz (parametre nastavené na známych génoch). Pre danú sekvenciu, ktorá anotácia je najpravdepodobnejšia? |
| − | * | + | * Evolúcia, Jukes-Cantorov model: model generujúci stĺpec zarovnania. Neznáme parametre: strom, dĺžky hrán. Pre danú sadu stĺpcov zarovnania, ktoré parametre povedú k najväčšej pravdepodobnosti? <math>\max_{param} \Pr(data|param)</math> |
| − | ** Trochu detailov: | + | ** Trochu detailov: pravdepodobnosť zmeny/nezmeny na hrane dĺžky t: <math>P(A|A,t) = (1+3e^{-\frac{4}{3} t})/4 </math>, <math>P(C|A,t)=(1-e^{-\frac{4}{3} t})/4</math> |
| − | ** Ak | + | ** Ak poznáme ancestrálne sekvencie, vieme spočítať pravdepodobnosť dát |
| − | ** | + | ** Ancestrálne sekvencie sú náhodné premenné, ktoré nás nezaujímajú: marginalizujeme ich (uvažujeme všetky ich možné hodnoty) |
==Zložitejšie evolučné modely== | ==Zložitejšie evolučné modely== | ||
| Riadok 64: | Riadok 64: | ||
* Nie všetky substitúcie sa dejú rovnako často: tranzície (v rámci pyrimidínov T<->C, v rámci purínov A<->G) sú pravdepodobnejšie ako tranzverzie (A,G)<->(C,T) | * Nie všetky substitúcie sa dejú rovnako často: tranzície (v rámci pyrimidínov T<->C, v rámci purínov A<->G) sú pravdepodobnejšie ako tranzverzie (A,G)<->(C,T) | ||
* Nie všetky nukleotidy sa v danom genóme vyskytujú rovnako často (napr. mitochondriálne genómy majú nízky obsah GC) | * Nie všetky nukleotidy sa v danom genóme vyskytujú rovnako často (napr. mitochondriálne genómy majú nízky obsah GC) | ||
| − | * Tieto javy | + | * Tieto javy zachytáva HKY model (Hasegawa, Kishino & Yano) |
| − | * Matica | + | * Matica rýchlostí zmeny (substitution rate matrix) |
<math>\left( | <math>\left( | ||
\begin{array}{cccc} | \begin{array}{cccc} | ||
| Riadok 74: | Riadok 74: | ||
\end{array} | \end{array} | ||
\right)</math> | \right)</math> | ||
| − | * <math>\kappa=\alpha/\beta</math> je pomer | + | * <math>\kappa=\alpha/\beta</math> je pomer rýchlostí, ktorými sa deju tranzície vs. transverzie |
* <math>\pi_j</math> je frekvencia bazy <math>j</math> v sekvencii | * <math>\pi_j</math> je frekvencia bazy <math>j</math> v sekvencii | ||
| − | * | + | * Rýchlosť, ako sa deje substitúcia z X do Y je súčin pravdepodobnosti Y a faktoru, ktorý zavisí od toho, či ide o tranzíciu alebo transverziu |
| − | * | + | * Súčet každého riadku matice má byť 0, t.j. <math>\mu_A=\beta\pi_C + \alpha\pi_G + \beta\pi_T</math> |
| − | * Matica sa znormalizuje tak, aby | + | * Matica sa znormalizuje tak, aby priemerný počet substitúcii za jednotku času bol 1 |
* Matica ma styri parametre: <math>\kappa</math> a tri frekvencie (stvrta musi doplnit do 1) plus dlzka hrany | * Matica ma styri parametre: <math>\kappa</math> a tri frekvencie (stvrta musi doplnit do 1) plus dlzka hrany | ||
* Zlozitejsi model lepsie zodpoveda skutocnym procesom, ale na odhad viac parametrov potrebujeme viacej dat. | * Zlozitejsi model lepsie zodpoveda skutocnym procesom, ale na odhad viac parametrov potrebujeme viacej dat. | ||
* Existuju metody, ktore pre dany cas t z matice rychlosti spocitaju pravdepodobnost, ze baza X zmutuje na bazu Y Pr(Y|X,t) | * Existuju metody, ktore pre dany cas t z matice rychlosti spocitaju pravdepodobnost, ze baza X zmutuje na bazu Y Pr(Y|X,t) | ||
* Napr. pre velmi maly cas <math>\epsilon</math> mame <math>\Pr(C|A,\epsilon)</math> je zhruba <math>\epsilon\beta\pi_C</math> | * Napr. pre velmi maly cas <math>\epsilon</math> mame <math>\Pr(C|A,\epsilon)</math> je zhruba <math>\epsilon\beta\pi_C</math> | ||
| − | * Pre rozumne dlhe casy toto neplati, preto sa pouzivaju algebraicke | + | * Pre rozumne dlhe casy toto neplati, preto sa pouzivaju algebraicke metódy, ktoré berú do úvahy možnosť viacerých substitúcií na tom istom mieste |
* Je aj vela inych modelov s mensim alebo vacsim poctom parametrov | * Je aj vela inych modelov s mensim alebo vacsim poctom parametrov | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Fitchov algoritmus== | ==Fitchov algoritmus== | ||
Aktuálna revízia z 15:20, 26. október 2023
Obsah
Fylogenetické stromy
Terminológia:
- zakorenený strom, rooted tree
- nezakorenený strom, unrooted tree
- hrana, vetva, edge, branch
- vrchol, uzol, vertex, node
- list, leaf, leaf node, tip, terminal node
- vnútorný vrchol, internal node
- koreň, root
- podstrom, subtree, clade
Zopár faktov o stromoch
- Majme zakorenený strom s n listami, v ktorom má každý vnútorný vrchol 2 deti. Takýto strom vždy má n-1 vnútorných vrcholov a 2n-2 vetiev (prečo?)
- Majme nezakorenený strom s n listami, v ktorom má každý vnútorný vrchol 3 susedov. Takýto strom vždy má n-2 vnútorných vrcholov a 2n-3 vetiev
- Koľkými spôsobmi môžeme zakoreniť nezakorenený strom s n listami?
- koreň môže byť na hociktorej vetve stromu, teda je 2n-3 možností zakorenenia
- Ak nakreslíme zakorenený strom obvyklým spôsobom, listy sú usporiadané zhora nadol (alebo zľava doprava). Koľko rôznych poradí listov vieme dostať rôznym zakresľovaním toho istého stromu s n listami?
- máme n-1 vnutornych vrcholov, v kazdom mozeme vymenit lave a prave dieta. Pre kazdu konfiguraciu takychto vymen dostavame ine poradie, celkovy pocet poradi je 2n-1
- Čo vieme zistiť o príbuznosti organizmov z nezakoreneného stromu (napr. kvartet 4 organizmov)?
- skúsime zakoreniť všetkými spôsobmi a vidíme, že o žiadnych dvoch listoch nevieme povedať, že by boli sesterské (evolučne bližšie než ostatné), lebo koreň stromu môže byť zrovna na niektorej hrane vedúcej ku nim
- vieme však zistiť, že niektoré dvojice sesterské nebudú
Iné použitie stromov v informatike:
- uvidíme hierarchické zhlukovanie, bayesovské siete, ale tiež efektívne dátové štruktúry
Bootstrap
- Náhodne vyberieme niektoré stĺpce zarovnania, zostrojíme strom vybranou metódou
- Celé to opakujeme veľa krát
- Značíme si, koľkokrát sa ktorá vetva opakuje v stromoch, ktoré dostávame
- Pri nezakorenených stromoch je vetva rozdelenie listov na dve skupiny (bipartícia)
- Nakoniec zostavíme strom z celých dát a pozrieme sa ako často sa ktorá jeho vetva vyskytovala
- Môžeme zostaviť aj strom z často sa vyskytujúcich hrán (napr. tých, ktoré sú vo viac ako 50% stromov)
- Bootstrap hodnoty nám dajú určitý odhad spoľahlivosti, hlavne ak máme celkovo málo dát (krátke zarovnanie)
- Ak však dáta nezodpovedajú vybranej metóde/modelu, tak aj pre zlý strom môžeme dostať vysoký bootstrap
Detail: pri náhodnom výbere stĺpcov pre bootstrap väčšinou používame rovnaký počet stĺpcov ako pôvodné zarovnanie, pričom vzorkujeme z pôvodného zarovnania s povolením opakovania stĺpca.
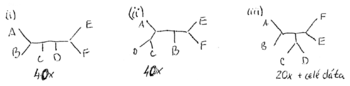
Príklad
- Robili sme 100x bootstrap, 40x sme dostali strom (i) na obrázku, 40x sme dostali strom (ii) a 20x sme dostali strom (iii)
- Strom (iii) sme dostali aj spustením metody na celých dátach
- Zistite úroveň bootstrap podpory pre jednotlivé vetvy stromu (iii)
- Ktoré ďalšie vetvy majú podporu aspoň 20%?
- Aký strom by sme dostali, ak by sme chceli nechať iba vetvy s podporou aspoň 80%?
Opakovanie pravdepodobnostných modelov
Keď počítame pravdepodobnosť, rozmýšľame o myšlienkovom experimente, v ktorom hádžeme kockou, ťaháme gulôčky z vreca a pod.
- Dôležité je vždy si poriadne uvedomiť, ako tento experiment prebieha
- Tieto myšlienkové experimenty však nastavujeme tak, aby odzrkadľovali nejaké aspekty reality, napr. skutočných DNA sekvencií, ich evolúcie a pod.
- Takže pravdepodobnosti, ktoré spočítame v idealizovanom svete nám možno niečo povedia o reálnom svete
- Slávny citát štatistika Georga Boxa "All models are wrong, but some are useful."
Aké sme doteraz videli modely
- Skórovacie matice: porovnávame model náhodných sekvencií a model náhodných zarovnaní
- E-value v BLASTe: náhodne vygenerujeme databázu a dotaz (query), koľko bude v priemere medzi nimi lokálnych zarovnaní so skóre aspoň S?
- Hľadanie génov: model generujúci sekvenciu+anotáciu naraz (parametre nastavené na známych génoch). Pre danú sekvenciu, ktorá anotácia je najpravdepodobnejšia?
- Evolúcia, Jukes-Cantorov model: model generujúci stĺpec zarovnania. Neznáme parametre: strom, dĺžky hrán. Pre danú sadu stĺpcov zarovnania, ktoré parametre povedú k najväčšej pravdepodobnosti?
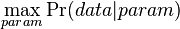
- Trochu detailov: pravdepodobnosť zmeny/nezmeny na hrane dĺžky t:
, 
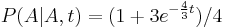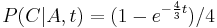
- Ak poznáme ancestrálne sekvencie, vieme spočítať pravdepodobnosť dát
- Ancestrálne sekvencie sú náhodné premenné, ktoré nás nezaujímajú: marginalizujeme ich (uvažujeme všetky ich možné hodnoty)
- Trochu detailov: pravdepodobnosť zmeny/nezmeny na hrane dĺžky t:
Zložitejšie evolučné modely
- Jukes-Cantorov model uvažuje len dĺžku hrany udanú ako priemerný počet substitúcií (vrátane tých, ktore nevidíme, kvôli tomu, že boli dve na tom istom mieste)
- Nie všetky substitúcie sa dejú rovnako často: tranzície (v rámci pyrimidínov T<->C, v rámci purínov A<->G) sú pravdepodobnejšie ako tranzverzie (A,G)<->(C,T)
- Nie všetky nukleotidy sa v danom genóme vyskytujú rovnako často (napr. mitochondriálne genómy majú nízky obsah GC)
- Tieto javy zachytáva HKY model (Hasegawa, Kishino & Yano)
- Matica rýchlostí zmeny (substitution rate matrix)
-
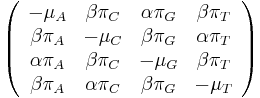
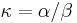je pomer rýchlostí, ktorými sa deju tranzície vs. transverzie
-
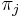je frekvencia bazy 
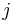v sekvencii
- Rýchlosť, ako sa deje substitúcia z X do Y je súčin pravdepodobnosti Y a faktoru, ktorý zavisí od toho, či ide o tranzíciu alebo transverziu
- Súčet každého riadku matice má byť 0, t.j.
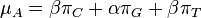
- Matica sa znormalizuje tak, aby priemerný počet substitúcii za jednotku času bol 1
- Matica ma styri parametre:
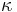a tri frekvencie (stvrta musi doplnit do 1) plus dlzka hrany
- Zlozitejsi model lepsie zodpoveda skutocnym procesom, ale na odhad viac parametrov potrebujeme viacej dat.
- Existuju metody, ktore pre dany cas t z matice rychlosti spocitaju pravdepodobnost, ze baza X zmutuje na bazu Y Pr(Y|X,t)
- Napr. pre velmi maly cas
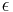mame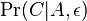 
je zhruba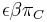 
- Pre rozumne dlhe casy toto neplati, preto sa pouzivaju algebraicke metódy, ktoré berú do úvahy možnosť viacerých substitúcií na tom istom mieste
- Je aj vela inych modelov s mensim alebo vacsim poctom parametrov
Fitchov algoritmus
Nerobili sme, uvedene pre zaujimavost
- Parsimony/uspornost
- Vstup: fylogeneticky strom, 1 stlpec zarovnania (jedna baza v kazdom liste stromu)
- Vystup: priradenie baz predkom minimalizujuce pocet substitucii
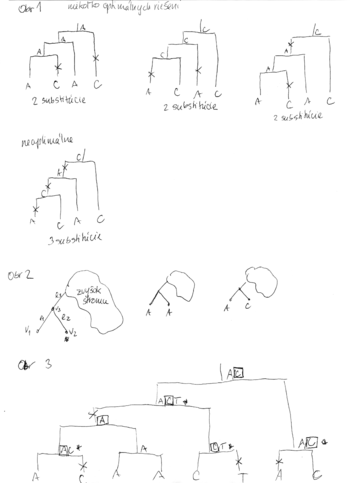
- Priklad - obr 1
- Uvazujme, co vieme povedat o strome s dvoma susednymi listami vo vacsom strome (oznacenie: obr. 2, listy v1 a v2, hrany do listov e1, e2, ich predok v3, hrana z v3 vyssie e3).
- Ak oba listy maju bazu rovnaku bazu, napr. A, predok v3 v optimalnom rieseni bude urcite mat bazu A
- Dokaz sporom: nech to tak nie je, nech optimalne riesenie ma nejaku inu bazu, napr. C. Vymenme v tomto rieseni toto C za A. Moze nam pribudnut jedna mutacia na hrane e3, ale ubudnu dve na hranach e1 a e2. Tym celkova cena riesenia klesne o 1, takze nebolo optimalne.
- Ak tieto dva listy maju rozne bazy, napr. A a C, tak existuje optimalne riesenie, ktore ma v predkovi v3 bazu A alebo C.
- Dokaz: vezmime optimalne riesenie. Ak ma v3 bazu A alebo C, tvrdenie plati. Ak ma v3 nejaku inu bazu, napr T, mozeme ju vymenit napr. za A, ci mozno pribudne jedna mutacia na e3 ale urcite ubudne mutacia na e1. Teda celkovy pocet mutacii sa nezvysi a nase nove riesenie je stale optimalne. Pozor, vo vseobecnosti nevieme povedat, ci ma v3 mat bazu A alebo C. V niektorych pripadoch su optimalne obe, v niektorych len jedna z nich.
- Fitchov algoritmus 1971
- Kazdemu vrcholu v priradime mnozinu baz M(v)
- M(v) pocitame od listov smerom ku korenu
- Pre list v bude M(v) obsahovat bazu v tomto liste
- Uvazujme vnutorny vrchol v s detmi x a y. Mame uz spocitane M(x) a M(y), chceme M(v)
- Ak M(x) a M(y) maju nejake spolocne bazy, vsetky tieto spolocne bazy dame do M(v), t.j.
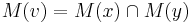
- Ak M(x) a M(y) nemaju spolocne bazy, do M(v) dame vsetky bazy z M(x) aj M(v), t.j.
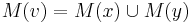
- V tomto pripade pocet mutacii vzrastie o jedna
- Ked mame M(v) spocitane pre vsetky vrcholy, ideme od korena smerom k listom a vyberieme vzdy jednu bazu z M(v).
- Ak sme vybrali pre rodica bazu x a x je v M(v), zvolime x aj pre v, inak zvolime lubovolnu bazu z M(v).
- Priklad algoritmu na obr 3
