1-BIN-301, 2-AIN-501 Methods in Bioinformatics

Website moved to https://fmfi-compbio.github.io/mbi/


Exam: Rozdiel medzi revíziami

Z MBI
Prejsť na: navigácia, hľadanie
(Vytvorená stránka „<!-- Nižšie uvádzame pre každý okruh učiva stručný zoznam najdôležitejších pojmov, ktoré by biológovia aj informatici mali poznať. Navyše uvádzame aj ni...“)
 
(→‎Additional important concepts for computer scientists)
 
(32 intermediate revisions by the same user not shown)
Riadok 1: Riadok 1:
 +
== Exam rules ==
 +
 +
Exam is for 1-BIN-301 (mainly AIN, BIN, DAV, INF students).
 +
 +
The exam is primarily '''written''':
 +
* You need at least 50% of points
 +
* Time 3 hours
 +
* About 50% of points for simple questions
 +
** examples on this page
 +
** in case of interest tutorial session before exam
 +
* The rest of the questions mostly designing/modifying an algorithm or model
 +
* You can use pen, simple calculator and a cheat sheet up to 2 A4 two-sided sheets
 +
 
<!--
 
<!--
−
Nižšie uvádzame pre každý okruh učiva stručný zoznam najdôležitejších pojmov, ktoré by biológovia aj informatici mali poznať. Navyše uvádzame aj niekoľko jednoduchých príkladov. Za príklady tohto typu bude možné pre biológov aj informatikov na skúške získať približne polovicu bodov. Samozrejme, na skúške nepoužijeme všetky tieto príklady a konkrétne reťazce, čísla, stromy a pod. budú iné. Na skúške máte dovolené používať kalkulačku s bežnými matematickými funkciami (nie však zložitejšie výpočtové zariadenia) a ťahák na dvoch listoch formátu A4, ktoré môžu byť z oboch strán popísané alebo potlačené ľubovoľným obsahom. Ostatné príklady na skúške budú prekvapením.
+
Na skúške máte dovolené používať kalkulačku s bežnými matematickými funkciami (nie však zložitejšie výpočtové zariadenia) a ťahák na dvoch listoch formátu A4, ktoré môžu byť z oboch strán popísané alebo potlačené ľubovoľným obsahom.  
 +
-->
 +
 
 +
If you do not pass the first written exam, part of your exam may be oral on the second and third attempts.
 +
 
 +
==Syllabus and examples of simple questions==
 +
 
 +
Below we list the most important concepts that both biologists and computer scientists should know from this course.
 +
 
 +
We also list simple questions. Questions of this type will comprise approximately 50% of the exam. Not all of these questions will be used on the exam and particular string, numbers, grammars and sequences will differ.
 +
 
 +
===Sequencing and genome assembly===
 +
 
 +
'''Main concepts in English and Slovak'''
 +
 
 +
DNA sequencing and its use, sequencing read, paired reads, contigs, shortest common superstring problem, de Bruijn graphs
  
−
===Sekvenovanie, zostavovanie genómov===
 
 
Sekvenovanie DNA a jeho využitie, čítanie (read), spárované čítania, kontig, problém najkratšieho spoločného nadslova, de Bruijnove grafy
 
Sekvenovanie DNA a jeho využitie, čítanie (read), spárované čítania, kontig, problém najkratšieho spoločného nadslova, de Bruijnove grafy
  
−
* Nájdite najkratšie spoločné nadslovo reťazcov GACAATAA, ATAACAC, GTATA, TAATTGTA.
+
'''Simple questions for the exam'''
−
* Zostavte deBruijnov graf pre k=2 (vrcholy budú dvojice) a čítania CCTGCC, GCCAAC
+
 
 +
* Find the shortest common superstring of strings GACAATAA, ATAACAC, GTATA, TAATTGTA.
 +
* Find the de Bruijn graph for k=2 (nodes will be pairs of nucleotides) and reads CCTGCC, GCCAAC
 +
 
 +
===Sequence alignment===
 +
 
 +
'''Main concepts in English and Slovak'''
 +
 
 +
The problem of local and global alignment of two sequences, dynamic programming algorithms, scoring matrix and its probabilistic meaning, statistical significance (E-value, P-value), heuristic search of local alignments (BLAST, minimizers), whole-genome and multiple alignments
 +
 
 +
Problém lokálneho a globálneho zarovnania dvoch sekvencií, jeho riešenie pomocou dynamického programovania, skórovacia matica a jej pravdepodobnostný význam, štatistická významnosť (E-value, P-value), heuristické hľadanie lokálnych zarovnaní (BLAST, minimizer-y), celogenómové a viacnásobné zarovnania
 +
 
 +
'''Simple questions for the exam'''
 +
 
 +
* Fill in the dynamic programing matrices for local and global alignment of sequences TACGT and CAGGATT, where the match has score +3, mismatch -1, gap -2. Reconstruct also the optimal alignments found by the dynamic programming algorithm.
  
−
===Zarovnávanie sekvencií===
+
* Compute the score of the alignment shown below using the scoring matrix shown below, gap opening penalty -5, gap extension penalty -2 for each additional base. Find a global alignment with a higher score for these two sequences and compute its score. (It is not necessary to find the optimal alignment; you can use any method to arrive at the answer.)
−
Problém lokálneho a globálneho zarovnania dvoch sekvencií, jeho riešenie pomocou dynamického programovania, skórovacia matica a jej pravdepodobnostný význam, štatistická významnosť (E-value, P-value), heuristické hľadanie lokálnych zarovnaní (BLAST), celogenómové a viacnásobné zarovnania
+
  
−
* Vyplňte maticu dynamického programovania pre lokálne (resp. globálne) zarovnanie reťazcov TACGT a CAGGATT, pričom zhodu skórujeme ako +3, nezhodu -1, medzeru -2. Napíšte aj optimálne zarovnanie, ktoré ste takto našli.
 
−
* Spočítajte skóre nižšie uvedeného zarovnania, pričom použijete skórovaciu maticu uvedenú nižšie, začatie medzery -5, rozšírenie medzery o jednu ďalšiu bázu -2. Nájdite globálne zarovnanie s vyšším skóre pre tieto dve sekvencie (netreba nájsť optimálne zarovnanie; pri hľadaní môžete použiť ľubovoľný postup alebo úvahu) a spočítajte aj skóre vášho nového zarovnania.
 
 
<pre>
 
<pre>
−
Zarovnanie:                            Matica:
+
Alignment:                            Matrix:
 
ATAGTTTAA                                A  C  G  T
 
ATAGTTTAA                                A  C  G  T
 
A-GGG--AA                            A  2  -2  -1  -2
 
A-GGG--AA                            A  2  -2  -1  -2
Riadok 22: Riadok 60:
 
</pre>
 
</pre>
  
−
* Uvažujme BLASTn, ktorý začína z jadier veľkosti w=3. Koľko jadier nájde pri porovnávaní sekvencií GATTACGGAT a CAGGATT? Ktoré to budú?
+
* Consider BLASTn algorithm starting from seeds of size w=3. How many seeds it finds while comparing sequences GATTACGGAT and CAGGATT? List all found seeds.
  
−
===Hľadanie génov===
+
===Gene finding===
−
Gén, exón, intrón, mRNA, zostrih a alternatívny zostrih, kodón, genetický kód, skrytý Markovov model (HMM), jeho stavy, pravdepodobnosti prechodu a emisie, použitie HMM na hľadanie génov
+
  
−
* Pre model na strane 16 prednášky o hľadaní génov (bol by v zadaní) spočítajte pravdepodobnosť vygenerovania báz AGT a stavov modrý,červený,modrý.
+
'''Main concepts in English and Slovak'''
  
−
===Evolúcia a komparatívna genomika===
+
Gene, exon, intron, mRNA, splicing and alternative splicing, genetic code, hidden Markov model (HMM), its states, transition and emission probabilities, use of HMMs in gene finding, Viterbi and forward algorithms
−
Fylogenetický strom (zakorenenený a nezakorenený), metóda maximálnej úspornosti (parsimony), metóda spájania susedov (neighbor joining), metóda maximálnej vierohodnosti (maximum likelihood), Jukes-Cantorov model substitúcií a zložitejšie substitučné matice, homológ, paralóg, ortológ, detekcia pozitívneho a negatívneho výberu, fylogenetické HMM, likelihood ratio test
+
  
−
* Na strome nižšie nájdite najúspornejšie ancestrálne znaky pre stĺpec zarovnania TTAAA (v poradí glum, hobit, človek, elf, ork). Odpoveď môžete spočítať ľubovoľným spôsobom.
+
Gén, exón, intrón, mRNA, zostrih a alternatívny zostrih, kodón, genetický kód, skrytý Markovov model (HMM), jeho stavy, pravdepodobnosti prechodu a emisie, použitie HMM na hľadanie génov, Viterbiho a dopredný algoritmus
 +
 
 +
'''Simple questions for the exam'''
 +
 
 +
* What is the probability of generating sequence AGT using sequence of states 1,2,1 in the HMM below?
 +
<pre>
 +
The HMM has three states 1, 2, 3. It always starts in state 1.
 +
Transition probabilities:
 +
From 1 to 1: 0.99
 +
From 1 to 2: 0.01
 +
From 2 to itself: 0.9
 +
From 2 to 1: 0.05
 +
From 2 to 3: 0.05
 +
From 3 to itself: 0.99
 +
From 3 to 2: 0.01
 +
Emmision probabilities in state 1:
 +
A 0.25, C 0.25, G 0.25, T 0.25
 +
Emmision probabilities in state 2:
 +
A 0.3, C 0.2, G 0.2, T 0.3
 +
Emmision probabilities in state 3:
 +
A 0.2, C 0.4, G 0.3, T 0.1
 +
</pre>
 +
 
 +
===Evolution and comparative genomics===
 +
 
 +
'''Main concepts in English and Slovak'''
 +
 
 +
Phylogenetic tree (rooted and unrooted), maximum parsimony method, neighbor joining method, maximum likelihood method,  Jukes-Cantor substitution model and more complex substitution matrices, Felsenstein algorithm, homolog, paralog, ortholog, detection of positive and negative selection, phylogenetic HMMs, likelihood ratio test
 +
 
 +
Fylogenetický strom (zakorenenený a nezakorenený), metóda maximálnej úspornosti (parsimony), metóda spájania susedov (neighbor joining), metóda maximálnej vierohodnosti (maximum likelihood), Jukes-Cantorov model substitúcií a zložitejšie substitučné matice, Felsensteinov algoritmus, homológ, paralóg, ortológ, detekcia pozitívneho a negatívneho výberu, fylogenetické HMM, test pomerom vierohodností (likelihood ratio test)
 +
 
 +
'''Simple questions for the exam'''
 +
 
 +
* Find the most parsimonious assignment of bases at the ancestral nodes in the tree below given a column of alignment TTAAA (in the order gollum, hobbit, human, elf, orc). You can derive your answer using any method (but it has to be the most parsimonious assignment).
 
<pre>
 
<pre>
−
Glum  ----|
+
Gollum ----|
 
           |----|
 
           |----|
−
Hobit  ----|    |----|
+
Hobbit ----|    |----|
 
                 |    |
 
                 |    |
−
Človek ---------|    |
+
Human  ---------|    |
 
                     |---
 
                     |---
 
Elf --------|        |
 
Elf --------|        |
 
             |--------|
 
             |--------|
−
Ork --------|
+
Orc --------|
 
</pre>
 
</pre>
−
* Nájdite najúspornejší strom pre zarovnanie uvedené nižšie. Aká je jeho cena (koľko mutácií je nutných na vysvetlenie týchto sekvencií)? Odpoveď môžete spočítať ľubovoľným spôsobom.
+
 
 +
* Find the most parsimonious tree for the alignment given below. What is its cost (i.e. how many mutations are necessary to explain these sequences)? You can derive your answer using any method (but it has to be the most parsimonious tree).
 
<pre>
 
<pre>
−
vtáčik biely      ACAACGTCT
+
whitebird ACAACGTCT
−
vtáčik čierny      TCTGAATCA
+
blackbird TCTGAATCA
−
vtáčik sivý        TGTGAAAGA
+
graybird  TGTGAAAGA
−
vtáčik modrý      ACTACGTCT
+
blubird  ACTACGTCT
−
vtáčik zelený      TGTGAAAGA
+
greenbird TGTGAAAGA
 
</pre>
 
</pre>
−
* Uvažujme maticu vzdialeností uvedenú nižšie. Ktorú dvojicu vrcholov spojí metóda spájania susedov ako prvú a aká bude nová matica po spojení?
+
 
 +
* Consider the tree for gollum, hobbit etc. given above, where each branch has the same length t. Let us assume that for any two different bases x and y, the probability of base x mutating to base y over time y is 0.1, and thus the probability of base x remaining the same after time t is 0.7. Probability of each base in the root is 0.25. Compute the probability that the tree will have base A in all internal nodes and in leaves bases TTAAA (from top to bottom). Find an assignment of bases in the ancestral nodes with a higher probability and compute this probability (you do not need to find the best possible assignment).
 +
 
 +
 
 +
* Consider the distance matrix given below. Which pair of nodes will be connected as first by the neighbor joining method and what will be the new distance matrix after joining these two nodes?
 
<pre>
 
<pre>
−
                 biely   čierny  sivý  modrý
+
                 white   black    gray    blue
−
vtáčik biely      0      5      7      4
+
whitebird        0      5      7      4
−
vtáčik čierny    5      0      8      5
+
blackbird        5      0      8      5
−
vtáčik sivý      7      8      0      5
+
graybird          7      8      0      5
−
vtáčik modrý      4      5      5      0
+
bluebird          4      5      5      0
 
</pre>
 
</pre>
−
* Uvažujme strom pre gluma, hobita atď uvedený v príklade vyššie (bol by v zadaní), pričom každá hrana má rovnakú dĺžku a pravdepodobnosť každej mutácie na jednej hrane je 0.1 (t.j. napr. Pr(C|A,t)=0.1) a teda pravdepodobnosť zachovania tej istej bázy je 0.7, pravdepodobnosť každej bázy v koreni je 0.25. Aká je pravdepodobnosť, že v listoch dostaneme TTAAA a vo vnútorných vrcholoch samé Áčka? Nájdite priradenie ancestrálnych báz vo vnútorných vrcholoch, ktoré má väčšiu pravdepodobnosť a spočítajte, aká tá pravdepodobnosť je (nemusíte nájsť najlepšie možné priradenie).
 
  
−
===Expresia génov, regulácia, motívy===
+
===Gene expression, regulation, motifs===
  
−
Určovanie génovej expresie pomocou microarray alebo sekvenovaním RNA-seq, hierarchické zhlukovanie, klasifikácia, reprezentácia sekvenčných motívov (väzobné miesta transkripčných faktorov) ako konsenzus, regulárny výraz a PSSM, hľadanie nových motívov v sekvenciách, consensus pattern problem, hľadanie motívu pomocou pravdepodobnostných modelov (EM algoritmus)
+
'''Main concepts in English and Slovak'''
 +
 
 +
Measuring gene expressing using microarray or RNA-seq, hierarchical clustering, classification, representation of sequence motifs (transcription factor binding sites) as a consensus, regular expression and PSSM, finding new motifs in sequences, consensus pattern problem, finding motifs using probability models, EM algorithm
 +
 
 +
Určovanie génovej expresie pomocou microarray alebo sekvenovaním RNA-seq, hierarchické zhlukovanie, klasifikácia, reprezentácia sekvenčných motívov (väzobné miesta transkripčných faktorov) ako konsenzus, regulárny výraz a PSSM, hľadanie nových motívov v sekvenciách, consensus pattern problem, hľadanie motívu pomocou pravdepodobnostných modelov, algoritmus EM
 
   
 
   
−
* Uvažujme microarray experimenty pre 5 génov. Medzi každými dvomi génmi sme spočítali vzdialenosť ich profilov expresie a dostali sme tabuľku vzdialeností uvedenú nižšie. Nájdite hierarchické zhlukovanie týchto génov, pričom vzdialenosť medzi dvoma zhlukmi (clustrami) bude vzdialenosť najbližších génov v nich. Uveďte aj v akom poradí ste jednotlivé zhluky tvorili.  
+
'''Simple questions for the exam'''
 +
 
 +
* After a series of expression measurements for 5 genes, we have computed distances between pairs of expression profiles and obtained the distance table shown below. Find the hierarchical clustering of these genes, where the distance between two clusters is computed as the minimum of the closest genes in these clusters (single linkage clustering). Show the order in which you were creating individual clusters.
 
<pre>
 
<pre>
−
        A    B    C    D    E
+
          A    B    C    D    E
−
gén A    0  0.6  0.1  0.3  0.7     
+
gene A    0  0.6  0.1  0.3  0.7     
−
gén B  0.6  0  0.5  0.5  0.4
+
gene B  0.6  0  0.5  0.5  0.4
−
gén C  0.1  0.5  0  0.6  0.6
+
gene C  0.1  0.5  0  0.6  0.6
−
gén D  0.3  0.5  0.6  0  0.8
+
gene D  0.3  0.5  0.6  0  0.8
−
gén E  0.7  0.4  0.6  0.8  0
+
gene E  0.7  0.4  0.6  0.8  0
 
</pre>
 
</pre>
  
−
* Uvažujte motív reprezentovaný profilom (skórovaciou maticou, PSSM) uvedenou nižšie. Spočítajte skóre reťazca GGAG. Ktorá sekvencia dĺžky 4 bude mať najmenšie a ktorá najväčšie skóre?
+
* Consider a motif represented by the PSSM shown below. Compute the score of string GGAG. Which sequences of length 4 will have the smallest and highest score in this PSSM?
 
<pre>
 
<pre>
 
A  -3    3  -2  -2
 
A  -3    3  -2  -2
Riadok 84: Riadok 163:
 
</pre>
 
</pre>
  
−
* Nájdite všetky výskyty regulárneho výrazu TA[CG][AT]AT v sekvencii GACGATATAGTATGTACAATATGC.
+
* We are running the EM algorithm for finding matrix W of base frequencies at individual motif positions. Motif length is 3 and we have 2 sequences of length 5 each, so there are 3 positions where the motif can start in each sequence. For each of these positions, we calculated the probability that the motif starts there based on the previous version of matrix W. What will be the new matrix W? (We do not use pseudocounts here, so for example base G will have probability 0 everywhere.)
  
−
===Proteíny===
+
<pre>
 +
Sequence 1: AACAT,
 +
probabilities of motif starting at positions 0,1,2: 0.4, 0.2, 0.4
 +
 
 +
Sequence 2: AAAAT,
 +
probabilities of motif starting at positions 0,1,2: 0.2, 0.2, 0.6
 +
</pre>
 +
 
 +
 
 +
* Find all occurrences of regular expression TA[CG][AT]AT in sequence GACGATATAGTATGTACAATATGC.
 +
 
 +
===Proteins===
 +
 
 +
'''Main concepts in English and Slovak'''
 +
 
 +
Primary, secondary and tertiary structure of a protein, protein domains and families, family representation by a profile (PSSM) and a profile HMM, protein threading, gene ontology.
 +
 
 +
Primárna, sekundárna a terciálna štruktúra proteínov, proteínové domény a rodiny, reprezentovanie rodiny pravdepodobnostným profilom a profilovým HMM, protein threading, gene ontology.
  
−
Primárna, sekundárna a terciálna štruktúra proteínov, proteínové domény a rodiny, reprezentovanie rodiny pravdepodobnostným profilom a profilovým HMM, protein threading, gene ontology.
+
'''Simple questions for the exam'''
  
−
* Zostavte profil (PSSM) pre zarovnanie sekvencií uvedené nižšie, pričom predpokladáme, že v celej databáze A tvorí 60% a G 40% všetkých sekvencií (iné aminokyseliny neuvažujeme). Použite prirodzený logaritmus (ln) a pseudocount 1.
+
* Construct a profile (PSSM) for the sequence alignment shown below, assuming that amino acid A comprises 60% of all sequences in a database, G 40% and we do not consider other amino acids. Use natural logarithm (ln) and pseudocount 1.
 
<pre>
 
<pre>
 
AAGA
 
AAGA
Riadok 101: Riadok 197:
 
===RNA===
 
===RNA===
  
−
Sekundárna štruktúra RNA, pseudouzol a dobre uzátvorkovaná štruktúra, Nussinovovej algoritmus, minimalizácia energie, stochastické bezkontextové gramatiky, kovariančné modely.
+
'''Main concepts in English and Slovak'''
  
−
* Doplňte chýbajúce hodnoty za otázniky v matici dynamického programovania (Nussinovovej algoritmus) pre nájdenie najväčšieho počtu dobre uzátvorkovaných spárovaných báz v RNA sekvencii GAACUAUCUGA (dovoľujeme len komplementárne páry A-U, C-G) a nakreslite sekundárnu štruktúru, ktorú algoritmus našiel.
+
Secondary structure of RNA, pseudoknot and well-parenthesized structures, Nussinov algorithm, energy minimization, stochastic context-free grammars, covariance models of RNA families
 +
 
 +
Sekundárna štruktúra RNA, pseudouzol a dobre uzátvorkovaná štruktúra, Nussinovovej algoritmus, minimalizácia energie, stochastické bezkontextové gramatiky, kovariančné modely rodín RNA.
 +
 
 +
'''Simple questions for the exam'''
 +
 
 +
* Fill in the missing values in the matrix of dynamic programming for Nussinov algorithm which finds the RNA secondary structure without pseudoknots with the highest number of paired bases in RNA sequence GAACUAUCUGA (we allow only complementary bases A-U, C-G) and show the secondary structure found by the algorithm.
 
<pre>
 
<pre>
 
  0 0 0 1 1 2 2 3 3 ? ?
 
  0 0 0 1 1 2 2 3 3 ? ?
Riadok 118: Riadok 220:
 
</pre>
 
</pre>
  
−
* Uvažujme RNA sekvenciu dĺžky 27, ktorá má v sekundárnej štruktúre spárované komplementárne bázy na pozíciách: (2,23), (3,22), (4,21), (5,13), (6,12), (8,16), (9,15), (10,14), (18,26) a (19,25). Koľko najmenej párov z tohto zoznamu musíme odstrániť, aby sme dostali štruktúru bez pseudouzlov? Ktoré páry to budú?
+
* Consider RNA sequence of length 27, which has secondary structure pairs on positions (2,23), (3,22), (4,21), (5,13), (6,12), (8,16), (9,15), (10,14), (18,26), (19,25). What is the smallest number of pairs that needs to be removed from this list to get a structure without pseudoknots? Which pairs will be removed?
  
−
* Uvažujme sekvenciu RNA ACUGAGUCCAAGG, ktorá má v sekundárnej štruktúre spárované bázy na pozíciách (1,7), (2,6), (3,5), (8,13) a (9,12). (Pozície číslujeme od 1.) (Táto RNA je uvedená ako príklad na strane 12 prednášky o RNA.) Ukážte akou postupnosťou pravidiel by sme ju mohli odvodiť v gramatike uvedenej nižšie tak, aby spárované bázy boli vždy vytvorené v jednom kroku odvodenia.
+
* Consider RNA sequence ACUGAGUCCAAGG, which has secondary structure pairs on positions (1,7), (2,6), (3,5), (8,13) a (9,12). (Positions are numbered started from 1.) (This RNA is shown as an example in the lecture on RNA structure.) Show a derivation of this sequence using a grammar show below so that paired bases are always generated in the same step of the derivation.
−
** Gramatika: S->aSu|uSa|cSg|gSc|aS|cS|gS|uS|Sa|Sc|Sg|Su|SS|epsilon
+
** Grammar 1: S->aSu|uSa|cSg|gSc|aS|cS|gS|uS|Sa|Sc|Sg|Su|SS|epsilon
−
** Iný príklad gramatiky: S->aSu|uSa|cSg|gSc|TS|ST|SS|epsilon; T->aT|cT|gT|tT|epsilon
+
** Grammar 2: S->aSu|uSa|cSg|gSc|TS|ST|SS|epsilon; T->aT|cT|gT|tT|epsilon
  
−
===Populačná genetika===
+
===Population genetics===
 +
 
 +
'''Main concepts in English and Slovak'''
 +
 
 +
Polymorphism, SNP, allele, homozygote, heterozygote, recombination, allele frequency as a Markov chain, random genetic drift, linkage disequilibrium, association mapping, LD block, subpopulation.
  
 
Polymorfizmus, SNP, alela, homozygot, heterozygot, rekombinácia, frekvencia polymorfizmu ako markovovský reťazec, náhodný genetický drift, väzbová nerovnováha (linkage disequilibrium), mapovanie asociácií, LD blok, subpopulácia.
 
Polymorfizmus, SNP, alela, homozygot, heterozygot, rekombinácia, frekvencia polymorfizmu ako markovovský reťazec, náhodný genetický drift, väzbová nerovnováha (linkage disequilibrium), mapovanie asociácií, LD blok, subpopulácia.
  
−
* Pre dvojice SNPov, ktorých tabuľky sú uvedené nižšie, určite, či môžeme štatisticky vylúčiť hypotézu, že sú v stave väzbovej rovnováhy (LE, linkage equilibrium) pri hladine významnosti p=0.05, resp. <math>\chi^2>3.841</math>. Pre každú dvojicu spočítajte veličinu <math>\chi^2</math>.
+
'''Simple questions for the exam'''
 +
 
 +
* For pairs of SNPs from the tables show below determine, if we can statistically reject the hypothesis that they are in linkage equilibrium (LE) at the significance level p=0.05, i.e. <math>\chi^2>3.841</math>. For each pair compute their <math>\chi^2</math> value.
 
<pre>
 
<pre>
 
     Q  q              Q  q            Q  q
 
     Q  q              Q  q            Q  q
Riadok 135: Riadok 243:
 
</pre>
 
</pre>
  
−
-->
+
===Additional important concepts===
 +
* Advanced dynamic programming algorithms (protein MS/MS, variants of sequence alignment, variants of Nussinov algorithm)
 +
* Integer linear programming

Aktuálna revízia z 15:27, 7. december 2023

Exam rules

Exam is for 1-BIN-301 (mainly AIN, BIN, DAV, INF students).

The exam is primarily written:

  • You need at least 50% of points
  • Time 3 hours
  • About 50% of points for simple questions
    • examples on this page
    • in case of interest tutorial session before exam
  • The rest of the questions mostly designing/modifying an algorithm or model
  • You can use pen, simple calculator and a cheat sheet up to 2 A4 two-sided sheets


If you do not pass the first written exam, part of your exam may be oral on the second and third attempts.

Syllabus and examples of simple questions

Below we list the most important concepts that both biologists and computer scientists should know from this course.

We also list simple questions. Questions of this type will comprise approximately 50% of the exam. Not all of these questions will be used on the exam and particular string, numbers, grammars and sequences will differ.

Sequencing and genome assembly

Main concepts in English and Slovak

DNA sequencing and its use, sequencing read, paired reads, contigs, shortest common superstring problem, de Bruijn graphs

Sekvenovanie DNA a jeho využitie, čítanie (read), spárované čítania, kontig, problém najkratšieho spoločného nadslova, de Bruijnove grafy

Simple questions for the exam

  • Find the shortest common superstring of strings GACAATAA, ATAACAC, GTATA, TAATTGTA.
  • Find the de Bruijn graph for k=2 (nodes will be pairs of nucleotides) and reads CCTGCC, GCCAAC

Sequence alignment

Main concepts in English and Slovak

The problem of local and global alignment of two sequences, dynamic programming algorithms, scoring matrix and its probabilistic meaning, statistical significance (E-value, P-value), heuristic search of local alignments (BLAST, minimizers), whole-genome and multiple alignments

Problém lokálneho a globálneho zarovnania dvoch sekvencií, jeho riešenie pomocou dynamického programovania, skórovacia matica a jej pravdepodobnostný význam, štatistická významnosť (E-value, P-value), heuristické hľadanie lokálnych zarovnaní (BLAST, minimizer-y), celogenómové a viacnásobné zarovnania

Simple questions for the exam

  • Fill in the dynamic programing matrices for local and global alignment of sequences TACGT and CAGGATT, where the match has score +3, mismatch -1, gap -2. Reconstruct also the optimal alignments found by the dynamic programming algorithm.
  • Compute the score of the alignment shown below using the scoring matrix shown below, gap opening penalty -5, gap extension penalty -2 for each additional base. Find a global alignment with a higher score for these two sequences and compute its score. (It is not necessary to find the optimal alignment; you can use any method to arrive at the answer.) 
Alignment:                             Matrix:
ATAGTTTAA                                 A   C   G   T
A-GGG--AA                             A   2  -2  -1  -2
                                      C  -2   1  -2  -1    
                                      G  -1  -2   1  -2
                                      T  -2  -1  -2   2
  • Consider BLASTn algorithm starting from seeds of size w=3. How many seeds it finds while comparing sequences GATTACGGAT and CAGGATT? List all found seeds.

Gene finding

Main concepts in English and Slovak

Gene, exon, intron, mRNA, splicing and alternative splicing, genetic code, hidden Markov model (HMM), its states, transition and emission probabilities, use of HMMs in gene finding, Viterbi and forward algorithms

Gén, exón, intrón, mRNA, zostrih a alternatívny zostrih, kodón, genetický kód, skrytý Markovov model (HMM), jeho stavy, pravdepodobnosti prechodu a emisie, použitie HMM na hľadanie génov, Viterbiho a dopredný algoritmus

Simple questions for the exam

  • What is the probability of generating sequence AGT using sequence of states 1,2,1 in the HMM below? 
The HMM has three states 1, 2, 3. It always starts in state 1.
Transition probabilities:
From 1 to 1: 0.99
From 1 to 2: 0.01
From 2 to itself: 0.9
From 2 to 1: 0.05
From 2 to 3: 0.05
From 3 to itself: 0.99
From 3 to 2: 0.01
Emmision probabilities in state 1:
A 0.25, C 0.25, G 0.25, T 0.25
Emmision probabilities in state 2:
A 0.3, C 0.2, G 0.2, T 0.3
Emmision probabilities in state 3:
A 0.2, C 0.4, G 0.3, T 0.1

Evolution and comparative genomics

Main concepts in English and Slovak

Phylogenetic tree (rooted and unrooted), maximum parsimony method, neighbor joining method, maximum likelihood method, Jukes-Cantor substitution model and more complex substitution matrices, Felsenstein algorithm, homolog, paralog, ortholog, detection of positive and negative selection, phylogenetic HMMs, likelihood ratio test

Fylogenetický strom (zakorenenený a nezakorenený), metóda maximálnej úspornosti (parsimony), metóda spájania susedov (neighbor joining), metóda maximálnej vierohodnosti (maximum likelihood), Jukes-Cantorov model substitúcií a zložitejšie substitučné matice, Felsensteinov algoritmus, homológ, paralóg, ortológ, detekcia pozitívneho a negatívneho výberu, fylogenetické HMM, test pomerom vierohodností (likelihood ratio test)

Simple questions for the exam

  • Find the most parsimonious assignment of bases at the ancestral nodes in the tree below given a column of alignment TTAAA (in the order gollum, hobbit, human, elf, orc). You can derive your answer using any method (but it has to be the most parsimonious assignment). 
Gollum ----|
           |----|
Hobbit ----|    |----|
                |    |
Human  ---------|    |
                     |---
Elf --------|        |
            |--------|
Orc --------|
  • Find the most parsimonious tree for the alignment given below. What is its cost (i.e. how many mutations are necessary to explain these sequences)? You can derive your answer using any method (but it has to be the most parsimonious tree). 
whitebird ACAACGTCT
blackbird TCTGAATCA
graybird  TGTGAAAGA
blubird   ACTACGTCT
greenbird TGTGAAAGA
  • Consider the tree for gollum, hobbit etc. given above, where each branch has the same length t. Let us assume that for any two different bases x and y, the probability of base x mutating to base y over time y is 0.1, and thus the probability of base x remaining the same after time t is 0.7. Probability of each base in the root is 0.25. Compute the probability that the tree will have base A in all internal nodes and in leaves bases TTAAA (from top to bottom). Find an assignment of bases in the ancestral nodes with a higher probability and compute this probability (you do not need to find the best possible assignment).


  • Consider the distance matrix given below. Which pair of nodes will be connected as first by the neighbor joining method and what will be the new distance matrix after joining these two nodes? 
                white   black    gray    blue
whitebird         0       5       7       4
blackbird         5       0       8       5
graybird          7       8       0       5
bluebird          4       5       5       0

Gene expression, regulation, motifs

Main concepts in English and Slovak

Measuring gene expressing using microarray or RNA-seq, hierarchical clustering, classification, representation of sequence motifs (transcription factor binding sites) as a consensus, regular expression and PSSM, finding new motifs in sequences, consensus pattern problem, finding motifs using probability models, EM algorithm

Určovanie génovej expresie pomocou microarray alebo sekvenovaním RNA-seq, hierarchické zhlukovanie, klasifikácia, reprezentácia sekvenčných motívov (väzobné miesta transkripčných faktorov) ako konsenzus, regulárny výraz a PSSM, hľadanie nových motívov v sekvenciách, consensus pattern problem, hľadanie motívu pomocou pravdepodobnostných modelov, algoritmus EM

Simple questions for the exam

  • After a series of expression measurements for 5 genes, we have computed distances between pairs of expression profiles and obtained the distance table shown below. Find the hierarchical clustering of these genes, where the distance between two clusters is computed as the minimum of the closest genes in these clusters (single linkage clustering). Show the order in which you were creating individual clusters. 
          A    B    C    D    E
gene A    0   0.6  0.1  0.3  0.7    
gene B   0.6   0   0.5  0.5  0.4
gene C   0.1  0.5   0   0.6  0.6
gene D   0.3  0.5  0.6   0   0.8
gene E   0.7  0.4  0.6  0.8   0
  • Consider a motif represented by the PSSM shown below. Compute the score of string GGAG. Which sequences of length 4 will have the smallest and highest score in this PSSM? 
A   -3    3   -2   -2
C   -2   -2    1   -2
G    0   -2   -1    3
T    1   -1    1   -2
  • We are running the EM algorithm for finding matrix W of base frequencies at individual motif positions. Motif length is 3 and we have 2 sequences of length 5 each, so there are 3 positions where the motif can start in each sequence. For each of these positions, we calculated the probability that the motif starts there based on the previous version of matrix W. What will be the new matrix W? (We do not use pseudocounts here, so for example base G will have probability 0 everywhere.) 
Sequence 1: AACAT, 
probabilities of motif starting at positions 0,1,2: 0.4, 0.2, 0.4

Sequence 2: AAAAT, 
probabilities of motif starting at positions 0,1,2: 0.2, 0.2, 0.6


  • Find all occurrences of regular expression TA[CG][AT]AT in sequence GACGATATAGTATGTACAATATGC.

Proteins

Main concepts in English and Slovak

Primary, secondary and tertiary structure of a protein, protein domains and families, family representation by a profile (PSSM) and a profile HMM, protein threading, gene ontology.

Primárna, sekundárna a terciálna štruktúra proteínov, proteínové domény a rodiny, reprezentovanie rodiny pravdepodobnostným profilom a profilovým HMM, protein threading, gene ontology.

Simple questions for the exam

  • Construct a profile (PSSM) for the sequence alignment shown below, assuming that amino acid A comprises 60% of all sequences in a database, G 40% and we do not consider other amino acids. Use natural logarithm (ln) and pseudocount 1. 
AAGA
GAGA
GAAA
GGAG
GGAA

RNA

Main concepts in English and Slovak

Secondary structure of RNA, pseudoknot and well-parenthesized structures, Nussinov algorithm, energy minimization, stochastic context-free grammars, covariance models of RNA families

Sekundárna štruktúra RNA, pseudouzol a dobre uzátvorkovaná štruktúra, Nussinovovej algoritmus, minimalizácia energie, stochastické bezkontextové gramatiky, kovariančné modely rodín RNA.

Simple questions for the exam

  • Fill in the missing values in the matrix of dynamic programming for Nussinov algorithm which finds the RNA secondary structure without pseudoknots with the highest number of paired bases in RNA sequence GAACUAUCUGA (we allow only complementary bases A-U, C-G) and show the secondary structure found by the algorithm. 
 0 0 0 1 1 2 2 3 3 ? ?
   0 0 0 1 1 2 2 3 3 ?
     0 0 1 1 2 2 2 3 3
       0 0 1 1 1 1 2 3
         0 1 1 ? 1 2 3
           0 1 1 1 2 2
             0 0 0 1 2
               0 0 1 1
                 0 0 1
                   0 0
                     0
  • Consider RNA sequence of length 27, which has secondary structure pairs on positions (2,23), (3,22), (4,21), (5,13), (6,12), (8,16), (9,15), (10,14), (18,26), (19,25). What is the smallest number of pairs that needs to be removed from this list to get a structure without pseudoknots? Which pairs will be removed?
  • Consider RNA sequence ACUGAGUCCAAGG, which has secondary structure pairs on positions (1,7), (2,6), (3,5), (8,13) a (9,12). (Positions are numbered started from 1.) (This RNA is shown as an example in the lecture on RNA structure.) Show a derivation of this sequence using a grammar show below so that paired bases are always generated in the same step of the derivation.
    • Grammar 1: S->aSu|uSa|cSg|gSc|aS|cS|gS|uS|Sa|Sc|Sg|Su|SS|epsilon
    • Grammar 2: S->aSu|uSa|cSg|gSc|TS|ST|SS|epsilon; T->aT|cT|gT|tT|epsilon

Population genetics

Main concepts in English and Slovak

Polymorphism, SNP, allele, homozygote, heterozygote, recombination, allele frequency as a Markov chain, random genetic drift, linkage disequilibrium, association mapping, LD block, subpopulation.

Polymorfizmus, SNP, alela, homozygot, heterozygot, rekombinácia, frekvencia polymorfizmu ako markovovský reťazec, náhodný genetický drift, väzbová nerovnováha (linkage disequilibrium), mapovanie asociácií, LD blok, subpopulácia.

Simple questions for the exam

  • For pairs of SNPs from the tables show below determine, if we can statistically reject the hypothesis that they are in linkage equilibrium (LE) at the significance level p=0.05, i.e. 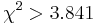\chi ^{2}>3.841. For each pair compute their 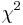\chi ^{2} value. 
    Q   q              Q  q             Q  q
P  100 200          P 10  20         P  1  2
p  300 200          p 30  20         p  3  2

Additional important concepts

  • Advanced dynamic programming algorithms (protein MS/MS, variants of sequence alignment, variants of Nussinov algorithm)
  • Integer linear programming
Zdroj: „https://compbio.fmph.uniba.sk/vyuka/mbi/index.php?title=Exam&oldid=3059“