CB05: Rozdiel medzi revíziami

Verzia zo dňa a času 13:44, 27. október 2022

Príklady stavových automatov pre HMM

Uvazujme HMM so specialnym zaciatocnym stavom b a koncovym stavom e, ktore nic negeneruju.

• Nakreslite HMM (stavovy diagram), ktory generuje sekvencie, ktore zacinaju niekolkymi cervenymi pismenami a potom obsahuju niekolko modrych
• Ako treba zmenit HMM, aby dovoloval ako "niekolko" aj nula?
• Ako treba zmenit HMM, aby pocet cervenych aj modrych bol vzdy parne cislo?
• Ako zmenit HMM, aby sa striedali cervene a modre kusy parnej dlzky?

V dalsich prikladoch uvazujeme aj to, ktore pismena su v ktorom stave povolene (pravdepodobnost emisie > 0) a ktore su zakazane

• cervena sekvencia dlzky dva, ktora zacina na A
• cervena sekvencia dlzky dva, ktora je hocico okrem AA
• toto sa da rozsirit na HMM, ktory reprezentuje ORF, teda nieco, co zacina start kodonom, potom niekolko beznych kodonov, ktore nie su stop kodonom a na koniec stop kodon

Dalsi biologicky priklad HMM: topologia transmembranovych proteinov.

E-hodnota (E-value) zarovnania

• Priklady k tejto casti v prezentacii pdf
• Mame dotaz dlzky m, databazu dlzky n, skore najlepsieho lokálneho zarovnania S
• E-value je ocakavany pocet zarovnani so skore aspon S ak dotaz aj databaza su nahodne
• Hrackarsky priklad: dotaz dlzky m=10, databaza dlzky n=300, S=6
• Zoberme nas nahodny model s obsahom GC 50%
• Mame vrece s gulockami oznacenymi A,C,G,T, z kazdej 25%
• Vytiahneme gulicku, zapiseme si pismeno, hodime ju naspat, zamiesame a opakujeme s dalsim pismenom atd az kym nevygenerujeme m pismen pre dotaz a n pismen pre databazu
• Pre nase vygenerovane sekvencie spocitame, kolkokrat sa dotaz vyskytuje v databaze
• Cely experiment opakujeme vela krat a spocitame priemerny pocet vyskytov, co bude odhad E-value

Vypocet strednej hodnoty vzorcom namiesto simulacie (rychlejsie)

• zlozita matematicka teoria [1]
• E-value sa priblizne da odhadnut vzorcom:

• n a m su dlzky porovnavanych sekvencii, S je skore, K a lambda su parametre, ktore zavisia od skorovacej schemy a od frekvencii vyskytu jednotlivych baz v nasom modeli nahodnej sekvencie.
• Napr blastn pre skorovaci system zhoda 1, nezhoda -1, medzera -2 používa lambda=0.800, K=0.0640
• .
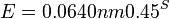• Zdvojnásobenie dĺžky databázy alebo dĺžky dotazu zdvojnásobí E-value
• Zníženie skóre o 1 tiež zhruba zdvojnásobí E-value (delenie 0.45, t.j. nasobenie 2.2)
  • Cislo, ktorym nasobime, zalezi od lambda a teda od skorovacej schemy a frekvencii vyskytu baz

Praktické príklady z predchádzajúcich cvičení

• CB04#Praktick.C3.A9_cvi.C4.8Denie_pri_po.C4.8D.C3.ADta.C4.8Di:_BLAT_vs_BLAST BLAT vs BLAST