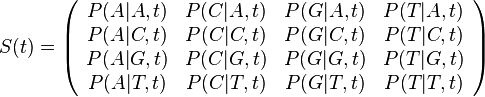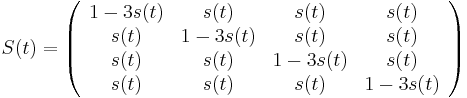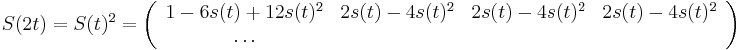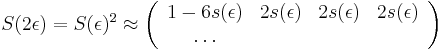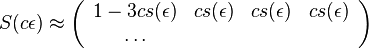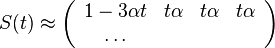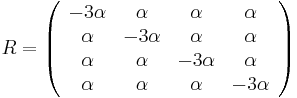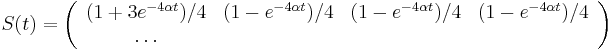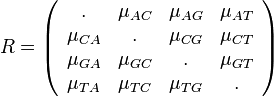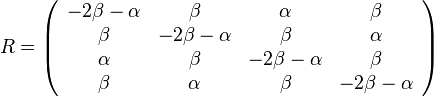CI07: Rozdiel medzi revíziami

Aktuálna revízia z 14:24, 5. november 2020

Obsah

1 Substitučné modely - odvodenie
2 Substitučné matice, zhrnutie
3 Použitie na odhad evolučnej vzdialenosti
4 Zložitejšie modely

Substitučné modely - odvodenie

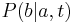Nech $P(b|a,t)$ je pravdepodobnosť, že ak začneme s bázou a, tak po čase t budeme mať bázu b.
Pre dané t môžeme také pravdepodobnosti usporiadať do matice 4x4 (ak študujeme DNA):

$S(t)=\left({\begin{array}{cccc}P(A|A,t)&P(C|A,t)&P(G|A,t)&P(T|A,t)\\P(A|C,t)&P(C|C,t)&P(G|C,t)&P(T|C,t)\\P(A|G,t)&P(C|G,t)&P(G|G,t)&P(T|G,t)\\P(A|T,t)&P(C|T,t)&P(G|T,t)&P(T|T,t)\\\end{array}}\right)$

Riadky zodpovedaju povodnej baze a, stlpce novej baze b
Sucet kazdeho riadku je 1

Požiadavky na S(t)

Intuitivne cim vacsie t, tym vacsia pravdepodobnost zmeny, pre nulovy cas este ziadna zmena nemala kedy nastat, mame teda 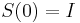$S(0)=I$ (jednotkova matica)
Naopak ked t ide do nekonecna, kazda baza velakrat zmutovala a teda uz prilis nezalezi, co to bolo na zaciatku. S(t) ma teda v limite pre velke t vsetky riadky rovnake.
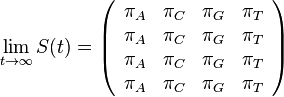
$\lim _{{t\rightarrow \infty }}S(t)=\left({\begin{array}{cccc}\pi _{A}&\pi _{C}&\pi _{G}&\pi _{T}\\\pi _{A}&\pi _{C}&\pi _{G}&\pi _{T}\\\pi _{A}&\pi _{C}&\pi _{G}&\pi _{T}\\\pi _{A}&\pi _{C}&\pi _{G}&\pi _{T}\\\end{array}}\right)$
Rozdelenie pravdepodobnosti $\pi$ nazyvame limitne (equilibrium)
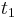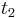Predpokladame tiez, ze pravdepodobnost mutacie zavisi len od aktualnej bazy, nie od minulych stavov a ze charakter procesu mutacii sa v case nemeni. Teda ak mame matice pre casy $t_{1}$ a $t_{2}$ , vieme spocitat maticu pre cas 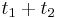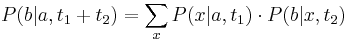$t_{1}+t_{2}$ : $P(b|a,t_{1}+t_{2})=\sum _{x}P(x|a,t_{1})\cdot P(b|x,t_{2})$ a teda v maticovej notacii 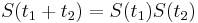$S(t_{1}+t_{2})=S(t_{1})S(t_{2})$ . Preto takyto model nazyvame multiplikativny.
Ak by sme uvazovali iba diskretne (celociselne) casy, stacilo by nam urcit iba 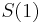$S(1)$ a vsetky ostatne casy dostaneme umocnenim tejto matice. Je vsak elegantnejsie mat 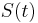$S(t)$ definovane aj pre realne t.
Tento typ modelu sa nazyva Markovov retazec so spojitym casom (continuous-time Markov chain)

Jukes-Cantorov substitučný model

Tento model predpoklada, ze vsetky substitucie su rovnako pravdepodobne, matica teda musí vyzerať nejako takto:

$S(t)=\left({\begin{array}{cccc}1-3s(t)&s(t)&s(t)&s(t)\\s(t)&1-3s(t)&s(t)&s(t)\\s(t)&s(t)&1-3s(t)&s(t)\\s(t)&s(t)&s(t)&1-3s(t)\\\end{array}}\right)$

Matica rýchlostí pre J-C model

$S(2t)=S(t)^{2}=\left({\begin{array}{cccc}1-6s(t)+12s(t)^{2}&2s(t)-4s(t)^{2}&2s(t)-4s(t)^{2}&2s(t)-4s(t)^{2}\\\dots \end{array}}\right)$

Pre velmi maly cas t je s(t) velmi male cislo (blizke 0) a pre velmi male s(t) su kvadraticke cleny 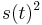$s(t)^{2}$ ovela mensie ako linearne cleny s(t) a teda

$S(2\epsilon )=S(\epsilon )^{2}\approx \left({\begin{array}{cccc}1-6s(\epsilon )&2s(\epsilon )&2s(\epsilon )&2s(\epsilon )\\\dots \end{array}}\right)$

Aj pre ine rozumne male nasobky

$S(c\epsilon )\approx \left({\begin{array}{cccc}1-3cs(\epsilon )&cs(\epsilon )&cs(\epsilon )&cs(\epsilon )\\\dots \end{array}}\right)$

Tento vztah dava zmysel: pre velmi male t mozeme zanedbat moznost, ze baza zmutovala viackrat a pravdepodobnost jednej mutacie linearne rastie s dlzkou casu.

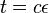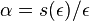Ak oznacime $t=c\epsilon$ a $\alpha =s(\epsilon )/\epsilon$ dostaneme pre velmi male t

$S(t)\approx \left({\begin{array}{cccc}1-3\alpha t&t\alpha &t\alpha &t\alpha \\\dots \end{array}}\right)$

Vytvorme si teraz maticu rychlosti (intenzit) (transition rate matrix, substitution rate matrix)

$R=\left({\begin{array}{cccc}-3\alpha &\alpha &\alpha &\alpha \\\alpha &-3\alpha &\alpha &\alpha \\\alpha &\alpha &-3\alpha &\alpha \\\alpha &\alpha &\alpha &-3\alpha \\\end{array}}\right)$

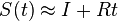
Dostavame, ze pre velmi male casy plati $S(t)\approx I+Rt$
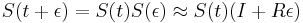$S(t+\epsilon )=S(t)S(\epsilon )\approx S(t)(I+R\epsilon )$ a teda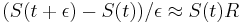 $(S(t+\epsilon )-S(t))/\epsilon \approx S(t)R$
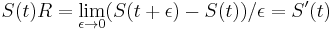
V limite dostaneme $S(t)R=\lim _{{\epsilon \rightarrow 0}}(S(t+\epsilon )-S(t))/\epsilon =S'(t)$
Dostali sme diferencialnu rovnicu S(t)R = S'(t), pociatocny stav $S(0)=I$ ).
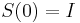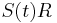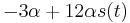Nasobenim matic S(t) a R dostavame, ze diagonalny prvok $S(t)R$ je $-3\alpha +12\alpha s(t)$ a nediagonalny 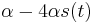$\alpha -4\alpha s(t)$ . Takze dostavame diferencialnu rovnicu 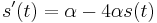$s'(t)=\alpha -4\alpha s(t)$ z rovnosti nediagonalnych prvkov (z rovnosti diagonalnych prvkov dostavame tu istu rovnicu len prenasobenu konstantou -3).

Poriadnejšie odvodenie diferenciálnej rovnice

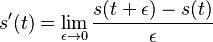$s'(t)=\lim _{{\epsilon \to 0}}{\frac {s(t+\epsilon )-s(t)}{\epsilon }}$ z definicie limity
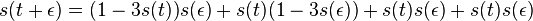$s(t+\epsilon )=(1-3s(t))s(\epsilon )+s(t)(1-3s(\epsilon ))+s(t)s(\epsilon )+s(t)s(\epsilon )$ podla multiplikativnosti S(t)
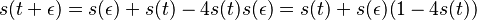
po úprave $s(t+\epsilon )=s(\epsilon )+s(t)-4s(t)s(\epsilon )=s(t)+s(\epsilon )(1-4s(t))$
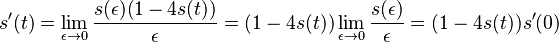
$s'(t)=\lim _{{\epsilon \to 0}}{\frac {s(\epsilon )(1-4s(t))}{\epsilon }}=(1-4s(t))\lim _{{\epsilon \to 0}}{\frac {s(\epsilon )}{\epsilon }}=(1-4s(t))s'(0)$
oznacme 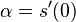$\alpha =s'(0)$ (alfa je konstanta, nezavisi od epsilon ani t)
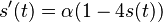$s'(t)=\alpha (1-4s(t))$ (finalna diferencialna rovnica, rovnaka ako predtym pre matice)
Riesenie diferencialnej rovnice 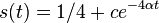$s(t)=1/4+ce^{{-4\alpha t}}$ pre kazdu konstantu c
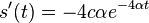
Mozeme overit dosadenim do rovnice, pricom $s'(t)=-4c\alpha e^{{-4\alpha t}}$
c=-1/4 dopocitame z pociatocnej podmienky s(0)=0
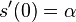
overime tiez, ze $s'(0)=\alpha$

Vlastnosti riešenia

Takže máme maticu:

$S(t)=\left({\begin{array}{cccc}(1+3e^{{-4\alpha t}})/4&(1-e^{{-4\alpha t}})/4&(1-e^{{-4\alpha t}})/4&(1-e^{{-4\alpha t}})/4\\\dots \end{array}}\right)$

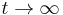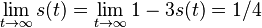Ked $t\rightarrow \infty$ , dostávame všetky prvky matice rovné 1/4, t.j. $\lim _{{t\to \infty }}s(t)=\lim _{{t\to \infty }}1-3s(t)=1/4$ .
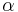$\alpha$ je teda pravdepodobnosť konkrétnej zmeny za jednotku času, ak uvažujeme veľmi krátke časy alebo presnejšie derivácia prvku s(t) vzhľadom na t v bode 0
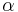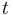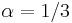Aby sme nemali naraz aj $\alpha$ aj $t$ , zvykneme maticu R normalizovat tak, aby priemerný počet substitúcii za jednotku času bol 1. V prípade Jukes-Cantorovho modelu je to keď $\alpha =1/3$ .

Substitučné matice, zhrnutie

S(t): matica 4x4, kde políčko 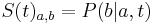$S(t)_{{a,b}}=P(b|a,t)$ je pravdepodobnosť, že ak začneme s bázou a, tak po čase t budeme mať bázu b.
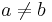
Jukes-Cantorov model predpokladá, že táto pravdepodobnosť je rovnaká pre každé dve bázy $a\neq b$
Pre daný čas t máme teda všade mimo diagonály s(t) a na diagonále 1-3s(t)
Matica rýchlostí R: pre Jukes-Cantorov model všade mimo diagonály 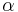$\alpha$ , na diagonále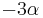 $-3\alpha$
Pre veľmi malý čas t je S(t) zhruba I-Rt
Rýchlost alpha je teda pravdepodobnosť zmeny za jednotku casu, ak uvažujeme veľmi krátke časy, resp. derivácia s(t) vzhľadom na t v bode 0
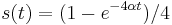
Riešením diferenciálnych rovníc pre Jukes-Cantorov model dostávame $s(t)=(1-e^{{-4\alpha t}})/4$
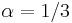
Matica rýchlostí sa zvykne normalizovať tak, aby na jednotku času pripadla v priemere jedna substitúcia, čo dosiahneme ak $\alpha =1/3$

Použitie na odhad evolučnej vzdialenosti

V case 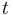$t$ je pravdepodobnost, ze uvidime zmenenu bazu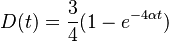 $D(t)={\frac {3}{4}}(1-e^{{-4\alpha t}})$
V realnom pouziti (vypocet matice vzdialenosti pre metodu spajania susedov) mame dve zarovnane sekvencie, medzi ktorymi vidime 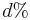zmenenych baz, chceme odhadnut t
- Spatne teda zratame t, ktore by hodnote 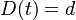$D(t)=d$ prinalezalo.
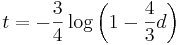
Dostavame teda vzorec pre vzdialenost, ktory sme videli na prednaske $t=-{\frac {3}{4}}\log \left(1-{\frac {4}{3}}d\right)$
Ak 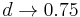$d\rightarrow 0.75$ , dostavame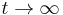 $t\rightarrow \infty$
Preco sme ten vzorec odvodili takto? V skutocnosti chceme najst najvierohodnejsiu hodnotu t, t.j. taku, pre ktore hodnota P(data|t) bude najvacsia. Zhodou okolnosti vyjde takto.

Zložitejšie modely

V praxi sa používajú komplikovanejsie substitučné modely, ktoré majú všeobecnejšiu maticu rýchlostí R

$R=\left({\begin{array}{cccc}.&\mu _{{AC}}&\mu _{{AG}}&\mu _{{AT}}\\\mu _{{CA}}&.&\mu _{{CG}}&\mu _{{CT}}\\\mu _{{GA}}&\mu _{{GC}}&.&\mu _{{GT}}\\\mu _{{TA}}&\mu _{{TC}}&\mu _{{TG}}&.\\\end{array}}\right)$

Hodnoty na diagonále matice sa dopočítavajú aby súčet každého riadku bol 0.

Hodnota 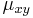$\mu _{{xy}}$ v tejto matici vyjadruje rýchlosť, akou sa určitá báza x mení na inú bázu y.
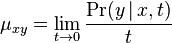Presnejšie $\mu _{{xy}}=\lim _{{t\rightarrow 0}}{\frac {\Pr(y\,|\,x,t)}{t}}$ .

Kimurov model napr. zachytáva, ze puríny sa častejšie menia na iné puríny (A a G) a pyrimidíny na ine pyrimidíny (C a T).

Má dva parametre: rýchlosť tranzícií alfa, transverzií beta

$R=\left({\begin{array}{cccc}-2\beta -\alpha &\beta &\alpha &\beta \\\beta &-2\beta -\alpha &\beta &\alpha \\\alpha &\beta &-2\beta -\alpha &\beta \\\beta &\alpha &\beta &-2\beta -\alpha \\\end{array}}\right)$

HKY model (Hasegawa, Kishino & Yano) tiež umožnuje rôzne pravdepodobnosti A, C, G a T v ekvilibriu.
Ak nastavíme čas v evolučnom modeli na nekonečno, nezáleží na tom, z ktorej bázy sme začali, frekvencia výskytu jednotlivých báz sa ustáli v tzv. ekvilibriu.
V Jukes-Cantorovom modeli je pravdepodobnosť ľubovoľnej bázy v ekvilibriu 1/4.
V HKY si zvolime aj frekvencie jednotlivých nukleotidov v ekvilibriu 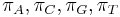$\pi _{A},\pi _{C},\pi _{G},\pi _{T}$ so súčtom 1
Parameter kapa: pomer tranzícií a transverzií (alfa/beta)
Matica rýchlostí:
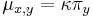- $\mu _{{x,y}}=\kappa \pi _{y}$ ak mutácia x->y je tranzícia,
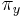- $\pi _{y}$ ak mutácia x->y je transverzia

Pre zložité modely nevieme odvodiť explicitný vzorec na výpočet S(t), ako sme mali pri Jukes-Cantorovom modeli
Ale vo všeobecnosti pre maticu rýchlostí 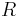dostávame .
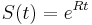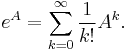
- Exponenciálna funkcia matice A sa definuje ako $e^{A}=\sum _{{k=0}}^{\infty }{1 \over k!}A^{k}.$
- Ak maticu rychlosti R diagonalizujeme (určite sa dá pre symetrické R) 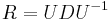$R=UDU^{{-1}}$ , kde D je diagonálna matica (na jej diagonále budu vlastné hodnoty R), tak 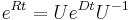$e^{{Rt}}=Ue^{{Dt}}U^{{-1}}$ , t.j. exponenciálnu funkciu uplatníme iba na prvky na uhlopriečke matice D.

CI07: Rozdiel medzi revíziami

Aktuálna revízia z 14:24, 5. november 2020

Obsah

Substitučné modely - odvodenie

Požiadavky na S(t)

Jukes-Cantorov substitučný model

Matica rýchlostí pre J-C model

Poriadnejšie odvodenie diferenciálnej rovnice

Vlastnosti riešenia

Substitučné matice, zhrnutie

Použitie na odhad evolučnej vzdialenosti

Zložitejšie modely

Navigačné menu

Osobné nástroje

Menné priestory

Varianty

Zobrazení

Operácie

Hľadať

Navigácia

Nástroje