CI08: Rozdiel medzi revíziami
Z MBI
(Vytvorená stránka „==Felsensteinov algoritmus 1981== * Mame dany strom T s dlzkami hran a bazy v listoch (jeden stlpec zarovnania) a model substitucii (zadany napr. maticou rychlosti R)....“) |
(Žiaden rozdiel)
|
Aktuálna revízia z 09:16, 12. november 2020
Felsensteinov algoritmus 1981
- Mame dany strom T s dlzkami hran a bazy v listoch (jeden stlpec zarovnania) a model substitucii (zadany napr. maticou rychlosti R). Spocitajme pravdepodobnost, ze z modelu dostaneme prave tuto kombinaciu baz v listoch.
- Oznacenie:
- Nech X_v je premenna reprezentujuca bazu vo vrchole v a nech x_v je konkretna baza v liste v.
- Nech listy su 1..n a vnut. vrcholy n+1..2n-1, pricom koren je 2n-1.
- Nech p_v je rodic vrchola v a nech dlzka hrany z v do rodica je t_v.
- Nech P(a|b,t) je pravdepodobnost, ze b sa zmeni na a za cas t (spocitame z matice R, vid minule cvicenia).
- Napr. v Jukes-Cantorovom modeli
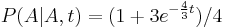 ,
, 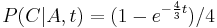
- Napr. v Jukes-Cantorovom modeli
- Nech q_a je pravdepodobnost bazy a v koreni (ekvilibrium matice R)
- Napr. v Jukes-Cantorovom modeli q_a = 1/4
- Ak by sme poznali bazy vo vsetkych vrcholoch, mame
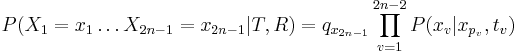
- Chceme pravdepodobnost
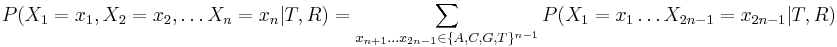
- Pocitat sucet cez exponencialne vela dosadeni hodnot za vnutorne vrcholy je neefektivne, spocitame rychlejsie dynamickym programovanim.
- Nech A[v,a] je pravdepodobnost dat v podstrome s vrcholom v ak X_v=a
- A[v,a] pocitame od listov ku korenu
- V liste A[v,a] = [a=x_v]
- Vo vnut. vrchole s detmi y a z mame
![A[v,a]=\sum _{{b,c}}A[y,b]A[z,c]P(b|a,t_{y})P(c|a,t_{z})](/vyuka/mbi/images/math/e/c/b/ecbada933fd6f145f641b4e2793e58df.png)
- Celkova pravdepodobnost je
![P(X_{1}=x_{1},X_{2}=x_{2},\dots X_{n}=x_{n}|T,R)=\sum _{a}A[r,a]q_{a}](/vyuka/mbi/images/math/3/0/d/30d167737e880c69f2a1cd08a5dfc5a5.png) pre koren r.
pre koren r.
Zlozitost, zlepsenie
- Zlozitost
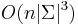
- Pre nebinarne stromy exponencialne
- Zlepsenie
![A[v,a]=(\sum _{{b}}A[y,b]P(b|a,t_{y}))(\sum _{c}A[z,c](c|a,t_{z}))](/vyuka/mbi/images/math/0/2/0/0201f86e4456366fe1c8944f7576e3b5.png)
- Zlozitost
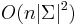 aj pre nebinarne stromy
aj pre nebinarne stromy
Chybajuce data
- Ak v niektorom liste mame neznamu bazu N, nastavime A[v,a]=1
- Podobne sa spracovavaju medzery v zarovnani, aj ked mohli by sme mat aj model explicitne ich modelujuci
Aposteriorna pravdepodobnost (nerobili sme)
- Co ak chceme spocitat pravdepodobnost P(X_v=a|X_1=x_1, X_2=x_2,\dots X_n=x_n,T,R)? Zaujimaju nas teda sekvencie genomov predkov.
- Potrebujeme B[v,a]=pravdpodobnost dat ak podstrom v nahradim listom s bazou a.
- B[v,a] pocitame od korena k listom
- V koreni B[v,a] = q_a
- Vo vrchole v s rodicom u a surodencom x mame
![B[v,a]=\sum _{{b,c}}B[u,b]A[x,c]P(a|b,t_{v})P(c|b,t_{v})](/vyuka/mbi/images/math/0/4/c/04cc0bf38cc6bbf3b4ddf7ce0e346560.png)
- Ziadana pravdepodobnost je
![B[v,a]A[v,a]/P(X_{1}=x_{1},X_{2}=x_{2},\dots X_{n}=x_{n}|T,R)](/vyuka/mbi/images/math/c/c/2/cc2c38f95bb6131cc0a4edfdc7db8bdb.png)