CI06
Obsah
HMM opakovanie
Parametre HMM:
-
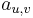 : prechodová pravdepodobnosť zo stavu
: prechodová pravdepodobnosť zo stavu 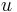 do stavu
do stavu 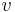
-
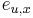 : pravdepodobnosť emisie
: pravdepodobnosť emisie 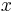 v stave
v stave 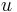
-
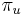 : pravdepodobnosť, že začneme v stave
: pravdepodobnosť, že začneme v stave 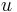
- Sekvencia
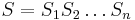
- Anotácia
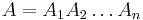
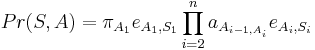
Trénovanie
- Proces, pri ktorom sa snažíme čo najlepšie odhadnúť pravdepodobnosti
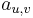 a
a 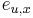 v modeli podľa trénovacích dát
v modeli podľa trénovacích dát
Usudzovanie (inferencia)
- Proces, pri ktorom sa snažíme pre sekvenciu
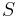 nájsť anotáciu
nájsť anotáciu 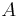 , ktorá sekvenciu
, ktorá sekvenciu 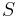 emituje s veľkou pravdepodobnosťou.
emituje s veľkou pravdepodobnosťou.
Inferencia pomocou najpravdepodobnejšej cesty, Viterbiho algoritmus
Hľadáme najpravdepodobnejšiu postupnosť stavov 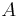 , teda
, teda 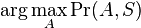 . Úlohu budeme riešiť dynamickým programovaním.
. Úlohu budeme riešiť dynamickým programovaním.
- Podproblém
![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) : Pravdepodobnosť najpravdepodobnejšej cesty končiacej po
: Pravdepodobnosť najpravdepodobnejšej cesty končiacej po 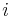 krokoch v stave
krokoch v stave 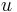 , pričom vygeneruje
, pričom vygeneruje 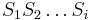 .
.
- Rekurencia:
-
![V[1,u]=\pi _{u}e_{{u,S_{1}}}](/vyuka/mbi/images/math/f/1/3/f13d26742a6a93123093e174c3fd90aa.png) (*)
(*)
-
![V[i,u]=\max _{w}V[i-1,w]a_{{w,u}}e_{{u,S_{i}}}](/vyuka/mbi/images/math/e/3/b/e3bf534bb50c39843ed166123ecc374b.png) (**)
(**)
-
Algoritmus:
- Nainicializuj
![V[1,*]](/vyuka/mbi/images/math/5/d/9/5d9f1d4ebd3080a0804a6501977b5dae.png) podľa (*)
podľa (*)
- for i=2 to n=dĺžka reťazca
- for u=1 to m=počet stavov
- vypočítaj
![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) pomocou (**)
pomocou (**)
- vypočítaj
- for u=1 to m=počet stavov
- Maximálne
![V[n,j]](/vyuka/mbi/images/math/1/2/9/12924883f1d662364326a1d3f0fed497.png) je pravdepodobnosť najpravdepodobnejšej cesty
je pravdepodobnosť najpravdepodobnejšej cesty
Aby sme vypísali anotáciu, pamätáme si pre každé ![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) stav
stav 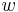 , ktorý viedol k maximálnej hodnote vo vzorci (**).
, ktorý viedol k maximálnej hodnote vo vzorci (**).
Zložitosť: 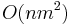
Poznámka: pre dlhé sekvencie budú čísla ![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) veľmi malé a môže dôjsť k podtečeniu. V praxi teda používame zlogaritmované hodnoty, namiesto násobenia súčet.
veľmi malé a môže dôjsť k podtečeniu. V praxi teda používame zlogaritmované hodnoty, namiesto násobenia súčet.
Inferencia - dopredný algoritmus
Aká je celková pravdepodobnosť, že vygenerujeme sekvenciu 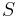 , t.j.
, t.j. 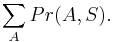 Podobný algoritmus ako Viterbiho.
Podobný algoritmus ako Viterbiho.
Podproblém ![F[i,u]](/vyuka/mbi/images/math/4/e/6/4e6962ec814d01e4ca0d1f2aa085a831.png) : pravdepodobnosť, že po
: pravdepodobnosť, že po 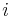 krokoch vygenerujeme
krokoch vygenerujeme 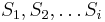 a dostaneme sa do stavu
a dostaneme sa do stavu 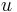 .
.
![F[i,u]=\Pr(A_{i}=u\wedge S_{1},S_{2},\dots ,S_{i})=\sum _{{A_{1},A_{2},\dots ,A_{i}=u}}\Pr(A_{1},A_{2},...,A_{i}\wedge S_{1},S_{2},...,S_{i})](/vyuka/mbi/images/math/9/c/5/9c51082607764a6c99095ebaa1ba26f4.png)
![F[1,u]=\pi _{u}e_{{u,S_{1}}}](/vyuka/mbi/images/math/f/e/a/fead9f93f8bf3927b34f49597d884996.png)
![F[i,u]=\sum _{v}F[i-1,v]a_{{v,u}}e_{{u,S_{i}}}](/vyuka/mbi/images/math/d/1/c/d1c9473aeb8cc364771bc9c575c7a73f.png)
Celková pravdepodobnosť ![\sum _{u}F[n,u]](/vyuka/mbi/images/math/1/b/2/1b2108be9d84620e173cb861e49c6b35.png)
Inferencia - posterior decoding
Aposteriórna pravdepodobnosť stavu u na pozícii i: 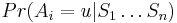
Pre každý index i chceme nájsť stav u s najväčšiou aposteriórnou pravdepodobnosťou, dostaneme tak inú možnú anotáciu.
Spustíme dopredný algoritmus a jeho symetrickú verziu, spätný algoritmus, ktorý počíta hodnoty
![B[i,u]=\Pr(A_{i}=u\wedge S_{{i+1}}\dots S_{n})](/vyuka/mbi/images/math/6/e/8/6e82648bde89df23b004629c06c05c23.png)
Aposteriórna pravdepodobnosť stavu u na pozícii i: ![Pr(A_{i}=u|S_{1}\dots S_{n})=F[i,u]B[i,u]/\sum _{u}F[n,u].](/vyuka/mbi/images/math/2/7/c/27cea5da3d3a25dfb8a677a41dc9e9b1.png)
Posterior decoding uvažuje všetky anotácie, nielen jednu s najvyššou pravdepodobnosťou. Môže však vypísať anotáciu, ktorá má sama o sebe nulovú pravdepodobnosť (napr. počet kódujúcich báz v géne nie je deliteľný 3).
Trénovanie HMM
- Stavový priestor + povolené prechody väčšinou ručne
- Parametre (pravdepodobnosti prechodu, emisie a počiatočné) automaticky z trénovacích sekvencií
- Ak máme anotované trénovacie sekvencie, jednoducho počítame frekvencie
- Ak máme iba neanotované sekvencie, snažíme sa maximalizovať vierohodnosť trénovacích dát v modeli. Používajú sa heuristické iteratívne algoritmy, napr. Baum-Welchov, ktorý je verziou všeobecnejšieho algoritmu EM (expectation maximization).
- Čím zložitejší model a viac parametrov máme, tým potrebujeme viac trénovacích dát, aby nedošlo k preučeniu, t.j. k situácii, keď model dobre zodpovedá nejakým zvláštnostiam trénovacích dát, nie však ďalším dátam.
- Presnosť modelu testujeme na zvláštnych testovacích dátach, ktoré sme nepoužili na trénovanie.
Tvorba stavového priestoru modelu
- Promótor + niekoľko prokaryotických génov
- Repeaty v intrónoch: multiple path problem
- Intrón má dĺžku aspoň 10
Zovšeobecnené HMM
- Predstavme si HMM s dvoma stavmi, napr. gén / negén, pričom každý stav má prechod do seba aj do druhého stavu
- Úloha: Nech p je pravdepodobnosť, že zostaneme v tom istom stave, (1-p), že prejdeme do druhého stavu. Aká je pravdepodobnosť, že v stave zostaneme presne k krokov (k>=1)?
- Riešenie:
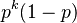
- Toto rozdelenie sa nazýva geometrické a pravdepodbnosť exponenciálne rýchlo klesá s rastúcim k
- Riešenie:
- Keď sa pozrieme na histogram reálny dĺžkov génov / exónov a iných oblastí, väčšinou sa enpodobá na geometrické rozdelnie, môže priponínať napr. normálne rozdelenie s určitou priemenrou dĺžkou a rozptylom okolo
- Jednoduché HMM teda dobre nemodeluje tento fenomén
- Zovšeobecnené HMM (semi-Markov) pracuje tak, že v stave má ľubovoľné rozdelenie pravdepodobnosti dĺžok. Model vôjde do stavu, vygeneruje dĺžku k z tohto rozdelenia, potom vygeneruje k znakov z príslušnej emisnej tabuľky a na záver sa rozhodne, ktorým prechodom opustí stav
- Úloha: ako spočítame pravdepodobnosť konkrétnej sekvencie a konkrétnej postupnosti stavov aj s dĺžkami? (zaveďme si aj nejaké vhodné označenie)
- Úloha: ako treba upraviť Viterbiho algoritmus pre tento model? Aká bude jeho zložitosť?
- Zložitosť bude kvadraticky rásť od dĺžky sekvencie, predtým rástla lineárne
- Predstavme si teraz, že rozdelenie dĺžok má hornú hranicu D takú, že všetky dĺžky väčšie ako D majú nulovú pravdepodobnosť.
- Úloha: ako sa toto obmedzenie prejaví v zložitosti Viterbiho algoritmu?
- Uloha: navrhnite, ako modelovať zovšeobecnený HMM s rozdelením dĺžok ohraničeným D pomocou normálneho stavu, kde sa jedne zovšeobecnený stav nahradí vhodnou postupnosťou D obyčajných stavov.
Párové HMM (pair HMM)
Nebrali sme, uvedene pre zaujimavost
- Emituje dve sekvencie
- V jednom kroku moze emitovat:
- pismenka v oboch sekvenciach naraz
- pismenko v jednej skevencii
- pismenko v druhej sekvencii
Priklad: HMM s jednym stavom v, takym, ze
-
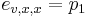
-
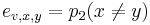 ,
,
-
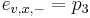 ,
,
-
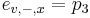
- tak, aby sucet emisnych pravdepodobnosti bol 1
- Co reprezentuje najpravdepodobnejsia cesta v tomto HMM?
Zlozitejsi HMM: tri stavy M, X, Y, uplne navzajom poprepajane
-
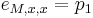
-
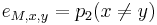 ,
,
-
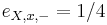 ,
,
-
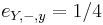 ,
,
- Co reprezentuje najpravdepodobnejsia cesta v tomto HMM?
Viterbiho algoritmus pre parove HMM
- V[i,j,u] = pravdepodobnost najpravdepodobnejsej postupnosti stavov, ktora vygeneruje x1..xi a y1..yj a skonci v stave u
-
![V[i,j,u]=\max _{w}\left\{{\begin{array}{l}V[i-1,j-1,w]\cdot a_{{w,u}}\cdot e_{{u,x_{i},y_{j}}}\\V[i-1,j,w]\cdot a_{{w,u}}\cdot e_{{u,x_{i},-}}\\V[i,j-1,w]\cdot a_{{w,u}}\cdot e_{{u,-,y_{j}}}\\\end{array}}\right.](/vyuka/mbi/images/math/d/5/0/d5064f1dc674bec18ec3404260675e81.png)
- Casova zlozitost O(mnk^2) kde m a n su dlzky vstupnych sekvencii, k je pocet stavov
Ako by sme spravili parove HMM na hladanie genov v dvoch sekvenciach naraz?
- Predpokladajme rovnaky pocet exonov
- V exonoch medzery len cele kodony (oboje zjednodusuje)
- Inde hocijake medzery