Programovanie (2) v Jave
1-INF-166, letný semester 2024/25
Prednáška 14: Rozdiel medzi revíziami
| Riadok 356: | Riadok 356: | ||
* Predchádzajúce implementácie sa ľahko dali upraviť na rôzne univerzá (celé čísla, desatinné čísla, smerníky na zložitejšie štruktúry, napr. struct, pole, reťazec) | * Predchádzajúce implementácie sa ľahko dali upraviť na rôzne univerzá (celé čísla, desatinné čísla, smerníky na zložitejšie štruktúry, napr. struct, pole, reťazec) | ||
* Na rozdiel od toho sa priame adresovanie dá použiť iba ak univerzum je ''U'' = {0,1,...,''m''-1} pre nejaké rozumne malé prirodzené číslo ''m'' | * Na rozdiel od toho sa priame adresovanie dá použiť iba ak univerzum je ''U'' = {0,1,...,''m''-1} pre nejaké rozumne malé prirodzené číslo ''m'' | ||
| − | * Podmnožinu 'A'' univerza ''U'' potom môžeme reprezentovať ako pole booleovských hodnôt dĺžky ''m'', kde ''i''-ty prvok | + | * Podmnožinu ''A'' univerza ''U'' potom môžeme reprezentovať ako pole booleovských hodnôt dĺžky ''m'', kde ''i''-ty prvok poľa bude <tt>true</tt> práve vtedy, keď ''i'' patrí do ''A''. |
| − | * Túto reprezentáciu sme používali napríklad v poli <tt>bolo</tt> | + | * Túto reprezentáciu sme používali napríklad v poli <tt>bolo</tt> pri prehľadávaní s návratom. |
| − | * Funkcie <tt>contains</tt> aj <tt>add</tt> sú potom veľmi | + | * Funkcie <tt>contains</tt> aj <tt>add</tt> sú potom veľmi jednoduché a rýchle. |
| − | * Problémom tohto prístupu je ale vysoká pamäťová zložitosť | + | * Problémom tohto prístupu je ale vysoká pamäťová zložitosť, ak je číslo ''m'' veľké. |
* Veľmi efektívne pre malé univerzá (napr. cifry ''0,...,9'', všetky znaky anglickej abecedy, všetky znaky s ASCII hodnotami od 0 po 255, a pod.). | * Veľmi efektívne pre malé univerzá (napr. cifry ''0,...,9'', všetky znaky anglickej abecedy, všetky znaky s ASCII hodnotami od 0 po 255, a pod.). | ||
| Riadok 370: | Riadok 370: | ||
const int m = 1000; | const int m = 1000; | ||
| − | /* Struktura | + | /* Struktura implementujuca mnozinu pomocou priameho adresovania: */ |
struct set { | struct set { | ||
bool *p; | bool *p; | ||
| Riadok 397: | Riadok 397: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | === Jednoduché | + | === Jednoduché hašovanie === |
| − | Priame adresovanie sa | + | Priame adresovanie sa nehodí pre veľké univerzá, lebo by vyžadovalo veľa pamäte. |
| − | '' | + | '''Hašovanie''' (angl. hashing) je jednoduchá finta, ktorá funguje nasledovne: |
| − | * Nech ''U'' je univerzum všetkých možných prvkov množiny | + | * Nech ''U'' je univerzum všetkých možných prvkov množiny. |
| − | * Vytvoríme | + | * Vytvoríme '''hašovaciu tabuľku''' (angl. hash table), čo je pole nejakej rozumnej veľkosti ''m''. |
| − | * Naprogramujeme '' | + | * Naprogramujeme ''hašovaciu funkciu'', ktorá transformuje prvky univerza ''U'' na indexy hašovacej tabuľky; pôjde teda o funkciu ''h'': ''U'' -> {0, 1, ... , ''m''−1}. |
| − | + | * Najjednoduchšia hašovacia funkcia pre celočíselné prvky je ''h''(''x'') = |''x''| mod ''m''. | |
| − | * Najjednoduchšia | + | ** |''x''| spočítame funkciou <tt>abs</tt> z knižnice <tt>cstdlib</tt> |
| − | ** '' | + | ** Absolútnu hodnotu používame, lebo napríklad <tt>-10 % 3</tt> je -1, čo mimo rozsahu indexov tabuľky |
| + | ** V praxi sa používajú zložitejšie hašovacie funkcie. Ideálne je hašovacia funkcia jednoduchá a rýchla, ale pritom by mal hodnoty do tabuľky distribuovať rovnomerne, aby sa príliš často nestávalo, že dva prvky sa namapujú na to isté políčko | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 419: | Riadok 420: | ||
[[Súbor:hash1.png]] | [[Súbor:hash1.png]] | ||
| − | + | Prvý pokus o prácu hašovacou tabuľkou by teda mohol vyzerať takto: | |
'''Vkladanie''' prvku ''x'': | '''Vkladanie''' prvku ''x'': | ||
| Riadok 434: | Riadok 435: | ||
=== Kolízie === | === Kolízie === | ||
| − | Pri vkladaní prvku sme narazili na problém, ak na už | + | * Pri vkladaní prvku sme narazili na problém, ak na už obsadené miesto chceme vložiť iný prvok. |
| − | * | + | * Ak sa dva prvky ''x'' a ''y'' sa zahašujú na rovnakú pozíciu ''h''(''x'') = ''h''(''y''), hovoríme, že nastala '''kolízia''' |
| − | * | + | * Existuje niekoľko metód na riešenie kolízií. |
| − | + | * Existujú rôzne prístupy na riešenie kolízií, môžeme napríklad hľadať iné voľné miesto v tabuľke. | |
| − | Existujú | + | * V našom programe kolízie vyriešime tak, že v každom políčku tabuľky uložíme spájaný zoznam všetkých prvkov, ktoré sa tam zahašovali. |
| − | + | ** Táto situácia je znázornená na nasledujúcom obrázku, v ktorom šípky zodpovedajú vkladaniam prvkov (celých čísel) do množiny reprezentovanej hašovacou tabuľkou. | |
| − | |||
| − | |||
| − | V každom políčku | ||
| − | v ktorom šípky zodpovedajú vkladaniam prvkov (celých čísel) do množiny reprezentovanej | ||
[[Súbor:Hash2.png]] | [[Súbor:Hash2.png]] | ||
| Riadok 450: | Riadok 447: | ||
#include <cstdlib> | #include <cstdlib> | ||
| − | + | /* Hasovacia funkcia: */ | |
| − | |||
| − | /* | ||
int h(int x, int m) { | int h(int x, int m) { | ||
return abs(x) % m; | return abs(x) % m; | ||
| Riadok 463: | Riadok 458: | ||
}; | }; | ||
| − | /* Struktura | + | /* Struktura implementujuca dynamicku mnozinu pomocou hasovania: */ |
struct set { | struct set { | ||
node **hashtable; // Pole smernikov na zaciatky jednotlivych zoznamov | node **hashtable; // Pole smernikov na zaciatky jednotlivych zoznamov | ||
| − | int m; // Velkost | + | int m; // Velkost hasovacej tabulky |
}; | }; | ||
| Riadok 472: | Riadok 467: | ||
s.m = m; | s.m = m; | ||
s.hashtable = new node *[m]; | s.hashtable = new node *[m]; | ||
| − | for (int i = 0; i < | + | for (int i = 0; i < m; i++) { |
s.hashtable[i] = NULL; | s.hashtable[i] = NULL; | ||
} | } | ||
| Riadok 478: | Riadok 473: | ||
bool contains(set &s, int x) { | bool contains(set &s, int x) { | ||
| − | int index = h(x, s.m); // Spocitame spravne policko | + | int index = h(x, s.m); // Spocitame spravne policko hasovacej tabulky |
node *p = s.hashtable[index]; // Smernik p ukazuje na prvy prvok spajaneho | node *p = s.hashtable[index]; // Smernik p ukazuje na prvy prvok spajaneho | ||
// zoznamu na danom policku | // zoznamu na danom policku | ||
| Riadok 491: | Riadok 486: | ||
void add(set &s, int x) { | void add(set &s, int x) { | ||
| − | int index = h(x, s.m); // Spocitame spravne policko | + | int index = h(x, s.m); // Spocitame spravne policko hasovacej tabulky |
| − | node *temp = new node; | + | node *temp = new node; // Vytvorime novy uzol do spajaneho zoznamu |
temp->data = x; | temp->data = x; | ||
temp->next = s.hashtable[index]; // Vlozime uzol temp na zaciatok zoznamu. | temp->next = s.hashtable[index]; // Vlozime uzol temp na zaciatok zoznamu. | ||
| Riadok 499: | Riadok 494: | ||
void destroy(set &s) { | void destroy(set &s) { | ||
| − | for (int i = 0; i < | + | for (int i = 0; i < s.m; i++) { |
node *p = s.hashtable[i]; // Uvolni zoznam s.hashtable[i] | node *p = s.hashtable[i]; // Uvolni zoznam s.hashtable[i] | ||
while (p != NULL) { | while (p != NULL) { | ||
| − | node * | + | node *p2 = p->next; |
delete p; | delete p; | ||
| − | p = | + | p = p2; |
} | } | ||
} | } | ||
| Riadok 511: | Riadok 506: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | '''Cvičenie:''' Ako bude vyzerať | + | '''Cvičenie:''' Ako bude vyzerať hašovacia tabuľka pri riešení kolízií pomocou spájaných zoznamov, ak hašovacia funkcia je |x| mod 5 a vkladáme prvky 13, -2, 0, 8, 10, 17? |
===Zložitosť=== | ===Zložitosť=== | ||
| − | * Rýchlosť závisí od | + | * Rýchlosť závisí od veľkosti tabuľky ''m'', hašovacej funkcie a počtu kolízií. |
| − | * V najhoršom prípade sa všetky prvky | + | * V najhoršom prípade sa všetky prvky zahašujú do toho istého políčka, a teda musíme pri hľadaní prejsť všetky prvky množiny. |
* Ak máme šťastie a v každom políčku máme len málo prvkov, bude aj vyhľadávanie rýchle. | * Ak máme šťastie a v každom políčku máme len málo prvkov, bude aj vyhľadávanie rýchle. | ||
| − | ** Ak je tabuľka dosť veľká a | + | ** Ak je tabuľka dosť veľká a hašovacia funkcia vhodne zvolená, tento prípad je pomerne obvyklý. |
| − | ** | + | ** Hašovacie tabuľky sa často používajú v praxi. |
* Viac budúci rok na predmete ''Algoritmy a dátové štruktúry''. | * Viac budúci rok na predmete ''Algoritmy a dátové štruktúry''. | ||
Verzia zo dňa a času 22:49, 7. november 2021
Obsah
Oznamy
- Tento týždeň bude okrem bežnej rozcvičky na utorňajších cvičeniach aj bonusová rozcvička počas piatkových doplnkových cvičení (za 1 bonusový bod). Termín odovzdania zvyšných úloh z týchto cvičení bude streda 18. novembra, 22:00.
- Druhú domácu úlohu treba odovzdať do piatku 13. novembra, 22:00.
- Budúci týždeň budú kvôli štátnemu sviatku iba piatkové cvičenia. V pondelok 16. novembra bude zverejnených niekoľko úloh na cvičenia č. 9 (menej, než obvykle).
- V piatok 20. novembra bude na začiatku doplnkových cvičení krátky test, body za ktorý budú riadnou súčasťou hodnotenia z cvičení č. 9. Pokyny ohľadom technickej realizácie testu budú upresnené neskôr.
Ešte k smerníkom
Opakovanie základnej práce so smerníkmi
int a = 7; // premenna typu int
int *b = NULL; // smernik na int
b = &a; // b obsahuje adresu premennej a
*b = 8; // v premennej a je teraz 8
a = (*b)+1; // v premennej a je teraz 9
Smerníky a struct
Smerník môže ukazovať aj na struct. Operátory . (prístup k prvku štruktúry) a [] (prístup k prvku poľa) majú vyššiu prioritu ako operátory * (dereferencia smerníka) a & (adresa). Preto napríklad:
- Zápis *s.cokolvek je to isté ako *(s.cokolvek) a vyjadruje dereferenciu smerníka s.cokolvek.
- Zápis (*p).cokolvek vyjadruje prvok cokolvek štruktúry získanej dereferenciou smerníka p.
- Zvyčajne je potrebnejší zápis (*p).cokolvek; existuje preň preto skratka p->cokolvek.
struct bod {
int x, y;
};
// ...
bod b;
b.x = 0;
b.y = 0;
bod *p = &b; // p ukazuje na bod b
bod *p2 = new bod; // alokovanie noveho bodu
(*p2).x = 20; // bod, na ktory ukazuje p2, bude mat x 20
p2->y = 10; // bod, na ktory ukazuje p2, bude mat y 10
delete p2; // uvolnenie pamate
Dynamická množina
Motivačný príklad
- Na fakulte sa dvere do niektorých miestností otvárajú priložením čipovej karty k čítačke
- Každá karta má v sebe uložené identifikačné číslo
- Čítačka má v pamäti zoznam identifikačných čísel oprávnených osôb (študenti, vyučujúci a pod.)
- Po priložení karty z nej prečíta číslo a zisťuje, či ho má vo svojom zozname
- Administrátor tiež potrebuje vedieť pridávať a uberať oprávnené osoby
- Ako asi môže byť systém pracujúci so zoznamom identifikačných čísel naprogramovaný?
Dynamická množina
Chceli by sme vytvoriť dátovú štruktúru s nasledujúcou špecifikáciou
- Máme množinu A, ktorá sa bude postupne meniť, preto ju nazývame dynamická množina
- Funkcia contains dostane množinu A a hodnotu x a zistí, či x patrí do A
- Funkcia add dostane množinu A a hodnotu x a pridá x do A
- Funkcia remove dostane množinu A a prvok x a odoberie x z A
- Pre jednoduchosť funkciu remove nebudeme dnes uvažovať
- Niekedy sa môžu zísť aj iné operácie.
Problém príslušnosti k množine sa vyskytuje aj v mnohých iných situáciách.
- Ako dnes uvidíme, dynamickú množinu môžeme implementovať rôznymi spôsobmi.
- Hovoríme, že dynamická množina je abstraktný dátový typ, špecifikuje totiž iba rozhranie, ktoré má dátová štruktúra poskytovať používateľovi, nie jeho implementáciu.
- Ak by sme zmenili implementáciu z jednej na inú, nemusíme nutne meniť programy, ktoré dynamickú množinu využívajú, pokiaľ k nej pristupujú iba pomocou uvedených funkcií.
Implementácie dynamických množín
- Pre jednoduchosť budeme uvažovať iba dynamickú množinu celých čísel.
- Dynamickú množinu budeme uchovávať v štruktúre set.
- Navyše budeme mať implementovaných niekoľko funkcií, ktoré s dynamickými množinami pracujú.
- Kostra programu teda bude vyzerať pre ľubovoľnú implementáciu dynamickej množiny takto:
/* Struktura reprezentujuca dynamicku mnozinu. */
struct set {
// ...
};
/* Funkcia, ktora vytvori prazdnu dynamicku mnozinu. */
void init(set &s) {
// ...
}
/* Funkcia, ktora zisti, ci prvok x patri do mnoziny s. */
bool contains(set &s, int x) {
// ...
}
/* Funkcia, ktora prida prvok x do mnoziny s. */
void add(set &s, int x) {
// ...
}
/* Funkcia, ktora uvolni mnozinu s z pamate. */
void destroy(set &s) {
// ...
}
Bez ohľadu na implementáciu štruktúry set a uvedených funkcií už teraz môžeme napísať program, ktorý ich využíva. Z konzoly číta príkazy a postupne ich vykonáva.
#include <iostream>
#include <cstring>
using namespace std;
// ...
const int maxlength = 100;
int main(void) {
set A;
init(A);
while (true) {
char prikaz[maxlength];
cin.width(maxlength);
cin >> prikaz;
if (strcmp(prikaz, "contains") == 0) {
int x;
cin >> x;
cout << contains(A, x) << endl;
} else if (strcmp(prikaz, "add") == 0) {
int x;
cin >> x;
add(A, x);
} else if (strcmp(prikaz, "end") == 0) {
break;
}
}
destroy(A);
}
Ukážeme si teraz niekoľko rôznych implementácii dynamickej množiny; začneme s dvoma, ktoré sú nám už v princípe známe.
Dynamická množina ako pole
Dynamickú množinu môžeme implementovať tak, že jej prvky budeme ukladať do poľa v ľubovoľnom poradí.
- Funkcia contains musí zakaždým prejsť celé pole lineárnym prehľadávaním (nie je teda zrovna rýchla).
- Funkcia add je naopak veľmi rýchla: stačí pridať prvok na koniec poľa.
- Je ale potrebné dávať pozor na prekročenie kapacity poľa (mohli by sme použiť dynamické pole).
#include <cassert>
// ...
const int maxN = 1000;
struct set {
int *p; // Smernik na nulty prvok pola.
int length; // Pocet prvkov v poli
};
void init(set &s) {
s.p = new int[maxN];
s.length = 0;
}
bool contains(set &s, int x) {
for (int i = 0; i < s.length; i++) {
if (s.p[i] == x) {
return true;
}
}
return false;
}
void add(set &s, int x) {
assert(s.length < maxN);
s.p[s.length] = x;
s.length++;
}
void destroy(set &s) {
delete[] s.p;
}
Dynamická množina ako utriedené pole
Prvky množiny môžeme v poli uchovávať aj utriedené od najmenšieho po najväčšie.
- Funkcia contains potom môže použiť binárne vyhľadávanie. Je teda rýchlejšia, ako v predchádzajúcom prípade (v poli veľkosti n sa pozrie len na približne log n pozícií; napríklad pre miliónprvkové pole sa pozrieme asi na 20 prvkov poľa).
- Funkcia add ale musí vložiť prvok na správne miesto v utriedenom poli; je teda o dosť pomalšia.
#include <cassert>
// ...
const int maxN = 1000;
struct set {
int *p; // Smernik na nulty prvok pola.
int length; // Momentalna dlzka pola.
};
void init(set &s) {
s.p = new int[maxN];
s.length = 0;
}
bool contains(set &s, int x) {
int left = 0;
int right = s.length - 1;
while (left <= right) {
int index = (left + right) / 2;
if (s.p[index] == x) {
return true;
} else if (s.p[index] > x) {
right = index - 1;
} else {
left = index + 1;
}
}
return false;
}
void add(set &s, int x) {
assert(s.length < maxN);
int kam = s.length;
while (kam > 0 && s.p[kam - 1] > x) {
s.p[kam] = s.p[kam - 1];
kam--;
}
s.p[kam] = x;
s.length++;
}
void destroy(set &s) {
delete[] s.p;
}
Ďalšie možnosti implementácie dynamickej množiny (plán na dnes)
Dnes uvidíme ďalšie dva spôsoby implementácie dynamickej množiny:
- Množina ako jednosmerne spájaný zoznam:
- Ľahko pridáme nové prvky, nepotrebujeme vopred vedieť veľkosť.
- Nedá sa rýchlo binárne vyhľadávať.
- Založené na smerníkoch.
- Množina pomocou hešovania:
- Často veľmi rýchle vyhľadávanie.
- Použijeme polia aj spájané zoznamy.
Spájané zoznamy
Spájaný zoznam (angl. linked list) je postupnosť uzlov rovnakého typu usporiadaných za sebou. Každý uzol pritom pozostáva z dvoch častí:
- Samotné dáta; v našom prípade jedno číslo typu int.
- Smerník, ktorý ukazuje na nasledujúci prvok zoznamu – ten umožňuje „pohybovať sa” po zozname zľava doprava.
Posledný uzol zoznamu nemá následníka – jeho smerník na následníka teda bude mať hodnotu NULL.
Štruktúra spájaného zoznamu je znázornená na nasledujúcom obrázku:
Keďže si v každom uzle pamätáme iba smerník na následníka (t.j. uzol „napravo” od daného uzla), hovoríme tiež o jednosmerne spájanom zozname. Často sú užitočné aj obojsmerne spájané zoznamy, kde sa v každom uzle uchováva aj smerník na predchodcu; takéto zoznamy sú ale o niečo náročnejšie na „údržbu”.
Uzol jednosmerne spájaného zoznamu budeme reprezentovať pomocou struct-u node:
/* Struktura reprezentujuca uzol jednosmerne spajaneho zoznamu: */
struct node {
int data; // Hodnota ulozena v danom uzle
node *next; // Smernik na nasledujuci uzol
};
Vo vnútri definície typu node teda používame smerník na samotný typ node.
Na rozdiel od poľa, v ktorom je poradie stanovené indexmi, je poradie v spájanom zozname určované ukazovateľmi next. Ak x je uzol zoznamu, tak x.next je:
- Smerník na nasledujúci uzol zoznamu, ak takýto uzol existuje.
- NULL v opačnom prípade.
Samotný spájaný zoznam – resp. množina ním reprezentovaná – je potom iba štruktúra set obsahujúca smerník na prvý prvok zoznamu. Ak je zoznam prázdny, bude tento smerník NULL. V štruktúre set by sme v prípade potreby mohli uchovávať aj iné údaje, ako napríklad počet prvkov v zozname a podobne.
/* Struktura realizujuca mnozinu prostrednictvom spajaneho zoznamu: */
struct set {
node *first; // Smernik na prvy uzol zoznamu
};
void init(set &s) {
s.first = NULL;
}
Vkladanie na začiatok zoznamu
Nasledujúca funkcia na začiatok zoznamu vloží nový uzol s dátami x:
void add(set &s, int x) {
node *p = new node; // Vytvoríme nový uzol ...
p->data = x; // ... jeho data nastavíme na x.
p->next = s.first; // ... jeho nasledníkom bude doposiaľ prvý prvok zoznamu
s.first = p; // ... a uzol p bude novým prvým prvkom
}
Vyhľadávanie v zozname
Funkcia vyhľadávajúca číslo x v zozname bude pracovať tak, že postupne prehľadáva zoznam od jeho začiatku, s využitím smerníkov na nasledujúce prvky:
bool contains(set &s, int x) {
node *p = s.first;
while (p != NULL) {
if (p->data == x) {
return true;
}
p = p->next;
}
return false;
}
Uvoľnenie zoznamu
Funkcia realizujúca uvoľnenie zoznamu z pamäti pracuje podobne: prechádza postupne zoznam od začiatku až po jeho koniec a uvoľňuje z pamäte jednotlivé uzly. Treba si tu však dať pozor na to, aby sme smerník na nasledujúci uzol získali ešte predtým, než z pamäti uvoľníme ten predošlý.
void destroy(set &s) {
node *p = s.first;
while (p != NULL) {
node *p2 = p->next;
delete p;
p = p2;
}
}
Výpis zoznamu
Môžeme napísať aj nasledujúcu funkciu, ktorá po zavolaní vypíše obsah celého zoznamu:
void print(set &s) {
node *p = s.first;
while (p != NULL) {
cout << p->data << " ";
p = p->next;
}
cout << endl;
}
Hešovanie
Implementácia množiny priamym adresovaním
Úplne odlišným spôsobom implementácie dynamickej množiny je tzv. priame adresovanie (angl. direct addressing).
- Množinu všetkých možných hodnôt, ktoré v danej implementácii môžeme chcieť do množiny pridať, nazveme univerzum U
- Predchádzajúce implementácie sa ľahko dali upraviť na rôzne univerzá (celé čísla, desatinné čísla, smerníky na zložitejšie štruktúry, napr. struct, pole, reťazec)
- Na rozdiel od toho sa priame adresovanie dá použiť iba ak univerzum je U = {0,1,...,m-1} pre nejaké rozumne malé prirodzené číslo m
- Podmnožinu A univerza U potom môžeme reprezentovať ako pole booleovských hodnôt dĺžky m, kde i-ty prvok poľa bude true práve vtedy, keď i patrí do A.
- Túto reprezentáciu sme používali napríklad v poli bolo pri prehľadávaní s návratom.
- Funkcie contains aj add sú potom veľmi jednoduché a rýchle.
- Problémom tohto prístupu je ale vysoká pamäťová zložitosť, ak je číslo m veľké.
- Veľmi efektívne pre malé univerzá (napr. cifry 0,...,9, všetky znaky anglickej abecedy, všetky znaky s ASCII hodnotami od 0 po 255, a pod.).
#include <cassert>
// ...
const int m = 1000;
/* Struktura implementujuca mnozinu pomocou priameho adresovania: */
struct set {
bool *p;
};
void init(set &s) {
s.p = new bool[m];
for (int i = 0; i <= m - 1; i++) {
s.p[i] = false;
}
}
bool contains(set &s, int x) {
assert(x >= 0 && x <= m - 1);
return s.p[x];
}
void add(set &s, int x) {
assert(x >= 0 && x <= m - 1);
s.p[x] = true;
}
void destroy(set &s) {
delete[] s.p;
}
Jednoduché hašovanie
Priame adresovanie sa nehodí pre veľké univerzá, lebo by vyžadovalo veľa pamäte.
Hašovanie (angl. hashing) je jednoduchá finta, ktorá funguje nasledovne:
- Nech U je univerzum všetkých možných prvkov množiny.
- Vytvoríme hašovaciu tabuľku (angl. hash table), čo je pole nejakej rozumnej veľkosti m.
- Naprogramujeme hašovaciu funkciu, ktorá transformuje prvky univerza U na indexy hašovacej tabuľky; pôjde teda o funkciu h: U -> {0, 1, ... , m−1}.
- Najjednoduchšia hašovacia funkcia pre celočíselné prvky je h(x) = |x| mod m.
- |x| spočítame funkciou abs z knižnice cstdlib
- Absolútnu hodnotu používame, lebo napríklad -10 % 3 je -1, čo mimo rozsahu indexov tabuľky
- V praxi sa používajú zložitejšie hašovacie funkcie. Ideálne je hašovacia funkcia jednoduchá a rýchla, ale pritom by mal hodnoty do tabuľky distribuovať rovnomerne, aby sa príliš často nestávalo, že dva prvky sa namapujú na to isté políčko
int hash(int x, int m) {
return abs(x) % m;
}
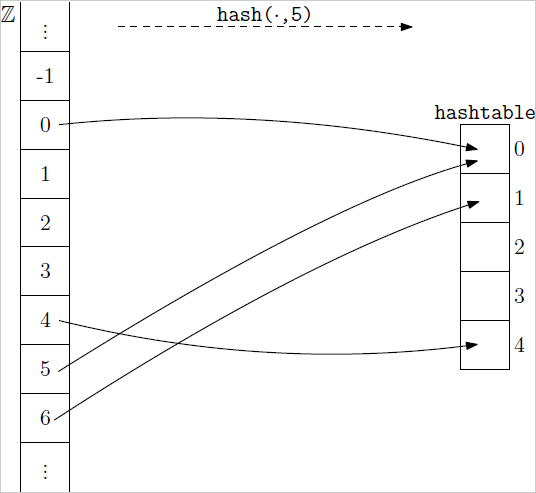
Pre m = 5 je táto funkcia znázornená na nasledujúcom obrázku.
Prvý pokus o prácu hašovacou tabuľkou by teda mohol vyzerať takto:
Vkladanie prvku x:
- Spočítame index = hash(x, m) a prvok vložíme na pozíciu hashtable[index].
Vyhľadávanie prvku x:
- Ak je prvok s kľúčom x v tabuľke, musí byť na indexe hash(x, m).
- Skontrolujeme túto pozíciu a ak tam je niečo iné ako x, prvok x sa v tabuľke nenachádza.
Problémy:
- Na akú hodnotu inicializovať prvky poľa hashtable?
- Čo ak budeme potrebovať vložiť prvok na miesto, kde je už niečo uložené?
Kolízie
- Pri vkladaní prvku sme narazili na problém, ak na už obsadené miesto chceme vložiť iný prvok.
- Ak sa dva prvky x a y sa zahašujú na rovnakú pozíciu h(x) = h(y), hovoríme, že nastala kolízia
- Existuje niekoľko metód na riešenie kolízií.
- Existujú rôzne prístupy na riešenie kolízií, môžeme napríklad hľadať iné voľné miesto v tabuľke.
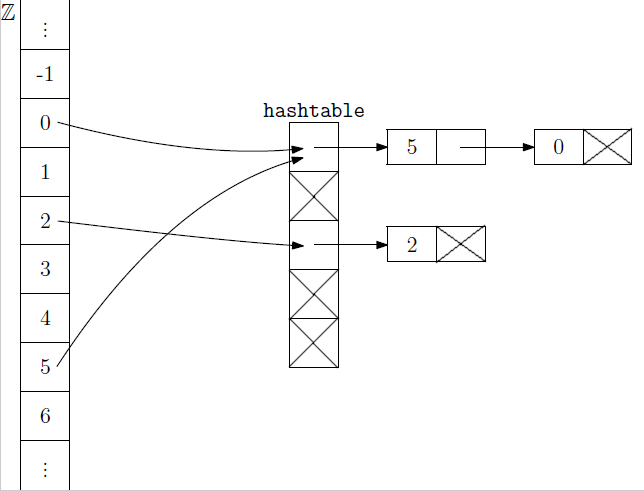
- V našom programe kolízie vyriešime tak, že v každom políčku tabuľky uložíme spájaný zoznam všetkých prvkov, ktoré sa tam zahašovali.
- Táto situácia je znázornená na nasledujúcom obrázku, v ktorom šípky zodpovedajú vkladaniam prvkov (celých čísel) do množiny reprezentovanej hašovacou tabuľkou.
#include <cstdlib>
/* Hasovacia funkcia: */
int h(int x, int m) {
return abs(x) % m;
}
/* Struktura reprezentujuca jeden prvok spajaneho zoznamu: */
struct node {
int data;
node *next;
};
/* Struktura implementujuca dynamicku mnozinu pomocou hasovania: */
struct set {
node **hashtable; // Pole smernikov na zaciatky jednotlivych zoznamov
int m; // Velkost hasovacej tabulky
};
void init(set &s, int m) { // Velkost tabulky bude parametrom funkcie init
s.m = m;
s.hashtable = new node *[m];
for (int i = 0; i < m; i++) {
s.hashtable[i] = NULL;
}
}
bool contains(set &s, int x) {
int index = h(x, s.m); // Spocitame spravne policko hasovacej tabulky
node *p = s.hashtable[index]; // Smernik p ukazuje na prvy prvok spajaneho
// zoznamu na danom policku
while (p != NULL) { // Prechadzame zoznam, hladame x
if (p->data == x) {
return true;
}
p = p->next;
}
return false;
}
void add(set &s, int x) {
int index = h(x, s.m); // Spocitame spravne policko hasovacej tabulky
node *temp = new node; // Vytvorime novy uzol do spajaneho zoznamu
temp->data = x;
temp->next = s.hashtable[index]; // Vlozime uzol temp na zaciatok zoznamu.
s.hashtable[index] = temp;
}
void destroy(set &s) {
for (int i = 0; i < s.m; i++) {
node *p = s.hashtable[i]; // Uvolni zoznam s.hashtable[i]
while (p != NULL) {
node *p2 = p->next;
delete p;
p = p2;
}
}
delete[] s.hashtable;
}
Cvičenie: Ako bude vyzerať hašovacia tabuľka pri riešení kolízií pomocou spájaných zoznamov, ak hašovacia funkcia je |x| mod 5 a vkladáme prvky 13, -2, 0, 8, 10, 17?
Zložitosť
- Rýchlosť závisí od veľkosti tabuľky m, hašovacej funkcie a počtu kolízií.
- V najhoršom prípade sa všetky prvky zahašujú do toho istého políčka, a teda musíme pri hľadaní prejsť všetky prvky množiny.
- Ak máme šťastie a v každom políčku máme len málo prvkov, bude aj vyhľadávanie rýchle.
- Ak je tabuľka dosť veľká a hašovacia funkcia vhodne zvolená, tento prípad je pomerne obvyklý.
- Hašovacie tabuľky sa často používajú v praxi.
- Viac budúci rok na predmete Algoritmy a dátové štruktúry.