Prednáška 22

Oznamy

Plán prednášok a cvičení na zvyšok semestra:

• Dnes pokračujeme stromy.
• V utorok 14.12. v rámci cvičení tréning na skúšku.
  • Na testovači už sú tréningové príklady na skúšku. Za niektoré budete môcť získať bonusový bod, ak ich vyriešite do 12.1. (ako tréning sa dajú riešiť aj neskôr). V utorok na cvičeniach pribudne ešte jeden tréningový príklad za 4 body. Ak prídete na cvičenia a odovzdáte na konci aspoň rozumne rozrobenú verziu programu, získate jeden bonusový bod, aj keď ho nestihnete dokončiť.
• V stredu 15.12. ak treba dokončíme stromy, potom nepovinná prednáška o nepreberaných črtách jazykov C a C++ (táto nepovinná časť učiva nebude vyžadovaná na skúške, ale môžete ju použiť).
• V piatok 17.12. od 12:00 predtermín skúšky, doplnkové cvičenia nebudú

Binárne vyhľadávacie stromy

Opakovanie

Príklad binárneho vyhľadávacieho stromu.

Binárny vyhľadávací strom (binary search tree) je dátová štruktúra určená na ukladanie dynamickej množiny prvkov.

• V binárnom vyhľadávacom strome má každý vrchol 0, 1 alebo 2 deti
• V každom vrchole máme položku s dátami (pre jednoduchosť typu int)
• Pre každý vrchol v stromu platí:
  • Každý vrchol v ľavom podstrome v má hodnotu data menšiu ako vrchol v
  • Každý vrchol v pravom podstrome v má hodnotu data väčšiu ako vrchol v

struct node {
    /* vrchol binárneho vyhľadávacieho stromu  */
    int data;       /* hodnota */
    node * parent;  /* rodič vrchola, NULL v koreni */
    node * left;    /* ľavé dieťa, NULL ak neexistuje */
    node * right;   /* pravé dieťa, NULL ak neexistuje */
};

/* Samotná štruktúra binárneho vyhľadávacieho stromu (obal pre používateľa). */
struct binarySearchTree {
    node *root;  /* koreň stromu, NULL pre prázdny strom */
};

Videli sme vyhľadávanie prvku v binárnom vyhľadávacom strome. Čas výpočtu je v najhoršom prípade úmerný výške stromu.

Vkladanie do binárneho vyhľadávacieho stromu

Nasledujúca funkcia insertNode vloží uzol *v na správne miesto podstromu zakoreneného v *root ako jeho list.

• Predpokladáme, že prvok v strome nie je.
• Putujeme po strome podobne ako pri vyhľadávaní prvku, až kým nenarazíme na nulový smerník.
  • Na tomto mieste by mal byť nový prvok, takže ho tam pridáme ako nový list
  • Uvádzame rekurzívnu verziu, dá sa aj cyklom, podobne ako pri hľadaní
• Funkcia bstInsert vytvorí uzol s daným kľúčom key a pomocou funkcie insertNode ho vloží do binárneho vyhľadávacieho stromu t.

/* Vloží uzol v na správne miesto podstromu zakoreneného v root */
void insertNode(node *root, node *v) {
    assert(root != NULL && v != NULL);
    if (v->data < root->data) {
        if (root->left == NULL) {
            root->left = v;
            v->parent = root;
        } else {
            insertNode(root->left, v);
        }
    } else {
        if (root->right == NULL) {
            root->right = v;
            v->parent = root;
        } else {
            insertNode(root->right, v);
        }
    }
}

/* Vloží do stromu t nový uzol s kľúčom key. */
void bstInsert(binarySearchTree &t, int key) {
    node *v = new node;
    v->data = key;
    v->left = NULL;
    v->right = NULL;
    v->parent = NULL;
    if (t.root == NULL) {
        t.root = v;
    } else {
        insertNode(t.root, v);
    }
}

Čas vkladania je tiež v najhoršom prípade úmerný hĺbke stromu.

Cvičenia

• Napíšte nerekurzívny variant funkcie insertNode.
• Napíšte funkciu treeSort, ktorá z poľa celých čísel a pomocou volaní funkcie bstInsert vytvorí binárny vyhľadávací strom a následne pomocou prehľadávania tohto stromu v poradí inorder pole a utriedi.
• Ako bude vyzerať strom po nasledujúcej postupnosti operácií?

    binarySearchTree t;
    bstInit(t);
    bstInsert(t, 2);
    bstInsert(t, 5);
    bstInsert(t, 3);
    bstInsert(t, 10);
    bstInsert(t, 7);  

Minimálny uzol

Nasledujúca funkcia minNode nájde v podstrome zakorenenom v root uzol s minimálnym kľúčom. Je pritom založená na skutočnosti, že všetky uzly tohto podstromu s kľúčom menším ako root->data sa musia nachádzať v ľavom podstrome uzla root.

Obalom pre používateľa bude funkcia bstMin, ktorá pomocou funkcie minNode nájde minimálny kľúč v danom binárnom vyhľadávacom strome t.

/* Vrati uzol s minimalnou hodnotou key v podstrome s korenom *root. */
node *minNode(node *root) {
    assert(root != NULL);
    if (root->left != NULL) {
        return minNode(root->left);
    } else {
        return root;
    }
}

/* Vrati minimalny kluc uzla v strome t. */
int bstMin(binarySearchTree &t) {
    assert(t.root != NULL);
    return minNode(t.root)->data; 
}

Cvičenie: napíšte nerekurzívny variant funkcie minNode.

Následník uzla

Funkcia successorNode nájde pre daný uzol v jeho následníka (angl. successor) v binárnom vyhľadávacom strome, čiže uzol, ktorý vo vzostupnom poradí podľa kľúčov nasleduje bezprostredne za uzlom v. Je pritom založená na nasledujúcich pozorovaniach:

• Ak má uzol v pravého syna, následník uzla v musí byť v jeho pravom podstrome – konkrétne pôjde o minimálny uzol z tohto podstromu.
• V opačnom prípade môže byť následníkom uzla *v jeho otec (ak *v je jeho ľavý syn). Ak je *v pravým synom svojho otca, môže to byť aj jeho starý otec (ak je otec uzla *v ľavým synom tohto starého otca), atď. Vo všeobecnosti teda ide o najbližšieho predka uzla *v takého, že *v patrí do jeho ľavého podstromu.
• V strome existuje práve jeden uzol bez následníka (jeden spomedzi najväčších prvkov).

/* Vrati uzol, ktory vo vzostupnom poradi uzlov podla klucov nasleduje za *v. Ak taky uzol neexistuje, vrati NULL. */
node *successorNode(node *v) {
    assert(v != NULL);
    if (v->right != NULL) {
        return minNode(v->right);
    }
    while (v->parent != NULL && v == v->parent->right) {
        v = v->parent;
    }
    return v->parent;
}

Mazanie z binárneho vyhľadávacieho stromu

Nasledujúca funkcia bstRemove zmaže z binárneho vyhľadávacieho stromu t práve jeden uzol s kľúčom key (ak sa taký uzol v strome vyskytuje). Pracuje tak, že najprv pomocou funkcie findNode nájde uzol *v s kľúčom key. V prípade úspechu zistí počet synov uzla *v. Ak totiž *v nemá žiadneho syna alebo má len jedného syna, možno ho zo stromu t zmazať jednoducho tak, že sa prípadný syn uzla *v stane synom otca uzla *v. V prípade, že má *v dvoch synov je však zrejmé, že jeho následník sa musí nachádzať v jeho neprázdnom pravom podstrome. Tento následník *rm navyše nemôže mať ľavého syna. Odstránenie kľúča key je teda možné realizovať tak, že sa kľúč uzla *rm presunie do uzla *v a následne sa odstráni uzol *rm tak, ako je popísané vyššie.

/* Zmaze zo stromu t prave jeden uzol s klucom key (ak tam taky je). */
void bstRemove(binarySearchTree &t, int key) {
    node *v = findNode(t.root, key);                   // Najde uzol v s hodnotou, ktoru treba vymazat.
    if (v == NULL) {
        return;
    }
    
    node *rm;                                          // Najde uzol *rm stromu t, ktory sa napokon realne zmaze.   
    if (v->left == NULL || v->right == NULL) {         
        rm = v;
    } else  {
        rm = successorNode(v);
    }
   
    if (rm != v) {                                     // Ak rm != v, presunie kluc uzla *rm do uzla *v. 
        v->data = rm->data;
    }
    
    node *child;                                       // Zmaze uzol *rm a uvolni pamat alokovanu pre tento uzol.
    if (rm->left != NULL) {
        child = rm->left;
    } else {
        child = rm->right;
    }                   
    if (child != NULL) {
        child->parent = rm->parent;
    }
    if (rm->parent == NULL) {
        t.root = child;
    } else if (rm == rm->parent->left) {
        rm->parent->left = child;    
    } else if (rm == rm->parent->right) {
        rm->parent->right = child;
    }
    delete rm;
}

Zložitosť jednotlivých operácií

• Časová zložitosť operácií bstFind(t), bstInsert(t) aj bstRemove(t) je úmerná hodnote height(t), čo je výška stromu t.
• Minule sme ukázali, že pre výšku h stromu s n vrcholmi je log₂(n+1)-1 ≤ h ≤ n-1.
• Zložitosť uvedených operácií je teda v najhoršom prípade lineárna od počtu uzlov stromu (tento prípad nastane, ak prvky vkladáme od najmenšieho po najväčší alebo naopak).
• Dá sa však ukázať, že v priemernom prípade je ich zložitosť rádovo logaritmická od počtu uzlov.
• Na predmete Algoritmy a dátové štruktúry (druhý ročník) sa tieto tvrdenia dokazujú poriadne a preberajú sa tam aj varianty vyhľadávacích stromov, pre ktoré je zložitosť uvedených operácií logaritmická aj v najhoršom prípade.

Zložitosť operácií na prácu s binárnymi vyhľadávacími stromami

• Časová zložitosť operácií bstFind(t), bstInsert(t) aj bstRemove(t) je úmerná hodnote height(t), čo je výška stromu t.
• Predminule sme ukázali, že pre výšku h stromu s n vrcholmi je log₂(n+1)-1 ≤ h ≤ n-1.
• Zložitosť uvedených operácií je teda v najhoršom prípade lineárna od počtu uzlov stromu (tento prípad nastane, ak prvky vkladáme od najmenšieho po najväčší alebo naopak).
• Dá sa však ukázať, že v priemernom prípade je ich zložitosť rádovo logaritmická od počtu uzlov.
• Na predmete Algoritmy a dátové štruktúry (druhý ročník) sa tieto tvrdenia dokazujú poriadne a preberajú sa tam aj varianty vyhľadávacích stromov, pre ktoré je zložitosť uvedených operácií logaritmická aj v najhoršom prípade.

Lexikografické stromy

Lexikografický strom reprezentujúci množinu reťazcov a, aj, ale, aleba, alebo, cez, na, nad.

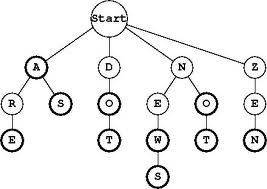
Lexikografické stromy (niekde tiež prefixové stromy; angl. trie zo slova retrieval) sú dátová štruktúra na uchovávanie množiny reťazcov. Ide o stromy, ktoré nemusia byť binárne:

• Každý uzol lexikografického stromu má najviac toľko synov, koľko je písmen v uvažovanej abecede. Každý zo synov zodpovedá práve jednému písmenu abecedy a každému písmenu abecedy zodpovedá najviac jeden syn daného uzla. Graficky možno písmená zodpovedajúce jednotlivým synom znázorniť ohodnotením hrán spájajúcich dané uzly.
• Koreň lexikografického stromu zodpovedá prázdnemu reťazcu.
• Uzol v hĺbke k zodpovedá reťazcu dĺžky k, ktorý dostaneme prečítaním písmen na ceste z koreňa do daného uzla.
• Každý uzol lexikografického stromu obsahuje informáciu (true alebo false) o tom, či k nemu prislúchajúci reťazec patrí do množiny reprezentovanej týmto lexikografickým stromom alebo nie.
• V korektnom lexikografickom strome všetky listy zodpovedajú reťazcom z reprezentovanej množiny; niektoré reťazce reprezentovanej množiny však môžu zodpovedať aj vnútorným vrcholom stromu. Každý uzol lexikografického stromu tak zodpovedá nejakému prefixu slova z ním reprezentovanej množiny – odtiaľ alternatívne pomenovanie prefixový strom.

Štruktúra node pre uzol lexikografického stromu tak obsahuje booleovskú premennú isWord, v ktorej je uložená informácia o tom, či reťazec prislúchajúci k danému uzlu patrí alebo nepatrí do reprezentovanej množiny a pole children smerníkov na jednotlivých synov daného uzla. Veľkosť alphSize tohto poľa je rovná veľkosti uvažovanej abecedy – pre písmená malej anglickej abecedy je táto hodnota rovná 'z' - 'a' + 1.

Pri rôznych praktických aplikáciách môže štruktúra node obsahovať aj rozličné ďalšie informácie – pre každé slovo z reprezentovanej množiny si napríklad môžeme pamätať jeho frekvenciu výskytu, preklad do nejakého iného jazyka a podobne.

const int alphSize = 'z' - 'a' + 1;

struct node {
    node *children[alphSize]; // pole smernikov na deti
    bool isWord;              // udava, ci uzol prislucha k slovu z reprezentovanej mnoziny
    // dalsie data (napriklad preklad slova, pocet vyskytov slova v texte, ...)
};

Samotný lexikografický strom je potom daný iba smerníkom na svoj koreň:

struct trie {
    node *root;      
};

Inicializácia lexikografického stromu

Nasledujúca funkcia inicializuje prázdny lexikografický strom t:

void trieInit(trie &t) {
    t.root = NULL; 
}

Likvidácia lexikografického stromu

Uvoľnenie pamäte alokovanej pre podstrom zakorenený v uzle root realizujeme obdobne ako pri binárnych vyhľadávacích stromoch. Jediný rozdiel spočíva v potenciálne väčšom počte synov uzla root.

void destroySubtree(node *root) {
    if (root != NULL) {
        for (int i = 0; i <= alphSize - 1; i++) {
            destroySubtree(root->children[i]);
        }
        delete root;
    }
}

Nasledujúca funkcia potom zlikviduje celý lexikografický strom t:

void trieDestroy(trie &t) {
    destroySubtree(t.root);
}

Vkladanie do lexikografického stromu

Pri vkladaní reťazca do množiny realizovanej lexikografickým stromom často vznikne potreba vytvárať nové uzly tohto stromu. Túto podúlohu realizuje funkcia createNode, ktorá vytvorí nový uzol s hodnotou isWord danou jej argumentom a so všetkými smerníkmi na synov rovnými NULL.

node *createNode(bool isWord) {
    node *v = new node;
    for (int i = 0; i <= alphSize - 1; i++) {
        v->children[i] = NULL;
    }
    v->isWord = isWord;
    return v;
}

Vloženie reťazca word do lexikografického stromu t potom realizuje funkcia trieInsert, ktorá pracuje nasledovne:

• Začne v koreni stromu, odkiaľ postupuje nižšie smerom k listom.
• V každom uzle sa pozrie na ďalšie písmeno slova word. Ak danému uzlu chýba syn pre toto písmeno, vytvorí ho pomocou funkcie createNode. Následne sa presunie do tohto syna.
• Ak v nejakom uzle v príde na koniec slova word, nastaví hodnotu v->isWord na true.

void trieInsert(trie &t, const char *word) {
    if (t.root == NULL) {
        t.root = createNode(false);
    }
    node *v = t.root;
    for (int i = 0; word[i] != 0; i++) {
        int c = word[i] - 'a';
        if (v->children[c] == NULL) {
            v->children[c] = createNode(false);
        }
        v = v->children[c];
    }
    v->isWord = true;
}

Hľadanie v lexikografickom strome

Funkcia trieFind pre daný lexikografický strom t a reťazec word zistí, či slovo word patrí do množiny reprezentovanej stromom t. Opäť pritom postupuje po písmenách reťazca word. Kým nedôjde na koniec slova, snaží sa ísť po hranách, ktoré zodpovedajú jednotlivým písmenám. V prípade, že v niektorom bode narazí na NULL, slovo word sa v strome nenachádza. V opačnom prípade toto slovo dočíta v nejakom uzle v. V takom prípade slovo word patrí do reprezentovanej množiny práve vtedy, keď v->isWord má hodnotu true.

bool trieFind(trie &t, const char *word) {
    node *v = t.root;
    if (v == NULL) {
        return false;
    }
    for (int i = 0; word[i] != 0; i++) {
        v = v->children[word[i] - 'a'];
        if (v == NULL) {
            return false;
        }
    }
    return v->isWord;
}

Vymazávanie z lexikografického stromu

Vymazávanie slov z množiny reprezentovanej lexikografickým stromom budeme realizovať prostredníctvom pomocnej rekurzívnej funkcie removeFromSubtree, ktorá z podstromu zakorenenom v uzle *root vymaže sufix reťazca word začínajúci na pozícii index. Táto funkcia vráti na výstupe booleovskú hodnotu podľa toho, či sa pri tomto vymazaní sufixu z daného podstromu vymazal jeho koreň *root (táto situácia nenastane vždy: napríklad pri mazaní slova a z podstromu reprezentujúceho množinu slov {a,ab} uzol prislúchajúci k reťazcu a v strome ostáva; zmení sa len jeho hodnota isWord).

Ak sa slovo word v reprezentovanej množine nenachádza, funkcia removeFromSubtree vyhlási chybu pomocou funkcie assert.

Funkcia removeFromSubtree pracuje nasledovne:

• Ak je sufix reťazca word začínajúci na indexe index prázdny, nastaví hodnotu root->isWord na false.
• V opačnom prípade funkcia removeFromSubtree zavolá rekurzívne samú seba pre syna zodpovedajúceho písmenu na pozícii index reťazca word. Ak toto volanie daného syna zmaže, prestaví smerník na tohto syna na NULL.
• V prípade, že po vykonaní jednej z predchádzajúcich dvoch operácií nemá uzol root žiadneho syna a súčasne má root->isWord hodnotu false, uvoľní pamäť alokovanú pre uzol root a informáciu o jeho zmazaní vráti na výstupe.

bool removeFromSubtree(node *root, const char *word, int index) {
    assert(root != NULL);
    if (word[index] == 0) {
        assert(root->isWord);
        root->isWord = false;
    } else {
        int c = word[index] - 'a';
        bool deleted = removeFromSubtree(root->children[c], word, index + 1);
        if (deleted) {          
            root->children[c] = NULL;
        }
    }
    int numChildren = 0;                        
    for (int i = 0; i <= alphSize - 1; i++) {
        if (root->children[i] != NULL) {
            numChildren++;
        }
    }
    if (numChildren == 0 && !root->isWord) {
        delete root;
        return true;
    }
    return false;
}

Samotné odstránenie reťazca word z množiny reprezentovanej stromom t potom realizuje nasledujúca funkcia trieRemove. Tá len zavolá funkciu removeFromSubtree pre koreň stromu t a v prípade, že volanie tejto funkcie koreň zo stromu odstráni, nastaví t.root na NULL.

void trieRemove(trie &t, const char *word) {
    bool rootRemoved = removeFromSubtree(t.root, word, 0);
    if (rootRemoved) {
        t.root = NULL;
    }
}

Výška lexikografického stromu

Nasledujúca funkcia vypočíta výšku podstromu zakoreneného v uzle *root (definovaná je rovnako ako pre binárne stromy):

int subtreeHeight(node *root) {
    if (root == NULL) {
        return -1;
    }
    int maxHeight = -1;
    for (int i = 0; i <= alphSize - 1; i++) {
        int height = subtreeHeight(root->children[i]);
        if (height > maxHeight) {
            maxHeight = height;
        }
    }
    return maxHeight + 1;
}

Výšku samotného lexikografického stromu t potom spočíta nasledujúca funkcia:

int trieHeight(trie &t) {
    return subtreeHeight(t.root);
}

Vypisovanie slov reprezentovaných lexikografickým stromom

Nasledujúca funkcia printSubtree prehľadáva podstrom zakorenený v uzle *root a v reťazci s postupne generuje všetky slová z reprezentovanej množiny, ktoré zároveň vypisuje na konzolu.

void printSubtree(node *root, char *s, int index) {
    if (root == NULL) {
        return;
    }
    if (root->isWord) {
        s[index] = 0;
        printf("%s\n", s);
    }
    for (int i = 0; i <= alphSize - 1; i++) {
        s[index] = 'a' + i;
        printSubtree(root->children[i], s, index + 1);
    }
}

Funkcia triePrint vypisujúca všetky slová v množine reprezentovanej lexikografickým stromom t najprv spočíta výšku stromu t, ktorá je rovná dĺžke najdlšieho reťazca tejto množiny. Následne dynamicky alokuje reťazec dostatočnej dĺžky na uchovanie každého slova množiny a zavolá funkciu printSubtree pre koreň stromu t.

void triePrint(trie &t) {
    int height = trieHeight(t);
    if (height >= 0) { 
        char *s = new char[height + 1];
        printSubtree(t.root, s, 0);
        delete[] s;
    }
}

Program pracujúci s lexikografickými stromami

Nasledujúci program načítava z konzoly príkazy zodpovedajúce operáciám na lexikografickom strome a za každým načítaným príkazom túto operáciu vykonáva.

#include <cstdio>
#include <cassert>
#include <cstring>
using namespace std;


// ...


int main(void) {
    trie t;
    trieInit(t);
    char command[20];
    char arg[20];
    while (true) {
        scanf("%19s", command);
        if (strcmp(command, "insert") == 0) {
            scanf("%19s", arg);
            trieInsert(t, arg);
        }
        if (strcmp(command, "find") == 0) {
            scanf("%19s", arg);
            bool b = trieFind(t, arg);
            if (b) {
                printf("YES\n");
            } else {
                printf("NO\n");
            }
        }
        if (strcmp(command, "remove") == 0) {
            scanf("%19s", arg);
            trieRemove(t, arg);
        }
        if (strcmp(command, "height") == 0) {
            printf("%d\n", trieHeight(t));
        }
        if (strcmp(command, "print") == 0) {
            triePrint(t);
        }
        if (strcmp(command, "exit") == 0) {
            break;
        }
    }
    trieDestroy(t);
    return 0;
}

Sylaby predmetu

Základy

Konštrukcie jazyka C

• premenné typov int, double, char, bool, konverzie medzi nimi
• podmienky (if, else, switch), cykly (for, while)
• funkcie (a parametre funkcií - odovzdávanie hodnotou, referenciou, smerníkom)

void f1(int x){}                                 //hodnotou
void f2(int &x){}                                //referenciou
void f3(int* x){}                                //smerníkom
void f(int a[], int n){}                         //polia bez & (ostanú zmeny)
void kresli(Turtle &t){}                         //korytnačky, SVGdraw a pod. s &

Polia, reťazce (char[])

int A[4]={3, 6, 8, 10}; 
int B[4];               
B[0]=3; B[1]=6; B[2]=8; B[3]=10;

char C[100] = "pes";
char D[100] = {'p', 'e', 's', 0};

• funkcie strlen, strcpy, strcmp, strcat

Súbory, spracovanie vstupu

• cin, cout alebo printf, scanf
• fopen, fclose, feof
• fprintf, fscanf
• getc, putc, ungetc, fgets, fputs
• spracovanie súboru po znakoch, po riadkoch, po číslach alebo slovách

Smerníky, dynamicky alokovaná pamäť, dvojrozmerné polia

int i;    // „klasická“ celočíselná premenná
int *p;   // ukazovateľ na celočíselnú premennú

p = &i;         // spravne
p = &(i + 3);   // zle i+3 nie je premenna
p = &15;        // zle konstanta nema adresu
i = *p;         // spravne ak p bol inicializovany

int * cislo = new int;  // alokovanie jednej premennej
*cislo = 50;
..
delete cislo;

int a[4];
int *b = a;  // a,b su teraz takmer rovnocenne premenne 

int *A = new int[n]; // alokovanie 1D pola danej dlzky
..
delete[] A;

int **a;       // alokovanie 2D matice
a = new int *[n];
for (int i = 0; i < n; i++) a[i] = new int[m];
..
for (int i = 0; i < n; i++) delete[] a[i];
delete[] a;

Abstraktné dátové typy

Abstraktný dátový typ dynamické pole (rastúce pole)

• operácie init, add, get, set, length

Abstraktný dátový typ dynamická množina (set)

• operácie init, find, insert, remove
• implementácie pomocou
  • neutriedeného poľa
  • utriedeného poľa
  • spájaných zoznamov
  • binárnych vyhľadávacích stromov
  • hašovacej tabuľky
  • lexikografického stromu (ak kľúč je reťazec)

Abstraktné dátové typy rad a zásobník

• operácie pre rad (frontu, queue): init, isEmpty, enqueue, dequeue, peek
• operácie pre zásobník (stack): init, isEmpty, push, pop
• implementácie: v poli alebo v spájanom zozname
• využitie: ukladanie dát na spracovanie, odstránenie rekurzie
• kontrola zátvoriek a vyhodnocovanie výrazov pomocou zásobníka

Dátové štruktúry

Spájané zoznamy

struct node {
    int data;
    item* next;
};
struct linkedList {
    item* first;
};
void insertFirst(linkedList &z, int d){
    /* do zoznamu z vlozi na zaciatok novy prvok s datami d */
    item* p = new item;   // vytvoríme nový prvok
    p->data = d;          // naplníme dáta
    p->next = z.first;    // prvok bude prvým prvkom zoznamu (ukazuje na doterajší začiatok)
    z.first = p;          // tento prvok je novým začiatkom
}

Strom pre výraz (65 – 3*5)/(2 + 3)

Binárne stromy

struct node {
    /* vrchol stromu  */
    dataType data;
    node * left;  /* lavy syn */
    node * right; /* pravy syn */
};

node * createNode(dataType data, node *left, node *right) {
    node *v = new node;
    v->data = data;
    v->left = left;
    v->right = right;
    return v;
}

• prehľadávanie inorder, preorder, postorder
• použitie na uloženie aritmetických výrazov

Binárne vyhľadávacie stromy

• vrcholy vľavo od koreňa menší kľúč, vpravo od koreňa väčší
• insert, find, remove v čase závisiacom od hĺbky stromu

Lexikografické stromy

• ukladajú množinu reťazcov
• nie sú binárne: vrchol môže mať veľa synov
• insert, find, remove v čase závisiacom od dĺžky kľúča, ale nie od počtu kľúčov, ktoré už sú v strome

struct node {
    /* vrchol lexikografickeho stromu  */
    char data; // pismeno ulozene v tomto vrchole
    bool isWord; // je tento vrchol koncom slova?
    node* next[Abeceda]; // pole smernikov na deti    
};

Hašovanie

• hašovacia tabuľka veľkosti m
• kľúč k premietneme nejakou funkciou na index v poli (0,...,m-1}
• každé políčko hašovacej tabuľky spájaný zoznam prvkov, ktoré sa tam zahašovali
• v ideálnom prípade sa prvky rozhodia pomerne rovnomerne, zoznamy krátke, rýchle hľadanie, vkladenie, mazanie
• v najhoršom prípade všetky prvky v jednom zozname, pomalé hľadanie a mazanie

int hash(int k, int m){ // veľmi jednoduchá hašovacia funkcia, v praxi väčšinou zložitejšie
    return abs(k) % m;
}
struct node {
    int item;
    node* next;
};

struct set {
    node** data;
    int m;
};

Algoritmy

Rekurzia

• Rekurzívne funkcie
• Vykresľovanie fraktálov
• Prehľadávanie s návratom (backtracking)
• Vyfarbovanie
• Prehľadávanie stromov

Triedenia

• nerekurzívne: Bubblesort, Selectionsort, Insertsort
• rekurzívne: Mergesort, Quicksort
• súvisiace algoritmy: binárne vyhľadávanie

Matematické úlohy

• Euklidov algoritmus, Eratostenovo sito
• Práca s aritmetickými výrazmi: vyhodnocovanie postfixovej formy, prevod z infixovej do postfixovej, reprezentácia vo forme stromu