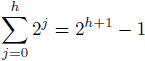Programovanie (1) v C/C++
1-INF-127, ZS 2024/25
Prednáška 20: Rozdiel medzi revíziami
| (8 medziľahlých úprav od 2 ďalších používateľov nie je zobrazených) | |||
| Riadok 36: | Riadok 36: | ||
* Decembrový termín odporúčame hlavne študentom, ktorým programovanie nerobí problémy. | * Decembrový termín odporúčame hlavne študentom, ktorým programovanie nerobí problémy. | ||
* Viac informácií o skúške je na stránke [[Zimný semester, skúška]], spolu cez to prejdeme budúcu stredu. | * Viac informácií o skúške je na stránke [[Zimný semester, skúška]], spolu cez to prejdeme budúcu stredu. | ||
| − | * Na | + | * Na testovači dnes po prednáške pribudne zopár tréningových príkladov na skúšku, všetky sa týkajú už prebraného učiva. Ďalšie dva tréningové príklady pridáme neskôr. |
==Opakovanie z minulej prednášky== | ==Opakovanie z minulej prednášky== | ||
| Riadok 200: | Riadok 200: | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | void printInorder( | + | /** Funkcia vypíše aritmetický výraz v inorder poradí */ |
| + | void printInorder(treeNode * root) { | ||
if (root->op == ' ') { | if (root->op == ' ') { | ||
| − | + | printf("%g", root->val); | |
} else { | } else { | ||
| − | + | printf("("); | |
| − | printInorder( | + | printInorder(root->left); |
| − | + | printf(" %c ", root->op); | |
| − | printInorder( | + | printInorder(root->right); |
| − | + | printf(")"); | |
} | } | ||
} | } | ||
| − | |||
| − | + | /** Funkcia vypíše aritmetický výraz v preorder poradí */ | |
| − | void printPreorder( | + | void printPreorder(treeNode * root) { |
if (root->op == ' ') { | if (root->op == ' ') { | ||
| − | + | printf("%g ", root->val); | |
} else { | } else { | ||
| − | + | printf("%c ", root->op); | |
| − | printPreorder( | + | printPreorder(root->left); |
| − | printPreorder( | + | printPreorder(root->right); |
} | } | ||
} | } | ||
| − | |||
| − | + | /** Funkcia vypíše aritmetický výraz v postorder poradí */ | |
| − | void printPostorder( | + | void printPostorder(treeNode * root) { |
if (root->op == ' ') { | if (root->op == ' ') { | ||
| − | + | printf("%g ", root->val); | |
} else { | } else { | ||
| − | printPostorder( | + | printPostorder(root->left); |
| − | printPostorder( | + | printPostorder(root->right); |
| − | + | printf("%c ", root->op); | |
} | } | ||
} | } | ||
| Riadok 371: | Riadok 370: | ||
* Ak je strom neprázdny, jeden jeho vrchol nazývame ''koreň'' (angl. root) | * Ak je strom neprázdny, jeden jeho vrchol nazývame ''koreň'' (angl. root) | ||
* Každý uzol ''u'' okrem koreňa je spojený hranou s práve jedným ''rodičom'' (angl. ''parent''), ktorým je nejaký uzol ''v''. Naopak uzol ''u'' je ''dieťaťom'' (angl. ''child'') uzla ''v''. | * Každý uzol ''u'' okrem koreňa je spojený hranou s práve jedným ''rodičom'' (angl. ''parent''), ktorým je nejaký uzol ''v''. Naopak uzol ''u'' je ''dieťaťom'' (angl. ''child'') uzla ''v''. | ||
| − | * Vo všeobecnom strome môže mať každý uzol ľubovoľný počet detí (aj nula) | + | * Vo všeobecnom strome môže mať každý uzol ľubovoľný počet detí (aj nula). |
* Strom je ''binárny'', ak má každý uzol ''najviac'' dve deti. Budeme pritom rozlišovať medzi pravým a ľavým dieťaťom. | * Strom je ''binárny'', ak má každý uzol ''najviac'' dve deti. Budeme pritom rozlišovať medzi pravým a ľavým dieťaťom. | ||
| − | * Uzly zakoreneného stromu, ktoré nemajú žiadne dieťa, nazývame ''listami''; zvyšné uzly | + | * Uzly zakoreneného stromu, ktoré nemajú žiadne dieťa, nazývame ''listami''; zvyšné uzly nazývame ''vnútornými uzlami''. |
* ''Predkom'' uzla ''u'' nazveme ľubovoľný uzol ''v'' ležiaci na ceste z ''u'' do koreňa stromu (vrátane ''u'' a koreňa). Naopak potom hovoríme, že ''u'' je ''potomkom'' uzla ''v''. | * ''Predkom'' uzla ''u'' nazveme ľubovoľný uzol ''v'' ležiaci na ceste z ''u'' do koreňa stromu (vrátane ''u'' a koreňa). Naopak potom hovoríme, že ''u'' je ''potomkom'' uzla ''v''. | ||
* ''Podstromom'' stromu ''T'' zakoreneným v nejakom uzle ''v'' stromu ''T'' budeme rozumieť strom s koreňom ''v'' pozostávajúci zo všetkých jeho potomkov a všetkých hrán stromu ''T'' vedúcich medzi týmito uzlami. | * ''Podstromom'' stromu ''T'' zakoreneným v nejakom uzle ''v'' stromu ''T'' budeme rozumieť strom s koreňom ''v'' pozostávajúci zo všetkých jeho potomkov a všetkých hrán stromu ''T'' vedúcich medzi týmito uzlami. | ||
| Riadok 384: | Riadok 383: | ||
=== Štruktúra pre uzol binárneho stromu === | === Štruktúra pre uzol binárneho stromu === | ||
| − | V nasledujúcom budeme pracovať výhradne s ''binárnymi stromami''. Štruktúra pre uzol všeobecného binárneho stromu je podobná, ako pri stromoch pre aritmetické výrazy, namiesto operátora alebo hodnoty si však v každom uzle budeme pamätať hodnotu ľubovoľného typu <tt>dataType</tt> | + | V nasledujúcom budeme pracovať výhradne s ''binárnymi stromami''. Štruktúra pre uzol všeobecného binárneho stromu je podobná, ako pri stromoch pre aritmetické výrazy, namiesto operátora alebo hodnoty si však v každom uzle budeme pamätať hodnotu ľubovoľného typu <tt>dataType</tt>, napríklad <tt>int</tt>. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | /* Typ prvkov | + | /* Typ prvkov ukladaných v uzloch binárneho stromu */ |
typedef int dataType; | typedef int dataType; | ||
| − | /* Uzol | + | /* Uzol binárneho stromu */ |
struct node { | struct node { | ||
| − | // hodnota | + | // hodnota uložená v uzle |
dataType data; | dataType data; | ||
| − | // | + | // smerníky na podstromy |
| − | + | treeNode * left, * right; | |
| − | |||
| − | |||
| − | |||
}; | }; | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 440: | Riadok 436: | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | /* Funkcia pre | + | /* Funkcia pre výpis hodnoty typu dataType */ |
void printDataType(dataType data) { | void printDataType(dataType data) { | ||
printf("%d ", data); // pre int | printf("%d ", data); // pre int | ||
} | } | ||
| − | /* | + | /* Vypíše podstrom s koreňom *root v poradí preorder */ |
void printPreorder(node *root) { | void printPreorder(node *root) { | ||
| − | if (root | + | if (root != NULL) { |
| − | + | printDataType(root->data); | |
| − | + | printPreorder(root->left); | |
| − | + | printPreorder(root->right); | |
| − | + | } | |
| − | |||
} | } | ||
| − | /* | + | /* Vypíše podstrom s koreňom *root v poradí inorder */ |
void printInorder(node *root) { | void printInorder(node *root) { | ||
| − | if (root | + | if (root != NULL) { |
| − | + | printInorder(root->left); | |
| + | printDataType(root->data); | ||
| + | printInorder(root->right); | ||
} | } | ||
| − | |||
| − | |||
| − | |||
} | } | ||
| − | /* | + | /* Vypíše podstrom s koreňom *root v poradí postorder */ |
void printPostorder(node *root) { | void printPostorder(node *root) { | ||
| − | if (root | + | if (root != NULL) { |
| − | + | printPostorder(root->left); | |
| + | printPostorder(root->right); | ||
| + | printDataType(root->data); | ||
} | } | ||
| − | |||
| − | |||
| − | |||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 495: | Riadok 488: | ||
=== Výška binárneho stromu === | === Výška binárneho stromu === | ||
| − | ''Hĺbkou uzla'' binárneho stromu nazveme jeho vzdialenosť od koreňa. Koreň má teda hĺbku ''0'', jeho deti majú hĺbku ''1'', atď. ''Výškou binárneho stromu'' potom nazveme maximálnu hĺbku niektorého z jeho vrcholov. Strom s jediným vrcholom má teda | + | * ''Hĺbkou uzla'' binárneho stromu nazveme jeho vzdialenosť od koreňa. |
| + | ** Koreň má teda hĺbku ''0'', jeho deti majú hĺbku ''1'', atď. | ||
| + | * ''Výškou binárneho stromu'' potom nazveme maximálnu hĺbku niektorého z jeho vrcholov. | ||
| + | ** Strom s jediným vrcholom má teda výšku ''0''; pre ostatné stromy je ich výška daná ako 1 plus maximum z výšok ľavého a pravého podstromu. | ||
Nasledujúca funkcia počíta výšku stromu (kvôli elegancii zápisu pritom pracuje s rozšírením definície výšky stromu na prázdne stromy, za ktorých výšku sa považuje číslo ''-1''). | Nasledujúca funkcia počíta výšku stromu (kvôli elegancii zápisu pritom pracuje s rozšírením definície výšky stromu na prázdne stromy, za ktorých výšku sa považuje číslo ''-1''). | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | /* | + | /* Spočíta výšku podstromu s koreňom *root. Pre root == NULL vráti -1. */ |
int height(node *root) { | int height(node *root) { | ||
if (root == NULL) { | if (root == NULL) { | ||
return -1; | return -1; | ||
} | } | ||
| − | // | + | // rekurzívne spočíta výšku ľavého a pravého podstromu |
int hLeft = height(root->left); | int hLeft = height(root->left); | ||
int hRight = height(root->right); | int hRight = height(root->right); | ||
| − | // | + | // vráti max(hLeft, hRight) + 1 |
if (hLeft >= hRight) { | if (hLeft >= hRight) { | ||
return hLeft + 1; | return hLeft + 1; | ||
| Riadok 544: | Riadok 540: | ||
return NULL; | return NULL; | ||
} | } | ||
| − | node *v = createNode(count | + | node *v = createNode(count, NULL, NULL); |
| + | count++; | ||
v->left = createFullTree(height - 1); | v->left = createFullTree(height - 1); | ||
v->right = createFullTree(height - 1); | v->right = createFullTree(height - 1); | ||
| Riadok 753: | Riadok 750: | ||
/** Funkcia vypíše aritmetický výraz v inorder poradí */ | /** Funkcia vypíše aritmetický výraz v inorder poradí */ | ||
| − | void printInorder( | + | void printInorder(treeNode * root) { |
if (root->op == ' ') { | if (root->op == ' ') { | ||
| − | + | printf("%g", root->val); | |
} else { | } else { | ||
| − | + | printf("("); | |
| − | printInorder( | + | printInorder(root->left); |
| − | + | printf(" %c ", root->op); | |
| − | printInorder( | + | printInorder(root->right); |
| − | + | printf(")"); | |
} | } | ||
} | } | ||
/** Funkcia vypíše aritmetický výraz v preorder poradí */ | /** Funkcia vypíše aritmetický výraz v preorder poradí */ | ||
| − | void printPreorder( | + | void printPreorder(treeNode * root) { |
if (root->op == ' ') { | if (root->op == ' ') { | ||
| − | + | printf("%g ", root->val); | |
} else { | } else { | ||
| − | + | printf("%c ", root->op); | |
| − | printPreorder( | + | printPreorder(root->left); |
| − | printPreorder( | + | printPreorder(root->right); |
} | } | ||
} | } | ||
/** Funkcia vypíše aritmetický výraz v postorder poradí */ | /** Funkcia vypíše aritmetický výraz v postorder poradí */ | ||
| − | void printPostorder( | + | void printPostorder(treeNode * root) { |
if (root->op == ' ') { | if (root->op == ' ') { | ||
| − | + | printf("%g ", root->val); | |
} else { | } else { | ||
| − | printPostorder( | + | printPostorder(root->left); |
| − | printPostorder( | + | printPostorder(root->right); |
| − | + | printf("%c ", root->op); | |
} | } | ||
} | } | ||
| Riadok 800: | Riadok 797: | ||
// vypíšeme vo všetkých troch notáciách | // vypíšeme vo všetkých troch notáciách | ||
printf(" inorder: "); | printf(" inorder: "); | ||
| − | printInorder( | + | printInorder(root); |
printf("\n predorder: "); | printf("\n predorder: "); | ||
| − | printPreorder( | + | printPreorder(root); |
printf("\n postdorder: "); | printf("\n postdorder: "); | ||
| − | printPostorder( | + | printPostorder(root); |
printf("\n"); | printf("\n"); | ||
// uvoľníme pamäť | // uvoľníme pamäť | ||
Aktuálna revízia z 09:26, 3. december 2023
Obsah
Oznamy
- Oznamy z pondelka
Prednášky
- Tento týždeň a budúci pondelok ešte prednášky v normálnom režime.
- Budúcu stredu 6.12. v prvej polovici prednášky informácie k skúške a rady k skúškovému všeobecne, potom doberieme posledné povinné učivo.
- Posledný týždeň semestra v pondelok 11.12. nepovinná prednáška o nepreberaných črtách jazykov C a C++, v stredu 13.12. prednáška pravdepodobne nebude.
Cvičenia a úlohy
- Cvičenia bežia normálne každý utorok, piatkové cvičenia už iba 2x.
- Ak ste na cvičení nezískali 5 bodov, sú pre vás povinné cvičenia v piatok. Dobrá príležitosť spýtať sa na nejasné veci v cvičeniach, prednáškach, domácej úlohe. Môžete aj trénovať prvý príklad zo skúšky alebo preriešiť si ukážkový test.
- Budúci utorok bude teoretická rozcvička na papieri, bude zahŕňať učivo po prednášku 19.
- Tretiu domácu úlohu treba odovzdať do budúceho utorka 5.12. 22:00.
Semestrálny test
- V stredu 13.12. o 18:10.
- Treba získať aspoň 50% bodov.
- Opravný termín v januári.
- Môžete si priniesť ťahák v rozsahu 1 listu A4.
- Na semestrálnom teste budú podobné typy príkladov, aké poznáte z teoretických cvičení, napríklad napíšte funkciu, ktorá robí zadanú činnosť, doplňte chýbajúce časti funkcie, zistite, čo funkcia robí.
- Vyskytnú sa ale aj príklady, kde je úlohou napísať, ako bude na nejakom vstupe fungovať algoritmus alebo dátová štruktúra z prednášky. Ukážky takýchto príkladov nájdete na stránke Zimný semester, semestrálny test
- Môžete si pozrieť aj ukážkový test pre pokročilých, ktorý má podobné typy príkladov ako semestrálny test.
Termíny skúšok
- Piatok 15.12. 13:10
- Piatok 12.1. 9:00
- Piatok 19.1. 9:00
- Piatok 26.1. 9:00, hlavne 1. opravný termín
- Piatok 9.2. 9:00, hlavne 2. opravný termín
Na termíny sa bude dať prihlasovať od dnes 20:00.
- Kapacita termínov bude obmedzená, prihláste sa teda radšej skôr, neskôr to môžete zmeniť.
- Hláste sa iba na jeden termín!
- Ak vidíte konflikt niektorého termínu s hromadnou skúškou alebo písomkou z iného predmetu, dajte mi prosím vedieť čím skôr.
- Decembrový termín odporúčame hlavne študentom, ktorým programovanie nerobí problémy.
- Viac informácií o skúške je na stránke Zimný semester, skúška, spolu cez to prejdeme budúcu stredu.
- Na testovači dnes po prednáške pribudne zopár tréningových príkladov na skúšku, všetky sa týkajú už prebraného učiva. Ďalšie dva tréningové príklady pridáme neskôr.
Opakovanie z minulej prednášky
Aritmetické výrazy
- Bežná infixová notácia, napr. (65 – 3*5)/(2 + 3)
- Postfixová notácia 65 3 5 * - 2 3 + /
- Prefixová notácia / - 65 * 3 5 + 2 3
- Prefixová a postfixová notácia nepotrebujú zátvorky
- Prevod z infixovej notácie na postfixovú pomocou zásobníka
- Čo si ukladáme do zásobníka?
- Vyhodnocovanie postfixovej notácie pomocou zásobníka
- Čo si ukladáme do zásobníka?
Aritmetický výraz ako strom
Aritmetické výrazy možno reprezentovať aj vo forme stromu
- Operátory a čísla tvoria tzv. uzly (alebo vrcholy) stromu.
- Operátory tvoria tzv. vnútorné uzly stromu, každý z nich má dve deti zodpovedajúce podvýrazom pre jednotlivé operandy.
- Pre jednoduchosť na dnešnej prednáške neuvažujeme unárne mínus, dalo by sa však ľahko dorobiť.
- Čísla tvoria tzv. listy stromu, tie už nemajú žiadne deti.
- Strom obsahuje jediný uzol, ktorý nemá rodiča. Tento sa nazýva koreň stromu a reprezentuje celý aritmetický výraz.
- Informatici stromy väčšinou kreslia „hore nohami”, s koreňom na vrchu.
Uzol takéhoto stromu tak môžeme reprezentovať napríklad nasledujúcou štruktúrou:
struct treeNode {
// číselná hodnota (len v listoch)
double val;
// operátor vo vnútorných uzloch, pre listy medzera
char op;
// smerníky na podstromy
treeNode * left, * right;
};
Pre vnútorné uzly stromu (zodpovedajúce operátorom) pritom:
- Smerníky left a right budú ukazovať na korene podstromov reprezentujúcich ľavý resp. pravý podvýraz.
- Znak op bude zodpovedať danému operátoru (napríklad '+').
- Hodnota val ostane nevyužitá.
Pre listy (zodpovedajúce číselným hodnotám) naopak:
- Smerníky left a right budú mať hodnotu NULL.
- Znak op bude medzera ' ' (podľa op teda môžeme rozlišovať, či ide o číslo alebo o operátor).
- Vo val bude uložená hodnota daného čísla.
Celý strom pritom budeme reprezentovať jeho koreňom.
V tejto reprezentácii sú niektoré položky štruktúry treeNode nevyužité (napr. val vo vnútorných vrcholoch). S využitím objektového programovania (letný semester) budeme vedieť stromy pre aritmetické výrazy reprezentovať elegantnejšie.
Vytvorenie uzlu
Nasledujúce funkcie vytvoria nový vnútorný uzol (pre operátor) resp. nový list (pre číslo):
treeNode *createOp(char op, treeNode *left, treeNode *right) {
treeNode *v = new treeNode;
v->left = left;
v->right = right;
v->op = op;
return v;
}
treeNode *createNum(double val) {
treeNode *v = new treeNode;
v->left = NULL;
v->right = NULL;
v->op = ' ';
v->val = val;
return v;
}
„Ručne” teraz môžeme vytvoriť strom pre výraz (65 – 3 * 5)/(2 + 3):
treeNode *root = createOp('/',
createOp('-',
createNum(65),
createOp('*', createNum(3), createNum(5))),
createOp('+', createNum(2), createNum(3)));
Alebo po častiach:
treeNode *v65 = createNum(65);
treeNode *v3 = createNum(3);
treeNode *v5 = createNum(5);
treeNode *v2 = createNum(2);
treeNode *v3b = createNum(3);
treeNode *vKrat = createOp('*', v3, v5);
treeNode *vMinus = createOp('-', v65, vKrat);
treeNode *vPlus = createOp('+', v2, v3b);
treeNode *vDeleno = createOp('/', vMinus, vPlus);
Vyhodnotenie výrazu reprezentovaného stromom
Nasledujúca rekurzívna funkcia vypočíta hodnotu aritmetického výrazu reprezentovaného stromom s koreňom root.
- Ak je zadaný vrchol listom, vrátime hodnotu uloženú v položke val.
- V opačnom prípade rekurzívne spočítame hodnoty pre obidva podvýrazy a skombinujeme ich podľa typu znamienka.
- Celkovo veľmi jednoduchý a prirodzený výpočet, nie je potrebný explicitný zásobník.
- Funkcia nižšie nefunguje pre unárne mínus, nebolo by však ťažké ho dorobiť.
Rekurziu budeme používať vždy, keď potrebujeme prejsť všetky uzly stromu. Cyklom sa to programuje ťažko, lebo z uzla potrebujeme ísť doľava aj doprava.
double evaluateTree(treeNode *root) {
assert(root != NULL);
if (root->op == ' ') {
return root->val;
} else {
double valLeft = evaluateTree(root->left);
double valRight = evaluateTree(root->right);
switch (root->op) {
case '+':
return valLeft + valRight;
break;
case '-':
return valLeft - valRight;
break;
case '*':
return valLeft * valRight;
break;
case '/':
return valLeft / valRight;
break;
default:
assert(false);
break;
}
}
return 0; // realne nedosiahnutelny prikaz
}
Uvoľnenie pamäte
Nasledujúca funkcia uvoľní z pamäte celý strom s koreňom root.
- Opäť používa rekurziu na prejdenie celého stromu.
- Pozor na poradie príkazov, treba najskôr uvoľniť podstromy až potom zavolať delete na root, inak by sme stratili prístup k deťom.
- Všimnite si, ako sú riešené triviálne prípady, funkcia ani nezisťuje, s akým typom uzla pracuje.
void destroyTree(treeNode *root) {
if (root != NULL) {
destroyTree(root->left);
destroyTree(root->right);
delete root;
}
}
Vypísanie výrazu reprezentovaného stromom v rôznych notáciách
Infixovú, prefixovú, resp. postfixovú reprezentáciu aritmetického výrazu reprezentovaného stromom s koreňom root možno získať pomocou nasledujúcich funkcií.
- Opäť používajú rekurziu na prejdenie celého stromu.
- Líšia sa hlavne umiestnením príkazu na vypísanie operátora (pred, medzi alebo za rekurzívnym vypísaním podvýrazov).
- Infixová notácia potrebuje aj zátvorky. Táto funkcia ich pre istotu dáva všade. Rozmyslite si, ako by sme ich vedeli vypísať iba tam, kde treba.
- Ako by sme funkcie rozšírili pre unárne mínus?
/** Funkcia vypíše aritmetický výraz v inorder poradí */
void printInorder(treeNode * root) {
if (root->op == ' ') {
printf("%g", root->val);
} else {
printf("(");
printInorder(root->left);
printf(" %c ", root->op);
printInorder(root->right);
printf(")");
}
}
/** Funkcia vypíše aritmetický výraz v preorder poradí */
void printPreorder(treeNode * root) {
if (root->op == ' ') {
printf("%g ", root->val);
} else {
printf("%c ", root->op);
printPreorder(root->left);
printPreorder(root->right);
}
}
/** Funkcia vypíše aritmetický výraz v postorder poradí */
void printPostorder(treeNode * root) {
if (root->op == ' ') {
printf("%g ", root->val);
} else {
printPostorder(root->left);
printPostorder(root->right);
printf("%c ", root->op);
}
}
Vytvorenie stromu z postfixového výrazu
Pripomeňme si z minulej prednášky funkciu na vyhodnocovanie postfixového výrazu:
/** Funkcia vyhodnotí a vráti hodnotou výrazu v postfixovom tvare. */
double evaluatePostfix(tokenSequence & tokens) {
// zásobník, do ktorého ukladáme čísla
stack numberStack;
init(numberStack);
for (int i = 0; i < tokens.length; i++) {
// aktuálny token zo vstupu
token curToken = tokens.items[i];
if (curToken.op == ' ') {
// čísla rovno ukladáme na zásobník
push(numberStack, curToken);
} else {
// spracovanie operátora
token num1, num2, result;
// najskôr vyberieme 1 alebo 2 čísla zo zásobníka
if (curToken.op == '~') {
num1 = pop(numberStack);
} else {
num2 = pop(numberStack);
num1 = pop(numberStack);
}
// na operandy aplikujeme operátor
applyOp(curToken, num1, num2, result);
// výsledné číslo uložíme na zásobník
push(numberStack, result);
}
}
// zo zásobníka vyberieme výsledné číslo
token result = pop(numberStack);
// skontrolujeme, že zásobník je prázdny a výsledok je číslo
assert(isEmpty(numberStack) && result.op == ' ');
// uvoľníme pamäť zásobníka
destroy(numberStack);
return result.val;
}
- Túto funkciu možno jednoducho prepísať tak, aby namiesto vyhodnocovania výrazu konštruovala zodpovedajúci aritmetický strom.
- Namiesto hodnôt jednotlivých podvýrazov stačí na zásobníku uchovávať korene stromov, ktoré tieto podvýrazy reprezentujú.
- Aplikácii aritmetickej operácie bude zodpovedať spojenie dvoch podstromov do jedného stromu.
- V tomto prípade nepoužívame postupnosť symbolov (tokenov), ale priamo spracovávame postfixový výraz vo forme reťazca.
typedef treeNode *dataType;
/* Sem príde definícia štruktúry pre zásobník a všetkých funkcií poskytovaných zásobníkom. */
treeNode * postfixToTree(char * str) {
// zásobník, do ktorého ukladáme korene podstromov
stack treeStack;
init(treeStack);
int strPos = 0; // pozícia v rámci reťazca
while (str[strPos] != 0) { // kým nie sme na konci str
if (isspace(str[strPos])) { // preskakujeme biele znaky
strPos++;
} else if (isdigit(str[strPos]) || str[strPos] == '.') {
// keď nájdeme cifru alebo bodku (začiatok čísla)
double val;
int skip;
// načítame toto číslo pomocou sscanf,
// do skip uložíme počet znakov čísla
sscanf(&(str[strPos]), "%lf%n", &val, &skip);
// preskočíme všetky znaky čísla
strPos += skip;
// vytvoríme list a uložíme na zásobník
push(treeStack, createNum(val));
} else {
// spracovanie operátora
assert(strchr("+-/*", str[strPos]) != NULL);
treeNode * left, * right;
// najskôr vyberieme 2 podstromy zo zásobníka
// vytvoríme nový koreň,
// ktorý bude ich rodičom a vložíme na zásobník
right = pop(treeStack);
left = pop(treeStack);
push(treeStack, createOp(str[strPos], left, right));
strPos++;
}
}
// zo zásobníka vyberieme výsledný strom
treeNode * result = pop(treeStack);
// skontrolujeme, že zásobník je prázdny
assert(isEmpty(treeStack));
// uvoľníme pamäť zásobníka
destroy(treeStack);
return result;
}
Ukážkový program pracujúci so stromami pre aritmetické výrazy
Nasledujúci program prečíta z konzoly aritmetický výraz v postfixovom tvare, skonštruuje jeho aritmetický strom a následne preň zavolá funkcie na výpočet hodnoty výrazu a jeho výpis v rôznych notáciách. Celý program je na konci prednášky.
int main() {
// načítame postfixový výraz do reťazca
const int maxLine = 100;
char postfix[maxLine];
fgets(postfix, maxLine, stdin);
// výraz konvertujeme na strom
treeNode * root = postfixToTree(postfix);
// spočítame hodnotu výrazu
double value = evaluateTree(root);
printf(" value: %g\n", value);
// vypíšeme vo všetkých troch notáciách
printf(" inorder: ");
printInorder(stdout, root);
printf("\n predorder: ");
printPreorder(stdout, root);
printf("\n postdorder: ");
printPostorder(stdout, root);
printf("\n");
// uvoľníme pamäť
destroyTree(root);
}
Binárne stromy
Stromy pre aritmetické výrazy sú špeciálnym prípadom binárnych stromov. V informatike majú binárne stromy množstvo rozličných uplatnení. Ukážeme si teda všeobecnú dátovú štruktúru binárneho stromu.
Terminológia stromov
- Strom obsahuje množinu uzlov alebo vrcholov prepojených hranami. (uzol angl. node, vrchol vertex, hrana edge).
- Ak je strom neprázdny, jeden jeho vrchol nazývame koreň (angl. root)
- Každý uzol u okrem koreňa je spojený hranou s práve jedným rodičom (angl. parent), ktorým je nejaký uzol v. Naopak uzol u je dieťaťom (angl. child) uzla v.
- Vo všeobecnom strome môže mať každý uzol ľubovoľný počet detí (aj nula).
- Strom je binárny, ak má každý uzol najviac dve deti. Budeme pritom rozlišovať medzi pravým a ľavým dieťaťom.
- Uzly zakoreneného stromu, ktoré nemajú žiadne dieťa, nazývame listami; zvyšné uzly nazývame vnútornými uzlami.
- Predkom uzla u nazveme ľubovoľný uzol v ležiaci na ceste z u do koreňa stromu (vrátane u a koreňa). Naopak potom hovoríme, že u je potomkom uzla v.
- Podstromom stromu T zakoreneným v nejakom uzle v stromu T budeme rozumieť strom s koreňom v pozostávajúci zo všetkých jeho potomkov a všetkých hrán stromu T vedúcich medzi týmito uzlami.
Každý binárny strom je teda buď prázdny, alebo je tvorený jeho koreňom a dvoma podstromami – ľavým a pravým.
Takéto stromy sa nazývajú zakorenené. Presnejšiu matematickú definíciu zakorenených aj nezakorenených stromov uvidíte na predmete Úvod do kombinatoriky a teórie grafov (letný semester).
Štruktúra pre uzol binárneho stromu
V nasledujúcom budeme pracovať výhradne s binárnymi stromami. Štruktúra pre uzol všeobecného binárneho stromu je podobná, ako pri stromoch pre aritmetické výrazy, namiesto operátora alebo hodnoty si však v každom uzle budeme pamätať hodnotu ľubovoľného typu dataType, napríklad int.
/* Typ prvkov ukladaných v uzloch binárneho stromu */
typedef int dataType;
/* Uzol binárneho stromu */
struct node {
// hodnota uložená v uzle
dataType data;
// smerníky na podstromy
treeNode * left, * right;
};
Vytvorenie binárneho stromu
Nasledujúca funkcia vytvorí uzol binárneho stromu s dátami data, ľavým podstromom zakoreneným v uzle *left a pravým podstromom zakoreneným v uzle *right (parametre left a right sú teda smerníkmi na uzly). Ako výstup funkcia vráti smerník na novovytvorený uzol.
/* Vytvori uzol binarneho stromu */
node *createNode(dataType data, node *left, node *right) {
node *v = new node;
v->data = data;
v->left = left;
v->right = right;
return v;
}
Nasledujúca volanie tak napríklad vytvorí binárny strom so šiestimi uzlami zakorenený v uzle *root.
node *root = createNode(1,
createNode(2,
createNode(3, NULL, NULL),
createNode(4,NULL,NULL)),
createNode(5,
NULL,
createNode(6, NULL, NULL)));
Cvičenie: nakreslite binárny strom vytvorený predchádzajúcim volaním.
Prehľadávanie stromov a vypisovanie ich uzlov
Často je potrebné prejsť celý strom a spracovať (napríklad vypísať) hodnoty vo všetkých uzloch. Toto prehľadávanie možno, podobne ako pri stromoch pre výrazy, realizovať v troch základných poradiach: preorder, inorder a postorder.
Pri vypisovaní predpokladáme, že pre hodnoty typu dataType máme k dispozícii funkciu printDataType, ktorá ich v nejakom vhodnom formáte vypisuje.
/* Funkcia pre výpis hodnoty typu dataType */
void printDataType(dataType data) {
printf("%d ", data); // pre int
}
/* Vypíše podstrom s koreňom *root v poradí preorder */
void printPreorder(node *root) {
if (root != NULL) {
printDataType(root->data);
printPreorder(root->left);
printPreorder(root->right);
}
}
/* Vypíše podstrom s koreňom *root v poradí inorder */
void printInorder(node *root) {
if (root != NULL) {
printInorder(root->left);
printDataType(root->data);
printInorder(root->right);
}
}
/* Vypíše podstrom s koreňom *root v poradí postorder */
void printPostorder(node *root) {
if (root != NULL) {
printPostorder(root->left);
printPostorder(root->right);
printDataType(root->data);
}
}
Cvičenie: ako by sme spočítali súčet hodnôt uložených v uzloch stromu?
Likvidácia binárneho stromu
Nasledujúca rekurzívna funkcia zlikviduje celý podstrom zakorenený v uzle *root (t. j. uvoľní pamäť pre všetky jeho uzly). Veľmi sa podobá na funkciu pre strom reprezentujúci aritmetický výraz.
/* Zlikviduje podstrom s korenom *root (uvolni pamat) */
void destroyTree(node *root) {
if (root != NULL) {
destroyTree(root->left);
destroyTree(root->right);
delete root;
}
}
Výška binárneho stromu
- Hĺbkou uzla binárneho stromu nazveme jeho vzdialenosť od koreňa.
- Koreň má teda hĺbku 0, jeho deti majú hĺbku 1, atď.
- Výškou binárneho stromu potom nazveme maximálnu hĺbku niektorého z jeho vrcholov.
- Strom s jediným vrcholom má teda výšku 0; pre ostatné stromy je ich výška daná ako 1 plus maximum z výšok ľavého a pravého podstromu.
Nasledujúca funkcia počíta výšku stromu (kvôli elegancii zápisu pritom pracuje s rozšírením definície výšky stromu na prázdne stromy, za ktorých výšku sa považuje číslo -1).
/* Spočíta výšku podstromu s koreňom *root. Pre root == NULL vráti -1. */
int height(node *root) {
if (root == NULL) {
return -1;
}
// rekurzívne spočíta výšku ľavého a pravého podstromu
int hLeft = height(root->left);
int hRight = height(root->right);
// vráti max(hLeft, hRight) + 1
if (hLeft >= hRight) {
return hLeft + 1;
} else {
return hRight + 1;
}
}
Cvičenie: prepíšte funkciu tak, aby triviálnym prípadom bol list, nie prázdny strom. Funkcia teda vždy dostane smerník na neprázdny strom a nebude volať rekurziu na prázdne podstromy. Ktorá verzia je jednoduchšia? Ktorá sa vám zdá jednoduchšia na pochopenie?
Aká môže byť výška binárneho stromu?
Pre výšku h binárneho stromu s n uzlami platia nasledujúce vzťahy:
- Určite h ≤ n-1. Tento prípad nastáva, ak sú všetky uzly „navešané jeden pod druhý”.
- Strom s výškou h má najviac
- Z toho h ≥ log2(n+1)-1.
- Dostávame teda log2(n+1)-1 ≤ h ≤ n-1.
- Napríklad strom s milión vrcholmi má teda hĺbku medzi 19 a 999999.
Príklad: plné binárne stromy
Binárny strom výšky h s maximálnym počtom vrcholov 2h+1-1 sa nazýva plný binárny strom. Nasledujúca funkcia createFullTree vytvorí takýto strom a vráti smerník na jeho koreň. Jeho uzly pritom očísľuje 1, 2, 3,... (predpokladáme, že dataType je int) pomocou globálnej premennej count.
// ...
int count;
/* Vytvori plny binarny strom vysky height s datami uzlov count, count + 1, ... */
node *createFullTree(int height) {
if (height == -1) {
return NULL;
}
node *v = createNode(count, NULL, NULL);
count++;
v->left = createFullTree(height - 1);
v->right = createFullTree(height - 1);
return v;
}
int main() {
count = 1;
node *root = createFullTree(3);
printf("Vyska: %d\n", height(root));
printf("Inorder: ");
printInorder(root);
printf("\n");
printf("Preorder: ");
printPreorder(root);
printf("\n");
printf("Postorder: ");
printPostorder(root);
printf("\n");
destroyTree(root);
}
Cvičenie:
- Nakreslite strom aj s hodnotami v uzloch, ktorý vznikne pre výšku 2.
- Vo všeobecnosti opíšte poradie, v ktorom sa v uvedenom programe jednotlivým uzlom priraďujú ich hodnoty.
- Ako by ste v programe odstránili globálnu premennú count?
Program pre aritmetické výrazy ako stromy
#include <cstdio>
#include <cctype>
#include <cassert>
#include <cstring>
using namespace std;
struct treeNode {
// číselná hodnota (len v listoch)
double val;
// operátor vo vnútorných uzloch, pre listy medzera
char op;
// smerníky na podstromy
treeNode * left, * right;
};
/** Funkcia vráti nový uzol pre operátor */
treeNode * createOp(char op, treeNode * left, treeNode * right) {
treeNode * v = new treeNode;
v->left = left;
v->right = right;
v->op = op;
return v;
}
/** Funkcia vráti nový uzol pre číslo */
treeNode * createNum(double val) {
treeNode * v = new treeNode;
v->left = NULL;
v->right = NULL;
v->op = ' ';
v->val = val;
return v;
}
// Nasleduje kód pre zásobník uzlov stromu
typedef treeNode * dataType;
/** Uzol spájaného zoznamu pre zásobník */
struct node {
dataType data; // dáta uložené v uzle
node * next; // smerník na ďalší uzol zoznamu
};
/** Štruktúra pre zásobník implementovaný pomocou zoznamu*/
struct stack {
node * top; // Smernik na vrch zasobníka alebo NULL
};
/** Funkcia inicializuje prázdny zásobník */
void init(stack & s) {
s.top = NULL;
}
/** Funkcia zistí, či je zásobník prázdny */
bool isEmpty(stack & s) {
return s.top == NULL;
}
/** Funkcia pridá prvok item na vrch zásobníka */
void push(stack & s, dataType item) {
node * tmp = new node;
tmp->data = item;
tmp->next = s.top;
s.top = tmp;
}
/** Funkcia odoberie prvok z vrchu zasobnika a vráti ho */
dataType pop(stack & s) {
assert(!isEmpty(s));
dataType result = s.top->data;
node * tmp = s.top->next;
delete s.top;
s.top = tmp;
return result;
}
/** Funkcia vráti prvok na vrchu zásobníka, ale nechá ho v zásobníku */
dataType peek(stack & s) {
assert(!isEmpty(s));
return s.top->data;
}
/** Funkcia uvoľní pamäť zásobníka */
void destroy(stack & s) {
while (!isEmpty(s)) {
pop(s);
}
}
/** Funkcia konvertuje výraz v postfixovom tvare na strom */
treeNode * postfixToTree(char * str) {
// zásobník, do ktorého ukladáme korene podstromov
stack treeStack;
init(treeStack);
int strPos = 0; // pozícia v rámci reťazca
while (str[strPos] != 0) { // kým nie sme na konci str
if (isspace(str[strPos])) { // preskakujeme biele znaky
strPos++;
} else if (isdigit(str[strPos]) || str[strPos] == '.') {
// keď nájdeme cifru alebo bodku (začiatok čísla)
double val;
int skip;
// načítame toto číslo pomocou sscanf,
// do skip uložíme počet znakov čísla
sscanf(&(str[strPos]), "%lf%n", &val, &skip);
// preskočíme všetky znaky čísla
strPos += skip;
// vytvoríme list a uložíme na zásobník
push(treeStack, createNum(val));
} else {
// spracovanie operátora
assert(strchr("+-/*", str[strPos]) != NULL);
treeNode * left, * right;
// najskôr vyberieme 2 podstromy zo zásobníka
// vytvoríme nový koreň,
// ktorý bude ich rodičom a vložíme na zásobník
right = pop(treeStack);
left = pop(treeStack);
push(treeStack, createOp(str[strPos], left, right));
strPos++;
}
}
// zo zásobníka vyberieme výsledný strom
treeNode * result = pop(treeStack);
// skontrolujeme, že zásobník je prázdny
assert(isEmpty(treeStack));
// uvoľníme pamäť zásobníka
destroy(treeStack);
return result;
}
/** Funkcia spočíta hodnotu výrazu reprezentovaného stromom */
double evaluateTree(treeNode * root) {
assert(root != NULL);
if (root->op == ' ') {
return root->val;
} else {
double valLeft = evaluateTree(root->left);
double valRight = evaluateTree(root->right);
switch (root->op) {
case '+':
return valLeft + valRight;
break;
case '-':
return valLeft - valRight;
break;
case '*':
return valLeft * valRight;
break;
case '/':
return valLeft / valRight;
break;
default:
assert(false);
break;
}
}
return 0; // realne nedosiahnutelny prikaz
}
/** Funkcia uvoľní pamäť daného stromu */
void destroyTree(treeNode * root) {
if (root != NULL) {
destroyTree(root->left);
destroyTree(root->right);
delete root;
}
}
/** Funkcia vypíše aritmetický výraz v inorder poradí */
void printInorder(treeNode * root) {
if (root->op == ' ') {
printf("%g", root->val);
} else {
printf("(");
printInorder(root->left);
printf(" %c ", root->op);
printInorder(root->right);
printf(")");
}
}
/** Funkcia vypíše aritmetický výraz v preorder poradí */
void printPreorder(treeNode * root) {
if (root->op == ' ') {
printf("%g ", root->val);
} else {
printf("%c ", root->op);
printPreorder(root->left);
printPreorder(root->right);
}
}
/** Funkcia vypíše aritmetický výraz v postorder poradí */
void printPostorder(treeNode * root) {
if (root->op == ' ') {
printf("%g ", root->val);
} else {
printPostorder(root->left);
printPostorder(root->right);
printf("%c ", root->op);
}
}
int main() {
// načítame postfixový výraz do reťazca
const int maxLine = 100;
char postfix[maxLine];
fgets(postfix, maxLine, stdin);
// výraz konvertujeme na strom
treeNode * root = postfixToTree(postfix);
// spočítame hodnotu výrazu
double value = evaluateTree(root);
printf(" value: %g\n", value);
// vypíšeme vo všetkých troch notáciách
printf(" inorder: ");
printInorder(root);
printf("\n predorder: ");
printPreorder(root);
printf("\n postdorder: ");
printPostorder(root);
printf("\n");
// uvoľníme pamäť
destroyTree(root);
}