Programovanie (2) v Jave
1-INF-166, letný semester 2023/24
Prednáška 9: Rozdiel medzi revíziami
(→Oznamy) |
d |
||
| (39 medziľahlých úprav od 2 ďalších používateľov nie je zobrazených) | |||
| Riadok 1: | Riadok 1: | ||
== Oznamy == | == Oznamy == | ||
| − | Domáca úloha do | + | Domáca úloha do utorka |
* Časť bodov môžete dostať aj za neúplný program | * Časť bodov môžete dostať aj za neúplný program | ||
| − | * Na | + | * Na piatkových cvičeniach vám môžeme poradiť, ak máte otázky |
| + | * Nenechávajte všetku prácu na poslednú chvíľu | ||
Cvičenia | Cvičenia | ||
* Dnes pribudne do cvičení ďalší príklad na rekurziu, v piatok bonusová rozcvička za jeden bod | * Dnes pribudne do cvičení ďalší príklad na rekurziu, v piatok bonusová rozcvička za jeden bod | ||
| − | * Študentom, ktorí ešte nepracovali s rekurziou, | + | * Bonusovú rozcvičku môžete riešiť od hocikade, ale len v čase piatkových cvičení |
| + | * Študentom, ktorí ešte nepracovali s rekurziou, odporúčame prísť na cvičenia v piatok | ||
| + | * V rekurzii pokračujeme aj budúci týždeň. Pondelkovú prednášku ľahšie pochopíte, ak si dovtedy vyriešite aspoň tieto dva ľahké rekurzívne príklady | ||
== Klasické úvodné príklady na rekurziu == | == Klasické úvodné príklady na rekurziu == | ||
| Riadok 30: | Riadok 33: | ||
Rekurzívna definícia faktoriálu: | Rekurzívna definícia faktoriálu: | ||
| − | + | * ''n! = 1'' ak ''n≤1'' | |
| + | * ''n! = n ⋅ (n-1)!'' inak | ||
Túto matematickú definíciu môžeme priamočiaro prepísať do rekurzívnej funkcie: | Túto matematickú definíciu môžeme priamočiaro prepísať do rekurzívnej funkcie: | ||
| Riadok 46: | Riadok 50: | ||
===Najväčší spoločný deliteľ (Euklidov algoritmus)=== | ===Najväčší spoločný deliteľ (Euklidov algoritmus)=== | ||
Ďalším tradičným príkladom na rekurziu je počítanie najväčšieho spoločného deliteľa. | Ďalším tradičným príkladom na rekurziu je počítanie najväčšieho spoločného deliteľa. | ||
| − | * [[Prednáška_3# | + | * [[Prednáška_3#Euklidov_algoritmus|Euklidov algoritmus z prednášky 3]] bol založený na rovnosti gcd(''a'',''b'') = gcd(''b'', ''a'' mod ''b'') |
* Tú sme použili v cykle: | * Tú sme použili v cykle: | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 64: | Riadok 68: | ||
if (b == 0) return a; | if (b == 0) return a; | ||
else return gcd(b, a % b); | else return gcd(b, a % b); | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 131: | Riadok 95: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | V rekurzívnej verzii | + | V rekurzívnej verzii okraje aktuálneho úseku poľa posielame ako parametre: |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
int find(int a[], int left, int right, int x) { | int find(int a[], int left, int right, int x) { | ||
| Riadok 154: | Riadok 118: | ||
* Táto funkcia má dva triviálne (nerekurzívne) prípady. Ktoré? | * Táto funkcia má dva triviálne (nerekurzívne) prípady. Ktoré? | ||
* Aká veličina klesá v každom rekurzívnom volaní? | * Aká veličina klesá v každom rekurzívnom volaní? | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Zhrnutie=== | ===Zhrnutie=== | ||
| Riadok 185: | Riadok 123: | ||
* výpočet ''n!'' vyjadríme pomocou výpočtu ''(n-1)!'' a násobenia | * výpočet ''n!'' vyjadríme pomocou výpočtu ''(n-1)!'' a násobenia | ||
* výpočet ''gcd(a, b)'' vyjadríme pomocou výpočtu gcd(b, a % b) | * výpočet ''gcd(a, b)'' vyjadríme pomocou výpočtu gcd(b, a % b) | ||
| − | |||
* binárne vyhľadávanie v dlhšom intervale vyjadríme pomocou binárneho vyhľadávania v kratšom intervale | * binárne vyhľadávanie v dlhšom intervale vyjadríme pomocou binárneho vyhľadávania v kratšom intervale | ||
Všimnite si, že občas musíme zoznam parametrov nejakej funkcie rozšíriť pre potreby rekurzie | Všimnite si, že občas musíme zoznam parametrov nejakej funkcie rozšíriť pre potreby rekurzie | ||
| − | * napr. funkcia find by prirodzene dostávala pole ''a'', dĺžku ''n'' a hľadaný prvok, ale kvôli rekurzii potrebuje ľavý a pravý okraj | + | * napr. funkcia <tt>find</tt> by prirodzene dostávala pole ''a'', dĺžku ''n'' a hľadaný prvok, ale kvôli rekurzii potrebuje ľavý a pravý okraj |
* pre pohodlie užívateľa môžeme pridať pomocnú funkciu (wrapper): | * pre pohodlie užívateľa môžeme pridať pomocnú funkciu (wrapper): | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 201: | Riadok 138: | ||
=== Nepriama rekurzia === | === Nepriama rekurzia === | ||
| − | Všetky doteraz uvedené funkcie sú príkladom priamej rekurzie | + | * Všetky doteraz uvedené funkcie sú príkladom priamej rekurzie, kde definovaná funkcia používa seba samú priamo. |
| − | seba samú priamo. | + | * V nepriamej rekurzii funkcia neodkazuje vo svojej definícii priamo na seba, ale využíva inú funkciu, ktorá sa odkazuje naspäť na prvú (všeobecnejšie sa kruh môže uzavrieť na viac krokov). |
| − | funkcia neodkazuje vo svojej definícii priamo na seba, ale využíva inú funkciu, ktorá sa odkazuje | + | * Ilustračný príklad nižšie (veľmi neefektívne) testuje párnosť a nepárnosť čísla (párnosť je samozrejme lepšie testovať pomocou <tt>n % 2</tt>): |
| − | naspäť na prvú (všeobecnejšie sa kruh môže uzavrieť na viac krokov). | + | * Nakoľko vo funkcii vieme použiť len funkcie definované v programe nad ňou, máme tu problém. Vyriešime ho tzv, deklaráciou, kde napíšeme len hlavičku funkcie bez tela a telo dáme nižšie. |
| − | |||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| + | // deklaracia funkcie odd, aby sa dala pouzit v even | ||
| + | bool odd(int n); | ||
| + | |||
bool even(int n) { | bool even(int n) { | ||
if (n == 0) return true; | if (n == 0) return true; | ||
| Riadok 232: | Riadok 171: | ||
* na spodku je záznam pre funkciu <tt>main</tt> | * na spodku je záznam pre funkciu <tt>main</tt> | ||
| − | Teraz si môžeme jednoduchý zásobník odsimulovať napríklad na výpočte faktoriálu. | + | Teraz si môžeme jednoduchý zásobník odsimulovať napríklad na výpočte faktoriálu, ktorý sme rozpísali na viac riadkov, aby sa nám simulácia lepšie robila. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| + | // Pôvodná verzia | ||
| + | int factorial(int n) { | ||
| + | if (n <= 1) return 1; | ||
| + | else return n * factorial(n - 1); | ||
| + | } | ||
| + | |||
| + | // Rozpísaná verzia | ||
int factorial(int n) { | int factorial(int n) { | ||
| − | if (n < 2) | + | int result; |
| − | else | + | if (n < 2) result = 1; |
| + | else { | ||
| + | int rest = factorial(n - 1); // rekurzia | ||
| + | result = n * rest; | ||
| + | } | ||
| + | return result; | ||
| + | } | ||
| + | |||
| + | int main() { | ||
| + | int f = factorial(3); | ||
| + | cout << f << endl; | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 249: | Riadok 205: | ||
== Odbočka: korytnačia grafika v SVGdraw == | == Odbočka: korytnačia grafika v SVGdraw == | ||
| − | Náš prvý dnešný príklad rekurzie budú rekurzívne obrázky, fraktály. Aby sa nám lepšie vykresľovali, v knižnici SVGdraw je možnosť kresliť pomocou korytnačej grafiky. | + | Náš prvý dnešný príklad rekurzie budú rekurzívne obrázky, fraktály. Aby sa nám lepšie vykresľovali, v knižnici [[SVGdraw]] je možnosť kresliť pomocou korytnačej grafiky. |
* Vytvoríme si virtuálnu korytnačku, ktorá má určitú polohu a natočenie. | * Vytvoríme si virtuálnu korytnačku, ktorá má určitú polohu a natočenie. | ||
* Môžeme jej povedať, aby sa otočila doľava alebo doprava o určitý počet stupňov (<tt>turtle.turnLeft(uhol)</tt> a <tt>turtle.turnRight(uhol)</tt>). | * Môžeme jej povedať, aby sa otočila doľava alebo doprava o určitý počet stupňov (<tt>turtle.turnLeft(uhol)</tt> a <tt>turtle.turnRight(uhol)</tt>). | ||
| Riadok 256: | Riadok 212: | ||
Napríklad na vykreslenie štvorca s dĺžkou strany 100 môžeme korytnačke striedavo prikazovať ísť o 100 dopredu a otáčať sa o 90 stupňov doľava. | Napríklad na vykreslenie štvorca s dĺžkou strany 100 môžeme korytnačke striedavo prikazovať ísť o 100 dopredu a otáčať sa o 90 stupňov doľava. | ||
| − | * Na obrázku sa animuje pohyb korytnačky ([[: | + | * Na obrázku sa animuje pohyb korytnačky ([[:Media:P8-stvorec.svg|pozri tu]]) |
* Program by sa dal ľahko rozšíriť na vykresľovanie pravidelného n-uholníka (stačí zmeniť uhol otočenia a počet opakovaní cyklu) | * Program by sa dal ľahko rozšíriť na vykresľovanie pravidelného n-uholníka (stačí zmeniť uhol otočenia a počet opakovaní cyklu) | ||
| Riadok 264: | Riadok 220: | ||
int main(void) { | int main(void) { | ||
/* Vytvor korytnačku na súradniciach (25,175) | /* Vytvor korytnačku na súradniciach (25,175) | ||
| − | * otočenú doprava na obrázku s rozmermi 200x200 | + | * otočenú doprava na obrázku s rozmermi 200x200, |
| − | * ktorý bude uložený | + | * ktorý bude uložený v súbore stvorec.svg. */ |
Turtle turtle(200, 200, "stvorec.svg", 25, 175, 0); | Turtle turtle(200, 200, "stvorec.svg", 25, 175, 0); | ||
for (int i = 0; i < 4; i++) { | for (int i = 0; i < 4; i++) { | ||
| − | turtle.forward(150); / | + | // vykresli čiaru dĺžky 150 |
| − | turtle.turnLeft(90); | + | turtle.forward(150); |
| + | // otoč sa doľava o 90 stupňov | ||
| + | turtle.turnLeft(90); | ||
} | } | ||
| − | /* strany | + | /* strany boli vykreslené v poradí |
| + | * dolná, pravá, horná, ľavá */ | ||
/* Ukonči vypisovanie obrázka. */ | /* Ukonči vypisovanie obrázka. */ | ||
| Riadok 283: | Riadok 242: | ||
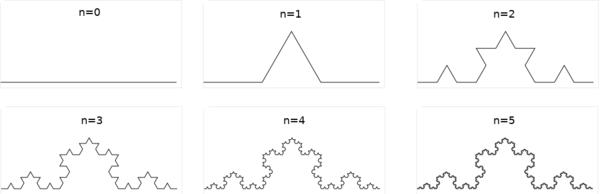
Fraktály sú útvary, ktorých časti na rôznych úrovniach zväčšenia sa podobajú na celý útvar. Mnohé fraktály vieme definovať a vykresliť pomocou jednoduchej rekurzie. | Fraktály sú útvary, ktorých časti na rôznych úrovniach zväčšenia sa podobajú na celý útvar. Mnohé fraktály vieme definovať a vykresliť pomocou jednoduchej rekurzie. | ||
| − | === | + | ===Kochova krivka=== |
| + | |||
| + | [[Image:koch.png|600px|Kochove krivky stupňov 0-5]] | ||
| + | |||
| − | |||
Príkladom fraktálu je Kochova krivka. Ako vzniká? | Príkladom fraktálu je Kochova krivka. Ako vzniká? | ||
* Predstavme si úsečku, ktorá meria ''d'' centimetrov. | * Predstavme si úsečku, ktorá meria ''d'' centimetrov. | ||
* Spravíme s ňou nasledujúcu transformáciu: | * Spravíme s ňou nasledujúcu transformáciu: | ||
** Úsečka sa rozdelí na tretiny a nad strednou tretinou sa zostrojí rovnostranný trojuholník. Základňa trojuholníka v krivke nebude. | ** Úsečka sa rozdelí na tretiny a nad strednou tretinou sa zostrojí rovnostranný trojuholník. Základňa trojuholníka v krivke nebude. | ||
| − | ** Dostávame tak útvar pozostávajúci zo | + | ** Dostávame tak útvar pozostávajúci zo 4 úsečiek s dĺžkou ''d/3''. |
| − | * Tú istú | + | * Tú istú transformáciu môžeme teraz spraviť na každej zo 4 nových úsečiek, t.j. dostávame 16 úsečiek dĺžky ''d/9''. |
| − | * Takéto transformácie môžeme robiť do | + | * Takéto transformácie môžeme robiť do nekonečna. |
Druhá možnosť je popísať krivku pomocou dvoch parametrov: dĺžka ''d'' a stupeň ''n'' | Druhá možnosť je popísať krivku pomocou dvoch parametrov: dĺžka ''d'' a stupeň ''n'' | ||
* Kochova krivka stupňa 0 je úsečka dĺžky ''d'' | * Kochova krivka stupňa 0 je úsečka dĺžky ''d'' | ||
* Kochova krivka stupňa ''n'' pozostáva zo štyroch kriviek stupňa ''n-1'' a dĺžky ''n/3'' | * Kochova krivka stupňa ''n'' pozostáva zo štyroch kriviek stupňa ''n-1'' a dĺžky ''n/3'' | ||
| − | ** | + | ** Na presný popis umiestnenia a natočenia týchto kriviek nižšieho stupňa použijeme korytnačiu grafiku, čo máme spravené vo funkcii nižšie. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 323: | Riadok 284: | ||
/* Vytvor korytnačku otočenú doprava. */ | /* Vytvor korytnačku otočenú doprava. */ | ||
| − | Turtle turtle(width, height, "fraktal.svg", 1, height-10, 0); | + | Turtle turtle(width, height, "fraktal.svg", |
| + | 1, height-10, 0); | ||
/* nakresli Kochovu krivku rekurzívne */ | /* nakresli Kochovu krivku rekurzívne */ | ||
| Riadok 338: | Riadok 300: | ||
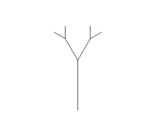
* strom má dva parametre: veľkosť ''d'' a stupeň ''n'' | * strom má dva parametre: veľkosť ''d'' a stupeň ''n'' | ||
* strom stupňa 0 je prázdna množina | * strom stupňa 0 je prázdna množina | ||
| − | * strom stupňa ''n'' pozostáva z kmeňa, ktorý tvorí úsečka dĺžky ''d'' a z dvoch podstromov, ktoré sú stromy stupňa ''n-1'', veľkosti ''d/2'' a otočené o 30 | + | * strom stupňa ''n'' pozostáva z kmeňa, ktorý tvorí úsečka dĺžky ''d'' a z dvoch podstromov, ktoré sú stromy stupňa ''n-1'', veľkosti ''d/2'' a otočené o 30 stupňov doľava a doprava od hlavnej osi stromu (pozri obrázky nižšie) |
<gallery widths=155 heights=115> | <gallery widths=155 heights=115> | ||
| Riadok 348: | Riadok 310: | ||
Rekurzívnu funkciu na vykresľovanie stromu napíšeme tak, aby sa po skončení vrátila na miesto a otočenie, kde začala | Rekurzívnu funkciu na vykresľovanie stromu napíšeme tak, aby sa po skončení vrátila na miesto a otočenie, kde začala | ||
| − | * Bez toho by | + | * Bez toho by sme nevedeli, kde korytnačka je po vykreslení ľavého podstromu a nemohli by sme teda kresliť pravý |
| − | * Korytnačka teda prejde po každej vetve dvakrát, raz smerom dopredu a raz naspäť. | + | * Korytnačka teda prejde po každej vetve dvakrát, raz smerom dopredu a raz naspäť ([[:Media:Strom3.svg|animácia]]) |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 395: | Riadok 357: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | == | + | ==Fibonacciho čísla== |
| + | |||
| + | ''[https://en.wikipedia.org/wiki/Fibonacci_number Fibonacciho postupnosť]'' je postupnosť čísel taká, že: | ||
| + | * Nultý člen je 0. | ||
| + | * Prvý člen je 1. | ||
| + | * Každý ďalší člen postupnosti je daný súčtom dvoch predchádzajúcich. | ||
| + | |||
| + | Prvých niekoľko členov Fibonacciho postupnosti je | ||
| + | :0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, ... | ||
| + | |||
| + | Formálnejšiu definíciu ''n''-tého Fibonacciho čísla ''F''(''n'') môžeme zapísať ako rekurzívny vzťah: | ||
| + | * ''F''(0) = 0, | ||
| + | * ''F''(1) = 1, | ||
| + | * Pre všetky prirodzené čísla ''n'' ≥ 2: ''F''(''n'') = ''F''(''n'' - 1) + ''F''(''n'' - 2). | ||
| + | |||
| + | Z tejto definície vieme opäť urobiť rekurzívnu funkciu jednoducho: | ||
| + | <syntaxhighlight lang="C++"> | ||
| + | int fib(int n){ | ||
| + | if (n == 0) { | ||
| + | return 0; | ||
| + | } else if (n == 1) { | ||
| + | return 1; | ||
| + | } else { | ||
| + | return fib(n - 1) + fib(n - 2); | ||
| + | } | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | ===Fibonacciho čísla nerekurzívne=== | ||
| + | |||
| + | Jedna možnosť je ukladať ''F''[0], ''F''[1], ..., ''F''[''n''] do poľa | ||
| + | |||
| + | <ul class="mw-collapsible mw-collapsed" data-expandtext="ukáž program" data-collapsetext="schovaj program"> | ||
| + | <li> | ||
| + | <syntaxhighlight lang="C++"> | ||
| + | int fibonacci(int n) { | ||
| + | int F[MAXN + 1]; | ||
| + | F[0] = 0; | ||
| + | F[1] = 1; | ||
| + | for(int i = 2; i <= n; i++) { | ||
| + | F[i] = F[i-1] + F[i-2]; | ||
| + | } | ||
| + | return F[n]; | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | </ul> | ||
| + | |||
| + | Všimnite si ale, že z poľa vždy potrebujeme len posledné dve vyplnené čísla, takže stačili by nám dve premenné typu <tt>int</tt>. | ||
| + | <syntaxhighlight lang="C++"> | ||
| + | int fibonacci(int n) { | ||
| + | if (n == 0) { | ||
| + | return 0; | ||
| + | } else if (n == 1) { | ||
| + | return 1; | ||
| + | } else { | ||
| + | int F_posledne = 1; | ||
| + | int F_predposledne = 0; | ||
| + | for (int i = 2; i <= n; i++) { | ||
| + | int F_n = F_posledne + F_predposledne; | ||
| + | F_predposledne = F_posledne; | ||
| + | F_posledne = F_n; | ||
| + | } | ||
| + | return F_posledne; | ||
| + | } | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | ===Cvičenie=== | ||
| + | |||
| + | Ako by sme bez počítača zistili, čo robí rekurzívna funkcia, napríklad takáto obmena Fibonacciho postupnosti? | ||
| − | + | <syntaxhighlight lang="C++"> | |
| − | + | int f(int n) { | |
| − | + | if (n <= 2) return 1; | |
| − | + | else return f(n-1) + f(n-3); | |
| + | } | ||
| + | </syntaxhighlight> | ||
| − | + | ===Ako pracuje rekurzívna verzia Fibonacciho čísel=== | |
| − | * | + | * Rekurzívna verzia výpočtu Fibonacciho čísel je krátka a elegantná, podobá sa na matematickú definíciu |
| − | + | * Je ale neefektívna | |
| − | |||
| − | * | ||
| − | |||
| − | + | * Skúsme napríklad odsimulovať, čo sa deje, ak chceme rekurzívne spočítať ''F''[3] | |
| − | * | + | * Kvôli prehľadnosti si rekurzívnu funkciu <tt>fib</tt> rozpíšeme na viac riadkov: |
| − | * | ||
| − | |||
| − | |||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | + | #include <iostream> | |
| − | if (n == 1) { | + | using namespace std; |
| − | + | ||
| − | + | int fib(int n) { | |
| + | if (n == 0) { | ||
| + | return 0; | ||
| + | } else if (n == 1) { | ||
| + | return 1; | ||
} else { | } else { | ||
| − | + | int a = fib(n - 1); // riadok (A) | |
| − | + | int b = fib(n - 2); // riadok (B) | |
| − | + | return a+b; | |
| − | |||
| − | |||
| − | |||
} | } | ||
} | } | ||
| − | int main ( | + | int main() { |
| − | // | + | int x = fib(3); // riadok (C) |
| − | + | cout << x << endl; | |
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | + | Tu je priebeh programu (obsah zásobníka) | |
| − | * | + | <pre> |
| − | + | (1) (2) (3) | |
| − | + | ||
| + | fib n=2 | ||
| + | fib n=3 fib n=3, a=?, b=?, riadok A | ||
| + | main, x=? main, x=?, riadok C main, x=?, riadok C | ||
| + | |||
| + | (4) (5) | ||
| + | |||
| + | fib n=1 | ||
| + | fib n=2, a=?, b=?, riadok A fib n=2, a=1, b=?, riadok A | ||
| + | fib n=3, a=?, b=?, riadok A fib n=3, a=?, b=?, riadok A | ||
| + | main, x=?, riadok C main, x=?, riadok C | ||
| + | |||
| + | |||
| + | (6) (7) | ||
| + | |||
| + | fib n=0 | ||
| + | fib n=2, a=1, b=?, riadok B fib n=2, a=1, b=0, riadok B | ||
| + | fib n=3, a=?, b=?, riadok A fib n=3, a=?, b=?, riadok A | ||
| + | main, x=?, riadok C main, x=?, riadok C | ||
| + | |||
| + | |||
| + | (8) (9) | ||
| + | |||
| + | fib n=1 | ||
| + | fib n=3, a=1, b=?, riadok A fib n=3, a=1, b=?, riadok B | ||
| + | main, x=?, riadok C main, x=?, riadok C | ||
| + | |||
| + | |||
| + | (10) (11) | ||
| + | |||
| + | fib n=3, a=1, b=1, riadok B | ||
| + | main, x=?, riadok C main, x=2, riadok C | ||
| + | </pre> | ||
| + | |||
| + | Postupnosť volaní počas výpočtu vieme znázorniť aj stromovým diagramom: | ||
| + | |||
| + | [[Súbor:fib.png|400px]] | ||
| + | |||
| + | Priamočiary rekurzívny zápis výpočtu Fibonacciho čísel je neefektívny, lebo výpočet Fibonacciho čísel sa opakuje | ||
| + | * Napr. pre ''n=5'' počítame <tt>fib(2)</tt> trikrát, pre ''n=6'' päťkrát a pre ''n=20'' až 4181-krát | ||
Aktuálna revízia z 23:22, 22. október 2024
Obsah
Oznamy
Domáca úloha do utorka
- Časť bodov môžete dostať aj za neúplný program
- Na piatkových cvičeniach vám môžeme poradiť, ak máte otázky
- Nenechávajte všetku prácu na poslednú chvíľu
Cvičenia
- Dnes pribudne do cvičení ďalší príklad na rekurziu, v piatok bonusová rozcvička za jeden bod
- Bonusovú rozcvičku môžete riešiť od hocikade, ale len v čase piatkových cvičení
- Študentom, ktorí ešte nepracovali s rekurziou, odporúčame prísť na cvičenia v piatok
- V rekurzii pokračujeme aj budúci týždeň. Pondelkovú prednášku ľahšie pochopíte, ak si dovtedy vyriešite aspoň tieto dva ľahké rekurzívne príklady
Klasické úvodné príklady na rekurziu
Rekurzia je metóda, pri ktorej definujeme objekt (funkciu, pojem, . . . ) pomocou jeho samého.
Na začiatok sa pozrieme na klasické príklady algoritmov využívajúcich rekurziu.
Výpočet faktoriálu
Faktoriál prirodzeného čísla n značíme n! a je to súčin všetkých celých čísel od 1 po n. Pre úplnosť 0! definujeme ako 1.
Výpočet pomocou cyklu z prednášky 3:
int factorial(int n) {
int result = 1;
for (int i = 1; i <= n; i++) {
result = result * i;
}
return result;
}
Rekurzívna definícia faktoriálu:
- n! = 1 ak n≤1
- n! = n ⋅ (n-1)! inak
Túto matematickú definíciu môžeme priamočiaro prepísať do rekurzívnej funkcie:
int factorial(int n) {
if (n <= 1) return 1;
else return n * factorial(n-1);
}
Aby sa rekurzia nezacyklila, mali by sme dodržiavať nasledujúce zásady:
- Rekurzívna funkcia musí obsahovať vetvu pre triviálny prípad niektorého vstupu. Táto vetva nebude obsahovať rekurzívne volanie funkcie, ktorú práve definujeme.
- Rekurzívne volanie funkcie by malo mať vhodne redukovaný niektorý vstup, aby sme sa časom dopracovali k triviálnemu prípadu.
Najväčší spoločný deliteľ (Euklidov algoritmus)
Ďalším tradičným príkladom na rekurziu je počítanie najväčšieho spoločného deliteľa.
- Euklidov algoritmus z prednášky 3 bol založený na rovnosti gcd(a,b) = gcd(b, a mod b)
- Tú sme použili v cykle:
int gcd(int a, int b) {
while (b != 0) {
int r = a % b;
a = b;
b = r;
}
return a;
}
Avšak opäť to isté môžeme ešte kratšie a elegantnejšie napísať rekurziou:
int gcd(int a, int b) {
if (b == 0) return a;
else return gcd(b, a % b);
}
Binárne vyhľadávanie
Aj binárne vyhľadávanie prvku v utriedenom poli z prednášky 7 sa dá pekne zapísať rekurzívne.
Pôvodná nerekurzívna funkcia vrátila polohu prvku x v poli a alebo hodnotou -1, ak sa tam nenachádzal:
int find(int a[], int n, int x) {
int left = 0, right = n - 1;
while (left <= right) {
int index = (left + right) / 2;
if (a[index] == x) {
return index;
}
else if (a[index] < x) {
left = index + 1;
}
else {
right = index - 1;
}
}
return -1;
}
V rekurzívnej verzii okraje aktuálneho úseku poľa posielame ako parametre:
int find(int a[], int left, int right, int x) {
if (left > right) {
return -1;
}
int index = (left + right) / 2;
if (a[index] == x) {
return index;
}
else if (a[index] < x) {
return find(a, index+1, right, x);
}
else {
return find(a, left, index - 1, x);
}
}
Ak chceme vyhľadať x v poli a s n prvkami, voláme find(a, 0, n-1, x).
Na zamyslenie:
- Táto funkcia má dva triviálne (nerekurzívne) prípady. Ktoré?
- Aká veličina klesá v každom rekurzívnom volaní?
Zhrnutie
Pri rekurzii vyjadríme riešenie nejakej úlohy pomocou riešenia jednej alebo viacerých úloh toho istého typu, ale s menším vstupom plus ďalšie potrebné nerekurzívne výpočty
- výpočet n! vyjadríme pomocou výpočtu (n-1)! a násobenia
- výpočet gcd(a, b) vyjadríme pomocou výpočtu gcd(b, a % b)
- binárne vyhľadávanie v dlhšom intervale vyjadríme pomocou binárneho vyhľadávania v kratšom intervale
Všimnite si, že občas musíme zoznam parametrov nejakej funkcie rozšíriť pre potreby rekurzie
- napr. funkcia find by prirodzene dostávala pole a, dĺžku n a hľadaný prvok, ale kvôli rekurzii potrebuje ľavý a pravý okraj
- pre pohodlie užívateľa môžeme pridať pomocnú funkciu (wrapper):
int find(int a[], int n, int x) {
return find(a, 0, n-1, x);
}
Viac o rekurzii
Nepriama rekurzia
- Všetky doteraz uvedené funkcie sú príkladom priamej rekurzie, kde definovaná funkcia používa seba samú priamo.
- V nepriamej rekurzii funkcia neodkazuje vo svojej definícii priamo na seba, ale využíva inú funkciu, ktorá sa odkazuje naspäť na prvú (všeobecnejšie sa kruh môže uzavrieť na viac krokov).
- Ilustračný príklad nižšie (veľmi neefektívne) testuje párnosť a nepárnosť čísla (párnosť je samozrejme lepšie testovať pomocou n % 2):
- Nakoľko vo funkcii vieme použiť len funkcie definované v programe nad ňou, máme tu problém. Vyriešime ho tzv, deklaráciou, kde napíšeme len hlavičku funkcie bez tela a telo dáme nižšie.
// deklaracia funkcie odd, aby sa dala pouzit v even
bool odd(int n);
bool even(int n) {
if (n == 0) return true;
else return odd(n - 1);
}
bool odd(int n) {
if (n == 0) return false;
else return even(n - 1);
}
Rekurzia pomocou zásobníka - ako je rekurzia implementovaná
O rekurzívne volania sa stará zásobník volaní (call stack)
- Ide o všeobecnú štruktúru potrebnú aj v nerekurzívnych programoch s funkciami
- Po zavolaní nejakej funkcie f sa pre ňu vytvorí na zásobníku záznam, ktorý obsahuje všetky lokálne premenné a argumenty funkcie
- Keď potom z funkcie f zavoláme nejakú funkciu g (pričom v rekurzii môže byť aj f=g), tak sa vytvorí nový záznam pre g. Navyše v zázname pre f si uložíme aj to, v ktorom kroku sme prestali s výpočtom, aby sme vedeli správne pokračovať
- Po skončení výpočtu funkcie g sa jej záznam zruší zo zásobníka. Vrátime sa k záznamu pre funkciu f a pokračujeme vo výpočte so správnymi hodnotami všetkých premenných a od správneho miesta.
Záznamy v zásobníku si môžeme predstaviť uložené v stĺpci jeden nad druhým
- vrchný záznam je aktuálny, pre funkciu, ktorá sa vykonáva
- pod ním je záznam pre funkciu, ktorá ju volala atď
- na spodku je záznam pre funkciu main
Teraz si môžeme jednoduchý zásobník odsimulovať napríklad na výpočte faktoriálu, ktorý sme rozpísali na viac riadkov, aby sa nám simulácia lepšie robila.
// Pôvodná verzia
int factorial(int n) {
if (n <= 1) return 1;
else return n * factorial(n - 1);
}
// Rozpísaná verzia
int factorial(int n) {
int result;
if (n < 2) result = 1;
else {
int rest = factorial(n - 1); // rekurzia
result = n * rest;
}
return result;
}
int main() {
int f = factorial(3);
cout << f << endl;
}
Zložitejšie príklady rekurzie
Každý z predchádzajúcich príkladov sme vedeli pomerne jednoducho zapísať aj bez rekurzie, aj keď rekurzívny výpočet bol často prehľadnejší, zrozumiteľnejší, kratší a krajší.
Ukážeme si však aj príklady, ktoré by sa bez rekurzie písali obtiažne (aj keď ako si neskôr ukážeme, rekurzia sa dá vždy odstrániť, v najhoršom prípade simuláciou zásobníka). Príklady, kde rekurzia veľmi pomáha, uvidíme na zvyšku dnešnej prednášky, ale aj na dvoch ďalších a k rekurzii sa vrátime aj neskôr v semestri a samozrejme na ďalších predmetoch.
Odbočka: korytnačia grafika v SVGdraw
Náš prvý dnešný príklad rekurzie budú rekurzívne obrázky, fraktály. Aby sa nám lepšie vykresľovali, v knižnici SVGdraw je možnosť kresliť pomocou korytnačej grafiky.
- Vytvoríme si virtuálnu korytnačku, ktorá má určitú polohu a natočenie.
- Môžeme jej povedať, aby sa otočila doľava alebo doprava o určitý počet stupňov (turtle.turnLeft(uhol) a turtle.turnRight(uhol)).
- Môžeme jej povedať, aby išla o určitú dĺžku dopredu (turtle.forward(dlzka))
- Keď ide korytnačka dopredu, zanecháva v piesku chvostom čiarku (vykreslí teda čiaru do nášho obrázku).
Napríklad na vykreslenie štvorca s dĺžkou strany 100 môžeme korytnačke striedavo prikazovať ísť o 100 dopredu a otáčať sa o 90 stupňov doľava.
- Na obrázku sa animuje pohyb korytnačky (pozri tu)
- Program by sa dal ľahko rozšíriť na vykresľovanie pravidelného n-uholníka (stačí zmeniť uhol otočenia a počet opakovaní cyklu)
#include "SVGdraw.h"
int main(void) {
/* Vytvor korytnačku na súradniciach (25,175)
* otočenú doprava na obrázku s rozmermi 200x200,
* ktorý bude uložený v súbore stvorec.svg. */
Turtle turtle(200, 200, "stvorec.svg", 25, 175, 0);
for (int i = 0; i < 4; i++) {
// vykresli čiaru dĺžky 150
turtle.forward(150);
// otoč sa doľava o 90 stupňov
turtle.turnLeft(90);
}
/* strany boli vykreslené v poradí
* dolná, pravá, horná, ľavá */
/* Ukonči vypisovanie obrázka. */
turtle.finish();
}
Fraktály
Fraktály sú útvary, ktorých časti na rôznych úrovniach zväčšenia sa podobajú na celý útvar. Mnohé fraktály vieme definovať a vykresliť pomocou jednoduchej rekurzie.
Kochova krivka
Príkladom fraktálu je Kochova krivka. Ako vzniká?
- Predstavme si úsečku, ktorá meria d centimetrov.
- Spravíme s ňou nasledujúcu transformáciu:
- Úsečka sa rozdelí na tretiny a nad strednou tretinou sa zostrojí rovnostranný trojuholník. Základňa trojuholníka v krivke nebude.
- Dostávame tak útvar pozostávajúci zo 4 úsečiek s dĺžkou d/3.
- Tú istú transformáciu môžeme teraz spraviť na každej zo 4 nových úsečiek, t.j. dostávame 16 úsečiek dĺžky d/9.
- Takéto transformácie môžeme robiť do nekonečna.
Druhá možnosť je popísať krivku pomocou dvoch parametrov: dĺžka d a stupeň n
- Kochova krivka stupňa 0 je úsečka dĺžky d
- Kochova krivka stupňa n pozostáva zo štyroch kriviek stupňa n-1 a dĺžky n/3
- Na presný popis umiestnenia a natočenia týchto kriviek nižšieho stupňa použijeme korytnačiu grafiku, čo máme spravené vo funkcii nižšie.
#include "SVGdraw.h"
void drawKoch(double d, int n, Turtle& turtle){
if (n==0) turtle.forward(d);
else {
drawKoch(d/3, n-1, turtle);
turtle.turnLeft(60);
drawKoch(d/3, n-1, turtle);
turtle.turnRight(120);
drawKoch(d/3, n-1, turtle);
turtle.turnLeft(60);
drawKoch(d/3, n-1, turtle);
}
}
int main(void) {
int width = 310; /* rozmery obrazku */
int height = 150;
double d = 300; /* velkost krivky */
int n = 5; /* stupen krivky */
/* Vytvor korytnačku otočenú doprava. */
Turtle turtle(width, height, "fraktal.svg",
1, height-10, 0);
/* nakresli Kochovu krivku rekurzívne */
drawKoch(d, n, turtle);
/* Schovaj korytnačku. */
turtle.finish();
}
Rekurzívny strom
A ešte jeden príklad fraktálu: strom definovaný nasledovne:
- strom má dva parametre: veľkosť d a stupeň n
- strom stupňa 0 je prázdna množina
- strom stupňa n pozostáva z kmeňa, ktorý tvorí úsečka dĺžky d a z dvoch podstromov, ktoré sú stromy stupňa n-1, veľkosti d/2 a otočené o 30 stupňov doľava a doprava od hlavnej osi stromu (pozri obrázky nižšie)
Rekurzívnu funkciu na vykresľovanie stromu napíšeme tak, aby sa po skončení vrátila na miesto a otočenie, kde začala
- Bez toho by sme nevedeli, kde korytnačka je po vykreslení ľavého podstromu a nemohli by sme teda kresliť pravý
- Korytnačka teda prejde po každej vetve dvakrát, raz smerom dopredu a raz naspäť (animácia)
#include "SVGdraw.h"
void drawTree(double d, int n, Turtle& turtle) {
if (n == 0) {
/* stupen 0 - nerob nic */
return;
} else {
/* kmen stromu */
turtle.forward(d);
turtle.turnLeft(30);
/* lava cast koruny */
drawTree(d / 2, n - 1, turtle);
turtle.turnRight(60);
/* prava cast koruny */
drawTree(d / 2, n - 1, turtle);
turtle.turnLeft(30);
/* navrat na spodok kmena */
turtle.forward(-d);
}
}
int main(void) {
/* rozmery obrazku */
int width = 150;
int height = 200;
/* velkost stromu */
double d = 100;
/* stupen krivky */
int n = 5;
/* vytvor korytnačku otočenú hore */
Turtle turtle(width, height, "fraktal.svg",
width / 2, height - 10, 90);
/* nakresli strom rekurzívne */
drawTree(d, n, turtle);
/* schovaj korytnačku */
turtle.finish();
}
Fibonacciho čísla
Fibonacciho postupnosť je postupnosť čísel taká, že:
- Nultý člen je 0.
- Prvý člen je 1.
- Každý ďalší člen postupnosti je daný súčtom dvoch predchádzajúcich.
Prvých niekoľko členov Fibonacciho postupnosti je
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, ...
Formálnejšiu definíciu n-tého Fibonacciho čísla F(n) môžeme zapísať ako rekurzívny vzťah:
- F(0) = 0,
- F(1) = 1,
- Pre všetky prirodzené čísla n ≥ 2: F(n) = F(n - 1) + F(n - 2).
Z tejto definície vieme opäť urobiť rekurzívnu funkciu jednoducho:
int fib(int n){
if (n == 0) {
return 0;
} else if (n == 1) {
return 1;
} else {
return fib(n - 1) + fib(n - 2);
}
}
Fibonacciho čísla nerekurzívne
Jedna možnosť je ukladať F[0], F[1], ..., F[n] do poľa
-
int fibonacci(int n) { int F[MAXN + 1]; F[0] = 0; F[1] = 1; for(int i = 2; i <= n; i++) { F[i] = F[i-1] + F[i-2]; } return F[n]; }
Všimnite si ale, že z poľa vždy potrebujeme len posledné dve vyplnené čísla, takže stačili by nám dve premenné typu int.
int fibonacci(int n) {
if (n == 0) {
return 0;
} else if (n == 1) {
return 1;
} else {
int F_posledne = 1;
int F_predposledne = 0;
for (int i = 2; i <= n; i++) {
int F_n = F_posledne + F_predposledne;
F_predposledne = F_posledne;
F_posledne = F_n;
}
return F_posledne;
}
}
Cvičenie
Ako by sme bez počítača zistili, čo robí rekurzívna funkcia, napríklad takáto obmena Fibonacciho postupnosti?
int f(int n) {
if (n <= 2) return 1;
else return f(n-1) + f(n-3);
}
Ako pracuje rekurzívna verzia Fibonacciho čísel
- Rekurzívna verzia výpočtu Fibonacciho čísel je krátka a elegantná, podobá sa na matematickú definíciu
- Je ale neefektívna
- Skúsme napríklad odsimulovať, čo sa deje, ak chceme rekurzívne spočítať F[3]
- Kvôli prehľadnosti si rekurzívnu funkciu fib rozpíšeme na viac riadkov:
#include <iostream>
using namespace std;
int fib(int n) {
if (n == 0) {
return 0;
} else if (n == 1) {
return 1;
} else {
int a = fib(n - 1); // riadok (A)
int b = fib(n - 2); // riadok (B)
return a+b;
}
}
int main() {
int x = fib(3); // riadok (C)
cout << x << endl;
}
Tu je priebeh programu (obsah zásobníka)
(1) (2) (3)
fib n=2
fib n=3 fib n=3, a=?, b=?, riadok A
main, x=? main, x=?, riadok C main, x=?, riadok C
(4) (5)
fib n=1
fib n=2, a=?, b=?, riadok A fib n=2, a=1, b=?, riadok A
fib n=3, a=?, b=?, riadok A fib n=3, a=?, b=?, riadok A
main, x=?, riadok C main, x=?, riadok C
(6) (7)
fib n=0
fib n=2, a=1, b=?, riadok B fib n=2, a=1, b=0, riadok B
fib n=3, a=?, b=?, riadok A fib n=3, a=?, b=?, riadok A
main, x=?, riadok C main, x=?, riadok C
(8) (9)
fib n=1
fib n=3, a=1, b=?, riadok A fib n=3, a=1, b=?, riadok B
main, x=?, riadok C main, x=?, riadok C
(10) (11)
fib n=3, a=1, b=1, riadok B
main, x=?, riadok C main, x=2, riadok C
Postupnosť volaní počas výpočtu vieme znázorniť aj stromovým diagramom:
Priamočiary rekurzívny zápis výpočtu Fibonacciho čísel je neefektívny, lebo výpočet Fibonacciho čísel sa opakuje
- Napr. pre n=5 počítame fib(2) trikrát, pre n=6 päťkrát a pre n=20 až 4181-krát