Prednáška 10

Oznamy

• Dnes 22:00 termín odovzdania DÚ1
• Zajtra alebo v stredu zverejníme DÚ2
• Cvičenia tento týždeň:
  • Zajtrajšia rozcvička bude z dnešnej prednášky (a teda je fajn si prednášku pozrieť pred cvičením)
  • V stredu sa objaví ešte jeden príklad týkajúci sa stredňajšej prednášky
  • Na dokončenie príkladov z utorkových cvičení budete mať dva týždne
• Tento týždeň neplánujeme na piatok bonusovú rozcvičku, cvičenia sa však budú konať
• Budúci utorok je sviatok a pondelok rektorské voľno, budeme mať teda iba prednášku v stredu a cvičenia v piatok
• V piatok 4.11. na cvičeniach bude krátky test podobne ako na prednáške 4.10.
  • Bude zahŕňať učivo po dnešnú prednášku
  • Môžete si priniesť ťahák 1 list A4. Používanie počítača nebude povolené.

• Všímajte si varovania kompilátora, môžu vás upozorniť na chybu

main.cpp:15:22: warning: 
  array subscript 1 is above array bounds of 'char [1]' 
  [-Warray-bounds]
        char str[0];
        str [0] = '\n';

main.cpp:16:1: warning: 
  no return statement in function 
  returning non-void [-Wreturn-type]

main.cpp:12:31: warning: 
  comparison of integer expressions 
  of different signedness: 'int' and 'size_t' 
  {aka 'long unsigned int'} [-Wsign-compare]
 for (int i = 0; i < strlen(retazec); i ++) {

Opakovanie rekurzie

• Rekurzívna definícia: určitý objekt definujeme pomocou menších objektov toho istého typu
  • Napr. Fibonacciho čísla F(n) = F(n-1) + F(n-2)
  • Nezabudnime na triviálne prípady, napr. F(0)=0, F(1)=1

• Rekurzívne definície vieme často priamočiaro zapísať do rekurzívnych funkcií

int fib(int n){
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        return fib(n - 1) + fib(n - 2);
    }
}

• V rekurzívnej funkcii riešime problém pomocou menších podproblémov toho istého typu
  • Napríklad aby sme našli číslo x v utriedenom poli medzi indexami left a right, potrebujeme ho porovnať so stredným prvkom tohoto intervalu a potom riešiť tú istú úlohu pre menší interval
  • Aj keď sme pôvodne chceli hľadať prvok v celom poli, úlohu rozšírime o parametre left a right, aby sa dala spraviť rekurzia

int find(int a[], int left, int right, int x) {
    if (left > right) {
        return -1;
    }
    int index = (left + right) / 2;
    if (a[index] == x) {
        return index;
    }
    else if (a[index] < x) {
        return find(a, index+1, right, x);
    }
    else {
        return find(a, left, index - 1, x);
    }
}

Zásobník volaní

Druhý pohľad na rekurziu je dynamický: môžeme simulovať, čo sa v programe deje so zásobníkom volaní (call stack)

• Skúsme napríklad odsimulovať, čo sa deje ak vo funkcii main zavoláme fib(3)
• Kvôli prehľadnosti si fib rozpíšeme na viac riadkov:

#include <iostream>
using namespace std;

int fib(int n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        int a = fib(n - 1); // riadok (A)
        int b = fib(n - 2); // riadok (B)
        return a+b;
    }
}

int main() {
    int x = fib(3);    // riadok (C)
    cout << x << endl; 
}

Tu je priebeh programu (obsah zásobníka)

(1)          (2)                      (3)

                                       fib n=2
              fib n=3                  fib n=3, a=?, b=?, riadok A
main, x=?     main, x=?, riadok C      main, x=?, riadok C

(4)                             (5)
 
fib n=1                         
fib n=2, a=?, b=?, riadok A     fib n=2, a=1, b=?, riadok A
fib n=3, a=?, b=?, riadok A     fib n=3, a=?, b=?, riadok A
main, x=?, riadok C             main, x=?, riadok C             


(6)                             (7)
 
fib n=0                         
fib n=2, a=1, b=?, riadok B     fib n=2, a=1, b=0, riadok B
fib n=3, a=?, b=?, riadok A     fib n=3, a=?, b=?, riadok A
main, x=?, riadok C             main, x=?, riadok C             


(8)                             (9)

                                fib n=1
fib n=3, a=1, b=?, riadok A     fib n=3, a=1, b=?, riadok B 
main, x=?, riadok C             main, x=?, riadok C                 


(10)                            (11)

fib n=3, a=1, b=1, riadok B     
main, x=?, riadok C             main, x=2, riadok C 

Postupnosť volaní počas výpočtu vieme znázorniť aj stromovým diagramom:

Pozor, priamočiary rekurzívny zápis výpočtu Fibonacciho čísel je neefektívny, lebo výpočet Fibonacciho čísel sa opakuje

• Napr. pre n=5 počítame fib(2) trikrát, pre n=6 päťkrát a pre n=20 až 4181-krát

Vypisovanie variácií s opakovaním

Vypíšte všetky trojice cifier, pričom každá cifra je z množiny {0..n-1} a cifry sa môžu opakovať (variácie 3-tej triedy z n prvkov). Napr. pre n=2:

000
001
010
011
100
101
110
111

Veľmi jednoduchý program s troma cyklami:

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n;
    for(int i=0; i<n; i++) {
        for(int j=0; j<n; j++) {
            for(int k=0; k<n; k++) {
                cout << i << j << k << endl;
            }
        }
    }
}

Rekurzívne riešenie pre všeobecné k

Čo ak chceme k-tice pre všeobecné k? Využijeme rekurziu.

• Variácie k-tej triedy vieme rozdeliť na n skupín podľa prvého prvku:
  • tie čo začínajú na 0, tie čo začínajú na 1, ..., tie čo začínajú na n-1.
• V každej skupine ak odoberieme prvý prvok, dostaneme variácie triedy k-1

#include <iostream>
using namespace std;

void vypis(int a[], int k) {
    for (int i = 0; i < k; i++) {
        cout << a[i];
    }
    cout << endl;
}

void generuj(int a[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        vypis(a, k);
    } else {
        for (int x = 0; x < n; x++) {
            a[i] = x;
            generuj(a, i + 1, k, n);
        }
    }
}

int main() {
    const int maxK = 100;
    int a[maxK];
    int k, n;
    cout << "Zadajte k a n: ";
    cin >> k >> n;
    generuj(a, 0, k, n);
}

Strom rekurzívnych volaní pre k=3, n=2 (generuj je skrátené na gen, červenou je zobrazený obsah poľa a):

Ďalšie rozšírenia

• Čo ak chceme všetky k-tice písmen A-Z?
• Čo ak chceme všetky DNA reťazce dĺžky k (DNA pozostáva z "písmen" A,C,G,T)?

// pouzi n=26
void vypis(int a[], int k) {
    for (int i = 0; i < k; i++) {
        char c = 'A'+a[i];
        cout << c;
    }
    cout << endl;
}

// pouzi n=4
void vypis(int a[], int k) {
    char abeceda[5] = "ACGT";
    for (int i = 0; i < k; i++) {
        cout << abeceda[a[i]];
    }
    cout << endl;
}

Cvičenia

• Ako by sme vypisovali všetky k-ciferné hexadecimálne čísla (šestnástková sústava), kde používame cifry 0-9 a písmená A-F?
• Ako by sme vypisovali všetky k-tice písmen v opačnom poradí, od ZZZ po AAA?

Variácie bez opakovania

Teraz chceme vypísať všetky k-tice cifier z množiny {0, ..., n-1}, v ktorých sa žiaden prvok neopakuje (pre k=n dostávame permutácie)

Príklad pre k=3, n=3

012
021
102
120
201
210

Skúšanie všetkých možností

• Jednoduchá možnosť: použijeme predchádzajúci program a pred výpisom skontrolujeme, či je riešenie správne

Prvý pokus:

bool spravne(int a[], int k, int n) {
    /* je v poli a dlzky k kazde cislo 
     * od 0 po n-1 najviac raz? */
    bool bolo[maxN];
    for (int i = 0; i < n; i++) {
        bolo[i] = false;
    }
    for (int i = 0; i < k; i++) {
        if (bolo[a[i]]) return false;
        bolo[a[i]] = true;
    }
    return true;
}

void generuj(int a[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        if (spravne(a, k, n)) {
            vypis(a, k);
        }
    } else {
        for (int x = 0; x < n; x++) {
            a[i] = x;
            generuj(a, i + 1, k, n);
        }
    }
}

Cvičenie: ako by sme napísali funkciu spravne, ak by nedostala ako parameter hodnotu n?

Prehľadávanie s návratom, backtracking

• Predchádzajúce riešenie je neefektívne, lebo prechádza cez všetky variácie s opakovaním a veľa z nich zahodí.
  • Napríklad pre k=7 a n=10 pozeráme 10⁷ variácií s opakovaním, ale iba 604800 z nich je správnych, čo je asi 6%
• Len čo sa v poli a vyskytne opakujúca sa cifra, chceme túto vetvu prehľadávania ukončiť, lebo doplnením ďalších cifier problém neodstránime
• Spravíme funkciu moze(a,i,x), ktorá určí, či je možné na miesto i v poli a dať cifru x
• Testovanie správnosti vo funkcii generuj sa dá vynechať

bool moze(int a[], int i, int x) {
    /* Mozeme dat hodnotu x na poziciu i v poli a?
     * Mozeme, ak sa nevyskytuje v a[0..i-1] */
    for (int j = 0; j < i; j++) {
        if (a[j] == x) return false;
    }
    return true;
}

void generuj(int a[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        vypis(a, k);
    } else {
        for (int x = 0; x < n; x++) {
            if (moze(a, i, x)) {
                a[i] = x;
                generuj(a, i + 1, k, n);
            }
        }
    }
}

Možné zrýchlenie: vytvoríme trvalé pole bolo, v ktorom bude zaznamené, ktoré cifry sa už vyskytli a to použijeme namiesto funkcie moze.

• Po návrate z rekurzie nesmieme zabudúť príslušnú hodnotu odznačiť!

void generuj(int a[], bool bolo[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * v poli bolo su zaznamenane pouzite cifry,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        vypis(a, k);
    } else {
        for (int x = 0; x < n; x++) {
            if (!bolo[x]) {
                a[i] = x;
                bolo[x] = true;
                generuj(a, bolo, i + 1, k, n);
                bolo[x] = false;
            }
        }
    }
}

int main() {
    const int maxK = 100;
    const int maxN = 100;
    int a[maxK];
    bool bolo[maxN];
    int k, n;
    cout << "Zadajte k a n (k<=n): ";
    cin >> k >> n;
    for (int i = 0; i < n; i++) {
        bolo[i] = false;
    }
    generuj(a, bolo, 0, k, n);
}

Cvičenie: ako potrebujeme zmeniť program, aby sme generovali všetky postupnosti k cifier z množiny {0,..,n-1}, také, že z každej cifry sú v postupnosti najviac 2 výskyty?

Technika rekurzívneho prehľadávania všetkých možností s orezávaním beznádejných vetiev sa nazýva prehľadávanie s návratom alebo backtracking.

• Hľadáme všetky postupnosti, ktoré spĺňajú nejaké podmienky
  • Vo všeobecnosti nemusia byť rovnako dlhé
• Ak máme celú postupnosť, vieme otestovať, či spĺňa podmienku (funkcia spravne)
• Ak máme časť postupnosti a nový prvok, vieme otestovať, či po pridaní tohto prvku má ešte šancu tvoriť časť riešenia (funkcia moze)
  • Funkcia moze nesmie vrátiť false, ak ešte je možné riešenie
  • Môže vrátiť true, ak už nie je možné riešenie, ale nevie to ešte odhaliť
  • Snažíme sa však odhaliť problém čím skôr

Všeobecná schéma

void generuj(int a[], int i) {
    /* v poli a dlzky k mame prvych i cisel z riesenia */
    if (spravne(a, i)) { 
        /* ak uz mame cele riesenie, vypiseme ho */
        vypis(a, i);
    } else {
        pre vsetky hodnoty x {
            if (moze(a,i,x)) {
                a[i] = x;
                generuj(a, i + 1);
            }
        }
    }
}

Prehľadávanie s návratom môže byť vo všeobecnosti veľmi pomalé, čas výpočtu exponenciálne rastie.

Generovanie všetkých podmnožín

Chceme vypísať všetky podmnožiny množiny {0,..,m-1}. Na rozdiel od variácií nám v podmnožine nezáleží na poradí (napr. {0,1} = {1,0}), prvky teda budeme vždy vypisovať od najmenšieho po najväčší. Napr. pre m=2 máme podmnožiny

{}
{0}
{1}
{0,1}

Podmnožinu vieme vyjadriť ako binárne pole dĺžky m,

• a[i]=0 znamená, že i nepatrí do množiny a a[i]=1 znamená, že patrí.
• Napríklad podmnožina {0,2,3} množiny {0,1,2,3,4} sa zapíše ako pole 1,0,1,1,0.

Teda môžeme použiť program variácie s opakovaním pre n=2, k=m a zmeniť iba výpis:

void vypis(int a[], int m) {
    cout << "{";
    bool prve = true;
    for (int i = 0; i < m; i++) {
        if (a[i] == 1) {
            if (prve) {
                cout << "" << i;
                prve=false;
            } else {
                cout << "," << i;
            }
        }
    }
    cout << "}" << endl;
}

• V premennej prve si pamätáme, či máme oddeliť ďalšie vypisované číslo od predchádzajúceho.
  • Ak ešte žiadne nebolo, oddeľovač je prázdny reťazec.
  • Ak už sme niečo vypísali, oddeľovač je čiarka.

Namiesto poľa intov môžeme použiť pole boolovských hodnôt a celý program trochu prispôsobiť tomu, že generujeme podmnožiny:

#include <iostream>
#include <cstring>
using namespace std;

void vypis(bool a[], int m) {
    cout << "{";
    bool prve = true;
    for (int i = 0; i < m; i++) {
        if (a[i]) {
            if (prve) {
                cout << "" << i;
                prve=false;
            } else {
                cout << "," << i;
            }
        }
    }
    cout << "}" << endl;
}

void generuj(bool a[], int i, int m) {
    /* v poli a dlzky k mame rozhodnutie o prvych i
     * prvkoch, chceme vygenerovat vsetky podmnoziny
     * prvkov {i..m-1} */
    if (i == m) {
        vypis(a, m);
    } else {
        a[i] = true;
        generuj(a, i + 1, m);
        a[i] = false;
        generuj(a, i + 1, m);
    }
}

int main() {
    const int maxM = 100;
    int m;
    cin >> m;
    bool a[maxM];
    generuj(a, 0, m);
}

Pre n=3 program vypíše:

{0,1,2}
{0,1}
{0,2}
{0}
{1,2}
{1}
{2}
{}

Cvičenie: Čo by program vypísal, ak by sme prehodili true a false v rekurzii?

Generovanie podmnožín využijeme na budúcej prednáške na riešenie problému batoha, čo je jeden z dôležitých praktických problémov, pre ktoré nepoznáme efektívne algoritmy.

Problém 8 dám

Prehľadávanie s návratom sa dá využiť aj na riešenie rôznych hlavolamov. Tu si ukážeme jeden z nich.

Cieľom je rozmiestniť n dám na šachovnici nxn tak, aby sa žiadne dve navzájom neohrozovali, tj. aby žiadne dve neboli v rovnakom riadku, stĺpci, ani na rovnakej uhlopriečke.

Príklad pre n=4:

 . * . .
 . . . *
 * . . .
 . . * .

• V každom riadku bude práve jedna dáma, teda riešenie môžeme reprezentovať ako pole damy dĺžky n, kde damy[i] je stĺpec, v ktorom je dáma na riadku i
  • Príklad vyššie by v poli damy mal čísla 1,3,0,2
• Podobne ako pri generovaní variácií bez opakovania chceme do poľa dať čísla od 1 po n, aby spĺňali ďalšie podmienky (v každom stĺpci a na každej uhlopriečke najviac 1 dáma)
• Vytvoríme polia, kde si pre každý stĺpec a uhlopriečku pamätáme, či už je obsadená
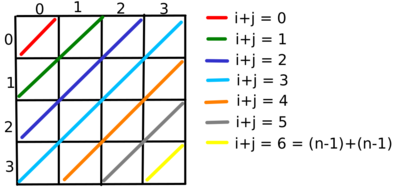
• Uhlopriečky v oboch smeroch očíslujeme číslami od 0 po 2n-2
  • V jednom smere majú miesta na uhlopriečke rovnaký súčet, ten teda bude číslom uhlopriečky
  • V druhom smere majú rovnaký rozdiel, ten však môže byť aj záporný, pričítame n-1
• Pre jednoduchosť použijeme niekoľko globálnych premenných, aby si rekurzívne funkcie nemuseli posielať veľa argumentov
  • Krajšie by bolo dať tieto premenné do struct-u a posielať ten ako argument

#include <iostream>
using namespace std;

/* globalne premenne */
const int maxN = 100;
int n;
int damy[maxN];       /* damy[i] je stlpec s damou v riadku i*/
bool bolStlpec[maxN]; /* bolStlpec[i] je true ak stlpec i obsadeny */

/* polia ktore obsahuju true ak uhlopriecky obsadene */
bool bolaUhl1[2 * maxN - 1];  
bool bolaUhl2[2 * maxN - 1];
int pocet;       /* pocet najdenych rieseni */

int uhl1(int i, int j) {
    /* na ktorej uhlopriecke je riadok i, stlpec j v smere 1? */
    return i + j;
}

int uhl2(int i, int j) {
    /* na ktorej uhlopriecke je riadok i, stlpec j v smere 2? */
    return n - 1 + i - j;
}

void vypis() {
    /* vypis sachovnicu textovo a zvys pocitadlo rieseni */
    pocet++;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (damy[i] == j) cout << " *";
            else cout << " .";
        }
        cout << endl;
    }
    cout << endl;
}

void generuj(int i) {
    /* v poli damy mame prvych i dam, dopln dalsie */
    if (i == n) {
        vypis();
    } else {
        for (int j = 0; j < n; j++) {
            /* skus dat damu na riadok i, stlpec j */
            if (!bolStlpec[j]
                && !bolaUhl1[uhl1(i, j)] 
                && !bolaUhl2[uhl2(i, j)]) {
                damy[i] = j;
                bolStlpec[j] = true;
                bolaUhl1[uhl1(i, j)] = true;
                bolaUhl2[uhl2(i, j)] = true;
                generuj(i + 1);
                bolStlpec[j] = false;
                bolaUhl1[uhl1(i, j)] = false;
                bolaUhl2[uhl2(i, j)] = false;
            }
        }
    }
}

int main() {
    cout << "Zadajte velkost sachovnice: ";
    cin >> n;
    for (int i = 0; i < n; i++) {
        bolStlpec[i] = false;
    }
    for (int i = 0; i < 2 * n + 1; i++) {
        bolaUhl1[i] = false;
        bolaUhl2[i] = false;
    }

    /* rekuzia */
    pocet = 0;
    generuj(0);
    cout << "Pocet rieseni: " << pocet << endl;
}

Zhrnutie

• Videli sme ako rekurzívne generovať všetky postupnosti spĺňajúce určité požiadavky
• Ak máme špeciálne požiadavky, napr. že žiadne číslo sa neopakuje, môžeme buď generovať všetky k-tice a testovať to pred výpisom, alebo už počas generovania urezávať neperspektívne vetvy výpočtu, čo je rýchlejšie
• Táto technika sa volá prehľadávanie s návratom (backtracking)
• Pozor, čas výpočtu prudko (exponenciálne) rastie s dĺžkou postupností, takže vhodné len pre malé vstupy.
• Dve ukážky: problém 8 dám, problém batoha (budúca prednáška),