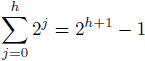Programovanie (1) v C/C++
1-INF-127, ZS 2024/25
Prednáška 20: Rozdiel medzi revíziami
| Riadok 122: | Riadok 122: | ||
* Celkovo veľmi jednoduchý a prirodzený výpočet, nie je potrebný explicitný zásobník | * Celkovo veľmi jednoduchý a prirodzený výpočet, nie je potrebný explicitný zásobník | ||
| − | Rekurziu budeme používať vždy, keď potrebujeme prejsť všetky uzly stromu | + | Rekurziu budeme používať vždy, keď potrebujeme prejsť všetky uzly stromu. Cyklom sa to programuje ťažko, lebo z uzla potrebujeme ísť doľava aj doprava. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 212: | Riadok 212: | ||
=== Vytvorenie stromu z postfixového výrazu === | === Vytvorenie stromu z postfixového výrazu === | ||
| − | Pripomeňme si z [[ | + | Pripomeňme si z [[Prednáška 19|minulej prednášky]] funkciu na vyhodnocovanie postfixového výrazu: |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
typedef double dataType; | typedef double dataType; | ||
| Riadok 381: | Riadok 381: | ||
/* Uzol binarneho stromu */ | /* Uzol binarneho stromu */ | ||
struct node { | struct node { | ||
| − | + | // hodnota ulozena v uzle | |
| − | + | dataType data; | |
| − | node * | + | |
| + | // smernik na lave dieta (NULL, ak toto dieta neexistuje) | ||
| + | node *left; | ||
| + | |||
| + | // smernik na prave dieta (NULL, ak toto dieta neexistuje) | ||
| + | node *right; | ||
}; | }; | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 433: | Riadok 438: | ||
=== Výška binárneho stromu === | === Výška binárneho stromu === | ||
| − | ''Hĺbkou uzla'' binárneho stromu nazveme jeho vzdialenosť od koreňa. Koreň má teda hĺbku ''0'', jeho | + | ''Hĺbkou uzla'' binárneho stromu nazveme jeho vzdialenosť od koreňa. Koreň má teda hĺbku ''0'', jeho deti majú hĺbku ''1'', atď. ''Výškou binárneho stromu'' potom nazveme maximálnu hĺbku niektorého z jeho vrcholov. Strom s jediným vrcholom má teda hĺbku ''0''; pre ostatné stromy je ich výška daná ako 1 plus maximum z výšok ľavého a pravého podstromu. |
Nasledujúca funkcia počíta výšku stromu (kvôli elegancii zápisu pritom pracuje s rozšírením definície výšky stromu na prázdne stromy, za ktorých výšku sa považuje číslo ''-1''). | Nasledujúca funkcia počíta výšku stromu (kvôli elegancii zápisu pritom pracuje s rozšírením definície výšky stromu na prázdne stromy, za ktorých výšku sa považuje číslo ''-1''). | ||
| Riadok 443: | Riadok 448: | ||
return -1; | return -1; | ||
} | } | ||
| − | int hLeft = height(root->left); | + | // rekurzivne spocita vysku laveho a praveho podstromu |
| − | int hRight = height(root->right); // | + | int hLeft = height(root->left); |
| − | if (hLeft >= hRight) { | + | int hRight = height(root->right); |
| + | // vrati max(hLeft, hRight) + 1 | ||
| + | if (hLeft >= hRight) { | ||
return hLeft + 1; | return hLeft + 1; | ||
} else { | } else { | ||
| Riadok 453: | Riadok 460: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Pre výšku ''h'' binárneho stromu s ''n'' uzlami | + | Cvičenie: prepíšte funkciu tak, aby triviálnym prípadom bol list, nie prázdny strom. Funkcia teda vždy dostane smerník na neprázdny strom a nebude volať rekurziu na prázdne podstromy. |
| + | |||
| + | === Aká môže byť výška binárneho stromu? === | ||
| + | |||
| + | Pre výšku ''h'' binárneho stromu s ''n'' uzlami platia nasledujúce vzťahy: | ||
* Určite ''h ≤ n-1''. Tento prípad nastáva, ak sú všetky uzly „navešané jeden pod druhý”. | * Určite ''h ≤ n-1''. Tento prípad nastáva, ak sú všetky uzly „navešané jeden pod druhý”. | ||
* Strom s výškou ''h'' má najviac | * Strom s výškou ''h'' má najviac | ||
Verzia zo dňa a času 12:24, 28. november 2022
Oznamy
- Tretiu domácu úlohu treba odovzdať do budúceho pondelka 5.12. 22:00.
- Príďte v piatok na cvičenia, ak potrebujete pomôcť s DÚ alebo s príkladmi z cvičení.
- Dnes a budúci pondelok ešte prednášky v normálnom režime
- Budúcu stredu 7.12. v prvej polovici prednášky informácie k skúške a rady k skúškovému všeobecne, potom doberieme posledné učivo
- Posledný týždeň semestra v pondelok 12.12. nepovinná prednáška o nepreberaných črtách jazykov C a C++, v stredu 14.12. cez prednášku semestrálny test
- Cvičenia bežia normálne každý utorok, piatkové cvičenia už iba 2x
Semestrálny test
- Treba získať aspoň 50% bodov
- Opravný termín v januári
- Môžete si priniesť ťahák v rozsahu 1 listu A4
- Na semestrálnom teste budú podobné typy príkladov, aké poznáte z teoretických cvičení, napríklad napíšte funkciu, ktorá robí zadanú činnosť, doplňte chýbajúce časti funkcie, zistite, čo funkcia robí.
- Vyskytnú sa ale aj príklady, kde je úlohou napísať, ako bude na nejakom vstupe fungovať algoritmus alebo dátová štruktúra z prednášky. Ukážky takýchto príkladov nájdete na stránke Zimný semester, semestrálny test
Termíny skúšok
- Piatok 16.12. 13:10 v H6 a H3
- Pondelok 9.1. 13:00 v H6 a H3
- Utorok 17.1. 13:00 v H6 a H3, hlavne 1. opravný termín
- Pondelok 30.1. 13:00 v H6, hlavne 2. opravný termín
Na termíny sa bude dať prihlasovať od dnes 20:00
- Kapacita termínov bude obmedzená, prihláste sa teda radšej skôr, neskôr to môžete zmeniť
- Hláste sa iba na jeden termín!
- Ak vidíte konflikt niektorého termínu s hromadnou skúškou alebo písomkou z iného predmetu, dajte mi prosím vedieť čím skôr, najlepšie ešte dnes
- Decembrový termín odporúčame hlavne študentom, ktorým programovanie nerobí problémy
Aritmetické stromy
Aritmetické výrazy možno reprezentovať aj vo forme stromu nazývaného aj aritmetickým stromom:
- Operátory a čísla tvoria tzv. uzly (alebo vrcholy) stromu.
- Operátory tvoria tzv. vnútorné uzly stromu, každý z nich má dve deti zodpovedajúce podvýrazom pre jednotlivé operandy.
- Čísla tvoria tzv. listy aritmetického stromu, tie už nemajú žiadne deti.
- Strom obsahuje jediný uzol, ktorý nemá rodiča. Tento sa nazýva koreň stromu a reprezentuje celý aritmetický výraz.
- Informatici stromy väčšinou kreslia „hore nohami”, s koreňom na vrchu.
Uzol aritmetického stromu tak môžeme reprezentovať napríklad nasledujúcou štruktúrou:
struct treeNode {
// ciselna hodnota (zmysluplna len v listoch)
double val;
// operator vo vnutornych uzloch, pre listy rovny medzere
char op;
// smernik na koren podstromu reprezentujuceho lavy podvyraz
// alebo NULL v liste
treeNode *left;
// smernik na koren podstromu reprezentujuceho pravy podvyraz
// alebo NULL v liste
treeNode *right;
};
Pre vnútorné uzly stromu (zodpovedajúce operátorom) pritom:
- Smerníky left a right budú ukazovať na korene podstromov reprezentujúcich ľavý resp. pravý podvýraz.
- Znak op bude zodpovedať danému operátoru (napríklad '+').
- Hodnota val ostane nevyužitá.
Pre listy (zodpovedajúce číselným hodnotám) naopak:
- Smerníky left a right budú mať hodnotu NULL.
- Znak op bude medzera ' ' (podľa op teda môžeme rozlišovať, či ide o číslo alebo o operátor).
- Vo val bude uložená hodnota daného čísla.
Celý strom pritom budeme reprezentovať jeho koreňom.
Ide tu o jednoduchú, no nie veľmi elegantnú reprezentáciu aritmetických stromov, keďže viaceré položky štruktúry treeNode môžu byť nevyužité. S využitím objektového programovania (letný semester) možno aritmetické stromy reprezentovať omnoho krajšie.
Vytvorenie uzlu aritmetického stromu
Nasledujúce funkcie vytvoria nový vnútorný uzol (pre operátor) resp. nový list (pre číslo):
treeNode *createOp(char op, treeNode *left, treeNode *right) {
treeNode *v = new treeNode;
v->left = left;
v->right = right;
v->op = op;
return v;
}
treeNode *createNum(double val) {
treeNode *v = new treeNode;
v->left = NULL;
v->right = NULL;
v->op = ' ';
v->val = val;
return v;
}
„Ručne” teraz môžeme vytvoriť strom pre výraz (65 – 3 * 5)/(2 + 3):
treeNode *root = createOp('/',
createOp('-',
createNum(65),
createOp('*', createNum(3), createNum(5))),
createOp('+', createNum(2), createNum(3)));
Alebo po častiach:
treeNode *v65 = createNum(65);
treeNode *v3 = createNum(3);
treeNode *v5 = createNum(5);
treeNode *v2 = createNum(2);
treeNode *v3b = createNum(3);
treeNode *vKrat = createOp('*', v3, v5);
treeNode *vMinus = createOp('-', v65, vKrat);
treeNode *vPlus = createOp('+', v2, v3b);
treeNode *vDeleno = createOp('/', vMinus, vPlus);
Vyhodnotenie výrazu reprezentovaného stromom
Nasledujúca rekurzívna funkcia vypočíta hodnotu aritmetického výrazu reprezentovaného stromom s koreňom root.
- Ak je zadaný vrchol listom, vrátime hodnotu uloženú v položke val
- V opačnom prípade rekurzívne spočítame hodnoty pre obidva podvýrazy a skombinujeme ich podľa typu znamienka
- Celkovo veľmi jednoduchý a prirodzený výpočet, nie je potrebný explicitný zásobník
Rekurziu budeme používať vždy, keď potrebujeme prejsť všetky uzly stromu. Cyklom sa to programuje ťažko, lebo z uzla potrebujeme ísť doľava aj doprava.
double evaluateTree(treeNode *root) {
assert(root != NULL);
if (root->op == ' ') {
return root->val;
} else {
double valLeft = evaluateTree(root->left);
double valRight = evaluateTree(root->right);
switch (root->op) {
case '+':
return valLeft + valRight;
break;
case '-':
return valLeft - valRight;
break;
case '*':
return valLeft * valRight;
break;
case '/':
return valLeft / valRight;
break;
default:
assert(false);
break;
}
}
return 0; // realne nedosiahnutelny prikaz
}
Uvoľnenie pamäte
Nasledujúca funkcia uvoľní z pamäte celý strom s koreňom root:
void destroyTree(treeNode *root) {
if (root != NULL) {
destroyTree(root->left);
destroyTree(root->right);
delete root;
}
}
Vypísanie výrazu reprezentovaného stromom v rôznych notáciách
Infixovú, prefixovú, resp. postfixovú reprezentáciu aritmetického výrazu reprezentovaného stromom s koreňom root možno získať pomocou nasledujúcich funkcií:
void printInorder(FILE *fw, treeNode *root) {
if (root->op == ' ') {
fprintf(fw, "%.2f", root->val);
} else {
fprintf(fw, "(");
printInorder(fw, root->left);
fprintf(fw, " %c ", root->op);
printInorder(fw, root->right);
fprintf(fw, ")");
}
}
void printPreorder(FILE *fw, treeNode *root) {
if (root->op == ' ') {
fprintf(fw, "%.2f ", root->val);
} else {
fprintf(fw, "%c ", root->op);
printPreorder(fw, root->left);
printPreorder(fw, root->right);
}
}
void printPostorder(FILE *fw, treeNode *root) {
if (root->op == ' ') {
fprintf(fw, "%.2f ", root->val);
} else {
printPostorder(fw, root->left);
printPostorder(fw, root->right);
fprintf(fw, "%c ", root->op);
}
}
Vytvorenie stromu z postfixového výrazu
Pripomeňme si z minulej prednášky funkciu na vyhodnocovanie postfixového výrazu:
typedef double dataType;
/* Sem pride definicia struktury pre zasobnik a vsetkych funkcii poskytovanych zasobnikom. */
double evaluatePostfix(char *expr) {
stack s;
init(s);
int i = 0;
while (true) {
while (expr[i] != 0 && expr[i] != '\n' && isspace(expr[i])) {
i++;
}
if (expr[i] == 0 || expr[i] == '\n') {
break;
} else if (isdigit(expr[i])) {
double num;
sscanf(&expr[i], "%lf", &num);
push(s, num);
while (isdigit(expr[i]) || expr[i] == '.') {
i++;
}
} else {
double num2 = pop(s);
double num1 = pop(s);
switch (expr[i]) {
case '+':
push(s, num1 + num2);
break;
case '-':
push(s, num1 - num2);
break;
case '*':
push(s, num1 * num2);
break;
case '/':
push(s, num1 / num2);
break;
}
i++;
}
}
double result = pop(s);
assert(isEmpty(s));
destroy(s);
return result;
}
Túto funkciu možno jednoducho prepísať tak, aby namiesto vyhodnocovania výrazu konštruovala zodpovedajúci aritmetický strom. Namiesto hodnôt jednotlivých podvýrazov stačí na zásobníku uchovávať korene stromov, ktoré tieto podvýrazy reprezentujú. Aplikácii aritmetickej operácie potom bude zodpovedať „spojenie” dvoch podstromov do jedného stromu:
typedef treeNode *dataType;
/* Sem pride definicia struktury pre zasobnik a vsetkych funkcii poskytovanych zasobnikom. */
treeNode *parsePostfix(char *expr) {
stack s;
init(s);
int i = 0;
while (true) {
while (expr[i] != 0 && expr[i] != '\n' && isspace(expr[i])) {
i++;
}
if (expr[i] == 0 || expr[i] == '\n') {
break;
} else if (isdigit(expr[i])) {
double num;
sscanf(&expr[i], "%lf", &num);
push(s, createNum(num));
while (isdigit(expr[i]) || expr[i] == '.') {
i++;
}
} else {
treeNode *right = pop(s);
treeNode *left = pop(s);
push(s, createOp(expr[i], left, right));
i++;
}
}
treeNode *result = pop(s);
assert(isEmpty(s));
destroy(s);
return result;
}
Ukážkový program pracujúci s aritmetickými stromami
Nasledujúci program prečíta z konzoly aritmetický výraz v postfixovom tvare, skonštruuje jeho aritmetický strom a následne preň zavolá funkcie na výpočet hodnoty výrazu a jeho výpis v rôznych notáciách:
int main(void) {
char expr[100];
fgets(expr, 100, stdin);
treeNode *root = parsePostfix(expr);
printf("Hodnota vyrazu je: %.2f\n", evaluateTree(root));
printf("Vyraz v infixovej notacii: ");
printInorder(stdout, root);
printf("\n");
printf("Vyraz v prefixovej notacii: ");
printPreorder(stdout, root);
printf("\n");
printf("Vyraz v postfixovej notacii: ");
printPostorder(stdout, root);
printf("\n");
destroyTree(root);
}
Binárne stromy
Aritmetické stromy sú špeciálnym prípadom binárnych stromov. V informatike nachádzajú binárne stromy množstvo rozličných uplatnení. Ukážeme si teda všeobecnú dátovú štruktúru binárneho stromu.
Terminológia stromov
- Strom obsahuje množinu uzlov alebo vrcholov prepojených hranami. (uzol angl. node, vrchol vertex, hrana edge).
- Ak je strom neprázdny, jeden jeho vrchol nazývame koreň (angl. root)
- Každý uzol u okrem koreňa je spojený hranou s práve jedným rodičom (angl. parent), ktorým je nejaký uzol v. Naopak uzol u je dieťaťom (angl. child) uzla v.
- Vo všeobecnom strome môže mať každý uzol ľubovoľný počet detí (aj nula)
- Strom je binárny, ak má každý uzol najviac dve deti. Budeme pritom rozlišovať medzi pravým a ľavým dieťaťom.
Takéto stromy sa nazývajú zakorenené. Presnejšiu matematickú definíciu zakorenených aj nezakorenených stromov uvidíte na predmete Úvod do kombinatoriky a teórie grafov (letný semester).
- Uzly zakoreneného stromu, ktoré nemajú žiadne dieťa, nazývame listami; zvyšné uzly potom nazývame vnútornými uzlami.
- Predkom uzla u nazveme ľubovoľný uzol v ležiaci na ceste z u do koreňa stromu (vrátane u a koreňa). Naopak potom hovoríme, že u je potomkom uzla v.
- Podstromom stromu T zakoreneným v nejakom uzle v stromu T budeme rozumieť strom s koreňom v pozostávajúci zo všetkých jeho potomkov a všetkých hrán stromu T vedúcich medzi týmito uzlami.
Každý binárny strom je teda buď prázdny, alebo je tvorený jeho koreňom a dvoma podstromami – ľavým a pravým.
Štruktúra pre uzol binárneho stromu
V nasledujúcom budeme pracovať výhradne s binárnymi stromami. Štruktúra pre uzol všeobecného binárneho stromu je podobná, ako pri aritmetických stromoch – namiesto operátora alebo hodnoty si však v každom uzle môžeme pamätať hodnotu ľubovoľného typu dataType.
Keďže neskôr budeme binárne stromy vypisovať, budeme predpokladať, že pre hodnoty typu dataType máme k dispozícii funkciu printDataType, ktorá ich v nejakom vhodnom formáte vypisuje. Nasledujúci kus kódu zodpovedá situácii, keď dataType je int.
#include <cstdio>
using namespace std;
// ...
/* Typ prvkov ukladanych v uzloch binarneho stromu -- moze byt prakticky lubovolny */
typedef int dataType;
/* Funkcia pre vypis hodnoty typu dataType */
void printDataType(dataType d) {
printf("%d ", d); // pre int
}
// ...
/* Uzol binarneho stromu */
struct node {
// hodnota ulozena v uzle
dataType data;
// smernik na lave dieta (NULL, ak toto dieta neexistuje)
node *left;
// smernik na prave dieta (NULL, ak toto dieta neexistuje)
node *right;
};
Vytvorenie binárneho stromu
Nasledujúca funkcia vytvorí uzol binárneho stromu s dátami data, ľavým podstromom zakoreneným v uzle *left a pravým podstromom zakoreneným v uzle *right (parametre left a right sú teda smerníkmi na uzly). Ako výstup funkcia vráti smerník na novovytvorený uzol.
/* Vytvori uzol binarneho stromu */
node *createNode(dataType data, node *left, node *right) {
node *v = new node;
v->data = data;
v->left = left;
v->right = right;
return v;
}
Nasledujúca volanie tak napríklad vytvorí binárny strom so šiestimi uzlami zakorenený v uzle *root.
node *root = createNode(1,
createNode(2,
createNode(3, NULL, NULL),
createNode(4,NULL,NULL)),
createNode(5,
NULL,
createNode(6, NULL, NULL)));
Cvičenie: nakreslite binárny strom vytvorený predchádzajúcim volaním.
Likvidácia binárneho stromu
Nasledujúca rekurzívna funkcia zlikviduje celý podstrom zakorenený v uzle *root (t. j. pouvoľňuje pamäť pre všetky jeho uzly).
/* Zlikviduje podstrom s korenom *root (pouvolnuje pamat) */
void destroyTree(node *root) {
if (root != NULL) {
destroyTree(root->left);
destroyTree(root->right);
delete root;
}
}
Výška binárneho stromu
Hĺbkou uzla binárneho stromu nazveme jeho vzdialenosť od koreňa. Koreň má teda hĺbku 0, jeho deti majú hĺbku 1, atď. Výškou binárneho stromu potom nazveme maximálnu hĺbku niektorého z jeho vrcholov. Strom s jediným vrcholom má teda hĺbku 0; pre ostatné stromy je ich výška daná ako 1 plus maximum z výšok ľavého a pravého podstromu.
Nasledujúca funkcia počíta výšku stromu (kvôli elegancii zápisu pritom pracuje s rozšírením definície výšky stromu na prázdne stromy, za ktorých výšku sa považuje číslo -1).
/* Spocita vysku podstromu s korenom *root. Pre root == NULL vrati -1. */
int height(node *root) {
if (root == NULL) {
return -1;
}
// rekurzivne spocita vysku laveho a praveho podstromu
int hLeft = height(root->left);
int hRight = height(root->right);
// vrati max(hLeft, hRight) + 1
if (hLeft >= hRight) {
return hLeft + 1;
} else {
return hRight + 1;
}
}
Cvičenie: prepíšte funkciu tak, aby triviálnym prípadom bol list, nie prázdny strom. Funkcia teda vždy dostane smerník na neprázdny strom a nebude volať rekurziu na prázdne podstromy.
Aká môže byť výška binárneho stromu?
Pre výšku h binárneho stromu s n uzlami platia nasledujúce vzťahy:
- Určite h ≤ n-1. Tento prípad nastáva, ak sú všetky uzly „navešané jeden pod druhý”.
- Strom s výškou h má najviac
- Z toho h ≥ log2(n+1)-1.
- Dostávame teda log2(n+1)-1 ≤ h ≤ n-1.
- Napríklad strom s milión vrcholmi má teda hĺbku medzi 19 a 999999.
Prehľadávanie stromov a vypisovanie ich uzlov
Často je potrebné prejsť celý strom a spracovať (napríklad vypísať) hodnoty vo všetkých uzloch. Toto prehľadávanie možno, podobne ako pri aritmetických stromoch, realizovať v troch základných poradiach: preorder, inorder a postorder.
/* Vypise podstrom s korenom *root v poradi preorder */
void printPreorder(node *root) {
if (root == NULL) {
return;
}
printDataType(root->data);
printPreorder(root->left);
printPreorder(root->right);
}
/* Vypise podstrom s korenom *root v poradi inorder */
void printInorder(node *root) {
if (root == NULL) {
return;
}
printInorder(root->left);
printDataType(root->data);
printInorder(root->right);
}
/* Vypise podstrom s korenom *root v poradi postorder */
void printPostorder(node *root) {
if (root == NULL) {
return;
}
printPostorder(root->left);
printPostorder(root->right);
printDataType(root->data);
}
Príklad: plné binárne stromy
Binárny strom výšky h s maximálnym počtom vrcholov 2h+1-1 sa nazýva plný binárny strom. Nasledujúca funkcia createFullTree vytvorí takýto strom a vráti smerník na jeho koreň. Jeho uzlom pritom priradí po dvoch rôzne hodnoty typu int (predpokladáme teda, že dataType je int) podľa globálnej premennej count.
// ...
int count;
/* Vytvori plny binarny strom vysky height s datami uzlov count, count + 1, ... */
node *createFullTree(int height) {
if (height == -1) {
return NULL;
}
node *v = createNode(count++, NULL, NULL);
v->left = createFullTree(height - 1);
v->right = createFullTree(height - 1);
return v;
}
int main(void) {
count = 1;
node *root = createFullTree(3);
printf("Vyska: %d\n", height(root));
printf("Inorder: ");
printInorder(root);
printf("\n");
printf("Preorder: ");
printPreorder(root);
printf("\n");
printf("Postorder: ");
printPostorder(root);
printf("\n");
destroyTree(root);
return 0;
}
Cvičenie: opíšte poradie, v ktorom sa v uvedenom programe jednotlivým uzlom priraďujú ich hodnoty.