CB02
Z MBI
Obsah
Úvod do pravdepodobnosti
- Myšlienkový experiment, v ktorom vystupuje náhoda, napr. hod ideálnou kockou/korunou
- Výsledkom experimentu je nejaká hodnota (napr. číslo, alebo aj niekoľko čísel, reťazec)
- Túto neznámu hodnotu budeme volať náhodná premenná
- Zaujíma nás pravdepodobnosť, s akou náhodná premenná nadobúda jednotlivé možné hodnoty
- T.j. ak experiment opakujeme veľa krát, ako často uvidíme nejaký výsledok
Príklad 1: hodíme idealizovanou kockou, premenná X bude hodnota, ktorú dostaneme
- Možné hodnoty 1,2,..,6, každá rovnako pravdepodobná
- Píšeme napr. Pr(X=2)=1/6
Príklad 2: hodíme 2x kockou, náhodná premenná X bude súčet hodnôt, ktoré dostaneme
- Možné hodnoty: 2,3,...,12
- Každá dvojica hodnôt (1,1), (1,2),...,(6,6) na kocke rovnako pravdepodobná, t.j. pravdepodobnosť 1/36
- Súčet 5 môžeme dostať 1+4,2+3,3+2,4+1 - t.j. P(X=5) = 4/36
- Súčet 11 môžeme dostať 5+6 alebo 6+5, t.j. P(X=11) = 2/36
- Rozdelenie pravdepodobnosti: (tabuľka udávajúca pravdepodobnosť pre každú možnú hodnotu)
hodnota i: 2 3 4 5 6 7 8 9 10 11 12 Pr(X=i): 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36
- Overte, ze súčet pravdepodobností je 1
Stredná hodnota E(X):
- priemer z možných hodnôt váhovaných ich pravdepodobnosťami
- v našom príklade
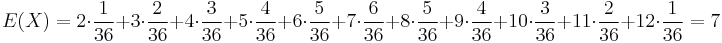
- Ak by sme experiment opakovali veľa krát a zrátali priemer hodnôt X, ktoré nám vyšli, dostali by sme číslo blízke E(X)
- Iný výpočet strednej hodnoty:
- X=X1+X2, kde X1 je hodnota na prvej kocke a X2 je hodnota na druhej kocke
-
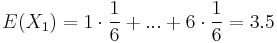 , podobne aj E(X2) = 3.5
, podobne aj E(X2) = 3.5
- Platí, že E(X1+X2)=E(X1) + E(X2) a teda E(X) = 3.5 + 3.5 = 7
- Pozor, pre súčin a iné funkcie takéto vzťahy platiť nemusia, napr.
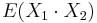 nie je vždy
nie je vždy 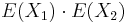
Pravdepodobnostný model náhodnej sekvencie
- Napríklad chceme modelovať náhodnú DNA sekvenciu dĺžky n s obsahom GC 40%
- Máme vrece s guľôčkami označenými A,C,G,T, pričom guľôčok označených A je 30%, C 20%, G 20% a T 30%.
- Vytiahneme guľôčku, zapíšeme si písmeno, hodíme ju naspäť, zamiešame a opakujeme s ďalším písmenom atď, až kým nevygenerujeme n písmen
- Vytiahnime z mechu 2x guľôčku. Prvé písmeno, ktoré nám vyjde, označme X1 a druhé X2
- Pr(X1=A) = 0.3, Pr(X2=C)=0.2
- Pr(X1=A a X2=C) = Pr(X1=A)*Pr(X2=C) = 0.3*0.2 = 0.06
- T.j. šanca, že dostaneme sekvenciu AC po dvoch ťahoch je 6%
- Ak rátame pravdepodobnosť, že sa dve nezávislé udalosti stanú súčasne, ich pravdepodobnosti násobíme. V tomto prípade to, či X1=A je nezávislé od toho, či X2=C
- Pr(X1 je A alebo C) = Pr(X1=A)+Pr(X1=C) = 0.3+0.2 = 0.5
- Pravdepodobnosť, že prvé písmeno bude A alebo C je 50%
- Pravdepodobnosti navzájom sa vylučujúcich udalostí (X1=A a X1=C) sa môžu sčítať, čím dostaneme pravdepodobnosť, že aspoň jedna z nich nastane
- Pr(v sekvencii je aspoň jedno A) = Pr(X1=A alebo X2=A) nemôžeme počítať ako Pr(X1=A)+Pr(X2=A), lebo sa navzájom nevylučujú a prípad, že X1=A a X2=A by sme započítali dvakrát
- Správne je Pr(X1 je A alebo X2 je A) = Pr(X1=A) + Pr(X1 <> A a X2=A) = Pr(X1=A) + Pr(X1 <> A) * Pr(X2=A) = 0.3+0.7*0.3 = 0.51
- Pr(X1=X2) = Pr(X1=X2=A) + Pr(X1=X2=C) + Pr(X1=X2=G) + Pr(X1=X2=T) = 0.3*0.3+0.2*0.2+0.2*0.2+0.3*0.3 = 0.26.
- Ak u označíme pravdepodobnosť u = Pr(X1=A)=Pr(X1=T)=Pr(X2=A)=Pr(X2=T) a v=Pr(X1=C)=Pr(X1=G)=Pr(X2=C)=Pr(X2=G), aký bude vzorec pre Pr(X1=X2)?
Príklad použitia modelu: Máme krátky primer AACAT. Koľko bude mať v priemere výskytov v sekvencii dĺžky 1000 v našom modeli?
- Pravdepodobnosť, ze AACAT je v náhodnej sekvencii hneď na začiatku je Pr(X1=A a X2=A a X3=C a X4=A a X5=A) = 0.3*0.3*0.2*0.3*0.3 = 0.00162
- Rovnaká pravdepodobnosť aj na pozícii 2,3,...996
- Nech V je počet výskytov v celej sekvencii (náhodná premenná s možnými hodnotami 0,1,...,996, aj keď napr. 996 to určite nemôže byť)
- Ideálne by sme chceli spočítať celú tabuľku pravdepodobností pre V, ale uspokojíme sa aj so strednou hodnotou E(V)
- Nech Vi je počet výskytov na pozícii i (co je vzdy 0 alebo 1)
-
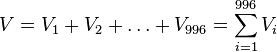
-
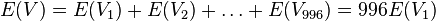
-
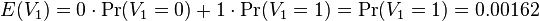
- E(V) = 996*0.00162 = 1.61352
- Takze primer AACAT sa v priemere bude v náhodnej sekvencii dĺžky 1000 s 40% obsahom GC vyskytovať v priemere cca 1,6 krát
- Primery byvaju dlhsie, takze sanca nahodnych vyskytov je ovela mensia, co je to co vacsinou chceme (chceme primer cielit na konkretnu poziciu, nie na vela nahodnych zhod)
Použitie pravdepodobnosti na analýzu potrebného pokrytia pri sekvenovaní
Pozri cvičenia pre informatikov
Dynamické programovanie
- Túto techniku uvidíme na ďalšej prednáške na hľadanie zarovnaní (alignments)
- Uvažujme problém platenia pomocou najmenšieho počtu mincí
- Napr. máme mince hodnoty 1,2,5 centov, z každej dostatok kusov
- Ako môžeme zaplatiť určitú sumu, napr. 13 centov, s čo najmenším počtom mincí?
- Aké je riešenie? 5+5+2+1 (4 mince)
- Všeobecná formulácia:
- Vstup: hodnoty k mincí m_1,m_2,...,m_k a cieľová suma X (všetko kladné celé čísla)
- Výstup: najmenší počet mincí, ktoré potrebujeme na zaplatenie X
- V našom príklade k=3, m_1 = 1, m_2 = 2, m_3 = 5, X=13
- Jednoduchý spôsob riešenia: použi najväčšiu mincu, ktorá je najviac X, odčítaj od X, opakuj
- Príklad: najprv použijeme mincu 5, zostane X=8, použijeme opäť mincu 5, zostane X=3, použijeme mincu 2, zostane X=1, použijeme mincu 1.
- Nefunguje vždy: zoberme mince hodnôt 1,3,4. Pre X=6 najlepšie riešenie je 2 mince: 3+3, ale náš postup (algoritmus) nájde 3 mince 4+1+1
- Ukážeme si algoritmus na základe dyn. programovania, ktorý pre každý vstup nájde najlepšie riešenie
- Zrátame najlepší počet mincí nielen pre X, ale pre všetky možné cieľové sumy 1,2,3,...,X-1,X
- To sa zdá byť ťažšia úloha, ale ukáže sa, že z riešenia pre menšie sumy vieme zostaviť riešenie pre väčšie sumy, takže nám to vlastne pomôže
- Spravíme si tabuľku, kde si pre každú sumu i=0,1,2,...X pamätáme A[i]=najmenší počet mincí, ktoré treba na vyplatenie sumy i
- Ukážme si to na príklade s mincami 1,3,4
i 0 1 2 3 4 5 6 7 8 9 A[i] 0 1 2 1 1 2 2 2 2 3
- Nevypĺňali sme ju žiadnym konkrétnym postupom, nejde o algoritmus
- Ale predstavme si, ze teraz chceme vyplniť A[10].
- V najlepšom riešení je prvá minca, ktorú použijeme 1,3, alebo 4
- ak je prvá minca 1, máme ešte zaplatiť sumu 10-1=9, tú podľa tabuľky vieme najlepšie zaplatiť na 3 mince, takže potrebujeme 4 mince na zaplatenie 10
- ak je prvá minca 3, máme ešte zaplatiť 10-3 = 7, na čo potrebujeme podla tabuľky 2 mince, takže spolu 3 mince na zaplatenie 10
- ak je prvá minca 4, máme ešte zaplatiť 10-4 = 6, na čo treba 2 mince, t.j. 3 mince na 10
- Nevieme, ktorá z týchto možností je naozaj v najlepšom riešení, ale pre druhé dva prípady dostávame menej mincí, takže výsledok budu 3 mince (napr. 3+3+4)
- Zovšeobecníme: A[i] = min { A[i-1]+1, A[i-3]+1, A[i-4]+1 }
- A[11] = min { 3+1, 2+1, 2+1} = min {4, 3, 3 } = 3
- Pre sústavu mincí 1,2,5, máme A[i] = 1+ min { A[i-1], A[i-2], A[i-5] }
- Vo všeobecnosti A[i] = 1+ min { A[i-m_1], A[i-m_2], ..., A[i-m_k] }
- Vzorec treba modifikovať pre malé hodnoty i, ktoré sú menšie ako najväčšia minca, lebo A[-1] a pod. nie je definované
- Pre zaujímavosť, program v Pythone, stačí meniť hodnoty m a X:
m = [1,3,4]
X = 11
k = len(m)
nekonecno = math.inf
A = [0]
for i in range(1, X + 1):
min = nekonecno
for j in range(k):
if i >= m[j] and A[i - m[j]] < min:
min = A[i - m[j]]
A.append(1 + min)
print(A)
- Ako nájsť, ktoré mince použiť?
- Pridáme druhú tabuľku B, kde v B[i] si pamätáme, ktorá bola najlepšia prvá minca, keď sme počítali A[i] (ak je viac možností, zoberieme ľubovoľnú, napr. najväčšiu)
i 0 1 2 3 4 5 6 7 8 9 10 A[i] 0 1 2 1 1 2 2 2 2 3 3 B[i] - 1 1 3 4 4 3 4 4 4 4
- Potom ak chceme nájsť napr. mince pre 10, vidíme, že prvá bola B[10]=4. Zvyšok je 6 a prvá minca na vyplatenie 6 je B[6]=3. Zostáva nám 3 a B[3]=3. Potom nám už zostáva 0, takže sme hotoví. Takže najlepšie vyplatenie je 4+3+3
- Celý program v Pythone:
m = [1,3,4]
X = 11
k = len(m)
nekonecno = math.inf
A = [0]
B = [-1]
for i in range(1, X + 1):
min = nekonecno
min_minca = -1
for j in range(k):
if i >= m[j] and A[i - m[j]] < min:
min = A[i - m[j]]
min_minca = m[j]
A.append(1 + min)
B.append(min_minca)
while X > 0:
print(B[X])
X = X - B[X]
Dynamické programovanie vo všeobecnosti
- Okrem riešenia celého problému vyriešime aj veľa menších podproblémov
- Riešenia podproblémov ukladáme do tabuľky
- Pri riešení väčšieho podproblému používame už vypočítané hodnoty pre menšie podproblémy
Aká je časová zložitosť tohto algoritmu?
- Dva parametre: X a k
- Tabuľka veľkosti O(X), každé políčko čas O(k). Celkovo O(Xk)