CI09
Z MBI
Obsah
Hľadanie motívov zadefinovaných pravdepodobnostnou maticou
- Mame danych n sekvencii
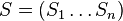 , kazda dlzky m, dlzku motivu L, nulova hypoteza q (frekvencie nukleotidov v genome)
, kazda dlzky m, dlzku motivu L, nulova hypoteza q (frekvencie nukleotidov v genome)
- Hladame motiv vo forme pravdepodobnostneho profilu dlzky L a jeho vyskyt v kazdej sekvencii
- Nech
![W[a,i]](/vyuka/mbi/images/math/0/3/2/032862e9742350e6fd5f134812164f21.png) je pravdepodobnost, ze na pozicii i motivu bude baza a, W cela matica
je pravdepodobnost, ze na pozicii i motivu bude baza a, W cela matica
-
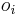 je pozicia vyskytu v sekvencii
je pozicia vyskytu v sekvencii 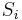 ,
, 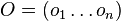 su vsetky vyskyty
su vsetky vyskyty
-
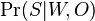 je jednoduchý súčin, kde pre pozície v oknách použijeme pravdepodobnosti z W, pre pozície mimo okna použijeme q
je jednoduchý súčin, kde pre pozície v oknách použijeme pravdepodobnosti z W, pre pozície mimo okna použijeme q
-
- Hľadáme W a O, ktoré maximalizujú tuto vierohodnosť Pr(S|W,O)
- Nepozname efektivny algoritmus, ktory by vedel vzdy najst maximum
- Dali by sa skusat vsetky moznosti O, pre dane O je najlepsie W frekvencie z dat
- Naopak ak pozname W, vieme najst najlepsie O
- v kazdej sekvencii i skusame vsetky pozicie
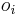 a zvolime tu, ktora ma najvyssiu hodnotu
a zvolime tu, ktora ma najvyssiu hodnotu 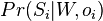
- v kazdej sekvencii i skusame vsetky pozicie
EM algoritmus
- Iterativne zlepsuje W, pricom berie vsetky O vahovane podla ich pravdepodobnosti vzhladom na W z minuleho kola
- Videli sme na prednaske, tu je trochu prepisany:
- Inicializácia: priraď každej pozícii j v sekvencii
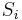 nejaké skóre
nejaké skóre 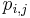
- Iteruj:
- Spočítaj W zo všetkých možných výskytov v
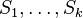 váhovaných podľa
váhovaných podľa 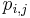
- Prepočítaj všetky skóre
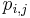 tak, aby zodpovedali pomerom pravdepodobností výskytu W na pozícii j v
tak, aby zodpovedali pomerom pravdepodobností výskytu W na pozícii j v 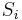 , t.j.
, t.j. 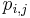 je umerne
je umerne 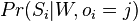 , pricom hodnoty normalizujeme tak, aby sucet v riadku bol 1
, pricom hodnoty normalizujeme tak, aby sucet v riadku bol 1
- Spočítaj W zo všetkých možných výskytov v
Gibbsovo vzorkovanie (Gibbs sampling)
- Inicializácia: Vezmi náhodné pozície výskytov O
- Iteruj:
- Spočítaj W z výskytov O
- Vyber náhodne jednu sekvenciu
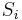
- Pre každú možnú pozíciu j v
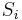 spočítaj skóre
spočítaj skóre 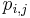 (ako v EM) výskytu W na tejto pozícii
(ako v EM) výskytu W na tejto pozícii
- Zvoľ
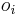 náhodne s váhovaním podľa
náhodne s váhovaním podľa 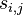
- Takto dostavame postupnost vzoriek
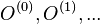 .
.
- Za sebou iduce vzorky sa podobaju (lisia sa len v jednej zlozke
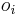 ) nie su teda nezavisle
) nie su teda nezavisle
- Pre kazdu vzorku
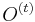 najdeme najlepsie
najdeme najlepsie 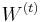 a spocitame vierohodnost
a spocitame vierohodnost 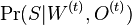 . Nakoniec vyberieme O a W, kde bola vierohodnost najvyssia.
. Nakoniec vyberieme O a W, kde bola vierohodnost najvyssia.
- Tento algoritmus (s malymi obmenami) bol pouzity v clanku Lawrence, Charles E., et al. (1993) "Detecting subtle sequence signals: a Gibbs sampling strategy for multiple alignment." Science.
- V clanku v kazdej iteracii maticu W rataju zo vsetkych sekvencii okrem
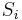
- Obcas robia krok, kde nahodne skusaju posunut vsetky vyskyty o jedna dolava alebo doprava
- Tento algoritmus nie je uplne matematicky korektne Gibbsovo vzorkovanie (nema ani poradne zadefinovane rozdelenie, z ktoreho vzorkuje). Na spodku stranky pre informaciu uvadzame algoritmus Gibbsovho vzorkovanie pre hladanie motivov z ineho clanku.
- V clanku v kazdej iteracii maticu W rataju zo vsetkych sekvencii okrem
Vzorkovanie z pravdepodobnostného modelu vo všeobecnosti
- Majme pravdepodobnostny model, kde D su nejake pozorovane data a X nezname nahodne premenne (napr pre nas D su sekvencie S a X su vyskyty O, pripadne aj matica W)
- mozeme hladat X pre ktore je vierohodnost Pr(D|X) najvyssia
- alebo mozeme nahodne vzorkovat rozne X z Pr(X|D)
Pouzitie vzoriek
- spomedzi ziskanych vzoriek zvolime tu, pre ktoru je vierohodnost Pr(D|X) najvacsia (iny pristup k maximalizovaniu vierohodnosti)
- ale vzorky nam daju aj informaciu o tom, aka je velka neurcitost v odhade X
- mozeme odhadovat stredne hodnoty a odchylky roznych velicin
- napr. pri hladani motivov mozeme sledovat ako casto je ktora pozicia vyskytom motivu
- generovat nezavisle vzorky z Pr(X|D) moze byt tazke
- metoda Markov chain Monte Carlo (MCMC) generuje postupnost zavislych vzoriek
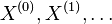 , konverguje v limite k cielovej distribucii Pr(X|D)
, konverguje v limite k cielovej distribucii Pr(X|D)
- Gibbsovo vzorkovanie je specialnym pripadom MCMC
Markovove reťazce
- Markovov reťazec je postupnosť náhodných premenných
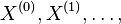 taká, že
taká, že 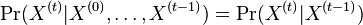 , t.j. hodnota v čase
, t.j. hodnota v čase 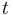 závisí len od hodnoty v čase
závisí len od hodnoty v čase 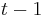 a nie ďalších predchádzajúcich hodnôt.
a nie ďalších predchádzajúcich hodnôt.
- Nás budú zaujímať homogénne Markovove reťazce, v ktorých
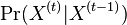 nezávisí od
nezávisí od 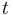 .
.
- Tiez nas zaujimaju len retazce v ktorych nahodne premenne
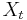 nadobudaju hodnoty z konecnej mnoziny (mozne hodnoty
nadobudaju hodnoty z konecnej mnoziny (mozne hodnoty 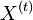 nazyvame stavy)
nazyvame stavy)
- Napriklad stavy A,C,G,T
- V Gibbsovom vzorkovani pre motivy je stav konfiguracia premennych O (t.j. mame (m-L+1)^n stavov)
- Vzorka v kroku t zavisi od vzorky v kroku t-1 (a lisi sa len v hodnote jedneho o_i)
Matica
- Pravdepodobnosti prechodu medzi stavmi za jeden krok mozeme vyjadrit maticou pravdepodobnosti P, ktorej prvok
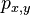 oznacuje pravdepodobnost prechodu zo stavu x do stavu y
oznacuje pravdepodobnost prechodu zo stavu x do stavu y 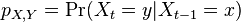
- Sucet kazdeho riadku je 1, cisla nezaporne
- Ako
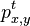 budeme oznacovat
budeme oznacovat 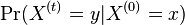 , tieto hodnoty dostaneme umocnenim matice P na t
, tieto hodnoty dostaneme umocnenim matice P na t
Stacionarne rozdelenie
- Rozdelenie
 na mnozine stavov sa nazyva stacionarne pre Markovov retazec
na mnozine stavov sa nazyva stacionarne pre Markovov retazec 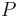 , ak pre kazde j plati
, ak pre kazde j plati 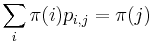 (alebo v maticovej notacii
(alebo v maticovej notacii 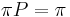 )
)
- Ak matica P splna urcite podmienky (je ergodicka), existuje pre nu prave jedno stacionarne rozdelenie
 . Navyse pre kazde x a y plati
. Navyse pre kazde x a y plati 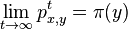
Priklady Markovovskych retazcov v bioinformatike
- V HMM stavy tvoria Markovov retazec
- Ine varianty: nekonecne stavove priestory (zlozitejsia teoria), spojity cas (videli sme pri evolucnych modeloch), retazce vyssieho radu, kde urcujeme
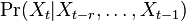 a pod.
a pod.
- Pouzitie v bioinformatike: charakterizacia nahodnych sekvencii (nulova hypoteza), pre DNA sa pouzivaju rady az do 5, lepsie ako nezavisle premenne
Ergodické Markovove reťazce
- Vravime ze matica je ergodicka, ak
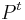 pre nejake t>0 ma vsetky polozky nenulove
pre nejake t>0 ma vsetky polozky nenulove
- Priklady neergodickych matic
1 0 0.5 0.5 0 1 0.5 0.5 0 1 0 1 1 0 1 0 nesuvisla slabo suvisla periodicka ergodicka
- V HMM stavy tvoria Markovov retazec; hladanie genov ergodicky stavovy priestor, profilove HMM nie
Markov chain Monte Carlo MCMC
- Chceme generovať náhodné vzorky z nejakeho cieloveho rozdelenia
 , ale toto rozdelenie je prilis zlozite.
, ale toto rozdelenie je prilis zlozite.
- Zostavime ergodicky Markovov retazec, ktoreho stacionarne rozdelenie je rozdelenie
 , tak aby sme efektivne vedeli vzorkovat
, tak aby sme efektivne vedeli vzorkovat 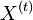 ak vieme
ak vieme 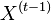 .
.
- Ak zacneme z lubovolneho bodu
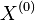 , po urcitom case t rozdelenie
, po urcitom case t rozdelenie 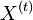 priblizne
priblizne 
- Ale za sebou iduce vzorky nie su nezavisle!
- Vieme vsak odhadovat ocakavane hodnoty roznych velicin
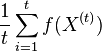 konverguje k
konverguje k ![E_{\pi }[f(X)]](/vyuka/mbi/images/math/a/a/4/aa4ecd5f5f91f0aaf04047c7435e1922.png)
Gibbsovo vzorkovanie
- Cielove rozdelenie
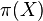 je cez vektory dlzky n
je cez vektory dlzky n 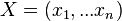
- V kazdom kroku vzorkujeme jednu zlozku vektora
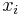 z podmienenej pravdepodobnosti
z podmienenej pravdepodobnosti 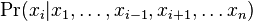
- Ostatne hodnoty nechame rovnake ako v predchadzajucom kroku
- Hodnotu
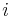 zvolime nahodne alebo periodicky striedame
zvolime nahodne alebo periodicky striedame 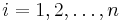
Dôkaz správnosti Gibbsovho vzorkovania
- Pozor! Gibbsovo vzorkovanie nie je vzdy ergodicke, ak niektore kombinacie hodnot maju nulovu pravdepodobnost!
- Treba dokazat, ze ak je ergodicky, tak ma ako stacionarnu distribuciu nase zvolene

- Definicia: Vravime, ze matice P a rozdelenie
 splnaju detailed balance, ak pre kazde stavy (dva vektory hodnot) x a y mame
splnaju detailed balance, ak pre kazde stavy (dva vektory hodnot) x a y mame 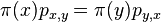
- Lema: ak pre nejaky retazec P a nejake rozdelenie
 plati detailed balance,
plati detailed balance,  je stacionarna distribucia pre P
je stacionarna distribucia pre P
- Dokaz:
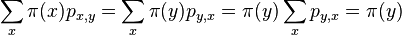
- Dokaz:
- Lema: pre retazec Gibbsovo vzorkovania plati detailed balance vzhladom na cielove rozdelnie

- Dokaz: uvazujme dva za sebou iduce vektory hodnot x a y, ktore sa lisia v i-tej suradnici. Nech
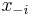 su hodnoty vsetkych ostatnych premennych okrem
su hodnoty vsetkych ostatnych premennych okrem 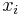
-
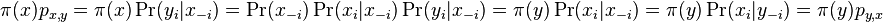
- Dokaz: uvazujme dva za sebou iduce vektory hodnot x a y, ktore sa lisia v i-tej suradnici. Nech
Poriadnejšie Gibbsovo vzorkovanie pre motívy
Uvedene pre zaujimavost - podla clanku Siddharthan R, Siggia ED, van Nimwegen E (December 2005). "PhyloGibbs: a Gibbs sampling motif finder that incorporates phylogeny". PLoS Comput. Biol. 1 (7): e67. doi:10.1371/journal.pcbi.0010067. PMID 16477324.
Pravdepodobnostny model
- Rozsirime model, aby aj O a W boli nahodne premenne, takze mame rozdelenie Pr(S,W,O)
- Potom chceme vzorkovat z Pr(O|S) (marginalizujeme cez vsetky hodnoty W)
- Vygeneruje sa nahodne matica pravdepodobnosti W (napr z roznomernej distribucie cez vsetky matice)
- V kazdej sekvencii i sa zvoli okno
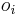 dlzky L (rovnomerne z m-L+1 moznosti)
dlzky L (rovnomerne z m-L+1 moznosti)
- V okne sa generuje sekvencia podla profilu W a mimo okna sa generuje sekvencia z nulovej hypotezy (ako predtym)
Gibbsovo vzorkovanie
- Mame dane S, vzorkujeme O (
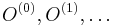 ) (ak treba, z
) (ak treba, z 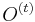 mozeme zostavit maticu
mozeme zostavit maticu 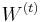 )
)
- zacni s nahodnymi oknami
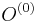
- v kroku t+1 zvol jednu sekvenciu i a pre vsetky pozicie
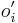 spocitaj
spocitaj 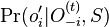 (kde
(kde 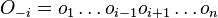 , t.j. všetky pozície výskytov okrem i-tej).
, t.j. všetky pozície výskytov okrem i-tej).
- nahodne zvol jedno
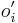 umerne k tymto pravdepodobnostiam
umerne k tymto pravdepodobnostiam
-
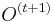 dostaneme z
dostaneme z 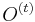 vymenou pozicie v sekvencii i za prave zvolenu
vymenou pozicie v sekvencii i za prave zvolenu
- opakuj vela krat
- zacni s nahodnymi oknami
- Konverguje k cielovemu rozdeleniu
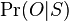 , ale vzorky nie su nezavisle
, ale vzorky nie su nezavisle
- Dalsie mozne kroky vo vzorkovani: posun vsetky okna o konstantu vlavo alebo vpravo
- Dalsie moznosti rozsirenia modelu/algoritmu: pridaj rozdelenie cez L a nahodne zvacsuj/zmensuj L, dovol vynechat motiv v niektorych sekvenciach, hladaj viac motivov naraz,...
Ako spocitat 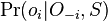 ?
?
- nezaujimaju nas normalizacne konstanty, lahko znormalizujeme scitanim cez vsetky
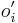
-
 , ale menovatel konstanta
, ale menovatel konstanta
-
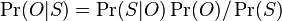 , kde
, kde 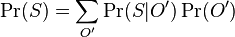
- Menovatel nas nezaujima (normalizacna konstanta)
-
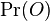 je tiez konstanta (rovnomerne rozdelenie pozicii okien)
je tiez konstanta (rovnomerne rozdelenie pozicii okien)
- Teda mame
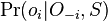 je umerne
je umerne 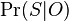
- Lahko vieme spocitat
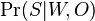 , potrebujeme "zrusit" W, da sa spocitat vzorec...
, potrebujeme "zrusit" W, da sa spocitat vzorec...
- Skusame vsetky mozne hodnoty
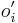 , pocitame pravdepodobnost
, pocitame pravdepodobnost 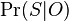 , vzorkujeme umerne k tomu
, vzorkujeme umerne k tomu
Dalsie detaily vypoctu 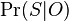 :
:
- Nech
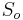 su len sekvencie v oknach a
su len sekvencie v oknach a 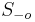 mimo okien. Mame
mimo okien. Mame 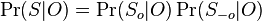
-
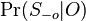 lahko spocitame (nezavisi od W)
lahko spocitame (nezavisi od W)
-
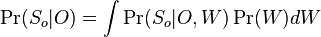 kde integral ide cez hodnoty, kde
kde integral ide cez hodnoty, kde 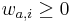 a
a 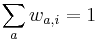
-
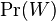 je konstanta (rovnomerne rozdelenie; nejde o pravdepodobnost ale hustotu),
je konstanta (rovnomerne rozdelenie; nejde o pravdepodobnost ale hustotu), 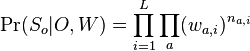 , kde
, kde 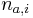 je pocet vyskytov bazy a na pozicii i v oknach
je pocet vyskytov bazy a na pozicii i v oknach 
-
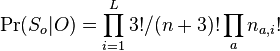 (bez dokazu)
(bez dokazu)
![\Pr(S_{i}|W,o_{i})=\prod _{{j=1}}^{{L}}W[S_{i}[j+o_{i}-1],j]\prod _{{j=1}}^{{o_{i}-1}}q[S_{i}[j]]\prod _{{j=o_{i}+L}}^{m}q[S_{i}[j]]](/vyuka/mbi/images/math/5/f/a/5fadd02fa29abf436fdd8a9d2f225bfe.png)