1-DAV-202 Data Management 2024/25
Difference between revisions of "HWr1"
| Line 214: | Line 214: | ||
Clustering is a wide group of methods that split data points into groups with similar properties. We will group together genes that have a similar reaction to cold, i.e. their rows in gene expression data matrix have similar values. We will consider two simple clustering methods | Clustering is a wide group of methods that split data points into groups with similar properties. We will group together genes that have a similar reaction to cold, i.e. their rows in gene expression data matrix have similar values. We will consider two simple clustering methods | ||
* '''K means''' clustering splits points (genes) into ''k'' clusters, where ''k'' is a parameter given by the user. It finds a center of each cluster and tries to minimize the sum of distances from individual points to the center of their cluster. Note that this algorithm is randomized so you will get different clusters each time. | * '''K means''' clustering splits points (genes) into ''k'' clusters, where ''k'' is a parameter given by the user. It finds a center of each cluster and tries to minimize the sum of distances from individual points to the center of their cluster. Note that this algorithm is randomized so you will get different clusters each time. | ||
| + | |||
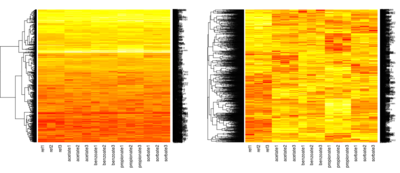
| + | [[Image:HW08-heatmap.png|thumb|400px|right|Examples of a heatmaps]] | ||
* '''Hierarchical clustering''' puts all data points (genes) to a hierarchy so that smallest subtrees of the hierarchy are the most closely related groups of points and these are connected to bigger and more loosely related groups. | * '''Hierarchical clustering''' puts all data points (genes) to a hierarchy so that smallest subtrees of the hierarchy are the most closely related groups of points and these are connected to bigger and more loosely related groups. | ||
| − | + | ||
<syntaxhighlight lang="r"> | <syntaxhighlight lang="r"> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
# Create a new version of frame a in which row is scaled so that | # Create a new version of frame a in which row is scaled so that | ||
# it has mean 0 and standard deviation 1 | # it has mean 0 and standard deviation 1 | ||
b=t(scale(t(a))) | b=t(scale(t(a))) | ||
# this matrix shows relative movements of each gene, disregarding its overall high or low expression | # this matrix shows relative movements of each gene, disregarding its overall high or low expression | ||
| + | |||
| + | # Heatmap: creates hierarchical clustering of rows | ||
| + | # then shows every value in the table using color ranging from red (lowest) to white (highest) | ||
| + | heatmap(as.matrix(a), Colv=NA, scale="none") | ||
| + | heatmap(as.matrix(b), Colv=NA, scale="none") | ||
| + | # compare the two matrices - which phenomena influenced clusters in each of them? | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Line 234: | Line 235: | ||
# k means clustering to 7 clusters | # k means clustering to 7 clusters | ||
k = 7 | k = 7 | ||
| − | cl <- kmeans( | + | cl <- kmeans(b, k) |
# Each gene has assigned a cluster (number between 1 and k) | # Each gene has assigned a cluster (number between 1 and k) | ||
# the command below displays the first 10 elements, i.e. clusters of first 10 genes | # the command below displays the first 10 elements, i.e. clusters of first 10 genes | ||
| Line 240: | Line 241: | ||
# Draw heatmap of cluster number 3 out of k, no further clustering applied | # Draw heatmap of cluster number 3 out of k, no further clustering applied | ||
# Do you see any common pattern? | # Do you see any common pattern? | ||
| − | heatmap(as.matrix( | + | heatmap(as.matrix(b[cl$cluster==3,]), Rowv=NA, Colv=NA, scale="none") |
# Reorder genes in the whole table according to their cluster cluster number | # Reorder genes in the whole table according to their cluster cluster number | ||
| − | heatmap(as.matrix( | + | # Can you spot our seven clusters? |
| + | heatmap(as.matrix(b[order(cl$cluster),]), Rowv=NA, Colv=NA, scale="none") | ||
# Compare overall column means with column means in cluster 3 | # Compare overall column means with column means in cluster 3 | ||
# Function apply runs mean on every column (or row if 2 changed to 1) | # Function apply runs mean on every column (or row if 2 changed to 1) | ||
| − | apply( | + | apply(b, 2, mean) |
# Now means within cluster 3 | # Now means within cluster 3 | ||
| − | apply( | + | apply(b[cl$cluster==3,],2,mean) |
# Clusters have centers which are also computed as means | # Clusters have centers which are also computed as means | ||
Revision as of 11:29, 15 April 2020
See also the lecture
In this homework, try to read the text, execute given commands, potentially trying some small modifications. Then do tasks A-D
- Submit the required files (3x .png)
- In your protocol, enter the commands used in tasks A-D, with explanatory comments in more complicated situations
- In task B also enter the required output to the protocol
- Protocol template in /tasks/r1/protocol.txt
Contents
The first steps
Type a command, R writes the answer, e.g.:
> 1+2 [1] 3
We can store values in variables and use them later:
> # population of Slovakia in millions, 2019 > population = 5.457 > population [1] 5.457 > # area of Slovakia in thousands of km2 > area = 49.035 > density = population / area > density [1] 0.1112879
Surprises in the R language:
- dots are used as parts of id's, e.g. read.table is name of a single function (not a method for the object read)
- assignment via <- or =
- vectors etc are indexed from 1, not from 0
Vectors, basic plots
A vector is a sequence of values of the same type (all are numbers or all are strings or all are booleans)
# Vector can be created from a list of numbers by function named c
a = c(1,2,4)
a
# prints [1] 1 2 4
# c also concatenates vectors
c(a,a)
# prints [1] 1 2 4 1 2 4
# Vector of two strings
b = c("hello", "world")
# Create a vector of numbers 1..10
x = 1:10
x
# prints [1] 1 2 3 4 5 6 7 8 9 10
Vector arithmetics
Many operations can be easily applied to each member of a vector
x = 1:10
# Square each number in vector x
x*x
# prints [1] 1 4 9 16 25 36 49 64 81 100
# New vector y: logarithm of a number in x squared
y = log(x*x)
y
# prints [1] 0.000000 1.386294 2.197225 2.772589 3.218876 3.583519 3.891820 4.158883
# [9] 4.394449 4.605170
# Draw the graph of function log(x*x) for x=1..10
plot(x,y)
# The same graph but use lines instead of dots
plot(x,y,type="l")
# Addressing elements of a vector: positions start at 1
# Second element of the vector
y[2]
# prints [1] 1.386294
# Which elements of the vector satisfy certain condition?
# (vector of logical values)
y>3
# prints [1] FALSE FALSE FALSE FALSE TRUE TRUE TRUE TRUE TRUE TRUE
# write only those elements from y that satisfy the condition
y[y>3]
# prints [1] 3.218876 3.583519 3.891820 4.158883 4.394449 4.605170
# we can also write values of x such that values of y satisfy the condition...
x[y>3]
# prints [1] 5 6 7 8 9 10
Alternative plotting facilities: ggplot2 library, lattice library
Task A
Create a plot of the binary logarithm with dots in the graph more densely spaced (from 0.1 to 10 with step 0.1)
- Store it in file log.png and submit this file
Hints:
- Create x and y by vector arithmetics
- To compute binary logarithm check help ? log
- Before running plot, use command png("log.png") to store the result, afterwards call dev.off() to close the file (in Rstudio you can also export plots manually)
Data frames and simple statistics
Data frame: a table similar to a spreadsheet. Each column is a vector, all are of the same length.
We will use a table with the following columns:
- Country name
- Region (continent)
- Area in thousands of km2
- Population in millions in 2019
(source of data UN)
The table is stored in the csv format (columns separated by commas).
# reading a data frame from a file
a = read.csv("countries.csv",header = TRUE)
# display mean, median, etc. of each column
summary(a);
# Compactly display structure of a
# (good for checking that import worked etc)
str(a)
# print the column with the name "Area"
a$Area
# population density: divide the population by the area
a$Population / a$Area
# Add density as a new column to frame a
a = cbind(a, Density = a$Population / a$Area)
# Scatter plot of area vs population
plot(a$Area, a$Population)
# we will data better in log-scale (both axes)
plot(a$Area, a$Population, log='xy')
# or in linear scale but omitting the biggest countries
plot(a$Area, a$Population, xlim=c(0,1500), ylim=c(0,150))
# average country population 33.00224 million
mean(a$Population)
# median country population 5.3805 million
median(a$Population)
# median country population in Europe
median(a$Population[a$Region=="Europe"])
# Standard deviation
sd(a$Population)
# Histogram of country populations in Europe
hist(a$Size)
Task B
Create frame europe which contains data for European countries selected from frame a. Also create a similar frame for African countries. Hint:
- To select the first three rows of a frame: a[c(1,2,3),].
- Here we want to select rows based on values not position (see computation of median country size in Europe above)
Run the command summary separately for each new frame. Comment on how their characteristics differ. Write output and your conclusion to the protocol.
Task C
Draw a graph comparing the area vs population in Europe and Africa; use different colors for points representing European and African countries. Apply log scale on both axes.
- Submit the plot in file countries.png
To draw the graph, you can use one of the options below, or find yet another way.
Option 1: first draw the Europe with one color, then add Africa in another color
- Color of points can be changed by as follows: plot(1:10,1:10, col="red")
- After the plot command, you can add more points to the same graph by command points, which can be used similarly as plot
- Warning: command points does not change the ranges of x and y axes. You have to set these manually so that points from both groups are visible. You can do this using options xlim and ylim, e.g. plot(x,y, col="red", xlim=c(0.1,100), ylim=c(0.1,100))
Option 2: plot both Europe and Africa in one plot command, and give it a vector of colors, one for each point. Command plot(1:10,1:10,col=c(rep("red",5),rep("blue",5))) will plot the first 5 points red and the last 5 points blue
Bonus task: add a legend to the plot, showing which color is Europe and which is Africa.
Expression data and clustering
# Read gene expression data table
a = read.csv("/tasks/r1/microarray.csv", row.names=1)
# Visual check of the first row
a[1,]
# Plot control (reference) replicate 1 vs. acetate acid replicate 1
plot(a$ref1, a$acetate1)
# Plot control replicate 1 vs. control replicate 2
plot(a$ref1, a$ref2)
# To show density in dense clouds of points, use this plot
smoothScatter(a$ref1, a$acetate1)
# Outliers away from diagonal in the plot above are most strongly differentially expressed genes
# These are more easy to see in MA plot:
# x-axis: average expression in the two conditions
# y-axis: difference between values (they are log-scale, so difference 1 means 2-fold)
plot((a$ref1+a$acetate1)/2, a$ref1-a$acetate1)
Clustering is a wide group of methods that split data points into groups with similar properties. We will group together genes that have a similar reaction to cold, i.e. their rows in gene expression data matrix have similar values. We will consider two simple clustering methods
- K means clustering splits points (genes) into k clusters, where k is a parameter given by the user. It finds a center of each cluster and tries to minimize the sum of distances from individual points to the center of their cluster. Note that this algorithm is randomized so you will get different clusters each time.
- Hierarchical clustering puts all data points (genes) to a hierarchy so that smallest subtrees of the hierarchy are the most closely related groups of points and these are connected to bigger and more loosely related groups.
# Create a new version of frame a in which row is scaled so that
# it has mean 0 and standard deviation 1
b=t(scale(t(a)))
# this matrix shows relative movements of each gene, disregarding its overall high or low expression
# Heatmap: creates hierarchical clustering of rows
# then shows every value in the table using color ranging from red (lowest) to white (highest)
heatmap(as.matrix(a), Colv=NA, scale="none")
heatmap(as.matrix(b), Colv=NA, scale="none")
# compare the two matrices - which phenomena influenced clusters in each of them?
# k means clustering to 7 clusters
k = 7
cl <- kmeans(b, k)
# Each gene has assigned a cluster (number between 1 and k)
# the command below displays the first 10 elements, i.e. clusters of first 10 genes
head(cl$cluster)
# Draw heatmap of cluster number 3 out of k, no further clustering applied
# Do you see any common pattern?
heatmap(as.matrix(b[cl$cluster==3,]), Rowv=NA, Colv=NA, scale="none")
# Reorder genes in the whole table according to their cluster cluster number
# Can you spot our seven clusters?
heatmap(as.matrix(b[order(cl$cluster),]), Rowv=NA, Colv=NA, scale="none")
# Compare overall column means with column means in cluster 3
# Function apply runs mean on every column (or row if 2 changed to 1)
apply(b, 2, mean)
# Now means within cluster 3
apply(b[cl$cluster==3,],2,mean)
# Clusters have centers which are also computed as means
# so this is the same as the previous command
cl$centers[3,]
Task D
Draw a plot in which x-axis is the time and y-axis is the expression level and the center of each cluster is shown as a line
- Use command matplot(x, y, type="l") which gets two matrices x and y and plots columns of x vs columns of y
- Command matplot(, y, type="l") will use numbers 1,2,3... as columns of the missing matrix x
- Create y from cl$centers by applying function t (transpose)
- To create an appropriate matrix x, first create a vector of times for individual experiments in minutes or hours (do it manually, no need to parse column names automatically). Using functions rep and matrix you can create a matrix x in which this vector is used as every column
- Then run matplot(x, y, type="l")
- Since time points are not evenly spaced, it would be better to use logarithmic scale on the x-axis: matplot(x, y, type="l", log="x")
- to avoid log(0), change the first timepoint from 0min to 1min
- Submit file clusters.png with your final plot