CI03
Z MBI
Obsah
[skryť]Dynamické programovanie
- Pozri Cvičenia pre biológov
Uvod do proteomiky
- Viac informacii: [1], Bafna, Reinert 2004
- Pozri tiež prezentáciu k cvičeniu
Gélová elektroforéza (gel electrophoresis) - uvedene pre zaujimavost, nerobili sme
- Izolovanie jednotlivých proteínov, porovnávanie ich množstva.
- Negatívne nabité proteíny migrujú v géli v elektrickom poli. Väčšie proteíny migrujú pomalšie, dochádza v oddeleniu do pruhov. Táto metóda sa používa aj na DNA a RNA. Pre proteíny možno tiež robiť 2D gél (podľa hmotnosti a náboja).
- Bioinformatický problém: zisti, ktoré fliačiky na dvoch 2D géloch zodpovedajú tým istým proteínom.
- Automatizovanejšia technológia: kvapalinová chromatografia (liquid chromatography) - separácia proteínov v tenkom stĺpci
Hmotnostná spektrometria (mass spectrometry)
- Hmotnostná spektrometria meria pomer hmostnosť/náboj molekúl vo vzorke.
- Používa sa na identifikáciu proteínov, napr. z 2D gélu.
- Proteín nasekáme enzýmom trypsín (seká na [KR]{P}) na peptidy
- Meriame hmostnosť kúskov, porovnáme s databázou proteínov.
- Tandemová hmotnostná spektrometria (MS/MS) ďalej fragmentuje každý kúsok a dosiahne podrobnejšie spektrum, ktoré obsahuje viac informácie
- v niektorých prípadoch vieme sekvenciu proteínu určiť priamo z MS/MS, bez databázy proteínov
Sekvenovanie proteinov pomocou MS/MS
Vsetky hmotnosti budeme povazovat za cele cisla
Vstup:
- celková hmotnosť peptidu M,
- hmotnosti aminokyselín a[1],...,a[20],
- spektrum ako tabuľka f[0],...,f[M], ktorá hmotnosti m určí skóre f[m] podľa signálu v okolí príslušného bodu grafu
Označenie:
- Uvažujme postupnosť aminokyselín
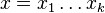
- Nech
![m(x)=\sum _{{j=1}}^{k}a[x_{j}]](/vyuka/mbi/images/math/5/1/e/51e47d7db5cc3125eee0a57b9e19c12c.png) je hmotnosť x
je hmotnosť x
- Nech
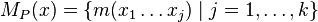 sú hmotnosti prefixov x
sú hmotnosti prefixov x
- Nech
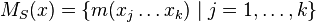 sú hmotnosti sufixov x
sú hmotnosti sufixov x
Problém 1
Berme do uvahy len b-iony, ktore zodpovedaju hmotnosti prefixu
Výstup:
- postupnosť aminokyselín x taká, že
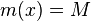 a
a ![\sum _{{m\in M_{P}(x)}}f[m]](/vyuka/mbi/images/math/e/f/c/efca77d5389ed7769b65877ff30a2c69.png) je maximálna možná
je maximálna možná
- Chceme teda najst peptid, ktory maximalizuje sucet skore svojich prefixov
Riešenie
- Dynamicke programovanie s podproblemom S[m] je skore najlepsieho prefixu s hmotnostou m
- Rekurencia? Zlozitost? Je to polynomialny algoritmus? (Aky velky je vlastne vstup?)
Problém 2
Berme do uvahy aj y-iony, ktore meraju hmotnost sufixu, scitame skore prefixov a sufixov
Výstup:
- postupnosť aminokyselín x taká, že
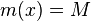 a
a ![\sum _{{m\in M_{P}(x)}}f[m]+\sum _{{m\in M_{S}(x)}}f[m]](/vyuka/mbi/images/math/6/9/9/699ef640d8249b3456c1241580179964.png) je maximálna možná
je maximálna možná
Riešenie
- pouzijeme upravenu skorovaciu tabulku g[m]=f[m]+f[M-m] a algoritmus pre problem 1
Problem tejto formulacie:
- jeden signal sa moze ratat dvakrat, raz ako b-ion, raz ako y-ion, algoritmus ma tendenciu pridavat taketo artefakty
Problém 3
Ak hmotnost nejakeho prefixu a nejakeho sufixu su rovnake, zarataj ich skore iba raz (skore peptidu je skore mnoziny hmotnosti jeho prefixov a sufixov)
Výstup:
- postupnosť aminokyselín x taká, že
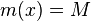 a
a ![\sum _{{m\in M_{P}(x)\cup M_{S}(x)}}f[m]](/vyuka/mbi/images/math/6/6/5/665a026ed145fe16ec6b27b6044972b8.png) je maximálna možná
je maximálna možná
Riesenie:
- Ina formulacia: maximalizujeme
![\sum _{{m\in M_{p}(x)\cup M_{S}(x),m\leq M/2}}h[m]](/vyuka/mbi/images/math/d/2/0/d20e9653e2a74d027573395f12f2f0f1.png)
-
![h[m]=\left\{{\begin{array}{ll}f[m]+f[M-m]&{\mbox{ak }}m<M/2\\f[m]&{\mbox{ak }}m=M/2\end{array}}\right.](/vyuka/mbi/images/math/6/b/9/6b9baa42bbaae35399de43cab3712d19.png)
- Definuj novy podproblem: S[p,s] je najlepsie skore, ktore moze dosiahnut prefix s hmotnostou p a sufix s hmotnostou s, kde 0<=p,s<=M/2,
- Rekurencia
![S[p,s]=\left\{{\begin{array}{ll}\max _{{i=1\dots 20}}S[p,s-a[i]]+h[s]&{\mbox{ak }}p<s\\\max _{{i=1\dots 20}}S[p-a[i],s]+h[p]&{\mbox{ak }}p>s\\\max _{{i=1\dots 20}}S[p-a[i],s]&{\mbox{ak }}p=s\\\end{array}}\right.](/vyuka/mbi/images/math/f/b/1/fb198e39be6b286cd92f4e0a8c0bbddf.png)
- Ako ukoncime dynamicke programovanie? Zlozitost?
- Zrychlenie: staci uvazovat s od p-w po p+w kde w je maximalna hmotnost aminokyseliny
Detekcia znamych proteinov pomocou MS (nerobili sme)
- Predikcia spektra pre dany peptid, porovnanie s realnym spektrom, zlozite skorovacie schemy
- Filtrovanie kandidatov na proteiny, ktore obsahuju peptidy s pozorovanou hmotnostou
- Problem: mame danu databazu proteinov a cielovu hmotnost peptidu M, pozname hmotnost kazdej aminokyseliny. Najdite vsetky podretazce s hmotnostou M.
- Databazu proteinov si vieme predstavit aj ako postupnost cisel - hmotnosti aminokyselin, hladame intervaly so suctom M.
- Trivialny algoritmus: zacni na kazdej pozicii, pricitavaj kym nedosiahnes hmotnost>=M. Zlozitost? Vieme zlepsit?
- Predspracovanie: pocitajme hmotnosti vsetkych podretazcov, potom vyhladajme binarne. Zlozitost?
- Zlozitejsi alg. s predspracovanim pomocou FFT (Fast Fourier Transform) Bansal, Cieliebak, Liptak 2004