2011/12 Programovanie (1) v C/C++

Táto stránka obsahuje archívnu kópiu materiálov zo školského roku 2011/12. Niektoré odkazy nemusia byť funkčné. V ďalších školských rokoch sa obsah predmetu môže mierne alebo výraznejšie meniť.

Prehľad a obsah

• #Zimný semester, úvodné informácie
• #Zimný semester, pravidlá
• #Zimný semester, test a skúška
• #Netbeans
• #Grafická knižnica SimpleDraw

Týždeň 19.-25.9.

Úvod, použitie grafickej knižnice, premenné, podmienky, cyklus for

#Prednáška 1 · #Prednáška 2 · #Cvičenia 1 · #DÚ1

Týždeň 26.9.-2.10.

Cykly (for, while), Euklidov algoritmus, funkcie

#Prednáška 3 · #Prednáška 4 · #Cvičenia 2 · #DÚ2

Týždeň 3.-9.10.

Polia, Eratostenovo sito, polynómy, triedenia

#Prednáška 5 · #Prednáška 6 · #Cvičenia 3 · #DÚ3

Týždeň 10.-16.10.

Binárne vyhľadávanie, zložitosť, znaky a reťazce

#Prednáška 7 · #Prednáška 8 · #Cvičenia 4 · #DÚ4

Týždeň 17.-23.10.

Súbory

#Prednáška 9 · #Prednáška 10 · #Cvičenia 5 · #DÚ5

Týždeň 24.-30.10.

Smerníky, dvojrozmerné polia

#Prednáška 11 · #Prednáška 12 · #Cvičenia 6 · #DÚ6

Týždeň 31.10.-6.11.

Slovník

#Prednáška 13

Týždeň 7.-13.11.

Rekurzia, backtracking

#Prednáška 14 · #Prednáška 15 · #Cvičenia 7 · #DÚ7

Týždeň 14.-20.11.

Rekurzívne triedenia, ešte backtracking, vyfarbovanie

#Prednáška 16 · #Prednáška 17 · #Cvičenia 8 · #DÚ8

Týždeň 21.-27.11.

Spájané zoznamy, zásobník a rad, odstraňovanie rekurzie

#Prednáška 18 · #Prednáška 19 · #Cvičenia 9 · #DÚ9

Týždeň 28.11.-4.12.

Vyfarbovanie bez rekurzie, aritmetické výrazy, stromy

#Prednáška 20 · #Prednáška 21 · #Cvičenia 10 · #DÚ10

Týždeň 5.-11.12.

Vyhľadávacie a lexikografické stromy

#Prednáška 22 · #Prednáška 23 · #Cvičenia 11 · #DÚ11

Týždeň 12.-18.12.

Zhrnutie, opakovanie, príprava na písomku, ďalšie črty jazykov C a C++

#Prednáška 24 · #Prednáška 25 · #Cvičenia 12

Zimný semester, úvodné informácie

Rozvrh

• Prednášky: utorok 9:50 a streda 14:50 F1-109
• Cvičenia:
  • 1i1 (prvý krúžok) utorok 14:50 M-218
  • 1i2 (druhý krúžok) a študenti iných odborov alebo ročníkov pondelok 13:10 H3
  • 1i3 (tretí krúžok) utorok 14:50 M-217
  • Rozdelenie na krúžky [1]

Vyučujúce

• RNDr. Jana Katreniaková PhD., miestnosť M-263,

Konzultácie v utorok 13:10-14:50 alebo po dohode e-mailom

• Mgr. Broňa Brejová, PhD., miestnosť M-163,

Konzultácie v stredu 13:00-14:00 alebo po dohode e-mailom

Cvičiaci

• Mgr. Martin Králik, miestnosť M-25 (oproti akváriu X),
• Mgr. Marika Mitrengová, miestnosť M-211

Ciele predmetu

• Tento predmet (1-INF-127 Programovavanie (1) v C/C++) je určený študentom prvého ročníka bakalárskeho študijného programu Informatika a spolu s predmetom 1-INF-166 Programovanie (2) v Jave v letnom semestri tvoria alternatívu k povinným predmetom 1-INF-126 Programovanie (1) a 1-INF-165 Programovanie (2).
• Každý študent sa môže rozhodnúť, či absolvuje 1-INF-127 a 1-INF-166 alebo 1-INF-126 a 1-INF-165. Nie je však možné absolvovať obe verzie programovania ani sa po prvom semestri presunúť z jednej verzie do druhej.
• Predmety 1-INF-126 a 1-INF-165 sa vyučujú v jazyku FreePascal a majú na našej fakulte už dlhú tradíciu. Predmety 1-INF-127 a 1-INF-166 budú vyučované v jazykoch C resp. C++ a Java. Výhodou je, že tieto jazyky využijete aj v ďalších nadväzujúcich predmetoch (Systémové programovanie, Programovanie (3) a podobne) a sú to aj jazyky využívané v praxi. Nevýhodu je, že sa po prvom semestri budete musieť preorientovať na iný jazyk.

• Ciele predmetu 1-INF-126:
  • naučiť sa algoritmicky uvažovať, písať kratšie programy a hľadať v nich chyby, porozumieť existujúcemu kódu
  • oboznámiť sa so základnými programovými a dátovými štruktúrami jazyka C resp. C++, nie je však nutne so všetkými črtami týchto jazykov
  • oboznámiť sa s niektorými základnými algoritmami a dátovými štruktúrami

Literatúra

• Predmet sa nebude striktne riadiť žiadnou učebnicou. Prehľad preberaných tém a stručné poznámky nájdete na stránke predmetu, doporučujeme Vám si na prednáškach a cvičeniach robiť vlastné poznámky.
• Pri štúdiu Vám môžu pomôcť knihy o jazykoch C a C++, o programovaní všeobecne a o algoritmoch preberaných na prednáške. Tu je výber z vhodných titulov, ktoré sú k dispozícii na prezenčné štúdium vo fakultnej knižnici:
  • Prokop: Algoritmy v jazyku C a C++ praktický pruvodce, Grada 2008, I-INF-P-26
  • Sedgewick: Algorithms in C. Parts 1-4 I-INF-S-43/I-IV
  • Kochan: Programming in C, 2005 D-INF-K-7a
• Referenčnú príručku k jazyku C++ nájdete napríklad na tejto webstránke: http://cplusplus.com/

Priebeh semestra

• Na prednáškach budeme preberať obsah predmetu. Prednášky budú štyri vyučovacie hodiny do týždňa.
• Cvičenia budú dve vyučovacie hodiny do týždňa v počítačovej učebni a ich cieľom je aktívne si precvičiť učivo. Na začiatku cvičenia bude krátka diskusia o prípadných nejasnostiach ohľadom materiálu z minulého cvičenia. Potom nasleduje rozcvička (krátky test) písaný na papieri. Ďalšou časťou cvičenia je precvičovanie príkladov k predchádzajúcim prednáškam (spoločne alebo individuálne). Na konci cvičenie spravidla budete môcť začať pracovať na domácej úlohe, pričom cvičiaci Vám v prípade potreby odpovie na Vaše otázky.
• Domáce úlohy navrhujeme tak, aby Vám ich riešenie pomohlo osvojiť si a precvičiť si učivo, čím sa okrem iného pripravujete aj na záverečnú skúšku. Okrem tohto sú za domáce úlohy body do záverečného hodnotenia. Najviac sa naučíte, ak sa Vám domácu úlohu podarí samostatne vyriešiť, ale ak sa vám to napriek vášmu usilu nedarí, neváhajte sa spýtať o pomoc prednášajúcich alebo cvičiacich. Možno s malou radou od nás sa Vám podarí úlohu spraviť. Treba však na domácej úlohe začať pracovať v predstihu, aby ste nás v prípade problémov stihli kontaktovať.
• Cieľom vyučujúcich tohto predmetu je vás čo najviac naučiť, ale musíte aj vy byť aktívni partneri. Ak Vám na prednáške alebo cvičení nie je niečo jasné, spýtajte sa. Môžete nám klásť tiež otázky počas našich konzultačných hodín alebo emailom. Ak sa dostanete do väčších problémov s plnením študijných povinností, poraďte sa s vyučujúcimi alebo s tútorom, ako tieto problémy riešiť.
• 40% známky dostávate za prácu cez semester, preto netreba nechávať štúdium učebnej látky až na skúškové obdobie.

Zimný semester, pravidlá

Známkovanie

• 20% známky je na základe rozcvičiek, ktoré sa píšu na (takmer) každom cvičení
• 20% známky je za domáce úlohy
• 30% známky je za záverečný písomný test
• 30% známky je za praktickú skúšku pri počítači

Pozor, body získavané za jednotlivé príklady nezodpovedajú priamo percentám záverečnej známky. Body za každú formu známkovania sa preváhujú tak, aby maximálny získateľný počet zodpovedal váham uvedených vyššie. Úlohy označené ako bonusové sa nerátajú do maximálneho počtu získateľných bodov v danej aktivite.

Stupnica

• Na úspešné absolvovanie predmetu je potrebné splniť nasledovné tri podmienky:
  • Získať aspoň 50% bodov v celkovom hodnotení
  • Získať aspoň 50% zo záverečného písomného testu
  • Získať aspoň 50% zo skúšky
• Ak niektorú z týchto troch podmienok nesplníte, dostávate známku Fx.
• V prípade úspešného absolvovania predmetu získate známku podľa bodov v celkovom hodnotení takto:

A: 90% a viac, B:80...89%, C: 70...79%, D: 60...69%, E: 50...59%

Rozcvičky

• Rozcvičky sú krátke testy (cca 15 minút), ktoré sa píšu na začiatku (takmer) každého cvičenia. Za každú rozcvičku môžete získať najviac 5 bodov.
• Pri rozcvičke môžete použiť ľubovoľné písomné materiály (poznámky, knihy,...), nie však počítače a iné elektronické pomôcky. Počas rozcvičky nie je možné zdieľať materiály so spolužiakmi.
• Ak bude počas semestra celkovo N rozcvičiek, do výslednej známky sa vám zaráta iba N-2 najlepších, t.j. dve rozcvičky, na ktorých ste získali najmenej bodov (alebo ste sa ich ani nezúčastnili) sa vám škrtajú.

Domáce úlohy

• Domáce úlohy budú vypisované takmer každý týždeň. Maximálny počet bodov za domácu úlohu bude uvedený v zadaní a bude sa pohybovať spravidla v rozsahu 5-10 bodov podľa náročnosti úlohy.
• Domáce úlohy treba odovzdať elektronicky pomocou systému Moodle do termínu určeného v zadaní. Neskoršie odovzdané úlohy nebudú akceptované.
• Niektoré týždne budú vypísané aj špeciálne bonusové domáce úlohy, za ktoré môžete získať body navyše alebo dohnať body stratené na iných domácich úlohách. Bonusové úlohy sú však náročnejšie.
• Program, ktorý odovzdáte ako domácu úlohu by mal byť skompilovateľný a spustiteľný v prostredí používanom na cvičeniach. Budeme kontrolovať správnosť celkovej myšlienky, správnosť implementácie ale body môžete stratiť aj za neprehľadný štýl.

Záverečný písomný test

• Záverečný test bude trvať 90 minút a bude obsahovať úlohy podobné tým, ktoré sa riešili na cvičeniach.
• Riadny termín testu sa bude konať v pondelok 19.12. o 10:00 v posluchárni B, opravný termín neskôr počas skúškového obdobia.
• Pri teste nemôžete používať žiadne pomocné materiály (písomné ani elektronické) okrem povoleného ťaháku v rozsahu jedného listu formátu A4 s ľubovoľným obsahom na oboch stranách.

Skúška

• Na skúške budete riešiť 2 úlohy pri počítači v celkovom trvaní 120 minút.
• Na skúške nemôžete používať žiadne pomocné materiály okrem povoleného ťaháku v rozsahu jedného listu formátu A4 s ľubovoľným obsahom na oboch stranách. Nebude k dispozícii ani internet. Budete používať rovnaké programátorské prostredie ako na cvičeniach.
• Po skončení skúšky sa koná krátky ústny pohovor s vyučujúcim, počas ktorého sa prediskutujú programy, ktoré ste odovzdali a uzavrie sa vaša známka.
• Opakovanie skúšky sa riadi študijným poriadkom fakulty.
• Ak si po konaní skúšky ešte opravíte body zo záverečného testu a nepotrebujete už opravovať samotnú skúšku, musíte prísť aj tak na ďalší ústny pohovor, ktorý sa vám bude rátať ako opravný termín skúšky.

Opisovanie

• Máte povolené sa so spolužiakmi a ďalšími osobami rozprávať o domácich úlohách a stratégiách na ich riešenie. Kód, ktorý odovzdáte, musí však byť vaša samostatná práca. Je zakázané opisovať kód z literatúry alebo z internetu a ukazovať svoj kód spolužiakom. Domáce úlohy môžu byť kontrolované softvérom na detekciu plagiarizmu.
• Počas rozcvičiek, testov a skúšok môžete používať iba povolené pomôcky a nesmiete komunikovať s žiadnymi osobami okrem vyučujúcich.
• Ak nájdeme prípady opisovania alebo nepovolených pomôcok, všetci zúčastnení študenti získajú za príslušnú domácu úlohu alebo test nula bodov (t.j. aj tí, ktorí dali spolužiakom odpísať). Opakované alebo obzvlášť závažné prípady opisovania budú podstúpené na riešenie dekanovi fakulty.

Neprítomnosť

• Účasť na cvičeniach veľmi silne doporučujeme a v prípade neprítomnosti stratíte body za rocvičky.
• V prípade kratšieho ochorenia alebo iných problémov môžete využiť možnosť, že dve najhoršie rozcvičky sa škrtajú a stratené body za domáce úlohy je možné dohoniť riešením bonusových príkladov.
• V prípade dlhšieho ochorenia (aspoň dva týždne alebo opakovaná neprítomnosť) alebo iných závažných prekážok sa príďte poradiť s prednášajúcimi o možných riešeniach. Treba tak spraviť čím skôr, nie až spätne cez skúškové. Prineste si potvrdenku od lekára.

Netbeans

Ako spustiť Netbeans v učebni

• Po spustení počítača zvoľte Linux a prihláste sa pomocou toho istého mena a hesla, ako používate v systéme AIS
• V ľavom dolnom rohu obrazovky je menu s ponukou programov, v oddelení Development nájdete Netbeans

Základy práce v Netbeans

Vytvorenie nového projektu

• Každý program v Netbeans potrebuje svoj "projekt", čo je adresár so všetkými potrebnými súbormi.
• V menu zvoľte File, potom New project
• V Categories zvoľte C/C++, v Project: C/C++ Application
• Na ďalšej obrazovke projekt nejako nazvite a zvoľte do akého adresára sa má uložiť. Doproučujeme cestu na svieťovom disku net, ku ktorému máte prístup zo všetkých počítačov v učebniach, napríklad v adresári /home/x/vasemeno/net/NetBeansProjects
• Stlačte Finish

Editovanie programu

• V ľavej časti okna máte panel Project, v ktorom nájdite projekt, ktorý ste práve vytvorili.
• V projekte rozbaľte Source Files a nájdete tam main.cpp, ktorý si dvojitým kliknutím otvoríte v editore. Jeho obsah môžete modifikovať alebo celý zmazať a nahradiť programom z prednášky.
• Súbor main.cpp nezabudnite uložiť (menu File, Save, alebo Ctrl-S)

Kompilovanie a spúšťanie

• V menu Run zvoľte Build main project (F11), program sa skompiluje. Prípadné chyby sa objavia v dolnej časti okna.
• V menu Run zvoľte Run main project (F6), program sa spustí.
• Ak máte naraz otvorených viac projektov, jeden z nich je hlavný, vyznačený hrubým písmom. Kompilovanie a spúšťanie sa aplikuje na hlavný projekt.
  • Ak chcete nastaviť nejaký projekt ako hlavný, kliknite na jeho meno v paneli Project pravým tlačidlom a zvoľte Set as main project

Prenášanie programov a odovzdávanie domácich úloh

• Pri odovzdávaní domácich úloh odovzdávajte súbor main.cpp s vašim programom (prípadne ďalšie súbory ak to vyžaduje zadanie). Tento súbor nájdete v adresári net/NetBeansProjects/menoprojektu
• Ak pracujete na rôznych počítačoch v rámci FMFI učební, svoje projekty si ukladajte na sieťovom disku net
• Dáta zo sieťového disku si môžete stiahnuť v učebni na USB kľúčik, alebo aj cez sieť z domu prihlásením sa na študentský Linuxový klaster daVinci (davinci.fmph.uniba.sk). Na prenos dát môžete použiť napríklad windowsovský program winscp
• Ak chcete prenášať projekt medzi rôznymi počítačmi, doporučujeme skopírovať iba main.cpp, prípadne ďalšie potrebné súbory.
  • Na druhom počítači vytvoríte nový projekt, nakopírujete main.cpp do jeho adresára.
  • Potom pridáte main.cpp do projektu takto: kliknite pravým tlačidlom na Source Files v paneli Projects, zvoľte Add Existing Item

Práca v Netbeans s grafickou knižnicou

• Stiahnite si knižnicu vo verzii určenej pre učebňu
  • Stiahnuté súbory libsimpleDraw.a a SimpleDraw.h uložte do adresára NetBeansProjects, v ktorom podadresáre obsahujú jednotlivé projekty
• Pri vytváraní nového projektu je potrebné zvoliť C/C++ Qt Application namiesto C/C++ Application
• Po vytvorení kliknite pravým tlačidlom na meno projektu v paneli Projects a zvoľte Properties
  • V paneli Categories zvoľte Linker v časti Build, v pravom paneli stlačte tri bodky pri Libraries, potom Add Library File, potom zvoľte súbor libsimpleDraw.a
• Teraz môžete editovať, kompilovať a spúšťať program rovnako ako bez použitie knižnice

Kopírovanie projektov

• Keď už máte jeden grafický program hotový a chcete si vytvoriť ďalší, môžete vynechať niektoré z krokov uvedených vyššie tým, že si otvoríte starý projekt, v paneli Project kliknete na jeho meno pravým tlačidlom, v menu zvolíte Copy a zadáte nové meno projektu.
• Teraz môžete editovať, kompilovať a spúšťať program bez zadávania ďalších nastavení.

Ako nainštalovať Netbeans na svojom počítači

Ak máte na počítači operačný systém Linux, budete potrebovať nainštalovať nasledujúce softvérové balíčky:

• Prostredie netbeans (v učebni máme verziu 6.9.1, mala by však postačovať aj iná verzia)
• Komplilátor g++
• Debuger gdb
• Knižnicu qt4 (balíček libqt4-dev)

Všetky tieto balíčky existujú napríklad v distribúcii Ubuntu. Ak vo vašej distribúcii nie je k dispozícii balíček pre Netbeans, stiahnite si ho zo stránky http://netbeans.org/downloads/

Po nainštalovaní týchto balíčkov spustite Netbeans, v menu Tools zvoľte Plugins a pridajte si plugin C/C++.

Ak máte na počítači operačný systém Windows, je možné tiež si nainštalovať Netbeans, o niečo ťažšie je však rozchodiť knižnicu Qt, ktorá je potrebná na použitie našej grafickej knižnice používanej na predmete.

• Informácia o inštalovaní Netbeans http://netbeans.org/community/releases/69/cpp-setup-instructions.html
• Odskúšaný návod na zvláštnej stránke.
• Môžete pracovať aj vo virtuálnom počítači so systémom Linux (pozri nižšie)

Používanie grafickej knižnice na svojom počítači

• Stiahnite si verziu knižnice určenú na kompilovanie.
• Vytvorte si v Netbeans nový projekt typu C/C++ Qt Static Library, nazvite ho simpleDraw
• Do adresára NetBeansProjects/simpleDraw/ rozzipujte stiahnuté súbory
• V projekte simpleDraw kliknite na Source files pravým tlačidlom a zvoľte Add Existing Item, potom medzi súbormi vyberte SimpleDraw.cpp a SimpleDraw.h (viac súborov naraz môžete pridať ak súčasne stlačíte Ctrl a kliknete na meno ďalšieho súboru)
• V projekte simpleDraw kliknite na Resource files pravým tlačidlom a zvoľte Add Existing Item, potom medzi súbormi zvoľte SimpleDrawWindow.cpp, SimpleDrawWindow.h a SimpleDrawWindow.ui
• Spustite Build Main Project
• Niekde v podadresároch adresára NetBeansProjects/simpleDraw/dist by vám mal vzniknúť súbor libsimpleDraw.a. Tento potom môžete použiť na vašom počítači rovnako ako používate jeho verziu pre učebne stiahnutú zo stránky.
• Podrobnejší návod pre Windows na zvláštnej stránke.

Netbeans vo virtuálnom počítači

• Jedna z možností, ako sa vysporiadať s problémami okolo bežania Netbeans a grafickej knižnice na Windowsovom počítači je bežať ho vo virtuálnom serveri s nainštalovaným Linuxom
• Doporučujeme túto možnosť, len ak Váš počítač má aspoň 2G pamäte
• Na cvičeniach môžete získať tri súbory prog.mf, prog.ovf, prog.vmdk celkovej veľkosti cca 2G (doneste si veľký USB kľúčik) obsahujúci nainštalovaný virtuálny počítač aj s prostredím Netbeans.
• Potrebujete si stiahnuť aj softvér na spúšťanie virtuálneho počítača, ten získate na stránke https://www.virtualbox.org/
• Po nainštalovaní softvéru Virtualbox pridáte do neho pridáte virtuálny počítač pomocou možnosti Import appliance, zvolíte prog.ovf (ďalšie dva súbory musia byť v tom istom priečinku)
• Virtuálnemu počítaču môžete nastaviť veľkosť pamäte, alebo zdieľanie pričinkov s vašim počítačom.
• Heslo na prihlasovanie a administrátorské úkony je také isté, aké ste použili pri prihlasovaní sa na predmet v prostredí Moodle (dve slová)
• Na pravom okraji obrazovky je lišta s často používanými programami, vrátane Netbeans a Firefoxu.

Grafická knižnica SimpleDraw

Knižnica SimpleDraw umožňuje zobraziť grafické okno a vykresľovať do neho rôzne geometrické útvary.

• Návod na použitie knižnice v prostredí Netbeans
• Stiahnutie knižnice
• Príklady programov na prvej prednáške
• Manuál ku knižnici

Príkazy na prácu s grafickou plochou

• Ako prvé musíme vytvoriť grafické okno s určitou veľkosťou plochy príkazom typu SimpleDraw window(300, 400);
• V každom programe vytvárajte iba jedno okno.
• Do okna môžeme kresliť príkazmi drawRectangle, drawEllipse, drawLine, drawText. Presný zoznam parametrov každého príkazu nájdete v manuáli. Príklad: window.drawRectangle(100, 200, 100, 100);
• Môžeme vykresľovať aj celé bitmapy načítané napr z .jpg alebo .png súboru, a to príkazom drawPixmap
• Ak chceme vykresľovať mnohouholníky alebo lomené čiary, použijeme skupinu príkazov startPath, lineTo a drawPath alebo drawClosedPath. Pomocou startPath a lineTo postupne vymenujeme vrcholy a pomocou drawPath alebo drawClosedPath čiaru uzavrieme a vykreslíme.
• Pomocou príkazov setPenColor, setBrushColor, unsetBrush, setFontColor vieme nastavovať farbu čiar, písma a vyfarbovania. Farby zadávame buď troma číslami od 0 do 255 určujúcimi intenzitu červenej, zelenej a modrej, alebo názvom, napr. "red" (zoznam mien farieb). Príkazom setFontSize nastavujeme veľkosť písma.
• Príkaz showAndClose vykreslí okno a čaká, kým užívateľ stlačí Exit, potom zavrie okno. Príkaz show čaká kým užívateľ stlačí Next, potom môžeme pokračovať vo vykresľovaní. Príkaz wait čaká zadaný počet sekúnd, čo sa dá využiť na spomalenie animácie.
• Príkaz clear vymaže obsah okna. Príkaz removeItem zmaže objekt (napr. čiaru) so zadaným číslom. Každý kresliaci príkaz vráti číslo práve vykresleného objektu, takže si ho stačí uložiť v nejakej premennej pre neskoršie mazanie.
• Príkaz savePng uloží zobrazený obrázok do png súboru.
• Príkazy startDebugging a stopDebugging zapínajú a vypínajú ladiaci mód, v ktorom program čaká na stlačenie Next po vykreslení každej čiary alebo iného objektu.

Príkazy na korytnačiu grafiku

• Pred vytvorením korytnačky musíme vytvoriť grafickú plochu.
• Korytnačka si pamätá svoju polohu a natočenie na ploche. Príkaz forward posunie korytnačku dopredu, príkaz turnLeft ju otočí.
• Ak má korytnačka spustené pero, kreslí pri pohybe čiaru. Toto sa mení príkazmi penUp a penDown.
• Príkazmi show a hide vieme nastaviť, či sa má nasmerovanie korytnačky zobrazovať ako šípka.
• Príkaz setWait umožňuje zapnúť čakanie po každom pohybe, aby sme lepšie videli, ako sa postupne hýbe.

SimpleDraw vo Windows

Inštalácia softvéru

Ak nemáme Netbeans, stiahneme si ho tu: http://netbeans.org/downloads/index.html (priamy link na inštalátor pre lenivých)

Mala by stačiť verzia pre C/C++.

Ak už Netbeans máme, tak si skontrolujeme, či v ňom máme plugin pre C++. To sa dá spraviť skontrolovaním dostupných pluginov tu:

Ak medzi nimi je, to znamená, že ho nemáme a treba si ho v danom okne doinštalovať.

Po inštalácii Netbeans je ďalším krokom je nainštalovanie Qt SDK z http://qt.nokia.com/downloads/ (priamy link na inštalátor pre lenivých).

V prípade inštalácie na počítači s internetom postačí online verzia inštalátora.

Pri inštalácii je dôležité zvoliť správne komponenty. Budeme potrebovať nasledovné:

Nakoniec je ešte potrebné nainštalovať MSYS.

"MSYS is a collection of GNU utilities such as bash, make, gawk and grep to allow building of applications and programs which depend on traditionally UNIX tools to be present. It is intended to supplement MinGW and the deficiencies of the cmd shell."

Sťahujeme odtiaľto: http://downloads.sourceforge.net/mingw/MSYS-1.0.11.exe

Ku koncu inštalácie je nutné odpovedať na dve otázky "yes" a následne vpísať cestu k nainštalovanému MinGW.

Pri použití predvolenej cesty pri inštalácii Qt to má vyzerať takto:

Dôležité je v ceste použiť presne tie lomítka, ktoré sú na obrázku.

Nastavenie Windows

Aby nám v Netbeans šlo spúštať konzolové (negrafické programy), potrebujeme do premennej prostredia PATH pridať cestu k MinGW: C:\QtSDK\mingw\bin

Objavili sa prípady, kedy bolo do PATH potrebné pridať aj cestuku Qt knižniciam: C:\QtSDK\Desktop\Qt\4.7.4\mingw\bin

Premenná PATH sa dá nastaviť v pravý klik na tento počítač > properties > advanced system settings > environment variables > system variables > variable path > edit. Na jej konci treba pridať bodkočiarku a danú cestu.

Po úprave PATH je nutné Windows reštartovať.

Nastavenie Netbeans

V Netbeans treba nastaviť správne cesty k jednotlivým súčastiam. Prejdeme preto cez menu do Tools -> Options -> C/C++ a klikneme na "Add...".

Objaví sa dialóg, do ktorého je treba vyplniť cestu k mingw, ktorá pri použití predvolených ciest vyzerá takto:

Následne ostanú nevyplnené dve cesty - k príkazom make a qmake. Tie vyplníme nasledovne (za predpokladu predvolených ciest):

Vytvorenie knižnice

V Netbeans si vytvoríme nový projekt - Qt Static Library:

Po kliknutí na "Next >" nastavíme "Tool Collection" na MinGW.

Zdrojové súbory knižnice si stiahneme tu: http://compbio.fmph.uniba.sk/vyuka/prog/data/simpleDraw.zip a rozbalíme do priečinku s novovytvoreným projektom. Následne tieto súbory musíme pridať do projektu tak, aby o tom Netbeans vedel. Najprv pridáme hlavičkové (.h) súbory:

Rovnakým spôsobom pridáme zdrojové súbory (.cpp) do Source Files.

Konfiguráciu projektu prepneme z "Debug" na "Release" a celé to skompilujeme stlačením tlačidla s obrázkom kladiva.

O úspechu nás bude informovať konzola v spodnej časti Netbeans hláškou "BUILD SUCCESSFUL (total time: XYs)".

Vytvorenú knižnicu nájdeme v adresári projektu v podadresári "dist\Release\MinGW-Windows", v závislosti od mena nášho projektu sa môže volať napríklad "libsimpleDraw.a"

Použitie knižnice

Tak ako na cvikách (Qt Application, pridať library file) ale miesto "main(void)" treba dať "main(int argc, char** argv)".

Zimný semester, test a skúška

Na tejto stránke sú informácie týkajúce sa záverečného písomného testu a praktickej skúšky pri počítači v zimnom semestri. Doporučujeme tiež si preštudovať

• pravidlá predmetu
• rady a informácie na prednáške 24

Termíny

Písomný test

• Riadny termín pondelok 19.12. o 10:00 v posluchárni B
• Opravný/náhradný termín pondelok 9.1. o 10:00 v F1/328

Termíny skúšok vždy o 9:00 v H3 (väčšie termíny aj M218):

• 4.1.2012 (15)
• 11.1.2012 (24)
• 25.1.2012 (24)
• 1.2.2012 (opravný termín) (24)
• 8.2.2012 (2. opravný termín) (15)

Na termín skúšky sa zapisujte v systéme AIS. Ústna časť skúšky sa koná v poobedňajších hodinách ten istý deň.

Ukážkové príklady na písomný test

V texte nižšie je niekoľko príkladov, ktoré sa svojim charakterom a obtiažnosťou podobajú na príklady, aké budú na záverečnej písomke. Tieto ukážkové príklady sú prevažne vybrané z cvičení a prednášok, na skutočnej písomke však budú nové, zatiaľ nepoužité príklady.

• Svoje odpovede si môžete skontrolovať nižšie

• Príklad 1: Zistite, čo vypíše nasledujúca funkcia, ak ju spustíme ako generuj(a, pocet, 0, 2, 3), pričom polia a a pocet majú dĺžku n=3 a obe sú naplnené nulami. Funkcia vypis(a,n) vypíše prvky poľa a.
  • Ako musíme funkciu opraviť, aby vypisovala všetky usporiadané n-tice čísel z množiny {0,...,n-1}, v ktorých sa každé číslo opakuje najviac k krát?

void generuj(int a[], int pocet[], int i, int k, int n) {
    if (i == n) {
        vypis(a, n);
    } else {
        for (int x = 0; x < n; x++) {
            if (pocet[x]<k) {
                a[i] = x;
                pocet[x]++;
                generuj(a, pocet, i + 1, k, n);
            }
        }
    }
}

• Príklad 2: Prepíšte výraz 8 3 4 * + 2 3 + / z postfixovej notácie do bežnej infixovej notácie

• Príklad 3: Prepíšte výraz ((2+4)/(3*5))/(1-2) do postfixovej a prefixovej notácie

• Príklad 4: Vyhodnocujeme výraz 8 3 4 * + 2 3 - / v postfixovej notácii algoritmom z prednášky. Aký bude obsah zásobníka v čase, keď začneme spracovávať znamienko +?

• Príklad 5: Máme zásobník s a rad q, pričom obidve štruktúry uchovávajú dáta typu char. Aký bude ich obsah po nasledujúcej postupnosti príkazov?

init(s);
init(q);
push(s, 'A');
push(s, 'B');
push(s, 'C');
enqueue(q, pop(s));
enqueue(q, pop(s));
push(s, 'D');
push(s, dequeue(q));

• Príklad 6: Máme binárny strom, v ktorom má každý vrchol buď dve deti a v dátovom poli uložený znak '#' alebo nemá žiadne deti a v dátovom poli má uložený znak '*'. Keď tento strom vypíšeme v preorder poradí, dostaneme postupnosť ##*#*** Nakreslite, ako vyzerá tento strom.

• Príklad 7: Nakreslite binárny vyhľadávací strom, ktorý dostaneme, ak do prázdneho slovníka postupne vkladáme záznamy s kľúčami 3, 4, 1, 2, 5, 6 (v tomto poradí).

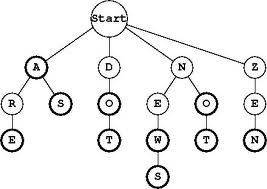
• Príklad 8: Nakreslite lexikografický strom s abecedou {a,b}, do ktorého sme vložili reťazce aba, aaab, baa, bab, ba. Vrcholy, ktoré zodpovedajú niektorému reťazcu zo vstupu zvýraznite dvojitým krúžkom.

• Príklad 9: Uvažujme nasledujúcu rekurzívnu funkciu na vyfarbovanie. Predpokladajme, že a je matica s troma riadkami a troma stĺpcami vyplnená nulami, pričom funkciu spustíme na stredné políčko, t.j. stlpec=riadok=1 a nová farba je tiež 1. V akom poradí vyfarbí políčka matice novou farbou?

void vyfarbi(int **a, int n, int m, int riadok, int stlpec, int farba) {
    /* prefarbi suvislu jednofarebnu oblast obsahujucu 
     * a[riadok][stlpec] na farbu farba */

    if (a[riadok][stlpec] != farba) {
        int stara_farba = a[riadok][stlpec];
        a[riadok][stlpec] = farba;
        if (riadok > 0 && a[riadok - 1][stlpec] == stara_farba) {
            vyfarbi(a, n, m, riadok - 1, stlpec, farba);
        }
        if (riadok + 1 < n && a[riadok + 1][stlpec] == stara_farba) {
            vyfarbi(a, n, m, riadok + 1, stlpec, farba);
        }
        if (stlpec > 0 && a[riadok][stlpec - 1] == stara_farba) {
            vyfarbi(a, n, m, riadok, stlpec - 1, farba);
        }
        if (stlpec + 1 < m && a[riadok][stlpec + 1] == stara_farba) {
            vyfarbi(a, n, m, riadok, stlpec + 1, farba);
        }
    }
}

• Príklad 10: Napíšte funkciu vyhod(zoznam &z), ktorá z jednosmerného spájaného zoznamu vyhodí všetky záznamy, v ktorých má položka data nulovú hodnotu. Pozor, takéto záznamy sa môžu vyskytovať aj na začiatku zoznamu. Vyhodené položky zoznamu treba odalokovať.

• Príklad 11: Napíšte funkciu dvojicky(node *root), ktorá spočíta počet všetkých vnútorných vrcholov v strome s koreňom root takých, že ich ľavé aj pravé dieťa majú v svojom dátovom poli uloženú tú istú hodnotu.

• Príklad 12: Nasledujúci program načíta od užívateľa počet kruhov, zoznam údajov pre jednotlivé kruhy (celočíselné súradnice a polomer), posunie každý kruh o 10 nižšie a zase kruhy vypíše. Doplňte do programu chýbajúce časti vyznačené čiarami (typy premenných, parametre a návratové typy funkcií).

#include <iostream>
using namespace std;

struct kruh {
   ________________
};

_______ posunKruh(__________) {
  k.y-=10;
}

_______ nacitajKruhy(__________) {
  _________ a;
  a = new kruh[n];
  for(int i=0; i<n; i++) {
    cin >> a[i].x >> a[i].y >> a[i].r;
  }
  return a;
}

______ vypisKruhy(________________) {
  for(int i=0; i<n; i++) {
    cout << " " << a[i].x << " " << a[i].y << " " << a[i].r << endl;
  }  
}

int main(void) {
  _______ n;
  _______ a;
  cin >> n;
  a = nacitajKruhy(n);
  for(int i=0; i<n; i++) {
    posunKruh(a[i]);
  }
  vypisKruhy(a, n);
  delete[] a;
}

• Príklad 13: Funkcia jeRastuci kontroluje, či sa hodnoty v spájanom jednosmernom zozname zvyšujú v smere od začiatku ku koncu zoznamu, t.j. či každý prvok je väčší ako jeho predchodca. Ak áno, vráti true, inak vráti false. Doplňte podmienky na podčiarknuté miesta tak, aby funkcia správne fungovala. V prípade, že zoznam je prázdny alebo obsahuje jeden prvok, odpoveď má byť true.

struct item {
    int data;
    item* next;
};

struct zoznam {
    item* zaciatok;
};

bool jeRastuci(zoznam &z) {
  item *v = z.zaciatok;
  while(____________) {
    if(_____________) {
      return false;
    }
    v = v->next;
  }
  return true;
}

• Príklad 14: Uvažujme funkciu na triedenie vkladaním uvedenú nižšie.
  • Koľkokrát sa vykoná riadok označený (**) na vstupnom poli (5,2,3,4,1)?
  • Koľkokrát sa vykoná riadok označený (**) na vstupnom poli dĺžky n, ktoré je celé utriedené okrem toho, že najmenší a najväčší prvok sú vymenené teda (n,2,3,4,...,n-2,n-1,1)? Počet vykonaní zapíšte ako funkciu od dĺžky poľa n.

void insertionSort(int a[], int n) {
    /* usporiadaj prvky v poli a od najmenšieho po najväčší */

    for (int i = 1; i < n; i++) {
        int prvok = a[i];
        int kam = i;
        while (kam > 0 && a[kam - 1] > prvok) {
            a[kam] = a[kam - 1];  // (**) 
            kam--;
        }
        a[kam] = prvok;
    }
}

Vzorové riešenia ukážkových príkladov na písomný test

• Príklad 1: funkcia vypíše tri trojice: 0 0 1, 0 0 2, 0 1 2. Nevypisuje to čo má, lebo po vynorení z rekurzie nezníži od pocet[x], aj keď hodnota a[i] bude zmenená z x na x+1. Tu je funkcia po oprave:

void generuj(int a[], int pocet[], int i, int k, int n) {
    if (i == n) {
        vypis(a, n);
    } else {
        for (int x = 0; x < n; x++) {
            if (pocet[x]<k) {
                a[i] = x;
                pocet[x]++;
                generuj(a, pocet, i + 1, k, n);
                pocet[x]--; /* pridany prikaz */
            }
        }
    }
}

• Príklad 2: (8+3*4)/(2+3)
• Príklad 3: postfix 2 4 + 3 5 * / 1 2 - / prefix: / / + 2 4 * 3 5 - 1 2
• Príklad 4: na zásobníku budú čísla 8 a 12 (8 je na spodku zásobníka). Číslo 12 vzniklo vynásobením 3 a 4.
• Príklad 5: na zásobníku budú znaky A, D, C (A na spodku zásobníka), v rade bude písmeno B
• Príklad 6:

        #
       / \
      #   *
     /\
    *  #
      /\
     *  *

• Príklad 7:

        3
       / \
      1   4
      \    \
       2    5
             \
              6

• Príklad 8: (namiesto dvojiteho krúžku používame *)

          .
         / \
        /   \
       /     \ 
      a       b
     / \     /
    a   b   a*
   /   /   / \
  a   a*  a*  b*
 /
b*

• Príklad 9: do každého políčka sme vpísali poradové číslo, kedy bude vyfarbené:

3 2 9
4 1 8
5 6 7

• Príklad 10: Jedna možnosť je použiť dvojitý smerník, ktorý môže ukazovať buď na premennú zaciatok v zozname alebo na premennú next v niektorom jeho prvku.

void vyhod(zoznam &z) {
  /* vytvorime si smernik na miesto,
   * kde je ulozeny smenrik na dalsi prvok*/
  item **smernik = &(z.zaciatok);
  /* kym nie sme na konci zoznamu */
  while((*smernik)!=NULL) {
      /* dalsi prvok je nula, zmazeme ju a prevesime zvysok zoznamu */
      if((*smernik)->data==0) {
          item *remove = *smernik;
          (*smernik) = (*smernik)->next;
          delete remove;
      }
      /* dalsi prvok nie je nula, posunieme smernik */
      else {
          smernik = &((*smernik)->next);
      }
  }
}

Druhá možnosť je použiť dva cykly: jedným mažeme nuly na začiaktu a druhým mažeme nuly vo zvyšku zoznamu.

void vyhod(zoznam &z) {
    /* vyhadzujeme nuly na zaciatku */
    while (z.zaciatok != NULL && z.zaciatok->data == 0) {
        item * remove = z.zaciatok;
        z.zaciatok = remove->next;
        delete remove;
    }
    /* node bude ukazovat vzdy na nenulovy prvok,
     * kontrolujeme prvok za nim */
    item * node = z.zaciatok;
    while (node != NULL && node->next != NULL) {
        if (node->next->data == 0) {
            item * remove = node->next;
            node->next = remove->next;
            delete remove;
        }
        else {
            node = node->next;
        }
    }
}

• Príklad 11:

int dvojicky(node *root) {
    /* prazdny strom neobsahuje dvojicky */
    if(root == NULL) return 0;
    
    int result = 0;
    /* ak su deti korena dvojicky, pricitaj 1*/
    if(root->left != NULL && root->right != NULL
            && root->left->data == root->right->data) {
        result++;
    }
    /* spocitaj dvojicky v lavom a pravom podstrome */
    result += dvojicky(root->left);
    result += dvojicky(root->right);
    return result;
}

• Príklad 12:

#include <iostream>
using namespace std;

struct kruh {
    int x, y, r;
};

void posunKruh(kruh &k) {
  k.y-=10;
}

kruh * nacitajKruhy(int n) {
  kruh * a;
  a = new kruh[n];
  for(int i=0; i<n; i++) {
    cin >> a[i].x >> a[i].y >> a[i].r;
  }
  return a;
}

void vypisKruhy(kruh *a, int n) {
  for(int i=0; i<n; i++) {
    cout << " " << a[i].x << " " << a[i].y << " " << a[i].r << endl;
  }
}

int main(void) {
  int n;
  kruh * a;
  cin >> n;
  a = nacitajKruhy(n);
  for(int i=0; i<n; i++) {
    posunKruh(a[i]);
  }
  vypisKruhy(a, n);
  delete[] a;
}

• Príklad 13:

bool jeRastuci(zoznam &z) {
    item *v = z.zaciatok;
    while (v != NULL && v->next != NULL) {
        if (v->data >= v->next->data) {
            return false;
        }
        v = v->next;
    }
    return true;
}

• Príklad 14:
  • Čísla 2,3,4 musia preskočiť číslo 5, riadok sa teda pre každé z nich vykoná raz a pre číslo 1 sa vykoná 4 krát, spolu teda 7 krát.
  • Čísla 2,3,4,...,n-2,n-1 musia preskočiť číslo n, riadok sa teda pre každé z nich vykoná raz a pre číslo 1 sa vykoná n-1 krát. Spolu sa teda riadok vykoná n-2+n-1=2n-3 krát.

Ukážkové príklady na skúšku pri počítači

Prvý príklad, verzia A

V súbore muzeum.txt sú údaje o počte navštevníkov múzea za jednotlivé dni, pričom súbor je rozdelený na niekoľko časových období, ktoré môžu byť rôzne dlhé. Na prvom riadku súboru je počet období. Na každom z ďalších riadkov je vždy najskôr uvedený počet dní v období a potom počet návštevníkov pre každý deň v danom období.

Načítajte tieto údaje zo súboru a vykreslite ich graficky, pričom každý deň bude vykreslený ako biely štvorček (farba "white"), ak v tom dni neprišiel žiadny návštevník alebo ako čierny štvorček (farba "black"), ak prišiel aspoň jeden. Štvorčeky pre každé obdobie budú v jednom riadku obrázku. Každý štvorček bude mať rámik farby "lightgray". Navyše nájdite časové obdobie, v ktorom bolo najviac dní, v ktorých prišiel do múzea aspoň jeden návštevník a toto obdobie zarámikujte červenou farbou (farba "red").

Príklad vstupu a vygenerovaného obrázku:

4
5 0 5 0 10 0
4 1 3 0 4
0
2 3 1

Pri vytváraní SimpleDraw okna nastavte veľkosť plochy podľa počtu období a dĺžky najdlhšieho obdobia na vstupe. Použite konštantu stvorcek=15, ktorá udáva veľkosť jedného štvorčeka. Naopak nepoužívajte polia konštantných veľkostí, program by mal vedieť spracovať ľubovoľné dáta, ktoré sa zmestia do pamäte (alokujte polia dynamicky alebo použite štruktúry, ktoré menia veľkosť podľa potreby).

Prvý príklad, verzia B

V súbore muzeum.txt sú údaje o počte navštevníkov múzea za jednotlivé dni. Na prvom riadku súboru je počet sledovaných dní. V ďalších riadkoch sú udaje pre jednotlivé dni oddelené medzerami alebo koncami riadkov. Nájdite najdlhší súvislý časový úsek za sledované obdobie, kedy nikto múzeum nenavštívil. Ak je viac úsekov s maximálnou dĺžkou, vypíšte prvý v poradí. Na konzolu vypíšte dve čísla oddelené medzerou: poradové číslo dňa, kedy tento úsek začal a jeho dĺžku. Dni čísľujeme od nuly.

Príklad vstupu:

10
1 0 0 1 0 0 0 2 0 0

V tomto príklade v dni 1 začína úsek dĺžky 2 kedy nikto neprišiel, v dni 4 začína úsek dĺžky 3 a v dni 8 začína ďalší úsek dĺžky 2. Najdlhší je teda úsek, ktorý začína v dni 4, výstup teda bude nasledovný:

4 3

Nepoužívajte polia konštantných veľkostí, program by mal vedieť spracovať ľubovoľné dáta, ktoré sa zmestia do pamäte (ak treba, alokujte polia dynamicky alebo použite štruktúry, ktoré menia veľkosť podľa potreby).

Druhý príklad, verzia A

Tento príklad je prevzatý z prednášky, na skúške budú príklady, ktoré doteraz neboli použité.

Úlohou je napísať program, ktorý bude riešiť hlavolam Sudoku. V tomto hlavolame máme danú plochu 9x9 políčok, pričom niektoré sú prázdne, iné obsahujú číslo z množiny {1..9}. Plocha je rozdelená do 9 štvorcov 3x3. Cieľom je doplniť čísla do všetkých prázdnych políčok tak, aby v každom riadku plochy, v každom stĺpci plochy a v každom štvorci 3x3 bola každá cifra {1..9} práve raz.

Tu je príklad hlavolamu aj s naznačeným rozdelením plochy na štvorce 3x3. Bodky označujú prázdne políčka.

. 3 . | . 7 . | . . .
6 . . | 1 9 5 | . . .
. 9 8 | . . . | . 6 .
---------------------
8 . . | . 6 . | . . 3
4 . . | 8 . 3 | . . 1
. . . | . 2 . | . . 6
---------------------
. 6 . | . . . | 2 8 .
. . . | 4 . 9 | . . 5
. . . | . 8 . | . 7 .

Náš program dostane vstup ako maticu 9x9 čísel, pričom nuly označujú prázdne políčka. Cieľom je vypísať na konzolu všetky riešenia hlavolamu, pričom každé riešenie je matica 9x9 a za ňou voľný riadok. Nakoniec má program vypísať celkový počet riešení hlavolamu. Matica je zadaná v súbore sudoku.txt Príklad vstupu a výstupu:

Vstup:          
0 3 0 0 7 0 0 0 0
6 0 0 1 9 5 0 0 0
0 9 8 0 0 0 0 6 0
8 0 0 0 6 0 0 0 3
4 0 0 8 0 3 0 0 1
0 0 0 0 2 0 0 0 6
0 6 0 0 0 0 2 8 0
0 0 0 4 0 9 0 0 5
0 0 0 0 8 0 0 7 0
  
Vystup:
5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9
                         
Pocet rieseni: 1

Program nižšie načíta maticu a obsahuje aj funkciu na výpis riešenia. Doprogramujte rekurzívnu funkciu generuj a ďalšie pomocné funkcie (najdiVolne a moze). Vaša rekurzívna funkcia by mala postupovať nasledovne:

• Pomocou funkcie najdiVolne nájde na ploche prázdne políčko, ak také nie je, vypíše riešenie a skončí.
• Do prázdneho políčka skúša vložiť čísla 1...9 a testuje, či nenastane konflikt v riadku, stĺpci alebo štvorci. Túto kontrolu robí pomocou funkcie moze.
• Vždy, keď niektoré číslo sedí, zavolá sa rekurzívne na vyplnenie zvyšných bielych miest.

V prípade potreby navrhnite a naprogramujte aj ďalšie pomocné funkcie.

#include <fstream>
#include <iostream>
using namespace std;

void vypis(int **a) {
    /* vypis riesenia sudoku */
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            cout << " " << a[i][j];
        }
        cout << endl;
    }
    cout << endl;
}

void najdiVolne(int **a, int &riadok, int &stlpec) {
    /* najdi volne policko na ploche a uloz jeho suradnice
     * do premennych riadpk a stlpec. Ak nie je, uloz do oboch
     * premennych hodnotu -1. */


}

bool moze(int **a, int riadok, int stlpec, int hodnota) {
    /* Mozeme ulozit danu hodnotu na dane policko?
     * Da sa to, ak riadok, stlpec, ani stvorec nema
     * tuto hodnotu este pouzitu. */
}

int generuj(int **a) {
    /* mame ciastocne vyplnenu plochu sudoku,
     * chceme najst vsetky moznosti, ako ho dovyplnat
     * a vratit ich pocet.  */

}

int main(void) {
    ifstream in;
    in.open("sudoku.txt");

    /* alokujeme a nacitame 2D maticu so vstupom */
    int **a = new int *[9];
    for (int i = 0; i < 9; i++) {
        a[i] = new int[9];
    }
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            in >> a[i][j];
        }
    }
    in.close();

    /* rekurzivne prehladavanie s navratom */
    int pocet = generuj(a);

    /* vypis riesenia */
    cout << "Pocet rieseni: " << pocet << endl;
}

Druhý príklad, verzia B

Tento príklad je prevzatý z cvičení, na skúške budú príklady, ktoré doteraz neboli použité.

Napíšte program, ktorý udržuje množinu celých čísel, pričom od užívateľa jeden po druhom načítava príkazy, ktoré aj hneď aj vykonáva. Každý príkaz pozostáva z jednopísmenového kódu a z celočísleného parametra, ktoré užívateľ zadá na jednom riadku. Príkazy sú štyroch typov:

• Príkaz s kódom 'I' vloží zadané číslo do množiny (na začiatku programu je množina prázdna). Vypíše buď reťazec OK, ak sa podarilo číslo vložiť, alebo reťazec ERR, ak už číslo v množine bolo.
• Príkaz s kódom 'R' dostane ako parameter niektorý z prvok množiny x a zistí, koľký v utriedenom poradí tento prvok je. Ak zadané číslo nie je z množiny, vypíše reťazec ERR, v opačnom prípade vypíše výsledok, ktorý by mal byť číslo od 1 po počet prvkov množiny.
• Príkaz s kódom 'S' nájde k-te najmenšie číslo v množine, pričom k je zadaný parameter, ktorý by mal byť v rozsahu od 1 po počet prvkov množiny. Ak k nie je v tomto rozsahu, program vypíše reťazec ERR, v opačnom prípade vypíše nájdený prvok.
• Príkaz s kódom 'E' ukončí program, parameter ignoruje.

Príklad:

I 20
OK
I 20
ERR
I 10
OK
R 20
2
S 2
20
R 30
ERR
E 0

Tento problém budeme riešiť modifikáciou binárnych vyhľadávacích stromov. Každý vrchol bude obsahovať kľúč typu int, smerník na ľavého a pravého syna, smerník na otca a počet vrcholov v celom podstrome zakorenenom v danom vrchole (položka count). Napríklad pre list by mal byť count 1, pre vrchol s dvoma synmi, ktorí sú obaja listami, by hodnota count mala byť 3.

V programe uvedenom nižšie máte funkcie z prednášky na vkladanie prvku do vyhľadávacieho stromu a jeho vyhľadávanie ako aj základ funkcie main. Vašou úlohou je doprogramovať nasledovné časti kódu:

• Funkcie createLeaf a insert zmeňte tak, aby správne inicalizovali a udržiavali položku count pre všetky vrcholy v strome.
• Funkcie rank a select (pozri nižšie)
• Dopísať spracovanie príkazov R a S do hlavného programu.

Čiastočné body môžete dostať aj ak sa vám podarí spraviť správne iba niektoré z týchto podúloh, nemeňte však celkovú kostru programu. V prípade potreby si napíšte aj ďalšie funkcie, ktoré budete z uvedených funkcií volať.

• Funkcia int rank(dictionary &d, int key) má nájsť prvok key v strome a vrátiť, koľký v utriedenom poradí spomedzi iných prvkov v strome je. V tejto funkcii predpokladajte, že hľadaný kľúč sa v strome určite nachádza (prípad, že sa nenachádza doriešte v hlavnom programe). V tejto funkcii využite položku count. Ak totiž pokračujeme v hľadaní v pravom podstrome určitého vrcholu v, tak vrchol v aj všetky vrcholy v jeho ľavom podstrome sú pred hľadaným prvkom. A aj bez toho, aby sme ľavý podstrom celý prechádzali, vieme koľko prvkov v ňom je.

• Funkcia int select(dictionary &d, int k) má vrátiť k-ty najmenší prvok vo vyhľadávacom strome. Aj v tejto funkcii využite položku count. Ak je totiž k najviac rovné počtu vrcholov v ľavom podstrome, k-ty najmenší prvok musí byť niekde v tomto podstrome. Ak je naopak k veľké, hľadaný prvok musí byť v pravom podstrome a vieme spočítať aj to, koľký najmenší v rámci tohto podstromu je.

#include <iostream>
#include <cassert>
using namespace std;

struct node {
    /* vrchol binarneho vyhladavacieho stromu  */
    int key; /* kluc podla ktoreho vyhladavame */
    int count; /* pocet vrcholov v podstrome */
    node * parent; /* otec vrchola */
    node * left; /* lavy syn */
    node * right; /* pravy syn */
};

struct dictionary {
    node *root;
};

void init(dictionary &d) {
    /* inicializuje prazdny slovnik */
    d.root = NULL;
}

node * createLeaf(int key, node * parent) {
    /* vytvor novy vrchol s danymi hodnotami, obe deti nastav na NULL */
    node *v = new node;
    v->key = key;
    v->left = NULL;
    v->right = NULL;
    v->parent = parent;
    return v;
}

node * findNode(node *root, int key) {
    /* V binarnom vyhladavacom strom s korenom root najdi a vrat
     * vrchol s klucom a ak neexistuje, vrat NULL. */
    node * v = root;
    while (v != NULL && v->key != key) {
        if (key < v->key) {
            v = v->left;
        } else {
            v = v->right;
        }
    }
    return v;
}

void findNode(node *root, int key, node *&v, node *&parent) {
    /* Do v uloz smernik na vrchol s klucom key alebo NULL ak neexistuje.
     * Do parent uloz otca v, NULL ak neexistuje a ak key nie je v strome
     * tak smernik na vrchol, ktory by mal byt otcom pre vrchol
     * s hodnotou key.*/
    parent = NULL;
    v = root;
    while (v != NULL && v->key != key) {
        parent = v;
        if (key < v->key) {
            v = v->left;
        } else {
            v = v->right;
        }
    }
}

bool find(dictionary &d, int key) {
    /* Zisti, ci sa v slovniku d nachadza kluc key. */
    node *v = findNode(d.root, key);
    if (v != NULL) {
        assert(v->key == key);
        return true;
    } else {
        return false;
    }
}

void insert(dictionary &d, int key) {
    /* Do slovnika d vlozi kluc key.
     * Predpokladame, ze takyto kluc este v slovniku nie je. */
    if (d.root == NULL) {
        /* prazdny strom - treba vytvorit koren */
        d.root = createLeaf(key, NULL);
    } else {
        node *v;
        node *parent;
        findNode(d.root, key, v, parent);
        /* parent je teraz vrchol, ktoreho syn ma byt novy vrchol */
        assert(v == NULL && parent != NULL);
        /* zisti, ci mame byt lave alebo prave dieta otca */
        if (key < parent->key) {
            assert(parent->left == NULL);
            parent->left = createLeaf(key, parent);
        } else {
            assert(parent->right == NULL);
            parent->right = createLeaf(key, parent);
        }
    }
}

int rank(dictionary &d, int key) {
    /* vrati kolky je key v utriedenom poradi prvkov v strome.
     * Predpoklada, ze key sa v strome nachadza. */
}

int select(dictionary &d, int k) {
    /* vrati k-ty najmensi prvok v strome.
     * Predpoklada, ze 1 <= k <= celkovy pocet prvkov v strome. */
}

int main() {
    dictionary d;
    init(d);

    while (true) {
        char command;
        int param;
        cin >> command >> param;
        switch (command) {
            case 'I':
                if (find(d, param)) {
                    cout << "ERR" << endl;
                } else {
                    insert(d, param);
                    cout << "OK" << endl;
                }
            case 'S':
                break;
            case 'R':
                break;
            case 'E': return 0;
        }
    }
}

Zimný semester, vzorové riešenia ukážkových príkladov k testu

• Príklad 1: funkcia vypíše tri trojice: 0 0 1, 0 0 2, 0 1 2. Nevypisuje to čo má, lebo po vynorení z rekurzie nezníži od pocet[x], aj keď hodnota a[i] bude zmenená z x na x+1. Tu je funkcia po oprave:

void generuj(int a[], int pocet[], int i, int k, int n) {
    if (i == n) {
        vypis(a, n);
    } else {
        for (int x = 0; x < n; x++) {
            if (pocet[x]<k) {
                a[i] = x;
                pocet[x]++;
                generuj(a, pocet, i + 1, k, n);
                pocet[x]--; /* pridany prikaz */
            }
        }
    }
}

• Príklad 2: (8+3*4)/(2+3)
• Príklad 3: postfix 2 4 + 3 5 * / 1 2 - / prefix: / / + 2 4 * 3 5 - 1 2
• Príklad 4: na zásobníku budú čísla 8 a 12 (8 je na spodku zásobníka). Číslo 12 vzniklo vynásobením 3 a 4.
• Príklad 5: na zásobníku budú znaky A, D, C (A na spodku zásobníka), v rade bude písmeno B
• Príklad 6:

        #
       / \
      #   *
     /\
    *  #
      /\
     *  *

• Príklad 7:

        3
       / \
      1   4
      \    \
       2    5
             \
              6

• Príklad 8: (namiesto dvojiteho krúžku používame *)

          .
         / \
        /   \
       /     \ 
      a       b
     / \     /
    a   b   a*
   /   /   / \
  a   a*  a*  b*
 /
b*

• Príklad 9: do každého políčka sme vpísali poradové číslo, kedy bude vyfarbené:

3 2 9
4 1 8
5 6 7

• Príklad 10: Jedna možnosť je použiť dvojitý smerník, ktorý môže ukazovať buď na premennú zaciatok v zozname alebo na premennú next v niektorom jeho prvku.

void vyhod(zoznam &z) {
  /* vytvorime si smernik na miesto,
   * kde je ulozeny smenrik na dalsi prvok*/
  item **smernik = &(z.zaciatok);
  /* kym nie sme na konci zoznamu */
  while((*smernik)!=NULL) {
      /* dalsi prvok je nula, zmazeme ju a prevesime zvysok zoznamu */
      if((*smernik)->data==0) {
          item *remove = *smernik;
          (*smernik) = (*smernik)->next;
          delete remove;
      }
      /* dalsi prvok nie je nula, posunieme smernik */
      else {
          smernik = &((*smernik)->next);
      }
  }
}

Druhá možnosť je použiť dva cykly: jedným mažeme nuly na začiaktu a druhým mažeme nuly vo zvyšku zoznamu.

void vyhod(zoznam &z) {
    /* vyhadzujeme nuly na zaciatku */
    while (z.zaciatok != NULL && z.zaciatok->data == 0) {
        item * remove = z.zaciatok;
        z.zaciatok = remove->next;
        delete remove;
    }
    /* node bude ukazovat vzdy na nenulovy prvok,
     * kontrolujeme prvok za nim */
    item * node = z.zaciatok;
    while (node != NULL && node->next != NULL) {
        if (node->next->data == 0) {
            item * remove = node->next;
            node->next = remove->next;
            delete remove;
        }
        else {
            node = node->next;
        }
    }
}

• Príklad 11:

int dvojicky(node *root) {
    /* prazdny strom neobsahuje dvojicky */
    if(root == NULL) return 0;
    
    int result = 0;
    /* ak su deti korena dvojicky, pricitaj 1*/
    if(root->left != NULL && root->right != NULL
            && root->left->data == root->right->data) {
        result++;
    }
    /* spocitaj dvojicky v lavom a pravom podstrome */
    result += dvojicky(root->left);
    result += dvojicky(root->right);
    return result;
}

• Príklad 12:

#include <iostream>
using namespace std;

struct kruh {
    int x, y, r;
};

void posunKruh(kruh &k) {
  k.y-=10;
}

kruh * nacitajKruhy(int n) {
  kruh * a;
  a = new kruh[n];
  for(int i=0; i<n; i++) {
    cin >> a[i].x >> a[i].y >> a[i].r;
  }
  return a;
}

void vypisKruhy(kruh *a, int n) {
  for(int i=0; i<n; i++) {
    cout << " " << a[i].x << " " << a[i].y << " " << a[i].r << endl;
  }
}

int main(void) {
  int n;
  kruh * a;
  cin >> n;
  a = nacitajKruhy(n);
  for(int i=0; i<n; i++) {
    posunKruh(a[i]);
  }
  vypisKruhy(a, n);
  delete[] a;
}

• Príklad 13:

bool jeRastuci(zoznam &z) {
    item *v = z.zaciatok;
    while (v != NULL && v->next != NULL) {
        if (v->data >= v->next->data) {
            return false;
        }
        v = v->next;
    }
    return true;
}

• Príklad 14:
  • Čísla 2,3,4 musia preskočiť číslo 5, riadok sa teda pre každé z nich vykoná raz a pre číslo 1 sa vykoná 4 krát, spolu teda 7 krát.
  • Čísla 2,3,4,...,n-2,n-1 musia preskočiť číslo n, riadok sa teda pre každé z nich vykoná raz a pre číslo 1 sa vykoná n-1 krát. Spolu sa teda riadok vykoná n-2+n-1=2n-3 krát.

Prednáška 1

Čo je programovanie

Algoritmus

Algoritmus: Postupnosť konečného počtu elementárnych krokov vedúca k vyriešeniu daného typu úlohy

Príklady:

1. Ako sčítať dve celé čísla v desiatkovej sústave
2. Ako nájsť najväčšieho spoločného deliteľa dvoch čísel
3. Ako riešiť Sudoku

Správnosť algoritmu

• Keď program dáva "správne" výsledky.
• Keď vždy skončí.

Program

• Predpis, pomocou ktorého počítač môže vykonávať algoritmus
• Zapísaný v programovacom jazyku

Programátorské prostredie

• Na tomto predmete budeme programovať v jazyku C++, budeme však z neho používať len malú časť.
• Budeme používať programátorské prostredie NetBeans, ktoré vám spríjemňuje a zjednodušuje prácu.
• Cvičenia a skúšky budú v operačnom systéme Linux, Netbeans a ďalšie potrebné nástroje si však môžete nainštalovať zadarmo aj vo Windows.

• Návod k práci v prostredí Netbeans

Prvý program

• Tradične sa v učebniciach programovania ako prvý uvádza program, ktorý iba vypíše na obrazovku text "Hello world!". Tu je v jazyku C++:

#include <iostream>
using namespace std;

int main(void) {
    cout << "Hello world!" << endl;
}

• Samotný text je vypísaný príkazom cout << "Hello world!" << endl;
• Všimnite si, že text Hello world! sme dali do úvodzoviek, čím poukazujeme na to, že to nie sú príkazy programovacieho jazyka, ale text, s ktorým treba niečo robiť.
• Za príkazom sme dali bodkočiarku, ktorá ho ukončuje.
• O vypisovaní si povieme viac neskôr, ale už teraz môžete vypisovať rôzne texty tým, že zmeníte text medzi úvodzovkami.

• Riadok int main(void) { označuje začiatok programu, program ide až po ukončovaciu zloženú zátvorku }
• Jazyk C++ sám o sebe neobsahuje príkazy na vypisovanie (cout <<...). Na to potrebujeme použiť knižnicu: súbor príkazov, ktoré niekto už naprogramoval a my ich len používame. Prvé dva riadky programu nám umožnia používať štandardnú knižnicu iostream, ktorá je súčasťou C++ a ktorá obsahuje príkazy na vypisovanie.

Spúšťanie programu

• Na to, aby sme náš program mohli spustiť na počítači, potrebujeme ho najskôr skompilovať, t.j. preložiť do spustiteľného strojového kódu.
• Ako na to, nájdete v návode k práci v prostredí Netbeans
• V prostredí Netbeans vieme program aj spustiť, môžeme si ho však aj skopírovať a spúšťať na iných počítačoch nezávisle od Netbeans.

Prvý grafický program

• Občas budeme vykresľovať obrázky pomocou knižnice SimpleDraw vytvorenej špeciálne pre tento predmet. (Tu je návod na jej používanie)
• Nasledujúci program vypíše text Hello world! pomocou tejto knižnice.

#include "../SimpleDraw.h"

int main(void) {
    /* Vytvor obrázok s rozmermi 100x100 pixelov */
    SimpleDraw window(100, 100);

    /* Nastav farbu písma na červenú. */
    window.setFontColor("red");

    /* Vypíš text vystredený na súradniciach 50,50. */
    window.drawText(50, 50, "Hello world!");

    /* Ulož obrázok do súboru hello s príponou png. */
    window.savePng("hello.png");

    /* Zobraz na obrazovke a čakaj, kým užívateľ stlačí Exit,
       potom zavri okno. */
    window.showAndClose();
}

Obsah súboru hello.png

• Po spustení program vypíše text červenou farbou, uloží ho vo forme obrázku do súboru hello.png a zobrazí ho v grafickom okne s tlačidlom "Exit". Keď užívateľ stlačí tlačidlo, okno sa zavrie.
• Prvý riadok programu teraz obsahuje inú knižnicu (SimpleDraw). Nie je súčasťou jazyka, preto si ju musíme skopírovať na náš počítač a umiestniť do vhodného adresára. Viac v návode.

• Medzi int main(void) { a koncovou zátvorkou } máme teraz viacero príkazov, každý ukončený bodkočiarkou. Vykonávajú sa v tom poradí, v ako sú napísané.
• Text medzi /* a */ bude počítač ignorovať, ide o komentár určený pre čitateľa. V tomto prípade vždy popisuje, čo bude robiť nasledujúci riadok.

Cvičenia

Aj keď sme si nepovedali toho veľa o jednotlivých príkazoch v tomto programe, mali by ste z komentárov vedieť uhádnuť, ako meniť program aby napríklad:

• mal inú veľkosť obrázku
• použil na vypisovanie inú farbu
• vypísal text na iné miesto v rámci obrázku
• vypísal dva rôzne texty na rôzne miesta obrazovky rôznou farbou (napr. červeným Hello world! a pod to modrým Good morning, starshine!)
• uložil obrázok do súboru s iným menom
• vôbec neukladal nič do súboru

Vykreslenie domčeka

Tradičný preškrtnutý domček

Domček so súradnicami

• Ukážeme si ešte program, ktorý vykreslí tradičný prečiarknutý domček, ako je na obrázku vpravo.
• Pozor, grafická obrazovka má súradnicu 0,0 v ľavom hornom rohu a smerom nadol y-ová súradnica stúpa, čo je naopak, než je zvykom v matematike.

#include "../SimpleDraw.h"

int main(void) {
    /* Vytvor obrázok s rozmermi 300x400 pixelov */
    SimpleDraw window(300, 400);

    /* Nakresli obdĺžnik (štvorec) s ľavým horným rohom v 100, 200
     * a šírkou aj dĺžkou 100. */
    window.drawRectangle(100, 200, 100, 100);

    /* Prečiarkni štvorec dvomi čiarami po uhlopriečke. */
    window.drawLine(100, 300, 200, 200);
    window.drawLine(100, 200, 200, 300);

    /* Nakresli strechu ako dve čiary. */
    window.drawLine(100, 200, 150, 100);
    window.drawLine(200, 200, 150, 100);

    /* Ulož obrázok do súboru domcek1 s príponou png. */
    window.savePng("domcek1.png");

    /* Zobraz na obrazovke a čakaj, kým užívateľ stlačí Exit,
       potom zavri okno. */
    window.showAndClose();
}

• Obmenou týchto dvoch programov by ste mali vedieť vykresliť hocijaký obrazec z rovných čiar a pridať k nim text.
• Knižnica SimpleDraw umožnuje vykresľovať aj kružnice a elipsy, lomené čiary, obrázky načítané zo súboru, meniť farbu čiary, vyfarbovať útvary a podobne. Viac sa dočítate v návode.

Domček korytnačou grafikou

• Pointa preškrtnutého domčeka je, že sa má kresliť jedným ťahom. To náš program vyššie nerobil.
• Knižnica SimpleDraw obsahuje aj príkazy na korytnačiu grafiku, ktorou môžeme domček nakresliť jedným ťahom.
  • Na obrazovke si vytvoríme virtuálnu korytnačku, ktorá má určitú polohu a natočenie.
  • Môžeme jej povedať, aby sa otočila doľava o určitý počet stupňov (turtle.turnLeft(uhol)).
  • Môžeme jej povedať, aby išla o určitú dĺžku dopredu (turtle.forward(dlzka))
  • Keď ide korytnačka dopredu, zanecháva v piesku chvostom čiarku (vykreslí teda čiaru do nášho obrázku).

#include "../SimpleDraw.h"
#include <cmath>

int main(void) {
    /* Vytvor obrázok s rozmermi 300x400 pixelov. */
    SimpleDraw window(300, 400);

    /* Vytvor korytnačku v ľavom dolnom rohu domu
     * otočenú doprava. */
    Turtle turtle(window, 100, 300, 0);

    /* Zobraz korytnačku ako šípku. */
    turtle.show();

    /* Korytnačka bude čakať 1 sekundu po každom ťahu. */
    turtle.setWait(1);

    /* Nakresli dolnú čiaru a otoč sa smerom hore. */
    turtle.forward(100);
    turtle.turnLeft(90);

    /* Nakresli pravú zvislú čiaru, hornú vodorovnú a ľavú zvislú. */
    turtle.forward(100);
    turtle.turnLeft(90);
    turtle.forward(100);
    turtle.turnLeft(90);
    turtle.forward(100);

    /* Otoč sa smerom na uhlopriečku.
       Dĺžku uhlopriečky vyrátame Pytagorovou vetou. */
    turtle.turnLeft(135);
    turtle.forward(sqrt(100 * 100 + 100 * 100));

    /* Otoč sa smerom na pravú časť strechy.
     * Strecha bude rovnostranný trojuholník so stranou
     * dĺžky 100. */
    turtle.turnLeft(75);
    turtle.forward(100);
    turtle.turnLeft(120);
    turtle.forward(100);

    /* A posledná čiara - uhlopriečne prečiarknutie. */
    turtle.turnLeft(75);
    turtle.forward(sqrt(100 * 100 + 100 * 100));

    /* Schovaj korytnačku. */
    turtle.hide();

    /* Zobraz na obrazovke. */
    window.showAndClose();
}

• Pre jednoduchosť tento domček má trochu nižšiu strechu v tvare rovnostranného trojuholníka s každou stranou dĺžky 100 (a vnútornými uhlami 60 stupňov)
• Keďže domček je štvorec, uhlupriečka ide pod uhlom 45 stupňov. Jej dĺžku však musíme spočítať. Na sčítavanie používame znamieko +, na násobenie *, a na odmocninu funkciu sqrt (skratka z anglického square root), ktorá je v knižnici cmath
• Po každom príkaze forward korytnačka na sekundu zastane, aby sme videli, čo robí.

Zhrnutie

• Programy, ktoré sme doteraz videli, vyzerali takto:
  • Najprv sme zapli používanie niekoľkých knižníc
  • Samotný program začínal int main(void) { a končil zloženou zátvorkou }
  • Program mohol mať niekoľko príkazov ukončených bodkočiarkami, ktoré sa vykonávajú jeden po druhom.
  • Okrem toho môžu byť v programe komentáre medzi /* a */, ktoré počítač ignoruje.

• Logiku za tým, prečo jednotlivé príkazy píšu tak, ako sa píšu, sme zatiaľ ešte nevysvetľovali, mali by ste však byť schopní modifikovať príklady uvedené v prednáške menením čísel, textov v úvodzovkách, pridávaním ďalších príkazov a podobne.

• Upozornenia:
  • Je rozdiel medzi malými a veľkými písmenami
  • Všetky čiarky, bodkočiarky, zátvorky a podobne sú dôležité
  • Na väčšine miest v programe môžeme voľne pridávať medzery a konce riadku, snažíme sa tým program spraviť prehľadný

• Programy, ktoré sme videli doteraz nie sú veľmi zaujímavé, lebo vždy robia to isté a robia pevný počet krokov, ktoré sme museli ručne všetky vypísať. Ďalej uvidíme
  • príkazy na načítanie vstupu od užívateľa
  • premenné, v ktorých si môžeme uchovávať vstupy a iné hodnoty
  • podmienky, ktoré nám umožnia vykonávať príkazy podľa okolností
  • cykly, ktoré nám umožnia opakovať tie isté príkazy veľa krát

Organizačné poznámky

• Utorok 20.9. o 14:50 prvé cvičenia, rozdeľte sa rovnomerne medzi M217 a M218
  • Ak vás bude viac ako počítačov, pracujte po dvojiciach resp. sa vystriedajte
  • Skúste odovzdat DÚ1 v moodli (treba heslo)
• V stredu ďalšia prednáška
• Koncom týždňa zverejnenie DÚ2 s termínom 3.10.
• V piatok termín odovzdania DÚ1
• V pondelok zverejníme rozdelenie do skupín na cvičenia
• Budúci utorok prvá rozcvička

Prednáška 2

Premenné

Spomeňme si na program na vykresľovanie domčeka. Ak by sme v ňom chceli zmeniť napríklad výšku domčeka, museli by sme pomeniť veľa súradníc v celom programe. Navyše keď vidíme v programe nejaké číslo, napr. 200, nevieme, ako sme k nemu prišli.

Program na kreslenie domčeka teraz prepíšeme tak, aby sme polohu a veľkosť domčeka mali zapísané symbolicky a mohli ich meniť na jednom mieste.

#include "../SimpleDraw.h"

int main(void) {
    /* x a y sú súradnice ľavého dolného rohu domčeka,
     * width a height sú jeho šírka a dĺžka,
     * roof je výška strechy. */
    int x = 100;
    int y = 300;
    int width = 100;
    int height = 100;
    int roof = 10;

    /* Vytvor obrázok s rozmermi 300x400 pixelov */
    SimpleDraw window(300, 400);

    /* Nakresli obdĺžnik */
    window.drawRectangle(x, y - height, width, height);

    /* Prečiarkni štvorec dvomi čiarami po uhlopriečke. */
    window.drawLine(x, y, x + width, y - height);
    window.drawLine(x, y - height, x + width, y);

    /* Nakresli strechu ako dve čiary. */
    window.drawLine(x, y - height, x + width / 2, y - height - roof);
    window.drawLine(x + width, y - height, x + width / 2, y - height - roof);

    /* Ulož obrázok do súboru domcek3 s príponou png. */
    window.savePng("domcek3.png");

    /* Zobraz na obrazovke a čakaj, kým užívateľ stlačí Exit,
       potom zavri okno. */
    window.showAndClose();
}

Symbolickým hodnotám x,y,width,height,roof sa hovorí premenné.

V programe teda môžeme používať nejaké parametre, ktoré nám program zprehľadnia, alebo nám poskytnú možnosť uložiť nejakú čiastočnú informáciu. Princíp premenných si môžeme predstaviť veľmi jednoducho. V pamäti počítača si vyhradíme priečinok potrebnej veľkosti, v programe si to nazveme nejakým názvom a na toto miesto si môžeme zapisovať hodnotu, ku ktorej zase pomocou názvu premennej vieme pristupovať.

Príkaz int x=100; vytvorí novú premennú a uloží do nej hodnotu 100. Každá premenná má určitý typ, ktorý určuje, aké hodnoty do nej môžeme ukladať. Tieto premenné majú typ int, čo je skratka zo slova integer, celé číslo.

Domček s height=200, roof=50

Ak v programe premenným priradíme iné čísla, môžeme vytvárať domčeky, ktorú budú vyššie alebo širšie, alebo budú mať strechu inej výšky. Tu vidíme jeden príklad.

    int x = 100;
    int y = 300;
    int width = 100;
    int height = 200;
    int roof = 50;

Príkaz int x=100; vieme rozpísať aj na dva príkazy int x; x=100;. Prvý z nich vytvorí premennú x, ktorá teraz bude mať nejakú ľubovoľnú hodnotu a druhý túto počiatočnú hodnotu zmení na nula.

Textový výpis a načítanie

Ďalší dôvod, kedy potrebujeme v programe využiť nejaký „parameter“ je situácia, kedy nejakú informáciu potrebujeme od používateľa. Vieme už vypísať niečo na obrazovku (výstup - output) a podobne môžeme aj čítať, čo nám používateľ napíše na klávesnici (vstup - input).

Nasledujúci program od užívateľa vypýta dve čísla a vypíše ich súčet.

#include <iostream>
using namespace std;

int main(void) {
    int x, y;

    cout << "Please enter the first number: ";
    cin >> x;
    cout << "Please enter the second number: ";
    cin >> y;

    int result = x + y;
    cout << x << "+" << y << "=" << result << endl;
}

Tu je príklad behu programu, keď užívateľ zadal čísla 10 a 3:

Please enter the first number: 10
Please enter the second number: 3
10+3=13

• Tento program používa na vstup a výstup príkazy z knižnice iostream a teda do hlavičky programu dáme #include <iostream> a using namespace std;
• Program najskôr vytvorí dve premenné x a y typu int (a nepriradzuje im zatiaľ žiadne hodnoty)
• Potom príkazom cout vypíše text "Please enter the first number: " aby užívateľ vedel, čo má robiť.
• Potom pomocou príkazu cin načíta číslo od používateľa do premennej x
• To isté opakuje pre premennú y
• Potom vytvorí novú premennú result a uloží do nej súčet x a y.
• Nakoniec vypíše výsledok aj s výrazom, ktorý sme počítali, pomocou príkazu cout.

Viac o príkaze cout

• Pomocou cout vypisujeme na konzolu, t.j. textovú obrazovku
• To, čo chceme vypísať pošleme na cout pomocou šípky <<
• cout << endl; vypíše koniec riadku
• Môžeme naraz vypísať aj viac vecí oddelených šípkami <<
  • Napr. cout << x << "+" << y << "=" << result << endl; vypíše najskôr obsah premennej x (napr. hodnotu 10), potom znamieko plus (ktoré máme v úvodzovkách), potom obsah premennej y, potom znaminko rovnosti, potom obsah premennej result a nakoniec koniec riadku.

Viac o príkaze cin

• Pomocu cin načítavame z konzoly údaje od užívateľa
• Tieto údaje pošleme do premenných pomocou šípky >>
• Opäť môžeme načítať aj viac vecí naraz, napr. nasledovný úryvok si vypýta obe čísla naraz a uloží ich do premenných x a y

   cout << "Please enter two numbers separated by space: ";
   cin >> x >> y;

• Pozor, cin nekontroluje, že užívateľ zadáva rozumné hodnoty. Čo sa stane, ak namiesto čísla zadá nejaké písmená a podobne?

Výrazy

Pri využívaní premenných by sme si mali niečo povedať aj o výrazoch a ich vyhodnocovaní. Na vytváranie výrazov v programe môžeme používať aritmetické a logické výrazy, zátvorky, čísla, konštanty a premenné.

Premenné

• Pre začiatok budeme pracovať s premennými typu int a double.
• Premenná typu int reprezentuje celé číslo.
• Premenná typu double reprezentuje reálne číslo.
• Ich rozsah je však obmedzený.
  • Typ int väčšinou zaberá 4 bajty (32 bitov) pamäte a vie ukladať čísla z intervalu <-2 147 483 648, +2 147 483 647>
  • Typ double väčšinou zaberá 8 bajtov a je uložený vo formáte s pohyblivou rádovou čiarkou, t.j. vo forme <tex>z\cdot a\cdot 2^b</tex>, kde z je znamienko, a je reálne číslo z intervalu <1,2) (mantisa) a b je celé číslo (exponent). Na uloženie mantisy sa používa 52 bitov a na uloženie exponentu 11 bitov. Vieme teda spracovávať zhruba čísla v rozsahu od Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10^{-300}} po Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10^{300}} s presnosťou na 15 až 16 platných cifier.
• Keď priradíme hodnotu typu double do hodnoty typu int, dôjde k jej zaokrúhleniu (nadol pri kladných číslach, nahor pri záporných).

Aritmetické výrazy

• +, -, * (násobenie), / (delenie)
  • delenie celočíselných premenných vráti dolnú celú časť podielu, napr. 5/3 je 1 (pre záporné čísla to môže horná celá časť)
•  % je modulo, napr. 5%3 bude 2, lebo 5 má zvyšok 2 po delení 3
• ++, -- je pridanie resp. odobranie 1
• ďalšie matematické funkcie vyžadujú #include <cmath> v hlavičke programu
  • napríklad cos(x), sin(x), tan(x) (tangens), acos(x) (arkus kosínus), exp(x) (Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e^x} ), log(x) (prirodzený logaritmus), pow(x,y) (Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^y} ), sqrt(x) (odmocnina), abs(x) (absolútna hodnota), floor(x) (dolná celá časť)
  • pozri tiež zoznam tu

Konštanty

• Celočíselné konštanty, ako napríklad 0, 1, 100, -5, majú typ int
• Konštanty s desatinnou bodkou, ako napríklad 1.5, 1.0, 3.13, -0.5 majú typ double. Môžeme tiež používať semilogaritmický zápis typu 1.5e3, čo znamená Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1.5\cdot 10^3} , t.j. 1500.

Logické konštanty a výrazy

• Logické konštanty: true (1) a false (0)
• Logické výrazy dávajú ako výsledok pravdivostnú hodnotu -- logickú konštantu
  • == (rovnosť), != (nerovnosť), <, <=
  • && (logický AND), || (logický OR), ! (logický NOT)

Vyhodnocovanie výrazov

Výrazy sa vyhodnocujú s preferenciou podľa nasledovnej tabuľky. Pritom výrazy v jednom riadku majú rovnakú prednosť a vyhodnocujú sa teda zľava doprava.

• logický NOT
• *, /, %
• +, -
• <, >, <=, >=
• ==, !=
• && (logický AND)
• || (logický OR)
• priradenie

Poradie vyhodnocovania môžeme meniť zátvorkami, napr. 4*(5-3)

Viac o operátoroch v C++ nájdete napríklad tu.

Podmienka (if)

Niekedy chceme vykonať určité príkazy len ak sú splnené nejaké podmienky. To nám umožňuje príkaz podmienky if. Jej použitie si najskôr ukážeme na priklade.

• Nasledujúci program si vypýta od užívateľa číslo a vypíše, či je toto číslo párne (even) alebo nepárne (odd).

 #include <iostream>
using namespace std;

int main(void) {
    int x;
    cout << "Please enter some number: ";
    cin >> x;

    if (x % 2 == 0) {
        cout << "Number " << x << " is even." << endl;
    } else {
        cout << "Number " << x << " is odd." << endl;
    }

}

• Tu je príklad dvoch behov programu:

Please enter some number: 10
Number 10 is even.

Please enter some number: 3
Number 3 is odd.

• Ako vidíme, za príkazom if je zátvorka s podmienkou. V našom príklade podmienka je x % 2 == 0. Zoberieme teda hodnotu x, pomocou operátora % zistíme zvyšok po delení 0 a pomocou dvoch rovnítok == testujeme, či je tento zvyšok rovný nule.
• Ak je podmienka v zátvorke splnená (t.j. ak je zvyšok rovný nule), vykonáme príkazy v zloženej zátvorke za príkazom if.
• Ak podmienka nie je splnená (t.j. ak zvyšok nie je rovný nule), vykonáme príkazy v zloženej zátvorke za slovom else
• Časť else {...} je možné vynechať, ak nechceme vykonávať žiadne príkazy.
• Nateraz píšeme zátvorky { a } za if aj za else. Napriek tomu, že v prípade, že za nimi nasleduje iba jeden príkaz to nie je nutné, odporúčame to robiť.

Vnorené podmienky

Pritom príkazy if môžeme navzájom vnárať, čím vzniknú vcelku komplikované výrazy.

• Načítaj čislo a zisti, či je kladné, záporné alebo nula.

#include <iostream>
using namespace std;

int main(void) {
    int x;
    cout << "Please enter some number: ";
    cin >> x;

    if (x == 0) {
        cout << "Null" << endl;
    } else {
        if (x > 0) {
            cout << "Positive" << endl;
        } else {
            cout << "Negative" << endl;
        }
    }

}

Upozornenie

Častá chyba, ktorá sa vyskytuje pri podmienke je použitie priradenia namiesto porovnania. Keby sme napísali

   if (x=0) cout << “Null” << endl; 

tak by odpoveď vypísalo v každom prípade. Namiesto toho, či používateľ napísal 0 by sme totiž zisťovali, či sa do premennej x dá priradiť 0.

Ďalšia bežná chyba sa vyskytuje v prípade, že prikaz je vlastne viacero príkazov.

  if (x==0) cout << “Null” << endl;
            cout << x;

je zle, pretože príkaz cout << x sa vykoná vždy – nezávisle od podmienky. V prípade, že chceme vykonať viacero príkazov, nesmieme zabudnúť ich uzátvorkovať podobne ako funkciu main. Teda

   if (x==0) {cout << “Null” << endl;
	      cout << x; 
   }

je správne.

Cyklus (for)

Teraz si ukážeme príkaz for, ktorý nám umožňuje opakovať viackrát nejakú skupinu príkazov.

Na úvod trochu motivácie. Skúste napísať nasledovné jednoduché programy:

• Vypíšte čísla od 0 do 9. A následne od 0 do 24. (pre vytrvalých od 0 do 99)
• Vykreslite pravidelný štvoruholník. Šesťuholník? Devätnásťuholník?

Vypisovanie čísiel

Nasledujúci program vypíše čísla 0 až 9 oddelené medzerami bez toho, aby sme ich niekde v programe explicitne vymenovali.

#include <iostream>
using namespace std;

int main(void) {
    for (int i = 0; i < 10; i++) {
        cout << " " << i;
    }
    cout << endl;
}

Tu je výstup programu.

0 1 2 3 4 5 6 7 8 9

Ak by sme v programe číslo 10 zmenili napr. na 25, vypíše čísla 0 do 24.

• Novou črtou tohto programu je príkaz for pre cyklus: for (int i = 0; i < 10; i++)
• Cyklus nám umožňuje opakovať určitú časť programu viackrát.
• V zátvorke za for sú tri časti oddelené bodkočiarkami.
  • Príkaz int i = 0 vytvorí novú celočíselnú premenú i a priradí jej hodnotu 0.
  • Podmienka i < 10 určuje dokedy sa má cyklus opakovať, t.j. kým hodnota i je menšia ako 10.
  • Príkaz i++ hovorí, že v každom kroku sa má premenná i zvýšiť o jedna.
• Medzi zložené zátvorky { a } môžeme dať jeden alebo viac príkazov, ktoré sa budú opakovať pre rôzne hodnoty premennej i.
  • V našom príklade máme vo vnútri cyklu iba príkaz cout << " " << i;, ktorý vypíše medzeru a hodnotu premennej i.
• Po skončení cyklu sa pokračuje príkazmi za končiacou zloženou zátvorkou, v našom prípade vypíšeme ešte koniec riadku.
• Všimnite si, že náš program obsahuje dve sady zložených zátvoriek vnorených v sebe: jedna ohraničuje celý program, jedna ohraničuje príkazy, ktorá sa robia vo vnútri cyklu.

• O presnom fungovaní príkazu for si povieme viac neskôr, ale teraz sa pozrime, čo spraví jednoduchá zmena v tomto príkaze:

for (int i = 1; i <= 10; i++) {

• Počiatočnú príkaz sme zmenili z int i = 0 na int i = 1, premenná i teda začne s hodnotou 1, nie 0. Cyklus môže začať od ľubovoľnej hodnoty (napríklad aj zápornej)
• Podmienku ukončenia sme zmenili z i < 10 na i <= 10, t.j. cyklus sa opakuje kým je hodnota premennej i menšia alebo rovná 10 (to isté by sme dosiahli aj pomocou i < 11)
• Program teda vypíše čísla od 1 po 10:

 1 2 3 4 5 6 7 8 9 10

Cvičenia 1

Cieľom prvých cvičení je vyskúšať si prostredie Netbeans a jednoduché úpravy textových aj grafickcýh programov z prednášky. Podobné programy budete písať budúci týždeň na rozcvičke, takže doporučujeme si priniesť papier s poznámkami z prvej prednášky.

Príklad 1

• Prihláste sa na počítač a spustite Netbeans podľa návodu tu
• Vytvorte nový projekt a skopírujte si tam Hello world program z prvej prednášky
• Skúste ho skompilovať a spustiť.
• Zmodifikujte ho tak, aby vypisoval slovenskú hlášku Ahoj svet! a opäť ho skompilujte a spustite.

Príklad 2

• Vytvorte nový projekt s programom na vykreslenie domčeka z prvej prednášky
  • Postupujte podľa návodu tu
  • Stiahnite si grafickú knižnicu SimpleDraw a správne ju umiestnite
  • Nezabudnite nastaviť novému projektu typ C/C++ Qt Application a nastaviť použitie knižnice
• Program skompilujte a spustite
• Zmodifikujte ho tak, aby nad domčekom v hornej časti obrázku bol zelený nápis Domcek

Príklad 3

Nakreslite korytnačou grafikou jedným ťahom obrázok napravo. Všetky malé trojuholníky na obrázku sú rovnostranné s dĺžkou hrany 100, veľký trojuholník má teda dĺžku hrany 200. Pripomíname, že v rovnostrannom trojuholníku majú vnútorné uhly 60 stupňov.

Príklad 4

Prihláste sa do prostredia moodle a odovzdajte prvú domácu úlohu.

DÚ1

2 body

Cieľom tejto domácej úlohy je oboznámiť sa so systémom Moodle, ktorý budete používať na odovzdávanie úloh aj neskôr a potvrdiť svoj záujem o tento predmet, aby sme s Vami rátali pri rozdelovaní do skupín na cvičenia.

Postup:

• Vytvorte textový súbor (napríklad v textovom editore alebo v prostredí Netbeans)
• Napíšte do neho odpovede na otázky uvedené nižšie
• Prihláste sa do systému Moodle pomocou AIS prihlasovacieho mena a hesla
• Zapíšte sa na predmet Programovanie (1) v C/C++ s použitím kľúča, ktorý dostanete na prednáške resp. cvičení
• Odovzdajte vytvorený textový súbor
• Termín odovzdania je piatok 23.9. 23:55

Otázky

1. Meno a priezvisko
2. Emailová adresa
3. Učili ste sa už programovať? Ak áno, v akom jazyku (jazykoch)?

Prednáška 3

Doteraz sme videli:

• Vypisovanie a načítavanie v textovom režime
• Vykresľovanie pomocou grafickej knižnice SimpleDraw
• Aritmetické a logické výrazy, premenné typu int a double
• Podmienku if
• Cyklus for

Dnes:

• Ďalšie príklady na cykly a podmienky, zopár menších noviniek.

Oprava:

• Priorita && je vyššia ako priorita ||, t.j. x>0 || y>0 && z>0 je to isté ako x>0 || (y>0 && z>0)

Viac príkladov na cyklus for

Vykreslenie náhodných kruhov

Nasledujúci program vykreslí na obrazovku náhodne rozmiestnené kruhy.

#include "../SimpleDraw.h"
#include <cstdlib>
#include <ctime>

int main(void) {
    int size = 300; /* veľkosť obrázku */
    int count = 30; /* počet kruhov */
    int radius = 10; /* polomer kruhu */

    /* inicializácia generátora pseudonáhodných čísel */
    srand(time(NULL));

    SimpleDraw window(size, size);

    for (int i = 0; i < count; i++) {
        /* vykresli kruh s polomerom radius na náhodné miesto */
        window.drawEllipse(rand() % size, rand() % size, radius, radius);
    }

    window.showAndClose();
}

• Program využíva príkaz rand(), ktorý generuje pseudonáhodné celé čísla. (Nie sú v skutočnosti náhodné, lebo ide o pevne definovanú matematickú postupnosť, ktorá však má mnohé vlastnosti náhodných čísel).
  • Výsledkom rand() je celé nezáporné číslo medzi 0 a nejakou veľkou konštantou.
  • rand() % size je číslo medzi 0 a size-1
  • vygenerujeme dve také čísla a použijeme ich ako súradnice kruhu (presnejšie ľavého horného rohu štorca opísaného kruhu)
• Príkaz srand inicializuje generátor pseudonáhodných čísel na určitú hodnotu, my použijeme aktuálny čas.
• Potrebujeme knižnice cstdlib a ctime.

Skúsme pred príkaz window.drawEllipse dať ešte príkaz window.setBrushColor, ktorý nastaví farbu výplne kruhu. Túto farbu chceme tiež nastaviť na náhodnú hodnotu, t.j. vygenerujeme tri náhodné čísla pre červenú, zelenú a modrú zložku tejto farby. Tieto čísla majú byť medzi 0 a 255.

/* nastav náhodnú farbu */
window.setBrushColor(rand() % 256, rand() % 256, rand() % 256);

Cvičenie: nastavme aj polomer kruhu ako náhodné číslo od 0 do 19. Čo ak chceme polomer od 10 do 19?

Výpočet faktoriálu

Tento program si od užívateľa vypýta číslo n a spočíta n!, t.j. súčin celých čísel od 1 po n.

#include <iostream>
using namespace std;

int main(void) {
    int n;

    cout << "Please enter n: ";
    cin >> n;

    int result = 1;
    for (int i = 1; i <= n; i++) {
        result = result * i;
    }
    cout << n << "!=" << result << endl;
}

Tu je príklad behu programu pre n=4 (1*2*3*4=24)

Please enter n: 4
4!=24

• Program používa premennú result, v ktorej sa ukladá dočasný výsledok. Na začiatok ju nastavíme na 1 a postupne ju násobíme číslami 1, 2, ..., n.
• Riadok result = result * i; zoberie pôvodnú hodnotu premennej result, vynásobí ju hodnotou premennej i (t.j. jedným z čísel 1, 2, ..., n) a výsledok uloží naspäť do premennej result (prepíše pôvodnú hodnotu). To isté sa dá napísať ako result *= i;

Krokovanie programu

• Skúsme si odkrokovať, ako sa budú postupne meniť hodnoty premenných počas behu programu
• Krokovanie programu a vypisovanie hodnôt premenných je možné robiť v prostredí Netbeans, mali by ste však byť schopní to robiť aj ručne, lebo tým lepšie pochopíte, ako program pracuje.
• Krokovanie v prostredí Netbeans:
  • Klikneme pravým na meno projeku v záložke Projects, zvolíme Step into
  • Tým sa naštaruje a hneď aj zastaví náš program, ďalej sa môžeme púšťať program riadok po riadku ikonkou Step Over (F8)
  • V dolnej časti okna v záložke Variables vidíme hodnoty vybraných premenných, ďalšie si môžeme ručne pridať

Int má obmedzený rozsah

Funkcia n! veľmi rýchlo rastie a už pre n=13 sa výsledok nezmestí do premennej typu int. Dostávame nezmyselné hodnoty:

12!=479001600
13!=1932053504
14!=1278945280
15!=2004310016
16!=2004189184
17!=-288522240

Správne hodnoty sú:

12!=479001600
13!=6227020800
14!=87178291200
15!=1307674368000
16!=20922789888000
17!=355687428096000

Cvičenie: Prepíšme program na počítanie faktoriálu tak, aby vypísal aj faktoriál ako súčin čísel, napríklad

Please enter n: 4
4! = 1*2*3*4 = 24

Vypisovanie deliteľov: podmienka v cykle

Nasledujúci program načíta číslo od užívateľa a vypíše zoznam jeho deliteľov.

#include <iostream>
using namespace std;

int main(void) {
    int n;
    cout << "Please enter some number: ";
    cin >> n;

    cout << "Divisors of " << n << ":";
    for (int i = 1; i <= n; i++) {
        if (n % i == 0) {
            cout << " " << i;
        }
    }
    cout << endl;
}

Beh programu:

Please enter some number: 12
Divisors of 12: 1 2 3 4 6 12

Malá odbočka: úprava a čitateľnosť programov

Okrem počítača budú váš program čítať aj ľudia: vy sami, keď v ňom potrebujete nájsť chybu alebo ho v budúcnosti rozširovať, vaši kolegovia vo firme, učitelia v škole. Preto treba programy písať tak, aby boli nielen správne, ale aj prehľadné a ľahko pochopiteľné. Tu sú zásady, ktoré takejto čitateľnosti pomáhajú:

• Odsadzovanie: príkazy vykonávané v cykle alebo podmeinke (medzi { a }) odsaďte o niekoľko pozícií doprava. Pri vnorených cykloch a podmienkach odsaďte každú ďalšiu úroveň viac.
  • V Netbeans sa dá odsadzovanie napraviť na vybranom texte pomocou položky meno Source->Format
• Medzery a voľné riadky: prehľadnosť zvýšite, ak oddelíte ucelené časti programu voľným riadkom. V zložitejších výrazoch doporučujeme vkladať medzery okolo operátorov:
  • for(int i=0;i<count;i++){
  • for (int i = 0; i < count; i++) {
• Dĺžka riadku: doporučujeme sa vyhýbať sa dlhým riadkom nad 80 znakov. Sú problémy s ich tlačením alebo zobrazovaním v menších oknách, aj na veľkom monitore namáhajú čitateľa. V prípade potreby je možné dlhšiu podmenku alebo iný výraz rozdeliť na viac riadkov.
• Názvy premenných: je vhodné používať názvy premenných, ktoré vyjadrujú ich obsah (po anglicky príp. slovensky). Pri premenných v kratších programoch, alebo ktoré sa používajú len lokálne v kratšom kúsku programu môžete použiť aj krátke zaužívané názvy, napr. i a j pre premenné v cykloch, n pre počet, a pre pole.
• Komentáre: význam jednotlivých úsekov kódu je dobré popísať v komentároch.

Pri známkovaní budeme brať do úvahy aj prehľadnosť vašich programov.

Cyklus while

Okrem cyklu for môžeme použiť aj cyklus while, ktorý vyzerá nasledovne:

while (podmienka) { 
  príkaz; 
}

Čítame: kým je splnená podmienka vykonávaj príkaz. Podrobnejšie:

• podmienka je výraz, ktorý sa najskôr vyhodnotí:
  • ak je jeho hodnota logická nepravda, cyklus je ukončený a program pokračuje ďalším príkazom za while{...}
  • ak je jeho hodnota logická pravda, vykoná sa príkaz a celý cyklus sa opäť opakuje.

Úroky v banke

Na začiatku každého roku uložíme 1000 EUR na úrokovú vkladnú knižku s ročným úrokom 5%. Zistite, za koľko rokov naše úspory dosiahnu sumu aspoň 20 000 EUR.

Vieme určite, že budeme musieť peniaze vkladať niekoľko rokov. Problém je v tom, že dopredu nevieme povedať koľko, pretože počet rokov je vlastne výstupom programu. Neformálne by sme algoritmus na vyriešenie mohli popísať takto:

• Založ si účet v banke (zatiaľ šetríš nula rokov)
• Kým nemáš na začiatku roka našetrené 20 000 EUR opakuj:
  • Vlož čiastku a čakaj na nový rok, kým sa zúročia

Potrebujeme cyklus, ktorý sa bude vykonávať, kým platí nejaká podmienka - práve na to je vhodný while cyklus. Pomocou neho zapíšeme algoritmus nasledovne:

#include <iostream>
using namespace std;

int main(void) {
    double ucet = 0;
    int rok = 0;

    while (ucet < 20000) {
        ucet = (ucet + 1000) * 1.05;
        rok++;   /* to isté ako rok = rok + 1 */
        cout << "Na konci roku " << rok << " máme na účte " << ucet << " EUR" << endl;
    }
}

Na konci roku 1 máme na účte 1050 EUR
Na konci roku 2 máme na účte 2152.5 EUR
Na konci roku 3 máme na účte 3310.12 EUR
Na konci roku 4 máme na účte 4525.63 EUR
Na konci roku 5 máme na účte 5801.91 EUR
Na konci roku 6 máme na účte 7142.01 EUR
Na konci roku 7 máme na účte 8549.11 EUR
Na konci roku 8 máme na účte 10026.6 EUR
Na konci roku 9 máme na účte 11577.9 EUR
Na konci roku 10 máme na účte 13206.8 EUR
Na konci roku 11 máme na účte 14917.1 EUR
Na konci roku 12 máme na účte 16713 EUR
Na konci roku 13 máme na účte 18598.6 EUR
Na konci roku 14 máme na účte 20578.6 EUR

Euklidov algoritmus na nájdenie najväčšieho spoločného deliteľa

• Jeden z najstarších dodnes používaných algoritmov, Euklides ho popísal v svom diele Základy, cca 300 pred Kr.
• Máme dané dve kladné celé čísla a a b a chceme nájsť najväčšie číslo d, ktoré delí a aj b.
• Skratka nsd(a,b), po anglicky gcd(a,b) (greatest common divisor)

• Príklad:
  • Delitele 12: 1, 2, 3, 4, 6, 12
  • Delitele 8: 1, 2, 4, 8
  • Spoločné delitele 8 a 12: 1, 2, 4
  • gcd(8,12)=4

• Lema: pre všetky kladné celé čísla a a b platí: gcd(a,b) = gcd(b, a mod b)
  • nech Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x = a \bmod b, y = \lfloor a/b\rfloor}
  • nech A je množina spoločných deliteľov a a b, B je množina spoločných deliteľov b a x
  • ukážeme, že A=B (a teda aj Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \max A = \max B} )
  • x = a - yb a preto každý deliteľ a aj b delí aj x, t.j. Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A\subseteq B}
  • taktiež a = yb + x a preto každý deliteľ b a x delí aj a, t.j. Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B\subseteq A}

#include <iostream>
using namespace std;

int main(void) {
    int a, b;
    cout << "Enter two positive integers a and b: ";
    cin >> a >> b;
    while(b != 0) {
        int x = a % b;
        a = b;
        b = x;
    }
    cout << "Their gcd: " << a << endl;
}

Príklad behu programu:

Enter two positive integers a and b: 30 8
Their gcd: 2

Tento výpočet prešiel cez dvojice:

30 8
8 6
6 2
2 0

Nekonečný cyklus

while (true) {
 prikaz;
}

Opakuje príkaz donekonečna (kým program nezastavíme).

Napríklad môžeme donekonečna vykresľovať náhodné kruhy, ale pozor, každý kruh berie trochu miesta v pamäti, po čase zaplníte pamäť a počítač môže dramaticky spomaliť, alebo program skončí s chybovou hláškou.

#include "../SimpleDraw.h"
#include <cstdlib>
#include <ctime>

int main(void) {
    int size = 300; /* veľkosť obrázku */
    int radius = 10; /* polomer kruhu */

    /* inicializácia generátora pseudonáhodných čísel */
    srand(time(NULL));

    SimpleDraw window(size, size);

    while (true) {
        /* vykresli kruh s polomerom radius na náhodné miesto */
        window.drawEllipse(rand() % size, rand() % size, radius, radius);
    }

    window.showAndClose();
}

Hra hádaj číslo

V nasledujúcom programe si počítač "myslí číslo" od 1 do 100 a užívateľ háda, o ktoré číslo ide.

Program používa premennú typu bool, do ktorej môžeme priraďovať logické hodnoty true alebo false.

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

int main(void) {
    /* vygenerujeme náhodné číslo medzi 1 a 100 */
    srand(time(NULL));
    int number = rand() % 100 + 1;

    /* Pamätáme si, či sme už uhádli alebo nie. */
    bool guessed = false;
    cout << "Guess a number between 1 and 100: ";
    /* Kým užívateľ neuhádne, spýtame sa ho na ďalšiu
       odpoveď. */
    while (!guessed) {
        int guess;
        cin >> guess;
        /* Vyhodnotíme odpoveď. */
        if (guess < number) {
            cout << "Too low, try again: ";
        } else if (guess > number) {
            cout << "Too high, try again: ";
        } else if (guess == number) {
            guessed = true;
            cout << "Correct guess" << endl;
        }
    }
}

Príklad priebehu programu:

Guess a number between 1 and 100: 50
Too low, try again: 75
Too high, try again: 63
Too low, try again: 69
Too high, try again: 66
Too low, try again: 67
Correct guess

Príkazy break a continue (používať s mierou)

• Príkaz break: skončí sa cyklus, v ktorom práve sme, pokračuje sa prvým príkazom za cyklom.
• Príkaz continue: ide na ďalšiu iteráciu cyklu, nevykoná zvyšok tela cyklu.

Používať s mierou, robia program menej prehľadný, ľahko zavlečú chyby.

Program uvedený vyššie môžeme prepísať bez boolovskej premennej s použitím nekonečného cyklu, z ktorého ale vyskočíme príkazom break, keď užívateľ uhádne.

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

int main(void) {
    /* vygenerujeme náhodné číslo medzi 1 a 100 */
    srand(time(NULL));
    int number = rand() % 100 + 1;

    cout << "Guess a number between 1 and 100: ";
    /* Kým užívateľ neuhádne, spýtame sa ho na ďalšiu
       odpoveď. */
    while (true) {
        int guess;
        cin >> guess;
        /* Vyhodnotíme odpoveď. */
        if (guess < number) {
            cout << "Too low, try again: ";
        } else if (guess > number) {
            cout << "Too high, try again: ";
        } else if (guess == number) {
            cout << "Correct guess" << endl;
            break;
        }
    }
}

Späť k cyklu for

Cyklus for má tvar

for(prikaz1; podmienka; prikaz2) {
    prikaz3;
}

Je ekvivalentný nasledujúcemu príkazu while:

prikaz1;
while(podmienka) {
    prikaz3;
    prikaz2;
}

Napríklad, nasledujúce kúsky kódu oba vypisujú čísla 0 až 9:

for (int i = 0; i < 10; i++) {
     cout << " " << i;
}

int i = 0;
while(i < 10) {
     cout << " " << i;
     i++;
}

Cyklus for spravidla používame, ak má náš cyklus krátky a jednoduchý iterátor (prikaz2) a jednoduchú podmienku. V opačnom prípade väčšinou používame cyklus while.

Ešte vypisovanie deliteľov

Ak chceme vypísať deliteľov od najväčších, stačí prepísať for cyklus:

• od najmenších: for (int i = 1; i <= n; i++) {
• od najväčších: for (int i = n; i > 0; i--) {

#include <iostream>
using namespace std;

int main(void) {
    int n;
    cout << "Please enter some number: ";
    cin >> n;

    cout << "Divisors of " << n << ":";
    for (int i = n; i > 0; i--) {
        if (n % i == 0) {
            cout << " " << i;
        }
    }
    cout << endl;
}

Príklad behu programu:

Please enter some number: 30
Divisors of 30: 30 15 10 6 5 3 2 1

Zrýchlime program na vypisovanie deliteľov: ak i je deliteľ n, aj n/i je deliteľ, môžeme ho rovno vypísať. Aspoň jeden z tejto dvojice je najviac odmocnina z n.

#include <iostream>
using namespace std;

int main(void) {
    int n;
    cout << "Please enter some number: ";
    cin >> n;

    cout << "Divisors of " << n << ":";

    for(int i=1; i*i<=n; i++) {
        if (n % i == 0) {
            int j = n / i;
            cout << " " << i << " " << j;
        }
    }
    cout << endl;
}

Cvičenie: Tento program nefunguje celkom správne, občas vypíše nejaké číslo dvakrát. Kedy? Ako ho vieme opraviť?

Pomalší program, ktorý skúša všetky čísla po n trvá pre n=1234567890 na mojom počítači 4.5s. Program, ktorý ide iba po odmocninu trvá 0.0002s.

Zhrnutie

• Videli sme niekoľko príkladov využitia cyklov for a while.
• Cyklus for je možné zapísať ako while (a naopak).
• Pseudonáhodné čísla generujeme príkazom rand(), inicializácia cez srand(time(NULL)).
• Logické hodnoty true a false vieme ukladať do premenných typu bool.
• Z cyklu vieme vyskočiť príkazom break, prejsť na ďalšiu iteráciu príkazom continue. Používať s mierou.
• Euklidov algoritmus rýchlo nájde najväčšieho spoločného deliteľa dvoch čísel.
• Dôležitá je prehľadná úprava programov a názvy premenných súvisiace s ich obsahom.
• Netbeans umožňuje krokovať program, mali by ste to však vedieť robiť aj ručne.

Organizačné poznámky

• Dnes (utorok) o 14:50 cvičenia krúžok 1 a 3 (učivo z minulého týždňa)
• Zajtra prednáška, téma podprogramy
• Do pondelka 3.10.2011 22:00 odovzdávajte DÚ2
• Koncom týždňa bude verejnená DÚ3 (pozrite si pred cvičením)
• Budúci týždeň rozcvička z tohtotýždenného cvičenia

Vnorené cykly

Vykreslime šachovnicu s n x n štvorčekmi, ktoré sú striedavo čierne a žlté.

• Potrebujeme na to dva vnorené cykly, jeden pôjde cez riadky šachovnice, druhý pre stĺpce.
• Ak row + column je párne, kreslíme čierny štvorec, inak kreslíme žltý.

#include "../SimpleDraw.h"

int main(void) {
    int n = 8; /* počet štvorcov v riadku a stĺpci*/
    int square = 20; /* veľkosť jedného štvorca */
    int size = n * square; /* veľkosť obrázku */

    SimpleDraw window(size, size);

    for (int row = 0; row < n; row++) {
        for (int column = 0; column < n; column++) {
            if ((row + column) % 2 == 0) {
                window.setBrushColor("black");
            } else {
                window.setBrushColor("yellow");
            }
            window.drawRectangle(column * square, row * square,
                    square, square);
        }
    }
    window.showAndClose();
}

To isté, ale najskôr vykreslíme veľký žltý štvorec, potom do neho vkresľujeme malé čierne štvorčeky.

• V cykle pre stĺpce preskakujeme každý druhý štvorec, pričom ak row je párny, začíname od 0, ak je nepárny, začíname od 1
  • for (int column = row % 2; column < n; column += 2) {
  • príkaz column += 2 je to isté ako column = column + 2

#include "../SimpleDraw.h"

int main(void) {
    int n = 8; /* počet štvorcov v riadku a stĺpci*/
    int square = 20; /* veľkosť jedného štvorca */
    int size = n * square; /* veľkosť obrázku */

    SimpleDraw window(size, size);

    /* veľký žltý štvorec */
    window.setBrushColor("yellow");
    window.drawRectangle(0,0,size,size);

    /* nastavíme farbu na čiernu */
    window.setBrushColor("black");
    
    for (int row = 0; row < n; row++) {
        for (int column = row % 2; column < n; column += 2) {
            window.drawRectangle(column * square, row * square,
                    square, square);
        }
    }
    window.showAndClose();
}

Prednáška 4

Fukcie sme už používali.

• V grafických programoch sme mali v knižnice SimpleDraw niečo, čo nám vykreslilo obdĺždnik. Stačilo nám napísať window.drawRectangle( , , , ) s patričnými parametrami a v grafickej obrazovke sa objavil obdĺždnik.
• Podobne aj sqrt() je funkcia, ktorá nám povie druhú odmocninu čísla.

Teraz sa pozrieme na to, ako vytvoriť v programe vlastnú funkciu. Doteraz sme vytvorili jedinu funkciu - funkciu main.

Fibonacciho čísla

Fibonacciho postupnosť je postupnosť čísiel, v ktorej každý ďalší člen F je súčtom dvoch predchádzajúcich. Jednotlivé členy postupnosti sa nazývajú Fibonacciho čísla.

   0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393… 

Na výpočet Fibonacciho čísel používame nasledovný vzťah:

• F(0) = 0
• F(1) = 1
• F(n)=F(n-1)+F(n-2)

Napíšeme program, ktorý bude počítať Fibonacciho čísla. Chceme teda funkciu, ktorá na otázku "Aké je ôsme Fibonacciho číslo?" odpovie "21".

Ako teda naprogramujeme funckiu? Potrebujeme zadefinovať nasledovné časti funkcie:

• Návratovú hodnotu funkcie: Naša funkcia vracia hodnotu Fibonacciho čísla na používateľom zadanej pozícii. Fibonacciho číslo je celé číslo a tak hodnota, ktorú má naša funkcia vrátiť je typu int. V prípade, že by funkcia nemala vrátiť nič je jej návratová hodnota typu void. Takou by bola napríkald funkcia, ktorá má za úlohu vypísať Fibonacciho postupnosť po nejakú pozíciu a potom skončiť.
• Názov funkcie: je na tom podobne ako pri premenných. Môžeme využiť obľúbený nič nehovoriaci názov funkcie foo ale radsšej použijeme názov, ktorý vystihuje čo funkcia počíta. Napríklad fibon_elem() alebo podobne.
• Zoznam parametrov funkcie: V zátvorkách za názvom funkcie je zoznam typov a názvov premenných, ktoré funkcia očakáva. V našom príklade funkcia očakáva poradie prvku, ktorý má vypísať. Teda jeden celočíselný parameter. Funkcie môžu mať zoznam parametrov aj prázdny. Napríklad funkcia, ktorá má pozdraviť používateľa a zistiť jeho meno asi žiadne parametre nepoužije.
• Telo funkcie: V zložených zátovrkách za definíciou funkcie je jej vlastný obsah - telo.

int fibon_elem(int pos) {

    int elem = 1;
    int n_1 = 1;
    int n_2 = 1;

    for (int i = 3; i <= pos; i++) {
        elem = n_1 + n_2;
        n_2 = n_1;
        n_1 = elem;
    }

    return elem;
}

Prácu funkcie fibon_elem() by ste mali byť schopní prečítať a pochopiť. Jediná nová vec je príkaz return.

Return

Príkaz return vracia hodnotu funkcie.

• V prípade výskytu príkazu return je funkcia okamžite zastavená a jej výstupná hodnota je výraz za slovom return.
• Funkcia, ktorá nič nevracia nemusí mať return - je implicitne definovaný na konci funkcie. Takáto funkcia však napriek tomu môže mať jeden (alebo viac) príkazov return.
• V prípade, že funkcia má niečo vrátiť, musí obsahovať return. Môže ich však obsahovať viac.

int max(int a, int b) {
    if (a > b) {
        return a;
    } else {
        return b;
    }
}

int max(int a, int b) {
    int maxval;
    if (a > b) {
        maxval = a;
    } else {
        maxval = b;
    }
    return maxval;
}

Parametre funkcií

Doteraz sme mali parametre funkcii nejaké hodnoty, ktoré fungovali nasledovne:

• Pri volaní funkcie sa hodnota samotného parametra stala vlastne lokálnou premennou funkcie.
• Táto hodnota sa síce dala meniť, ale táto zmena sa do miesta odkiaľ sme funkciu volali nedostala.

Parameter, ktorý nie je priamo hodnota, ale iba adresa, kde nejakú hodnotu nájdeme je referencia. Dôvodov môže byt niekoľko

Viac ako jedna návratová hodnota

Odovzdávanie parametra referenciou je potrebné vždy, keď máme vrátiť viac ako jednu hodnotu.

void stred(double x1, double y1, double x2, double y2, double &xs, double &ys){
  xs=(x1+x2)/2;
  ys=(y1+y2)/2;
}

int main(void){

double x1, y1, x2,y2;
double x,y;

cout << "Napiste suradnice jedneho konca usecky (oddelene medzerou): ";
cin << x1 << y1;

cout << "Napiste suradnice druheho konca usecky (oddelene medzerou): ";
cin << x2 << y2;

stred(x1,y1,x2,y2,x,y);
cout << "Stred usecky je ["<< x << "," << y << "]." << endl;
}

Funkcia, ktorej úlohou je zmeniť svoj parameter

#include <iostream>
using namespace std;

void duplicate (int& a, int& b, int& c)
{
  a=a*2;
  b=b*2;
  c=c*2;
}

int main ()
{
  int x=1, y=3, z=7;
  duplicate (x, y, z);
  cout << "x=" << x << ", y=" << y << ", z=" << z;
  return 0;
}

Keby sme funkcii odovzdali parameter priamo hodnotou tj, void duplicate (int a, int b, int c) tak by sa hodnoty nezmenili.

Potrebné odovzdať parameter a či funkcia prebehla správne

Čo vlastne môžeme urobiť, keď dostaneme zlý parameter.

• Môžeme okamžite ukončiť celý program. V knižnici cstdlib je funkcia exit(), ktorá robí presne to. Má ako parameter hodnotu, ktorú nastaví
• Bežný spôsob, o ktorom si niečo povieme neskôr, sú takzvané výnimky exceptions
• Môžeme vrátiť nejakú špeciálnu hodnotu a veriť, že používateľ z toho pochopí, že je to divné a že to rozozná od správneho výstupu funkcie. Ale dôvera v schopnosti a inteligenciu používateľa sa všeobecne v softvérovom inžinierstve neodporúča.
• Môžeme teda ako výstup funkcie vrátiť, či sa podarilo alebo nepodarilo správne vypočítať hodnotu. Teda výstupom funkcie bude logická hodnota bool a potrebujeme parameter - referenciu, v ktorom vrátime hodnotu.

Ďalšie poznámky o funkciách a premenných v nich

Kde definovať funkciu?

Funkcia musí byť definovaná pred tým, ako ju v programe použijeme, aby kompilátor vedel skontrolovať korektnosť jej použitia (počet parametrov, ich typ..).

V prípade, že to nie je možné urobiť, potrebujeme aspoň dopredu oznámiť, že takéto funkcie budú. Urobíme to pomocou prototypu funkcie type name ( argument_type1, argument_type2, ...);

// declaring functions prototypes
#include <iostream>
using namespace std;

void odd (int a);
void even (int a);

int main ()
{
  int i;
  do {
    cout << "Type a number (0 to exit): ";
    cin >> i;
    odd (i);
  } while (i!=0);
  return 0;
}

void odd (int a)
{
  if ((a%2)!=0) cout << "Number is odd.\n";
  else even (a);
}

void even (int a)
{
  if ((a%2)==0) cout << "Number is even.\n";
  else odd (a);
}

Kde má byť return?

Vo funkcii, ktorá vracia neprázdnu hodnotu (tj. nie void) musí byť return (alebo viac returnov) tak, aby každé možné prejdenie funkciou bolo ukončené príkazom return. Vo funkciách, ktoré vracajú void, môže ale nemusí byť return - to znamená, že oba nasledovné programy sú v poriadku.

void printmessage ()
{
  cout << "I'm a function!";
}

void printmessage ()
{
  cout << "I'm a function!";
  return;
}

Lokálne a globálne premenné

void Fnc () {
//  i=13; – nemôžeme používať premennú i – žiadna premenná i nie je viditeľná
}

int i;

void Fnc2 () {
  i=50; // priradí sa do globálne premennej i!
  Fnc ();
}

void Fnc1 () {
  int i;
  i=2; // priradí sa do lokálnej premennej i, ktorá vznikla v tejto funkcii
    // uvedomte si, že v tomto okamihu existujú 3 premenné s menom i :
    //   i – globálna premenná,
    //   lokálna premenná i, ktorá vznikla vo funkcii main,
    //   a lokálna premenná i, ktorá vznikla v tejto funkcii.
}

void main () {
int i;
  i=1;
    // priraďuje sa do lokálnej premennej i a nie do globálnej premennej i,
    // globálna premenná i je prekrytá – identifikátor i označuje lokálnu premennú i.
  Fnc1 ();
    // lokálna premenná i má stále hodnotu 1
  Fnc2 ();
    // lokálna premenná i má stále hodnotu 1, globálna premenná i má hodnotu 50,
  ::i=25; // priraďujem do globálne premennej i
}

Funkcia main

Má od ostatných funkcií niekoľko odlišností

• Síce má návratový typ (int), ale nemusí nič vracať.
• V programe sa nemôže volať - jediné jej volanie je automatické (začína sa ním beh programu)
• Má predpísané argumenty, ktoré sa dajú vynechať (alebo ich časť od konca)

Príklad: obmena problému z cvičení

Úlohou na cvičení bolo napísať program, ktorý zistí, či sú intervaly disjunktné, jeden podintervalom druhého alebo majú iný prienik. V tomto príklade chceme opäť načítať dva intervaly a vypísať ich prienik alebo informáciu, že sú disjunktné.

#include <iostream>
using namespace std;

void swap(int &x, int &y) {
    int tmp = x;
    x = y;
    y = tmp;
}

int min(int x, int y) {
    if (x < y) {
        return x;
    } else {
        return y;
    }
}

int main(void) {
    int a, b, c, d;
    cout << "Zadajte zaciatok a koniec prveho intervalu: ";
    cin >> a >> b;
    cout << "Zadajte zaciatok a koniec druheho intervalu: ";
    cin >> c >> d;

    /* Chceme, aby zaciatok prveho intervalu bol <= zaciatku druheho. */
    if (c < a) {
        swap(a, c);
        swap(b, d);
    }

    if (b < c) {
        cout << "Intervaly su disjunktne." << endl;
    } else {
        cout << "Ich prienik je interval [" << c << "," << min(b, d) << "]" << endl;
    }
}

• Intervaly si po načítaní usporiadame tak, aby prvý interval začínal skôr. Ak to neplatilo (tj c<a), tak sme vymenili ich vymenili.
• Ak už vieme, že prvý interval začína skôr, tak potom sú intervaly disjunktné, ak aj skôr skončí.
• V opačnom prípade je prienik od začiatku druhého intervalu po prvý koniec, teda menšie z čísel b,d.

Perličky na záver

• Inline funkcie: Teoreticky to hovori prekladaču, že pri preklade má miesto volania tej funkcie na to miesto dať priamo telo tej funkcie. Takze se ušetrí ten skok. Drobný problém je, že ten pokyn môže prekladac ignorovať a neurobiť to. A naopak, môze to urobiť sám od seba pri ľubovoľnej funkcii. Takze v reále to prekladač považuje len za nápovedu alebo to ignoruje úplne.

Formát inline type name ( arguments ... ) { instructions ... }

• Preťažovanie funkcii: Bude hlavne v budúcom semestri. Ide o možnosť použiť jeden názov funkcie pre rôzne ak má odlišný počet alebo typ parametrov. Bežne sa využíva napríklad ak chceme sa ináč správať na celých a na desatinných číslach.

• Konštantný parameter: Keď chceme z nejakého dôvodu dávať parameter referenciou (aby sa napr. zbytočne nekopíroval) ale pritom nechceme aby sa menil. Napríklad nasledovná funkcia je chybná a kompilátor vyhlási chybu:

void foo(const int &x){
   x = 6;  // x is a const reference and can not be changed!
}

Cvičenia 2

Úlohou dnešného cvičenia je precvičiť si logické a aritmetické výrazy, podmienky a jednoduché použitie cyklu for.

• Nasledujúce dva úryvky programu robia to isté, pričom prvý používa logický operátor && (and) a druhý používa dva príkazy if:

//Verzia 1:
if(x>0 && y>0) { cout << "Yes!"; }

//Verzia 2:
if(x>0) {
  if(y>0) { cout << "Yes!"; }
}

• Podobne nahraďte logické operátory && a || aj v nasledujúcich príkazoch:

if(x>0 || y>0) { cout << "Yes!"; }
if (x>0 || (x<0 && y<0)) { cout << "Yes!"; }
if (x<0 && (y<0 || z<0)) { cout << "Yes!"; }

• Nech x je nejaký logický výraz. Čomu sa rovnajú nasledovné výrazy?

x && true 
x && false 
x || true 
x || false
x && x
x || x 
x && !x
x || !x
x == true 
x == false

• Napíšte program, ktorý načíta dve čísla a vypíše to väčšie z nich.

• Napíšte program, ktorý korytnačou grafikou vykreslí pravidelný n-uholník. V programe si zadefinujte a použite nasledujúce premenné

    int size = 300; /* veľkosť obrázku */
    int length = 200; /* dĺžka strany */
    int n = 4; /* počet strán */

Vyskúšajte meniť hodnoty premenných a pozrite si výsledok.

• Napíšte program, ktorý načíta tri celé čísla a vypíše, či môžu byť stranami jedného trojuholníka.

• Napíšte program, ktorý vypíše tabuľku druhých mocnín čísel 1,2,...,n. Výstup bude mať takúto formu:

1 squared is 1
2 squared is 4
3 squared is 9
...

• Napíšte program, ktorý načíta štyri celé čísla a,b,c,d, ktoré predstavujú dva uzavreté intervaly [a,b] a [c,d]. Program vypíše tú z nasledujúcich viet, ktorá pre ne platí:

   Intervaly su disjunktne (maju prazdny prienik).
   Jeden z intervalov je podmnozinou druheho.
   Intervaly sa pretinaju, ale ziaden nie je podmnozinou druheho.

• Napíšte program, ktorý načíta dĺžku základne a výšku rovnoramenného trojuholníka a vykreslí ho pomocou drawLine. Veľkosť obrázku môžete zvoliť pevne 300x300 a horný vrchol trojuholníka (150,20).
  • Prepíšte predchádzajúci program, aby používal korytnačiu grafiku. Potrebné dĺžky spočítajte Pytagorovou vetou a uhly spočítajte napr. funkciou atan (arkus tangens). Pozor, atan vracia radiány, treba prepočítať na stupne. Zadefinujte si a použite premennú double pi = 3.1415926536; Ak budete kresliť obrázok obidvoma spôsobmi do tej iste plochy, môžete si overiť, či dostanete to isté.

Špirála pre n=10

• Napíšte program, ktorý vykreslí špirálu korytnačou grafikou ako na obrázku vpravo. Špirála pozostáva z n úsečiek, pričom prvá má dĺžku d a každá ďalšia je o d dlhšia od predchádzajúcej. Čísla n a d sú uložené v premenných. Veľkosť obrázku uložte do ďalšej premennej size. Korytnačka nech začína v strede plochy.

DÚ2

max. 5 bodov, termín odovzdania pondelok 3.10.o 22:00

Cieľom tejto domácej úlohy je precvičiť si prácu s grafickou knižnicou, textovým vstupom a výstupom, jednoduchými premennými a aritmetickými výrazmi, ako aj použitie podmienok.

Na prednáške 2 sme kreslili domček, ktorého výška, šírka a iné parametre boli uložené v premenných a použité viackrát na výpočet rôznych súradníc. Na tejto domácej úlohe tento program zlepšíme tromi rozšíreniami, pričom čiastočné body môžete získať aj keď naprogramujete len niektoré z nich.

• Program z prednášky vytvára okno veľkosti 300x400, aj keď sa tento rozmer nemusí pre daný domček hodiť. Zmeňte vykresľovanie obrázku tak, aby používalo štyri celkové parametre: width (šírka domčeka), height (výška hlavnej obdĺžnikovej časti domčeka), roof (výška strechy), margin (voľný okraj okolo domčeka). Na všetkých stranách (naľavo, napravo, dole aj hore nad vrcholom strechy) má byť rovnaký voľný okraj. Z týchto parametrov vypočítajte potrebnú veľkosť obrázku aj súradnice ľavého dolného rohu domčeka, ktoré si môžete uložiť do ďalších premenných.

• Parametre width, height, roof a margin si vypýtajte od užívateľa. Váš program bude používať knižnicu iostream aj simpleDraw. Najskôr si na konzole vypýtajte parametre, až potom vytvárajte grafické okno s výsledkom.

• Skôr než začnete vytvárať grafické okno, skontrolujte, či parametre zadané užívateľom sú správne. Ak nie sú správne, vypíšte na textovú konzolu "Wrong parameters". Ak sú správne, vykreslite domček. Parametre budeme považovať za správne, ak sú všetky zadané hodnoty (width, height, roof a margin) kladné a ak celková šírka ani výška obrázku neprevýši 1000. Môžete predpokladať, že užívateľ zadal celé čísla (kontrolovanie správnosti formátu čísel sme ešte nepreberali).

Váš program by mal byť skompilovateľný a spustiteľný v prostredí používanom na cvičeniach. V prostredí moodle odovzdajte súbor main.cpp obsahujúci váš program.

Prednáška 5

Štatistika z N čísel

Úlohou je zistiť o N prečítaných číslach nejaké štatistické údaje.

Maximum a minimum

Zrejme stačí čítať čísla postupne a pamätať si zatiaľ najväčšie a zatiaľ najmenšie číslo.

• Ako ale začať? Ako nastaviť maximum a minumum na začiatok?
  • Jedna možnosť je nastaviť ich tak, aby to boli nezmyselné hodnoty a iste sa zmenili - napriklad maximum veľmi malé a minumum veľké. Kto nám ale zaručí, že používateľ nedá všetky čísla ešte menšie? Riešením je použiť najväčšie resp. najmenšie možné číslo - ale je to škaredé.
  • Druhá možnosť je si pamätať, že ešte nemáme správne nastavené minimum a maximum a pri prvej príležitosti ich nastaviť.
  • A prvá príležitosť je pri prvom čísle. Môžeme to teda urobiť priamo. Minimum iste nebude väčšie ako toto prvé číslo a maximum iste nebude menšie.

#include <iostream>
#include <cstdlib>

using namespace std;

int main(void){
  int max, min, x, N;

  cout << "Zadaj pocet cisel: ";
  cin >> N;

  cout << "Zadavajte cisla: ";
  cin >> x;

  min=x; max=x;
  for (int i=1; i<N; i++){
    cin >> x;
    if (x<min) {min=x;}
    if (x>max) {max=x;}
  }

  cout << endl << "Maximum je " << max << " a minumum je " << min << endl;  
}

Výskyty čísel 0..9

Ak vieme, že na vstupe sú iba čísla od 0 do 9, tak by sme chceli vedieť, koľko jednotlivých čísel je. Mohli by sme to riesiť takto:

• Pre každú možnú hodnotu si vytvoríme jednu premennú (dokopy ich bude teda 10 - napríklad p0, p1 .. p9) na začiatku nastavenú na 0.
• V prípade, že prečítané číslo bolo 0 zväčšíme hodnotu p0, ak bolo 1 zväčšíme p1 ...

Je to však pomerne komplikovaný spôsob - a to máme iba 10 rôznych premenných. Problém je v tom, že štvrtá premenná je p4 vieme iba my ako programátori a počítač o tom nevie - nemá žiaden súvis medzi jednotlivými premennými.

Teraz ukážeme riešenie tohoto príkladu pomocou poľa.

#include <iostream>
using namespace std;

int main(void) {
  int p[10];
  int c,N;
 
  for (int i=0; i<10; i++) p[i]=0;   // inicializácia pola p[0]=0; p[1]=0; ... p[9]=0;

  cout << "Zadajte pocet cisel: ";
  cin >> N;
  cout << "Zadavajte " << N << "cisel z intervalu 0-9: ";
  for (int i=0; i<N; i++){
    cin >> c;
    if (c>=0 && c<10) p[c]++;    // test, či je číslo z požadovaného rozsahu
  }

  cout << endl; 
  for (int i=0; i<10; i++) cout << i << ": " << p [i] << endl; // výpis
}

Priemer

Podobne ako pri maxime a minime si aj priemer vieme počítať postupne.

• Budeme si počítať súčet doterajších čísel a na záver ho vydelíme ich počtom.
• Dá sa robiť aj postupne - aby sme nemali zapamätané príliš veľké číslo (súčet)?

Ak by sme chceli o každom čísle vedieť, či je nadpriemerné alebo podpriemerné zjavne by sme si museli čísla zapamätať.

• Keby sme vedeli dopredu, koľko ich bude vedeli by sme to urobiť podobne ako v predchádzajúcom príklade.

#include <iostream>

using namespace std; 

int main(void) {
  int N=20;
  int p[20];
  double sucet=0;
  double priemer;
 
  cout << "Zadavajte " << N << " cisel: ";
  for (int i=0; i<N; i++){
    cin >> p[i];
    sucet=sucet+p[i];
  }

  priemer=sucet/N;
  cout << "Priemer je " << priemer << "." << endl; 
  for (int i=0; i<N; i++) 
   if (p[i]>priemer) cout << p[i] << ": vacsie ako priemer." << endl;
   else if (p[i]<priemer) cout << p[i] << ": mensie ako priemer." << endl;
   else cout << p[i] << ": priemer." << endl;
}

• Ak by sme nevedeli počet čísel, môžeme aspoň odhadnúť, že ich nebude viac ako NMax, ktoré definujeme ako konštantu v programe.
• A prečo vlastne nemôžeme dať ako veľkosť poľa N, ktoré si prečítame od používateľa?

Polia

• Rozsah poľa je konštantný výraz väčší ako 0. Prvky sa indexujú od 0 po počet - 1
• Občas sa dá ako rozsah použiť aj dopredu zadefinovaná premenná, ale napr. nasledovný program v C++ skompilujete ale v C nie. Takže opatrne!

  int i=100;
  int p [i]; - i je premenná, ktorá vznikne až počas behu programu, a teda jej hodnota nie je počas kompilácie známa.

• Radšej použijeme konštantu const int N=100
• Veľkosť poľa môže byť ohraničená v závislosti od kompilátora.

Vytvorenie a inicializácia poľa

V C++ je niekoľko pravidiel, ktoré určujú kedy ich môže používať a čo sa stane, ak počet prvok neodpovedá počtu hodnôt v inicializácii. Pole je možné inicializovať iba v definícii.

int A[4]={3, 6, 8, 10}; //spravne
int B[4]; //spravne
B[4]={3, 6, 8, 10};  //nespravne
B[0]=3; B[1]=6; B[2]=8; B[3]=10;

Pri inicializácii sa dá dodať aj menej hodnôt ako má pole. Napr. inicializácia iba dvoch prvých hodnôt. Pri čiastočnej inicializácii nastaví prekladač ostatné prvky na nulu.

double C[5]={5.0, 13.9}; // inicializuje C[0]=5.0, C[1]=13.9 a C[2]..C[4]=0
double C[5]={0}; // jednoduchá inicializácia všetkých prvkov na 0

Ak pri inicializácii poľa necháme hranaté zátvorky prázdne prekladač si sám spočíta prvky poľa. Nie je to však odporúčaný postup.

int A[]={1, 5, 3, 8}; // zistí rozsah poľa 0..3

Indexovanie hodnotou mimo intervalu

  int a [10], b [10];
  int i;
  for (i=0; i<10; i++) a [i]=random (100); // náhodné hodnoty

Pozor, kompilátor nekontroluje indexy prvkov

 a [11]=1234;.

• Skompilujete, ale hodnota 12345 sa zapíše do pamäte na zlé miesto,
• Môže to mať nepredvídateľné následky: prepísanie obsahu iných premenných (chybný výpočet alebo „nevysvetliteľné“ správanie sa programu) alebo prepísane časti kódu vášho programu (čo vo väčšine prípadov spôsobí „zamrznutie“ alebo reset počítača),

Kopírovanie a testovanie rovnosti

V prípade, že chceme vytvoriť pole, ktoré je kópiou už existujúceho poľa, ponúka sa možnosť príkazu priradenia b=a;. Takýto príkaz však neskompilujete – nedá sa takto priraďovať, treba kopírovať prvok po prvku.

  for (i=0; i<10; i++) b[i]=a[i];

Podobne sa nedá porovnávať polia pomocou podmienky if (a==b) cout << "Ok";. Takúto podmienku síce skompilujete, ale nikdy to nebude pravda – neporovná sa obsah poľa, ale niečo úplne iné (adresy polí v pamäti). Treba to riešiť opäť prvok po prvku.

  bool r=true;
  for (i=0; i<10; i++) { r=r && (a [i]==b [i]); }
  if (r) cout << "Ok\n"; 

Príklady na prácu s poľom

• Načítajte pole čísel a vypíšte ho v opačnom poradí.
• Skúste poradie povymienať priamo v poli a nie iba pri výpise.

• Načítajte pole čísel a vypíšte ho v náhodnom poradí.
• Ako by ste pole náhodne povymieňali priamo v pamäti?

Vector

Aby sme predišli problémom s určením rozsahu poľa môžeme použiť typ vector z knižnice STL. Ide o pole s dynamickou alokáciou pamäte, čo znamená, že ak by priestor, ktorý si vyhradil nestačil vyrieši si to sám.

#include<iostream>
#include<vector>

using namespace std;

int main(void){

  vector<int> A;
  int c,N;

  cout << "Zadaj pocet cisel: ";
  cin >> N;
  cout << "Zadavaj cisla: ";

  for (int i=0; i<N; i++){
    cin >> c;
    A.push_back(c);
  }
 
  cout << endl << "Teraz ich vypisem:";
  for (int i=0; i<N; i++){
    cout << A[i];
  }

}

• Deklarovať vector môžeme jedným z nasledujúcich spôsobov

vector<int> A;       //vytvorí pole celých čísel
vector<int> A(10);   //vytvorí pole 10 celých čísel, ktoré všetky nastaví na default hodnotu
vector<int> A(5,1);  //vytvorí pole 5 celých čísel, ktoré nastaví na 1

• Prístup k prvkom vectora je možný dvoma spôsobmi
  • klasicky pomocou A[index] - má podobné problémy ako polia
  • A.at(index) je bezpečnejší spôsob, kedy v prípade indexu mimo rozsahu nebude robiť neplechu

• Vkladanie do poľa je možné tiež dvomi spôsobmi - ale pozor na miešanie
  • do už vytvoreného miesta (ak sme tak deklarovali vector) pomocou priradenia (ďalší priestor získam pomocou A.resize(nova hodnota))
  • pomocou A.push_back(x), kedy ako ďalší prvok nastaví x s tým, že o pamäť sa stará sám (veľkosť si potom môžeme zistiť pomocou A.size())

Kreslíme padajúce kruhy

• Vytvoríme si polia pre x-ovú a y-ovú súradnicu kruhu.
• Potrebujeme aj pole, do ktorého si budeme dávať celočíselné identifikátory nakreslených kruhov, aby sme ich neskôr mohli zmazať.

#include "../SimpleDraw.h"
#include <cstdlib>
#include <ctime>

int main(void) {
    const int count = 30; /* počet kruhov */
    int size = 300; /* veľkosť obrázku */
    int diameter = 15; /* polomer kruhu */
    int step = 4; /* o kolko padne dolu v jednom kroku */
    int repeat = 50; /* pocet iteracii */
    double wait = 0.1; /* cakaj po kazdej iteracii */

    /* inicializácia generátora pseudonáhodných čísel */
    srand(time(NULL));

    SimpleDraw window(size, size);
    window.setBrushColor("lightblue");

    int x[count]; /* x-ova poloha kruzku */
    int y[count]; /* y-ove poloha kruzku */
    int id[count]; /* id objektu na obrazovke */

    /* kazdemu kruzku vygeneruj nahodnu polohu */
    for (int i = 0; i < count; i++) {
        x[i] = rand() % (size - diameter);
        y[i] = rand() % (size - diameter);
    }

    /* opakuj repeat iteracii */
    for (int r = 0; r < repeat; r++) {
        /* chod cez vsetky kruhy */
        for (int i = 0; i < count; i++) {
            /* ak nie sme v prvej iteracii, treba zmazat kruh */
            if (r > 0) {
                window.removeItem(id[i]);
            }
            /* zvys y-ovu suradnicu o step */
            y[i] += step;
            /* ak sme prilis nizko, zacni na vrchu na nahodnom x */
            if (y[i] >= size - diameter) {
                y[i] = 0;
                x[i] = rand() % (size - diameter);
            }
            /* vykresli kruzok na novom mieste */
            id[i] = window.drawEllipse(x[i], y[i], diameter, diameter);
        }
        /* na konci iteracie chvilu pockaj */
        window.wait(wait);
    }
}

• Takéto polia nie sú ideálne, lebo údaje o jednom kruhu sú v troch rôznych poliach a bolo by logickejšie ich mať pokope.
• Situácia by bola ešte horšia, ak by každý kruh mal napr. aj náhodnú farbu s troma zložkami R,G,B. To by sme potrebovali päť polí.
• Na spojenie údajov k jednému kruhu použijeme dátovú štruktúru struct

Padajúce kruhy so struct

#include "../SimpleDraw.h"
#include <cstdlib>
#include <ctime>

struct kruh {
    int x, y; /* coordinates */
    int id;   /* id for deleting */
    int r, g, b; /* red, green, blue */
};

void generujKruh(kruh &k, int max) {
    k.x = rand() % max;
    k.y = rand() % max;
    k.r = rand() % 256;
    k.g = rand() % 256;
    k.b = rand() % 256;
    k.id = -1;
}

int main(void) {
    const int count = 30; /* počet kruhov */
    int size = 300; /* veľkosť obrázku */
    int diameter = 15; /* polomer kruhu */
    int step = 4; /* o kolko padne dolu v jednom kroku */
    int repeat = 50; /* pocet iteracii */
    double wait = 0.1; /* cakaj po kazdej iteracii */

    int max = size - diameter; /* maximum possible coordinate */

    /* inicializácia generátora pseudonáhodných čísel */
    srand(time(NULL));

    SimpleDraw window(size, size);
    window.setBrushColor("lightblue");

    /* pole kruhov */
    kruh kruhy[count];

    /* kazdemu kruzku vygeneruj nahodnu polohu */
    for (int i = 0; i < count; i++) {
        generujKruh(kruhy[i], max);
    }

    /* opakuj repeat iteracii */
    for (int r = 0; r < repeat; r++) {
        /* chod cez vsetky kruhy */
        for (int i = 0; i < count; i++) {
            /* ak nie sme v prvej iteracii, treba zmazat kruh */
            if (r > 0) {
                window.removeItem(kruhy[i].id);
            }
            /* zvys y-ovu suradnicu o step */
            kruhy[i].y += step;
            /* ak sme prilis nizko, zacni na vrchu na nahodnom x */
            if (kruhy[i].y >= max) {
                generujKruh(kruhy[i], max);
                kruhy[i].y = 0;
            }
            /* vykresli kruzok na novom mieste */
            window.setBrushColor(kruhy[i].r, kruhy[i].g, kruhy[i].b);
            kruhy[i].id = window.drawEllipse(kruhy[i].x, kruhy[i].y,
                    diameter, diameter);
        }
        /* na konci iteracie chvilu pockaj */
        window.wait(wait);
    }
}

Prednáška 6

Organizačné poznámky

• Do pondelka môžete ešte odovzdať DÚ1 (meno, priezvisko, email, jazyky), nie však DÚ2
• V moodli si vždy skontrolujte, či ste súbor správne odovzdali, priebežne si pozerajte známky a komentáre, upozornite nás na prípadné problémy
• DÚ3 do pondelka, DÚ4 zverejnená koncom týždňa
• Poriadne čítať a dodržiavať zadania úloh, spýtajte sa, ak niečo nie je jasné, alebo ak máte problémy úlohu riešiť
• Na cvičeniach si môžete nahrať na 2Gb kľúčik linuxový virtuálny stroj s nainštalovaným Netbeans

Parametre funkcií - prehľad, opakovanie

• Jednoduché typy, napr. int, double, bool
  • Bez & sa skopíruje hodnota
  • S & premenná dostane vo funkcii nové meno

void f1(int x) {
    x++; // zmena x sa nepresenie do main (y zostane rovnaká)
    cout << x << endl;
}

void f2(int &x) {
    x++; // zmena x sa prenesie ako zmena y v main
    cout << x << endl;
}

int main(void) {
    int y = 0;
    f1(y);
    f2(y);
    f1(y + 1);
    //zle: f2(y+1);
}

• Polia odovzdávame bez &
  • väčšinou potrebujeme poslať aj veľkosť poľa, ak nie je globálne známa
  • zmeny v poli zostanú aj po skončení funkcie

void f(int a[], int n) {
    for (int i = 0; i < n; i++) {
        cout << a[i] << endl;
    }
}

int main(void) {
    int b[3] = {1, 2, 3};
    f(b, 3);
}

• Vektory, korytnačky a grafické okná sú v skutočnosti objekty, väčšinou ich chcete posielať s &
  • všetky zmeny na nich spravené pretrvávajú aj po skončení funkcie

void kresli(Turtle &t, vector<double> &angles) {
  int n = angles.size();
  for(int i=0; i<n; i++) {
     t.turnLeft(angles[i]);
     t.forward(10);
  }
}
int main(void) {
    int n=10;
    vector <double> angles(n, 360.0/n);
    SimpleDraw window(500,500);
    Turtle turtle(window, 250, 450, 0);
    kresli(turtle, angles);
    window.showAndClose();
}

• Štruktúry (struct) väčšinou tiež posielame pomocou &
• Návratové hodnoty:
  • ak je výsledkom funkcie jedno číslo alebo pravdivostná hodnota, vrátime ju príkazom return
  • ak je výsledkom viac hodnôt, alebo niečo zložitejšie (pole, struct,...), odovzdáme ho ako parameter pomocou &, návratová hodnota môže zostať void
• Tieto pravidlá súvisia so smerníkmi a správou pamäti, povieme si viac o pár týždňov

Pole vs vector

• V príkladoch sme používali polia, na minulej prednáške sme videli aj vector
  • Polia sú o niečo rýchlejšie ako vectory, fungujú aj v čistom C
  • Vector oveľa pohodlnejší, veľa užitočných funkcií, iba v C++
  • Vector je pomerne zložitý objekt, o objektoch až budúci semester, preto budeme používať hlavne pole

Eratostenovo sito

Chceme vypísať všetky prvočísla medzi 2 a N. Mohli by sme ísť cez všetky čísla a pre každé testovať, koľko má deliteľov (deliteľov sme už hľadali predtým), ale vieme to spraviť aj rýchlejšie. Použijeme algoritmus zvaný Eratostenovo sito.

• Vytvoríme pole A pravdivostných hodnôt, kde A[i] nám hovorí, či je i ešte potenciálne prvočíslo.
• Na začiatku budú všetky hodnoty true, lebo sme ešte žadnu nevylúčili.
• Začneme číslom 2 - toto je iste prvočíslo (tak ho vypíšeme). O jeho násobkoch však vieme, že iste nemôžu byť prvočísla - nastavíme preto pre každý násobok j=2*k pravdivostnú hodnotu A[j] na false.
• Potom prechádzame v poli, kým nenájdeme najbližšiu ďalšiu hodnotu true. Toto číslo je prvočíslo (vypíšeme ho) a vyškrtáme jeho násobky.

#include <iostream>
using namespace std;

int main(void) {
    const int N = 25;
    bool A[N + 1];

    for (int i = 2; i <= N; i++) {
        A[i] = true;
    }
    for (int i = 2; i <= N; i++) {
        if (A[i]) {
            cout << i << " ";
            for (int j = 2 * i; j <= N; j = j + i) {
                A[j] = false;
            }
        }
    }
    cout << endl;
}

Výstup programu

2 3 5 7 11 13 17 19 23

Priebeh programu:

0  1  2  3  4  5  6  7  8  9 10 11 12 ...
?  ?  T  T  T  T  T  T  T  T  T  T  T ... na zaciatku
?  ?  T  T  F  T  F  T  F  T  F  T  F ... po vyskrtani i=2
?  ?  T  T  F  T  F  T  F  F  F  T  F ... po vyskrtani i=3
?  ?  T  T  F  T  F  T  F  F  F  T  F ... dalej sa uz skrtaju len vacsie cisla

Cvičenie: Napíšte funkciu, ktorá uloží prvočísla medzi 2 a N do poľa (ak by sme ich chceli použiť na ďalšie výpočty.

Polynómy

• Príklad polynómu: Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2x^3 + 3x -1} .
• Polynóm si môžeme uložiť do poľa, pričom koeficient pri Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^i} dáme do a[i]
• Pre náš príklad vytvoríme pole napríklad príkazom double a[4] = {-1, 3, 0, 2};
• Teraz si ukážeme niekoľko funkcií, ktoré s polynómami pracujú.

Vyhodnocovanie polynómu

• Chceme spočítať hodnotu polynómu pre nejaké konkrétne x
• Príklad: pre Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2x^3 + 3x -1} a pre x=2 dostaneme Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 21 = (2\cdot 2^3 + 3\cdot 2 -1)}

Pokus 1:

double evaluatePolynomial(double a[], int n, double x) {
    /* a je pole koeficientov s n hodnotami.
     * Funkcia vráti hodnotu tohto polynómu v bode x.
     *
     * Táto implementácia na výpočet x na i používa funkciu
     * pow, čo ale pomalé a potenciálne nie úplne presné.
     */
    double value = 0;
    for (int i = 0; i < n; i++) {
        value += a[i] * pow(x, i);
    }
    return value;
}

• Pripomíname: value += x je to isté ako value = value + x
• Všimnite si, že v komentári na začiatku funkcie popisujem, čo tá funkcia robí, to je väčšinou dobrý nápad spraviť.
• Aký najvyšší stupeň môže mať polynóm a (ako funkcia n)?

Pokus 2:

• Vyhneme sa volaniu pow tým, že budeme nejakú premennú opakovanie násobiť hodnotou x
• V cykle uvádzame ako komentár invariant, podmienku, ktorá na tom mieste vždy platí. Takýto invariant nám pomôže si uvedomiť, že je náš program správny.
• Čo by sa stalo, ak by sme prehodili dva príkazy vo vnútri cyklu?

double evaluatePolynomial(double a[], int n, double x) {
    /* a je pole koeficientov s n hodnotami.
     * Funkcia vráti hodnotu tohto polynómu v bode x.
     *
     * Táto implementácia počíta x na i v cykle spolu
     * s vyhodnocovaním polynómu.
     */
    double value = 0;
    double xpow = 1;
    for (int i = 0; i < n; i++) {
        /* Invariant: xpow sa rovna x na i */
        value += a[i] * xpow;
        xpow *= x;
    }
    return value;
}

Pokus 3: Hornerova schéma

• O kúsoček lepšia ako pokus 2 - nepotrebuje pomocnú premnnú a v každej iterácii cyklu robí iba jedno násobenie, nie dve
• Idea je začať od najvyšších mocnín x:
  • Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2x^3 + 0x^2 + 3x -1 = ((2\cdot x+0)x+3)x-1}

double evaluatePolynomial(double a[], int n, double x) {
    /* a je pole koeficientov s n hodnotami.
     * Funkcia vráti hodnotu tohto polynómu v bode x.
     *
     * Táto implementácia používa tzv. Hornerovu schému,
     * ktorá začína od najvyšších koeficentov a
     * a pre každé i robí iba jedno sčítanie a jedno násobenie.
     */
    double value = 0;
    for (int i = n - 1; i >= 0; i--) {
        value = value * x + a[i];
    }
    return value;
}

Cvičenie: aký je invariant po vykonaní príkazu v cykle?

Hlavný program:

#include <cstdlib>
#include <cmath>
#include <iostream>
using namespace std;

double evaluatePolynomial(double a[], int n, double x) {
  // jedna z funkcií vyššie
}

void enterPolynomial(double a[], int &n, int maxN) {
    /* Od užívateľa načíta koeficienty polynómu do a,
     * ich počet uloží do n, maxN je veľkosť poľa,
     * ktorú nemožno prekročiť. */
    cout << "Zadaj pocet koeficientov n: ";
    cin >> n;
    if (n > maxN) {
        cout << "Prilis velke n!" << endl;
        exit(1);
    }
    for (int i = 0; i < n; i++) {
        cout << "Zadaj koeficient pri x na " << i << ": ";
        cin >> a[i];
    }
}

int main(void) {
    const int maxN = 100;
    int n;
    double a[maxN];

    enterPolynomial(a, n, maxN);
    double x;
    cout << "Zadaj x: ";
    cin >> x;
    cout << "Hodnota pre x=" << x << " je " << evaluatePolynomial(a, n, x) << endl;
}

Zadaj pocet koeficientov n: 4
Zadaj koeficient pri x na 0: -1
Zadaj koeficient pri x na 1: 3
Zadaj koeficient pri x na 2: 0
Zadaj koeficient pri x na 3: 2
Zadaj x: 2
Hodnota pre x=2 je 21

Sčítanie polynómov

• Pri sčítaní polynómov len sčítame koeficienty pri zodpovedajúcich mocnicnách x
• Napr. Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (2x^3 + 3x -1) + (-4x^2+2x+7) = (2+0)x^3 + (0-4)x^2 +(3+2)x^1 + (-1+7)x^0 = 2x^3-4x^2+5x+6}
• Musíme dávať pozor na to, že dĺžky polynómov môžu byť rôzne a hondoty v poli za n ďalej sú nedefinované.

void addPolynomials(double a[], int na, double b[], int nb, double c[], int &nc) {
    /* a je pole koeficientov polynomu s na hodnotami,
     * b je pole koeficientov s nb hodnotami
     * do c zratame ich sucet, do nc pocet hodnot, ktory bude vacsie z
     * na, nb. Predpokladame, ze c je dost velke, aby sa do neho nc
     * prvkov zmestilo. */
    if (na > nb) {
        nc = na;
    } else {
        nc = nb;
    }

    for (int i = 0; i < nc; i++) {
        c[i] = 0;
        if (i < na) {
            c[i] += a[i];
        }
        if (i < nb) {
            c[i] += b[i];
        }
    }
}

Hlavný program: (teraz vidíme, načo nám je funkcia enterPolynomial, bez nej by sme cyklus na načítavanie museli písať dvakrát)

#include <cstdlib>
#include <iostream>
using namespace std;

void enterPolynomial(double a[], int &n, int maxN) {
  // pozri vyššie
}

void writePolynomial(double a[], int n) {
    /* a je pole koeficientov polynómu s n hodnotami */
    for (int i = 0; i < n; i++) {
        cout << "Koeficient polynomu pri x na " << i << " je " << a[i] << endl;
    }
}

int main(void) {
    const int maxN = 100;
    int na, nb;
    double a[maxN], b[maxN];
 
    cout << "Prvy polynom:" << endl;
    enterPolynomial(a, na, maxN);
    cout << endl << "Druhy polynom:" << endl;
    enterPolynomial(b, nb, maxN);

    double c[maxN];
    int nc;
    addPolynomials(a, na, b, nb, c, nc);
    cout << endl << "Ich sucet:" << endl;
    writePolynomial(c, nc);
}

Príklad behu:

Prvy polynom:
Zadaj pocet koeficientov n: 4
Zadaj koeficient pri x na 0: -1
Zadaj koeficient pri x na 1: 3
Zadaj koeficient pri x na 2: 0
Zadaj koeficient pri x na 3: 2

Druhy polynom:
Zadaj pocet koeficientov n: 3
Zadaj koeficient pri x na 0: 7
Zadaj koeficient pri x na 1: 2
Zadaj koeficient pri x na 2: -4

Ich sucet:
Koeficient polynomu pri x na 0 je 6
Koeficient polynomu pri x na 1 je 5
Koeficient polynomu pri x na 2 je -4
Koeficient polynomu pri x na 3 je 2

Ďalšie príklady s polynómami

Vieme napísať aj ďalšie funkcie alebo programy na prácu s polynómami:

• Vykresľovanie grafu (rátame hodnotu polynómu v husto rozmiestnených bodoch)
• Násobenie polynómov
• Delenie so zvyškom a Euklidov algoritmus
• Derivácia
• A mnohé ďalšie

Zdrojový kód celého programu

• #Zdrojový kód programu s polynómami

Načo sú v programovaní dobré funkcie

• Rozbijeme veľký problém na menšie dobre definované časti (napr. načítaj polynóm, spočítaj jeho hodnotu), každou časťou sa môžeme zaoberať zvlášť. Výsledný program je ľahšie pochopiteľný, najmä ak u každej funkcie napíšeme, čo robí.
• Vyhneme sa opakovaniu kusov kódu (napr. načítanie polynómu A a B). Pri kopírovaní kusov kódu ľahko narobíme chyby, a ak chceme niečo meniť, musím meniť na veľa miestach.
• Hotové funkcie môžeme použiť aj v ďalších programoch, prípadne z nich zostavovať nové knižnice, napríklad knižnicu na prácu s polynómami.

Triedenia

Máme pole čísel, chceme ich usporiadať od najmenšieho po najväčšie.

• Napr. pre pole 9 3 7 4 5 2 chcem dostať 2 3 4 5 7 9
• Jeden z najštudovanejších problémov v informatike.
• Súčasť mnohých zložitejších algoritmov.
• Veľa spôsobov, ako triediť, dnes si ukážeme zopár najjednoduchších.

Bublinkové triedenie (Bubble Sort)

Idea: Kontrolujeme všetky dvojice susedných prvkov a keď vidíme menšie číslo za väčším, vymeníme ich

       for (int i = 1; i < n; i++) {
            if (a[i] < a[i - 1]) {
                swap(a[i - 1], a[i]);
            }
        }

• Ak sme nenašli v poli žiadnu dvojicu, ktorú treba vymeniť, skončili sme.
• Inak celý proces opakujeme znova.

Celé triedenie:

void swap(int &x, int &y) {
    /* Vymeň hodnoty premenných x a y. */
    int tmp = x;
    x = y;
    y = tmp;
}

void sort(int a[], int n) {
    /* usporiadaj prvky v poli a od najmenšieho po najväčší */

    bool hotovo = false;
    while (!hotovo) {
        bool vymenil = false;
        /* porovnávaj všetky dvojice susedov, vymeň ak menší za väčším */
        for (int i = 1; i < n; i++) {
            if (a[i] < a[i - 1]) {
                swap(a[i - 1], a[i]);
                vymenil = true;
            }
        }
        /* ak sme žiadnu dvojicu nevymenili, môžeme skončiť. */
        if (!vymenil) {
            hotovo = true;
        }
    }
}

• Čo ak vo for cykle dám for (int i = 0; i < n; i++) {
• Ako nahradím premennú hotovo príkazom break?

Príklad behu:

prvá iterácia while cyklu
 9 3 7 4 5 2
 3 9 7 4 5 2
 3 7 9 4 5 2
 3 7 4 9 5 2
 3 7 4 5 9 2
 3 7 4 5 2 9

druhá iterácia while cyklu
 3 7 4 5 2 9
 3 4 7 5 2 9
 3 4 5 7 2 9
 3 4 5 2 7 9

tretia iterácia while cyklu
 3 4 5 2 7 9
 3 4 2 5 7 9

štvrtá iterácia while cyklu
 3 4 2 5 7 9
 3 2 4 5 7 9

piata iterácia while cyklu
 3 2 4 5 7 9
 2 3 4 5 7 9

Cvičenie: Ako sa bude správať algoritmus na nasledujúcich vstupoch, koľkokrát zopakuje vonkajší while cyklus?

• Utriedené pole 1,2,...,n
• Pole n,1,2,...,n-1
• Pole 2,3,...,n,1
• Pole n,n-1,...,1

Triedenie výberom (selection sort, max sort)

Idea: nájdime najväčší prvok a uložme ho na koniec. Potom nájdime najväčší medzi zvyšnými a uložme ho na druhé miesto odzadu atď.

int maxIndex(int a[], int n) {
    /* vráť index, na ktorom je najväčší prvok z prvkov a[0]...a[n-1] */
    int index = 0;
    for(int i=1; i<n; i++) {
        if(a[i]>a[index]) {
            index = i;
        }
        /* invariant: a[j]<=a[index] pre vsetky j=0,...,i*/
    }
    return index;
}

void sort(int a[], int n) {
    /* usporiadaj prvky v poli a od najmenšieho po najväčší */

    for(int kam=n-1; kam>=1; kam--) {
        /* invariant: a[kam+1]...a[n-1] sú utriedené
         * a pre každé i,j také že 0<=i<=kam, kam<j<n platí a[i]<=a[j] */
        int index = maxIndex(a, kam+1);
        swap(a[index], a[kam]);
    }
}

Príklad behu programu

Vstup           9 3 7 4 5 2 
Po výmene (9,2) 2 3 7 4 5 9
Po výmene (7,5) 2 3 5 4 7 9
Po výmene (5,4) 2 3 4 5 7 9
Po výmene (4,4) 2 3 4 5 7 9
Po výmene (3,3) 2 3 4 5 7 9
Po výmene (2,2) 2 3 4 5 7 9

Cvičenie: Bude čas behu algoritmu výrazne odlišný pre pole utriedené správne a pole utriedené v opačnom poradí?

Triedenie vkladaním (Insertion Sort)

Idea:

• v prvej časti poľa prvky v utriedenom poradí
• zober prvý prvok z druhej časti a vlož ho na správne miesto v utriedenom poradí

Príklad behu algoritmu:

 9 3 7 4 5 2
 3 9 7 4 5 2
 3 7 9 4 5 2
 3 4 7 9 5 2
 3 4 5 7 9 2
 2 3 4 5 7 9

Ako spraviť vkladanie:

• Vkladaný prvok si zamätáme v pomocnej premennej
• Utriedené prvky posúvame o jedno doprava, kým nenájdeme správne miesto pre odložený prvok

void sort(int a[], int n) {
    /* usporiadaj prvky v poli a od najmenšieho po najväčší */

    for (int i = 1; i < n; i++) {
        int prvok = a[i];
        int kam = i;
        while (kam > 0 && a[kam - 1] > prvok) {
            a[kam] = a[kam - 1];
            kam--;
        }
        a[kam] = prvok;
    }
}

• Všimnime si podmienku (kam > 0 && a[kam - 1] > prvok)
  • Ak kam==0, prvá časť je false, druhá časť sa už nevyhodnocuje
  • Ak by sme prehodili časti, program by mohol spadnúť (a[kam - 1] > prvok && kam > 0)

Cvičenie: Ako sa bude správať algoritmus na nasledujúcich vstupoch, koľkokrát zopakuje priradenie a[kam]=a[kam-1]?

• Utriedené pole 1,2,...,n
• Pole n,1,2,...,n-1
• Pole 2,3,...,n,1
• Pole n,n-1,...,1

Zdrojový kód celého programu

• #Zdrojový kód programu s triedeniami

Zhrnutie

• Videli sme niekoľko nových algoritmov:
  • Eratostenovo sito na hľadanie prvočísel
  • Vyhodnocovanie a sčítavanie polynómov
  • Tri jednoduché algoritmy na triedenie

• Precvičili sme si funkcie, parametre a polia
• K funkciám je dobré napísať, čo robia
• Do cyklov si môžeme písať invarianty
  • Používajú sa pri formálnom dokazovaní správnosti
  • Pomáhajú pochopeniu kódu
  • Môžeme ich použiť na ručnú alebo automatickú kontrolu správnosti hodnôt premenných
  • Príkaz assert v knižnici cassert kontroluje podmienku, napr. assert(i>=0 && i<n); ukončí program s chybovou hláškou ak podmienka neplatí

Zdrojový kód programu s polynómami

#include <cstdlib>
#include <cmath>
#include <iostream>
using namespace std;

const int maxN = 100;

double evaluatePolynomialPow(double a[], int n, double x) {
    /* a je pole koeficientov s n hodnotami.
     * Funkcia vráti hodnotu tohto polynómu v bode x.
     *
     * Táto implementácia na výpočet x na i používa funkciu
     * pow, čo ale pomalé a potenciálne nie úplne presné.
     */
    double value = 0;
    for (int i = 0; i < n; i++) {
        value += a[i] * pow(x, i);
    }
    return value;
}

double evaluatePolynomialMult(double a[], int n, double x) {
    /* a je pole koeficientov s n hodnotami.
     * Funkcia vráti hodnotu tohto polynómu v bode x.
     *
     * Táto implementácia počíta x na i v cykle spolu
     * s vyhodnocovaním polynómu.
     */
    double value = 0;
    double xpow = 1;
    for (int i = 0; i < n; i++) {
        /* Invariant: pow sa rovna x na i */
        value += a[i] * xpow;
        xpow *= x;
    }
    return value;
}

double evaluatePolynomialHorner(double a[], int n, double x) {
    /* a je pole koeficientov s n hodnotami.
     * Funkcia vráti hodnotu tohto polynómu v bode x.
     *
     * Táto implementácia používa tzv. Hornerovu schému,
     * ktorá začína od najvyšších koeficentov a
     * a pre každé i robí iba jedno sčítanie a jedno násobenie.
     */
    double value = 0;
    for (int i = n - 1; i >= 0; i--) {
        value = value * x + a[i];
    }
    return value;
}

void addPolynomials(double a[], int na, double b[], int nb, double c[], int &nc) {
    /* a je pole koeficientov polynomu s na hodnotami,
     * b je pole koeficientov s nb hodnotami
     * do c zratame ich sucet, do nc pocet hodnot, ktory bude vacsie z
     * na, nb. Predpokladame, ze c je dost velke, aby sa do neho nc
     * prvkov zmestilo. */
    if (na > nb) {
        nc = na;
    } else {
        nc = nb;
    }

    for (int i = 0; i < nc; i++) {
        c[i] = 0;
        if (i < na) {
            c[i] += a[i];
        }
        if (i < nb) {
            c[i] += b[i];
        }
    }
}

void enterPolynomial(double a[], int &n, int maxN) {
    /* Od užívateľa načíta koeficienty polynómu do a,
     * ich počet uloží do n, maxN je veľkosť poľa,
     * ktorú nemožno prekročiť. */
    cout << "Zadaj pocet koeficientov n: ";
    cin >> n;
    if (n > maxN) {
        cout << "Prilis velke n!" << endl;
        exit(1);
    }
    for (int i = 0; i < n; i++) {
        cout << "Zadaj koeficient pri x na " << i << ": ";
        cin >> a[i];
    }
}

void writePolynomial(double a[], int n) {
    /* a je pole koeficientov polynómu s n hodnotami */
    for (int i = 0; i < n; i++) {
        cout << "Koeficient polynomu pri x na " << i << " je " << a[i] << endl;
    }
}

void testEvaluate() {
    int n;
    double a[maxN];

    enterPolynomial(a, n, maxN);
    double x;
    cout << "Zadaj x: ";
    cin >> x;
    cout << "Hodnota pre x=" << x << " je " << evaluatePolynomialPow(a, n, x) << endl;
    cout << "Hodnota pre x=" << x << " je " << evaluatePolynomialMult(a, n, x) << endl;
    cout << "Hodnota pre x=" << x << " je " << evaluatePolynomialHorner(a, n, x) << endl;
}

void testAdd() {
    int na, nb;
    double a[maxN], b[maxN];
    cout << "Prvy polynom:" << endl;
    enterPolynomial(a, na, maxN);
    cout << endl << "Druhy polynom:" << endl;
    enterPolynomial(b, nb, maxN);
    double c[maxN];
    int nc;
    addPolynomials(a, na, b, nb, c, nc);
    cout << endl << "Ich sucet:" << endl;
    writePolynomial(c, nc);
}

int main(void) {

    testEvaluate();
    testAdd();

}

Zdrojový kód programu s triedeniami

#include <iostream>
using namespace std;

void swap(int &x, int &y) {
    /* Vymeň hodnoty premenných x a y. */
    int tmp = x;
    x = y;
    y = tmp;
}

void printArray(int a[], int n) {
   for (int i = 0; i < n; i++) {
       cout << " " << a[i];
   }
   cout << endl;
}

void bubbleSort(int a[], int n) {
    /* usporiadaj prvky v poli a od najmenšieho po najväčší */

    bool hotovo = false;
    while (!hotovo) {
        bool vymenil = false;
        /* porovnávaj všetky dvojice susedov, vymeň ak menší za väčším */
        for (int i = 1; i < n; i++) {
            if (a[i] < a[i - 1]) {
                swap(a[i - 1], a[i]);
                vymenil = true;
            }
        }
        /* ak sme žiadnu dvojicu nevymenili, môžeme skončiť. */
        if (!vymenil) {
            hotovo = true;
        }
    }
}
int maxIndex(int a[], int n) {
    /* vráť index, na ktorom je najväčší prvok z prvkov a[0]...a[n-1] */
    int index = 0;
    for(int i=1; i<n; i++) {
        if(a[i]>a[index]) {
            index = i;
        }
        /* invariant: a[j]<=a[index] pre vsetky j=0,...,i*/
    }
    return index;
}

void selectionSort(int a[], int n) {
    /* usporiadaj prvky v poli a od najmenšieho po najväčší */

    for(int kam=n-1; kam>=1; kam--) {
        /* invariant: a[kam+1]...a[n-1] sú utriedené
         * a pre každé i,j také že 0<=i<=kam, kam<j<n platí a[i]<=a[j] */
        int index = maxIndex(a, kam+1);
        swap(a[index], a[kam]);
    }
}

void insertionSort(int a[], int n) {
    /* usporiadaj prvky v poli a od najmenšieho po najväčší */

    for (int i = 1; i < n; i++) {
        // inv1
        int prvok = a[i];
        int kam = i;
        while (kam > 0 && a[kam - 1] > prvok) {
            // inv2
            a[kam] = a[kam - 1];
            kam--;
        }
        a[kam] = prvok;
    }
}

int main(void) {
    int n = 6;
    int a[6] = {9, 3, 7, 4, 5, 2};

    printArray(a, n);
    insertionSort(a, n);
    printArray(a,n);
}

Cvičenia 3

Vypisovanie čísel

Chceme vypísať štvorec veľkosti NxN obsahujúci čísla nasledovne:

• V prvom riadku budú samé 1, v druhom samé 2, .. v poslednom samé N
• V každom riadku budú čísla od 1 po N
• Rovnaké čísla budú uhlopriečne

1 1 1 1    1 2 3 4    1 2 3 4
2 2 2 2    1 2 3 4    2 3 4 5
3 3 3 3    1 2 3 4    3 4 5 6
4 4 4 4    1 2 3 4    4 5 6 7

Číselné sústavy

• Zistite koľko cifier má zadané číslo N.
• Zistite ciferný súčet zadaného čísla N.
• Prečítajte číslo a vypíšte ho odzadu v dvojkovej sústave.

Hádaj číslo

Na prednáške bola naprogramovaná hra Hádaj číslo, kde si počítač "myslí číslo" od 1 do 100 a používateľ háda, o ktoré číslo ide. Upravte program nasledovne:

• Program umožní používateľovi sa vzdať, napríklad keď používateľ zadá 0. V tom prípade program vypíše hľadané číslo a skončí.
• Program bude počítať počet kôl, ktoré používateľ potreboval k uhádnutiu čísla a na konci ho vypíše.
• Program porovná počet kôl, ktoré potreboval používateľ s optimálnym počtom kôl.

Kombinačné čísla

Iste poznáte kombinačné číslo Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {n\choose k}=\frac{n!}{k!(n-k)!}} , ktoré vyjadruje, koľkými možnosťami je možné vybrať k prvkov z n-prvkovej množiny.

• Vypočítajte kombinačné číslo Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {n\choose k}} priamo z definície, t.j. pomocou funkcie, ktorá počíta faktoriál čísla.
• Kombinačné čísla sa dajú počítať aj kúsok optimálnejšie. Napríklad Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {5 \choose 2} = \frac{5!}{2!3!} = \frac{5\cdot4\cdot 3\cdot 2\cdot 1}{2\cdot 1\cdot3\cdot2\cdot1}} sa zjavne dá zjednodušiť na Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {5 \choose 2} = \frac{5\cdot4}{2\cdot 1}} . Vytvorte funckiu, ktorá počíta kombinačné číslo týmto spôsobom. Vieme túto funkciu upraviť tak, aby nepočítala najskôr čitateľa a potom menovateľa a pritom ostal jej výsledok stále typu int?
• Pomocou predchádzajúcej funkcie vypíšte do jedného riadku hodnoty Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {n\choose i}} pre používateľom zadané n a všetky i od 0 po n.
• Funkciu pre vypísanie celého riadku vieme optimalizovať nasledovne: Na základe čísla Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {n\choose i}} budeme počítať Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {n\choose i+1}} . Vypíšte riadok Pascalovho trojuholníka takýmto spôsobom.

Grafická funkcia

• Vytvorte funkciu, ktorá vykreslí pravidelný n-uholník. Ako parameter funkcie budeme potrebovať okrem n a dĺžky strany aj okno, do ktorého vykresľujeme (prenesieme ho ako referenciu - pomocou &).

• Vytvorte funkciu, ktorá bude kreslit jeden kruh, ktory pada dolu obrazovkou. Kruh začína tak, aby ho bolo celý vidieť na x-ovej súradnici zadanej parametrom a padá dolu o krok, ktorý je tiež parametrom funkcie. Keď padne úplne dolu, tak funkcia skončí.

DÚ3

max. 5 bodov + 3 body bonus, termín odovzdania pondelok 10.10. o 22:00

Cieľom tejto domácej úlohy je precvičiť prácu s cyklami a funkciami. Nepoužívajte polia a iné dátové štruktúry, iba premenné typu int a prípadne bool.

Iste poznáte kombinačné čísla Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {n\choose k}=\frac{n!}{k!(n-k)!}} , ktoré vyjadrujú, koľkými možnosťami je možné vybrať k prvkov z n-prvkovej množiny. Keď kombinačné čísla usporiadame do tvaru trojuholníka, dostaneme Pascalov trojuholník. V každom riadku Pascalovho trojuholníka sú kombinačné čísla pre jednu hodnotu n, pričom uvažujeme všetky hodnoty k od 0 po n.

V tejto úlohe chceme zrátať zvyšok po delení dvoma pre jednotlivé čísla v Pascalovom trojuholníku a vykresliť ich graficky tak, že nepárne čísla zobrazíme ako čierny štvorček a párne ako biely štvorček. Ak tak urobíme pre veľa riadkov Pascalovho trojuholníka, dostaneme fraktálny útvar zvaný Sierpinského trojuholník. Problém však je, že keby sme priamočiaro rátali kombinačné čísla pre veľké hodnoty n a zisťovali či sú párne, nestačil by nám rozsah premennej int. Budeme teda postupovať prefíkanejšie: nebudeme rátať presnú hodnotu kombinačného čísla, zrátame iba najväčšiu mocninu dvojky, ktorá ho delí. Kombinačné číslo je podiel súčinov malých celých čísel. Ak zistíme pre každé z týchto čísel, aká najväčšia mocnina dvojky ho delí, sčitovaním a odčitovaním môžeme získať najväčšiu mocninu dvojky, ktorá delí výsledné kombinačné číslo. Napríklad Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {5 \choose 2} = \frac{5!}{2!3!} = \frac{5\cdot4\cdot 3\cdot 2\cdot 1}{2\cdot 1\cdot3\cdot2\cdot1}} V čitateli 5,3 a 1 sú deliteľné iba Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2^0 } , 4 je deliteľné Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2^2} a 2 je deliteľné Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2^1} . Spolu je teda čitateľ deliteľný Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2^3} . Podobne menovateľ je deliteľný Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2^2} , najvyššia mocnina dvojky, ktorá delí výsledné kombinačné číslo je teda Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2^1} . Toto kombinačné číslo je 10, takže vidíme, že odpoveď je správna.

• Časť a) Napíšte funkciu s hlavičkou int powerTwo(int n) ktorá spočíta pre dané kladné celé číslo n najvyššie k také, že Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2^k} delí n. Napríklad powerTwo(12) je 2, lebo Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 4=2^2} je najvyššia mocnina dvojky, ktorá delí 12.

Výsledok pre maxN=4

Výsledok pre maxN=4 s naznačenými hranicami jednotlivých políčok Pascalovho trojuholníka. Červené čiary vo vašom programe nekreslite.

• Časť b) Napíšte program, ktorý bude riadok po riadku počítať paritu kombinačných čísel v Pascalovom trojuholníku a keď nájde nepárne číslo, vykreslí na príslušné miesto grafickej plochy čierny štvorček.
  • Pri výpočte môžete použiť vzťah medzi susednými hodnotami v riadku: Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {n\choose k} = {n\choose k-1} \cdot \frac{n-k+1}{k}} pre Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1\le k \le n} .
  • Vyhnite sa problémom s veľmi veľkými číslami použitím funkcie powerTwo
  • V programe si uložte do premenných nasledujúce parametre obrázku (nenačítavajte ich od užívateľa, stačí ich nastaviť priamo v programe):
    • maxN - posledný riadok, ktorý vypisujeme
    • square - veľkosť jedného štvrčeka
  • Potrebnú veľkosť obrázku aj rozmiestnenie štvorcov spočítajte z týchto premenných.
  • Výsledok by mal vyzerať zhruba ako obrázok napravo (použili sme maxN=4, square=50). Pre veľké maxN program potrebuje veľa pamäte na uloženie jednotlivých štvorčekov, skúste však napríklad hodnotu square=2 a maxN=63 a maxN=255.

• Časť c) bonus: Napíšte vylepšený program taký, že ak ide v riadku za sebou niekoľko čiernych štvorčekov, vykreslíte ich ako jeden obdĺžnik. To by malo program zrýchliť a zmenšiť jeho pamäť. Program by mal tiež spočítať, koľko čiernych štvorčekov by vykreslil v základnej verzii, koľko vykreslil obdĺžnikov a aká je teda úspora v počte vykreslených útvarov. Hodnoty, ktoré dostanete pre maxN=63 uveďte v komentári programu.

Domácu úlohu odovzdávajte v systéme Moodle. Pre časť a) a b) odovzdajte súbor main.cpp. Ak robíte aj časť c), odovzdajte ju v zvláštnom súbore bonus.cpp.

Prednáška 7

Vyhľadávanie prvkov poľa

Úlohou je zistiť, či pole obsahuje prvok zadanej hodnoty.

• Zrejme budeme musieť prejsť celé pole, lebo nevieme, kde sa prvok môže nachádzať.

int Member(int A[], int N, int x){
 for (int i=0; i<N; i++){
   if (a[i]==x) return i;
 }  
 return -1;
}

• Toto môžeme urobiť aj v prípade, že máme pole usporiadané. Prejdením celého poľa prvok iste nájdeme alebo zistíme, že sa tam taký prvok nenachádza.
• Ale neexistuje lepšie riešenie?

Binárne vyhľadávanie

Lepšie riešenie samozrejme existuje a je založené na nasledovnej myšlienke:

• Ak pozriem v utriedenom poli na nejaký prvok A[i], tak v intervale 0..(i-1) sú čísla veľkosti nanajvýš A[i] a v intervale (i+1)..(N-1) sú čísla veľkosti aspoň A[i].
• Keď teda hľadám nejaký prvok x, tak po jednom nahliadnutí do poľa viem
  • buď priamo povedať, že ten prvok sa tam nachádza - ak som trafila priamo pozíciu i taku, že x=A[i]
  • vyhodiť (t.j. ďalej nepoužívať) časť poľa v intervale (i+1)..(N-1) - ak som trafila priamo pozíciu i taku, že x<A[i]
  • vyhodiť (t.j. ďalej nepoužívať) časť poľa v intervale 0..(i-1) - ak som trafila priamo pozíciu i taku, že x>A[i]
• V utriedenom poli teda môžem vyhľadávať nasledovne:
  • budem si pamätať ľavý a pravý kraj, kde ešte môže byť hľadaný prvok
  • vyberiem nejaký prvok z tohoto intervalu a patrične interval skrátim
  • ak už je interval zlý (t.j. pravý a ľavý kraj sú naopak) tak skončí
• Jediná nezodpovedaná otázka je, ako vyberám prvok, na ktorý sa pýtam

int Member(int A[], int N, int x){
 int left=0, right=N-1, index;
 while (left<=right){
   index=??;
   if (A[index]==x) {return index;}
   else if (A[index]<x) {left=index+1;}
        else {right=index-1;}
 }
 return =-1;
}

Pozrime sa na jednotlivé možnosti ako prvok vyberať (aj keď vám je už asi jasné, aký bude výsledok):

• Budeme vyberať vždy prvý prvok - tým vlastne máme skoro pôvodné hľadanie. Jediný rozdiel je, že v prípade, že už dojdeme na prvok poľa, ktorý je väčší ako hľadané x, tak zastavíme a odpovieme, že prvok tam nie je.
  • Beh programu si ukážeme na príklade

A[7]={2,5,41,68,72,100,156}
N=7 x=41
   left=0 right=6: index=0; A[index]<x
   left=1 right=6; index=1; A[index]<x
   left=2 right=6; index=2; A[index]=x  -> return 2
N=7 x=31
   left=0 right=6: index=0; A[index]<x
   left=1 right=6; index=1; A[index]<x 
   left=2 right=6; index=2; A[index]>x
   left=2 right=1; left>right           -> koniec while cyklu -> return -1

• Budeme vyberať vždy stredný prvok teda index=(left+right)/2, čím dosiahneme, že v každom ktorku zahodíme polovicu poľa.
  • Beh programu si ukážeme na príklade

A[7]={2,5,41,68,72,100,156}
N=7 x=41
   left=0 right=6: index=3; A[index]>x (68>41)
   left=0 right=2; index=2; A[index]<x (5<41)
   left=2 right=2; index=1; A[index]=x -> return 2
N=7 x=31
   left=0 right=6: index=3; A[index]>x (68>31)
   left=1 right=2; index=1; A[index]<x (5<31)
   left=2 right=2; index=2; A[index]>x (41>31)
   left=2 right=1; left>right           -> koniec while cyklu -> return -1

Tak nejako prirodzene máme pocit, že to druhé riešenie je lepšie. Že by malo byť asi rýchlejšie...

Zložitosť algoritmu

Ako sme viedli už napríklad na triedení a vyhľadávaní, jednu úlohu môžeme často riešiť viacerými spôsobmi. Tak intuitívne máme o niektorých pocit, že sú lepšie ako iné. Prečo a v čom sú niektoré riešenia lepšie a ako môžeme niečo také vlastne odhadovať (ináč ako intuitívne).

Čas

Často nás zaujíma, ako rýchlo nám program bude bežať. Vo väčšine prípadov táto rýchlosť nejakým spôsobom závisí od vstupných dát. Iste bude kratšie trvať utriedenie 3 prvkového poľa ako poľa s 100000 prvkami. Časovú zložitosť teda budeme odhadovať v závislosti od veľkosti vstupu.

Pre niektoré programy sa môže čas vypočítať jednoducho ako počet operácií, ktoré program vykoná. Avšak už pri použití podmienky dojdeme k situácii, kedy začneme uvažovať, čo započítať a co nie.

int main(void){
  int x,max,N;

  cout << "Zadajte N>0: ";
  cin >> N;
  cout << "Zadavajte cisla: ";

  cin >> max;
  for (int i=1; i<N; i++){
    cin >> x;
    if (x>max) {max=x;}
  }
}

• Na začiatku máme 3 príkazy (cout a cin).
• Pre prvý prvok následne potrebujeme jeho načítanie (priamo do premennej max v ktorej si pamätáme aktuálne maximum).
• Je jasné, že pre každý ďalší z N prvkov, potrebujeme prvok načítať a opýtať sa na podmienku.
• Avšak už nie pre každý prvok musíme následne použiť priradenie (tých priradení nemusíme potrebovať žiadne ale môžeme ho potrebovať v každom z N-1 prvkov)
• Celkový súčet bude teda niečo medzi 3+1+(N-1)+0 a 3+1+(N-1)+(N-1)

Vo väčších programoch však to rozmedzie nie je také jednoduché vypočítať a preto sa bavíme často o najhoršom prípade, ktorý môže nastať. Okrem toho nás nezaujímajú presné čísla ale iba akýsi odhad (približná funkcia) závislá od vstupu. Ukážeme si odhad zložitosti na niektorých príkladoch.

• Už spomínané hľadanie maxima. Pre každý z N prvkov potrebujeme urobiť niekoľko (aspoň jednu ale nie viac ako konštantu) operácií. Preto zložitosť bude lineárna.
• Pozrime sa, ako na tom bude binárne vyhľadávanie. Pozrieme sa na najhorší možný scénár a to, že prvok nájdeme až v poslednom kroku alebo v poli nebude vôbec, teda ho neobjavíme skôr.
  • V prvom kroku máme celé pole a v ňom sa pozrieme na stredný prvok a podľa jeho hodnoty zoberieme buď ľavú alebo pravú (zhruba) polovicu poľa.
  • Tým pádom v druhom kroku máme pole polovičnej veľkosti a robíme na ňom zase to isté.
  • V každom kroku teda máme pole o poloicu menšie až kým nemáme pole veľkosti 1 - potom buď už prbvok nájdeme alebo v ďalšom krku povieme, že tam nie je.
  • Akú zložitosť bude mať tento program? Zapíšeme si číslo N (počet prvkov) v dvojkovej sústave. Pri delení poľa na polovicu bude ďalšia veľkosť poľa vlastne toto číslo bez poslednej cifry. Počet krokov, ktoré potrebujeme je teda zhruba počet cifier takto zapísaného čísla, čo je Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle log_2 N} .
  • Iba tak pre úplnosť dodávam, že log N je menej ako N, čiže binárne vyhľadávanie beží rýchlejšie ako lineárne (v najhoršom prípade).

Na minulej prednáške boli niektoré triedenia. Pozrime, akú zložitosť majú. Odhad zložitosti urobím na jednom príklade, zvyšné si môžete skúsiť doma alebo na cvičeniach.

• Selection sort (max sort). Najprv pripomeniem hlavnú ideu: nájdeme najväčší prvok a uložme ho na koniec. Potom nájdime najväčší medzi zvyšnými a uložme ho na druhé miesto odzadu atď.

int maxIndex(int a[], int n) {
    /* vráť index, na ktorom je najväčší prvok z prvkov a[0]...a[n-1] */
    int index = 0;
    for(int i=1; i<n; i++) {
        if(a[i]>a[index]) {
            index = i;
        }
        /* invariant: a[j]<=a[index] pre vsetky j=0,...,i*/
    }
    return index;
}

void sort(int a[], int n) {
    /* usporiadaj prvky v poli a od najmenšieho po najväčší */

    for(int kam=n-1; kam>=1; kam--) {
        /* invariant: a[kam+1]...a[n-1] sú utriedené
         * a pre každé i,j také že 0<=i<=kam, kam<j<n platí a[i]<=a[j] */
        int index = maxIndex(a, kam+1);
        swap(a[index], a[kam]);
    }
}

• Opäť máme program, v ktorom postupujeme v nejakých krokoch - v tomto prípade máme for-cyklus. V každom kroku musíme nájsť maximum z poľa a veľkosti kam+1. Potom už iba vymeníme takto nájdené maximum a posledný provok poľa. Pričom premenná kam je riadiaca premenná for-cyklu a v každom kroku klesá.
• Otázka je, aký čas potrebujeme na hľadanie maxima z x prvkov. Odpoveď je jednoduchá - prvky musíme prejsť všetky a teda zložitosť bude lineárna, t.j. x.
• Teraz si už iba spočítame: V prvom kroku hľadáme maximum z n prvkov, v druhom z n-1 ...
• Teda čas, ktorý na to potrebujeme je Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n+(n-1)+...+1=\frac{n(n+1)}{2}=\frac{n^2}{2}+\frac{n}{2}} . Zložitosť tohoto triedenia bude teda kvadratická.

Pamäť

Ďalší bežný dôdov prečo povedať, že nejaký algoritmus je lepší ako druhý je, keď si toho musí menej pamätať. Majme napríklad klasickú úlohu - hľadanie najväčšieho prvku. To môžeme riešiť dvomi spôsobmi.

• Všetky čísla si zapamätáme do poľa a následne nájdeme maximum z poľa.
• Budeme zisťovať maximum priebežne a pamätať si ho v jednej premennej.

Na prvý spôsob si potrebujeme zapamätať pole čísel - teda pre N čísel potrebujeme N prvkov poľa a ešte nejaké pomocné premenné k tomu. Na rozdiel od toho, pre druhý spôsob (priebežné počítanie) si potrebujeme pamätať iba to priebežné maximum a nejakú pomocnú premennú. Zjavne teda pre nejaké väčšie N bude druhý spôsob výrazne vhodnejší.

Znaky

Znakové konštanty sa zapisujú v jednoduchých apostrofoch: 'A'. Špeciálne znaky sa dajú zapísať pomocou ich kódu v osmičkovej alebo šestnástkovej sústave: '\101' a '\x41' reprezentujú znak s kódom 65, t.j. 'A'.

Znaky majú teda svoje kódy. Najbežnejšie sa budeme stretávať s týmito:

• 32: medzera
• 27: escape
• 48...57: 0...9
• 65...90: A...Z
• 97...122: a...z
• -1 ... -128: (aby ste si nemysleli, že kódy sú iba kladné) rôzne symboly

Znakové premenné sú typu char. Ich veľkosť je vždy 1, teda sizeof(char) == 1

Do premennej môžem priraďovať, jej obsah zapísať alebo prečítať:

  char c='A';
  char z;
  z=c;
  cout << c;
  cin >> z;  // prečíta jeden znak (pozor, preskakujú sa biele znaky)

Znaky môžem porovnávať. Na konci programu vyššie platí nasledovné:

• c=='A' ... je pravda,
• c=='a' ... nie je pravda – rozlišujú sa malé a veľké písmená,
• c<='Z' ... je pravda – písmená sú usporiadané: A<B< ... <Z, a<b< ... <z, aj cifry sú usporiadané: 0<1< ... <9.

Ako už bolo spomínané, pri čítaní zo streamu sa preskakujú tzv. biele znaky. Toto nie je vždy žiadúce a preto môžeme streamu nastaviť modifikátor noskipws, ktorý zruší preskakovanie takýchto znakov. Do premennej teda budeme vedieť prečítať aj medzeru.

#include <iostream>
using namespace std;

int main(void) {
  char a,b,c;
 
  cin >> noskipws >> a >> b >> c;
  cout << a << b << c;
 }

Pretypovavanie

Znakové premenné, ako už bolo spomínané majú svoje kódy. Tieto kódy sú celé čísla a preto medzi znakmi a celými číslami môžeme prechádzať úplne jednoducho.

#include<iostream>

using namespace std;

int main(void){

  int N;
  char c;

  cout << "Napiste cislo: ";
  cin >> N;                     // prečíta číslo 
  c=N;                          // do znakovej premennej môžeme číslo priradiť bez problémov
  cout << c << endl;            // vieme vypísať znak
  cout << (c+1) << endl;          // ale keď už použijeme aritm. operáciu, je to ako číslo

  cout << "Napiste znak: ";     
  cin >> c;                     // prečíta znak
  N=c;                          // do celočíselnej premennej ho priamo vieme priradiť
  cout << N << endl;
}

Okrem toho však vieme urobiť aj tzv. pretypovávanie, keď chceme aby výsledok bol konkrétneho typu. Napríklad, aby nám v prvej časti vypísalo nie ďalší kód ale ďalší znak, mohli sme výsledok pretypovať.

  cout << (char)(c+1) << endl;          // vďaka pretypovaniu dostávame na výpise zase znak

Všeobecne môžeme takýmto spôsobom môžeme meniť typ - napr. výsledku nejakej operácie.

  double x=8.344;
  int N=x;
  cout << N/3 << " " << (double)(N/3) << " " << (double)N/3 << " " << x/3 << " " << (int)x/3<< endl;

Tento program vypíše nasledovný výstup:

2 2 2.66667 2.78133 2

Hádaj číslo (kým to niekoho baví)

Viacero programov čo sme tu mali sa mohlo vykonávať viac ráz. My si ukážeme, ako upraviť program "Hádaj číslo", aby po uhádnutí ponúkol možnosť hrať znovu, pokiaľ to niekoho baví.

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

void HadajCislo(int number) {
    /* Pamätáme si, či sme už uhádli alebo nie. */
    bool guessed = false;
    cout << "Guess a number between 1 and 10: ";
    /* Kým užívateľ neuhádne, spýtame sa ho na ďalšiu odpoveď. */
    while (!guessed) {
        int guess;
        cin >> guess;
        /* Vyhodnotíme odpoveď. */
        if (guess < number) {
            cout << "Too low, try again: ";
        } else if (guess > number) {
            cout << "Too high, try again: ";
        } else if (guess == number) {
            guessed = true;
            cout << "Correct guess" << endl;
        }
    }
}

int main(void) {
    /* vygenerujeme náhodné číslo medzi 1 a 10 */
    srand(time(NULL));
    int number;
    char c;
    bool pokracovat = true;

    while (pokracovat) {

        number = rand() % 10 + 1;
        HadajCislo(number);

        cout << "Do you want to play again? (Y/N) ";
        cin >> c;
        if (c=='Y') {
           cout << "OK. Play once more." << endl;
        }
        else if (c=='N') {
            pokracovat=false;
        }

    }
}

Switch

V prípade, že by možností bolo viac a napríklad by sme chceli ináč reagovať v prípade iných odpovedí tak sa podmienka stane príliš komplikovanou. Preto často používame príkaz na switch, ktorý podľa hodnoty výrazu pokračuje jednou vetvou.

V našom jednoduchom príklade, by mohol switch vyzerať nasledovne:

switch (c) {
  case 'Y': cout << "OK. Play once more." << endl; break;
  case 'N': pokracovat = false;
}

Vo všeobecnosti má príkaz switch viacero rôznych prípadov vyhodnotenia výrazu v podmienke.

switch (výraz)
{
case k1: príkazy1
case k2: príkazy2
default: príkazyd
}

Takýto príkaz funguje nasledovne:

• Vyhodnotí výraz.
  • Ak sa hodnota zhoduje s konštantným výrazom ki v niektorom case, pokračuje prvým príkazom v príkazyi
  • Ak sa nezhoduje, pokračuje prvým príkazom v prikazyd, ak existuje default, alebo pokračuje za koncom switch bloku.
• Narozdiel od pascalovského case vykonávanie nekončí vykonaním posledného príkazu v prikazyi, ale pokračuje ďalej, ak nie je prerušené príkazom break.

#include <iostream.h>

void main () {
  int n;
  cout << "\n" << "Zadaj n (1,2,3,4): ";
  cin >> n;
  switch (n) {
    case 1: cout << "Jeden\n";
    case 2: cout << "Dva\n";
    case 3:
    case 4: cout << "Tri alebo styri\n";
    default: cout << "Chyba!\n";
  }
  cout << "Koniec.\n";
}

Pre n=2 sa začnú vykonávať príkazy uvedené za vetvou case 2:. Vypíše sa:

    Dva
    Tri alebo styri
    Chyba!
    Koniec.

Výhodou je, že môžeme zlúčiť viacero prípadov do jednej vetvy tým, ze príkazy napíšeme až za posledný prípad (tu vidíme napr. v situácii n=3 a n=4).

Dôležité upozornenie: break switch while

Možno ste si všimli, že v príklade Hádaj číslo som použila na ukončenie cyklu premennú pokračuj. V prípade použitia podmienky if som mohla namiesto toho urobiť cyklus nekonečný a v prípade odpovede 'N' cyklus prerušiť príkazom break. Keby som podobnú vec skúsila urobiť v prípade použitia switch program by sa neskončil nikdy. Dôvod je, že príkaz break nevyskočí zo všetkých cyklov, ale iba z najvnútornejšieho - a tým je v tomto prípade switch.

Kontrola čísla

Vďaka znakom môžeme skúsiť urobiť prvú jednoduchú kontrolu toho, čo nám vlastne používateľ napísal na vstup. Napríklad, či zadal správne celé číslo a nenamiešal medzi cifry nejaký iný znak.

#include <iostream>

using namespace std;

int main(void){
    int N=0;
    char c;
    
    cout <<"Zadajte cele kladne cislo: ";

    cin >> noskipws >> c;
    while ((c>='0')&&(c<='9')) {                  // kym je nacitany znak cislo (t.j. jedna cifra)
        /* vsimnite si ze nepripocitavame priamo c ale c-48: ide totiz o kod znaku a '0' ma kod 48 */
        N=N*10+(c-48);                            // upravime cislo N
        cin >> noskipws >> c;                     // a nacitame dalsi znak
    }

    if ((c==' ')|| (c=='\n')){                    // ak sme skoncili medzerou alebo koncom riadku, tak je to pekne cislo
        cout << "Zadali ste " << N << endl;
    } 
    else cout << "Toto je cele cislo?" << endl;   // ak sme skoncili niecim divnym, tak to asi nebude ok
}

Vďaka načítaniu znakov a ich kontroly vieme zistiť, či doteraz zadané číslo alebo čokoľvek iné zodpovedá tomu, čo program očakáva.

Prednáška 8

Reťazec ako postupnosť znakov

Textový reťazec je v C chápaná ako postupnosť znakov char (v poli) ukončená znakom s kódom 0.

#include <iostream.h>

void main () {
    char r[100];
    int i;
    r[0] = 'A';
    r[1] = 'h';
    r[2] = 'o';
    r[3] = 'j';
    r[4] = '\n'; // znak pre koniec riadku
    r[5] = 0;

    // Vypíšeme po znakoch
    for (i = 0; r[i] != 0; i++) cout << r[i];

    // C++ podporuje výpis reťazca - vypíšeme naraz
    cout << r;
}

Jednoduchšie spôsoby incializácie

• Podobne ako ľubovoľné pole char r[100]={'A','h','o','j','\n',0};
• Špeciálna skratka: char r[100]="Ahoj";
• Ako vytvoríme prázdny reťazec?

Prvky reťazca (znaky) môžeme meniť

char A[100] = "Edo";
char ch = 'l';
char B[100] = "pes";

B[0] = ch;     // priradíme do jedného prvku reťazca premmennú typu char. Výsledkom je 'les'.
B[0] = 'v';    // priradíme do jedného prvku reťazca konštantný znak. Výsledkom je 'ves'. 
B[0] = A[1];   // priradíme do jedného prvku reťazca prvok iného reťazca. Výsledkom je 'des'. 

Kopírovanie

• Reťazec je normálne pole, nemôžeme ho teda jednoducho skopírovať, nemôžeme teda spraviť

char A[100];
A = "Ahoj";  // chyba
char B[100] = "Ahoj"; // ok - inicializacia
A = B; // chyba

Riešenie je podobné ako pri poliach - kopírovanie znak po znaku:

void kopirujRetazec(char A[], char B[]) {
    // skopiruj obsah retazca B do retazca A
    // A musi mat dost miesta
    int i;
    for (i = 0; B[i] != 0; i++) A[i] = B[i];
    A[i] = 0; // reťazec musí končiť 0
}

Porovnávanie

• Reťazce nemôžeme ani porovnávať pomocou ==, !=, < atď, zase musíme použiť cyklus.

bool rovnostRetazcov(char A[], char B[]) {
    // vrati true ak su retazce A a B rovnake, inak vrati false

    for (int i = 0; B[i] != 0 || A[i] != 0; i++) {
        if (A[i] != B[i]) return false;
    }
    return true;
}

• Ako bude prebiehať funkcia, ak jeden reťazec je začiatkom druhého?

Knižnica string.h v C

Obsahuje mnohé funkcie na prácu s reťazcami, napríklad tieto:

• strlen(retazec): vráti dĺžku reťazca
• strcpy(kam, co): skopíruje reťazec co do reťazca kam
• strcat(kam, co): za koniec reťazca kam pridá reťazec co
• strcmp(retazec1, retazec2): vráti nulu ak sa reťazce rovnajú, kladné číslo keď je prvý neskôr v abecednom poradí, záporné číslo ak je skôr. Pozor, to či je skôr alebo neskôr sa berie podľa kódov znakov, takže napr "Z" je skôr ako "a".

Reťazec pomocou knižnice string v C++

• Okrem klasických C-čkových reťazcov môžeme použiť aj C++ typ string.
• Majú elegantnejšie používanie, podobne ako vector si sami určujú potrebnú veľkosť pamäte
• Sú to objekty, do knižníc odovzdávame cez &

#include <string>
using namespace std;

int main(void) {

    char cstr[100] = "Ahoj\n";
    string str = "Ako sa mas?\n";
    string str2;

    /* mozeme priradovat konstantne retazce, C-ckove retazce (polia znamkov)
      aj C++ stringy. */
    str2 = "Ahoj\n";
    str2 = cstr;
    str2 = str;
    /* meranie dlzky */
    cout << "Dlzka je: " << str.length() << endl;

    /* Funguje porovnanie pomocou ==, !=, <,...
     * (bud dvoch C++ stringov, alebo C++ stringu a C stringu)
     * Znamienko + znamená zreťazenie. */
    str2 = cstr + str;
    str2.push_back('X');
    str2.push_back('\n');
    cout << str2;

    if (str < str2) {
        cout << "Prvy je skor" << endl;
    } else if (str == str2) {
        cout << "Rovnaju sa" << endl;
    } else {
        cout << "Druhy je skor" << endl;
    }
}

Jednotlivým znakom pristupujeme pomocou [] alebo at (ako pri vektore).

Načítavanie reťazcov

• Bežné načítanie z konzoly do reťazca (C alebo C++) načíta jedno slovo
  • Preskočí biele znaky (medzery konce riadkov, tabulátory), potom prečíta všetko po ďalší biely znak (alebo koniec vstupu) a uloží do premennej.
  • Pri čítaní do poľa znakov je vhodné nastaviť maximálny počet znakov na načítanie, aby sme nevyšli z poľa

• Na načítanie jedného riadku je možné použiť funkciu getline. Načíta až po koniec riadku, ten zahodí.

#include <iostream>
#include <string>
using namespace std;

int main(void) {
    const int maxN = 100;
    string str, str2;
    char cstr[maxN], cstr2[maxN];

    getline(cin, str); // cely riadok
    cin.getline(cstr, maxN); // cely riadok, ale najviac maxN-1 znakov

    cin >> str2; //jedno slovo
    cin.width(maxN); // najviac maxN-1 znakov pri najbližšom načítaní
    cin >> cstr2;

    cout << "str: \"" << str << "\"" << endl;
    cout << "cstr: \"" << cstr << "\"" << endl;
    cout << "str2: \"" << str2 << "\"" << endl;
    cout << "cstr2: \"" << cstr2 << "\"" << endl;
}

Príklad behu programu (prvé tri riadky zadal užívateľ, na začiatku a konci každého je medzera)

 a b c 
 d e f 
 g h i 
str: " a b c "
cstr: " d e f "
str2: "g"
cstr2: "h"

Algoritmy s textovými reťazcami

Prácu s reťazcami si precvičíme na niekoľkých menších príkladoch.

Prevod čísla na reťazec

Máme danú premennú x typu int, chceme ju uložiť v desiatkovej sústave do reťazca.

• Zvyšok po delení 10 je posledná cifra, uložíme si ju do reťazca, vydelíme x 10.
• Opakujeme, kým nespracujeme celé číslo.
• Prevod z čísla c (0..9) na cifru: '0'+c
• Nezabudneme na ukončovací znak 0
• Dostaneme číslo v opačnom poradí, napr pre x=12 budeme mať reťazec {'2', '1', 0}

void reverse(char A[]) {
    int n = strlen(A);
    int i = 0;
    int j = n - 1;
    while (i < j) {
        char tmp = A[i];
        A[i] = A[j];
        A[j] = tmp;
        i++; j--;
    }
}

void int2cstr(int x, char A[]) {
    /* prevedie kladne cele cislo x na retazec,
     * vysledok ulozi do retazca A, ktory musi mat dost miesta. */
    assert(x > 0);

    int n;
    for (n = 0; x > 0; n++) {
        A[n] = '0' + x % 10;
        x /= 10;
    }
    A[n] = 0;

    /* teraz je cislo naopak, treba otocit */
    reverse(A);
}

• Ako upravíme funkciu, aby fungovala aj pre x=0, prípadne záporné x?
• Ako by sme zapísali pomocou C++ reťazcov?
• Pozor na rozdiel medzi znakom 0 a '0' (a medzi reťazcom "0")

Formátovanie čísla

const int maxN = 100;

void formatInt(int x, char A[], int width) {
    /* číslo x konvertujeme na reťazec
     * a uložíme do poľa A zarované doprava na šírku width */

    /* najprv x uložíme do pomocného reťazca B  a zrátame jeho dĺžku n */
    char B[maxN];
    int2cstr(x, B);
    int n = strlen(B);

    /* do A dáme n-width medzier a ukončovaciu 0 */
    assert(n <= width);
    int i;
    for (i = 0; i < width - n; i++) {
        A[i] = ' ';
    }
    A[i] = 0;

    /* za A prikopírujeme B */
    strcat(A, B);
}

• Čo by sa stalo, ak by sme nedali do A ukončovaciu 0?
• Vedeli by sme prepísať program, aby pracoval priamo v poli A (bez poľa B)?

Využijeme na vypísanie pekne zarovnanej tabuľky faktoriálov:

int factorial(int n) {
    int result = 1;
    for (int i = 1; i <= n; i++) {
        result *= i;
    }
    return result;
}

int main(void) {
    char A[maxN];
    int n = 12;
    for (int i = 1; i <= n; i++) {
        int x = factorial(i);
        formatInt(i, A, 2);
        cout << A << "! = ";
        formatInt(x, A, 10);
        cout << A << endl;
    }
}

 1! =          1
 2! =          2
 3! =          6
 4! =         24
 5! =        120
 6! =        720
 7! =       5040
 8! =      40320
 9! =     362880
10! =    3628800
11! =   39916800
12! =  479001600

Dalo by sa aj jednoduchšie pomocou nastavenia width v cin:

int main(void) {
    int n = 12;
    for (int i = 1; i <= n; i++) {
        int x = factorial(i);
        cout.width(2);
        cout << i << "! = ";
        cout.width(10);
        cout << x << endl;
    }
}

Zalamovanie riadkov

• Máme reťazec s nejakým textom, v ktorom sa vyskytujú rôzne biele znaky, napríklad medzery a konce riadkov. Máme danú šírku riadku W, napr. 80 znakov. Úlohou je ho upraviť tak:
  • aby na každom riadku bolo najviac napr. W znakov, pričom nový riadok začína tam, kde by už ďalšie slovo presahovalo cez W
  • medzi dvoma slovami má byť vždy buď jedna medzera alebo jeden koniec riadku
  • predpokladáme, že žiadne slovo nemá viac ako W znakov

Zadavaj text ukonceny prazdnym riadkom.
A AA A AAA 
A  A AA AAA
AAA A AA AA  A

Zadaj sirku riadku:
5
Sformatovany odstavec:
A AA
A AAA
A A
AA
AAA
AAA A
AA AA
A

Zadavaj text ukonceny prazdnym riadkom.
Martin Kukucin: Do skoly.    Vakacie sa koncia. Ondrej Rybar sa vse zamysli nad marnostou sveta i vsetkeho, co je v nom. 
Predstupuje mu tu i tu pred oci profesor, ako stoji pred ciernou tabulou, drziac kruzidlo v ruke a demonstruje pamatnu poucku Pytagorovu. 
A zimomriavky naskakuju na chrbat, lebo s geometriou stoji od pociatku na nohe valecnej. 
Ani matematika nenie lepsia, menovite odvtedy, co sa do nej vplichtili miesto cisel vsakove litery. 
Neraz hutal, naco ich ucenci vpustili do matematiky - ved i bez nich je dost strapata: ci sa im malilo cisel a tak preto vsantrocili medzi ne a a b a ci fantazia sa im tak rozihrala, 
ze prekrocila hranice cisel celych, zlomkov obycajnych i desatinnych i bohvieakych, a zabludila na nivy, kde rastu nestastne litery? 
 ,Uz akokolvek,' huta Ondro, ,litery tam nemaju co hladat. Tazko je uverit, ze a/b = c, lebo nevies, co je a, alebo b.' 

Zadaj sirku riadku:
50
Sformatovany odstavec:
Martin Kukucin: Do skoly. Vakacie sa koncia.
Ondrej Rybar sa vse zamysli nad marnostou sveta i
vsetkeho, co je v nom. Predstupuje mu tu i tu pred
oci profesor, ako stoji pred ciernou tabulou,
drziac kruzidlo v ruke a demonstruje pamatnu
poucku Pytagorovu. A zimomriavky naskakuju na
chrbat, lebo s geometriou stoji od pociatku na
nohe valecnej. Ani matematika nenie lepsia,
menovite odvtedy, co sa do nej vplichtili miesto
cisel vsakove litery. Neraz hutal, naco ich ucenci
vpustili do matematiky - ved i bez nich je dost
strapata: ci sa im malilo cisel a tak preto
vsantrocili medzi ne a a b a ci fantazia sa im tak
rozihrala, ze prekrocila hranice cisel celych,
zlomkov obycajnych i desatinnych i bohvieakych, a
zabludila na nivy, kde rastu nestastne litery? ,Uz
akokolvek,' huta Ondro, ,litery tam nemaju co
hladat. Tazko je uverit, ze a/b = c, lebo nevies,
co je a, alebo b.'

Plán: úlohu si rozdelíme na viac častí

• Prerobíme reťazec tak, aby sme všetky biele znaky nahradili medzerami. Na rozpoznanie bielych znakov použijeme funkciu isspace z knižnice cctype.
• Každý súvislý úsek medzier nahradímke práve jednou medzerou, zmažeme medzery na začiatku a konci.
  • Podobá sa na príklad z vyhadzovaním núl z poľa z cvičení
  • Viac možnostá na riešenie, napríklad znaky presýpame do nového poľa. my ale použijeme len jedno pole
• Niektoré medzery nahradíme koncom riadku, aby každý riadok mal šírku najviac W
• Spravíme načítanie a vypísanie.

#include <iostream>
#include <cstring>
#include <cctype>
#include <cassert>
using namespace std;

void simplify(char A[]) {
    /* V retazci A nahradi kazdy suvisly usek bielych znakov prave jednou medzerou.
     * Na zaciatku a konci retazca nebudu medzery. */

    int i;

    /* prepis hocijake biele znaky na medzeru */
    for (int i = 0; A[i] != 0; i++) {
        if (isspace(A[i])) {
            A[i] = ' ';
        }
    }

    int kam = 0; /* prve este neobsadene miesto */
    char prev = ' '; /* predchadzajuci znak */

    for (int i = 0; A[i] != 0; i++) {
        /* ak nemame viac medzier po sebe, skopirujeme znak */
        if (A[i] != ' ' || prev != ' ') {
            A[kam] = A[i];
            kam++;
        }
        /* zapamatame si posledny znak */
        prev = A[i];
    }

    /* zrusime pripadnu medzeru na konci */
    if (kam > 0 && A[kam - 1] == ' ') {

        kam--;
    }

    /* retazec ukoncime nulou */
    A[kam] = 0;
}

bool breakLines(char A[], int width) {
    /* Preformatuje odstavec na sirku riadku width, vyhodi zbytocne medzery.
     * Dlzka kazdeho slova musi byt najviac width, inak funkcia vrati false */

    simplify(A);
    int n = strlen(A);

    int zac = 0;  /* prve pismeno v riadku */
    while (zac < n) {
        int kon = zac + width;  /* potencialny koniec riadku */
        /* ak uz nemame dost pismen na cely riadok */
        if (kon > n) {
            kon = n;
        }
        /* ak sme na konci, pridame koniec riadku za koniec retazca */
        if (kon == n) {
            A[kon] = '\n';
            A[kon + 1] = 0;
            n++;
        } else {
            /* ideme späť, kým nenájdeme medzeru */
            while (kon > zac && A[kon] != ' ') {
                kon--;
            }
            /* nenašli sme medzeru: slovo bolo príliš dlhé. */
            if (kon == zac) {
                return false;
            }
            /* medzeru prepíšeme na koniec riadku */
            assert(A[kon]==' ');
            A[kon] = '\n';
        }
        /* za koncom riadku bude novy zaciatok */
        zac = kon + 1;
    }
    return true;
}

int main(void) {
    const int maxN = 2000;
    char A[maxN];

    cout << "Zadavaj text ukonceny prazdnym riadkom." << endl;
    while (true) {
        /* nacitame jeden riadok */
        char tmp[maxN];
        cin.getline(tmp, maxN);
        /* ak je prazdny, koncime nacitavanie */
        if (strcmp(tmp, "") == 0) {
            break;
        }
        /* ak je miesto v poli A, pridame do neho novy riadok */
        if (strlen(A) + strlen(tmp) + 2 < maxN) {
            strcat(A, tmp);
            strcat(A, "\n");
        } else {
            cout << "Text je prilis dlhy." << endl;
            return 1;
        }
    }

    cout << "Zadaj sirku riadku:" << endl;
    int width;
    cin >> width;

    breakLines(A, width);
    cout << "Sformatovany odstavec:" << endl;
    cout << A;
}

• Akú zložitosť má načítanie vzhľadom na celkový počet načítaných písmen? Dalo by sa zlepšiť?

Vyhľadávanie podreťazca

Chceme zistiť, či a kde sa v reťazci nachádza určité slovo alebo iná vzorka.

#include <iostream>
#include <cstring>
#include <cctype>
#include <cassert>
using namespace std;

int find(char text[], char pattern[]) {
    /* Vráti -1 ak sa retazec pattern nevyskytuje v retazce text,
     * inak vráti polohu jeho prvého výskytu. */

    int n = strlen(text);
    int m = strlen(pattern);
    for (int i = 0; i < n - m + 1; i++) {
        int j = 0;
        while (j < m && text[i + j] == pattern[j]) {
            j++;
        }
        if (j == m) {
            return i;
        }
    }
    return -1;
}

int main(void) {
    const int maxN = 2000;
    char A[maxN], B[maxN];

    cout << "Zadaj text: ";
    cin.getline(A,maxN);
    cout << "Zadaj vzorku: ";
    cin.getline(B,maxN);
    cout << find(A,B) << endl;
}

• Predpočítame si dĺžky a uložíme do premenných, aby sa zbytočne nerátali unova a znova
• Vedeli by sme do poľa uložiť polohy všetkých výskytov?

Cvičenia 4

Manipulácia s poľom

V nasledujúcich zadaniach napíšte úryvok kódu alebo funkciu, ktorá bude pracovať s poľom intov a, pričom jeho veľkosť máte v premennej n.

• Nájdite všetky nuly a vyhoďte ich z poľa, pričom po skončení je v premnnej n nový počet prvkov.
  • Viete spraviť program tak, aby poradie nenulových prvkov zostalo to isté? T.j. z poľa {1,0,4,0,0,7} dostaneme {1,4,7}
• Otočte poradie prvkov v úseku poľa zadanom začiatkom a koncom.
• Posuňte pole cyklicky o 1 doprava, pričom posledný prvok sa dostane na prvé miesto.
• Posuňte pole cyklicky o k doprava.
  • Viete to spraviť tak, aby čas výpočtu nezávisel od k?

Triedenia

• Bublinkové triedenie z prednášky 6 v prvej iterácii dostane najväčší prvok na svoje miesto, po druhej už sú dva najväčšie na svojom mieste atď.
  • Využite tento fakt na zrýchlenie: porovnávajte dvojice len po n-k kde k je číslo aktuálnej iterácie.
• Bublinkové triedenie sa dá zrýchliť ešte viac v prípade, ak si budeme pamätať posledné miesto, kde sa uskutočnila výmena. Od tohoto miesta ďalej už je pole usporiadané.

Ladenie programu (debugovanie)

Šejkrové triedenie je veľmi podobné bublinkovému. Narozdiel od neho šejkrové po prejdení poľom jedným smerom až do konca nezačína znovu od začiatku, ale pokračuje opačným smerom od konca späť. Taktiež používa zrýchlenie spomenuté v predchádzajúcej úlohe k bublinkovému triedeniu. Šejkrové triedenie teda prechádza poľom stále tam a späť, pokiaľ sa usporiadaný začiatok nespojí s usporiadným koncom.

Nájdite všetky chyby v nasledujúcom programe. Doporučujeme najprv spraviť program skompilovateľný, potom si ho pozorne prečítať a odstrániť nezmysly a zvyšné chyby odladiť pomocou krokovania programu.

• #Shakersort pre cvičenia 4

Veľké čísla

• Veľké čísla, ktoré sa nemusia zmestiť do premennej typu int môžeme reprezentovať pomocou poľa, v ktorom si pamätáme jeho cifry v desiatkovom zápise.
  • Vytvorte program, ktorý načíta po cifrách a vypíše takto reprezentované veľké číslo.
  • Spravte funkcie na sčítanie, prípadne násobenie veľkých čísel.

Polynómy

• Na prednáške 6 sme mali program, v ktorom polynóm reprezentujeme ako pole jeho koeficientov. Napíšte funkciu, ktorá vynásobí takéto polynómy.
• Vykreslite graf polynómu.

Prvočísla

• Použite Eratostenovo sito na nájdenie prvočísel z prednášky 6. S pomocou týchto prvočísel napíšte program na rozklad čísla na súčin prvočíselných deliteľov.

Shakersort pre cvičenia 4

  #include <ioscream>
  #using namespace std;
  
  void swap(int x, int y) {
      /* Vymeň hodnoty premenných x a y. */
      int tmp = x;
      x = y;
      y = tmp;
  }
  
  void printArray(int a[], int n) {
      /* Vypíš celé pole. */
     for (int i = 0; i < n; i++) {
         cout << " " << a[n];
     }
     cout << endl;
  }
  
  void shakerSort(int a[], int n) {
      /* Usporiadaj prvky v poli a od najmenšieho po najväčší. */
      /* Chodíme tam a späť, pričom vždy menej,
       * lebo na koniec v každom prechode presunieme číslo,
       * ktoré tam patrí. */
  
      int begin = 0;
      int end = n;
      int i;
      while (begin<end)
      {
          /* spravíme prechod zľava doprava */
          for (i==begin; i<end; i++);
          {
              if (a[i]>=a[i+1]) swap(a[i], a[i+1]);
          }
          end--;
          /* spravíme prechod sprava doľava */
          for (i==end; i>begin; i++);
          {
              if (a[i]>=a[i-1]) swap(a[i], a[i+1]);
          }
          begin--;
      }
  }
  
  int main(void) {
      int n = 6;
      int a[6] = {9, 3, 7, 4, 5, 6};
  
      printArray(a, n);
      sharkSort(a, n);
      printArray(a, n);
  }

DÚ4

max. 8 bodov, termín odovzdania utorok 18.10. o 22:00

Cieľom tejto domácej úlohy je precvičiť si prácu s poliami a funkciami pri písaní o niečo dlhšieho programu. Budeme programovať hru Logik. V tejto hre máme hracie kamene F rôznych farieb. Prvý hráč (v našom prípade počítač) si zvolí N hracích kameňov a uloží ich do radu. Druhý hráč sa snaží túto postupnosť farieb uhádnuť. V každom kole si druhý hráč tiež zvolí N kameňov a zoradí ich. Prvý hráč mu povie, ako blízko je k správnej odpovedi pomocou bielych a čiernych bodov nasledujúcim spôsobom:

• Za každú pozíciu, na ktorej sa správna opoveď a najnovší pokus nelíšia, dostane čierny bod.

• Celkový počet bodov (bielych a čiernych spolu) zodpovedá tomu, koľko najviac čiernych bodov by sa dalo získať preusporiadaním kameňov v pokuse.

Ak sa teda v pokuse žiadna farba neopakuje, biele body zodpovedajú farbám, ktoré sú aj v správnej odpovedi, ale na inom mieste ako v pokuse. Ak sa farby v pokuse opakujú, musíme vziať do úvahy aj ich počty. Napríklad ak pokus obsahuje tri červené kamene a správna odpoveď iba dva červené kamene, hráč dostane iba dva biele (príp. čierne) body.

Hra sa končí, keď druhý hráč dostane N čiernych bodov, teda správne uhádol poradie farieb v správnej odpovedi.

V našej verzii budeme farby reprezentovať číslami 0,1,...,F-1. Biele body sa budú zapisovať ako malé x a veľké body ako veľké X. Vždy sa vypíšu najskôr všetky biele a potom všetky čierne body. Tu je príklad priebehu hry pre N=3, F=5 a správnu odpoveď 2,4,4.

Zadaj 3 cisel(cisla) od 0 po 4: 0 1 2
Hodnotenie: x

Zadaj 3 cisel(cisla) od 0 po 4: 0 3 4
Hodnotenie: X

Zadaj 3 cisel(cisla) od 0 po 4: 1 4 3
Hodnotenie: X                              

Zadaj 3 cisel(cisla) od 0 po 4: 3 2 4
Hodnotenie: xX

Zadaj 3 cisel(cisla) od 0 po 4: 3 2 2
Hodnotenie: x

Zadaj 3 cisel(cisla) od 0 po 4: 2 4 4
Hodnotenie: XXX

Uhadli ste!

Napíšte program, ktorý vygeneruje správnu odpoveď generátorom pseudonáhodných čísel a potom si opakovane od hráča vypýta jeho tip a spočíta mu body. Hra sa končí, keď hráč uhádne správnu odpoveď. Môžete predpokladať, že hráč zadáva korektné hodnoty (čísla od 0 do F-1).

Najzložitejšou časťou je spočítanie počtu bielych bodov. Ten môžete získať z celkového počtu bodov odčítaním čiernych bodov. Na spočítanie celkového počtu bodov doporučujeme vytvoriť pomocné pole dĺžky F, ktoré v políčku i bude mať počet výskytov čísla i v správnej odpovedi a druhé pole takého istého tvaru pre aktuálny pokus. Potom viete ľahko spracovať prípad typu, že v pokuse sú dve červené a v správnej odpovedi tri červené kamene.

Nižšie prikladáme kostru programu, ktorá celý problém rozkladá na menšie časti implementované v jednotlivých funkciách. Doporučujeme Vám postupovať podľa tohto návodu, nie je to však nevyhnutné. Vaše riešenie by však malo spĺňať nasledovné požiadavky:

• Váš program správne funguje a správa sa analogicky k vyššie uvedenému priebehu hry.
• Hodnoty N a F máte zadefinované ako konštanty, ktoré stačí zmeniť na jednom mieste v programe.
• Používate len príkazy, ktoré sme preberali na prednáške.
• Program je rozdelený na niekoľko funkcií s dobre logicky definovanými úlohami. Mená funkcií zodpovedajú tomu, čo tie funkcie robia a na začiatku každej funkcie v komentári podrobnejšie vysvetlíte jej účel.

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;

/* globalne konstanty: 
 * F je pocet vsetkych moznych farieb
 *   (farby budu od 0 po F-1 vratane)
 * N je pocet hadanych farieb
 */
const int F = 5;
const int N = 3;

void nacitaj(int a[]) {
  /* Do pola a od uzivatela nacita N cisel od 0 po F-1 */

}

void generuj(int a[]) {
  /* Do pola a vygeneruje N nahodnych cisel od 0 po F-1 */

}

int cierne(int a[], int b[]) {
  /* V poli a je spravne riesenie, v poli b je pokus.
   * Obidve polia obsahuju N cisel od 0 po F-1.
   * Funkcia vrati pocet ciernych bodov, 
   * ktore ma uzivatel dostat. */

}

void pocty(int a[], int p[]) {
  /* V poli a je riesenie (N cisel od 0 po F-1).
   * Do pola p spocitame pocty vyskytov
   * jednotlivych cisel, t.j. pre 0<=i<F
   * p[i] bude pocet vskytov cisla i v poli a
   */

}

int vsetky(int a[], int b[]) {
  /* V poli a je spravne riesenie, v poli b je pokus.
   * Obidve polia obsahuju N cisel od 0 po F-1.
   * Funkcia vrati pocet vsetkych bodov, 
   * ktore ma uzivatel dostat. */
  
}

void vypis(int vsetky, int cierne) {
  /* Dany je pocet vsetkych bodov a kolko 
   * z nich maju byt cierne (zvysne su biele).
   * Pre kazdy biely bod vypise x 
   * a pre kazdy cierny X. */

}

int main(void) {
  /* pole so spravnou odpovedou a pokusom */
  int spravne[N];
  int pokus[N];

  /* generovanie spravnej odpovede */
  srand(time(NULL));
  generuj(spravne);

  /* samotna hra */
  while(true) {
    nacitaj(pokus);
    int v = vsetky(spravne, pokus);
    int c = cierne(spravne, pokus);
    vypis(v, c);
    if(c==N) {
      cout << "Uhadli ste!" << endl;
      break;
    }
  }
}

Prednáška 9

Súbory ako streamy

Každý textový súbor môžeme chápať ako postupnosť znakov (podobne ako vstup/výstup z konzoly). Teda aj textový súbor je vlastne stream, ktorý môžeme postupne (zľava doprava) čítať alebo do neho zapisovať.

Ofstream

Budeme využívať typy a funkcie zadefinované v knižnici fstream. Na príklade ukážeme, ako vytvoriť súbor a ako doň zapisovať:

#include <fstream>

using namespace std;

int main (void) {
  ofstream o;
  o.open ("Test.txt");     // otvorenie súboru
  o << 'z';                // zapíše 1 znak
  o << "Toto je retazec";  // zapíše reťazec znakov (= postupnosť znakov)
  o << endl;               // 1 znak = nový riadok – znak \ má špeciálny význam
  o << "Text";             // v súbore bude toto na začiatku nového riadka
  o << endl;
  o << 10*32 ;             // môžeme zapísať hodnotu výrazu ako reťazec znakov
  o << endl;
  o << "10*32=" << 10*32 << endl;          // zapíše sa zľava doprava
  o << "1 rovna sa 4? " << (1==4) << endl; // pozor na priority operátorov ... 1==4 musí byť v zátvorkách !!!
  o.close ();              // zatvorenie súboru
}

ofstream o;

• premenná o je typu ofstream = Output File Stream = súbor, do ktorého budeme zapisovať – výstupný súbor,

o.open ("Test.txt");

• open (...) je funkcia, ktorá pracuje s premennou o,
• jej argumentom reťazec = meno súboru,
• otvorí súboru – na disku vnikne súbor s názvom Test.txt,
• premenná o od teraz obsahuje rôzne informácie o súbore Test.txt – pomocou premennej o budem pracovať so súborom Test.txt,

operátor << funguje rovnako ako pri vstupe/výstupe do konzoly:

• syntax: súbor << výraz;, kde súbor je premenná typu ofstream,
• vyhodnotí výraz a zapíše jeho hodnotu do súboru.

o.close ();

• close () je funkcia, ktorá ukončí prácu so súborom Test.txt – uzavrie súbor,
• Pravidlo: súbor, ktorý som otvoril musím uzavrieť – ak píšete jednoduché programy a neuzavriete súbor, nemusí sa nič zlé prihodiť, ale nepatrí sa to. Pri zložitejších programoch môžu vznikať "nepredvídateľné" chyby.

Ifstream

Podobne môžeme otvoriť aj súbor, z ktorého budeme čítať vstup. V príklade načítame pole celých čísel.

#include <fstream>
#include <iostream>

using namespace std;
const int MAX=100;

int main (void) {
  ifstream f;
  int pocet, A[MAX];
  
  f.open ("VSTUP.txt");
  if (f.fail ()) return 1;  // return = návrat z funkcie – koniec programu
  f >> pocet;
  for (int i=0; i<pocet; i++) {
    f >> A[i];
  }

  for (int i=0; i<pocet; i++) {
    cout<< A[i] << " ";
  }
  f.close();
}

ifstream f;

• premenná f je typu ifstream = Input File Stream = súbor, z ktorého môžeme čítať – vstupný súbor,

f.open ("VSTUP.txt");

• otvorí súboru – s názvom VSTUP.txt, premenná f od teraz obsahuje rôzne informácie o súbore VSTUP.txt – pomocou premennej f budem pracovať so súborom VSTUP.txt,

f.fail ()

• je funkcia, ktorá vráti logickú hodnotu pravda, ak nastala pri práci so súborom f chyba, najčastejšie chyby vzniknú, ak sa súbor nedá otvoriť (keď neexistuje).

operátor >> funguje ako pri šstandardnom vstupe

• syntax: súbor >> prem; kde súbor je premenná typu ifstream,
• podľa toho, akého typu je prem sa zo súboru prečítajú znaky, tie sa premenia na hodnotu, ktorá sa priradí do premennej prem. Pri čítaní sa preskakujú biele znaky (medzery a konce riadkov).

f.close ()

• ifstream data iba číta, takže tam nie je buffer, pri ktorom sa treba uistiť, že bol zapísaný na disk
• nie je teda nutné ifstream zatvárať - nič se nestane ak ho program na konci natvrdo zabije. Naopak keď by zabil ofstream, môžete prísť o dáta

Testovanie správneho otvorenia

Pri načítaní sme sa už stretli s funkciou f.fail(), ktorá vrátila logickú hodnotu pravda ak vznikla chyba (väčšinou pri otovrení neexistujúceho súboru). Druhou možnosťou je testovať správne otvorenie pomocou testovania premennej typu ofstream alebo ifstream. Je to ekvivalentné (snáď skoro vždy) funkcii fail.

  ifstream fin("VSTUP.txt"); // input
  if(!fin) {
    cout << "Cannot open VSTUP.txt file.\n";
    return 1;
  }

  ofstream fout("VYSTUP.txt"); // output, normal file
  if(!fout) {
    cout << "Cannot open VYSTUP.txt file.\n";
    return 1;
  }

Testovanie konca súboru

ifstream fin("VSTUP.txt"); // input
char c;

while(!fin.eof()) {
  fin>>c;
  cout<<c;
}

Čítanie a zápis v C

Doteraz sme čítanie a vypisovanie robili pomocou streamov. V jazyku C však streamy nie sú a tak je dobré poznať aj spôsob, ktoý funguje tam. Na rozdiel od streamov, ktoré boli v knižnici <iostream> používame na načítávanie a zápis v C knižnicu <stdio.h>

Najprv si ukážeme funkcie, ktoré pracujú s jedným znakom.

• Funckia getchar() vracia hodnotu typu celé číslo. Táto funkcia načíta jeden znak z obrazovky (až po stlačení klávesy enter). V prípade, že je znakov viac, funkcia načíta prvý z nich. Ak chceme načítať všetky potrebujeme funkciu volať v cykle.
• Funkcia putchar(int) má ako parameter celé číslo (vieme už o jednoznačnom vzťahu medzi znakmi a ich kódmi - celými číslami). Návratovou hodnotou funkcie je celé číslo - kód vytlačeného znaku alebo -1 (EOF) v prípade, že nastala chyba.

Okrem toho poznáme aj funkcie, ktoré umožnia prečítať dáta v požadovanej forme, napríklad čísla, znaky alebo reťazce. Na základe preddefinovaných znakov môžeme čítať niektoré formáty:

• %c - znak (character)
• %i - celé číslo (integer)
• %d - celé číslo (integer)
• %f, %Lf - reálne číslo (double)
• %s - reťazec (string)

• Funkcia printf vytlačí formátovaný reťazec a vracia počet znakov, ktoré vytlačila. V prípade chyby vracia záporné číslo. Jej tvar je printf(format, premenne). Každý reťazec sa uzatvára do dvojitých úvodzoviek. Ak chceme napríklad tlačiť premennú typu celé číslo, tak použijeme formát %d a za koncom formátu nasleduje po čiarke konkrétna premenná, ktorej hodnotu potrebujeme vytlačiť.
• Funkcia scanf vytlačí formátovaný reťazec a vracia počet úspešne priradených hodnôt. V prípade chyby vracia hodnotu EOF. Jej tvar je scanf(format, premenne). Každý reťazec sa uzatvára do dvojitých úvodzoviek. Ak chceme napríklad tlačiť premennú typu celé číslo, tak použijeme formát %d a za koncom formátu nasleduje po čiarke konkrétna premenná, ktorej hodnotu potrebujeme vytlačiť. Avšak jednoduché premenné odovzdávame funckii scanf pomocou adresy (&). Výnimkou je reťazec znakov, ktorý odovzdávame priamo.

#include <stdio.h>

int main (void)
{
  char str [80];
  int i;

  printf ("Enter your family name: ");
  scanf ("%s",str);  
  printf ("Enter your age: ");
  scanf ("%d",&i);
  printf ("Mr. %s , %d years old.\n",str,i);

}

Takto formátovaný vstup a výstup nám umožní mať lepšiu kontrolu ako vstup/výstup vyzerá. Ako si ukážeme, ide istý druh kontroly robiť aj pri streamoch, ale je to menej prehľadné.

Textové súbory v C

• Základný dátový typ: FILE *
  • ukazovateľ (pointer - *) na objekt typu FILE
  • dodržať veľké písmená (FILE *, nie file *)
• Definícia premennej f pre prácu so súborom FILE *f; (pre viac premenných FILE *fr, *fw;)
  • aj pre čítanie, aj pre zápis rovnaké
• Otvorenie súboru
  • pre čítanie: fr = fopen("SUBOR.TXT", "r");
  • pre zápis: fw = fopen("SUBOR.TXT", "w");
• Operácie podobné ako načítanie zo štandardného vstupu
  • c=getc(f)
  • putc(c,f)
  • fscanf(f, "format", argumenty)
  • fprintf(f, "format", argumenty)
• Keď už nebudeme zo súboru čítať ani doňho zapisovať - uzatvoriť súbor fclose(f);
  • nespoliehať sa, že po skončení programu sa v mnohých systémoch automaticky uzavrie súbor
  • počet súčasne otvorených súborov je obmedzený
  • zápis bufferu do súboru (preto uzatvárať ihneď) - pri spadnutí programu by zostali dáta v bufferi a stratili by sa
  • ak sa nepodarí otvoriť súbor - vracia fclose() konštantu EOF

Testovanie konca riadku

Koniec riadku označujeme EOLN (označenie, nie symbolická konštanta). Štandardne testujeme koniec riadku porovnaním na znak pre koniec riadku \n

• aj pre čítanie, aj pre zápis
• význam určuje prekladač podľa systému (<CR>, <LF>, alebo <CR><LF>)

#include <stdio.h>

int main(void) {
   FILE *fr;
   int c;

   fr = fopen("VSTUP.TXT", "r");
   while ((c = getc(fr)) != '\n') 
      putchar(c);
   putchar(c);    /* vypis \n */
   fclose(fr);
}

Testovanie konca súboru

• Pomocou symbolickej konštanty EOF
  • definovaná v stdio.h, väčšinou má hodnotu -1
  • premenná c nesmie byť definovaná ako char, pretože EOF je reprezentovaná ako int s hodnotou -1 (-1 by bola na char konvertovaná ako iný znak)

#include <stdio.h>

int main(void) {
   FILE *fr, *fw;
   int c;

   fr = fopen("LIST.TXT", "r");
   fw = fopen("KOPIA.TXT", "w");

   while ((c = getc(fr)) != EOF)
      putc(c, fw);

   fclose(fr);
   fclose(fw);
}

• Pomocou makra feof()

Štandardný vstup a výstup ako súbor

C pracuje s klávesnicou a obrazovkou ako so súborom - v stdio.h sú definované dva konštantné ukazovatele stdin a stdout.

FILE *stdin, *stdout;

• označujú štandardný vstupný/výstupný prúd (standard intput-output stream)
• stdin a stdout môžu byť použité v programe ako argumenty operácií so súbormi getc(stdin)

Vďaka tomu, že aj štandardný vstup a výstup sa dajú používať v takým istým spôsobom ako súbory je, že si používateľ môže vybrať, s čím chce pracovať. Program vypíše otázku, či má byť výstup vypísaný na obrazovku, alebo do súboru VYSTUP.TXT.

#include <stdio.h>

int main(void) {
  FILE *fw;
  int c;

  printf("Stlacte O pre vypis na Obrazovku\n");
  printf("alebo iny znak pre zapis do suboru VYSTUP.TXT: ");

  c = getchar();
  while (getchar() != '\n') 
     ;   
  if (c == 'o'  ||  c == 'O')
    fw = stdout;
  else 
    fw = fopen("VYSTUP.txt", "w");
    
  printf("Piste text a ukoncite ho znakom *\n");
  while ((c = getchar()) != '*')
    putc(c, fw);

  if (fw != stdout)                       // ak nemame standardny vystup, potrebujeme subor zavriet
    fclose(fw);

  return 0;
}

Prednáška 10

Pozor, toto je provizorna verzia prednasky

• Prednáška by už nemala obsahovať nesprávne programy
• Obsahuje každú oblasť niektorým spôsobom (časom pribudne aj druhý spôsob)

Spracovávanie vstupu

Tri najčastejšie schémy spracovania textového súboru:

• čítanie po znakoch (resp. premenných) - ignorujeme značky <Eoln> (považujeme ich len za biele znaky)
  • Príklad: Chceme zistiť počet medzier v texte

int main(void){
int c,poc=0;
FILE *f;

f=fopen("VSTUP.txt","r");
while ((c=getc(f))!=EOF){
 if (c==' ') poc++;
}

printf("%d\n",poc);
}

• čítanie celých riadkov - getline
  • Príklad: Chceme zistiť počet riadkov a najväčšiu dĺžku riadku
  • Skúste čo urobí nasledovný program pre prázdny súbor, pre súbor kde je na konci ešte Enter a podobne - počíta to správne?

#include <iostream>
#include <fstream>
#include <string>

using namespace std;

int main()
{
	ifstream f("VSTUP.txt");
	string line;
        int x,poc=0, max=-1;

	while(!f.eof()) {
          getline(f,line);
	  x=line.length();
          if (x>max) max=x;
          poc++;
	}
}

ifstream f;
char str[100];
int poc=0,max=-1;

while (f.getline(str,100)){
 poc++;
 x=strlen(str);
 if (x>max) max=x;
}

• čítanie po riadkoch - v každom riadku čítame po znakoch až do konca riadka
  • Príklad: V každom riadku chceme spočítať počet znakov '.'
    • Prvá možnosť čítanie riadkov do stringov a v nich potom spracovávame
    • Druhá možnosť je čítať každý riadok postupne

int main(void){
ifstream f("VSTUP.txt");;
string line;
int poc;

while (getline(f,line)){
 poc=0;
 for (int i=0; i<line.length(); i++){
   if (line[i]=='.') poc++;
 }
 cout << poc <<endl;
}

FILE *f;
int poc=0,c;

while ((c=getc(f))!=EOF){
 if (c=='\n'){
  // spracuj koniec riadku
  cout << poc << endl;
  poc=0;
 }
 else {
  //spracuj znak z riadku
  if (c=='.') poc++;
 }
}

V prípade, že máme v súbore zaručené čísla, bežne bývajú v niektorom z nasledujúcich formátov:

• N (počet čísel) a za tým N čísel
• čísla ukončené -1
• niekoľko sád z predchádzajúcich vecí

Kontrola správneho vstupu

• Určenie, či súbor obsahuje potrebný počet čísel na nejakú operáciu

Program načíta zo súboru tri double čísla zo súboru DATA.TXT a vypíše ich na obrazovku - testuje, či sú v súbore 3 čísla

#include <stdio.h>

int main() {
   FILE *fr;
   double x, y, z;

   fw = fopen("DATA.TXT", "r");
   if(fscanf(fr, "%lf %lf %lf\n", &x, &y, &z) == 3)
      printf("%lf \n", x + y + z);
   else 
      printf("Subor neobsahuje 3 realne cisla\n.");
   fclose(fr);
   return 0;
}

• Kontrola celého čísla, záporného čísla, desatinného čísla, čísla v x-kovej sústave

Ungetc

často zistíme, že máme prestať čítať znak až potom, čo prečítame o znak naviac - vrátiť do bufferu ungetc(c,fr) vráti znak do vstupného bufferu

• ak je vrátenie úspešné, ungetc() vracia vrátený znak
• ak je vrátenie neúspešné, vráti EOF

späť do bufferu môžeme zapísať aj iný ako práve prečítaný znak

Program konvertuje znakový reťazec na zodpovedajúcu číselnú hodnotu

int c, hodnota = 0;

while ((c = getchar()) >= '0' && c <= '9') {
  hodnota = hodnota * 10 + (c - '0');
}
ungetc(c, stdin);

Programu prečíta číslo pomocou fscanf() - predtým však musí prečítať neznámy počet znakov '$'.

int main(void){
 int c, hodnota = 0;
 FILE *fr;
  
  fr = fopen("VSTUP.txt", "r");
  while ((c = getc(fr)) == '$') 
      ;
  ungetc(c, fr);
  fscanf(fr, "%d", &hodnota);
  cout<< hodnota;
  fclose(fr);
}

Klávesnica

Využijeme funkcie z knižnice conio:

• kbhit () – vráti hodnotu logická pravda U je stlačený nejaký kláves,
• getch () – vráti kód stlačeného klávesu. Ak nie je stlačený žiadny kláves, funkcia čaká na stlačenie klávesu (až potom vráti jeho kód).

Príklad: Na klávesnici budeme stláčať tlačidlá a podľa nich vypisovať znaky. Program skončí, keď stlačíme kláves Esc.

#include <iostream>
#include <conio.h>

using namespace std;

int main(void){
  char c;
  c=getch();
  while (c!=27){
      cout << c << endl;
      c=getch();
  }
}

Alebo pomocou cyklu do-while:

#include <iostream>
#include <conio.h>

using namespace std;

int main(void){
  char c;
  do {
    c=getch();
    cout << c << endl;
  } while (c!=27);
}

Formátovanie výstupu

• Presnosť desatinného čísla v tomto kontexte znamená počet číslic zápisu desatinného čísla v desiatkovej sústave. Vyskúšame nasledovný program:

#include <iostream>
#include <iomanip>

using namespace std;

int main(void){
  double x = 800000.0/81.0;
  cout << setprecision(2) << x;
}

Tento program nie je pokazený, urobuilo presne to, čo sme od neho chceli - resp. čo sme mu napísali. Vypísal dve cifry z desiatkového zápisu. Pôvodným plánom však bolo vypísať dve desatinné miesta. V tomto prípade si musíme zmeniť formát z plávajúcej desatinnej čiarky (floating-point) na pevnú (fixed-point). Potom program bude vyzerať nasledovne:

#include <iostream>
#include <iomanip>

using namespace std;

int main(void){
  double x = 800000.0/81.0;
  cout << fixed << setprecision(2) << x;
}

• Úvodné nuly (alebo iné znaky) - bežný prípad, že v dátume by sme radi doplnili deň a mesiac na dvojciferné čísla a rok na štvorciferné.

#include <iostream>
#include <iomanip>

using namespace std;

void showDate(int m, int d, int y){
  cout << setfill('0');
  cout << setw(2) << m << '/'
  << setw(2) << d << '/'
  << setw(4) << y << endl;
}

int main(void){
  showDate(1,1,1999);
}

Kódovanie, šiforvanie

Cézarova šifra

Cézarova šifra je šifra, kde každé písmeno vstupného reťazca je posunuté v abecede o K miest. Ukážeme si použitie pre anglickú abecedu (t.j. znaky 'A'-'Z' bez diakritiky), ale je možné ju použiť napríklad aj na ASCI kódy.

int encryptCezar(FILE *fr, int K){
    int c;
    K=K%26;
    
    while ((c = getc(fr)) != EOF){
        if ((c<='Z') && (c>='A')){
            c=c+K;
            if (c>'Z'){c=c-26;}
            putc(c,stdout);
        }        
        else if (isspace(c)) {
            putc(c,stdout);
        }
        else return -1;
    }
    return 0;
}

• Text, ktorý chceme zašifrovať načítávame zo súboru fr a posúvame znaky 'A'-'Z' o nejakú konštantu K.
• V prípade, že narazíme na znak, ktorý nie je ani vhodným písmenom ani bielym znakom, tak vyhlásime chybu.
• Zašifrovaný text vypisujeme na obrazovku - nebol pri problém to zmeniť do súboru.
• Volanie funkcie šifrovania môže byť napríklad nasledovne: if (encryptCezar(fr,K)!=0) printf("Chyba pri kodovani");

Pri dešifrovaní postupujeme podobne, len číslo K od prečítaného znaku odrátame.

Vigenerova šifra

Vigenerova šifra je veľmi podobná Cézarovej, ale posun nie je konštantný, ale podľa kľúča. Tento kľúč samozrejme musí byť známy obidvom stranám - používa sa tak pri šifrovaní ako aj dešifrovaní.

int encryptVigenere(FILE *fr, char A[]){
    int i=0, c;
    
    while ((c = getc(fr)) != EOF){
        if ((c<='Z') && (c>='A')){
            c=c+A[i]-'A'; i++;
            if (c<'A'){c=c+26;}
            if (c>'Z'){c=c-26;}
            putc(c,stdout);
        }        
        else if (isspace(c)) {
            putc(c,stdout);
        }
        else return -1;

        if (A[i]=='\0') i=0; 
    }
    
    return 0;
}

• Funkcia zašifruje vstup zo súboru pomocou kľúča A, ktorý má svoj ako parameter.
• Opäť šifruje iba znaky 'A'-'Z' a biele znaky necháva ako sú.
• V prípade, že dojde po zašifrovaní znaku na koniec kľúča, ďalší znak bude znovu zašifrovaný pomocou prvého znaku kľúča. Kľúč totiž zvyčajne býva kratší ako samotný text a tým pádom je potrebné ho niekoľko krát použiť dokola.
• Volanie funkcie môže byť napríklad nasledovné: if (encryptVigenere(fr,"BABA")!=0) printf("Chyba pri kodovani");

Samoopravné kódy

V prípade, že očakávame, že na mieste, kadiaľ sa správa prenáša môže niekto/niečo správu poškodiť alebo zmeniť, je dobré, keď si vieme skontrolovať či prišla v poriadku. Najjednoduchším riešením je pridať nejaké dáta navyše, ktoré nenesú informáciu, ale robia iba kontrolu. Najjednoduchšou možnosťou je checksum - teda nejaký kontrolný súčet.

Pri zakódovaní spracujeme správu nasledovne:

• Všetky znaky, ktoré dostávame (opäť budeme akceptovať iba znaky 'A'-'Z') iba prepíšeme na výstup ale pamätáme si ich aktuálny súčet - postačí modulo 26.
• Na konci pridáme ešte tento jeden znak.

Pri odkódovani potrebujeme odlíšiť nejako posledný znak a pracovať nasledovne:

• Pamätáme si doteraz posledný znak a aktuálny súčet (opäť modulo 26)
• V prípade, že dojdeme na koniec súboru (správy) potrebujeme posledný znak odčítať (lebo nepatrí do správy) a zisiť, čí sa súčet rovná tomuto znaku.

Cvičenia 5

Funkcie zo string.h

Naprogramujte si vlastné funkcie bez použitia týchto funkcii z knižnice string.h

• MyStrlen(retazec): vráti dĺžku reťazca
• MyStrcat(kam, co): za koniec reťazca kam pridá reťazec co

Práca so stringami

• Upravte string tak, aby začiatočné písmeno každého slova bolo veľké (môžete použiť funkciu toupper z cctype).
• Upravte načítané slovo nasledovne: Prvý a posledný znak slova necháme, ostatné náhodne poprehadzujeme.
  • Vypíšte používateľovi takto upravené slovo a dajte mu hádať aké slovo ste pôvodne mali.

Jednoduchá kalkulačka

• Napíšte program, ktorý načíta dve čísla a ponúkne "Menu" operácií, ktoré s nimi môže vykonať (plus, mínus, krát, deleno). Na základe znaku, ktorý používateľ zadal vypíše výsledok.
• Rozšírte program tak, aby sa vždy po skončení pýtal, či ešte chce používateľ ďalej pokračovať.

Veľké čísla

Vytvorte program pre prácu s dlhými číslami. Čísla si reprezentujte v poli celých čísel, ktoré zodpovedá desiatkovému zápisu veľkého čísla.

• Vytvorte funkciu pre načítanie takéhoto čísla. Funkcia prečíta reťazec znakov a uloží ho do poľa reprezentujúceho toto číslo.
• Vytvorte funkciu pre vypísanie takéhoto čísla. Funkcia vypíše reťazec znakov na základe obsahu poľa.
• Vytvorte funkciu pre sčítanie dvoch takto reprezentovaných čísel. Výsledkom je tretie pole, ktoré reprezentuje výsledok sčítania.

DÚ5

max. 5 bodov plus 3 body bonus, termín odovzdania utorok 25.10. o 22:00

Napíšte program, ktorý animuje bublinkové triedenie, ktoré sme preberali na prednáške 6 pomocou grafickej knižnice SimpleDraw. Vaša animácia by mala vyzerať ako príklad na obrázku vpravo. Na začiatku každého prechodu poľom zobrazte všetky prvky v poli ako čierne paličky. Keď algoritmus porovnáva dve susedné hodnoty v poli, zobrazte pole tak, aby porovnávané prvky boli vyznačené červenou.

Aminácia pre počiatočnú hodnotu poľa {9, 3, 7, 5, 2}

Základná verzia programu (za 5 bodov):

• Pred každým vykreslením poľa môžete zmazať obrazovkou príkazom window.clear() a vykresľovať pole odznovu.
• Po každom vykreslení poľa čakajte určitý počet sekúnd príkazom window.wait(time);
• V programe si definujte nasledujúce konštanty, ktorými určíte parametre obrázku:

/* veľkosť medzery medzi paličkami a 
 * veľkosť okraja okolo obrázku */
const int gap = 10;  

/* šírka paličky */
const int width = 10;

/* výška jedného dieliku paličky, t.j. napr. palička pre hodnotu 8
 * bude výšky 8*height */
const int height = 10;

/* maximálna povolená hodnota v triedenom poli */
const int maxValue = 10;

/* dĺžka čakania po každom zobrazení poľa */
const double wait = 1;

/* maximálny povolený počet hodnôt v poli resp. počet paličiek */
const int maxN = 5; 

Konštanty môžete mať zadefinované globálne na vrchu programu, aby ste ich mohli používať vo všetkých funkciách. Potrebné rozmery obrázku a súradnice paličiek spočítajte z týchto hodnôt.

• Pole nenačítavajte od užívateľa, inicializujte ho n hodnotami priamo v programe.
• V poli budú iba kladné celé čísla medzi 1 a maxValue a ich počet bude najviac maxN.
• Dbajte na prehľadný štýl programu (členenie na funkcie, pomenovanie funkcií a premenných, komentáre, formátovanie)

Bonusové úlohy (spolu najviac 3 body)

• Prepíšte program tak, aby nevolal funkciu window.clear(), ale aby podľa potreby zmazal iba tie paličky, ktorým treba zmeniť farbu alebo výšku (zoznam id jednotlivých vykreslených paličiek si musíte pamätať v nejakom poli)
• Ak sa budú dve porovnávané paličky vymieňať, naznačte to v obrázku obojstrannou šípkou v medzere medzi nimi.

Odovzdávajte len jeden súbor, ktorý môže obsahovať základnú verziu, alebo verziu rozšírenú aj o bonusy.

Prednáška 11

Pointer, ukazovateľ, smerník

Pre pripomenutie: pamäť v počítači sú dieliky do ktorých sa zapisujú hodnoty premenných a následne k nim pomocou mien týchto premenných môžeme pristupovať. Ukazovateľ je premenná, ktorej hodnota je adresa v pamäti (teda nie hodnota, ktorá je tam napísaná, ale miesto, kde je niečo napísané).

• Ukazovateľ je definovaný pomocou *

int i // „klasická“ celočíselná premenná
int *p_i // ukazovateľ na celočíselnú premennú

• Ukazovateľ je teda 'rôzny' pre rôzne typy premenných
  • nedá sa priraďovať navzájom rôzne 'typy' ukazovateľov

int *pi;
char *pc;
pc=pi; // nevhodné

Inicializácia

Povedzme, že niečo na čo chceme ukazovať je obyčajná premenná typu int. Nadefinujem ju takto int x; Smerník sa urobí tak, že pridám hviezdičku. Smerník na int potom vyzerá takto int *a;

Je síce pekné, že si vytvorím smerník na int, ale treba aj nastaviť aby niekam ukazoval. Lebo takto z toho môžu vzniknúť chyby (ak budem chcieť na miesto kde (zatiaľ ne)ukazuje niečo uložiť, tak bude problém). Jednou z možností, ako povedať, že smerník má niekam ukazovať je povedať mu adresu.

int x;
int *a=&x;

Takýto zápis je ok, lebo smerník a hneď ukazuje na adresu kde je uložené x. Nepríjemné (alebo žiadúce?) je že keď mením teraz x mením aj to na čo ukazuje a, a naopak ak mením obsah toho kde ukazuje a, mením zároveň x.

Adresa, Dereferencovanie

Adresa miesta v pamäti, kde je umiestnená premenná x je &x.

Pomocou operátora dereferencie (*smernik) sa získajú dáta uložené na adrese, na ktorú ukazuje smerník.

Priradenie

Priradiť do premennej typu pointer na niečo môžeme iba adresu premennej typu niečo.

int i, *p_i;

p_i=&i; // spravne
p_i = &(i + 3); // zle i+3 nie je premenna
p_i=&15; //zle konstanta nema adresu
p_i=15; //zle priradovanie absolutnej adresy
i=p_i; // zle priradovanie adresy
i=&p_i; // zle priradovanie adresy
i=*p_i; // spravne ak p_i bol inicializovany
*p_i=4; // spravne ak p_i bol inicializovany

Keď nikam neukazuje

• Nulový ukazovateľ: NULL - symbolická konštanta definovaná v stdlib.h:
• Je možné priradiť ho ukazovateľom na ľubovoľný typ
• Testovanie prázdnosti: if (p_i == NULL) {...}
• V C++ môžeme používať namiesto NULL aj 0.

Parametre funkcií

• Volanie hodnotou

void print2X(int x) {
    x=2*x;
    cout << x;
}

int main(void){
    int x;
    ..
    print2X(x);
    ..
}

• Volanie referenciou

void print2X(int &x) {
    x = 2*x;
    cout << x;
}

int main(void){
    int x;
    ..
    print2X(x);
    ..
}

• Nové: volanie adresou

void print2X(int *p_x) {
    *p_x = *p_x * 2;
    cout << *p_x;
}

int main(void){
    int x;
    ..
    print2X(&x);
    ..
}

Príklad: Naša stará známa funkcia swap s použitím ukazovateľov:

void swap(int *p_x, int *p_y){ // ako parameter má dve adresy ukazujúce na celé čísla
    int pom = *p_x;             // do premennej pom nastavi hodnotu, ktorá je na adrese p_x                 
    *p_x = *p_y;                // hodnotu, ktorá je na adrese p_x zmení na hodnotu, ktorá je na adrese p_y 
    *p_y = pom;                 // hodnotu, ktorá je na adrese p_y nastaví na hodnotu premennej pom
} 

Ako budeme túto funkciu volať, ak chceme vymeniť hodnoty premenných i=5 a j=7

• swap(i, j); vymení obsah adries daných obsahom i, j: vymieňa hodnoty na adresách 5 a 7 - nemalo by asi ani skompilovať
• swap(*i, *j); vymieňa adresy adries z obsahu i, j: z adries 5 a 7 sa zoberú hodnoty a tie sa použijú ako adresy - nemalo by asi ani skompilovať
• swap(&i, &j); správne: vezme adresu premenných i a j a funkcia swap vymení hodnoty na týchto adresách

Polia a smerníky

Polia a smerníky spolu veľmi úzko súvisa. Dá sa totiž, povedať, že pole je vlastne smerník... Keď totiž vytvorím pole, tak sa jeho meno správa (väčšinou) ako ukazovateľ na jeho prvý prvok...

int pole[4] = {4, 3, 2, 1};

Na výpis takéhoto poľa môžeme použiť nasledujúci kód:

 for (int i = 0; i < 4; ++i){
   cout<<"Prvok "<<i<<" je "<<pole[i]<<endl;
 }

V tomto príklade sme použili operátor []. Ďalej si ukážeme ako napísať kód ktorý by mal rovnaký efekt s použitím smerníkov. Nasledujúce príklady slúžia len na pochopenie smerníkovej aritmetiky. Ak je to možné je lepšie použiť operátor [].

for (int i = 0; i < 4; ++i){
  cout<<"Prvok "<<i<<" je "<<*(pole + i)<<endl;
}

Namiesto použitia indexu je možné využiť fakt, že typ pole je v podstate smerník na prvý prvok. Preto sa dá k prvkom dostať pomocou operátora dereferencie (*).

Na typ smerník je možné používať smerníkové operácie.

Sizeof()

Na vysvetlenie aritmetických operácií s ukazovateľmi potrebujeme operátor sizeof():

• zistí veľkosť dátového typu v Bytoch
• vyhodnotí sa v čase prekladu (nezdržuje beh)

int i, *p_i;
i = sizeof(*p_i); //počet Bytov potrebných na uloženie typu int 

Smerníková aritmetika

• smerník + n: Posun smerníka o n. Ak napríklad smerník ukazuje na 0. prvok poľa potom po operácii smerník + n bude ukazovať na n-tý prvok poľa. Ak chceme zvýšiť smerník o 1 môžeme použiť smerník++.
• smerník - n: Posun smerníka o n prvkov smerom k začiatku.
• smerník - smerník: Výsledkom rozdielu smerníkov je vzdialenosť miest na ktoré ukazujú. Ak napríklad prvý smerník ukazuje na 5. prvok poľa a druhý smerník na 3. prvok poľa ich rozdiel je 2. Smerníky musia patriť do toho istého poľa ináč bude výsledok nedefinovaný.

int *smernik;
smernik = pole;
for (int i = 0; i < 4; ++i){
   cout<<"Prvok "<<i<<" je "<<*smernik<<endl;
   smernik++;
}

V tomto príklade je najskôr definovaný smerník na typ int. Tento typ je veľmi podstatný pretože pri smerníkových operáciách musí program poznať veľkosť prvku na ktorý smerník ukazuje. Potom do smerníka uložíme adresu prvého prvku poľa a. V cykle najskôr vypisujeme číslo uložené na adrese smerníka a potom ho zvyšujeme.

int *smernik;
smernik = &pole[0];
for (int i = 0; i < 4; ++i){
   cout<<"Prvok "<<i<<" je "<<*smernik<<endl;
   ++smernik;
}

Porovnávanie ukazovateľov

• operátory: < <= > >= == !=
• porovnávanie má zmysel len keď ukazovatele:
  • sú rovnakého typu
  • ukazujú do toho istého poľa
• výsledok porovnania: ak je podmienka splnená, tak 1 inak 0

for (int *smernik = pole; smernik < pole+4; ++smernik){
  cout<<"Prvok "<<i<<" je "<<*smernik<<endl;
}

New, delete

Pri programovaní si málokedy vystačíme s automatickými premennými. Pre prípady keď potrebujeme dynamicky vytvárať a rušiť premenné tu máme operátory new a delete. Alokovanie miesta pre 1 premennú

#include <iostream>

using namespace std;

int main(void){
    int * cislo = new int;
    *cislo = 50;
    cout<<*cislo<<endl;
    delete cislo;
}

Použitie operátora new je veľmi jednoduché. Stačí volať new názov typu a operátor new vráti smerník na alokovanú pamäť. V prípade neúspechu napríklad pre nedostatok pamäte vyvolá výnimku. Takto vytvorené premenné sa automaticky nerušia preto je potrebné po poslednom použití pamäť upratať operátorom delete.

Malloc, free

Funkcie malloc a free sú používané prevažne v čistých C programoch. Tieto funkcie majú na starosti iba alokáciu a dealokáciu zatiaľ čo operátory new a delete sa starajú aj o inicializáciu a deinicializáciu prvkov.

Príklad využitia new a delete

#include <iostream>
#include <fstream>
#include <cstdlib>
using namespace std;

struct kruh {
    int x, y, r;
};

const int maxN = 100;
const double pi = 3.1415926536;

int main(void) {
    /* zo suboru kruhy.txt chceme nacitat zoznam kruhov do pola */
    kruh * zoznam[maxN];
    int n = 0;

    /* otvorenie suboru */
    ifstream in;
    in.open("kruhy.txt");
    if (in.fail()) {
        cout << "Nenasiel som subor." << endl;
        exit(1);
    }

    /* citanie suboru */
    while (1) {
        /* vytvorime novy kruh */
        kruh * novy = new kruh;
        in >> novy->x;
        /* ak nenacital x, chceme skoncit, zrejme koniec suboru */
        if (in.fail()) {
            delete novy;
            break;
        }
        /* nacitame y a polomer */
        in >> novy->y >> novy->r;

        /* ulozime do zoznamu */
        zoznam[n] = novy;
        n++;
    }
    in.close();

    /* spracovavame zoznam kruhov, napr. spocitame sucet ich obsahov */
    double sucet = 0;
    for (int i = 0; i < n; i++) {
        sucet += zoznam[i]->r * zoznam[i]->r*pi;
    }
    cout << "Pocet kruhov:" << n << endl;
    cout << "Sucet obsahov kruhov: " << sucet << endl;

    /* na konci zmazeme kruhy */
    for (int i = 0; i < n; i++) {
        delete zoznam[i];
    }
}

Alokovanie miesta pre jednorozmerné pole

Veľmi podobným spôsobom je možné alokovať a dealokovať jednorozmerné pole. Operátor delete[] sa postará o upratanie každého prvku poľa.

int *cisla = new int[10];

// naplníme dátami
for (int i = 0; i < 10; i++)
{
	cisla[i] = i;
}

// vypíšeme
for (int i = 0; i < 10; i++)
{
	cout<<cisla[i]<<endl;
}
delete[] cisla;

Prednáška 12

Organizačné poznámky

• Budúci týždeň nebudú cvičenia a prednáška bude iba v stredu
• Termín domácej úlohy 6 do piatka 4.11.2011 22:00
• V piatok 4.11. bude zverejnené zadanie novej domácej úlohy
• Záverečná písomka bude po skončení semestra, v pondelok 19.12. o 10:00 v posluchárni B
• Na záverečnej písomke a na skúške môžete použiť ťahák v rozsahu jedného listu A4
• Viac v Pravidlách

Opakovanie smerníkov

Smerníky na jednoduché premenné:

int a = 7;         /* premenna typu int */
int *b = NULL;     /* smernik na premennu typu int */
b = &a;            /* b ukazuje na a */
*b = 8;            /* v premennej a je teraz 8 */
a = (*b)+1;        /* v premennej a je teraz 9 */

Smerníky na structy:

struct bod {
  int x,y;
};
bod *p;       /* smernik na structuru typu bod */
p = new bod;  /* alokovanie noveho bodu */
p->x = 10;    /* dve formy priradovania do sucasti structu */
(*p).y = 20;
delete p;     /* uvoľníme alokovanú pamäť */

Smerníky a polia, smerníková aritmetika:

int a[4];
int *b = a;  /* a,b su teraz takmer rovnocenne premenne */
*b = 3;
*(b+1) = 4;
b[2] = 5;
a[3] = 6; /* v poli sú teraz čísla 3,4,5,6 */

Vytvorenie poľa s danou veľkosťou

• Doteraz naše polia mali vždy vopred určenú veľkosť.
• Vieme však aj alokovať pole s n prvkami takto:

int *A;
A = new int[n];

• Odalokujeme ho potom pomocou delete[] A
• Nasledujúci program prečíta zo súboru číslo n a ďalších n celých čísel, ktoré uloží do poľa A veľkosti n
• V tomto poli potom nájde maximum.
  • Všimnite si, že do funkcie max posielame premennú A, ako keby bola pole

#include <iostream>
using namespace std;

int max(int n, int A[]) {
    int max = A[0];
    for (int i = 1; i < n; i++) {
        if (A[i] > max) {
            max = A[i];
        }
    }
    return max;
}

int main(void) {
    int n;
    int *A;
    cin >> n;
    A = new int[n];
    for (int i = 0; i < n; i++) {
        cin >> A[i];
    }
    cout << max(n, A) << endl;
    delete[] A;
}

Naša verzia vektora: rastúce pole

• Čo však ak vopred nevieme, koľko čísel bude v súbore, musíme jednoducho čítať až do konca?
• Môžeme použiť vector z C++, ktorý sa zväčšuje podľa potreby
• My si jednoduchšiu verziu vektora naprogramujeme.
  • Začneme s malým poľom (veľkosti 2)
  • Vždy keď sa pole zaplní, alokujeme nové pole dvojnásobnej veľkosti, prvky do neho skopírujeme a staré pole odalokujeme
  • Presúvanie prvkov dlho trvá, preto pole vždy zdvojnásobíme, aby sme nemuseli presúvať často
• Celý program s niekoľkými pomocnými funkciami na prístup k poľu s kontrolou hraníc je nižšie. Program načíta desatinné čísla v súbore a spočíta ich priemer.

#include <iostream>
#include <cassert>
using namespace std;

struct vektor {
    double *a; /* pole prvkov typu double */
    int velkost; /* velkost alokovaneho pola */
    int pocet;  /* pocet prvkov pridanych do pola */
};

double vytvorVektor(vektor &a) {
    /* inicializuj vektor s kratkym polom */
    a.velkost = 2;
    a.a = new double[a.velkost];
    a.pocet = 0;
}

void pridajPrvok(vektor &a, double x) {
    /* na koniec pola pridaj prvok x, zvacsi pole ak treba */

    if (a.pocet == a.velkost) {
        /* treba zvacsovat */
        double *nove = new double[a.velkost * 2];
        /* prekopirujeme zo stareho do noveho */
        for (int i = 0; i < a.pocet; i++) {
            nove[i] = a.a[i];
        }
        /* zmazeme stare */
        delete [] a.a;
        /* upravume premenne */
        a.a = nove;
        a.velkost *= 2;
    }
    /* teraz uz je pole dost velke, staci ulozit x */
    a.a[a.pocet] = x;
    a.pocet++;
}

double dajPrvok(vektor &a, int i) {
    /* vrat prvok v poli na pozicii i (s kontrolou i) */
    assert(i >= 0 && i < a.pocet);
    return a.a[i];
}

void ulozPrvok(vektor &a, int i, double x) {
    /* na poziciu i uloz hodnotu x (s kontrolou i) */
    assert(i >= 0 && i < a.pocet);
    a.a[i] = x;
}

void zmazVektor(vektor &a) {
    delete[] a.a;
}

int main(void) {
    vektor a;
    vytvorVektor(a);

    while (true) {
        double x;
        cin >> x;
        if (cin.fail()) break;
        pridajPrvok(a, x);
    }

    double sum = 0;
    for (int i = 0; i < a.pocet; i++) {
        sum += dajPrvok(a, i);
    }
    cout << sum / a.pocet << endl;

    zmazVektor(a);
}

Dvojrozmerné polia

• Doteraz sme stále pracovali s jednorozmerným poľom, čo však ak potrebujeme dvojrozmerné pole, maticu?
• Spravme teraz maticu s n=10 riadkami a m=20 stĺpcami
• Spravíme si pole n jednorozmerných polí, t.j. pole smerníkov na int: int *a[n];
• Naalokujeme si n jednorozmerných polí veľkosti m a smerník na každé uložíme do jedného prvku poľa a

const int n = 10;
const int m = 20;
int *a[n];
for (int i = 0; i < n; i++) {
    a[i] = new int[m];
}

Prvok v i-tom riadku a j-tom stĺpci dostaneme jedným z týchto spôsobov:

• a[i][j]
• *(*(a+i)+j)

Tu je kód, ktorý vynuluje pole:

for (int i = 0; i < n; i++) {
   for (int j = 0; j < m; j++) {
       a[i][j] = 0;
   }
}

Na konci sa patrí pamäť uvoľniť:

for (int i = 0; i < n; i++) {
    delete[] a[i];
}

Dynamicky alokovaná matica

Ak chceme n a m určiť dynamicky, napr. načítať ich zo súboru, musíme aj pole a alokovať pomocou new a nakoniec uvoľniť pomocou delete[]:

#include <iostream>
using namespace std;

int main(void) {
    int n, m;
    cin >> n >> m;
    int **a;
    a = new int *[n];
    for (int i = 0; i < n; i++) {
        a[i] = new int[m];
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            a[i][j] = 0;
        }
    }

    for (int i = 0; i < n; i++) {
        delete[] a[i];
    }
    delete[] a;
}

Funkcie pre alokáciu matice

Na alokáciu a dealokáciu matice si napíšeme funkcie, môžu sa nám hodiť:

int ** vytvorMaticu(int n, int m) {
    /* vytvor maticu s n riadkami a m stlpcami */
    int **a;
    a = new int *[n];
    for (int i = 0; i < n; i++) {
        a[i] = new int[m];
    }
    return a;
}

void zmazMaticu(int n, int m, int **a) {
    /* uvolni pamat matice s n riadkami a m stlpcami */
    for (int i = 0; i < n; i++) {
        delete[] a[i];
    }
    delete[] a;
}

void nacitajMaticu(istream &in, int n, int m, int **a) {
    /* matica je vytvorena, velkosti n, m, vyplnime ju cislami zo vstupu */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            in >> a[i][j];
        }
    }
}

Všimnite si, že všetkým funkciám dávame aj rozmery matice. Namiesto toho by sme si mohli spraviť štruktúru podobne ako pri vektore:

struct matica {
  int n, m;
  int **a;
}

Výšková mapa

V matici môžeme mať danú napr. mapu:

• 0 znamené more
• kladné číslo znamené pevninu a udáva nadmorskú výšku (napr. v metroch)

Táto reprezentácia neumožňuje zapísať pevninu pod úrovňou mora.

Pomocou funkcií vyššie môžeme takúto mapu načítať zo súboru a môžeme spraviť napr. program, ktorý zobrazí more modrou a pevninou odtieňami zelenej a hnedej podľa nadmorskej výšky. Príklad matice a obrázku:

22 11
 0 0 0 0 0 0 0 0 0 0 0
 0 20 40 60 80 100 120 140 120 0 0
 0 40 80 120 160 200 240 280 190 100 0
 0 60 120 180 240 300 360 420 260 100 0
 0 80 160 240 320 400 480 560 260 100 0
 0 100 200 300 400 500 600 700 330 100 0
 0 120 240 360 480 600 720 840 400 100 0
 0 140 280 420 560 700 840 980 470 100 0
 0 160 320 480 640 800 960 700 200 0 0
 0 180 360 540 720 900 700 500 0 0 0
 0 200 400 600 800 1000 1200 1400 680 100 0
 0 220 440 660 880 1100 1320 1540 750 100 0
 0 240 480 720 960 1200 1440 1680 820 100 0
 0 260 520 780 1040 1300 1560 1820 1200 400 0
 0 280 560 840 1120 1400 1680 1960 1500 600 0
 0 240 480 720 960 1200 1440 1680 1000 400 0
 0 200 400 600 800 1000 1200 1400 680 100 0
 0 160 320 480 640 800 960 1120 540 100 0
 0 120 240 360 480 600 720 840 400 100 0
 0 80 160 240 320 400 480 560 260 100 0
 0 40 80 120 160 200 240 280 120 0 0
 0 0 0 0 0 0 0 0 0 0 0

Okrem zobrazovania môžeme chcieť napríklad nájsť polohu najvyššieho vrchu a zobraziť ho v čiernom rámčeku, ako na obrázku vyššie.

• Čo spraví funkcia, ak je celá mapa pokrytá morom?

void najvyssiVrch(int n, int m, int **a, int &riadok, int &stlpec) {
    /* najdi polohu najvyssej hodnoty v matici */
    riadok = 0;
    stlpec = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if(a[i][j]>a[riadok][stlpec]) {
                riadok = i;
                stlpec = j;
            }
        }
    }
}

Príklad hlavného programu, ktorý hľadá najvyšší vrch.

int main(void) {
    /* nacitaj rozmery matice */
    int n, m;
    cin >> n >> m;

    /* vytvor a nacitaj maticu */
    int **a = vytvorMaticu(n, m);
    nacitajMaticu(cin, n, m, a);

    /* najdi najvyssi vrch */
    int riadok, stlpec;
    najvyssiVrch(n, m, a, riadok, stlpec);

    /* uvolni pamat matice */
    zmazMaticu(n, m, a);
}

Zdrojový kód celého programu

• Tento program načíta maticu, nájde najvyšší vrch a vykreslí obrázok: #Program mapa pre prednášku 12

Hra life

Hra life je jednoduchá simulácia kolónie buniek, ktorá má zaujímavé teoretické vlastnosti.

• Máme mriežku m x n štvorčekov, v každom žije najviac 1 bunka
• Bunky sa rodia a umierajú podľa toho, koľko majú susedov v ôsmych okolitých políčkach
  • Ak v čase t má bunka 2 alebo 3 susedov, zostane žiť aj v čase t+1, inak zomiera
  • Ak v čase t má prázden políčko presne 3 susedov, narodí sa tam v čase t+1 nová bunka

Stav hry si môžeme pamätať v matici boolovských hodnôt.

Rátanie zmeny v matici

• Stav v čase t máme v matici a, do matice b chceme dať stav v čase t+1

int zratajOkolie(int n, int m, bool **a, int riadok, int stlpec) {
    /* pocet zivych prvkov v okoli */
    int sucet = 0;
    for (int i = riadok - 1; i <= riadok + 1; i++) {
        for (int j = stlpec - 1; j <= stlpec + 1; j++) {
            /* treba osetrit okraje matice */
            if (i >= 0 && i < n && j >= 0 && j < m && a[i][j]) {
                sucet++;
            }
        }
    }
    /* samotny stvorcek nechceme zaratat */
    if (a[riadok][stlpec]) {
        sucet--;
    }
    return sucet;
}

void prepocitajMaticu(int n, int m, bool **a, bool **b) {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            int pocet = zratajOkolie(n, m, a, i, j);
            /* prirad do b[i][j] hodnotu podla okolia a[i][j] */
            b[i][j] = (pocet == 3 || (pocet == 2 && a[i][j]));
        }
    }
}

Hlavný program

• Prepočítavanie chceme opakovať v cykle pre viacero časových intervalov
• Môžeme prekopírovať celú maticu z b späť do a, ale rýchlejšie je len vymeniť smerníky

    for (int i = 0; i < 10; i++) {
        /* podla a spocitaj maticu do b */
        prepocitajMaticu(n, m, a, b);
        /* vymen smerniky, aby v a bola nova matica */
        bool **tmp = b;
        b = a;
        a = tmp;
    }

• vytvorMaticu, zmazMaticu a pod. prepíšeme tak, aby robili s maticou boolovských hodnôt namiesto intov

int main(void) {
    /* nacitaj rozmery matice */
    int n, m;
    cin >> n >> m;

    /* vytvor a nacitaj maticu */
    bool **a = vytvorMaticu(n, m);
    nacitajMaticu(cin, n, m, a);

    /* zobraz maticu */
    SimpleDraw window(m*stvorcek, n * stvorcek);
    zobrazMaticu(n, m, a, window);
    window.wait(2);

    /* pomocna matica na vypocty */
    bool **b = vytvorMaticu(n, m);

    /* simuluj 10 krokov hry life */
    for (int i = 0; i < 10; i++) {
        /* podla a spocitaj maticu do b */
        prepocitajMaticu(n, m, a, b);
        /* prekresli, co sa zmenilo */
        zobrazZmeny(n, m, a, b, window);
        window.wait(2);
        /* vymen smerniky, aby v a bola nova matica */
        bool **tmp = b;
        b = a;
        a = tmp;
    }

    /* uvolni pamat matic */
    zmazMaticu(n, m, a);
    zmazMaticu(n, m, b);
}

Detaily vykresľovania

• Na začiatku vykreslíme celú maticu, potom prekreslíme vždy len tie bunky, ktoré sa zmenili

void zobrazStvorcek(int i, int j, bool hodnota, SimpleDraw &window) {
    /* zobraz stvorcek v riadku i a stlpci j */
    window.setPenColor("white");
    if (hodnota) {
        window.setBrushColor("black");
    } else {
        window.setBrushColor("white");
    }
    window.drawRectangle(j*stvorcek, i*stvorcek, stvorcek, stvorcek);
}

void zobrazMaticu(int n, int m, bool **a, SimpleDraw &window) {
    /* zobraz prvky true ciernymi stvorcekmi */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            /* nastavenie farby podla hodnoty */
            if (a[i][j]) {
                zobrazStvorcek(i, j, true, window);
            }
        }
    }
}

void zobrazZmeny(int n, int m, bool **a, bool **b, SimpleDraw &window) {
    /* zobraz nove stvorceky na miestach, kde bola zmena */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (a[i][j] != b[i][j]) zobrazStvorcek(i, j, b[i][j], window);
        }
    }
}

Príklad vstupu

• Pre jednoduchosť vstup uvádzame ako nuly a jendnotky bez medzier (1=živá bunka)

20 20
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000111111111100000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000
00000000000000000000

Zdrojový kód celého programu

• Tento program načíta vstup a simuluje 10 krokov hry Life: #Program life pre prednášku 12

Načítanie reťazcov

Dvojrozmerné polia v C/C++ nemusia mať všetky riadky rovnako dlhé.

• Spomeňte si, že v C je reťazec jednoducho pole char-ov kde za posledným znakom ide špeciálny znak 0
• Pole reťazcov bude teda dvojrozmerné pole char-ov
• Môžeme načítavať napr. súbor po riadkoch, pričom každý riadok načítame do dlhého poľa, ktoré by malo stačiť a potom do prekopírujeme do akurát veľkého riadku v poli
• Na koniec program riadky vypíše odzadu
• Ak by sme vopred alokovali maxN riadkov, každý veľkosti maxRiadok, vyšlo by potenciálne na zmar oveľa viac pamäte.

#include <iostream>
#include <cstring>
using namespace std;

const int maxRiadok = 1000;
const int maxN = 1000;

int main(void) {
    char *a[maxN];
    char riadok[maxRiadok];
    int n = 0;
    while (true) {
        cin.getline(riadok, maxRiadok);
        if (cin.fail()) break;
        a[n] = new char[strlen(riadok)+1];
        strcpy(a[n], riadok);
        n++;
    }

    for(int i=n-1; i>=0; i--) {
        cout << a[i] << endl;
    }
}

Vstupy do funkcie main

• Netbeans vám vyrobí main funkciu s nasledujúcou hlavičkou:

int main(int argc, char** argv) {

• char **argv je pole C-čkových reťazcov a argc je počet reťazcov v tomto poli
• Prvý z nich, argv[0], je meno samotného programu a ostatné sú argumenty programu
• Užitočné, ak spúšťame program z príkazového riadku
• Dá sa nastaviť v Netbeans, Properties, Run
• Tento program jednoducho argumenty vypíše

#include <iostream>
using namespace std;

int main(int argc, char** argv) {
    for (int i = 0; i < argc; i++) {
        cout << argv[i] << endl;
    }
}

Smerníkové kuriozity

    int *a[3];                /* pole 3 smerníkov na int */
    int (*b)[3];              /* jeden smerník na pole troch intov, neinicializovaný */
    int c[3] = {0,1,2};       /* pole troch intov */
    b = &c;                   /* teraz b ukazuje na pole c */
    cout << (*b)[2] << endl;  /* pristup k prvku 2 pola c */
    cout << *b[2] << endl;    /* zle: tvarime sa, ze b je pole, pristupime k jeho prvku 2 a interpretujeme ho ako smernik */

Pre aké typy by dávali zmysel nasledujúce výrazy?

• (*p).x je to isté ako p->x
• *p.x je to isté ako *(p.x)

Zhrnutie

• 1D pole: int *a = new int[n]; cout << a[0];
• 2D pole: int **a = new int * [n]; for(int i=0; i<n; i++) a[i] = new int[m]; cout a[0][1];
  • Riadky 2D poľa nemusia byť rovnako dlhé
• 3D pole: int ***a = new int ** [n]; ...

Program mapa pre prednášku 12

#include "../SimpleDraw.h"
#include <iostream>
#include <iomanip>
using namespace std;

/* velkost stvorceka mapy v pixeloch */
const int stvorcek = 15;

int ** vytvorMaticu(int n, int m) {
    /* vytvor maticu s n riadkami a m stlpcami */
    int **a;
    a = new int *[n];
    for (int i = 0; i < n; i++) {
        a[i] = new int[m];
    }
    return a;
}

void zmazMaticu(int n, int m, int **a) {
    /* uvolni pamat matice s n riadkami a m stlpcami */
    for (int i = 0; i < n; i++) {
        delete[] a[i];
    }
    delete[] a;
}

void nacitajMaticu(istream &in, int n, int m, int **a) {
    /* matica je vytvorena, velkosti n, m, vyplnime ju cislami zo vstupu */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            in >> a[i][j];
        }
    }
}

void farba(SimpleDraw &window, int r, int g, int b) {
    /* nastav farbu ciary aj vyplne na dane hodnoty */
    window.setBrushColor(r, g, b);
    window.setPenColor(r, g, b);
}

void zobrazMaticu(int n, int m, int **a, SimpleDraw &window) {
    /* zobraz maticu farebnymi stvorcekmi :
     * modra: more (hodnota 0)
     * zelena: niziny 1..200,
     * hneda: pohoria 200..2000 */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            /* nastavenie farby podla hodnoty */
            if (a[i][j] == 0) {
                farba(window, 0, 0, 255);
            } else if (a[i][j] <= 200) {
                double x = a[i][j] / 200.0;
                farba(window, x * 255, 127 + x * 127, 0);
            } else {
                double x = (a[i][j] - 200) / 2000.0;
                farba(window, 255 - x * 150, 255 - x * 200, 0);
            }
            /* vykresleni stvorceka, pozor: vymena suradnic */
            window.drawRectangle(j*stvorcek, i*stvorcek, stvorcek, stvorcek);
        }
    }
}

void najvyssiVrch(int n, int m, int **a, int &riadok, int &stlpec) {
    /* najdi polohu najvyssej hodnoty v matici */
    riadok = 0;
    stlpec = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if(a[i][j]>a[riadok][stlpec]) {
                riadok = i;
                stlpec = j;
            }
        }
    }
}

int main(void) {
    /* nacitaj rozmery matice */
    int n, m;
    cin >> n >> m;

    /* vytvor a nacitaj maticu */
    int **a = vytvorMaticu(n, m);
    nacitajMaticu(cin, n, m, a);

    /* zobraz maticu */
    SimpleDraw window(m*stvorcek, n * stvorcek);
    zobrazMaticu(n, m, a, window);

    /* najdi najvyssi vrch a zobraz ho stvorcekom */
    int riadok, stlpec;
    najvyssiVrch(n, m, a, riadok, stlpec);
    window.unsetBrush();
    window.setPenColor("black");
    window.drawRectangle(stlpec*stvorcek, riadok*stvorcek, stvorcek, stvorcek);

    /* zobraz okno */
    window.showAndClose();

    /* uvolni pamat matice */
    zmazMaticu(n, m, a);
}

Program life pre prednášku 12

#include "../SimpleDraw.h"
#include <iostream>
#include <string>
#include <cassert>
using namespace std;

/* velkost stvorceka */
const int stvorcek = 15;

bool ** vytvorMaticu(int n, int m) {
    /* vytvor maticu s n riadkami a m stlpcami */
    bool **a;
    a = new bool *[n];
    for (int i = 0; i < n; i++) {
        a[i] = new bool[m];
    }
    return a;
}

void zmazMaticu(int n, int m, bool **a) {
    /* uvolni pamat matice s n riadkami a m stlpcami */
    for (int i = 0; i < n; i++) {
        delete[] a[i];
    }
    delete[] a;
}

void nacitajMaticu(istream &in, int n, int m, bool **a) {
    /* matica je vytvorena, velkosti n, m, vyplnime ju cislami zo vstupu */
    for (int i = 0; i < n; i++) {
        string riadok;
        in >> riadok;
        assert(riadok.length() == m);
        for (int j = 0; j < m; j++) {
            a[i][j] = (riadok[j] == '1');
        }
    }
}

void zobrazStvorcek(int i, int j, bool hodnota, SimpleDraw &window) {
    /* zobraz stvorcek v riadku i a stlpci j */
    window.setPenColor("white");
    if (hodnota) {
        window.setBrushColor("black");
    } else {
        window.setBrushColor("white");
    }
    window.drawRectangle(j*stvorcek, i*stvorcek, stvorcek, stvorcek);
}

void zobrazMaticu(int n, int m, bool **a, SimpleDraw &window) {
    /* zobraz prvky true ciernymi stvorcekmi */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            /* nastavenie farby podla hodnoty */
            if (a[i][j]) {
                zobrazStvorcek(i, j, true, window);
            }
        }
    }
}

int zratajOkolie(int n, int m, bool **a, int riadok, int stlpec) {
    /* pocet zivych prvkov v okoli */
    int sucet = 0;
    for (int i = riadok - 1; i <= riadok + 1; i++) {
        for (int j = stlpec - 1; j <= stlpec + 1; j++) {
            /* treba osetrit okraje matice */
            if (i >= 0 && i < n && j >= 0 && j < m && a[i][j]) {
                sucet++;
            }
        }
    }
    /* samotny stvorcek nechceme zarat */
    if (a[riadok][stlpec]) {
        sucet--;
    }
    return sucet;
}

void prepocitajMaticu(int n, int m, bool **a, bool **b) {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            int pocet = zratajOkolie(n, m, a, i, j);
            /* prirad do b[i][j] hodnotu podla okolia a[i][j]
             * ak dva susedia, preziva,
             * ak traja susedia, preziva alebo rodi sa
             * ak menej ako 2 alebo viac ako 3, nebude nic */
            b[i][j] = (pocet == 3 || (pocet == 2 && a[i][j]));
        }
    }
}

void zobrazZmeny(int n, int m, bool **a, bool **b, SimpleDraw &window) {
    /* zobraz nove stvorceky na miestach, kde bola zmena */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (a[i][j] != b[i][j]) zobrazStvorcek(i, j, b[i][j], window);
        }
    }
}

int main(void) {
    /* nacitaj rozmery matice */
    int n, m;
    cin >> n >> m;

    /* vytvor a nacitaj maticu */
    bool **a = vytvorMaticu(n, m);
    nacitajMaticu(cin, n, m, a);

    /* zobraz maticu */
    SimpleDraw window(m*stvorcek, n * stvorcek);
    zobrazMaticu(n, m, a, window);
    window.wait(2);

    /* pomocna matica na vypocty */
    bool **b = vytvorMaticu(n, m);

    /* simuluj 10 krokov hry life */
    for (int i = 0; i < 10; i++) {
        /* podla a spocitaj maticu do b */
        prepocitajMaticu(n, m, a, b);
        /* prekresli, co sa zmenilo */
        zobrazZmeny(n, m, a, b, window);
        window.wait(2);
        /* vymen smerniky, aby v a bola nova matica */
        bool **tmp = b;
        b = a;
        a = tmp;
    }

    /* uvolni pamat matic */
    zmazMaticu(n, m, a);
    zmazMaticu(n, m, b);
}

Cvičenia 6

Vstup

• Napíšte program, ktorý načíta desatinné čísla zo súboru a vypíše ich priemer. Spravte túto úlohu pre tri formáty súboru (všetky tri formáty obsahujú čísla oddelené medzerami alebo koncami riadkov):
  • Súbor začína číslom N, ktoré určuje počet čísel, za ním idú samotné čísla, z ktorých rátame priemer. Napr pre vstup 3 1 2 12 bude priemer 15/3=5.
  • Súbor obsahuje kladné čísla, z ktorých rátame priemer a za posledným je číslo nula. Nulu do priemeru nerátame. Napr. pre vstup 1 2 12 0 bude priemer 15/3=5.
  • Súbor obsahuje iba čísla, z ktorých rátame priemer, načítavať treba po koniec súboru. Napr. pre vstup 1 2 12 bude priemer 15/3=5. Na detekciu konca súboru využite napr. funkciu fscanf s kontrolou správneho načítania.
• Napíšte program, ktorý vypíše súbor VSTUP.TXT na obrazovku tak, že všetky riadky dlhšie ako 80 znakov ureže na 80-tom stĺpci

Výstup

• Do súboru vypíšte tabuľku hodnôt funkcie sin(x) pre x od -1 po 1 s krokom 0.2, pričom ich bude vypisovať na 5 desatinných miest a x aj sin(x) budú zarovnané doprava:

-1.0 -0.84147
-0.8 -0.71736
-0.6 -0.56464
-0.4 -0.38942
-0.2 -0.19867
-0.0 -0.00000
 0.2  0.19867
 0.4  0.38942
 0.6  0.56464
 0.8  0.71736
 1.0  0.84147

Štatistika

• Stiahnite si textový súbor [2], ktorý obsahuje frekvenciu, s akou užívatelia vyhľadávali výraz ice cream v Googli v jednotlivých týždňoch rokov 2004 až 2010. Každý riadok obsahuje údaje o jednom týždni: prvé tri slová sú dátum, štvrté relatívna frekvencia.
• Načítajte tento súbor do poľa záznamov so štruktúrou

struct tyzden {
  string mesiac;
  int den;
  int rok;
  double frekvencia;
};

• Vypíšte na konzolu, v ktorom týždni bola frekvencia vyhľadávania najvyššia.
• Pre každý rok od 2004 po 2010 spočítajte súčet frekvencií a vypíšte na konzolu v prehľadnom tvare, na dve desatinné miesta:

2004 63.14
2005 62.14
...
2010 72.02

Šifrovanie permutačnou šifrou

• Napíšte funkciu, ktorá zašifruje vstupný súbor tak, že v každom bloku dĺžky n povymieňa polohu znakov podľa zadaného kľúča. Kľúč je pole A dĺžky n, kde A[i] uvádza, ktoré písmeno z pôvodného bloku má ísť na i-te miesto v zašifrovanom bloku. Napr. pre n=4 a A={3,2,0,1} dostaneme pre blok "ABCD" výsledok "DCAB", lebo na pozíciu 0 vo výsledku sme dali písmeno na pozícii A[0] = 3, t.j. D, atď. Ak v poslednom bloku nemáme dosť písmen, doplníme ich medzerami. Hlavička funkcie: void encryptPermutation(FILE *f, int n, int A[]);

• Pre dešifrovanie môžeme použiť tú istú funkciu, akurát kľúč musíme zmeniť z pôvodnej permutácie A na novú permutáciu B tak, že B[A[i]]=i pre každé i. Napr. pre príklad vyššie to bude B={2,3,1,0}

• Vyskúšajte touto šifrou zašifrovať a potom spätne odšifrovať krátky text.

DÚ6

max. 5 bodov plus 2 body bonus, termín odovzdania piatok 4.11.2011 o 22:00

Cieľom tejto domácej úlohy je precvičiť si prácu so súbormi.

Váš program na vstupe načíta zo súboru telefónny zoznam a vypíše ho v prehľadnejšom tvare do iného súboru. Podrobne si prečítajte celé zadanie a dodržte všetky pokyny.

Popis vstupného súboru

• Súbor pozostáva zo slov oddelených medzerami, pričom pod slovom rozumieme postupnosť nebielych znakov ohraničenú bielymi znakmi, prípadne začiatkom a koncom súboru. Medzi dvoma slovami môže byť aj viac ako jeden biely znak. Na začiatku a konci súboru môžu a nemusia byť biele znaky.
• V súbore sú údaje o niekoľkých osobách a ich telefónnych číslach, pričom záznam o jednej osobe začína jedným alebo viacerými slovami tvoriacimi meno a za nimi ide jedno alebo viacero slov tvoriacich číslo. Slová tvoriace meno rozpoznáme podľa toho, že obsahujú aspoň jedno písmeno anglickej abecedy (malé alebo veľké, bez diakritiky). Naopak slová tvoriace telefónne čísla neobsahujú žiadne písmená.

Popis výstupného súboru

• Záznam o každej osobe je na zvláštnom riadku, pričom jednotlivé slová v mene aj v čísle sú oddelené práve jednou medzerou.
• Medzi koncom mena a začiatkom čísla je tiež práve jedna medzera.
• Mená zarovnajte doprava tak, aby najdlhšie meno v súbore začínalo na začiatku riadku a pred kratšie mená vložte na začiatok riadku medzery tak, aby všetky mená končili v tom istom stĺpci.
• Záznamy vo výstupnom súbore budú v rovnakom poradí ako na vstupe.

Príklad vstupu a výstupu

Janko
  Hrasko 02
/ 12 34 56 78 Jozko F. Mrkvicka
+421(911)999    888

     Janko Hrasko 02 / 12 34 56 78
Jozko F. Mrkvicka +421(911)999 888

Ďalšie pokyny

• Ako názov vstupného súboru zadajte zoznam.txt a výstupného súboru prehlad.txt. Pri otváraní súborov zadajte iba meno bez cesty, súbor sa vám podľa nastavení Netbeans vytvorí buď v domovskom adresári alebo v adresári s projektom.
• Pri načítavaní súboru kontrolujte, či:
  • súbor obsahuje najviac 100 záznamov
  • súbor nezačína telefónnym číslom (prvé musí ísť vždy meno)
  • súbor nekončí menom (za každým menom musí nasledovať číslo)

Ak niektorá z týchto podmienok nie je splnená, vypíšte na konzolu vhodnú chybovú hlášku a ukončite program príkazom exit(1) z knižnice cstdlib, prípadne príkazom return 1, ak ste vo funkcii main.

• Dbajte na čitateľnosť programu, rozdeľte ho na vhodne definované funkcie.

Dobré rady (ktoré nie je nutné dodržať, ak si myslíte, že to viete spraviť lepšie)

• Pri načítavaní ukladajte údaje do poľa struct-ov, napr.

struct osoba {
    string meno;
    string telefon;
};

• Ak zoznam je pole typu osoba, tak dĺžku mena i-tej osoby zistíme príkazom zoznam[i].meno.length()
• Na načítavanie použite operátor ifstream >> do premennej typu string. Tento operátor sa už postará o rozdelenie súboru na slová.
• Dajte pozor na správnu detekciu konca súboru. Pre ifstream f vráti f.eof() true, iba ak pri predchádzajúcom načítaní program narazil na koniec súboru. Vyskúšajte teda, či Váš program funguje aj v prípade, že súbor končí bielym znakom, aj v prípade, že končí napr. nejakým číslom.
• To, či je znak písmeno, môžete overiť funkciou isalpha z knižnice cctype.

Bonusová úloha

• V telefónnom zozname nájdite záznamy s tým istým menom (meno je také isté, ak sa skladá z tých istých slov v tom istom poradí). Každú takúto skupinu čísel pre rovnaké meno vypíšte na jednom riadku, pričom najprv ide meno zarovnané doprava a potom jednotlivé čísla oddelené čiarkou a medzerou.
• Tieto dáta vypíšte do súboru skupiny.txt
• Nemusíte dbať na rýchlosť, môžete porovnávať každé meno s každým.
• Poradie záznamov nemusíte zachovať.
• Bonusovú a hlavnú časť úlohy odovzdajte v tom istom programe, ktorý bude vypisovať obidva súbory.

Príklad

Janko M. 02/12 34 56 78
Misko 02/23 45 67 89
Janko 
M.  0949/123 456

Janko M. 02/12 34 56 78, 0949/123 456
   Misko 02/23 45 67 89

Prednáška 13

Problém slovníka

Do dátovej štruktúry slovník si ukladáme záznamy, kde každý záznam x obsahuje navyše položku key(x) – kľúč jedinečný pre tento záznam.

Dátová štruktúra D je slovník, ak podporuje nasledujúce operácie:

• Insert(D,(x,key(x))) do dátovej štruktúry D vloží záznam x so svojím kľúčom (ak v nej ešte nie je záznam s daným kľúčom),
• Find (D, k) vráti miesto, kde sa nachádza záznam x s kľúčom k, alebo špeciálnu hodnotu (NULL alebo -1 v závislosti od implementácie) ak sa taký záznam v D nenachádza
• Delete (D, k) vymaže záznam s kľúčom k z D

Hoci hlavným cieľom vyhľadávania je nájsť dáta prislúchajúce danému kľúču, väčšinou sa všetky dáta okrem kľúča zanedbávajú. Cieľom je ukázať spôsoby hľadania kľúča a pevne veríme, že ak nájdeme kľúč, podarí sa nám nájsť aj prislúchajúce dáta. V programoch budeme používať záznamy, kde nás vlastne nebudú zaujímať konkrétne hodnoty dát (na ukážku si môžeme dať dáta ako integer).

struct zaznam {
int key;
int data;
}

Príklady:

• Mená a rodné čísla
• Telefónnny zoznam (mená a telefónne čísla)
• Mapovanie host name na IP adresy

Implementácia slovníka pomocou poľa

Asi najjednoduchšia implementácia je pomocou poľa: Majme pole n záznamov A dĺžky MAX.

zaznam A[MAX];
n=0;

Vkladanie

Nový prvok vložíme jednoducho na koniec:

bool insert(zaznam z) {
    if (n == MAX) return false;
    else {
        A[n++] = z;
        return true;
    }
}

V prípade, že n=MAX, nastane pretečenie.

• Jedna možnosť, ako to riešiť, je zvoliť MAX dostatočne veľké a uistiť sa, že pretečeniene nenastane (v takom prípade stačí A[n++]=z ).
• Druhou možnosťou je pri pretečení pole realokovať: alokuje me nové pole dvojnásobnej dĺžky (MAX = 2*MAX), staré pole tam pre kopírujeme a uvoľníme jeho pamäť. V prípade, že počet prvkov klesne pod štvrtinu (n < MAX/4), môže me pole realokovať späť na polovičnú veľkosť. Kvôli tomu však musíme upraviť definíciu poľa, v ktorom slovník ukladáme. Vytvoríme si preň vlastnú štruktúru, ktorá bude obsahovať aktuálnu veľkosť, maximálnu veľkosť a samotné pole (dynamické).

struct slovnik {
 int n;
 int MAX;
 zaznam *A;
}

void vytvorSlovnik(slovnik &A){
 A.n=0;
 A.MAX=2;
 A.A=new zaznam[A.MAX];
}

void zvacsiSlovnik(slovnik &A){        
 zaznam *nove = new zaznam[A.MAX * 2];
 /* prekopirujeme zo stareho do noveho */
 for (int i = 0; i < A.n; i++) {
    nove[i] = A.A[i];
 }
 /* zmazeme stare */
 delete [] A.A;
 /* upravume premenne */
 A.A = nove;
 A.MAX *= 2;
}

void zmensiSlovnik(slovnik &A){        
 zaznam *nove = new zaznam[A.MAX/2];
 /* prekopirujeme zo stareho do noveho */
 for (int i = 0; i < A.n; i++) {
    nove[i] = A.A[i];
 }
 /* zmazeme stare */
 delete [] A.A;
 /* upravume premenne */
 A.A = nove;
 A.MAX /= 2;
}

void zmazSlovnik(slovnik &A) {
    delete[] A.A;
}


void insert(zaznam z, slovnik &A){
 if (A.n==A.MAX) zvacsiSlovnik(A);
 A.A[A.n++]=z;
}

int main(void){
 slovnik A;
 vytvorSlovnik(A);

 zaznam z;
 z.key=1; z.data=12345;
 insert(z,A);

 zmazSlovnik(A);
}

Vymazávanie

Vymazávanie je tiež jednoduché, daný prvok nahradíme prvkom na konci:

bool remove(int k, zaznam &z) {
    int i = find(k);
    if (i < 0) return false;
    z = A[i];
    A[i] = A[--n];
    return true;
}

Vyhľadávanie

Pri vyhľadávaní nám neostáva nič iné ako prezerať postupne všetky záznamy, kým daný kľúč nenájdeme, alebo nedôjdeme na koniec poľa (v tom prípade vieme, že záznam s daným kľúčom sa v poli nenachádza):

int find(int k){
    for (int i=0; i<n; i++){
        if (A[i].key==k){
            return i;
        }
    }
    return -1;
}

Implementácia slovníka pomocou utriedeného poľa

Ak potrebujeme rýchlo vyhľadávať, lepšia možnosť je udržiavať pole utriedené. Rýchle vyhľadávanie však bude na úkor väčšej zložitosti ostatných operácií.

Vkladanie

bool insert(zaznam z) {
    int i = 0;
    if (n==MAX) return false;
    while ((A[i].key < z.key) && (i < n)){ 
        i++;
    }    
    n++;
    for (int j = n - 1; j > i; j--){
        A[j] = A[j - 1];
    }    
    A[i] = z;
    return true;
}

Pri vkladaní musíme novému záznamu „spraviť miesto" – nájdeme miesto, kam nový záznam vložiť (while-cyklus) a počnúc daným miestom posunieme všetky záznamy o 1 doprava (FOR-cyklus).

Vymazávanie

Pri vymazávaní posunieme všetky prvky počnúc (i+1)-vým doľava.

bool remove(int k, zaznam &z){
    int i=find(k);
    if (i<0) {return false;}
    z=A[i];
    n--;
    for (int j=i; j<n; j++){
        A[j]=A[j+1];
    }    
    return true;
}

Vyhľadávanie

Zjavne pri utriedenom poli máme komplikovanejšie (a časovo zložitejšie) vkladanie a vymazávanie. Vieme však rýchlejšie výhľadávať. Binárne vyhľadávanie sme už mali na prednáške 7.

Pripomenieme myšlienku: začíname hľadať v intervale <l,r> a pozrieme sa na stredný prvok A[m], kde m = (l+ r )/2.

• ak A[m] = k , našli sme hľadaný záznam a sme hotoví.
• ak k < A[m], potom zjavne hľadaný kľúč patrí do prvej polovice intervalu <l,r>, t.j. do intervalu <l,m-1>.
• ak A[m] < k , zjavne patrí do druhej polovice intervalu <l,r>, t.j. do intervalu <m+1,r>.

Takto sa nám každým krokom zmenší hľadaný interval na polovicu

int find(int k) {
    int left = 0, right = n - 1, index;
    while (left <= right) {
        index = (left + right) / 2;
        if (A[index].key = k) {
            return index;
        } else if (A[index].key < k) {
            left = index + 1;
        } else {
            right = index - 1;
        }
    }
    return -1;
}

Hashovacie tabuľky

Hashovanie je metóda vyhľadávania, ktorá je založená na trochu inom princípe ako predchádzajúce možnosti. Tabuľka, do ktorej budeme ukladať záznamy, je výrazne väčšia, ako očakávaný počet záznamov. Do tabuľky budeme pristupovať pomocou funkcie, ktorá vypočíta, kam uložíme prvok, resp. kde ho máme hľadať.

const int MAX=524287;
zaznam Tab[MAX];

Konkrétne, nech K je množina všetkých kľúčov a hashovacia tabuľka je veľkosti MAX (teda používa indexy 0..MAX-1).

• Hashovacia funkcia bude transformovať kľúče na indexy poľa, teda pôjde o funkciu h:K \rightarrow {0 , 1 , . . . , MAX −1}.
• Snažíme sa, aby funkcia bola jadnoduchá ale pritom neprideľovala často rovnaké indexy (bude kľúče do tabuľky distribuovať rovnomerne).
• V triviálnom prípade, ak K = {0, 1, . . . , MAX −1}, stačí za h zvoliť identitu. Keďže v praxi však býva množina K príliš veľká, takúto funkciu nemôžeme použiť.
• Často sa používa funkcia h(k) = k mod MAX (je dobré, ak v tomto prípade MAX je prvočíslo nie blízko mocniny 2).

int hash(int k){
 return k mod MAX;
}

Jednoduché riešenie

Ak máme teda vhodnú funkciu hash a hashovaciu tabuľku, môžeme navrhnúť prvé funkcie na prácu s ňou.

• Vyhľadávanie je jednoduché - v prípade, že tam prvok s kľúčom k je, musí byť na mieste hash(k). Skontrolujeme teda, či na tomto mieste je prvok s kľúčom k - ak áno, je to hľadaný prvok a ak nie, tak hľadaný prvok neexistuje.

int find(int k){
 int i=hash(k);
 if (Tab[i].key==k) return i;
 else return -1;
}

• Vymazanie takéhoto prvku je tiež jednoduché. Ak sme prvok našli, tak ho vymažeme.

bool remove(int k, zaznam &z){
 int i=find(k);
 if (i<0) return false;
 else {
  z=Tab[i];
  return true;
 }
}

• Nakoniec si ukážeme vkladanie. Myšlienka je podobne jednoduchá - vypočítame si, kam prvok chceme vložiť a ak je tam miesto, tak ho tam vložíme.

bool insert(zaznam z){
 int i=hash(z.key); 
 if (Tab[i]== ??){
   Tab[i]=z;
   return true;
 }
 else return false;
}

• Ostávajú nám dve otvorené otázky:
  • Ako zistíme, že na niektorom mieste v tabuľke nič nie je?
  • Čo so situáciou, keď chceme vložiť na miesto, kde už niečo uložené máme?

Prázdne miesto v tabuľke

• Jednoduchá možnosť, ako zistiť, že v tabuľke na danom mieste nič nie je, je mať hodnotu 'nic' a touto inicializovať na začiatku celú tabuľku. Vytvoríme si konštantný záznam nic taký, že jeho kľúč nebude používaný a jeho dáta budú 0.

• Druhá možnosť je si tabuľku definovať ako pole pointrov na zaznamy a tieto vieme nastaviť na NULL.

zaznam * Tab[MAX];

Pre každé vloženie budeme musieť najprv vytvoriť záznam zaznam * novy=new zaznam; a tento vložiť na miesto v prípade, že tam zatiaľ nič nie je.

bool insert(zaznam z) {
    zaznam * novy = new zaznam;
    novy->data = z.data;
    novy->key = z.key;
    int i = hash(novy->key);
    if (Tab[i] == NULL) {
        Tab[i] = novy;
        return true;
    } else return false;
}

Samozrejme patrične k tomu treba upraviť aj hľadanie a vymazávanie prvku (máme smerníky na záznamy a nie priamo záznamy).

Kolízia

Pri vkladaní prvku sme narazili na problém, že na už obsadané miesto sme chceli vložiť iný prvok. Môže sa stať, že dva prvky x a y sa zahashujú na rovnakú pozíciu h(x) = h(y). Takémuto javu hovoríme kolízia. Existuje viacero spôsobov, ako ju riešiť. Najjednoduchším spôsobom bude to, že budeme nejako hľadať prvú voľnú pozíciu v tabuľke, buď postupným prezeraním nasledovných prvkov, alebo s pozeraním nie tesne nasledovných prvkov ale s nejakým krokom.

Pridáme teda novú konštantu

const int KROK=1; // s nastavením sa môžete pohrať a zistiť, čo to robí

Vkladanie

Pri vkladaní prvku do tabuľky budeme hľadať prvú voľnú pozíciu. Dôležité je si uvedomiť, že teoreticky sa môže stať, že už voľná pozícia nebude (resp. pri nevhodnej dĺžke kroku ju nenájdeme). Preto po MAX krokoch hľadanie voľného miesta skončíme a ak sme ho doteraz nenašli, vyhlásime, že vložiť sa nepodarilo.

bool insert(zaznam z) {
    zaznam * novy = new zaznam;
    novy->data = z.data;
    novy->key = z.key;
    int i = hash(novy->key);
    int poc = 0;
    while ((Tab[i] != NULL) && (poc < MAX)) {
        i = (i + KROK) % MAX;
        poc++;
    }
    if (Tab[i] == NULL) {
        Tab[i] = novy;
        return true;
    } else return false;
}

Vyhľadávanie

Vyhľadávanie je teraz o kúsok náročnejšie. Hľadaný prvok môže byť nielen na svojom mieste ale aj kdekoľvek za ním. Vieme však, že akonáhle narazíme na prvé voľné miesto, tak prvok s hľadaným kľúčom sme nenašli. lebo najneskôr na tomto voľnom mieste by sa musel objaviť.

Pozor, opäť nemá zmysel hľadať dlhšie ako MAX krokov, lebo by sme sa mohli zacykliť.

int find(int k) {
    int i = hash(k);
    int poc = 0;
    while (poc < MAX) {
        if (Tab[i] == NULL) return -1;
        else if (Tab[i]->key == k) return i;
        else {
            i = (i + KROK) % MAX;
            poc++;
        }
    }
}

Vymazávanie

Ak na vymazávanie použijeme správne vyhľadávanie, zdá sa, že okrem práce s uvoľnením pamäte nebudeme mať žiaden problém.

bool remove(int k, zaznam &z) {
    int i = find(k);
    if (i < 0) return false;
    else {
        z = *Tab[i];
        delete Tab[i];
        Tab[i] = NULL;
        return true;
    }
}

Opak je však pravdou. Máme tabuľku Tab[11] a uvažujme nasledovnú postupnosť príkazov (po každom kroku je vypísaný stav tabuľky).

insert(1,1);
Tab: (NULL) (1,1) (NULL) (NULL) (NULL) (NULL) (NULL) (NULL) (NULL) (NULL) (NULL)
insert(12,12); // všimnite si, že záznam s kľúčom 12 mal ísť na pozíciu 1 ale tá bola obsadená a teda bol umiestnený na pozíciu 2 
Tab: (NULL) (1,1) (12,12) (NULL) (NULL) (NULL) (NULL) (NULL) (NULL) (NULL) (NULL)
find(12);
2 // záznam s kľúčom 12 vieme nájsť
remove(1);
Tab: (NULL) (NULL) (12,12) (NULL) (NULL) (NULL) (NULL) (NULL) (NULL) (NULL) (NULL)
find(12);
-1 // záznam s kľúčom 12 nevieme nájsť

Potrebujeme teda pri vymazávaní nejakým spôsobom dosiahnuť, aby sme pri ďalšom hľadaní vedeli, že tu niečo bolo.

• Jedna možnosť je nevymazať naozaj prvok, ktorý sme vymazávali - ten však ostane obsadzovať miesto
• Najbežnejší spôsob je si vytvoriť záznam prázdne miesto, ktorý sa pri vkladaní tvári ako prázdne miesto a pritom nie je NULL, takže pri hľadaní nejakého záznamu sa nám na ňom cyklus nezastaví.

Prednáška 14

Bežné úvodné príklady na rekurziu

Vysvetlenie pojmu rekurzia sa dá zhrnúť do jednej vety: Rekurzia je metóda, pri ktorej definujeme objekt (funkciu, pojem, . . . ) pomocou jeho samého.

Na začiatok sa skúsme pozrieť na „klasické“ príklady algoritmov využívajúcich rekurziu. Prvým, azda najklasickejším príkladom je faktoriál. Ten pre prirodzené (0, 1, 2, . . .) číslo n vráti 1 pokiaľ n = 0 a súčin všetkých čísel od 1 po n inak.

int factorial(int n){
    if (n<2) return 1;
    else return n*factorial(n-1);
}

Výpočet faktorilu je založený na jeho rekurzívnej definícii. Pri prepisovaní rekurzívnych definícii (a všeobecne pri používaní rekurzie) je potrebné dodržiavať nasledujúce zásady, aby sme sa vyhli chybám:

• Príkazová časť rekurzívnej procedúry (funkcie) musí obsahovať vetvu pre triviálny prípad niektorého základného parametra alebo vstupnej hodnoty. Táto vetva nebude obsahovať (rekurzívne) volanie procedúry (funkcie), ktorú práve definujeme.
• Ľubovoľné volanie procedúry (funkcie) vo vnútri jej príkazovej časti musí mať vhodne redukovaný argument (alebo globálnu hodnotu). Pri tejto redukcii sa očakáva, že raz dosiahne triviálny prípad po konečnom počte opakovaní.

Ďalším tradičným príkladom na rekurziu s ktorým ste sa už stretli je počítanie najväčšieho spoločného deliteľa. Opäť dostvame jednoduchú rekurzívnu funkciu. Budeme si jej parametre udržovať usporiadané, tj. prvý parameter je vždy väčší ako druhý (ak by to tak nebolo, vieme jednuduchým testom na začiatku upraviť).

• Triviálny prípad nastáva, keď druhý parameter je 0. Potom je výsledkom prvý parameter.
• V opačnom prípade je NSD(a,b) = NSD(a mod b, b) - tu však vidíme, že Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a mod b < b} a preto zavoláme NSD(b,a mod b)

int nsd(int a, int b){
 if (b == 0) return a;
 else return nsd(b,a%b);
}

A nemôžeme vynechať obľúbený rekurzívny príklad - Fibonacciho čísla. Tam sa rekurzia priam pýta, keďže Fibonacciho čísla sú samé o sebe definované rekurzívne.

• F(0)=F(1)=1
• F(n)=F(n-1)+F(n-2) pre n>2

Z tejto definície vieme opäť urobiť rekurzívny príklad jednoducho:

int fib(int n){
    if (n<2) return 1;
    else return fib(n-1)+fib(n-2);
}

Nepriama rekurzia

Všetky doteraz uvedené funkcie sú príkladom priamej rekurzie – definovaná funkcia používa seba samú priamo. Druhým možným prípadom je nepriama rekurzia (alebo tiež vzájomná), kedy funkcia neodkazuje vo svojej definícii priamo na seba, ale využíva inú funkciu, ktorá sa odkazuje naspäť na prvú (všeobecnejšie sa kruh môže uzavrieť na krokov viac). Ako príklad uveďme rekurzívne definície predikátov párnosti a nepárnosti

bool even(int n) {
    if (n == 0) return true;
    else return odd(n - 1);
}

bool odd(int n) {
    if (n == 0) return false;
    else return even(n - 1);
}

Binárne vyhľadávanie

Binárne vyhľadávanie sme už mali skôr, avšak rekurzia značne zjednoduší a zprehľadní túto funkciu. Na rozdiel od pôvodnej verzie si nepotrebujeme pamätať okraje aktuálneho miesta - pamätá si ich za nás rekurzia (ako svoj parameter).

Ako funguje:

• V prípade, že už máme jednoprvkové pole dostávame triviálny prípad.
• Ak máme viac prvkov, tak sa rekurzívne zavoláme na pravú alebo ľavú stranu podľa vzťahu hodnoty x a stredného prvku.

bool binSearch(int x, int l, int r, int A[]){
    if (l==r) return (A[l]==x);
    if (x<=A[(l+r)/2]) return binSearch(x,l,(l+r)/2,A);
    else return binSearch(x,(l+r)/2+1,r,A);
}

int main(void){
    int A[9]={1,5,7,12,45,79,100,123,467};
    cout << binSearch(7,0,8,A);
}

Rekurzia

Predchádzajúce príklady boli príkladmi použitia rekurzie pri definícii jednoduchých funkcií. Samozrejme, funkcie, ktoré by počítali to isté, by sa dali naprogramovať aj bez pomoci rekurzie. Ale pravdepodobne vidíte, že rekurzívny spôsob je prehľadnejší, zrozumiteľnejší, kratší a krajší (teda aspoň v prvých príkladoch určite).

Načo to vôbec robíme, veď všetko toto sme už robili aj pred tým a nebolo to nič náročné (prečo vôbec riešiť niečo ako rekurzia)? Asi hlavný dôvod je, že nie všetko vieme prepísať bez rekurzie. Príklady, ktoré sme ukázali boli teda istým spôsobom ľahké - pomocou rekurzie vieme urobiť oveľa viac.

Vyhodnocovanie výrazu

Máme zadaný string, v ktorom je výraz obsahujúci celé čísla, znamienka '+', '-' a zátvorky. Pre jednoduchosť predpokladajme, že zátvorky sú všade (t.j. každý výraz je tvaru (Výraz Operátor Výraz) alebo Číslo)a celý výraz je správne uzátvorkovaný.

Príklady výrazov:

• 99
• (12+13)
• (((12-5)+7)-(6+8))

Na vyhodnotenie výrazu môžeme použiť nasledovný postup:

• Nájdeme si znamienko Z také, že výraz je tvaru ((Výraz1)Z(Výraz2))
• Zistíme, akú hodnotu majú Výraz1 a Výraz2
• Hodnota celého výrazu sa dá vypočítať pomocou týchto hodnôt a znamienka Z

Čo nutne ešte potrebujeme je nájsť správne znamienko Z.

int najdiZnamienko(char str[]){
    /*Vieme, ze vyraz je tvaru (Vyraz1 Z Vyraz2)*/
    int poc=0;
    for (int i=1; i<strlen(str)-1; i++){
        if (str[i]=='(') poc++;
        else if (str[i]==')') poc--;
        else if (((str[i]=='+')||(str[i]=='-'))&&(poc==0)) return i;
    }
    return -1;
}

Ďalej je dobre sa zamyslieť, kedy s vyhodnocovaním skončíme. Bude to v prípade, že už očakvame, že máme výraz iba celé číslo - na začiatku nie je zátvorka.

Potom vyhodnocovanie výrazu može pracovať nasledovne:

int vyhodnotVyraz(char str[]){
    if (str[0]!='(') return vyhodnotCislo(str);
    else {
        char s[100];
        int poz, hodnota1, hodnota2;

        poz=najdiZnamienko(str);

        strCopy(str,s,1,poz-1);      // od 1 po pozíciu pred znamienkom (pozícia 0 je '(' )
        hodnota1=vyhodnotVyraz(s);
        strCopy(str,s,poz+1,strlen(str)-2); // od pozície po znamienku po predposledný znak stringu (posledný znak - strlen()-1 je ')' )
        hodnota2=vyhodnotVyraz(s);

        switch (str[poz]){
            case '+': return hodnota1+hodnota2;
            case '-': return hodnota1-hodnota2;
        }

        return 0;
    }    
}

Fraktály

Kochova krivka stupňa 3

Príkladom fraktálu je Kochova krivka. Ako vzniká?

• Predstavme si úsečku, ktorá meria d centimetrov.
• Ďalej potrebujeme transformáciu, teda konkrétne presne definovaný súbor opakovateľných pravidiel: Úsečka sa rozdelí na tretiny a nad strednou tretinou sa zostrojí rovnostranný trojuholník. Základňa trojuholníka v krivke nebude. Opakovaní môžeme robiť nekonečno.
• Druhá možnosť je popísať krivku pomocou systému, ktorého vykonávanie sa podobá príkazom korytnačky.
  • Základným krokom je F (forward) vytvorenie rovnej čiary určitej dĺžky
  • Okrem toho poznáme príkazy + a - (turn left a turn right o určitý uhol - v našom prípade 60 stupňov)
  • Krivku môžeme popísať pomocou nasledovného pravidla F → F+F--F+F , ktoré kreslí z pôvodnej krivky komplikovanejšiu krivku.
  • Takže namiesto F (rovnej čiary určitej dĺžky) môžeme nakresliť rovnú čiaru, otočiť sa doľava, nakresliť rovnú čiaru, dva krát sa otočiť doprava, nakresliť čiaru, otočiť sa doľava a nakresliť čiaru.
  • Následne s každou čiarou môžeme opäť urobiť transformáciu a dostať zložitejšiu krivku.
  • Drobný problém, ktorý musíme vyriešiť je, že týmto spôsobom (ak by sme robili vždy čiary veľkosti d) by nám obrázok príliš rástol. My však chceme ostať v pôvodnej veľkosti preto pri každej transformácii zmenšíme dĺžku čiary na 1/3.

Z toho potom dostávame nasledovný program:

#include "../SimpleDraw.h"

void drawKoch(double d, int n, Turtle& turtle){
    if (n==0) turtle.forward(d);
    else {
        drawKoch(d/3, n-1, turtle);
        turtle.turnLeft(60);
        drawKoch(d/3, n-1, turtle);
        turtle.turnLeft(-120);
        drawKoch(d/3, n-1, turtle);
        turtle.turnLeft(60);
        drawKoch(d/3, n-1, turtle);
    }
}

int main(void) {
    int width = 310; /* rozmery obrazku */
    int height = 150;

    double d = 300; /* velkost krivky */
    int n = 3; /* stupen krivky */
    double wait = 0.2; /* kolko korytnacka caka */

    /* Vytvor obrázok */
    SimpleDraw window(width, height);

    /* Vytvor korytnačku otočenú doprava. */
    Turtle turtle(window, 1, height - 10, 0);
    /* Zobraz korytnačku ako šípku. */
    turtle.show();
    /* Korytnačka bude čakať po každom ťahu. */
    turtle.setWait(wait);

    /* nakresli Kochovu krivku rekurzívne */
    drawKoch(d, n, turtle);

    /* Schovaj korytnačku. */
    turtle.hide();
    /* Zobraz na obrazovke a čakaj, kým užívateľ stlačí Exit,
       potom zavri okno. */
    window.showAndClose();
}

Hanojské veže

• Problém hanojských veží pozostáva z troch stĺpcov (tyčiek) a niekoľkých kruhov rôznej veľkosti. Začína sa postavením pyramídy z kruhov (kameňov) na prvú tyčku.
• Úlohou je potom presunúť celú pyramídu na inú tyčku, avšak pri dodržaní nasledovných pravidiel:
  • v jednom ťahu (na jedenkrát) je možné premiestniť iba jeden hrací kameň
  • väčší kameň nesmie byť nikdy položený na menší

Ako budeme úlohu riešiť? Asi rekurzívne, nie?

• V prípade, že máme iba jeden kameň je úloha veľmi jednoduchá - preložíme ho z pôvodného stĺpika na cieľový stĺpik.
• Ak chceme preložiť viac kameňov (nech ich je N), tak
  • Všetky okrem posledného preložíme na pomocný stĺpik (na to použijeme taký istý postup len s N-1 kameňmi)
  • Premiestnime jeden kameň kam potrebujeme
  • Zatiaľ odložené kamene (na pomocnom stĺpiku) preložíme z pomocného na cieľový stĺpik (na to použijeme opäť taký istý postup s N-1 kameňmi)

Aby sme to popísali konkrétnejšie - preloženie N kameňov z A na C (s pomocným stĺpikom B) urobíme takto:

• Preložíme N-1 kameňov z A na B (s použitím C)
• Preložíme 1 kameň z A na C (s použitím B - ale reálne to potrebovať nebudeme)
• Preložíme N-1 kameňov z B na C (s použitím A)

Dôležité je si uvedomiť, že nasledovný postup dodržuje pravidlá.

void presunHanoi(int odkial, int cez, int kam, int n){
    if (n == 1) {
        cout << "Prelozim kamen z " << odkial <<" na " << kam << endl;
    } else {
        presunHanoi(odkial, kam, cez, n-1); // odlozime si n-1 na pomocny-cez
        presunHanoi(odkial, cez, kam, 1);   // prelozime najvacsi na finalne miesto
        presunHanoi(cez, odkial, kam, n-1); // zvysnych n-1 prelozime z docasneho odkladiska na finalne
    }
}

int main (void){
    presunHanoi(1, 2, 3, 3); // z veze 1 na vezu 3 (pomocou veze 2)
}

Rekurzia pomocou stacku - ako to funguje

O rekurzívne volania sa stará zásobník. Ako funguje?

• Pri vnáraní sa do rekruzívnej funkcie (keď volá funkcia sama seba) si potrebuje zapamätať stav v akom sa nachádza, aby sa pri vynorení vedel dostať do pôvodného stavu. Všetky informácie popisujúce stav si zapíše do zásobníka a až potom sa rekurzívne zavolá.
• Pri vynorení musí zo zásobníka vybrať v prvom rade miesto, kde v rekurzívnej funkcii pokračovať a ďalej všetky premenné.

Čo si teda musel zásobník pamätať?

• adresu návratu - teda miesto kde v rekurzívnej funkcii sa nachádza: dôležité je to hlavne v situácii, keď máme viacero rekurzívnych volaní (či už podľa podmienky alebo sa voláme vždy viac krát)
• lokálne premenné - hodnoty (a spôsob ako sa k nim dostať - v realite totiž zásobník funguje kúsok komplikovanejšie)

Keď už vieme, že o rekurzívne volania sa stará zásobník, možeme si taký jednoduchý zásobník osimulovať napríklad na výpočte faktoriálu.

int fact(int n){
    if (n<2) return 1;
    else return n*fact(n-1);
}

Chvostová rekurzia

Dôvod, prečo sme tieto príklady vedeli napísať už pred tým, ako sme sa dozvedeli niečo o rekurzii je to, že voláme rekurziu z každého volania iba raz. Napríklad na výpočet faktoriálu daného čísla potrebujeme jedenkrát rekurzívne zavolať faktoriál predchádzajúceho čísla. Navyše sa rekurzívne volanie nachádza iba ako posledný krok (niektorých vetiev) výpočtu funkcie. Dobrý kompilátor dokáže z takejto rekurzívnej funkcie vytvoriť nerekurzívnu.

A Fibonacci, ten sa predsa volá dve krát? Áno, ale iba ak je program napísaný neefektívne. Ak napíšeme program podľa uvedeného predpisu a pokúsime sa funkciu volať s rôznymi parametrami, tak čoskoro zistíme, že takto definovaná funkcia počíta celkom pomaly. Prečo? Jednotlivé hodnoty Fibonacciho čísel počítame totiž viackrát (čím menšie číslo, tým viackrát je spočítané). To sa dá napraviť celkom jednoducho použitím takzvaného akumulátora. Akumulátor je dodatočný parameter, v ktorom si predávame stav výpočtu. Konkrétne pri efektívnejšom počítaní Fibonacciho čísel zdola nahor si v akumulátore budeme odkladať posledné dve napočítané čísla. V podstate takto budeme napodobňovať to, ako by ste si napočítali konkrétne Fibonacciho číslo v hlave. Začnete od dvoch jednotiek a postupne si dopočítate ďalšie až po číslo, ktoré ste potrebovali.

int fib1(int a, int b, int n) {
    if (n == 0) return a;
    else return fib1(b,a+b,n-1);
}

int fib(int n){
    fib1(1,1,n);
}

V parametroch a a b si pamätáme dve susedné čísla a v parametri n si pamätáme, koľko rekurzívnych volaní ešte chceme urobiť. Takže takto naprogramovaná Fibonacciho funkcia je nielen rýchla, ale aj kopíruje spôsob nášho uvažovania, a preto je zrozumiteľnejšia. Navyše používa iba jedno rekurzívne volanie.

Prednáška 15

Vypisovanie variácií s opakovaním

Vypíšte všetky trojice cifier, pričom každá cifra je z množiny {0..n-1} a cifry sa môžu opakovať (variácie 3-tej triedy z n prvkov). Napr. pre n=2:

000
001
010
011
100
101
110
111

Veľmi jednoduchý program s troma cyklami:

#include <iostream>
using namespace std;

int main(void) {
    int n;
    cin >> n;
    for(int i=0; i<n; i++) {
        for(int j=0; j<n; j++) {
            for(int k=0; k<n; k++) {
                cout << i << j << k << endl;
            }
        }
    }
}

Rekurzívne riešenie pre všeobecné k

Čo ak chceme k-tice pre všeobecné k? Využijeme rekurziu.

#include <iostream>
using namespace std;

void vypis(int a[], int k) {
    for (int i = 0; i < k; i++) {
        cout << a[i];
    }
    cout << endl;
}

void generuj(int a[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        vypis(a, k);
    } else {
        for (int x = 0; x < n; x++) {
            a[i] = x;
            generuj(a, i + 1, k, n);
        }
    }
}

int main(void) {
    int k, n;
    cin >> k >> n;
    int *a;
    a = new int[k];
    generuj(a, 0, k, n);
    delete[] a;
}

Ďalšie rozšírenia

• Čo ak chceme všetky k-tice písmen A-Z?
• Čo ak chceme všetky DNA reťazce dĺžky k (DNA pozostáva z "písmen" A,C,G,T)?

// pouzi n=26
void vypis(int a[], int k) {
    for (int i = 0; i < k; i++) {
        char c = 'A'+a[i];
        cout << c;
    }
    cout << endl;
}

// pouzi n=4
void vypis(int a[], int k) {
    char *abeceda = "ACGT";
    for (int i = 0; i < k; i++) {
        cout << abeceda[a[i]];
    }
    cout << endl;
}

Cvičenia

• Ako by sme vypisovali všetky k-ciferné hexadecimálne čísla (šestnástková sústava), kde používame cifry 0-9 a písmená A-F?
• Ako by sme vypisovali všetky k-tice písmen v opačnom poradí, od ZZZ po AAA?

Variácie bez opakovania

Teraz chceme vypísať všetky k-tice cifier z množiny {0,..,n-1}, v ktorých sa žiaden prvok neopakuje (pre k=n dostávame permutácie)

Príklad pre k=3, n=3

012
021
102
120
201
210

Skúšanie všetkých možností

• Jednoduchá možnosť: použijeme predchádzajúci program a pred výpisom skontrolujeme, či je riešenie správne

Prvý pokus:

bool spravne(int a[], int k, int n) {
    /* je v poli a dlzky k kazde cislo od 0 po n-1 najviac raz? */
    bool *bolo = new bool[n];
    for (int i = 0; i < n; i++) {
        bolo[i] = false;
    }
    for (int i = 0; i < k; i++) {
        if (bolo[a[i]]) return false;
        bolo[a[i]] = true;
    }
    return true;
}

void generuj(int a[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        if (spravne(a, k, n)) {
            vypis(a, k);
        }
    } else {
        for (int x = 0; x < n; x++) {
            a[i] = x;
            generuj(a, i + 1, k, n);
        }
    }
}

Pozor, kontrola nie je celkom správna, lebo neodalokuje pole, míňame veľa pamäte!

• Pozor na takéto chyby pri prerušení cyklov pomocou break, continue alebo return.

Opravená verzia:

bool spravne(int a[], int k, int n) {
    /* je v poli a dlzky k kazde cislo od 0 po n-1 najviac raz? */
    bool *bolo = new bool[n];
    for (int i = 0; i < n; i++) {
        bolo[i] = false;
    }
    bool dobre = true;
    for (int i = 0; i < k; i++) {
        assert(0 <= a[i] && a[i] < n);
        if (bolo[a[i]]) { dobre = false; }
        bolo[a[i]] = true;
    }
    delete[] bolo;
    return dobre;
}

Cvičenie: ako by sme napísali kontrolu, ak by sme nepoznali n?

Prehľadávanie s návratom, backtracking

• Predchádzajúce riešenie je neefektívne, lebo prechádza cez všetky variácie s opakovaním a veľa z nich zahodí.
  • Napríklad pre k=7 a n=10 pozeráme Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 10^7} variácií s opakovaním, ale iba 604800 z nich je správnych, čo je asi 6%
• Len čo sa v poli a vyskytne opakujúca sa cifra, chceme túto vetvu prehľadávania ukončiť, lebo doplnením ďalších cifier problém neodstránime
• Spravíme funkciu moze(a,i,x), ktorá určí, či je možné na miesto i v poli a dať cifru x
• Testovanie správnosti vo funkcii generuj sa dá vynechať

bool moze(int a[], int i, int x) {
    /* Mozeme dat hodnotu x na poziciu i v poli a?
     * Mozeme, ak sa nevyskytuje v a[0..i-1] */
    for (int j = 0; j < i; j++) {
        if (a[j] == x) return false;
    }
    return true;
}

void generuj(int a[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        vypis(a, k);
    } else {
        for (int x = 0; x < n; x++) {
            if (moze(a, i, x)) {
                a[i] = x;
                generuj(a, i + 1, k, n);
            }
        }
    }
}

Možné zrýchlenie: vytvoríme si trvalé pole bolo, v ktorom bude zaznamené, ktoré cifry sa už vyskytli a to použijeme vo funkcii moze.

• Po návrate z rekurzie nesmieme zabudúť príslušnú hodnotu odznačiť!

void generuj(int a[], bool bolo[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * v poli bolo mame zaznamenane, ktore cifry su uz pouzite,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        vypis(a, k);
    } else {
        for (int x = 0; x < n; x++) {
            if (!bolo[x]) {
                a[i] = x;
                bolo[x] = true;
                generuj(a, bolo, i + 1, k, n);
                bolo[x] = false;
            }
        }
    }
}

int main(void) {
    int k, n;
    cin >> k >> n;
    int *a = new int[k];
    bool *bolo = new bool[n];
    for (int i = 0; i < n; i++) {
        bolo[i] = false;
    }
    generuj(a, bolo, 0, k, n);
    delete[] a;
    delete[] bolo;
}

Cvičenia: ako potrebujeme zmeniť program, aby sme generovali všetky postupnosti k cifier z množiny {0,..,n-1}, také, že:

• z každej cifry sú v postupnosti najviac 2 výskyty?
• žiadne dve po sebe idúce cifry nie sú rovnaké?
• súčet cifier je aspoň S?

Technika rekurzívneho prehľadávania všetkých možností s orezávaním beznádejných vetiev sa nazýva prehľadávanie s návratom alebo backtracking.

• Hľadáme všetky postupnosti, ktoré spĺňajú nejaké podmienky
  • Vo všeobecnosti nemusia byť rovnako dlhé
• Ak máme celú postupnosť, vieme otestovať, či spĺňa podmienku (funkcia spravne)
• Ak máme časť postupnosti a nový prvok, vieme otestovať, či po pridaní tohto prvku má ešte šancu tvoriť časť riešenia (funkcia moze)
  • Funkcia moze nesmie vrátiť false, ak ešte je možné riešenie
  • Môže vrátiť true, ak už nie je možné riešenie, ale nevie to ešte odhaliť
  • Snažíme sa však odhaliť problém čím skôr

Všeobecná schéma

void generuj(int a[], int i) {
    /* v poli a dlzky k mame prvych i cisel z riesenia */
    if (spravne(a, i)) { /* ak uz mame cele riesenie, vypisme ho */
        vypis(a, i);
    } else {
        pre vsetky hodnoty x {
            if (moze(a,i,x) {
                a[i] = x;
                generuj(a, i + 1);
            }
        }
    }
}

Prehľadávanie s návratom môže byť vo všeobecnosti veľmi pomalé, čas výpočtu exponenciálne rastie.

Problém 8 dám

Cieľom je rozmiestniť n dám na šachovnici nxn tak, aby sa žiadne dve navzájom neohrozovali, tj. aby žiadne dve neboli v rovnakom riadku, stĺpci, ani na rovnakej uhlopriečke.

Príklad pre n=4:

 . * . .
 . . . *
 * . . .
 . . * .

• V každom riadku bude práve jedna dáma, teda môžeme si riešenie reprezetovať ako pole damy dĺžky n, kde damy[i] je stĺpec, v ktorom je dáma na riadku i
• Podobne ako v predchádzajúcom príklade chceme do poľa dať čísla od 1 po n, aby spĺňali ďalšie podmienky (v každom stĺpci a na každej uhlopriečke najviac 1 dáma)
• Vytvoríme si polia, kde si budeme pamätať pre každý stĺpec a uhlopriečku, či už je obsadený
• Uhlopriečky v oboch smeroch očísľujeme číslami od 0 po 2n-2
  • V jednom smere majú miesta na uhlopriečke rovnaký súčet, ten teda bude číslom uhlopriečky
  • V druhom smere majú rovnaký rozdiel, ten však môže byť aj záporný, pričítame n-1
• Pre jednoduchosť použijeme globálne premenné, lebo potrebujeme veľa polí
  • Globálne premenné spôsobujú problémy vo väčších programoch: mená premenných sa môžu "biť", môžeme si omylom prepísať číslo dôležité v inej časti programu
  • Mohli by sme si tiež spraviť struct obsahujúci všetky premenné potrebné premenné v rekurzii a odvzdávať si ten (uvidíme v ďalšom programe).

#include <iostream>
using namespace std;

/* globalne premenne */
int n;
int *damy;   /* pole ktore obsahuje stlpec s damou v riadku i*/
bool *bolStlpec; /* pole ktore obsahuje true ak stlpec obsadeny damou */
bool *bolaUhl1;  /* polia ktore obsahuju true ak uhlopriecky obsadene */
bool *bolaUhl2;
int pocet;       /* pocet najdenych rieseni */

int uhl1(int i, int j) {
    /* na ktorej uhlopriecke je riadok i, stlpec j v smere 1? */
    return i + j;
}

int uhl2(int i, int j) {
    /* na ktorej uhlopriecke je riadok i, stlpec j v smere 2? */
    return n - 1 + i - j;
}

void vypis() {
    /* vypis sachovnicu textovo a zvys pocitadlo rieseni */
    pocet++;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (damy[i] == j) cout << " *";
            else cout << " .";
        }
        cout << endl;
    }
    cout << endl;
}

void generuj(int i) {
    /* v poli damy mame prvych i dam, dopln dalsie */
    if (i == n) {
        vypis();
    } else {
        for (int j = 0; j < n; j++) {
            /* skus dat damu na riadok i, stlpec j */
            if (!bolStlpec[j]
                    && !bolaUhl1[uhl1(i, j)] && !bolaUhl2[uhl2(i, j)]) {
                damy[i] = j;
                bolStlpec[j] = true;
                bolaUhl1[uhl1(i, j)] = true;
                bolaUhl2[uhl2(i, j)] = true;
                generuj(i + 1);
                bolStlpec[j] = false;
                bolaUhl1[uhl1(i, j)] = false;
                bolaUhl2[uhl2(i, j)] = false;
            }
        }
    }
}

int main(void) {
    cin >> n;
    /* alokacia poli */
    damy = new int[n];
    bolStlpec = new bool[n];
    bolaUhl1 = new bool[2 * n - 1];
    bolaUhl2 = new bool[2 * n - 1];
    for (int i = 0; i < n; i++) {
        bolStlpec[i] = false;
    }
    for (int i = 0; i < 2 * n + 1; i++) {
        bolaUhl1[i] = false;
        bolaUhl2[i] = false;
    }

    /* rekuzia */
    pocet=0;
    generuj(0);
    cout << "Pocet rieseni: " << pocet << endl;

    /* uvolnime polia */
    delete[] damy;
    delete[] bolStlpec;
    delete[] bolaUhl1;
    delete[] bolaUhl2;
}

Sudoku

Chceme riešiť hlavolam Sudoku. Máme danú plochu 9x9 políčok, pričom niektoré sú prázdne, iné obsahujú číslo z množiny {1..9}. Plocha je rozdelená do 9 štvorcov 3x3. Cieľom je doplniť čísla do prázdnych štvorčekov tak, aby v každom riadku plochy, v každom stĺpci plochy a v každom štvorci 3x3 bola každá cifra {1..9} práve raz.

. 3 . | . 7 . | . . .
6 . . | 1 9 5 | . . .
. 9 8 | . . . | . 6 .
---------------------
8 . . | . 6 . | . . 3
4 . . | 8 . 3 | . . 1
. . . | . 2 . | . . 6
---------------------
. 6 . | . . . | 2 8 .
. . . | 4 . 9 | . . 5
. . . | . 8 . | . 7 .

Príklad vstupu a výstupu:

Vstup:                   Vystup:
0 3 0 0 7 0 0 0 0	 5 3 4 6 7 8 9 1 2
6 0 0 1 9 5 0 0 0	 6 7 2 1 9 5 3 4 8
0 9 8 0 0 0 0 6 0	 1 9 8 3 4 2 5 6 7
8 0 0 0 6 0 0 0 3	 8 5 9 7 6 1 4 2 3
4 0 0 8 0 3 0 0 1	 4 2 6 8 5 3 7 9 1
0 0 0 0 2 0 0 0 6	 7 1 3 9 2 4 8 5 6
0 6 0 0 0 0 2 8 0	 9 6 1 5 3 7 2 8 4
0 0 0 4 0 9 0 0 5	 2 8 7 4 1 9 6 3 5
0 0 0 0 8 0 0 7 0        3 4 5 2 8 6 1 7 9

                         Pocet rieseni: 1

Naša rekurzívna funkcia bude postupovať nasledovne:

• nájde na ploche prázdne políčko, ak také nie je, vypíše riešenie a skončí
• do prázdneho políčka skúša vložiť čísla 1...9 a testuje, či nenastane konflikt v riadku, stĺpci alebo štvorci
• ak niektoré číslo sedí, zavolá sa rekurzívne na vyplnenie zvyšných bielych miest

Namiesto globálnych premenných si vytvoríme si struct sudoku, do ktorého uložíme všetky potrebné údaje pre rekurzívne vyhľadávanie. Rekurzia potom bude vyzerať takto:

void generuj(sudoku &s) {
    int i = najdiVolne(s);
    if (i < 0) {
        vypis(s);
    } else {
        for (int x = 1; x <= 9; x++) {
            if (moze(s, i, x)) {
                uloz(s, i, x);
                generuj(s);
                zmaz(s, i, x);
            }
        }
    }
}

Pre každý riadok (a podobne pre každý stĺpec a štvorec) si budeme pamätať, ktoré cifry sú v ňom už použité. Je to teda 2D pole typu bool.

• Aby sme takéto pole nemuseli robiť zvlášť pre riadky, stĺpce a štvorce, nazveme všetky tieto útvary skupiny
  • Máme teda 27 skupín, očísľujeme ich 0..26. Z nich je 9 riadkových (čísla 0..8), 9 stĺpcových (čísla 9..17) a 9 štvorcových (čísla 18..26)
  • Každá skupin má vektor 9 bool-ov označujúcich použité cifry
  • Každé políčko má pole 3 intov, obsahujúcich čísla jeho 3 skupín

Keď už máme skupiny, nezáleží na tom, ako máme údaje o políčkach usporiadané, namiesto 2D matice ich dáme do 1D poľa.

#include <iostream>
using namespace std;

/* kazde policko patri do 3 skupin: riadok, stlpec a stvorec */
const int SKUPIN = 3;

/* udaje o jednom policku plochy: suradnice,
 * hodnota (0 ak prazdne, alebo 1..9,
 * a zoznam skupin, do ktorych patri. */
struct policko {
    int riadok, stlpec;
    int hodnota;
    int skupiny[SKUPIN];
};

struct sudoku {
    policko *plocha;  /* pole vsetkych policok plochy */
    bool **obsadene;  /* pre kazdy skupiny ci je dana cifra uz pouzita */
    int pocetPolicok; /* clekovy pocet policok (9*9) */
    int pocetSkupin;  /* clekovy pocet skupin (3*9) */
    int rieseni;      /* pocet najdenych rieseni */
};

void vypis(sudoku &s) {
    /* vypis riesenie sudoku a zvys pocitadlo rieseni */
    s.rieseni++;
    int pozicia = 0;
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            cout << " " << s.plocha[pozicia].hodnota;
            pozicia++;
        }
        cout << endl;
    }
    cout << endl;
}

int najdiVolne(sudoku &s) {
    /* najdi volne policko na ploche */
    for (int i = 0; i < s.pocetPolicok; i++) {
        if (s.plocha[i].hodnota == 0) return i;
    }
    return -1;
}

bool moze(sudoku &s, int pozicia, int hodnota) {
    /* Mozeme ulozit danu hodnotu na policko s poradovym cislom pozicia?
     * Da sa to, ak ziadna so skupin tohto policka nema
     * tuto hodnotu uz pouzitu. */
    for (int i = 0; i < SKUPIN; i++) {
        /* cislo i-tej skupiny pre policko */
        int skupina = s.plocha[pozicia].skupiny[i];
        /* ak je uz hodnota obsadena, neda sa pouzit */
        if (s.obsadene[skupina][hodnota]) return false;
    }
    /* vo vsetkych skupinach je hdonota neobsadena */
    return true;
}

void uloz(sudoku &s, int pozicia, int hodnota) {
    /* na policko s poradovym cislom pozicia uloz danu
     * hodnotu. Ak je hodnota > 0, zaregistruj ju
     * tiez ako obsadenu vo vsetkych skupinach,
     * kam policko patri. */
    s.plocha[pozicia].hodnota = hodnota;
    if (hodnota > 0) {
        for (int i = 0; i < SKUPIN; i++) {
            int skupina = s.plocha[pozicia].skupiny[i];
            s.obsadene[skupina][hodnota] = true;
        }
    }
}

void zmaz(sudoku &s, int pozicia) {
    /* hodnotu v policku s pozicia zmen na nulu
     * a povodnu hodnotu odznac v poliach obsadene pre vsetky
     * skupiny tohto policka */
    int hodnota = s.plocha[pozicia].hodnota;
    s.plocha[pozicia].hodnota = 0;
    for (int i = 0; i < SKUPIN; i++) {
        int skupina = s.plocha[pozicia].skupiny[i];
        s.obsadene[skupina][hodnota] = false;
    }
}

void generuj(sudoku &s) {
    /* mame ciastocne vyplnenu plochu sudoku,
     * chceme najst vsetky moznosti, ako ho dovyplnat. */
    int i = najdiVolne(s);
    if (i < 0) {
        vypis(s);
    } else {
        for (int x = 1; x <= 9; x++) {
            if (moze(s, i, x)) {
                uloz(s, i, x);
                generuj(s);
                zmaz(s, i);
            }
        }
    }
}

void inicializuj(sudoku &s, int **a) {
    /* inicializuj strukturu sudoku na zaklade
     * vstupnej matice s cislami 0..9*/
    s.pocetPolicok = 9 * 9;
    s.pocetSkupin = 3 * 9;
    /* alokujeme polia a oznacime cifry ako neobsadene */
    s.plocha = new policko[s.pocetPolicok];
    s.obsadene = new bool*[s.pocetSkupin];
    for (int i = 0; i < s.pocetSkupin; i++) {
        s.obsadene[i] = new bool[10];
        for (int j = 1; j <= 9; j++) {
            s.obsadene[i][j] = false;
        }
    }
    /* pre kazde policko naplnime jeho strukturu
     * a vyplnime obsadene cifry */
    int pozicia = 0;
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            s.plocha[pozicia].riadok = i;
            s.plocha[pozicia].stlpec = j;
            s.plocha[pozicia].skupiny[0] = i;
            s.plocha[pozicia].skupiny[1] = 9 + j;
            s.plocha[pozicia].skupiny[2] = (i / 3)*3 + (j / 3) + 18;
            uloz(s, pozicia, a[i][j]);
            pozicia++;
        }
    }
    /* este sme nenasli ziadne riesenie */
    s.rieseni = 0;
}

int main(void) {
    /* alokujeme a nacitame 2D maticu so vstupom */
    int **a = new int *[9];
    for (int i = 0; i < 9; i++) {
        a[i] = new int[9];
    }
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            cin >> a[i][j];
        }
    }
    /* vytvorime struktury pre sudoku */
    sudoku s;
    inicializuj(s, a);
    /* rekurzivne prehladavanie s navratom */
    generuj(s);

    /* vypis riesenia */
    cout << "Pocet rieseni: " << s.rieseni << endl;

    /* este by sme mali odalokovat polia v sudoku */
}

Ak spustíme program na vstupe uvedenom vyššie, nájde jedno riešenie približne za stotinu sekundy. Ak všetky čísla v prvých dvoch riadkoch zmeníme na nuly, hľadá vyše tri minúty (bez vypisovania) a nájde 159800 riešení. Ak by sme vymazali ešte ďalšie čísla, program by mohol byť ešte výrazne pomalší.

Cvičenie:

• Zlepšite algoritmus tak, aby nezačínal vždy s prvým prázdnym políčkom, ale s takým, ktoré má najmenej neobsadených možností (v ideálnom prípade 1). Ak má niektoré nevyplnené políčko 0 možností, môžeme túto vetvu hľadania tiež ukončiť.
  • S touto zmenou zbehne program na ťažšom vstupe už za 8 sekúnd namiesto 3 minút
• Čo by bolo treba zmeniť v programe, aby zakazoval opakujúce sa cifry aj na hlavnej diagonále celej plochy?

Cvičenie:

• Ako by sme vypísali všetky podmnožiny veľkosti k danej množiny (kombinácie)?

Cvičenia 7

Pointre a typy

• Pre aké typy by dávali zmysel nasledujúce výrazy?
  • (*p).x je to isté ako p->x
  • *p.x je to isté ako *(p.x)
  • (x->y)[1]
  • (*x)[1].y

Matice

• Otočte poradie riadkov 2D matice (stačí vymeniť smerníky)
• Otočte poradie stĺcov 2D matice (treba vymienať čísla v riadkoch)
• K matici s n riadkami a m stĺpcami zostavte transponovanú, t.j. s m riadkami a n stĺcami

2D polia

• Vytvorte Pascalov trojuholník ako 2D pole, ktoré má v prvom riadku jedno číslo Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {0 \choose 0}} , v druhom dve Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {1 \choose 0}} a Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {1 \choose 1}} atď. Môžete využiť vzťah, že Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {n \choose 0} = {n \choose 0} = 1} a pre 0<k<n platí Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}} , t.j. n-tý riadok vieme ľahko spočítať z n-1-vého.
• Do programu s výškovou mapou doprogramujte hľadanie všetkých ostrovčekov veľkosti 1, t.j. políčka s pevninou, ktoré sa hranou nedotýkajú inej pevniny (môžu sa dotýkať rohom). Každý taký ostrovček zarámikujte. Spravte si vstup, v ktorom takéto ostrovčeky budú, aby ste mohli program vyskúšať.
• Zobrazovanie hry Life zmeňte tak, aby sa bunky, ktoré práve umreli, zobrazili ako sivé políčka a až v ďalšom kroku zmizli úplne. (T.j. v čase t bunka žije, teda je čierne, v čase t+1 umrela teda je sivá a v čase t+2 bude bielou, ak sa znova nenarodila). Pre jednoduchosť môžete v každom kole zmazať obrazovku a vykresľovať všetky políčka odzova.

Vektor

• Do programu na prácu s jednoduchým vektorom z prednášky 12 doprogramujte funkciu void zmazPosledny(vektor &a), ktorá z poľa vyhodí posledný prvok (zmenší sa teda pocet) a ak bude pocet menší ako tretina veľkosti, vytvorí nové pole polovičnej veľkosti, zvyšné prvky do neho premiestni, a staré pole uvoľní. Pole by malo mať vždy veľkosť aspoň 1.
• Vytvorte dvojrozmerný vektor, ktorý bude podporovať nasledovné operácie:
  • Inicializuj: Nastaví počiatočnú použiteľnú veľkosť na 2x2, N(počet riadkov)=0 a M(počet stĺpcov)=0.
  • Pridaj riadok: Ak sa do súčasnej veľkosti zmestí, pridá riadok (zväčší N) obsahujúci M núl. Ak sa nezmestí, zdvojnásobí počet riadkov.
  • Pridaj stĺpec: Ak sa do súčasnej veľkosti zmestí, pridá stĺpec (zväčší M) obsahujúci N núl. Ak sa nezmestí, zdvojnásobí počet stĺpcov.
  • Uvoľni: Uvoľní pamäť.

DÚ7

max. 5 bodov, termín odovzdania utorok 15.11. o 22:00

Cieľom tejto domácej úlohy je precvičiť si prácu s maticami a alokáciou pamäte.

Možno si z prípravného sústredenia pamätáte hru Proboj, na ktorej ste programovali stratégiu pre červíka, ktorý sa mal pohybovať po ploche, hľadať jedlo a vyhýbať sa prekážkam. V tejto domácej úlohe si napíšete program, ktorý bude simulovať pohyb jednoduchého červíka, pričom jednoduché pravidlo pre jeho náhodný pohyb dostanete hotové.

Príklad hernej situácie. Stena je zobrazená čiernou, červík červenou a jedlo zelenou. Hlava je v najpravejšom dieliku červíka.

Hracia plocha je matica s n riadkami a m stĺpcami. Každé políčko je buď prázdne, alebo je na ňom jedlo alebo stena alebo jeden dielik červíka. Celkovo červík pozostáva z viacerých dielikov, pričom jeden z jeho koncov nazveme hlavou. V každom kroku sa hlava červíka posunie na niektoré zo susedných políčok, pričom môže ísť iba na také políčko, kde nie je nič, alebo kde je jedlo. Ostatné dieliky sa presúvajú za hlavou tak, že každý sa presunie na miesto, kde bol dovtedy predchádzajúci. Ak červík stúpil na políčko, kde bolo jedlo, toto jedlo zje a narastie o jeden dielik, takže jeho chvost vlastne ostane tam isto, kde bol v predchádzajúcom ťahu. Simulácia pokračuje až kým sa červík nepokúsi prejsť na políčko, kde to nie je možné, alebo kým neprejde vopred daný počet ťahov.

Vašou úlohou je dopísať chýbajúce funkcie do kostry programu uvedeného nižšie. Nemeňte použité dátové štruktúry ani hlavičky funkcií a riaďte sa popisom každej funkcie uvedeným na jej začiatku.

Popis dátových štruktúr

Herná plocha je dvojrozmerné pole int-ov s n riadkami a m stĺpcami. Hodnota každého políčka je číslo medzi 0 a 3 a určuje jeho obsah (pozri konštanty NIC, STENA, JEDLO a CERVIK). Okrem samotného poľa máme v štruktúre plocha aj jej rozmery n a m. Červík je daný poľom dielikov a premennou pocet, ktorá určuje koľko dielikov červík práve má. Tieto dieliky sú uložené v poli od chvosta k hlave, pričom chvost je na pozícii 0 a hlava na pozícii pocet-1. Keď sa červík posunie, treba v poli poposúvať aj jeho dieliky. Polia pre plochu aj červíka sú dynamicky alokované podľa rozmerov plochy, pričom pre červíka alokujeme n*m políčok, čo je najväčšia dĺžka, akú teoreticky môže dosiahnuť.

Činnosť programu je uľahčená niekoľkými konštantami. V poli farby sú mená farieb pre jednotlivé typy obsahu políčka. Smer pohybu červíka sa v programe označuje číslami 0,1,2,3, pričom 0 znamená natočenie doprava, 1 hore, 2 doľava a 3 dole. V poliach delta_stlpec a delta_riadok sú pre každý smer uvedené dĺžky, o ktoré sa má hlava červíka v danom smere posunúť. Napr. pre smer 0 je delta_riadok[0]=0 a delta_stlpec[0]=1, čo znamená, že červík zostáva v tom istom riadku a ide o jedno políčko doprava.

Popis vstupného súboru

Počiatočnú situáciu hry má program načítať zo vstupného súboru cervik.txt. Tento súbor začína číslami n a m udávajúcimi počet riadkov a stĺpcov hracej plochy. Za nimi nasleduje n riadkov po m čísel, každé číslo udáva obsah jedného políčka, pričom tento obsah môže byť 0 (nič), 1 (stena) alebo 2 (jedlo). Za maticou nasleduje číslo k, udávajúce počet dielikov červíka a potom zoznam týchto dielikov, pričom každý dielik je daný svojim číslom riadku a stĺpca (riadky a stĺpce sú číslované od nuly). Dieliky sú v zozname vypísané smerom od chvosta k hlave. Môžete predpokladať, že vstupný súbor obsahuje iba korektné údaje. Na miestach, kde je červík, bude na hracej ploche prázdne miesto.

Príklad vstupného súboru

Pre tento vstup by po načítaní mal program vykresliť obrázok uvedený vyššie.

10 30
 1 1 0 1 0 2 0 2 1 0 0 0 0 0 0 1 0 0 1 2 0 0 0 2 2 2 2 1 1 0
 0 0 0 1 0 0 0 1 0 1 2 0 0 1 0 0 0 1 0 2 1 0 0 1 1 1 2 0 2 2
 2 0 0 0 1 1 0 0 0 0 1 0 1 2 0 2 1 0 0 0 1 1 1 0 0 1 0 0 2 0
 0 0 1 0 0 2 2 1 2 1 0 1 1 0 2 1 0 0 2 0 1 2 1 0 1 0 1 0 0 0
 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 2 0 0
 0 0 0 0 2 2 2 0 1 0 1 1 1 1 0 0 1 0 0 2 2 0 0 1 0 1 0 1 2 2
 0 2 1 0 0 1 1 1 2 1 0 0 1 1 1 1 0 0 0 0 0 0 2 1 0 1 1 0 1 0
 0 0 0 2 2 0 2 0 1 0 0 0 0 2 2 2 0 2 0 1 0 0 1 1 1 2 0 0 0 0
 0 1 0 2 2 0 1 0 0 1 1 0 0 1 2 1 0 0 1 0 1 2 0 1 1 0 1 1 0 2
 0 0 0 1 0 0 1 1 0 0 0 0 2 0 1 0 0 1 2 0 1 2 0 0 1 2 1 0 0 2
3 4 10 4 11 4 12

Kostra programu

Do tejto kostry doprogramujte chýbajúce časti.

#include "../SimpleDraw.h"
#include <iostream>
#include <fstream>
#include <cstdlib>
#include <ctime>

using namespace std;

/* velkost stvorceka mapy v pixeloch */
const int stvorcek = 15;
/* dlzka cakania medzi dvoma krokmi simulacie */
const double wait = 1.5;
/* maximalny pocet krokov */
const int maxKrokov = 50;

/* konstanty urcujuce obsah policka plochy */
const int NIC = 0;
const int STENA = 1;
const int JEDLO = 2;
const int CERVIK = 3;

/* farby pre jednotlive typy obsahu policka */
string farby[4] = {"lightgrey", "black", "green", "brown"};

/* o kolko sa pohne cervik v riadku a stlpci,
 * ak je natoceny urcitym smerom */
const int delta_stlpec[4] = {1, 0, -1, 0};
const int delta_riadok[4] = {0, -1, 0, 1};

/* suradnice jedneho dieliku červika */
struct dielik {
    int riadok, stlpec;
};

/* samotny cervik */
struct cervik {
    int pocet; /* pocet dielikov cervika */
    dielik *dieliky; /* pole dielikov cervika */
};

/* hracia plocha */
struct plocha {
    int n, m; /* n: pocet riadkov, m: pocet stlpcov */
    int **a; /* dvojrozmenra matica, kazdy dielik obsahuje jednu z
             * hodnot NIC, STENA, JEDLO alebo CERVIK */
};

void nacitajPlochu(istream &in, plocha &a) {
    /* nacita zo suboru in cisla n a m, nanalokuje pamat 
     * a vyplni ju cislami zo vstupneho suboru. */

}

void nacitajCervika(istream &in, cervik &c, plocha &a) {
    /* Pre cervika c naalokuje pole dielikov dost velke,
     * aby sa tam zmestil aj cervik velkosti m*n. 
     * Zo suboru in nacita pocet dielikov cervika a ich suradnice
     * dielikov a ulozi ich do struktury c. Cervika tiez vyznaci
     * na ploche pomocou konstanty CERVIK */
}

void zobrazStvorcek(SimpleDraw &window, int riadok, int stlpec, int typ) {
    /* zobrazi na pozicii (riadok, stlpec) stvorcek s farbou pre dany typ */

    /* nastav farbu ciary aj vyplne na dane hodnoty */
    window.setBrushColor(farby[typ]);
    window.setPenColor("white");
    window.drawRectangle(stlpec*stvorcek, riadok*stvorcek, stvorcek, stvorcek);
}

void zobrazPlochu(plocha &a, SimpleDraw &window) {
    /* zobrazi celu plochu s vyuzitim funkcie zobrazStvorcek */
}

void kamCervik(cervik &c, int smer, int &riadok, int &stlpec) {
    /* do premennych riadok a stlpec ulozi,
     * kam sa pohne cervik, ak pojde danym smerom */

    riadok = c.dieliky[c.pocet - 1].riadok + delta_riadok[smer];
    stlpec = c.dieliky[c.pocet - 1].stlpec + delta_stlpec[smer];
}

int coNajde(plocha &a, int riadok, int stlpec) {
    /* vrati hodnotu, ktoru cervik najde na ploche, ak pojde
     * na policko (riadok, stlpec). Ak su suradnice policka
     * mimo plochu, vrati hodnotu STENA */

}

bool posunCervika(SimpleDraw &window, plocha &a, cervik &c, int smer) {
    /* cervika c posunie o jedno policko v smere smer, ak sa da,
     * pricom spravi prislusne zmeny v strukture cervik, na ploche,
     * aj na obrazovke. Ak cervik nasiel jedlo, jeho dlzka sa zvysi.
     * Funkcia vrati true, ak sa posun podaril, alebo false, ak cervik narazil. */

}

int urciSmer(plocha &a, cervik &c) {
    /* Urci smer, akym sa cervik bude hybat.
     * Pozrie sa na vsetky styri policka susediace s hlavou
     * Ak je na policku prekazka (stena, cervik), smer dostane 0 bodov
     * Ak je na policko prazdne, tento smer dostane 1 bod,
     * Ak je na policku jedlo, tento smer dostane 2 body.
     * Nakoniec sa nahodne vyberie smer s pravdedpodbnostami
     * umernymi poctu bodov. Ak ziaden smer nie je mozny,
     * vyberieme smer 0  */

    int body[4];
    int sucet = 0;
    for (int smer = 0; smer < 4; smer++) {
        int riadok, stlpec;
        kamCervik(c, smer, riadok, stlpec);
        int policko = coNajde(a, riadok, stlpec);
        switch (policko) {
            case STENA:
            case CERVIK: body[smer] = 0;
                break;
            case JEDLO:
                body[smer] = 2;
                break;
            case NIC:
                body[smer] = 1;
                break;
        }
        sucet += body[smer];
    }
    if (sucet == 0) return 0;

    int r = rand() % sucet;
    for (int smer = 0; smer < 4; smer++) {
        if (body[smer] && body[smer] > r) {
            return smer;
        }
        r -= body[smer];
    }

    return 0;
}

void zmazPlochu(plocha &a) {
    /* uvolni pamat matice v ploche */

}

void zmazCervika(cervik &c) {
    /* uvolni pamat na ulozenie dielikov cervika */

}

int main(void) {
    ifstream in;
    in.open("cervik.txt");
    if (in.fail()) {
        cout << "Nepodarilo sa otvorit subor";
        return 1;
    }

    srand(time(NULL));

    /* vytvor a nacitaj plochu */
    plocha a;
    nacitajPlochu(in, a);

    /* vytvor a nacitaj cervika */
    cervik c;
    nacitajCervika(in, c, a);

    /* zobraz plochu */
    SimpleDraw window(a.m * stvorcek, a.n * stvorcek);
    zobrazPlochu(a, window);

    window.wait(wait);

    for (int krok = 0; krok < maxKrokov; krok++) {
        /* jeden krok simulacie: urci smer, posun sa, cakaj */
        int smer = urciSmer(a, c);
        bool ok = posunCervika(window, a, c, smer);
        if (!ok) break;
        window.wait(wait);
    }

    /* zobraz okno */
    window.showAndClose();

    /* uvolni pamat matice */
    zmazPlochu(a);

    /* uvolni pamat cervika */
    zmazCervika(c);
}

Prednáška 16

Rozdeľuj a panuj

Rekurzívne triedenia sú založené na princípe Rozdeľuj a panuj. Tento spôsob všeobecne funguje nasledovne

• Rozdeľuj: Prvá fáza algoritmu je rozdelenie problému na nejaké menšie časti, ktoré sa dajú riešiť ďalej samostatne (teda by nemali mať prienik).
• Vyrieš podproblémy: Rekurzívne sa zavolám na podproblémy a keď dostanem ich výsledky, tak ..
• Panuj: Poslednou časťou je spojenie výsledkov do výsledku celkového problému.

MergeSort

V triedení zlučovaním sa pole veľkosti N rozdelí na polovicu najjednoduchším spôsobom - na prvú a druhú polovicu. Tieto rekurzívne utriedime, čím dostávame 2 utriedené postupnosti. Preto vo fáze panuj potrebujeme tieto dve polia zlúčiť (merge) do výsledného poľa.

int mergesort(int a[], int low, int high){
    if (low>=high) return 0;

    // rozdeluj
    int mid=(low+high)/2;

    //rekurzivne volanie na dva podpripady
    mergesort(a,low,mid);
    mergesort(a,mid+1,high);

    //panuj 
    return merge(a,low,high,mid);
}

Zlučovanie utriedených podpolí

Zaujímavým problémom je zlúčenie dvoch utriedených postupností. Máme dve utriedené postupnosti A[0..N-1] a B[0..M-1].

• Je úplne jasné, že prvým prvkom výslednej postupnosti bude menší z prvkov A[0] a B[0].

Potom ostávajú postupnosti A[1..N-1] a B[0..M-1] alebo A[0..N-1] a B[1..M-1].

• Vo všeobecnosti máme teraz postupnosti A[i..N-1] a B[j..M-1]. Ďalším prvkom postupnosti bude buď A[i] alebo B[j] a ostanú nám postupnosti A[i+1..N-1] a B[j..M-1] alebo A[i..N-1] a B[j-1..M-1].
• Toto robíme dovtedy, kým s jedným poľom neskončíme. Vtedy na koniec dokopírujeme zyvšok druhého poľa.

Z toho dostávame nasledovný program.

void merge(int A[],int B[],int N, int M){
 int i=0,j=0;
 int C[100];

 while((i<N)&&(j<M)){
  if(A[i]<=B[j]){
   C[i+j]=A[i++]; // vysledok ukladame na (i+j)-te miesto
  }
  else{
   C[i+j]=B[j++]; // vysledok ukladame na (i+j)-te miesto
  }
 }

 if (i<N){        // skoncilo pole B
  for(;i<N;i++){
   C[i+j]=A[i];
  }
 }
 else {           // skoncilo pole A
  for(;j<M;j++){
   C[i+j]=B[j];
  }
 }
}

Tento postup sa dá mierne upraviť, ak si uvedomíme, že vlastne vieme, ako dlho zapisujeme z jednej postupnosti (napríklad A). Je to do chvíle, kým jej prvý prvok nebude väčší, ako prvý prvok z postupnosti druhej (B).

void merge(int A[],int B[],int N, int M){
 int i=0,j=0;
 int* C=new int[N+M];

 while((i<N)&&(j<M)){
  while ((A[i]<=B[j])&&(i<N)){
      C[i+j]=A[i++];
  }

  while (B[j]<=A[i]&&(j<M)){
      C[i+j]=B[j++];
  }  
 }

  for(;i<N;i++){  // ktore pole skoncilo testovat netreba, lebo cyklus prinajhorsom neprebehne
   C[i+j]=A[i];
  }
  for(;j<M;j++){
   C[i+j]=B[j];
  }
 delete[] C;
}

Výsledný MergeSort

Ostáva už iba drobnosť. My nezlučujeme dve nezávislé polia ale prvky jedného poľa a navyše by sme radi, aby tie prvky v tomto poli aj skončili.

• Prvá časť sa bude riešiť jednoducho. Nepotrebujeme teda ako parameter dve polia ale iba jedno (A[]) ale zato potrebujeme miesta odkiaľ a pokiaľ sú jednotlivé úseky.
  • Pre začiatok by sme teda mali parametre int A[], int zaciatok1, int koniec1, int zaciatok2, int koniec2.
  • Avšak jediné úseky, ktoré zlučujeme sú úseky idúce za sebou, ktoré sme iba rozdelili na nejakom mieste - pôvodne sme mali interval (low, high) a my sme ho rozdelili na intervaly (low, mid) a (mid+1,high). Na identifikáciu takýchto úsekov potom stačia parametre low a high.
• Druhý problém vieme vyriešiť jednoducho - pomocné pole na konci nakopírujeme naspäť.
  • A nič oveľa inteligentnejšie nebudeme robiť - zbytočne by sme si niečo prepísali - toto nie je rekurzívna fáza, tu sa to pole vždy umaže hned po využití.

#include<iostream>

using namespace std;

void merge(int A[],int low, int high){
 int i=low, j=(high+low)/2+1;      // indexy v poli A
 int k=0;                          // index v poli C
 int N=j, M=high+1;                // zarazky indexov i a j
 int* C=new int[high-low+1];

 while((i<N)&&(j<M)){
  while ((A[i]<=A[j])&&(i<N)){
      C[k++]=A[i++];
  }

  while (A[j]<=A[i]&&(j<M)){
      C[k++]=A[j++];
  }  
 }

  for(;i<N;i++){  // ktore pole skoncilo testovat netreba, lebo cyklus prinajhorsom neprebehne
   C[k++]=A[i];
  }
  for(;j<M;j++){
   C[k++]=A[j];
  }
 
 for (int kk=low; kk<=high; kk++) A[kk]=C[kk-low];
 
 delete[] C;
 
}


void mergesort(int A[], int low, int high){
    if (low>=high) return;

    // rozdeluj
    int mid=(low+high)/2;

    //rekurzivne volanie na dva podpripady
    mergesort(A,low,mid);
    mergesort(A,mid+1,high);

    //panuj 
    merge(A,low,high);
}

int main(void){
    int A[]={135,1,58,75,12,45,7,100,23,467};
    mergesort(A,0,9);
    for (int i=0; i<10; i++) cout<< A[i]<< " ";
}

Ukážka na príklade

Pole A[]={135,1,58,75,12,45,7,100,23,467}

Merge (0,0,1): 135     1  -> 1 135 
Merge (0,1,2): 1 135     58  -> 1 58 135 
Merge (3,3,4): 75     12  -> 12 75 
Merge (0,2,4): 1 58 135     12 75  -> 1 12 58 75 135 
Merge (5,5,6): 45     7  -> 7 45 
Merge (5,6,7): 7 45     100  -> 7 45 100 
Merge (8,8,9): 23     467  -> 23 467 
Merge (5,7,9): 7 45 100     23 467  -> 7 23 45 100 467 
Merge (0,4,9): 1 12 58 75 135     7 23 45 100 467  -> 1 7 12 23 45 58 75 100 135 467 

Quicksort

Quicksort je tiež založený na metóde rozdeľuj a panuj. Aby utriedil pole N prvkov, rozdelí si ich na menšie a väčšie prvky, ktoré potom utriedi. Štruktúra programu je nasledovná:

• Rozdeľuj: prvky rozdelí na dve skupiny (menšie a väčšie prvky). Ako uvidíme neskôr, čo sú väčšie a menšie prvky závisí na spracovávaných prvkoch. Celkovo môžeme povedať, že menšie prvky sú menšie ako väčšie prvky (logické, nie?)
• Rekurzívne sa zavolá na každú skupinu prvkov a dostáva dve utriedené postupnosti - utriedenú postupnosť menších prvkov a utriedenú postupnosť väčších prvkov.
• Panuj: Keďže menšie prvky sú všetky menšie ako prvky väčšie pole N prvkov je utriedené, ak dáme tieto dve postupnosti proste za seba, najskôr utriedené menšie prvky, potom utriedené väčšie prvky.

void quicksort(int A[], int l, int r){
if (l>=r) return;

// rozdelenie
pivot=divide(A, l, r);

// reukrzivne volanie na mensie a vacsie prvky
quicksort(A,l,pivot);
quicksort(A,pivot+1,r);

//zlucenie nebude treba - su spravne za sebou
}

Jednoduché rozdelenie prvkov

Najprv si ukážeme jednoduchý spôsob, ako pole správne rozdeliť. Budeme si naozaj vytvárať 2 polia (Cmensie a Cvacsie), do ktorého prvky z poľa A (teda z jeho podpoľa A[l..r]) budeme rozdeľovať. Každé z týchto polí bude mať veľkosť najviac r-l.

Špeciálne si oddelíme pivot, aby sme si ho niekde neprepísali (mohli sme si vytvárať polia 3 - väčšie, menšie a rovné).

Následne do poľa A[l..r] nakopírujeme najskôr pole Cmensie, potom pivot (jeho pozíciu si zapamatáme) a nakoniec pole Cvacsie. Takto upravené pole a hodnotu na ktorej sa nachádza pivot môžeme vrátiť.

int divide(int A[], int l, int r){
    int pivot=l;    //alebo lubovolny iny prvok z intervalu
    int pivothodnota=A[pivot];
    int* Cmensie=new int[r-l];
    int* Cvacsie=new int[r-l];
    
    int i1=0,i2=0;
    for (int i=l; i<=r; i++){
        if (i==pivot) continue;
        else if (A[i]<=A[pivot]) Cmensie[i1++]=A[i];
        else Cvacsie[i2++]=A[i];
    }
    for (int i=0; i<i1; i++){
        A[l+i]=Cmensie[i];
    }

    pivot=l+i1;
    A[pivot]=pivothodnota;
    
    for (int i=0; i<i2; i++){
        A[pivot+1+i]=Cvacsie[i];
    }
    
    delete[] Cmensie;
    delete[] Cvacsie;
    
    return pivot; // hodnota na ktorej je teraz realne pivot
}

Pri takomto rozdeľovaní poľa by sme sa mohli rekurzívne volať iba na časti A[l..pivot-1] a A[pivot+1..r] resp. na ešte kratšie úseky ak by sme si pamätali aj prvky rovné pivotu.

Rozdelenie prvkov priamo v poli (inplace quicksort)

Rozdelenie prvkov na menšie a väčšie sa dá vykonávať aj priamo v poli - bez pomocných polí. Myšlienka je nasledovná:

• Zvolíme si hodnotu, na základe ktorej budeme prvky deliť.
• Zľava pozeráme na prvky v poli - ktoré môžu byť v tejto polovici (sú menšie ako pivot), tak tam necháme a keď narazíme na väčší (alebo rovný), zastavíme.
• Podobne sprava - ktoré môžu byť v tejto polovici (sú väčšie ako pivot), tak tam necháme a keď narazíme na menší (alebo rovný), zastavíme.
• V jednej chvíli sme zastavili z oboch krajov a máme dva prvky - jeden je menší a druhý väčší ako pivot. V prípade, že sú v tých nesprávnych poloviciach (teda ak ten väčší je naľavo od menšieho) tak ich vymeníme.
• V prípade, že sme našli prvky, ktoré však už sú v správnych poloviciach znamená to, že sa nám už naše dva indexy niekedy stretli. V tom pripade viem, že naľavo od j máme iste iba čísla menšie od pivota (lebo touto časťou už index i prechádzal) - podobne to platí aj napravo od i.

int divide(int A[], int l, int r){
    int i=l, j=r;
    int pivothodnota=A[1]; 
    
    while (i<j){
        while (A[i]<pivothodnota) i++;
        while (A[j]>pivothodnota) j--;
        if (i<j) {
            int temp=A[i]; A[i]=A[j]; A[j]=temp; 
        }
    }
    return j;
}

Takto napísaná funkcia funguje iba pre rôzne čísla. Uvedomte si, že pri výmene dvoch rovnakých čísel (môže sa stať, ak sú vybraným pivotom) sa zacyklíme. Preto vo finálnej verzii upravíme rozdelenie tak, aby fungovalo aj pre opakované čísla.

Výsledný quicksort

int divide(int A[], int l, int r){
    int v=A[r]; // zvolim si pivot a odlozim si ho na kraj (alebo rovno zvolim krajny prvok)
    int i=l-1, j=r;
    int temp;
    while (i<j){
        while (A[++i]<v);
        while (A[--j]>v);
        if (i>=j) break;
        temp=A[i]; A[i]=A[j]; A[j]=temp;
    }
    temp=A[i]; A[i]=A[r]; A[r]=temp; // vratim pivot kam patri
    return i;
} 

void quicksort(int A[], int l, int r){
if (l>=r) return;

// rozdelenie
int pivot=divide(A, l, r);

// reukrzivne volanie na mensie a vacsie prvky
quicksort(A,l,pivot-1);
quicksort(A,pivot+1,r);

//zlucenie nebude treba - su spravne za sebou
}

Občas sa môžete stretnúť aj s takto napísaným quicksortom. Skúste si premyslieť, prečo funguje a prečo si môžem dovoliť niektoré prvky vynechať.

void quickSort(int A[], int left, int right) {
    if (left>=right) return;
    int i = left, j = right;
    int pivot = A[(left + right) / 2];

    /* partition */
    while (i <= j) {
        while (A[i] < pivot) i++;
        while (A[j] > pivot) j--;
        if (i <= j) {
            int tmp = A[i]; A[i] = A[j]; A[j] = tmp;
            i++; j--;
        }
    };

    /* recursion */
    quickSort(A, left, j);
    quickSort(A, i, right);
}

Príklad

Divide (0,8): 1 2 5 7 3       14 7 26 12 
Divide (0,4): 1 2 3       7 5 
Divide (0,2): 1    2    3 
Divide (3,4): 5       7 
Divide (5,8): 7       14 26 12 
Divide (6,8): 14 12       26 
Divide (6,7): 12       14 

Odhad zložitosti

Zjavne sa vyskytujú dobré a zlé prípady. Ideálne je, keď sa nám podarí rozdeliť pole na dve rovnaké časti. Vtedy má quicksort zložitosť O(N.log N), čiže lepšiu, ako triedenia, ktoré sme ukázali na prednáške 6.

Nepríjemné je, keď sa nám podarí pole vždy rozdeliť na dve podpolia, z ktorých jedno má iba jeden prvok. Toto spôsobí, že v takýchto prípadoch potrebujeme až Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle O(N^2)} . Dobrá správa je, že takýchto prípadov nie je príliš veľa.

• Vymyslite príklad, kde by nastalo nevhodné rozdelenie. Závisí to samozrejme od toho, ako vyberáme pivota. Zamyslite sa nad prípadmi pivot=A[1] a pivot=A[(l+r)/2].

Medián

Medián z prvkov je prvok, ktorý po utriedení je v strede poľa. Pre N prvkové pole je teda (N/2)-ty najmenší prvok. Ako hľadať medián.

Jednoduché riešenie

Najjednoduchšie bude prvky si utriediť a následne pozrieť na A[n/2].

k-ty najmenší prvok

Druhá možnosť je si uvedomiť, že pri triedení quicksortom sme vlastne niektoré časti nemuseli triediť, keď by sme vedeli, že v nich medián nie je. Všeobecne budeme hľadať k-ty najmenší prvok.

• Pole si rozdelíme ako pri quicksorte. Nech prvá časť má x prvkov. Potom
  • ak k<x, stačí nám hľadať k-ty najmenší prvok v prvej časti
  • ak k>x, potrebujeme nájsť (k-x)-tý prvok v druhej časti

int Select(int A[], int l, int r, int k){
    if ((l==r)&&(k==0)) return A[l];
    else if (l>=r) return -1;

    int pivot=divide2(A,l,r);
    if (k<pivot-l) Select(A,l,pivot-1,k);
    else if (k>pivot-l) Select(A,pivot+1,r, k-pivot+l-1);
    else return A[pivot];
}

Prednáška 17

Oznamy

• Aj napriek dekanskému voľnu bežíme podľa normálneho rozvrhu: v piatok sa objaví domáca úloha 9, budúci utorok termín domácej úlohy 8, budúci týždeň rozcvička z rekurzie.
• Ešte stále sa neprihlásil majiteľ nepodpísanej rozcvičky č. 5.
• Reklamácie známok z DÚ 1-5 a rozcvičiek 1-6 do budúceho piatku (25.11.).
• Ak máte problémy s domácimi úlohami alebo učivom tak vôbec, príďte sa poradiť.

Opakovanie: generovanie všetkých variácií s opakovaním

Vypíšte všetky usporiadané k-tice čísel, pričom každé číslo je z množiny {0..n-1} a čísla sa môžu opakovať (variácie k-tej triedy z n prvkov). Napr. pre k=3, n=2:

000
001
010
011
100
101
110
111

#include <iostream>
using namespace std;

void vypis(int a[], int k) {
    for (int i = 0; i < k; i++) {
        cout << a[i];
    }
    cout << endl;
}

void generuj(int a[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        vypis(a, k);
    } else {
        for (int x = 0; x < n; x++) {
            a[i] = x;
            generuj(a, i + 1, k, n);
        }
    }
}

int main(void) {
    int k, n;
    cin >> k >> n;
    int *a;
    a = new int[k];
    generuj(a, 0, k, n);
    delete[] a;
}

Generovanie všetkých podmnožín

Chceme vypísať všetky podmnožiny množiny {0,..,m-1}. Na rozdiel od variácií nám v podmnožine nezáleží na poradí (napr. {0,1} = {1,0}), prvky teda budeme vždy vypisovať od najmenšieho po najväčší. Napr. pre m=2 máme podmnožiny

{}
{0}
{0,1}
{1}

Podmnožinu vieme vyjadriť ako binárne pole dĺžky m, kde a[i]=0 znamená, že i nepatrí do množiny a a[i]=1 znamená, že patrí. Teda môžeme použiť predchádzajúci program pre n=2,k=m a zmeniť iba výpis:

void vypis(int a[], int m) {
    cout << "{";
    string oddelovac = "";
    for (int i = 0; i < m; i++) {
        if (a[i] == 1) {
            cout << oddelovac;
            oddelovac = ",";
            cout << i;
        }
    }
    cout << "}" << endl;
}

• V premennej oddeľovač si pamätáme, akým reťazcom máme oddeliť ďalšie vypisované číslo od prechdádzajpceho.
  • Ak ešte žiadne nebolo, oddeľovač je prázdny reťazec.
  • Ak už sme niečo vypísali, oddeľovač je čiarka.

Namiesto poľa intov môžeme použiť pole boolovských hodnôt a celý program trochu prispôsobiť tomu, že generujeme podmnožiny:

#include <iostream>
using namespace std;

void vypis(bool a[], int m) {
    cout << "{";
    string oddelovac = "";
    for (int i = 0; i < m; i++) {
        if (a[i]) {
            cout << oddelovac;
            oddelovac = ",";
            cout << i;
        }
    }
    cout << "}" << endl;
}

void generuj(bool a[], int i, int m) {
    /* v poli a dlzky k mame rozhodnutie o prvych i
     * prvkoch, chceme vygenerovat vsetky podmnoziny
     * prvkov {i..m-1} */
    if (i == m) {
        vypis(a, m);
    } else {
        a[i] = true;
        generuj(a, i + 1, m);
        a[i] = false;
        generuj(a, i + 1, m);
    }
}

int main(void) {
    int m;
    cin >> m;
    bool *a;
    a = new bool[m];
    generuj(a, 0, m);
    delete[] a;
}

Pre n=3 program vypíše:

{0,1,2}
{0,1}
{0,2}
{0}
{1,2}
{1}
{2}
{}

Čo by vypísal, ak by sme prehodili true a false v rekurzii?

Problém batoha, Knapsack problem

Zlodej sa vlúpal do obchodu a vidí n vecí, pričom pre každú z nich vie odhadnúť jej hmostnosť a cenu, za ktorú by ju vedel predať. V svojom batohu však vie odniesť len veci s celkovou hmotnosťou najviac W kilogramov. Ako má vybrať veci, aby mali čo najväčšiu cenu a aby ich celková hmostnosť neprekročila W?

Príklad: majme n=3 veci, pričom vec 0 má hmostnoť 10 a cenu 6, vec 1 má hmotnosť 8 a cenu 4 a vec 2 má hmotnosť 6 a cenu 3. Zlodej unesie najviac 15. Do súboru to zapíšeme takto:

3
10 6
8 4
6 3
15

Najlepšie je zobrať veci 1 a 2. Ich cena je 7 a súčet hmotností 14.

Tento problém ešte stretnete v ďalších ročníkoch štúdia, teraz si ukážeme jednoduchý program, ktorý prehľadáva všetky možnosti.

Jednoduché riešenie: pozeráme všetky podmnožiny

Ako predtým, generujeme všetky podmnožiny a pre každú spočítame, či jej hmotnosť nepresahuje nosnosť batoha. Podmnožiny však nevypisujeme, ale porovnávame s najlepšou nájdenou doteraz.

#include <iostream>
using namespace std;

/* struktura na ukladanie udajov o jednej veci */
struct vec {
    int hmotnost;
    int cena;
};

/* globalne premenne pouzivane v rekurzii */
int n;           /* celkovy pocet veci v obchode */
vec *a;          /* pole veci */
int maxCena;     /* najlepsie doteraz najdene riesenie */
bool *maxZober;  /* ktore veci su v najlepsom rieseni */
int nosnost;     /* kolko unesie batoh */

/* spocitaj sucet hmotnosti vybranych predmetov */
int sucetHmotnosti(bool zober[]) {
    int sucet = 0;
    for (int i = 0; i < n; i++) {
        if(zober[i]) sucet += a[i].hmotnost;
    }
    return sucet;
}

/* spocitaj sucet cien vybranych predmetov */
int sucetCien(bool zober[]) {
    int sucet = 0;
    for (int i = 0; i < n; i++) {
        if(zober[i]) sucet += a[i].cena;
    }
    return sucet;
}

/* vypis zoznam vybranych predmetov */
void vypis(bool zober[]) {
    cout << "Zober predmety ";
    string oddelovac = "";
    for (int i = 0; i < n; i++) {
        if (zober[i]) {
            cout << oddelovac;
            oddelovac = ", ";
            cout << i;
        }
    }
    cout << ". Ich cena je " << sucetCien(zober) << "." << endl;
}

void generuj(bool zober[], int i) {
    /* v poli a dlzky k mame rozhodnutie o prvych i
     * prvkoch, chceme vygenerovat vsetky podmnoziny
     * prvkov {i..n-1} a kazdu skontrolovat a porovnat s maximom */
    if (i == n) {
        /* uz sme sa rozhodli o kazdom prvku. Zistime, ci mame hmostnost
         * vybranych predmetov <= nosnost */
        if(sucetHmotnosti(zober)<=nosnost) {
            /* ak ano, zistime, ci cena vybranych predmetov
             * je viac ako doteraz najlepsie maximum */
            int cena = sucetCien(zober);
            if(cena>maxCena) {
                /* prekopiruj sucasny vyber do najlepsieho */
                maxCena = cena;
                for(int i=0; i<n; i++) {
                    maxZober[i] = zober[i];
                }
            }
        }
    } else {
        /* dosad true aj false na miesto i
         * a skusaj vsetky moznosti pre zvysok pola */
        zober[i] = true;
        generuj(zober, i+1);
        zober[i] = false;
        generuj(zober, i+1);
    }
}

int main(void) {
    /* nacitame pocet predmetov n */
    cin >> n;
    /* alokujeme pole a nacitame hmotnost a cenu predmetov */
    a = new vec[n];
    for(int i=0; i<n; i++) {
        cin >> a[i].hmotnost >> a[i].cena;
    }
    /* nacitame nostnost */
    cin >> nosnost;

    /* alokuj polia potrebne pre rekurziu*/
    bool *zober = new bool[n];
    maxZober =  new bool[n];
    maxCena = -1; /* doteraz najlepsie riesenie ma cenu -1 */

    generuj(zober, 0); /* prehladavj vsetky moznosti */

    vypis(maxZober); /* vypis najlepsie najdene riesenie */

    /* uvolni pamat */
    delete[] a;
    delete[] zober;
    delete[] maxZober;
}

• Ako by sme mohli globálne premenné odstrániť?
• Aké sú ich výhody a nevýhody?

Trochu rýchlejší program: skončíme vždy keď prekročíme nosnosť

Ked uz sme sa rozhodli o prvých i prvkoch, spočítame hmotnosť tých, čo sme vybrali, a ak prekračuje nosnosť, túto vetvu hľadania ukončíme - nemá zmysel dopĺňať ďalšie hodnoty do zvyšku poľa, ak už zvolené veci sú príliš ťažké.

/* spocitaj sucet hmotnosti vybranych predmetov,
 * ale uvazujme iba prvych k predmetov  */
int sucetHmotnosti(bool zober[], int k) {
    int sucet = 0;
    for (int i = 0; i < k; i++) {
        if(zober[i]) sucet += a[i].hmotnost;
    }
    return sucet;
}

void generuj(bool zober[], int i) {
    /* v poli a dlzky k mame rozhodnutie o prvych i
     * prvkoch, chceme vygenerovat vsetky podmnoziny
     * prvkov {i..n-1} a kazdu skontrolovat a porovnat s maximom */

    /* ak uz sme prekrocili nosnost, nemusime pokracovat v hladani */
    if(sucetHmotnosti(zober, i) > nosnost) return;
    if (i == n) {
        /* uz sme sa rozhodli o kazdom prvku.
         * Sucasne vieme, ze hmostnost
         * vybranych predmetov <= nosnost.
         * Zistime teda, ci cena vybranych predmetov
         * je viac ako doteraz najlepsie maximum */
        int cena = sucetCien(zober);
        if (cena > maxCena) {
            /* prekopiruj sucasny vyber do najlepsieho */
            maxCena = cena;
            for (int i = 0; i < n; i++) {
                maxZober[i] = zober[i];
            }
        }
    } else {
        /* dosad true aj false na miesto i
         * a skusaj vsetky moznosti pre zvysok pola */
        zober[i] = true;
        generuj(zober, i + 1);
        zober[i] = false;
        generuj(zober, i + 1);
    }
}

Ešte rýchlejší program: neprepočítavame nosnosť a cenu vždy znovu a znovu

Predchádzajpci program vždy znovu a znovu prepočítava hmotnosť a cenu, aj keď sa zoznam vybraných predmetov zmení iba trochu. Namiesto toho si môžeme v rekurzii udržiavať aktuálnu hmotnosť aj cenu doteraz vybraných predmetov.

void generuj(bool zober[], int i, int hmotnost, int cena) {
    /* v poli a dlzky k mame rozhodnutie o prvych i
     * prvkoch, hmotnost je sucet hmotnosti uz vybranych predmetov
     * a cena je sucet ich cien.
     * Chceme vygenerovat vsetky podmnoziny
     * prvkov {i..n-1} a kazdu skontrolovat a porovnat s maximom */

    /* ak uz sme prekrocili nosnost, nemusime pokracovat v hladani */
    if(hmotnost > nosnost) return;
    if (i == n) {
        /* uz sme sa rozhodli o kazdom prvku.
         * Sucasne vieme, ze hmostnost
         * vybranych predmetov <= nosnost.
         * Zistime teda, ci cena vybranych predmetov
         * je viac ako doteraz najlepsie maximum */
        if (cena > maxCena) {
            /* prekopiruj sucasny vyber do najlepsieho */
            maxCena = cena;
            for (int i = 0; i < n; i++) {
                maxZober[i] = zober[i];
            }
        }
    } else {
        /* dosad true aj false na miesto i
         * a skusaj vsetky moznosti pre zvysok pola */
        zober[i] = true;
        generuj(zober, i + 1, hmotnost + a[i].hmotnost, cena + a[i].cena);
        zober[i] = false;
        generuj(zober, i + 1, hmotnost, cena);
    }
}

Späť k Sudoku

Chceme riešiť hlavolam Sudoku. Máme danú plochu 9x9 políčok, pričom niektoré sú prázdne, iné obsahujú číslo z množiny {1..9}. Plocha je rozdelená do 9 štvorcov 3x3. Cieľom je doplniť čísla do prázdnych štvorčekov tak, aby v každom riadku plochy, v každom stĺpci plochy a v každom štvorci 3x3 bola každá cifra {1..9} práve raz.

. 3 . | . 7 . | . . .
6 . . | 1 9 5 | . . .
. 9 8 | . . . | . 6 .
---------------------
8 . . | . 6 . | . . 3
4 . . | 8 . 3 | . . 1
. . . | . 2 . | . . 6
---------------------
. 6 . | . . . | 2 8 .
. . . | 4 . 9 | . . 5
. . . | . 8 . | . 7 .

Príklad vstupu a výstupu:

Vstup:                   Vystup:
0 3 0 0 7 0 0 0 0	 5 3 4 6 7 8 9 1 2
6 0 0 1 9 5 0 0 0	 6 7 2 1 9 5 3 4 8
0 9 8 0 0 0 0 6 0	 1 9 8 3 4 2 5 6 7
8 0 0 0 6 0 0 0 3	 8 5 9 7 6 1 4 2 3
4 0 0 8 0 3 0 0 1	 4 2 6 8 5 3 7 9 1
0 0 0 0 2 0 0 0 6	 7 1 3 9 2 4 8 5 6
0 6 0 0 0 0 2 8 0	 9 6 1 5 3 7 2 8 4
0 0 0 4 0 9 0 0 5	 2 8 7 4 1 9 6 3 5
0 0 0 0 8 0 0 7 0        3 4 5 2 8 6 1 7 9

                         Pocet rieseni: 1

Naša rekurzívna procedúra bude postupovať nasledovne:

• nájde na ploche prázdne políčko, ak také nie je, vypíše riešenie a skončí
• do prázdneho políčka skúša vložiť čísla 1...9 a testuje, či nenastane konflikt v riadku, stĺpci alebo štvorci
• ak niektoré číslo sedí, zavolá sa rekurzívne na vyplnenie zvyšných bielych miest

Na konci prednášky 15 sme videli dosť zložitý program na riešenie Sudoku, tu je o niečo jednoduchší. Používa len obyčajnú maticu čísel 0..9, kde 0 znamená prázdne políčko a vo funkcii moze testuje, či sa určité číslo dá dať na určité políčko.

#include <iostream>
using namespace std;

void vypis(int **a) {
    /* vypis riesenie sudoku */
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            cout << " " << a[i][j];
        }
        cout << endl;
    }
    cout << endl;
}

void najdiVolne(int **a, int &riadok, int &stlpec) {
    /* najdi volne policko na ploche a uloz jeho suradnice
     * do premennych riadpk a stlpec. Ak nie je, uloz -1. */
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            if (a[i][j] == 0) {
                riadok = i;
                stlpec = j;
                return;
            }
        }
    }
    riadok = -1;
    stlpec = -1;
}

bool moze(int **a, int riadok, int stlpec, int hodnota) {
    /* Mozeme ulozit danu hodnotu na dane policko?
     * Da sa to, ak riadok, stlpec, ani stvorec nema
     * tuto hodnotu este pouzitu. */
    for (int i = 0; i < 9; i++) {
        if (a[riadok][i] == hodnota) return false;
        if (a[i][stlpec] == hodnota) return false;
    }
    /* lavy horny roh stvorca */
    int riadok1 = riadok - riadok % 3;
    int stlpec1 = stlpec - stlpec % 3;
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
            if (a[riadok1 + i][stlpec1 + j] == hodnota) return false;
        }
    }
    return true;
}

int generuj(int **a) {
    /* mame ciastocne vyplnenu plochu sudoku,
     * chceme najst vsetky moznosti, ako ho dovyplnat
     * a vratit ich pocet.  */

    /* najdeme volne policko */
    int riadok, stlpec;
    najdiVolne(a, riadok, stlpec);

    /* ak uz ziadne nie je, vypiseme riesenie */
    if (riadok < 0) {
        vypis(a);
        return 1;
    } else {
        /* Do volneho policka dosadzujeme cifry 1..9,
         * volame rekurzivne vyplnanie ostatnych policok. */
        int pocet = 0; /* pocet rieseni */
        for (int x = 1; x <= 9; x++) {
            if (moze(a, riadok, stlpec, x)) {
                a[riadok][stlpec] = x;
                pocet += generuj(a);
                a[riadok][stlpec] = 0;
            }
        }
        return pocet;
    }

}

int main(void) {
    /* alokujeme a nacitame 2D maticu so vstupom */
    int **a = new int *[9];
    for (int i = 0; i < 9; i++) {
        a[i] = new int[9];
    }
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            cin >> a[i][j];
        }
    }
    /* rekurzivne prehladavanie s navratom */
    int pocet = generuj(a);

    /* vypis riesenia */
    cout << "Pocet rieseni: " << pocet << endl;
    /* este by sme mali odalokovat polia v sudoku */
}

Program na konci prednášky 15 si udržiaval pre každý riadok, stĺpec a štvorec boolovské hodnoty, či je dané číslo už použité. Tým pádom vedel funkciu moze spraviť rýchlejšie, program však bol zložitejší a ťažšie pochopiteľný.

Vyfarbovanie súvislých oblastí

Máme daný obrázok pozostávajúci z m riadkov a n stĺpcov pixelov, každý pixel určitej farby. V našom jednoduchom príklade budeme uvažovať iba 4 farby, ktoré budeme zapisvať číslami 0,..,3 a ktorých význam bude daný týmto poľom, takže napr. farba 0 je biela:

const string farby[4] = {"white", "green", "black", "brown"};

Užívateľ si zvolí určitý pixel obrázku a chce vyfarbiť celú súvislú jednofarebnú oblasť obsahujúcu tento pixel novou farbou. Ak napríklad začneme vyfarbovať v obrázku vľavo farbou 3 (hnedou) od pixelu (0,0), dostaneme obrázok napravo:

• 
• 

Tu je pôvodný obrázok v textovej forme, ako matica čísel.

11 17
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0
 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0
 0 0 0 1 0 0 0 0 0 2 2 1 2 2 2 2 0
 0 0 0 1 0 0 0 0 0 2 0 1 0 0 0 2 0
 0 2 2 2 2 2 2 2 0 2 2 1 2 2 2 2 0
 0 2 0 1 0 0 0 2 0 0 0 1 0 0 0 0 0
 0 2 0 1 0 0 0 2 0 0 0 1 0 1 1 1 1
 0 2 0 1 1 1 1 2 1 1 1 1 0 1 0 0 1
 0 2 0 0 0 0 0 2 0 0 0 0 0 1 1 1 1
 0 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 0

Túto úlohu vieme vyriešiť nasledujúcou rekurzívnou funkciou, ktorá prefarbí zadané políčko a potom rekurzívne pokračuje vo vyfarbovaní vo všetkých susedoch, ktorí majú rovnakú farbu, ako pôvodne malo toto políčko.

void vyfarbi(int **a, int n, int m, int riadok, int stlpec, int farba) {
    /* prefarbi suvislu jednofarebnu oblast obsahujucu 
     * a[riadok][stlpec] na farbu farba */

    if (a[riadok][stlpec] != farba) {
        int stara_farba = a[riadok][stlpec];
        a[riadok][stlpec] = farba;
        if (riadok > 0 && a[riadok - 1][stlpec] == stara_farba) {
            vyfarbi(a, n, m, riadok - 1, stlpec, farba);
        }
        if (riadok + 1 < n && a[riadok + 1][stlpec] == stara_farba) {
            vyfarbi(a, n, m, riadok + 1, stlpec, farba);
        }
        if (stlpec > 0 && a[riadok][stlpec - 1] == stara_farba) {
            vyfarbi(a, n, m, riadok, stlpec - 1, farba);
        }
        if (stlpec + 1 < m && a[riadok][stlpec + 1] == stara_farba) {
            vyfarbi(a, n, m, riadok, stlpec + 1, farba);
        }
    }
}

Susedov náš program pozerá v poradí hore, dole, doľava, doprava.

• V akom poradí vyfarbí políčka nulovej matice 2x2 ak začne v ľavom hornom rohu?
• V akom poradí vyfarbuje jednoriadkovú maticu, ak začneme niekde v strede?

Zdrojový kód celého programu

• Tento program vytvorí maticu a vyfarbí v ňom jednu oblasť aj s animáciou: #Ukážkový program vyfarbovanie

Použitie vyfarbovania na mape

Spomeňme si na program na prácu s výškovou mapu z prednášky 12. Máme zadanú mapu ako maticu celých čísel, v ktorej 0 znamená more a kladné čísla nadmorskú výšku pevniny. Budeme predpokladať, že na mape je niekoľko ostrovov, ktoré sú plne obkolesené morom a nemajú žiadne vnútorné moria ani jazerá. Chceme spočítať, koľko tam tých ostrovov je.

Použijeme na to vyfarbovanie z predchádzajúceho programu.

• Prejdeme maticu a všetky kladné čísla prepíšeme na 1. Máme teda 0 vyznačené more a 1 ostrovy.
• Prechádzame maticu a vždy, keď nájdeme 1 (ešte nepreskúmaný ostrov), vyfarbíme ho farbou 2 a zvýšime počet ostrovov.
• Nakoniec máme more ako 0 a všetky ostrovy ako 2.

Príklad mapy a jej zobrazenie po prepísaní kladných čísel na 1 (zelená), po vyfarbení prvého ostrova číslom 2 (čiernou) a po vyfarbení všetkých ostrovov.

11 17
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 1 9 1 1 1 0 0 1 1 0 0 0 0 0
 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0
 0 0 0 1 0 0 0 0 0 1 1 1 0 0 1 1 0
 0 0 0 1 0 0 0 0 0 2 0 0 0 0 0 1 0
 0 1 0 0 2 2 2 2 0 2 2 1 7 1 1 1 0
 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 7 0 1 0 0 0 2 0 0 0 1 0 1 1 1 0
 0 0 0 1 5 1 1 2 1 1 3 1 0 1 2 2 0
 0 1 0 0 0 1 1 2 2 0 0 0 0 1 1 1 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

• 
• 
• 

Takto to naprogramujeme:

   for(int i=0; i<n; i++) {
        for(int j=0; j<m; j++) {
            if(a[i][j]>0) a[i][j] = 1;
        }
    }

    int ostrovov = 0;
    for(int i=0; i<n; i++) {
        for(int j=0; j<m; j++) {
            if(a[i][j]==1) {
                ostrovov++;
                vyfarbi(a, n, m, i, j, 2);
            }
        }
    }
    cout << "Pocet ostrovov: " << ostrovov << endl;

Zdrojový kód celého programu

• Tento program načíta maticu a zobrazuje vyfarbovanie ostrovov: #Ukážkový program ostrovy

Ukážkový program vyfarbovanie

Program vytvorí maticu a vyfarbí v nej jednu oblasť aj s animáciou.

#include "../SimpleDraw.h"
#include <iostream>

const string farby[4] = {"white", "green", "black", "brown"};
/* velkost stvorceka mapy v pixeloch */
const int stvorcek = 15;
/* cakanie po kazdom kroku vysvetlovania */
double waitTime = 0.3;

int ** vytvorMaticu(int n, int m) {
    /* vytvor maticu s n riadkami a m stlpcami */
    int **a;
    a = new int *[n];
    for (int i = 0; i < n; i++) {
        a[i] = new int[m];
    }
    return a;
}

void zmazMaticu(int n, int m, int **a) {
    /* uvolni pamat matice s n riadkami a m stlpcami */
    for (int i = 0; i < n; i++) {
        delete[] a[i];
    }
    delete[] a;
}

void zobrazStvorcek(int i, int j, int farba, string farbaCiary, SimpleDraw &window) {
    /* zobraz stvorcek v riadku i a stlpci j */
    window.setPenColor(farbaCiary);
    window.setBrushColor(farby[farba]);
    window.drawRectangle(j*stvorcek, i*stvorcek, stvorcek, stvorcek);
}

void zobrazMaticu(int **a, int n, int m, SimpleDraw &window) {
    /* zobraz vsetky stvorceky matice */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            zobrazStvorcek(i, j, a[i][j], "lightgray", window);
        }
    }
}

void obdlznik(int **a, int riadok, int stlpec, int vyska, int sirka, int farba) {
    /* do matice vykresli ram obdlznika urcitej farby */
    for (int i = 0; i < sirka; i++) {
        a[riadok][stlpec + i] = farba;
        a[riadok + vyska - 1][stlpec + i] = farba;
    }
    for (int i = 0; i < vyska; i++) {
        a[riadok + i][stlpec] = farba;
        a[riadok + i][stlpec + sirka - 1] = farba;
    }
}

void naplnMaticu(int **a, int n, int m) {
    /* do matice vykrelsi tri obdlzniky. Rozmery musia byt aspon
     * 11 riadkov a 17 stlpcov */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            a[i][j] = 0;
        }
    }
    obdlznik(a, 3, 9, 3, 7, 2);
    obdlznik(a, 1, 3, 8, 9, 1);
    obdlznik(a, 5, 1, 6, 7, 2);
    obdlznik(a, 7, 13, 3, 4, 1);
}

void vyfarbi(int **a, int n, int m, int riadok, int stlpec, 
             int farba, SimpleDraw &window) {
    /* prefarbi suvislu jednofarebnu oblast obsahujucu
     * a[riadok][stlpec] na farbu farba */

    if (a[riadok][stlpec] != farba) {
        int stara_farba = a[riadok][stlpec];
        a[riadok][stlpec] = farba;
        zobrazStvorcek(riadok, stlpec, a[riadok][stlpec], "red", window);
        window.wait(waitTime);
        if (riadok > 0 && a[riadok - 1][stlpec] == stara_farba) {
            vyfarbi(a, n, m, riadok - 1, stlpec, farba, window);
        }
        if (riadok + 1 < n && a[riadok + 1][stlpec] == stara_farba) {
            vyfarbi(a, n, m, riadok + 1, stlpec, farba, window);
        }
        if (stlpec > 0 && a[riadok][stlpec - 1] == stara_farba) {
            vyfarbi(a, n, m, riadok, stlpec - 1, farba, window);
        }
        if (stlpec + 1 < m && a[riadok][stlpec + 1] == stara_farba) {
            vyfarbi(a, n, m, riadok, stlpec + 1, farba, window);
        }
        zobrazStvorcek(riadok, stlpec, a[riadok][stlpec], "lightgray", window);
        window.wait(waitTime);
    }
}


int main(void) {
    int n = 11;
    int m = 17;
    int **a = vytvorMaticu(n, m);
    naplnMaticu(a, n, m);

    SimpleDraw window(m*stvorcek, n * stvorcek);
    zobrazMaticu(a, n, m, window);

    //vyfarbi(a, n, m, 1, 6, 3, window);
    vyfarbi(a, n, m, 0, 0, 3, window);

    window.showAndClose();

    zmazMaticu(n, m, a);
}

Ukážkový program ostrovy

Program načíta maticu s mapou a spočíta v nej ostrovy postupným vyfarbovaním, vykresľuje maticu graficky.

#include "../SimpleDraw.h"
#include <iostream>

const string farby[3] = {"white", "green", "black"};
/* velkost stvorceka mapy v pixeloch */
const int stvorcek = 15;

int ** vytvorMaticu(int n, int m) {
    /* vytvor maticu s n riadkami a m stlpcami */
    int **a;
    a = new int *[n];
    for (int i = 0; i < n; i++) {
        a[i] = new int[m];
    }
    return a;
}

void zmazMaticu(int n, int m, int **a) {
    /* uvolni pamat matice s n riadkami a m stlpcami */
    for (int i = 0; i < n; i++) {
        delete[] a[i];
    }
    delete[] a;
}


void nacitajMaticu(istream &in, int n, int m, int **a) {
    /* matica je vytvorena, velkosti n, m, vyplnime ju cislami zo vstupu */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            in >> a[i][j];
        }
    }
}

void zobrazStvorcek(int i, int j, int farba, string farbaCiary, SimpleDraw &window) {
    /* zobraz stvorcek v riadku i a stlpci j */
    window.setPenColor(farbaCiary);
    window.setBrushColor(farby[farba]);
    window.drawRectangle(j*stvorcek, i*stvorcek, stvorcek, stvorcek);
}

void zobrazMaticu(int **a, int n, int m, SimpleDraw &window) {
    /* zobraz vsetky stvorceky matice */
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            zobrazStvorcek(i, j, a[i][j], "lightgray", window);
        }
    }
}

void vyfarbi(int **a, int n, int m, int riadok, int stlpec, int farba) {
    /* prefarbi suvislu jednofarebnu oblast obsahujucu
     * a[riadok][stlpec] na farbu farba */

    if (a[riadok][stlpec] != farba) {
        int stara_farba = a[riadok][stlpec];
        a[riadok][stlpec] = farba;
        if (riadok > 0 && a[riadok - 1][stlpec] == stara_farba) {
            vyfarbi(a, n, m, riadok - 1, stlpec, farba);
        }
        if (riadok + 1 < n && a[riadok + 1][stlpec] == stara_farba) {
            vyfarbi(a, n, m, riadok + 1, stlpec, farba);
        }
        if (stlpec > 0 && a[riadok][stlpec - 1] == stara_farba) {
            vyfarbi(a, n, m, riadok, stlpec - 1, farba);
        }
        if (stlpec + 1 < m && a[riadok][stlpec + 1] == stara_farba) {
            vyfarbi(a, n, m, riadok, stlpec + 1, farba);
        }
    }
}


int main(void) {
    /* nacitaj rozmery matice */
    int n, m;
    cin >> n >> m;

    /* vytvor a nacitaj maticu */
    int **a = vytvorMaticu(n, m);
    nacitajMaticu(cin, n, m, a);

    for(int i=0; i<n; i++) {
        for(int j=0; j<m; j++) {
            if(a[i][j]>0) a[i][j] = 1;
        }
    }


    SimpleDraw window(m*stvorcek, n * stvorcek);
    zobrazMaticu(a, n, m, window);

    int ostrovov = 0;
    for(int i=0; i<n; i++) {
        for(int j=0; j<m; j++) {
            if(a[i][j]==1) {
                ostrovov++;
                vyfarbi(a, n, m, i, j, 2);
                window.clear();
                zobrazMaticu(a, n, m, window);
                window.show();
            }
        }
    }

    cout << "Pocet ostrovov: " << ostrovov << endl;

    window.showAndClose();
    zmazMaticu(n, m, a);
}

Cvičenia 8

Backtracking, prehľadávanie s návratom

• Napíšte rekurzívny program, ktorý pre dané čísla n a k (1<=k<=n) vypíše všetky podmnožiny veľkosti k množiny {0..n-1}. Na rozdiel od variácií nám v podmnožine nezáleží na poradí (napr. {0,1} = {1,0}), prvky teda budeme vždy vypisovať od najmenšieho po najväčší. Napr. pre n=3 a k=2 vypíšte

0 1
0 2
1 2

• Napíšte program, ktorý pre dané n, k a S vypíše všetky k-tice čísel z množiny {0..n-1}, ktorých súčet je aspoň S. Prehľadávanie zastavte vždy keď nie je možné súčet S dosiahnuť, ani keby všetky zvyšné čísla mali hodnotu n-1. Napríklad pre k=3, n=3, S=5 vypíšte

1 2 2
2 1 2
2 2 1
2 2 2

Rekurzívne vykresľovanie korytnačou grafikou

Napíšte rekurzívny program, ktorý bude vykresľovať strom korytnačou grafikou. Strom má dva parametre: veľkosť d a stupeň n. Strom stupňa 0 je prázdna množina. Strom stupňa n pozostáva z kmeňa, ktorý tvorí úsečka dĺžky n a z dvoch podstromov, ktoré sú stromy stupňa n-1, veľkosti d/2 a otočené o 30 stupnov doľava a doprava od hlavnej osi stromu (pozri obrázky nižšie). Pri vykresľovaní stromu sa s korytnačkou vráťte na miesto a otočenie, v ktorom ste začali (bez toho by sa len ťažko písala rekuzívna funkcia). Korytnačka teda prejde po každej vetve dvakrát, raz smerom dopredu a raz naspäť.

• 

  Strom stupňa 1

• 

  Strom stupňa 2

• 

  Strom stupňa 3

• 

  Strom stupňa 5

Grayov kód

• Vypíšte všetky k-tice binárnych hodnôt 0 a 1 tak, aby sa každé dve po sebe idúce k-tice sa líšili na najvaic jednom mieste a tiež posledná k-tica s prvou, ako v tomto príklade:

000
001
011
010
110
111
101
100

Takáto postupnosť sa nazýva Grayov kód. Ako vidno v tomto príklade, Grayov kód stupňa k sa dá zostaviť rekurzívne: horná polovica kódu stupňa k je Grayov kód stupňa k-1 s cifrou 0 pridanou na najlavejšiu pozíciu a druhá polovica kódu stupňa k je kód stupňa k-1 vypísaný odzadu s cifrou 1 pridanou na najlavejšiu pozíciu. Môžete použiť nasledovnú hlavičku rekurzívnej funkcie:

void gray(int a[], int k, int i, bool reverse) {
  /* Prvych i pozicii v poli a obsahuje hodnoty 0 a 1,
   * Do zvysnych k-i postupne dosadte Grayov kod stupna k-i
   * a zakazdym vypiste cele pole. 
   * Ak reverse = true, Grayov kod generujte odzadu. */
}

DÚ8

max. 5 bodov, termín odovzdania utorok 22.11. o 22:00

Cieľom tejto domácej úlohy je precvičiť si prácu s rekurziou.

Napíšte program, ktorý pomocou korytnačej grafiky a rekurzie vykreslí fraktálnu krivku, ktorá je pre stupne 1,2 a 5 zobrazená na obrázkoch nižšie. Pre stupeň 1 má táto krivka tvar T-čka, pričom vodorovná aj zvislá úsečka majú dĺžku d. Pre stupeň n z každého konca vodorovnej časti T-čka zavesíme fraktály stupňa n-1 a veľkosti d/2, pričom jeden je otočený nahor a jeden nadol. (Fraktál stupňa 0 môžeme pre úplnosť zadefinovať ako prázdnu množinu.)

V programe si zadefinujte nasledujúce konštanty, ktorých zmenou môžete ovplyvniť správanie sa programu:

    const int width = 400; /* rozmery obrázku */
    const int height = 400;

    const double d = 200;    /* dĺžka úsečiek T-čka na najvyššej úrovni rekurzie */
    const int n = 5;         /* stupeň fraktálu */
    const double wait = 0.2; /* koľko korytnačka čaká po každom ťahu */

Korytnačka by mala začať v strede spodnej strany obrázka natočené nahor, po nakreslení celého fraktálu by mala skončiť na tom istom mieste a s tým istým natočením (po každej čiare prejde dvakrát -- tam aj späť). Táto podmienka vám pomôže správne pospájať fraktály stupňa n-1 do fraktálu stupňa n.

Pomôcky:

• Doporučujeme program najskôr odladiť pre stupeň n=1 a 2 a dlhšie čakanie (napr. wait=2), až potom skúšať vyššie hodnoty n a kratší wait.
• Inšpirovať sa môžete programom na Kochovu krivku z prednášky 14.
• Ak dáme korytnačke ako argument do turnLeft záporné číslo, bude sa otáčať o toľko stupňov doprava. Ak jej do forward dáme záporné číslo, pôjde o toľko dozadu.

• 

  Krivka stupňa 1

• 

  Krivka stupňa 2

• 

  Krivka stupňa 5

Prednáška 18

Spájaný zoznam

Doteraz sme sa už stretli s niekoľkými typmi dynamickej pamäte.

• Videli sme typ vektor, ktorý nám pamäť alokoval dynamicky a podľa potreby sám.
• Neskôr sme si dynamicky sami alokovali pole s n prvkami takto:

int *A;
A = new int[n];

//Odalokujeme ho potom pomocou 
delete[] A; 

• Pomocou toho sme vedeli vytvoriť vlastný vektor s zväčšením alebo zmenšením veľkosti podľa potreby.

Teraz si ukážeme ďalší spôsob, ako si prvky nejakého typu ukladať. Veľmi dobre by sme ho využili napríklad v hashovacej tabuľke (prednáška 13), keď sme riešili kolízie. V prípade, že by ku kolízii došlo by sme mohli proste zapojiť ďalší prvok na to isté miesto.

Štruktúra jednoduchého spájaného zoznamu

Spájaný zoznam je teda vlastne postupnosť uzlov rovnakého typu usporiadaných za sebou. Každý uzol pozostáva z dvoch častí:

• referencie (smerníky), ktoré ukazujú na nasledovníka (v komplikovanejších prípadoch aj inde) a pomáhajú nám sa pohybovať po zozname
• samotné dáta (pôvodný prvok) - v našom prípade pre jednoduchosť int

Uzol spájaného zoznamu je teda pre naše účely nasledovného typu:

struct item {
    int data;
    item* next;
};

Na rozdiel od poľa, v ktorom je poradie stanovené indexmi, je teda poradie v spájanom zozname určované ukazovateľmi. Ak x je prvok zoznamu, tak x.next je

• nasledujúci prvok zoznamu
• NULL (ak x je posledným prvkom zoznamu)

OBR zoznam1.png

Samotný typ zoznam potrebuje nejakým spôsobom riešiť prístup k jeho prvkom. Najjednoduchšia možnosť je smerník na úvodný prvok.

struct zoznam {
    item* zaciatok;
};

Potom očakávateľne pokiaľ máme prázdny zoznam z, tak z.zaciatok bude NULL, v opačnom prípade bude ukazovať na prvý prvok zoznamu. Inicializácia zásobníka je teda veľmi jednoduchá:

void init(zoznam &z){
    z.zaciatok=NULL;
}

int main(void){
    zoznam z;
    init(z); 
}

Tiež vieme veľmi jednoducho určiť, či je zoznam prázdny.

bool empty(const zoznam &z){
    if (!z.zaciatok) return true; // resp. (z.zaciatok==NULL) 
    else return false;
}

Vkladanie a vymazanie na začiatku

Na to, aby sme zoznam nejakým spôsobom naplnili, potrebujeme vedieť vôbec vytvoriť prvok zoznamu. To robíme dynamicky nasledovne:

item* p=new item;
p->data=NEJAKE_DATA;
p->next=NEJAKY_SMERNIK_NIEKAM;

Teda vytvoríme si smerník na uzol zoznamu, vyhradíme mu patričný kus pamäte a naplníme ho vhodnými dátami.

Môžeme si teda skúsiť vytvoriť zoznam z, ktorý bude mať 3 prvky 1,2 a 3.

zoznam z;
item* p=new item;
item* q=new item;
item* r=new item;
p->data=1; 
q->data=2; 
r->data=3;
p->next=q;
q->next=r;
r->next=NULL;
z.zaciatok=p;

Pravdepodobne nechceme vytvárať zoznam ako v príklade a potrebujeme teda funkciu na vloženie prvku. Najjednoduchšia možnosť je vkladanie na začiatok zoznamu. Samozrejme prvku budeme musieť vhodne nastaviť jeho smerník next a asi aj nejaké smerníky v zozname.

OBR zoznamInsert.png

void insertZac(zoznam &z, int d){
    item* p=new item;   // vytvoríme nový prvok
    p->data=d;          // naplníme dáta
    p->next=z.zaciatok; // prvok bude prvým prvkom zoznamu (ukazuje na doterajší začiatok)
    z.zaciatok=p;       // tento prvok je novým začiatkom
}

Pre vymazanie prvého prvku postupujeme podobne, len nesmieme zabudnúť okrem presmerovania začiatku aj uvoľniť pamäť pôvodne prvého prvku. Funkcia deleteZac nám vráti hodnotu prvého prvku a tento prvok vymaže.

int deleteZac(zoznam &z){
     if (z.zaciatok==NULL) return ERR; // teda niečo o čom vieme, že je chyba 
 
     item* p=(z.zaciatok->next); // prvok, ktorý bude ďalej začiatkom
     int d=z.zaciatok->data;     // to čo máme vrátiť
     delete z.zaciatok;          // uvoľnenie pamäte
     z.zaciatok=p;               // nový začiatok
     return d;
}

Prechádzanie zoznamu

Veľmi dôležité je vedieť zoznamom prechádzať a postupne pracovať s jeho prvkami. Prechádzanie zoznamom je potrebné napríklad pre hľadanie konkrétneho prvku, hľadanie najväčšieho prvku, atď. My si ukážeme vypisovanie všetkých prvkov zoznamu.

Ako budeme postupovať? Vytvorím si jeden smerník na prvky zoznamu - x.

• Začneme prvým prvkom zoznamu. Na ten nám ukazuje smerník z.zaciatok.
• Kým x nebude na konci zoznamu (t.j. nebude NULL) tak si vypíšem patričné dáta (x->data) a presuniem sa na ďalší prvok (x->next)
• Vo chvíli keď je NULL znamená to, že ďalší prvok už nemám (a je jedno, či sa mi to stalo hneď na začiatku - t.j. že z.zaciatok je NULL - alebo neskôr)

void vypis(zoznam z){
    item* x=z.zaciatok;
    while (x!=NULL){
        cout<<x->data<<" ";
        x=x->next;
    }
}

Prejsť celý zoznam potrebujem aj v prípade, že chcem uvoľniť pamäť (na konci programu).

void uvolni(zoznam &z){
    while (z.zaciatok!=NULL){
     item* p=(z.zaciatok);
     z.zaciatok=z.zaciatok->next;
     delete p;
    }
}

Utriedený zoznam

Občas sa nám hodí, aby sme si zoznam udržiavali utriedený. Má to však jeden problém oproti vkladaniu na začiatok alebo koniec. Vkladanie doprostred zoznamu (pred nejaký prvok) môže spôsobiť niekoľko špeciálnych prípadov, ktoré potrebujeme ošetriť.

Vo chvíli, keď chceme vkladať pred prvok x, potrebujeme totiž vyriešiť aj jeho repdchodcu, teda prvok, ktorý pôvodne ukazoval na x. Po vložení už nemá ukazovať na x, ale na novo vložený prvok. Preto potrebujeme celú dobu hľadania vhodného miesta pamätať na to, že aj predchodca je potrebný a niekde si ho pamätať.

Rozlišujeme teda 3 prípady:

• Zoznam je prázdny - vytvoríme prvok, naplníme dátami, nemá nasledovníka a je novým začiatkom
• Chceme vložiť na začiatok zoznamu - vytvoríme prvok, naplníme dátami, nasledovník je pôvodný začiatok a on je nový začiatok
• Ostatné prípady - nájdeme miesto, s tým, že sme o krok pozadu (teda všetko riešime z pozície predchodcu), vytvoríme prvok a upravíme

void insert(zoznam& z, int data) {
    //máme prázdny zoznam
    if (z.zaciatok==NULL) {
        item* p = new item;
        p->data=data;
        p->next=NULL;
        z.zaciatok = p;
        return;
    }

    // chceme vkladať pred prvý prvok
    if (data < z.zaciatok->data) {
        item* p = new item;
        p->data=data;
        p->next = z.zaciatok;
        z.zaciatok = p;
        return;
    }

    //prvok nepatrí na začiatok
    item* prev = z.zaciatok;
    while ((prev->next!=NULL) && (prev->next->data < data)){
        prev = prev->next;
    }    
    item* p = new item;
    p->data=data;
    p->next = prev->next;
    prev->next = p;
}

Riešenie ako je popísané je správne, avšak je náročné na napísanie, aby sme vyriešili špeciálne prípady. Jedna možnosť, ako špeciálne prípady neriešiť, je použiť tzv. zarážku (sentinel node). Zarážka označuje začiatok (koniec) zoznamu a nemá žiadnu hodnotu kľúča. Používa sa hlavne na zjednodušenie a zrýchlenie niektorých operácií. Použitím zarážky sa docieli, že každý uzol má predchodcu (nasledovníka) a že každý zoznam má prvý (posledný) uzol. V princípe to znamená, že miesto toho, aby smerníky mali hodnotu nil, budú ukazovať na zarážku.

Druhá možnosť je pomôcť si drobnou fintou. Je jasné, že z.zaciatok je iný typ, ako uzol zoznamu. Avšak smerník na začiatok je rovnakého typu ako smerník na ľubovoľný ďalší prvok. Môžeme si teda vytvoriť smerník na tento typ. Ním si budeme ukazovať, kde sa v zozname aktuálne nachádzame a nebude rozdiel medzi začiatkom a iným prepojením.

void insert2(zoznam &z, int data){
    item** it=&z.zaciatok;
    while(*it && (*it)->data<data) it=&((*it)->next);
    item* p=new item;
    p->data=data;
    p->next=*it;
    *it=p;
}

Podobne by sa dalo riešiť aj vymazávanie prvkov zo zoznamu. Vo funkcii remove budeme vymazávať prvok určený hodnotou. Nájdeme ho teda a vymažeme. Potrebné je si opäť pamätať jeho predchodcu, nakoľko tomuto prvku meníme nasledovníka.

void remove(zoznam &z, int data) {
    // prvok sa v zozname nenachádza resp. je zoznam prázdny
    if (!z.zaciatok || z.zaciatok->data > data) return; 
    
    // vymazávam prvý prvok
    if (data == z.zaciatok->data) {
        item* to_del = z.zaciatok;
        z.zaciatok = z.zaciatok->next;
        delete to_del;
        return;
    }

    //ostatné prípady
    item* prev = z.zaciatok;
    while (prev->next && prev->next->data < data) prev = prev->next;
    if (prev->next && prev->next->data == data) {
        item* to_del = prev->next;
        prev->next = prev->next->next;
        delete to_del;
    }
}

Dvojsmerne spájaný zoznam

Je to typ spájaného zoznamu, ktorý má smerník na svojho nasledovníka a aj smerník na svojho predchodcu. Ak je uzol prvý, hodnota smerníka na predchodcu má hodnotu NULL a obdobne, ak je uzol posledný, tak hodnota smerníka na nasledovníka je NULL.

Prvok zoznamu teda vyzerá takto:

struct item {
    int data;
    item* next;
    item* prev;
};

Obvykle sa potom okrem začiatku zoznamu udržuje aj smerník na koniec (teda posledný prvok zoznamu). Teda zoznam vyzerá nasledovne:

struct zoznam {
    item* zaciatok;
    item* koniec;
};

Pre inicializáciu je potrebné okrem začiatku nastaviť aj koniec. Uvoľnovanie pamäti funguje úplne rovnako ako v jednosmerne spájanom.

Vkladanie a vymazávanie na začiatku

Podobne ako pri jednosmernom zozname na vkladanie si potreujeme vytvoriť prvok, ktorý budeme vkladať a následne upravíme smerníky v ňom a v zozname. Ukážeme si, ako vkladať a vymazavať na začiatku zoznamu. Podobne sa dá pracovať aj na konci zoznamu, keďže smerník na koniec si tiež udržujeme.

void insertZac(zoznam &z, int d){
    item* p=new item;
    p->next=z.zaciatok;
    p->prev=NULL;
    p->data=d;
    if (z.zaciatok!=NULL){
        (z.zaciatok)->prev=p;
    }
    else {
        z.koniec=p;
    }
    z.zaciatok=p;
}

Čo je rozdiel oproti jednosmerne spájanému zoznamu je odlišné správanie pri prázdnom zozname.

• Ak je zoznam prázdny, potom potrebujem po vložení správne nastaviť smerník na koniec zoznamu.
• Ak zoznam nie je prázdny, potom potrebuem zase správne nastaviť predchádzajúci prvok pôvodnému začiatku, teda smerník (z.zaciatok)->prev.

Pri vymazávaní potrebujeme tiež ošetriť, či sme nevymazali posledný prvok. V tom prípade potrebujeme nastaviť správne aj koniec zoznamu.

int deleteZac(zoznam &z){
     item* p=(z.zaciatok->next);
     int d=z.zaciatok->data;
     delete z.zaciatok;
     z.zaciatok=p;
     if (p!=NULL) p->prev=NULL;
     else z.koniec=NULL;
     return d;
}

Prechádzanie zoznamu odpredu/odzadu

Na prechádzanie dvojsmerne spájaného zoznamu je možné použiť rovnaký postup ako pri prechádzaní jednosmerného (tie smerníky smerom dopredu v zozname sú). Okrem toho máme možnosť urobiť aj prechádzanie/výpis zoznamu odzadu.

void vypisOdzadu(zoznam z){
    item* x=z.koniec;
    while (x!=NULL){
        cout<<x->data<<" ";
        x=x->prev;
    }
}

Vďaka tejto možnosti teda vieme jednoducho nájsť k-ty prvok odzadu zoznamu.

int kOdzadu(zoznam z, int k){
    item* x=z.koniec;
    int data;
    for (int i=0; i<k; i++){
      if (x==NULL) return -1;
      data=x->data;
      x=x->prev;
    }
    return data;
}

Prednáška 19

Oznamy

• Nezabudnite si skontrolovať body z DÚ 1-5 a rozcvičiek 1-6 a nahlásiť problémy do piatku
• V knižnici dve nové knihy na prezenčné čítanie:
  • Sedgewick: Algorithms in C. Parts 1-4 I-INF-S-43/I-IV
  • Prokop: Algoritmy v jazyku C a C++. I-INF-P-26
  • Kochan: Programming in C, 2005 D-INF-K-7a (od začiatku semestra)

Zásobník (stack) a rad (queue)

• Jednoduché dátové štruktúry, ktoré udržujú zoznam nejakých prvkov
• Tieto prvky sú dosť často úlohy, resp. dáta čakajúce na spracovanie
• Vieme do nich vkladať a vyberať
• Líšia sa tým, v ako poradí vyberáme

Rad, fronta (queue)

• Vyberáme prvok, ktorý je v rade najdlhšie (first in, first out, FIFO)
• Podobá sa na státie v rade pri pokladni: ten kto tam stojí najdlhšie bude prvý obslúžený
• Základné operácie

/* inicializuje prázdny rad */
void init(queue &q);

/* zisti, ci je rad prazdny */
bool isEmpty(queue &q);

/* prida prvok s hodnotou item na koniec radu */
void enqueue(queue &q, dataType data); 

/* odoberie prvok zo začiatku radu a vráti jeho hodnotu */
dataType dequeue(queue &q);

/* vrati prvok zo zaciatku radu, ale necha ho v rade */
dataType peek(queue &q);

Zásobník (stack)

• Vyberáme prvok, ktorý je v rade najkratšie (last in, first out, LIFO)
• Podobá sa na umývača tanierov v reštaurácii, vždy vezme horný tanier z kopy

/* inicializuje prázdny zásobník */
void init(stack &s);

/* zisti, ci je zasobnik prazdny */
bool isEmpty(stack &s);

/* prida prvok s hodnotou item na vrch zasobnika */
void push(stack &s, dataType data); 

/* odoberie prvok z vrchu zásobníka a vráti jeho hodnotu */
dataType pop(stack &q);

Ešte potenciálne potrebujeme uvoľniť pamäť nejakou ďalšou funkciou, napr. destroy.

Príklad:

typedef int dataType;
/* sem pride definicia typov stack a queue a vsetky potrebne funkcie */

int main() {
    cout << "Stack:" << endl;
    stack s;
    init(s);
    push(s, 1);
    push(s, 2);
    push(s, 3);
    cout << pop(s) << endl;
    cout << pop(s) << endl;
    cout << pop(s) << endl;

    cout << "Queue:" << endl;
    queue q;
    init(q);
    enqueue(q, 1);
    enqueue(q, 2);
    enqueue(q, 3);
    cout << dequeue(q) << endl;
    cout << dequeue(q) << endl;
    cout << dequeue(q) << endl;
}

Zásobník prevracia poradie prvkov, rad zachováva.

Stack:
3
2
1
Queue:
1
2
3

Abstraktný dátový typ (ADT)

• Aj bez toho aby sme videli, ako presne sú stack a queue naprogramované, vieme, čo by mal program vypísať (za predpokladu, že sú naprogramované podľa špecifikácie).
• Môžeme teda meniť implementáciu týchto štruktúr bez toho, aby sme menili programy, ktoré ich používajú.
• Už sme videli ADT slovník (operácie insert, find, delete), ktorý sa dal implementovať napr. utriedeným poľom, neutriedeným poľom, hashovacou tabuľkou, ale aj spájaným zoznamom a ďalšími zložitejšími štruktúrami
• Dnes si ukážeme implementácie zásobníka a radu pomocou polí aj spájaných zoznamov
• Zmenou definície typu dataType môžeme spraviť zásobník obsahujúci prvky typu int, double, char, string, ale aj zložitejšie štruktúry, alebo smerníky na ne (aby sa zbytočne nekopírovalo)

Zásobník implementovaný pomocou poľa

Dve prirodzené možnosti:

• vrch zásobníka v prvku 0
• spodok zásobníka v prvku 0

Prvá možnosť by bola pomalá, na operácie push aj pop by sme museli posúvať všetky prvky v zásobníku. Použijeme teda druhú možnosť, v prvku 0 bude spodok zásobníka, v premennej top si pamätáme pozíciu vrchného prvku.

struct stack {
    int top;  /* pozicia vrchného prvku zásobníka */
    dataType *items; /* pole prvkov */
};

/* inicializuje prázdny zásobník */
void init(stack &s) {
    s.top = -1;
    s.items = new dataType[maxN];
}

/* zisti, ci je zasobnik prazdny */
bool isEmpty(stack &s) {
    return s.top == -1;
}

/* prida prvok s hodnotou item na vrch zasobnika */
void push(stack &s, dataType item) {
    s.top++;
    assert(s.top < maxN);
    s.items[s.top] = item;
}

/* odoberie prvok z vrchu zásobníka a vráti jeho hodnotu */
dataType pop(stack &s) {
    assert(s.top >= 0);
    s.top--;
    return s.items[s.top + 1];
}

Rad implementovaný pomocou poľa

• Rad sa nedá implemetovať tak jednoducho ako zásobník, lebo na jednej strane potrebujeme vkladať a na druhej vyberať.
• Takže ak by sme chceli mať napr. prvý prvok v rade vždy na pozícii 0, museli by sme pri vyberaní posúvať všetky prvky.
• Namiesto toho si budeme pamätať pozíciu prvého prvku (premenná first) a keď vyberieme prvok, len zvýšime first
• Tým sa postupne zaplnený úsek posúva doprava
• Keď dôjdeme na koniec poľa, zatočíme sa, ako keby za prvkom maxN-1 nasledoval prvok 0

struct queue {
    int first;  /* prvý prvok v rade */
    int count;  /* počet prvkov v rade */
    dataType *items; /* pole prvkov */
};

/* inicializuje prázdny rad */
void init(queue &q) {
    q.first = 0;
    q.count = 0;
    q.items = new dataType[maxN];
}

/* zisti, ci je rad prazdny */
bool isEmpty(queue &q) {
    return q.count == 0;
}

/* prida prvok s hodnotou item na koniec radu */
void enqueue(queue &q, dataType item) {
    assert(q.count < maxN);
    int last = (q.first + q.count) % maxN;
    q.items[last] = item;
    q.count++;
}

/* odoberie prvok zo začiatku radu a vráti jeho hodnotu */
dataType dequeue(queue &q) {
    assert(q.count > 0);
    int index = q.first; /* kde je prvok, ktory chceme vratit */
    q.first = (q.first + 1) % maxN;
    q.count--;
    return q.items[index];
}

/* vrati prvok zo zaciatku radu, ale necha ho v rade */
dataType peek(queue &q) {
    assert(q.count > 0);
    return q.items[q.first];
}

Zásobník implementovaný pomocou spájaného zoznamu

• V zásobníku v poli sme na začiatku poľa spodok zásobníka
• V zozname budeme mať na začiatku zoznamu vrchol zásobníka, lebo na začiatok zoznamu sa dobre vkladá a vyberá.
• Použijeme kód na vkladanie a vyberanie zo zoznamu z minulej prednášky (prvok zoznamu sme premenovali na node, začiatok zoznamu na top)
• Nepotrebujeme vopred stanovavať maximálny počet prvkov, zásobník podľa potreby rastie alebo sa zmenšuje (kým je voľná pamäť)

struct node {
    dataType data;
    node* next;
};

struct stack {
    node *top; /* vrchný prvok zásobníka */
};

/* inicializuje prázdny zásobník */
void init(stack &s) {
    s.top = NULL;
}

/* zisti, ci je zasobnik prazdny */
bool isEmpty(stack &s) {
    return s.top == NULL;
}

/* prida prvok s hodnotou item na vrch zasobnika */
void push(stack &s, dataType item) {
    node *temp = new node;
    temp->data = item;
    temp->next = s.top;
    s.top = temp;
}

/* odoberie prvok z vrchu zásobníka a vráti jeho hodnotu */
dataType pop(stack &s) {
    assert(s.top != NULL);
    node *temp = s.top->next; // prvok, ktorý bude ďalej top
    dataType val = s.top->data; // to čo máme vrátiť
    delete s.top;
    s.top = temp;
    return val;
}

Rad implementovaný pomocou spájaného zoznamu

• Potrebujeme na jednom konci zoznamu vkladať, na opačnom vyberať.
• Použijeme kruhový zoznam, v ktorom posledný prvok ukazuje pomocou next na prvý prvok v zozname
• Prvý prvok radu bude prvý v zozname, bude ukazovať na druhý prvok atď.
• V štruktúre queue si pamätáme iba smerník na posledný prvok radu
  • Ak je rad prázdny, tento smerník je NULL
  • Z posledného prvku sa jedným krokom vieme dostať k prvému prvku

struct queue {
    node *last; /* posledný prvok v rade */
};

/* inicializuje prázdny rad */
void init(queue &q) {
    q.last = NULL;
}

/* zisti, ci je rad prazdny */
bool isEmpty(queue &q) {
    return q.last == NULL;
}

/* prida prvok s hodnotou item na koniec radu */
void enqueue(queue &q, dataType item) {
    node *temp = new node;
    temp->data = item;
    if (q.last == NULL) {
        q.last = temp;
        temp->next = temp;
    } else {
        temp->next = q.last->next;
        q.last->next = temp;
        q.last = temp;
    }
}

/* odoberie prvok zo začiatku radu a vráti jeho hodnotu */
dataType dequeue(queue &q) {
    assert(q.last != NULL);
    node *first = q.last->next;
    if (first->next == first) { /* ak v zozname iba jeden prvok */
        q.last = NULL;
    } else { /* v zozname viac prvkov, preskocime first */
        q.last->next = first->next;
    }
    dataType val = first->data;
    delete first; /* zmazeme node pre first */
    return val;
}

/* vrati prvok zo zaciatku radu, ale necha ho v rade */
dataType peek(queue &q) {
    assert(q.last != NULL);
    return q.last->next->data;
}

Použitie rady a zásobníka

• Zvyčajne uchovávajú dáta, ktoré ešte treba spracovať, resp. zoznam úloh

Rad použijeme, ak chceme zachovať poradie.

• Jeden proces pridáva úlohy, druhý ich rieši (prípadne aj viac procesov môže vkladať alebo vyberať)
• Príklady:
  • Textový procesor pripravuje strany na tlač, vkladá ich do radu, tlačiareň ich tlačí
  • Výpočtové úlohy čakajú na veľkom serveri v rade na spustenie
  • Zákazníci čakajú na zákazníckej linke na voľného operátora
  • Pasažieri na stand-by čakajú na voľné miesto v lietadle

Zásobník je jednoduchší, používame ho, ak nám nezáleží na poradí, alebo ak chceme poradie prevracať

• Hlavný príklad je zásobník, ktorý kompilátor vytvorí na ukladanie lokálnych premenných funkcií, čo nám umožňuje použiť rekurziu (call stack)
• Pri nekonečnej rekurzii nám zásobník "pretečie" a program spadne, napr. s chybou Segmentation fault

void pokus() {
    int i;
    pokus();
}

int main() {
    pokus();
}

• Rekurzívne programy vieme prepísať na nerekurzívne, napríklad pomocou ručne vytvoreného zásobníka
  • Mohli by sme mechanicky simulovať to, ako zásobník používa kompilátor, to by však bolo veľmi neprehľadné
  • Väčšinou trochu zmeníme ako presne program funguje
  • Ukážeme si niekoľko príkladov

Nerekurzívny QuickSort

• Quicksort zvolí nejakú hodnotu, prvky menšie ako táto hodnota dá do ľavej časti poľa, väčšie prvky do pravej časti poľa
• Potom rekurzívne volá Quicksort na obe časti poľa

void quicksort(int A[], int l, int r) {
    if (l >= r) return;

    // rozdelenie
    int pivot = divide(A, l, r);

    // reukrzivne volanie na mensie a vacsie prvky
    quicksort(A, l, pivot - 1);
    quicksort(A, pivot + 1, r);
}
int main() {
  ...
  quicksort(A, 0, n-1);
  ...
}

Namiesto rekurzie si spravíme zásobník dvojíc l,r, ktoré ešte treba dotriediť

struct usek {
    int l, r;
};

typedef usek dataType;

void quicksort(int A[], int n) {
    stack s;
    init(s);
    
    /* do stacku vlozime usek pre cele pole */
    usek u;
    u.l = 0;
    u.r = n - 1;
    push(s, u);

    while (!isEmpty(s)) {
        u = pop(s);
        /* spracovavame usek od u.l po u.r */
        if (u.l >= u.r) continue;

        /* rozdelenie */
        int pivot = divide(A, u.l, u.r);

        /* ľavý a pravý úsek vložíme do stacku na neskoršie dotriedenie */
        usek u1;
        u1.l = u.l;
        u1.r = pivot - 1;
        usek u2;
        u2.l = pivot + 1;
        u2.r = u.r;
        push(s, u2);
        push(s, u1);
    }
}

• Tento program triedi úseky v rovnakom poradí, ako rekurzívny Quicksort, lebo po rozdelení intervalu [0..n-1] na dve časti dá na vrchol zásobníka ľavú časť. Až keď sa táto ľavá časť a všetky podúlohy, ktoré z nej vzniknú, spracuje, vytiahne sa zo zásobníka pravá časť.
• V Quicksorte však na poradí nezáleží, takže by sme mohli vložiť úseky aj naopak push(s, u1); push(s, u2); (potom by najprv dotriedil pravú časť až potom ľavú)
• Alebo by sme namiesto zásobníka mohli použiť rad. Potom by najskôr rozdelil ľavú aj pravú časť na ďalšie podčasti a potom by delil každú z týchto podčastí atď

Na zamyslenie: ako by sme spravili nerekurzívny MergeSort? Prečo to nejde tak isto ako Quicksort?

• Pomocou zásobníka môžeme rekurziu aj z rekuzívneho vyfarbovania súvislých úsekov, pozri prednášku 20

Kontrola uzátvorkovania

• Jednoduchý príklad na použitie zásobníka
• Máme daný reťazec obsahujúci zátvorky rôznych typov (,),[,],{,} a chceme zistiť, či je dobre uzátvorkovaný
• Ak zoberieme prvých i znakov reťazca, počet uzátvaracích zátvoriek nesmie prevýšiť počet otváracích
• Ku každej otváracej zátvorke musí byť zatváracia toho istého typu

+2
Vyraz je dobre uzatvorkovany

(x+2)
Vyraz je dobre uzatvorkovany

[((({}[])[]))]
Vyraz je dobre uzatvorkovany

[[))
Vyraz nie je dobre uzatvorkovany

())(
Vyraz nie je dobre uzatvorkovany

Do zásobníka si budeme ukladať pre každú začínajúcu zátvorku jej zodpovedajúcu končiacu. Keď príde končiaca zátvorka, skontorlujeme, či na vrchu zásobníka je to isté (a vyberieme to zo zásobníka).

typedef char dataType;

    string vyraz;
    cin >> vyraz;
    stack s;
    init(s);
    bool spravny = true;
    for (int i = 0; i < vyraz.length(); i++) {
        switch (vyraz[i]) {
            case '(':
                push(s, ')');
                break;
            case '[':
                push(s, ']');
                break;
            case '{':
                push(s, '}');
                break;
            case ')':
            case ']':
            case '}':
                if (isEmpty(s)) {
                    spravny = false;
                } else {
                    char c = pop(s);
                    if (c != vyraz[i]) {
                        spravny = false;
                    }
                }
                break;
        }
    }
    if (spravny) {
        cout << "Vyraz je dobre uzatvorkovany" << endl;
    } else {
        cout << "Vyraz nie je dobre uzatvorkovany" << endl;
    }
}

Cvičenia 9

Čítanie programov

• Skúste zistiť bez použitia počítača, čo vypíše nasledujúca funkcia, ak ju spustíme ako generuj(a, pocet, 0, 2, 3), pričom polia a a pocet majú dĺžku n=3 a obe sú naplnené nulami. Funkcia vypis(a,n) vypíše prvky poľa a.
• Ako musíme funkciu opraviť, aby vypisovala všetky usporiadané n-tice čísel z množiny {0,...,n-1}, v ktorých sa každé číslo opakuje najviac k krát?

void generuj(int a[], int pocet[], int i, int k, int n) {
    if (i == n) {
        vypis(a, n);
    } else {
        for (int x = 0; x < n; x++) {
            if (pocet[x]<k) {
                a[i] = x;
                pocet[x]++;
                generuj(a, pocet, i + 1, k, n);
            }
        }
    }
}

Vyfarbovanie ostrovov

• Na prednáške 17 sme mali program, ktorý počítal počet ostrovov na mape. Upravte ho tak, aby našiel ostrov s najväčšou plochou a vyfarbil ho inou farbou ako ostatné ostrovy.
  • Upravte funkciu vyfarbi tak, aby vracala celé číslo udávajúce počet políčok, ktoré prefarbila. Tým zistíte plochu jednotlivých ostrovov.

Zrýchlenie MergeSortu

• MergeSort z prednášky 16 je pre veľké polia oveľa rýchlejší ako napríklad InsertionSort z prednášky 6, ale pre veľmi malé polia je pomalší, lebo zbytočne stráca čas rekurziou, kopírovaním prvkov hore dole a podobne. Spravte do MergeSortu takú zmenu, že ak je dĺžka úseku, ktorý máme triediť, menšia ako 20, nebudeme ho triediť rekurzívne delením na dve časti a zlučovaním, ale namiesto toho na celý úsek použijeme InsertionSort. Pre dlhé úseky postupujeme tak ako predtým.
  • Funkciu na InsertionSort z prednášky 6 musíte upraviť tak, aby netriedila celé pole od 0 po n-1 ale iba určitý úsek od low po high vrátane.
  • Použite nasledujúcu funkciu main, ktorá vygeneruje 5 miliónov náhodných čísel a zmerajte čas, koľko trvá MergeSortu ich utriedenie bez vašej zmeny a koľko s vašou zmenou (NetBeans vypisuje čas behu programu).
  • Môžete prípadne skúsiť porovnať aj čas MergeSortu a InsertionSortu samotného, ale doporučujeme nastaviť n na menšie číslo, napr n=100000, lebo pre n=5000000 by ste sa výsledku InsertionSortu tak skoro nedočkali.

#include <cstdlib>
#include <ctime>
using namespace std;

/* tu pridu potrebne funkcie */

int main(void) {
    /* inicializácia generátora pseudonáhodných čísel */
    srand(time(NULL));

    /* naalokuj pole velkosti n a vygeneruj nahodne cisla */
    const int n = 5000000;
    int *A = new int[n];
    for (int i = 0; i < n; i++) {
        A[i] = rand() % n;
    }

    mergesort(A, 0, n-1);

    // kontrola, ze je pole utriedene
    for (int i = 1; i < n; i++) {
        if (A[i] < A[i - 1]) {
            cout << "Zle utriedene pole!" << endl;
            return 1;
        }
    }
    delete[] A;
}

Obmena problému batoha

• Na prednáške 17 sme riešili problém batoha, kde sme mali daných n predmetov, každý s určitou hmotnosťou a cenou a o každom sme sa rozhodovali, či ho dáme do batoha alebo nie. Teraz zmeníme zadanie tak, že z každého predmetu máme neobmedzený počet kópií, takže z jedného typu predmetu s určitou hmotnosťou a cenou môžeme dať do batoha aj viac kusov. Zmeňte program tak, aby zlodejovi vybral najlepšie zaplnenie batoha za týchto podmienok. Riešenie reprezentuje ako pole zober typu int, kde zober[i] je počet kusov i-teho predmetu, ktoré zlodej naloží do batoha.

DÚ9

max. 5 bodov plus 3 body bonus, termín odovzdania utorok 29.11. o 22:00

Cieľom tejto domácej úlohy je precvičiť si prácu s rekurzívnym prehľadávaním všetkých možností.

V tejto hre sa vrátime k hre Logik, ktorú ste programovali v domácej úlohe 4. Tentokrát je vašou úlohou napísať program, ktorý zo súboru načíta niekoľko ťahov tejto hry (pokusy hráča a body, ktoré dostal) a vypíše všetky možné riešenia, ktoré sú kompatibilné s týmto priebehom hry aj ich počet.

V programe generujte všetky variácie s opakovaním zodpovedajúce potenciálnym riešeniam a pre každú skontrolujte, či je naozaj kompatibilná s celou históriou hry.

Vstupný súbor na prvom riadku obsahuje počet farieb a počet hracích kameňov, ktoré má hráč uhádnuť. Na druhom riadku je potom počet ťahov hry a na každom z ďalších riadkov je pokus hráča a odpoveď, akú dostal. Pre prvé tri ťahy ukážkovej hry z DÚ4 by vstupný súbor vyzeral takto:

5 3
3
0 1 2 x
0 3 4 X
1 4 3 X    

Pre tento vstup existujú dve riešenia, program teda vypíše

2 3 3
2 4 4
2

V programe použite kostru uvedenú na spodku zadania. V tejto kostre je už naprogramované načítanie vstupu zo súboru vstup.txt do štruktúry hra. Doprogramujte funkcie generuj, spravne a zmaz podľa popisu v hlavičke. Pridajte aj ďalšie funkcie, ktoré budete v programe potrebovať. Môžete použiť aj modifikované funkcie z domácej úlohy 4 (napr. cierne a vsetky). Na rozdiel od DÚ4 už ale nemáme globálne konštanty N a F, ale premenné pocetFarieb a pocetHadanych v štruktúre hra. Všetky polia v programe alokujte príkazom new a po skončení uvoľnite. Nezabudnite na prehľadnú úpravu programu a komentáre.

Bonusová úloha: Napíšte program, ktorý umožní užívateľovi hrať hru Logik, podobne ako v domácej úlohe 4, ale hru užívateľovi trochu sťaží. Nezvolí si hneď na začiatku náhodnú kombináciu farieb, ale v každom kroku dá užívateľovi taký počet bielych a čiernych bodov, aby v hre zostalo čo najviac rôznych riešení. Váš program si teda udržuje celú doterajšiu históriu hry. Po pridaní nového pokusu od užívateľa skúša tomuto pokusu dosadiť všetky možné počty bielych a čiernych bodov a pre každú takto rozšírenú históriu použije prehľadávanie v hlavnej časti domácej úlohy na zistenie počtu riešení. Potom užívateľovi vypíše také počty bodov, pri ktorých bol počet riešení najvyšší.

Napríklad ak pre 5 farieb a 3 hádané kamene užívateľ v prvom kroku zadá pokus 0 1 2, program vypíše jeden biely bod (v hre zostáva 30 riešení). Ak potom v druhom ťahu užívateľ zadá pokus 3 3 4, program vypíše jedne biely a jeden čierny bod (v hre zostáva 8 riešení).

Bonus odovzdajte v súbore bonus.cpp (hlavnú časť úlohy odovzdajte zvlášť). V programe môžete predpokladať, že počet ťahov je najviac 100, počet farieb a počet hádaných kameňov načítajte od užívateľa na začiatku hry. Upozorňujeme, že za nefunkčné, neúplné alebo ťažko čitateľné bonusové programy budeme dávať nula bodov.

Kostra programu pre základnú časť úlohy

#include <iostream>
#include <string>
#include <fstream>
using namespace std;

struct tah {
  int *pokus; /* pole cisel (farieb), ktore zadal hrac */
  int vsetkyBody; /* kolko dostal spolu bodov */
  int cierneBody; /* kolko dostal ciernych bodov */
};

struct hra {
  int pocetFarieb; /* celkovy pocet roznych farieb v hre */
  int pocetHadanych; /* pocet farieb, ktore sa hadaju v kazdom tahu */
  int pocetTahov; /* kolko tahov prebehlo */
  tah *tahy; /* pole tahov */
};

void nacitaj_hru(hra &h, istream &in) {
  /* z otvoreneho suboru in nacitaj hru h, naalokuj potrebne polia */

  /* nacitaj parametre hry */
  in >> h.pocetFarieb >> h.pocetHadanych;
  /* nacitaj pocet tahov hry */
  in >> h.pocetTahov;
  /* alokuj pole tahov */
  h.tahy = new tah[h.pocetTahov];
  for (int i = 0; i < h.pocetTahov; i++) {
    /* pre kazdy tah alokuj pole hadanych farieb  a nacitaj ho */
    h.tahy[i].pokus = new int[h.pocetHadanych];
    for (int j = 0; j < h.pocetHadanych; j++) {
      in >> h.tahy[i].pokus[j];
    }
    /* nacitaj body vo forme xxxXXX
     * a spocitaj pocet ciernych a pocet vsetkych  */
    string slovo;
    in >> slovo;
    h.tahy[i].vsetkyBody = slovo.length();
    h.tahy[i].cierneBody = 0;
    for (int pos = 0; pos < slovo.length(); pos++) {
      if (slovo[pos] == 'X') {
        h.tahy[i].cierneBody++;
      }
    }
  }
}

void vypis(int a[], int n) {
  /* na konzolu vypise cisla v poli a dlzky n */
  for (int i = 0; i < n; i++) {
    if (i > 0) cout << " ";
    cout << a[i];
  }
  cout << endl;
}

bool spravne(hra &h, int a[]) {
  /* V poli a je potencialne spravne riesenie.
   * Funkcia vrati true, ak by pre toto spravne riesenie
   * sedeli v celej hre body pridelene jednotlivym pokusom. */

}

int generuj(hra &h, int a[], int i) {
  /* V poli a mame prvych i farieb, chceme
   * generovat moznosti pre dalsich h.pocetHadanych-i farieb
   * a pre kazdu zistit moznost, ci je spravna.
   * Spravne riesenia vypisujeme a ich pocet vratime. */
  if (i == h.pocetHadanych) {
    if (spravne(h, a)) {
      vypis(a, h.pocetHadanych);
      return 1;
    } else {
      return 0;
    }
  } else {
     /* doprogramujte zvysok funkcie */
  }
}

void zmaz(hra &h) {
  /* odalokuje polia v strukture hra */
}

int main(void) {
  /* nacitanie vstupu do struktury h typu hra */
  ifstream in;
  in.open("vstup.txt");
  if(in.fail()) return 1;
  hra h;
  nacitaj_hru(h, in);
  in.close();

  /* naalokujeme pole pre riesenie a zavolame rekurzivne prehladavanie */
  int *a = new int[h.pocetHadanych];
  int pocet = generuj(h, a, 0);

  /* vypiseme pocet rieseni */
  cout << pocet << endl;

  /* odalokujeme pouzite polia */
  delete[] a;
  zmaz(h);
}

Prednáška 20

Organizačné záležitosti

Záverečná písomka:

• 19.12.2011 o 10:00 v B
• opravný termín/náhradný 9.1.2012 o 10:00 v F1/328

Termíny skúšok vždy o 9:00 v H3 (väčšie termíny aj M218):

• 4.1.2012 (15)
• 11.1.2012 (24)
• 25.1.2012 (24)
• 1.2.2012 (opravný termín) (24)
• 8.2.2012 (2. opravný termín) (15)

Nerekurzívne vyfarbovanie

Rekurziu sme použili aj na prefarbovanie súvislých úsekov na novú farbu:

void vyfarbi(int **a, int n, int m, int riadok, int stlpec, int farba) {
    /* prefarbi suvislu jednofarebnu oblast obsahujucu 
     * a[riadok][stlpec] na farbu farba */

    if (a[riadok][stlpec] != farba) {
        int stara_farba = a[riadok][stlpec];
        a[riadok][stlpec] = farba;
        if (riadok > 0 && a[riadok - 1][stlpec] == stara_farba) {
            vyfarbi(a, n, m, riadok - 1, stlpec, farba);
        }
        if (riadok + 1 < n && a[riadok + 1][stlpec] == stara_farba) {
            vyfarbi(a, n, m, riadok + 1, stlpec, farba);
        }
        if (stlpec > 0 && a[riadok][stlpec - 1] == stara_farba) {
            vyfarbi(a, n, m, riadok, stlpec - 1, farba);
        }
        if (stlpec + 1 < m && a[riadok][stlpec + 1] == stara_farba) {
            vyfarbi(a, n, m, riadok, stlpec + 1, farba);
        }
    }
}

Prepíšme si štyri volania rekurzívne do jedného cyklu pomocou polí delta_riadok a delta_stlpec, podobne ako sme mali na DÚ o červíkovi.

const int delta_stlpec[4] = {1, 0, -1, 0};
const int delta_riadok[4] = {0, -1, 0, 1};

void vyfarbi(int **a, int n, int m, int riadok, int stlpec, int farba) {
    /* prefarbi suvislu jednofarebnu oblast obsahujucu
     * a[riadok][stlpec] na farbu farba */

    if (a[riadok][stlpec] != farba) {
        int stara_farba = a[riadok][stlpec];
        a[riadok][stlpec] = farba;
        for (int smer = 0; smer < 4; smer++) {
            /* skus susedne policko so suradnicami r,s */
            int r = riadok + delta_riadok[smer];
            int s = stlpec + delta_stlpec[smer];
            if (r >= 0 && r < n && s >= 0 && s < m && a[r][s] == stara_farba) {
                vyfarbi(a, n, m, r, s, farba);
            }
        }
    }
}

Namiesto rekurzie si do zásobníka môžeme uložiť štyroch susedov aktuálneho políčka, pretože z nich ešte treba vyfarbovať ďalej. Ale spravíme malú zmenu: pred uložením do stacku ich už prefarbíme novou farbou, aby sme vedeli, že ich už viackrát do zásobníka nemáme dať.

struct policko {
    int r, s;
};

typedef policko dataType;

void vyfarbi(int **a, int n, int m, int riadok, int stlpec, int farba) {
    /* prefarbi suvislu jednofarebnu oblast obsahujucu
     * a[riadok][stlpec] na farbu farba */

    stack s;
    init(s);

    /* vyfarbi startovacie policko a daj ho do stacku */
    int stara_farba = a[riadok][stlpec];
    if (stara_farba == farba) return;
    a[riadok][stlpec] = farba;
    policko p;
    p.r = riadok;
    p.s = stlpec;
    push(s, p);

    while (!isEmpty(s)) {
        /* vytiahni policko zo stacku */
        p = pop(s);
        /* skontroluj jeho susedov, vyfarbi ich a uloz to stacku */
        for (int smer = 0; smer < 4; smer++) {
            policko p2;
            p2.r = p.r + delta_riadok[smer];
            p2.s = p.s + delta_stlpec[smer];
            if (p2.r >= 0 && p2.r < n && p2.s >= 0 && p2.s < m
                    && a[p2.r][p2.s] == stara_farba) {
                a[p2.r][p2.s] = farba;
                push(s, p2);
            }
        }
    }
}

Namiesto zásobníka môžeme použiť aj rad, potom bude vyfarbovať v poradí podľa vzdialenosti od štartovacieho políčka (prehľadávanie do šírky)

void vyfarbi(int **a, int n, int m, int riadok, int stlpec, int farba) {
    /* prefarbi suvislu jednofarebnu oblast obsahujucu
     * a[riadok][stlpec] na farbu farba */

    queue q;
    init(q);

    /* vyfarbi startovacie policko a daj ho do radu */
    int stara_farba = a[riadok][stlpec];
    if (stara_farba == farba) return;
    a[riadok][stlpec] = farba;
    policko p;
    p.r = riadok;
    p.s = stlpec;
    enqueue(q, p);

    while (!isEmpty(q)) {
        /* vytiahni policko z radu */
        p = dequeue(q);
        zobrazStvorcek(p.r, p.s, a[p.r][p.s], "lightgray", window);
        window.wait(waitTime);
        /* skontroluj jeho susedov, vyfarbi ich a uloz to radu */
        for (int smer = 0; smer < 4; smer++) {
            policko p2;
            p2.r = p.r + delta_riadok[smer];
            p2.s = p.s + delta_stlpec[smer];
            if (p2.r >= 0 && p2.r < n && p2.s >= 0 && p2.s < m
                    && a[p2.r][p2.s] == stara_farba) {
                a[p2.r][p2.s] = farba;
                enqueue(q, p2);
                zobrazStvorcek(p2.r, p2.s, a[p2.r][p2.s], "red", window);
                window.wait(waitTime);
            }
        }
    }
}

Aritmetické výrazy

Reprezentácia výrazov : z matematiky sme zvyknutí na bežný zápis aritmetických výrazov, kde je každý binárny operátor medzi operandami, s ktorými sa bude vykonávať príslušná operácia. Poradie, v akom sa jednotlivé operácie vykonávajú, sa riadi umiestnením zátvoriek a prioritou operácií. Tomuto bežnému zápisu sa hovorí infixová forma (alebo notácia) aritmetického výrazu.

Napríklad vyhodnocujeme výraz : (65 – 3*5)/(2 + 3)

Vyhodnocovanie výrazov v infixovej notácii sme ukázali na prednáške 14 . Pracovali sme iba s úplne (a dobre) uzátvorkovanými výrazmi, kde sme nemuseli riešiť prioritu operácií. Pripomeňme si kostru programu:

int vyhodnotVyraz(char str[]){
    if (str[0]!='(') return vyhodnotCislo(str);
    else {
        char s[100];
        int poz, hodnota1, hodnota2;

        poz=najdiZnamienko(str);

        strCopy(str,s,1,poz-1);      // od 1 po pozíciu pred znamienkom (pozícia 0 je '(' )
        hodnota1=vyhodnotVyraz(s);
        strCopy(str,s,poz+1,strlen(str)-2); // od pozície po znamienku po predposledný znak stringu (posledný znak - strlen()-1 je ')' )
        hodnota2=vyhodnotVyraz(s);

        switch (str[poz]){
            case '+': return hodnota1+hodnota2;
            case '-': return hodnota1-hodnota2;
        }

        return 0;
    }    
}

V prípade, že by sme chceli výraz vyhodnocovať bez úplného uzátvorkovania, zmenila by sa hlavne funkcia, ktorá hľadá operand, ktorý potrebujeme vykonať.

Postfixová a prefixovová notácia

Okrem infixovej notácie se môžeme stretnúť s ďalšími formami zápisu aritmetických výrazov. A to s prefixovou a postfixovou formou. Postfixová notácia (obrátená poľská notácia) má v zápise výrazu operátor až po oboch operandoch.

Výraz (65 – 3*5)/(2 + 3) by teda v postfixovej forme mal notáciu 65 3 5 * - 2 3 + /

V prefixovej notácii je situácia opačná ako pri postfixovej notácii. Každý operátor stojí pred dvoma operandami, ku ktorým prislúcha.

Výraz (65 – 3*5)/(2 + 3) by v prefixovej forme bol / - 65 * 3 5 + 2 3

Postfixová a prefixová notácia sú na prvý pohľad pre človeka neprehľedné, ale ako uvidíme, dajú sa oveľa jednoduchšie vyhodnocovať. Okrem toho vidíme ešte jednu výhodu - nepotrebujú zátvorky.

Vyhodnocovanie postfixovej formy

Na vyhodnocovanie výrazov v postfixovej forme budeme používať zásobník. Budeme do neho vkladať operandy - teda hodnoty podvýrazov.

• Využijeme vlastnosť, že operátor má oba operandy pred sebou. Teda vo chvíli keď narazíme na operátor, jeho operandy už niekde máme prečítané.
• Navyše sú to tie posledné dva prečítané/vypočítané hodnoty.

Vyhodnotenie potom realizujeme nasledovne:

• Procházíme výraz z ľava doprava a ak narazíme na operand tak putuje do zásobníku.
• Akonáhle však narazíme na operátor tak vyberieme dva operandy zo zásobníku.
  • Ale pozor keďže máme zásobník (LIFO) tak musíme prehodiť poradie operandov tak ako sme ich vybrali postupne zo zásobníku
  • Napríklad pri delení (a/b je v postfixovej notácii a b /) sme zo zásobníku najskôr vybrali deliteľa (b) a ako druhého sme vybrali delenca (a), a preto pri vykonávaní operácie musíme prehodiť ich poradie.
• Vykonáme operáciu s vybranými operandami a výsledok tejto operácie umiestnime späť do zásobníku.
• Tento postup opakujeme kým nedojdeme na koniec výrazu. V okamžiku keď se tak stalo máme v zásobníku jeden prvok a to je výsledok výrazu.

int main(void){
    stack s;
    init(s);
    char postfix[size];
    int elem1, elem2, i=0;
    gets(postfix);
    
    while (postfix[i]!='\0'){
        switch (postfix[i]){
            case ' ': i++; break;
            case '+': {
                elem1=pop(s); elem2=pop(s); push(s, elem1+elem2); 
                i++;
                break;
            }
            case '-': {
                elem1=pop(s); elem2=pop(s); push(s, elem2-elem1);
                i++;
                break;
            }
            case '*': {
                elem1=pop(s); elem2=pop(s); push(s, elem1*elem2);
                i++;
                break;
            }
            case '/': {
                elem1=pop(s); elem2=pop(s); push(s, elem2/elem1);
                i++;
                break;
            }
            default: push(s, evaluateNumber(postfix, i));
        }
    }
    cout << pop(s);
}

Konverzia infixovej formy na postfixovú

Vidíme, že vyhodnocovanie postfixovej formuly je jednoduché. Väčšinou však pracujú bežní ľudia s infixovou formou zápisu a preto potrebujeme nejakým spôsobom

Pre jednoduchosť si najskôr ukážeme iba výrazy bez zátvoriek. Priorita operátorov je nasledovná (od najnižšej):

• + - (sčítanie odčítanie )
• * / (násobenie delenie )
• ^ (umocnenie )

Výraz máme reprezentovaný v reťazci a predpokladajme, že je správny (správny počet operátorov a pod.). Budeme potrebovať zásobník, do ktorého si budeme ukladať zatiaľ nevypísané časti infixovej formuly (teda operátory, ktoré ešte nemajú oba operandy).

Samotné vyhodnocovanie bude vyzerať nasledovne:

• Prechádzame výrazom z ľava doprava.
• Pokiaľ objavíme operand tak ho iba prepíšeme do postfixového reťazca a ďalej nás už nezaujíma.
• Ak narazíme na operátor, pozrieme sa na vrch zásobníka:
  • Kým operátor zo zásobníka má väčšiu alebo aspoň rovnakú prioritu, tak vyberáme zo zásobníka (a vybrané operátory prepíšeme do postfixového reťazca). Vypisujeme tak až dokiaľ nenarazíme na operátor s nižšou prioritou (alebo dno)
• Až po tomto kroku umiestnime aktuálny operátor do zásobníka.
• Tento postup opakujeme pokiaľ nenarazíme na konec výrazu. Potom sme narazili na koniec výrazu, preto len vyberieme operátory zo zásobníku a umiestnime ich na výstup.

Teraz ešte potrebujeme pridať zátvorky. Ľavá zátvorka nemá žiaden reálny význam, je iba zarážkou pre pravú. Preto keď na ňu narazíme, iba ju vložíme do zásobníka. Keď však narazíme na pravú znamená to, že všetky operátory, ktoré boli v zátvorke by mali byť už vypísané na výstup. Preto ich vypisujeme až kým nenarazíme na ľavú zátvorku.

int main(void) {
    char infix[size],postfix[size];
    dataType ele, elem, popped;
    stack s;

    int prep, pre, j = 0;

    init(s);
    push(s,'#'); // dno zasobnika

    gets(infix); // nacita aritmeticky vyraz v infixovej forme

    for (int i = 0; infix[i] != 0; i++) {
        /*cisla a ine znaky*/
        if (infix[i] != '(' && infix[i] != ')' && infix[i] != '^' && infix[i] != '*' && infix[i] != '/' && infix[i] != '+' && infix[i] != '-')
            postfix[j++] = infix[i];
        /*zaciatok zatvorky iba kopirujem*/
        else if (infix[i] == '(') {
            elem = infix[i];
            push(s,elem);
        } 
        /*koniec zatvorky znamena, ze vypisem vsetky operatory, co boli v tej zatvorke (a este nie su vypisane)*/
        else if (infix[i] == ')') {
            while ((popped = pop(s)) != '('){
                postfix[j++] = ' ';
                postfix[j++] = popped;
                postfix[j++] = ' ';
            }       
        } 
        /*operatory*/
        else {
            postfix[j++]=' ';
            elem = infix[i];
            pre = precedence(elem); // dolezitost prichadzajuceho operatora
            ele = topElement(s);
            prep = precedence(ele); //dolezitost operatora v zasobniku

            /*ak je prichadzajuci operator dolezitejsi tak ho dam do zasobnika - pojde skor */
            if (pre > prep) push(s,elem);
            /*inac vypisem vsetky dolezitejsie co uz tam su - mali ist pred nim - a jeho tam vlozim */
            else {
                while (prep >= pre) {
                    if (ele == '#') break;
                    popped = pop(s);
                    ele = topElement(s);
                    postfix[j++] = ' ';
                    postfix[j++] = popped;
                    postfix[j++] = ' ';
                    prep = precedence(ele);
                }
                push(s,elem);
            }
        }
    }

    /* vsetko co nam este na zasobniku ostalo vypisem */
    while ((popped = pop(s)) != '#'){
        postfix[j++] = ' ';
        postfix[j++] = popped;
        postfix[j++] = ' ';
    }
    postfix[j] = '\0';
    cout << endl << "Post fix : " << postfix << endl;
           
}

V programe sú ešte na niekoľkých miestach pridané medzery (často zbytočné, aby sa nám operandy nezliali do jedného čísla a vedeli sme ich následne vyhodnocovať.

Prednáška 21

Opakovanie: aritmetické výrazy

• Bežná infixová notácia, napr. (65 – 3*5)/(2 + 3)
• Úplne uzátvorkovaná, napr. ((65 – (3*5))/(2 + 3))
• Postfixová notácia 65 3 5 * - 2 3 + /
• Prefixová notácia / - 65 * 3 5 + 2 3
• Prefixová a postfixová notácia nepotrebujú zátvorky
• Prevod z infixovej notácie na postfixovú pomocou zásobníka
  • Čo si ukladáme do zásobníka?
• Vyhodnocovanie postfixovej notácie pomocou zásobníka
  • Čo si ukladáme do zásobníka?

Dnes:

• uloženie aritmetického výrazu vo forme stromu a práca so stromami všeobecne

Budúci týždeň a posledná DÚ:

• ďalšie príklady stromov v informatike

Aritmetický výraz ako strom

Strom pre výraz (65 – 3*5)/(2 + 3)

• Každý operátor a každé číslo tvorí vrchol stromu
• Vrchol pre operátor má pod sebou zavesené menšie stromy pre podvýrazy, ktoré spája
• Informatici stromy väčšinou kreslia hore nohami, s koreňom na vrchu
  • V našom príklade je koreň vrchol s operátorom /

Dátová štruktúra pre vrcholy stromu

struct node {
    /* vrchol stromu  */
    double val;     /* ciselna hodnota */
    char op;        /* operator '+', '-', *', '/', alebo ' ' ak ide o hodnotu */
    node * left;    /* lavy podvyraz */
    node * right;  /* pravy podvyraz */
};

Ak máme vrchol pre operátor:

• left a right sú smerníky na ľavý a pravý podvýraz
• znak op je znamienko operátora, napr. '+'
• hodnota val je nevyužitá

Ak máme vrchol pre číslo vo výraze:

• left a right majú hodnotu NULL (žiadne podvýrazy)
• znak op má hodnotu medzera ' '
• val obsahuje hodnotu čísla

Jednoduchá ale nie veľmi elegantná reprezentácia

• niektoré položky sú nevyužité (val v operátoroch, left a right pri číslach)
• budúci semester uvidíme krajšie riešenie pomocou objektov

Vytváranie vrcholov stromu

Nasledujúce dve funkcie vytvoria nový vrchol.

• Pre vrchol typu operátor už funkcia dostane smerníky na vrcholy pre podvýrazy

node * createOp(char op, node *left, node *right) {
    /* vytvori novy vrchol stromu s operatorom op
     * a do jeho laveho a praveho podvyrazu ulozi
     * smerniky left a right. */
    node *v = new node;
    v->left = left;
    v->right = right;
    v->op = op;
    return v;
}

node * createNum(double val) {
    /* Vytvori novy vrchol stromu s danou hodnotou,
     * lavy a pravy podvyraz bude prazdny, op bude medzera */
    node *v = new node;
    v->left = NULL;
    v->right = NULL;
    v->op = ' ';
    v->val = val;
    return v;
}

Vytvorme teraz ručne strom pre náš výraz (65 – 3*5)/(2 + 3):

node *v = createOp('/',
            createOp('-', createNum(65),
                          createOp('*', createNum(3), createNum(5))),
            createOp('+', createNum(2), createNum(3)));

Alebo to môžeme rozpísať po krokoch:

node *v65 = createNum(65);
node *v3 = createNum(3);
node *v5 = createNum(5);
node *v2 = createNum(2);
node *v3b = createNum(3);
node *vKrat = createOp('*', v3, v5);
node *vMinus = createOp('-', v65, vKrat);
node *vPlus = createOp('+', v2, v3b);
node *vDeleno = createOp('/', vMinus, vPlus);

Vyhodnocovanie výrazu

double evaluate(node *v) {
    /* vyhodnoti vyraz dany stromom s korenom vo vrchole v */
    assert(v != NULL);

    /* ak je operator medzera, vratime jednoducho hodnotu */
    if (v->op == ' ') {
        return v->val;
    }

    /* rekurzivne vyhodnotime lavy a pravy podvyraz */
    double valLeft = evaluate(v->left);
    double valRight = evaluate(v->right);

    /* Hodnotu laveho a praveho podvyrazu spojime podla typu operatora
     * a vratime. Prikaz break netreba, pouzivame return. */
    switch (v->op) {
        case '+': return valLeft + valRight;
        case '-': return valLeft - valRight;
        case '*': return valLeft * valRight;
        case '/': return valLeft / valRight;
        default: assert(0);
    }
}

Vytvorenie stromu z postfixového výrazu

Kód na vyhodnocovanie postfixového výrazu z minulej prednášky:

typedef node * dataType;

doube evaluatePostfix(char *postfix) {
    stack s;
    init(s);
    int elem1, elem2, i=0;

    while (postfix[i]!='\0'){
        switch (postfix[i]){
            case ' ': i++; break;
            case '+': {
                elem1=pop(s); elem2=pop(s); push(s, elem1+elem2); 
                i++;
                break;
            }
            case '-': {
                elem1=pop(s); elem2=pop(s); push(s, elem2-elem1);
                i++;
                break;
            }
            case '*': {
                elem1=pop(s); elem2=pop(s); push(s, elem1*elem2);
                i++;
                break;
            }
            case '/': {
                elem1=pop(s); elem2=pop(s); push(s, elem2/elem1);
                i++;
                break;
            }
            default: push(s, evaluateNumber(postfix, i));
        }
    }
    return pop(s);
}

Do zásobníka si ukladáme čísla - medzivýsledky už vahodnotených podvýrazov. Pri tvorbe stromu si tam namiesto toho budeme ukladať už vytvorené podstromy.

typedef node * dataType;

node *parsePostfix(char *postfix) {
    stack s;
    init(s);
    int i=0;
    double val;
    node * elem1, * elem2, *v;

    while (postfix[i]!=0){
        switch (postfix[i]){
            case ' ': i++; break;
            case '+':
            case '-':
            case '*':
            case '/':
                elem1 = pop(s);
                elem2 = pop(s);
                v = createOp(postfix[i], elem2, elem1);
                push(s, v);
                i++;
                break;
            default :
                val = evaluateNumber(postfix, i);
                push(s, createNum(val));
        }
    }
    return pop(s);
}

Funkcia evaluateNumber môže vyzerať napríklad takto:

double evaluateNumber(char str[], int &i) {
    /* Z retazca od pozicie i precitaj cislo az po prvy
     * iny znak (medzera, koniec retazca, operator).
     * Cislo i sa nastavi na prvu poziciu, ktora sa neda precitat. */
    double val = 0;
    while (str[i] >= '0' && str[i] <= '9') {
        val = val * 10 + (str[i] - '0');
        i++;
    }
    /* desatinna cast */
    if (str[i] == '.') {
        i++;
        double power = 0.1;
        while (str[i] >= '0' && str[i] <= '9') {
            val += (str[i] - '0') * power;
            power /= 10;
            i++;
        }
    }
    return val;
}

Terminológia stromov

• Strom má vrcholy (nodes, vertices) a tie sú pospájané hranami (edges)
• Nás zaujímajú zakorenené stromy, ktoré majú jeden vrchol zvolený ako koreň (root)
• Každý iný vrchol okrem koreňa je spojený hranou s jedným otcom (parent) a s niekoľkými (nula alebo viac) synmi (children)
• Listy sú vrcholy, ktoré nemajú deti, ostatné vrcholy voláme vnútorné
• V binárnom strome má každý vrchol najviac dve deti
• Predkovia vrchola sú všetky vrcholy na ceste od neho smerom ku koreňu, teda on sám, jeho otec, otec jeho otca atď, až kým nenarazíme na koreň
• Ak x predkom y, tak y je potomkom x
• Podstrom s koreňom vo vrchole v tvorí vrchol v a všetci jeho potomkovia
• Strom je teda buď prázdny, alebo je tvorený koreňom a dvoma podstromami: ľavým a pravým.

Náš aritmetický strom

• Je binárny
• V listoch sú čísla, vo vnútorných vrcholoch operácie
• Každý vnútroný vrchol má dve deti

Dátová štruktúra pre binárne stromy

Dátovú štruktúru pre vrcholy binárnych stromov môžeme zovšeobecniť a použiť v nej nejaký všeobecný typ dataType, podobne ako pri zásobníku. Spravíme si tiež všeobecnú funkciu na vytvorenie nového vrcholu, ktorá dostane smerníky na podstromy.

struct node {
    /* vrchol stromu  */
    dataType data;
    node * left;  /* lavy podstrom */
    node * right; /* pravy podstrom */
};

node * createNode(dataType data, node *left, node *right) {
    node *v = new node;
    v->data = data;
    v->left = left;
    v->right = right;
    return v;
}

Uvažujme strom, v ktorom každý vrchol obsahuje jeden znak. Ako bude vyzerať tento strom?

node *v = createNode('A',
            createNode('B', createNode('C', NULL, NULL),
                            createNode('D', NULL, NULL)),
            createNode('E', NULL, createNode('F', NULL, NULL)));

Použitie pre aritmetické výrazy

Ak by sme takýto všeobecný strom chceli použiť na aritmetické výrazy, definujeme si dataType ako šturktúru s dvoma položkami op a val, ktoré vo vrcholoch potrebujeme. Funckie createOp a createNum vieme napísať pomocou createNode

struct dataType {
    double val;     /* ciselna hodnota */
    char op;     /* operator '+', '-', *', '/', alebo ' ' ak ide o hodnotu */
};

node * createOp(char op, node *left, node *right) {
    dataType d;
    d.op = op;
    return createNode(d, left, right);
}

node * createNum(double val) {
    dataType d;
    d.op = ' ';
    d.val = val;
    return createNode(d, NULL, NULL);
}

Ak teraz máme premennú v ako smerník na nejaký vrchol stromu, namiesto v->op budeme písať v->data.op.

Prehľadávanie stromov

• Často potrebujeme prejsť celý strom a spracovať dáta vo všetkých vrcholoch.
• Napríklad chceme vypísať hodnotu v každom vrchole
• Opäť použijeme rekurziu, voláme na ľavý a pravý podstrom.

void print(dataType &d) {
    cout << d;
}

void preorder(node *v) {
    if (v == NULL) return;
    print(v->data);
    preorder(v->left);
    preorder(v->right);
}

• Pre príklad stromu uvedeného vyššie vypíše ABCDEF
• Takéto poradie sa volá preorder, lebo najprv vypíšeme (spracujeme) dáta vo vrchole, až potom v jeho podstromoch.
• Dáta vo vrchole môžeme vypísať aj po navštívení oboch podstromov, takéto poradie nazývame postorder.
  • Pre náš strom CDBFEA
• Alebo ich môžeme vypísať medzi navštívením ľavého a pravého vrcholu, takéto poradie nazývame inorder.
  • Pre náš strom CBDAEF

void postorder(node *v) {
    if (v == NULL) return;
    postorder(v->left);
    postorder(v->right);
    print(v->data);
}

void inorder(node *v) {
    if (v == NULL) return;
    inorder(v->left);
    print(v->data);
    inorder(v->right);
}

Vypisovanie aritmetických výrazov

• Preorder vypisovanie vypíše výraz v prefixovej notácii / - 65 * 3 5 + 2 3
• Postdorder vypisovanie vypíše výraz v postfixovej notácii 65 3 5 * - 2 3 + /

void print(dataType &d) {
    /* funkcia na tlac jedneho vrcholu pouzita v preorder a postorder */
    if(d.op == ' ') {
      cout << ' ' << d.val;
    }
    else {
        cout << ' ' << d.op;
    }
}

• Inorder vypisovanie nevypíše výraz v infixovej notácii, chýbajú zátvorky 65 - 3 * 5 / 2 + 3
  • Chceme úplne uzátvorkovaný výraz, napr. ( ( 65 - ( 3 * 5 ) ) / ( 2 + 3 ) )

void infix(node *v) {
    /* funkcia na tlac vyrazu v infixovej notacii */
    if(v->data.op == ' ') {
        cout << ' ' << v->data.val;
    }
    else {
        cout << " (";
        infix(v->left);
        cout << " " << v->data.op;
        infix(v->right);
        cout << " )";
    }
}

Cvičenia

• Napíšte funkciu na odalokovanie binárneho stromu
• Napíšte funkciu, ktorá každému uzlu prirobí smerník na rodiča do položky parent typu node *
• Vo výrazoch by sme mohli mať aj premenné, potom za ne dosadzovať hodnoty alebo celé podvýrazy
  • Ako by sme premenné reprezentovali v štruktúre dataType?
• Predstavme si, že v preorder poradí namiesto dát vypíšeme počet detí daného vrcholu. Napríklad pre náš strom so znakmi to bude 2 2 0 0 1 0 (preorder poradie je A B C D E F, vrcholy A a B majú po dve deti, vrcholy C a D majú 0 detí, vrchol E má jedno dieťa a vrchol F 0 detí). Ako z takejto postupnosti zostavíme strom? Je jednoznačne daný? Skúste si nakresliť strom pre postupnosť 2 0 2 1 2 0 0 2 0 0.

Cvičenia 10

• Majme zásobník, do ktorého ukladáme dáta typu char. Do nasledujúceho úryvku kódu vložte na tri miesta príkaz cout << pop(s) tak, aby program vypísal text BAC

stack s;
init(s);
push(s, 'A');
push(s, 'B');
push(s, 'C');

• Majme dva rady, do ktorých ukladáme dáta typu char. Do nasledujúce úryvku kódu vložte na vhodné miesta príkazy tak, aby program vypísal text BAC. Môžete použiť len tri typy príkazov, každý aj viackrát:
  • cout << dequeue(q1);
  • enqueue(q1, dequeue(q2));
  • enqueue(q2, dequeue(q1));

queue q1, q2;
init(q1);
init(q2);
enqueue(q1, 'A');
enqueue(q1, 'B');
enqueue(q1, 'C');

• Napíšte funkciu vyhod(zoznam &z), ktorá z jednosmerného spájaného zoznamu vyhodí všetky záznamy, v ktorých má položka data nulovú hodnotu. Pozor, takéto záznamy sa môžu vyskytovať aj na začiatku zoznamu. Vyhodené položky zoznamu treba odalokovať. V prednáške 18 nájdete funkcie na vytvorenie a vypísanie zoznamu, ktoré môžete použiť na testovanie vášej funkcie.

• Napíšte funkciu kopiruj(zoznam &kam, zoznam &odkial), ktorá vytvorí kópiu zoznamu odkial a uloží ju do zoznamu kam.

• Napíšte funkciu zip(zoznam &z1, zoznam &z2, zoznam &z3), ktorá vyvorí z dvoch zoznamov ich "zips" - vo výslednom zozname sa budú postupne striedať prvky z prvého a druhého zoznamu. Pokiaľ má jeden zoznam viac prvkov ako ten druhý, tak jeho zvyšné prvky budú na konci zoznamu.

 zip({1,2,3}, {10,11,12,13,14}) = {1,10,2,11,3,12,13,14}

• Napíšte funkciu reverse(zoznam &z), ktorá otočí poradie prvkov v zozname (jednosmernom spájanom).

• Do programu na kontrolu správne uzátvorkovaných výrazov z prednášky 19 dopíšte informatívne oznamy pre užívateľa, ktoré mu povedia, zátvorka na ktorom mieste v reťazci nemá ľavý pár alebo na ktorom mieste má ľavý pár iného typu ako pravý. Po prvej takejto chybe už ďalšie nevypisujte.

DÚ10

max. 7 bodov, termín odovzdania utorok 6.12. o 22:00

Cieľom tejto domácej úlohy je precvičiť si prácu so spájanými zoznamami a s rekurziou.

Napíšte verziu triedenia MergeSort, ktorá bude triediť dáta v spájanom zozname. Vo vašom programe použite jednosmerný spájaný zoznam, ktorý si udržuje smerník na prvý aj posledný prvok zoznamu. V kostre uvedenej nižšie najskôr naprogramujte dve podporné funkcie insertLast a length, ktoré pracujú s takýmito zoznamami. Potom naprogramujte rekurzívnu funkciu mergeSort, ktorá zoberie zoznam, rozdelí ho na dva približne rovnako veľké zoznamy, každý z nich zvlášť rekurzívne utriedi a potom ich spojí do jedného utriedeného zoznamu funkciou merge (ktorú tiež musíte naprogramovať). Zoznamy dĺžky 1 a 0 už netreba triediť.

Pri delení zoznamu na dve časti môžete buď vyberať prvky z jedného zoznamu a striedavo ich vkladať do dvoch ďalších zoznamov, alebo si môžete nájsť v zozname stred a ten "preseknúť".

Celý program načítava od užívateľa čísla až kým užívateľ nezadá číslo -1, potom ich utriedi a vypíše výsledok.

#include <iostream>
#include <cassert>
using namespace std;

struct item {
    /* prvok spajaneho zoznamu so smernikom na dalsi */
    int data;
    item* next;
};

struct list {
    /* spajany zoznam so smernikom na prvy a posledny prvok,
     * smerniky budu NULL ak je zoznam prazdny  */
    item *first;
    item *last;
};

void init(list &z) {
    /* inicializuje prazdny zoznam */
    z.first = NULL;
    z.last = NULL;
}

bool empty(const list &z) {
    /* testuje, ci je zoznam prazdny */
    return z.first == NULL;
}

int length(list &z) {
    /* vrati dlzku zoznamu */
}

void insertLast(list &z, int d) {
    /* Vlozi prvok na posledne miesto v zozname.
     * Pozor na pripad, ked je zoznam prazdny */
}

int deleteFirst(list &z) {
    /* Zmaz prvok zo zaciatku zoznamu a vrat jeho hodnotu. */
    assert(z.first != NULL);
    item* p = (z.first->next); // prvok, ktorý bude ďalej začiatkom
    int d = z.first->data; // to, čo máme vrátiť
    delete z.first; // uvoľnenie pamäte
    z.first = p; // nový začiatok
    if (z.first == NULL) { // ak je teraz zoznam prazdny, zmeni aj last
        z.last = NULL;
    }
    return d;
}

void print(list &z) {
    /* vypise vsetky prvky zoznamu oddelene medzerami */
    item* x = z.first;
    while (x != NULL) {
        cout << x->data << " ";
        x = x->next;
    }
    cout << endl;
}

void merge(list &z1, list &z2, list &z) {
    /* Dva neprazdne utriedene zoznamy z1 a z2 zluci do jedneho utriedeneho zoznamu z. */
}

void mergeSort(list &z) {
    /* utriedi zoznam z */
}

int main() {
    list z;
    init(z);

    /* nacitaj data zo vstupu: kladne cisla, za ktorymi ide cislo -1 */
    while (1) {
        int data;
        cin >> data;
        if (data == -1) break;
        insertLast(z, data);
    }

    /* utried */
    mergeSort(z);

    /* vypis vysledok */
    print(z);
}

Prednáška 22

Organizačné poznámky

• Dajte nám vedieť svoj názor: malá špecializovaná anketa v Moodli, celofakultná anketa na http://anketa.fmph.uniba.sk/
• Dnes vyhľadávacie stromy, zajtra dokončenie vyhľadávacích stromov, lexikografické stromy
• Budúci týždeň v utorok opakovanie, zhrnutie, vaše otázky k učivu, precvičovanie príkladov, rady k písomke a skúške
• Budúci týždeň v stredu: prehľad vecí, čo sme nebrali z C resp. C++, nebude na skúške
• Cvičenia tento a budúci týždeň normálne, vrátane rozcvičiek
• DÚ11 do budúceho utorka je posledná
• Pondelok 19.12. záverečná písomka, treba získať 50% bodov, nepodceniť
• Tento týždeň by sa mali na stránke objaviť ukážkové príklady na písomku

Opakovanie: binárne stromy

• V každom vrchole máme uložené nejaké dáta a smerník na ľavého a pravého syna.

struct node {
    /* vrchol stromu  */
    dataType data;
    node * left;  /* lavy syn */
    node * right; /* pravy syn */
};

• Príklad využitia: reprezentácia aritmetických výrazov
• Na prechádzanie všetkých vrcholov sa hodí rekurzia
  • videli sme preorder, inorder, postorder poradie vypisovania

Jednoduchá práca so stromami

Výška (hĺbka) stromu

• Hĺbka vrcholu v strome je jeho vzdialenosť od koreňa. T.j. koreň má hĺbku 0, jeho synovia hĺbku 1 atď.
• Výška stromu (niekedy nazývaná hĺbka stromu) je maximum z hĺbok jeho vrcholov
  • Ak máme strom s jedným vrcholom, výška je 0
  • Inak spočítame výšku ľavého a pravého podstromu
  • Ku každej pripočítame 1, lebo pridávame hranu k otcovi
  • Aby to fungovalo aj pre prázdne podstromy, dodefinujeme výšku prázdneho podstromu na -1

 int height(node *v) {
    /* Vrat vysku stromu s korenom v.
     * Ak v je NULL, vrati -1. */
    if (v == NULL) return -1;
    int left = height(v->left);
    int right = height(v->right);
    /* vrat max(left, right)+1 */
    if (left >= right) return left + 1;
    else return right + 1;
}

Ak máme binárny strom s n vrcholmi, aká môže byť jeho minimálna a maximálna výška?

• Výška stromu s n vrcholmi je najviac n-1, ak sú všetky navešané jeden pod druhý, t.j. každý okrem posledného má jedného syna
• Strom s výškou h má najviac Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2^{h+1}-1} vrcholov
  • Dá sa dokázať indukciou vzhľadom na h
• Takže vieme, že Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n\le 2^{h+1}-1} .
• Vyjadríme h: Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h\ge \log_2(n+1)-1}
• Takže dostávame Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \log_2(n+1)-1 \le h \le n-1}

Úplný binárny strom

• Strom, ktorý má pri určitej hĺbke h maximálny počet vrcholov, t.j. Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2^{h+1}-1} sa nazýva úplny binárny strom.
• Chceli by sme taký strom vytvoriť.

• Použijeme funkciu createNode na vytvorenie jedného vrcholu:

node * createNode(dataType data, node *left, node *right) {
    node *v = new node;
    v->data = data;
    v->left = left;
    v->right = right;
    return v;
}

• Rekurzívne tvoríme väčšie stromy z menších.
• Globálna premenná count priradí vrcholom do dátovej položky poradové číslo.

node* createTree(int height) {
    if (height == -1) return NULL;
    node* u = createNode(count++, NULL, NULL);
    u->left = createTree(height - 1);
    u->right = createTree(height - 1);
    return u;
}

Uvoľňovanie stromu

Pri ukončení práce by sme mali pamäť, ktorú sme potrebovali na strom uvoľniť.

void destroyTree(node* v){
  if(v!=NULL){
    destroyTree(v->left);
    destroyTree(v->right);
    delete v;
  }
}

Hľadanie prvku v strome

• Chceme zistiť, či sa v strome nachádza určitá hodnota, alebo spočítať, koľkokrát sa tam nachádza.
• Môže byť hocikde, preto musíme prejsť rekurzívne všetky vrcholy stromu

int count(node *v, dataType x) {
    /* Vrat pocet vyskytov hodnoty x v strome s korenom v. */
    if (v == NULL) return 0;
    int add = 0;
    if (v->data == x) add = 1;
    return count(v->left, x) + count(v->right, x) + add;
}

Binárne vyhľadávacie stromy

• Binárne vyhľadávacie stromy sú usporiadané tak, aby sme vedli pomerne rýchlo vyhľadať prvok s určitou hodnotou
• V každom vrchole máme položku kľúč (key), kľúče vieme porovnávať znamienkom < (napr. int, double, string...)
• Pre každý vrchol v stromu platí:
  • Každý vrchol u v ľavom podstrome v má kľúč menší ako vrchol v
  • Každý vrchol u v pravom podstrome v má kľúč väčší ako vrchol v
• Z toho vyplýva, že ak vypíšeme strom v inorder poradí, dostaneme prvky usporiadané
• Pre danú množinu kľúčov existuje veľa vyhľadávacích stromov

Hľadanie vo vyhľadávacom strome

• Porovnáme hľadaný kľúč s kľúčom v koreni
  • Ak sa rovnajú, našli sme čo hľadáme a končíme
  • Ak je hľadaná hodnota menšia ako kľúč v koreni, musí byť v ľavom podstrome, ak je väčšia v pravom
• V príslušnom podstrome sa rozhodujeme podľa tých istých pravidiel
• Keď narazíme na prázdny podstrom, kľúč sa v strome nenachádza

node * findNode(node *root, keyType key) {
    /* V binarnom vyhladavacom strom s korenom root najdi a vrat
     * vrchol s klucom a ak neexistuje, vrat NULL. */
    node * v = root;
    while (v != NULL && v->key != key) {
        if (key < v->key) {
            v = v->left;
        } else {
            v = v->right;
        }
    }
    return v;
}

• Dá sa zapísať rekurzívne alebo cyklom, lebo vždy ideme iba do jedného podstromu
• Čas výpočtu je v najhoršom prípade úmerný výške stromu

Vyhľadávací strom ako implementácia slovníka

Chceme implementovať slovník, v ktorom máme pre každý kľúč uložené nejaké dáta, napr. pre každé meno máme telefónne číslo.

• Ide o abstraktný dátový typ s nasledujúcimi funkciami:

void init(dictionary &d);
/* inicializuje prazdny slovnik */


bool find(dictionary &d, keyType key, dataType &data);
/* V slovniku s najde kluc key a do data ulozi data s nim 
 * spojene. Ak tam nie je, vrati false, inak vrati true. */

void insert(dictionary &d, keyType key, dataType data);
/* Do slovnika d vlozi kluc key a jeho data.
 * Predpokladame, ze takyto kluc este v slovniku nie je. */


void remove(dictionary &d, keyType key);
/* Zmaze kluc key zo slovnika d.
 * Predpokladame, ze tam taky kluc je. */

• Opäť vieme slovník použiť bez znalosti detailov implementácie
• Videli sme už slovník v neutriedenom poli, utriedenom poli, hashovacej tabuľke, spájanom zozname,...
• Dnes si ukážeme slovník v binárnom vyhľadávacom strome
• Pre úplnosť príklad použitia:

typedef string keyType;
typedef string dataType;

int main() {
    dictionary d;
    init(d);

    insert(d, "Janko Hrasko", "02 / 12 34 56 78");
    insert(d, "Jozko F. Mrkvicka", "+421(911)999 888");

    string cislo;
    bool nasiel = find(d, "Janko Hrasko", cislo);
    assert(nasiel);
    cout << cislo << endl;

    remove(d, "Janko Hrasko");

    nasiel = find(d, "Janko Hrasko", cislo);
    assert(!nasiel);
}

Použijeme nasledujúcu definíciu vrcholu, v ktorej máme zvlášť key a zvlášť data.

• Pamätáme si aj smerník na rodiča (ten má hodnotu NULL v koreni)
• Slovník je potom jednoducho smerník na koreň a inicializujeme ho na NULL.

struct node {
    /* vrchol binarneho vyhladavacieho stromu  */
    keyType key;    /* kluc podla ktoreho vyhladavame */
    dataType data;  /* data spojene s klucom */
    node * parent;  /* otec vrchola */
    node * left;    /* lavy syn */
    node * right;   /* pravy syn */
};

struct dictionary {
    node *root;
};

void init(dictionary &d) {
    /* inicializuje prazdny slovnik */
    d.root = NULL;
}

Funkciu find napíšeme jednoducho pomocou findNode, ktorú sme videli predtým:

bool find(dictionary &d, keyType key, dataType &data) {
    /* V slovniku s najde kluc key a do data ulozi data s nim
     * spojene. Ak tam nie je, vrati false, inak vrati true. */
    node *v = findNode(d.root, key);
    if (v != NULL) {
        assert(v->key == key);
        data = v->data;
        return true;
    } else {
        return false;
    }
}

Vkladanie prvku do vyhľadávacieho stromu

• Predpokladáme, že prvok v strome nie je.
• Putujeme po strome podobne ako po vyhľadávaní prvku, až kým nenarazíme na nulový smerník.
  • Na tomto mieste by mal byť nový prvok, takže ho tam pridáme ako nový list
• Použijeme rozšírenú verziu findNode, ktorá vráti miesto, kam by mal prvok patriť, aj jeho otca.

node * createLeaf(keyType key, dataType data, node * parent) {
    /* vytvor novy vrchol s danymi hodnotami, obe deti nastav na NULL */
    node *v = new node;
    v->key = key;
    v->data = data;
    v->left = NULL;
    v->right = NULL;
    v->parent = parent;
    return v;
}

void findNode(node *root, keyType key, node *&v, node *&parent) {
    /* Do v uloz smernik na vrchol s klucom key alebo NULL ak neexistuje.
     * Do parent uloz otca v, NULL ak neexistuje a ak key nie je v strome
     * tak smernik na vrchol, ktory by mal byt otcom pre vrchol
     * s hodnotou key.*/
    parent = NULL;
    v = root;
    while (v != NULL && v->key != key) {
        parent = v;
        if (key < v->key) {
            v = v->left;
        } else {
            v = v->right;
        }
    }
}

void insert(dictionary &d, keyType key, dataType data) {
    /* Do slovnika d vlozi kluc key a jeho data.
     * Predpokladame, ze takyto kluc este v slovniku nie je. */
    if (d.root == NULL) {
        /* prazdny strom - treba vytvorit koren */
        d.root = createLeaf(key, data, NULL);
    } else {
        node *v;
        node *parent;
        findNode(d.root, key, v, parent);
        /* parent je teraz vrchol, ktoreho syn ma byt novy vrchol */
        assert(v == NULL && parent != NULL);
        /* zisti, ci mame byt lave alebo prave dieta otca */
        if (key < parent->key) {
            assert(parent->left == NULL);
            parent->left = createLeaf(key, data, parent);
        } else {
            assert(parent->right == NULL);
            parent->right = createLeaf(key, data, parent);
        }
    }
}

• Čas vkladania je tiež v najhoršom prípade úmerný hĺbke stromu.

Odbočka: minimum a nasledovník

• Spravíme si dve funkcie, ktoré sa nám zídu pri mazaní prvku, ale môžu sa zísť aj inokedy.

• Prvá funkcia nájde vo vyhľadávacom strome minimum.
  • Všetky prvky menšie ako koreň sú v ľavom podstrome, bude tam zrejme aj minimum.
  • Tá istá úvaha platí pre koreň ľavého podstromu.
  • Ideme teda doľava kým sa dá, posledný vrchol vrátime (list alebo vrchol s pravým synom).
  • Dá sa tiež pekne napísať rekurzívne.

node *minimumNode(node *v) {
    /* vrati vrchol s minimalnym klucom vo vyhladavacom strome
     * s korenom v */
    assert(v != NULL);
    while (v->left != NULL) {
        v = v->left;
    }
    return v;
}

Druhá funkcia nájde vrchol, ktorý v utriedenom poradí nasleduje za daným vrcholom v.

• Ak má v pravého syna, nasledovník bude v pravom podstrome, konkrétne vrchol s minimálnym kľúčom v tomto podstrome
• V opačnom prípade to môže byť rodič, ak v je jeho ľavý syn
• Ak je pravý syn, môže to byť prarodič, ak je rodiť jeho ľavý syn, atď
• Nájdeme teda prvého predka, do ktorého ľavého podstromu patrí v a ten je hľadaný nasledovník

node *successorNode(node *v) {
    /* vrati vrchol, ktorý v utriedenom poradi nasleduje za vrcholom v,
     * alebo NULL ak taky vrchol nie je */
    assert(v != NULL);
    if (v->right != NULL) {
        return minimumNode(v->right);
    }
    while (v->parent != NULL && v == v->parent->right) {
        v = v->parent;
    }
    return v->parent;
}

Mazanie prvkov z vyhľadávacieho stromu

• Nájdeme mazaný vrchol v podľa kľúča obvyklým spôsobom
• Ak je v list, jednoducho ho zmažeme
• Ak má v jedno dieťa, toto dieťa prevesíme priamo pod otca v a v zmažeme
• Ak má v dve deti, nájdeme nasledovníka v, t.j. minimum v pravom podstrome v.
• Tento nasledovník nemá ľavé dieťa, vieme ho teda zmazať.
• Jeho údaje presunieme do vrcholu v.
• Tiež treba dať pozor na mazanie koreňa.

void remove(dictionary &d, keyType key) {
    /* Zmaze kluc key zo slovnika d.
     * Predpokladame, ze tam taky kluc je. */

    /* Najdi vrchol s klucom */
    node *v = findNode(d.root, key);
    assert(v != NULL && v->key == key);
    /* najdi vrchol rm s jednym synom child,
     * ktory vyhodime. */    
    node *rm, *child;
    if (v->left == NULL || v->right == NULL) rm = v;
    else rm = successorNode(v);
    assert(rm->left == NULL || rm->right == NULL);
    if (rm->left != NULL) child = rm->left;
    else child = rm->right;

    /* preves syna priamo pod otca rm */
    if (child != NULL) child->parent = rm->parent;
    if (rm->parent == NULL) d.root = child;
    else {
        /* ak rm nie je koren, jeho otcovi zaves child */
        node *parent = rm->parent;
        assert(rm == parent->left || rm == parent->right);
        if (rm == parent->left) parent->left = child;
        else parent->right = child;
    }
    /* ak rm nema mazany kluc, prekopiruj data z rm do v*/
    if (rm != v) {
        v->key = rm->key;
        v->data = rm->data;
    }
    delete rm;
}

Prednáška 23

Slovník

Na prednáške ?? sme pracovali s abstraktnou dátovou štruktúrou slovník. Na implementáciu sme využívali hashovacie tabuľky, ktoré pracovali vcelku optimálne, avšak potrebovali veľký pamäťový priestor. Pripomeňme si, aké operácie od slovníka požadujeme.

• Vloženie prvku
• Vymazanie prvku
• Hľadanie prvku

Budeme sa snažiť vytvoriť takú implementáciu slovníka, kde si nebudeme musieť pamätať nič zbytočné a pritom v ňom budeme vedieť vyhľadávať lepšie ako čisto v zozname slov.

Opakovanie binárne vyhľadávacie stromy

Aj binárne vyhľadávacie stromy môžeme chápať ako implementáciu slovníka a jeho operácií. Najvhodnejší je v prípade, ak sú kľúče (celé) čísla. Samozrejme vo všeobecnosti postačí, ak vieme na kľúčoch urobiť porovnanie (>,<,=).

Binárny vyhladávací strom je binárny strom v ktorom platí:

• Hodnota v koreni je väčšia ako všetky hodnoty v ľavom podstrome.
• Hodnota v koreni je menšia ako všetky hodnoty v pravom podstrome.
• Ľavý aj pravý podstrom sú binárne vyhľadávacie stromy.

Pre tie isté čísla existuje viacero binárnych vyhľadávacích stromov (skúste napríklad čísla 1..4). Čo však majú spoločné je inorder výpis.

• Prečo?

Zopakujeme si, ako boli implementované jednotlivé operácie.

Hľadanie v binárnom strome

Porovnáme hľadaný kľúč s kľúčom v koreni

• Ak sa rovnajú, našli sme čo hľadáme a končíme
• Ak je hľadaná hodnota menšia ako kľúč v koreni, musí byť v ľavom podstrome, ak je väčšia v pravom

node* findNode(node* root, keyType key) {
    node* v = root;
    while (v != NULL && v->key != key) {
        if (key < v->key) {
            v = v->left;
        } else {
            v = v->right;
        }
    }
    return v;
}  

node* findNode(node* root, keyType key) {
    if ((root==NULL)||(root->key==key)) return root;    
    
    if (key < root->key) return findNode(root->left);
    else return findNode(root->left);
}  

Vkladanie do binárneho vyhľadávacieho stromu

• Putujeme po strome podobne ako po vyhľadávaní prvku, až kým nenarazíme na nulový smerník.
• Na tomto mieste by mal byť nový prvok, takže ho tam pridáme ako nový list.
• Na to, aby sme vedeli pridať nový list potrebujeme vedieť predchodcu toho listu (takže si musíme pri hľadaní ťahať za sebou).

Vymazávanie z binárneho vyhľadávacieho stromu

• Putujeme po strome podobne ako po vyhľadávaní prvku, až kým nenarazíme na hľadaný prvok.
• Tento prvok chceme vymazať:
  • Ak je prvok listom, triviálne vymažeme.
  • Ak má iba jedného potomka, prevesíme.
  • Ináč nájdeme nasledovníka (minimum v pravom podstrome) a prekopírujeme ho na miesto hľadaného prvku a ten list zmažeme.

Zložitosť slovníkových operácií v BVS

Zložitosť operácií závisí od výšky stromu. Tá je

• V najhoršom prípade O(n)
• V priemernom prípade O(log n)ľ

Find, Insert, Delete:

• Najlepší prípad O(1)
• Najhorší prípad O(height(T))=O(n)
• Priemerný prípad O(height(T))=O(log n)

Pre porovnanie si pripomeňme implementáciu slovníka pomocou

• Usporiadaného zoznamu: Find - O(log n), Insert - O(n), Delete - O(n) (najhoršie prípady)
• Neusporiadaného zoznamu: Find - O(n), Insert - O(1), Delete - O(n) (najhoršie prípady)

Lexikografické stromy (trie)

Myšlienka je relatívne jednoduchá. Slová budem ukladať do stromu, kde sa budem rozhodovať na základe písmen. Každé slovo začína niektorým písmenom abecedy. Podľa neho sa v koreni stromu rozhodnem, do ktorého z jeho podstromov pokračujem. Podstromov je Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |Abeceda|} .

Vrchol lexikografického stromu obsahuje:

• dáta - môže byť čisto písmenko, na ktoré som sa do vrcholu dostala (alebo celé slovo, ktoré v tomto vrchole končí)
• smerníky na ďalšie podstromy (teda na ďalšie vrcholy stromu)
• počet koľko krát sme vrchol použili (nateraz asi nevidíte dôvod - ukážeme ho neskôr)

Vrchol je teda nasledovného tvaru:

struct node {
    /* vrchol stromu  */
    char data;
    int use_count;
    node* next[Abeceda]; 
};

alebo môžeme pole smerníkov alokovať vždy keď vznikne vrchol - nebude definícia závislá od veľkosti abecedy:

struct node {
    /* vrchol stromu  */
    char data;
    int use_count;
    node** next; 
};

Samotný strom je potom iba smerník na koreňový vrchol

struct trie {
    node* root;
};

Inicializácia a uvoľňovanie stromu

Pri práci s lexikografickým stromom začíname s jedným prázdnym vrcholom - koreňom, ktorého pole nasledovníkov su iba smerníky s hodnotou NULL. Koreň je vlastne špeciálny vrchol, ktorý neobsahuje žiadne dáta.

trie* initTrie(){
    node* root = initNode();
    trie* t=new trie;
    t->root=root;
    return t;
}

Pričom funkcia initNode() pracuje nasledovne:

• Vytvorí si smerník na nový vrchol (alokuje mu priestor)
• Ak máme pole nasledovníkov cez smerníky (teda nie pole konkrétnej veľkosti, ktoré by sa vytvorilo spolu s vrcholom), vytvoríme si takéto pole.
• Inicializujeme nasledovníkov na NULL.
• Nastavíme hodnoty data a use_count (zatiaľ na niečo neexistujúce, alebo si potrebné hodnoty môžeme odovzdať ako parameter funkcie initNode() ).

node* initNode(){
    node* v=new node;
    node** w=new node*[Abeceda];
    for (int i=0; i<Abeceda; i++) w[i]=NULL;
    v->next=w;
    v->use_count=0;
    v->data='x';
    return v;
}

Uvoľňovanie pamäti stromu je pomocou jednoduchej rekurzívnej funkcie freeNode(node*), pričom na uvoľnenie celého stromu potrebujeme zavolať freeNode(t->root)

void freeNode(node* v){
    if (v==NULL) return;
    for (int i=0; i<Abeceda; i++) freeNode(v->next[i]); 
    delete v->next; // táto časť by nebola potrebná, ak by sme mali next statické
    delete v;
}

Vkladanie do stromu

Do lexikografického stromu vkladáme string - tj reťazec znakov, zložený iba z písmen abecedy (pre jednoduchosť pracujeme s abecedou 'A'..'Z' resp. s jej začiatkom veľkosti |Abeceda|).

Postupujeme v cykle (po jednotlivých písmenách vkladaného slova) nasledovne:

• Začínam od koreňa stromu
• Ak nemám patričný smerník - tj. smerník na ďalšie potrebné písmkenko, tak si takýto vrchol (obsahujúci patričné písmenko) vytvoríme.
  • Všimnite si, že v úplne prvom otočení cyklu nemáme žiadne zmysluplné písmenko, ktoré by sme dali ako hodnotu koreňu.
• Tento vrchol používame aj pri tomto slove - zväčšíme teda počet jeho použití.
• Pozrieme si znak slova (pri prvom kroku vlastne na prvý) a ak je to koniec slova, tak skončíme cyklus.
• V opačnom prípade sa posunieme vhodnou hranou - máme už zaručené, že tam nebude NULL a tiež na ďalší znak slova.

void insertTrie(trie* t, char* key) {
    node **r; // opäť budeme používať smerník na smerník, aby sme mohli ukazovať priamo na hranu a nemali problém s NULL na konci
    node *v;
    char *p;
    int c;

    r = &t->root; 
    p = key;

    while (true) {
        v = *r;
        if (v == NULL) {
            v = initNode(); /* vrchol neexistuje, vytvor ho */
            (v->data)=c;
            *r = v;     /* smernik na smernik do trie */
        }

        /* Pouzijeme tento vrchol a nastavime jeho hodnotu */
        (v->use_count)++;

        c = *p;                /* Aktualny znak: */
        if (c == '\0') break;  /* ak je tam koniec vkladaneho slova, ukoncime cyklus */
        r = &v->next[c - 'A']; /* inac pokracujeme dalsim znakom */

        p++;
    }
}

Hľadanie v lexikografickom strome

Vyhľadávanie v strome opäť postupuje po písmenkáach vyhľadávaného slova. Kým nedojde na koniec slova snaží sa ísť po hranách, ktoré zodpovedajú písmenkám. V prípade, že na niektorom mieste chýba patričná hrana, znamená to, že takéto slovo sa v strome nenachádza.

bool searchTrie(trie* t, char* s){
    node *v = t->root;
    while(*s != '\0'){
        int c = *s - 'A';
        if (v->next[c] == NULL) return false;
        else v = v->next[c];
        *s++;
    }
    return true;
}

Teraz sa nad tým kúsok zamyslíme. Vo chvíli, keď uložím slovo "ahoj", mám vlaste vytvorené aj slová "a", "ah" a "aho", pričom tieto vôbec v slovníku nemusia byť. Po prečítaní slova sa teda potrebujem opýtať, či tam nejaké slovo naozaj končilo a na základe toho odpovedať.

bool searchTrie(trie* t, char* s){
    node *v = t->root;
    while(*s != '\0'){
        int c = *s - 'A';
        if (v->next[c] == NULL) return false;
        else v = v->next[c];
        *s++;
    }
    if(endOfWord(v) == true) return true;
    else return false;
}

Otázka je, ako zistím, že nejaké slovo v slovníku naozaj bolo a nejedná sa iba o prefix?

• Prvá možnosť je si vkaždom vrchole pamätať, či tam nejaké slovo končilo. Stačí nám na to ďalšia premenná v štruktúre node, ktorú budeme patrične nastavovať.
• Druhá možnosť je využiť existujúce súčasti štruktúry node, konkrétne číslo use_count. Do tejto premennej sme pripočítávali 1 vždy, keď sme vrchol používali.
  • Teda pre vrchol Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v} s potomkami Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v_1 .. v_k} je use_count vo vrchole v aspoň súčet use_count potomkoch. Vždy keď sme navštívili vrchol v, tak sme pokračovali v jednom z jeho potomkov.
  • Teda, vždy okrem prípadu, kedy sme vo v končili nejaké slovo. Počet slov, ktoré vo v končili je práve rozdielom v->use_count - SUMA (v_i->use_count).

bool endOfWord(node* p){
    int sum=0;
    for (int i=0; i<Abeceda; i++){
        if (p->next[i]!=NULL) sum+=(p->next[i])->use_count;
    }
    if (sum==p->use_count) return false;
    else return true;
}

Vymazávanie z lexikografického stromu

Pri vymazávaní slova postupujeme podobne ako pri hľadaní s tým rozdielom, že musíme patrične upravovať počet použití vrcholu. Nesmieme tiež zabudnúť vymazať vrchol, ktorý používame posledný krát.

void deleteTrie(trie* t, char* s){
    node* v = t->root;
    while(*s != '\0'){
        int c = *s - 'A';
        if(v->next[c] == NULL) return;  // Error
        else if ((v->next[c])->use_count == 1){ // Posledné použitie vrcholu
            freeNode(v->next[c]);
            v->next[c] = NULL;
            return;
        }
        else {
            v = v->next[c]; 
            v->use_count--;
        }    
        *s++;
    }
    (t->root)->use_count--;
}

Teraz si vyskúšajme takto napísanú funkciu na strome v ktorom máme iba slovo "ahoj" a skúsime z neho vymazať slovo "a". Takéto slovo v slovníku nemáme, napriek tomu nám ho dovolí vymazať a vymaže tým vlastne slovo "ahoj".

Aby sme tomu zabránili môžeme urobiť jednu z nasledujúcich vecí:

• Uvoľnovať vrcholy iba v prípade, že je tam niekde endOfWord() alebo
• Na začiatku sa opýtať, či sa také slovo vyskytuje a potom mazať v kľude. Tým vyriešime aj problém, že čo z rozpracovaným stromom vo chvíli, keď zistím, že som vlastne vymazávať nemala.

Vypisovanie stromu

Podobne ako pri binárnych stromoch aj lexikografický strom môžeme vypisovať napríklad funkciou Preorder(). Aby sa aspoň kúsok dalo sledovať, ako to so stromom vyzerá, pridali sme nejaké zátvorky (nie že by veľmi pomohli).

void preorder(node* v){
    if (v==NULL) {cout << "0 "; return;}
    else cout << "("<< v->data<<","<< v->use_count<<") ";

    cout << "[";
    for (int i=0; i<Abeceda; i++){
        preorder(v->next[i]);
    }
    cout <<"] ";
}

Oveľa viac by nám pomohlo vedieť vypísať všetky slová, ktoré sú v slovníku. Ich počet je zjavne (t->root)->use_count.

Funkcia na vypisovanie všetkých slov bude pracovať rekurzívne a do pomocnej premennej pre si bude zapisovať aktuálny prefix stav slova, ktoré vypisuje. Pracuje nasledovne -- vo vrchole v a mám aktuálny prefix pre

• Ak v je list, tak vypíše prefix
• Ak nie, tak sa rekurzívne zavolá na všetky podstromy, pričom k prefixu pridá postupne všetky potenciálne znaky Abecedy.
• Špeciálne ak je vo vrchole v koniec nejakého slova, tak ho vypíše.

void printTrie(int depth, node *p, char* prefix) {    
    if (leaf(p)) {              // ak sme na liste a nie je tam NULL
         cout << prefix << endl;
    }
    else {
       for (int i = 0; i<Abeceda; i++)
             if (p->next[i] != NULL) {       
                 prefix[depth] = (p->next[i])->data;   // pridám si ďalšie písmeno
                 prefix[depth+1] = '\0';               // a zaň koniec slova
                 printTrie(depth+1,p->next[i],prefix); // zavolám sa rekurzívne
             }
       if (endOfWord(p)) {                             // špeciálne aj v strede stromu môžem vypísať
            prefix[depth] = '\0';
            cout << prefix << endl;
         }
    }
}

Volanie tejto rekurzívnej funkcie je s použitím pomocnej premennej, ktorej dĺžku by sme mohli nastaviť ako dĺžku ajdlhšieho slova v strome.

    char* pre=new char[100];
    printTrie(0,t->root, pre);

Ďalšie použitie lexikografického stromu

Budeme riešiť takúto úlohu: na vstupe je daná množina slov z abecedy {a, b}. Takýchto slov môže byť aj niekoľko stotisíc a my potrebujeme vedieť, koľkokrát sa nachádza každé slovo v tejto množine.

Môžeme použiť lexikografický strom a jeho pripravené funkcie. Jedine pri výpise slov potrebujeme zistiť, koľko slov vo vrchole končí. To vieme s využitím premennej use_count.

Cvičenia 11

• Máme binárny strom, v ktorom má každý vrchol buď dve deti a v dátovom poli uložený znak '#' alebo nemá žiadne deti a v dátovom poli má uložený znak '*'. Keď tento strom vypíšeme v preorder poradí, dostaneme postupnosť ##*#*** Nakreslite, ako vyzerá tento strom.

• Napíšte rekurzívnu funkciu, ktorá každému uzlu binárneho stromu prirobí smerník na otca do položky parent typu node *. Funkcia bude mať hlavičku void assignParent(node *v, node *parent) kde vrchol parent je otcom vrchola v, alebo NULL ak v je koreň a teda nemá otca. Funkcia doplní otca vrcholu v aj všetkým jeho potomkom, t.j. napr. synom vrchola v nastaví ako otca smerník na v. Použite nasledujúcu štruktúru pre vrchol stromu:

struct node {
    /* vrchol stromu  */
    dataType data;
    node * left;  /* lavy podstrom */
    node * right; /* pravy podstrom */
    node * parent; /* otec vrcholu */
};

• Uvažujte binárne stromy pre aritmetické výrazy, v ktorých máme aj premennú x. Tá sa spozná podľa toho, že v položke op je uložený znak 'x' (položka val sa v takýchto vrcholoch nepoužíva). Napíšte funkciu, ktorá dostane nezáporné celé číslo n a zostaví strom, ktorý reprezentuje Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^n} , pričom použije len vrcholy pre premennú x a pre násobenie.
  • Modifikujte funkciu evaluate z prednášky 21 tak, aby pracovala aj pre výrazy s premennou x, pričom hodnotu tejto premennej dostane ako parameter, t.j. hlavička bude double evaluate(node *v, double x) {. Overte, že ak tútu funkciu spustíte pre váš strom zodpovedajúci Syntaktická analýza (parsing) neúspešná (MathML (experimentálne): Neplatná odpověď („Math extension cannot connect to Restbase.“) od serveru „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x^n} , dostanete správny výsledok.

• Napíšte funkciu, ktorá binárny strom upraví tak, že v dátovej časti vrcholov bude node * next ukazujúci na nasledujúci vrchol stromu v
  • infixovom poradí
  • prefixovom poradí

• Na prednáške prednáške 20 sú tri funkcie na vyfarbovanie súvislej plochy, ktoré používajú polia delta_x a delta_y. Vďaka týmto poliam skúma každé políčko svojich susedov v poradí vpravo, hore, vľavo, dole. Jedna z týchto funkcií je však rekurzívna, jedna používa zásobník a jedna rad. Každú funkciu spustíme na matici a s troma riadkami a troma stĺpcami, ktorá je vyplnená nulami, pričom funkciu spustíme na stredné políčko, t.j. stlpec=riadok=1 a nová farba je tiež 1. V akom poradí budú tieto funkcie vyfarbovať jednotlivé štvorčeky matice? Skúste túto úlohu riešiť bez použitia počítača.

DÚ11

max. 5 bodov plus 2 body bonus, termín odovzdania utorok 13.12. o 22:00

Cieľom tejto úlohy je precvičiť si prácu so stromami.

Vašou úlohou je napísať program, ktorý odkóduje text zapísaný Morseovou abecedou, pričom túto abecedu budete mať uloženú v binárnom strome. Samotnú Morseovu abecedu načítajte zo súboru s názvom morse.txt, ktorý si stiahnite tu. Na každom riadku súboru je jedno písmeno a za medzerou zápis tohto písmena v Morseovej abecede pomocou znakov bodka a pomlčka. Budeme pracovať len s kódmi pre písmená A až Z. Text na dekódovanie zadá užívateľ ako jeden riadok na konzole, pričom kódy pre jednotlivé písmená sú oddelené medzerou a dve medzery znamenajú medzeru medzi slovami. Napríklad ak užívateľ zadá text ".... . .-.. .-.. ---  .-- --- .-. .-.. -..", váš program by mal vypísať "HELLO WORLD". Ak text obsahuje neexistujúci kód, program vypíše namiesto takéhoto písmena otáznik, napríklad pre zadaný text "... ------ ..." vypíše "S?S".

Morseovu abecedu si uložte vo forme binárneho stromu, kde každý vrchol môže mať dve deti, jedno nazvané dot (bodka) a druhé dash (čiarka). Určitému kódu zodpovedá vrchol, do ktorého sa dostaneme z koreňa, pričom budeme vždy na bodku pokračovať do dieťaťa nazvaného dot a na pomlčku do dieťaťa nazvaného dash. V tomto vrchole máme ako dáta uložené písmeno, ktoré tomuto kódu zodpovedá. Príklad prvých troch vrstiev stromu je na obrázku nižšie. Písmeno A má kód .- a teda sa k jeho vrcholu dostaneme tak, že z koreňa pôjdeme do dieťaťa označeného dot a odtiaľ do dieťaťa označeného dash. Niektoré vrcholy, napríklad koreň, nezodpovedajú žiadnemu písmenu v Morseovej abecedy a teda v nich namiesto písmena máme uložený otáznik, t.j. znak '?'. Na uloženie stromu použite nasledovnú dátovú štruktúru:

struct node {
    /* vrchol stromu  */
    char letter;  /* pismeno vo vrchole alebo '?' */
    node * dot;   /* kod predlzeny o bodku */
    node * dash;  /* kod predlzeny o ciarku */
};

V svojom programe naprogramujte nasledujúce dve funkcie na základnú prácu s Morseovým kódom, ktoré potom použite vo vašom programe, ktorý načíta Morseovu abecedu zo súboru, zakódovaný text od užívateľa a vypíše výsledok. Vo funkciách môžete namiesto poľa char-ov použiť string, inak však ich definíciu nemeňte.

void addCode(char letter, char code[], node *root) {
  /* Do stromu s koreňom root pridá kód uložený v reťazci code 
   * ktorý zodpovedá písmenu letter. */
}

V tejto funkcii postupujte z koreňa hlbšie podľa zadaného kódu, kým nenanarazíte na nulový smerník. Ďalej vytvárajte nové vrcholy podľa potreby. Keď prídete do vrcholu zodpovedajúcemu celému kódu, uložte do neho dané písmeno. Môže sa stať, že nebudete musieť vytvárať žiadne nové vrcholy, lebo vrchol pre daný kód už bol vytvorený počas spracovávania nejakého dlhšieho kódu.

char findLetter(char message[], int &pos, node *root) {
  /* V strome s koreňom root nájde písmeno zodpovedajúce kódu,
   * ktorý v texte message začína na pozícii pos.
   * Toto písmeno vráti ako výsledok funkcie.
   * Ak takéto písmeno neexistuje, vráti znak '?'. 
   * Pozíciu pos posunie na najbližšiu medzeru za kódom alebo za 
   * posledné písmeno textu, ak za kódom je už koniec textu. */

V tejto funkcii nezabudnite na možnosť, že príslušný kód nie je v strome a vtedy treba vrátiť otáznik, ale aj správne posunúť pos za koniec kódu.

Bonusová úloha: Na vstupe dostanete od užívateľa text v Morseovej abecede, v ktorom ale chýbajú medzery oddeľujúce kódy pre jednotlivé znaky. Dostanete tiež počet písmen, ktorý je v texte zakódovaný. Napíšte rekurzívne prehľadávanie, ktoré nájde všetky texty danej dĺžky, ktoré majú takýto kód. Napríklad pre text "..." a počet znakov 2 by ste mali dostať možnosti EI a IE. Pre text "......-...-..---" a počet znakov 5, by ste mali dostať 62 možností, z ktorých jedna je HELLO. Bonusovú úlohu odovzdajte v tom istom programe ako základ domácej úlohy, pričom program si najskôr vypýta text s medzerami, odkóduje ho a potom si ešte vypýta text bez medzier a počet hľadaných znakov a vypisuje všetky možnosti.

Prednáška 24

Sylaby predmetu

Základy

• Konštrukcie jazyka C
  • premenné: int, double, char, bool (vzťah int a char)
  • podmienky (if, else, switch), cykly (for, while)
  • funkcie (a parametre funkcii - odovzdávanie hodnotou, referenciou, smerníkom)

void f1(int x){}                                 //hodnotou
void f2(int &x){}                                //referenciou
void f3(int* x){}                                //smerníkom
void f(int a[], int n){}                         //polia bez & (ostanú zmeny)
void kresli(Turtle &t, vector<double> &angles){} //korytnačky, okná a pod. s &

• Grafické programy - kreslenie geometrických útvarov, korytnačka (použitie grafickej knižnice)

#include "../SimpleDraw.h"

int main(void) {
    int width = 100;
    int n=6;

    /* Vytvor obrázok s rozmermi 300x400 pixelov */
    SimpleDraw window(300, 300);

    /* Nakresli obdĺžnik */
    window.drawRectangle(100, 100, width, width);

    /* Nakresli čiaru */
    window.drawLine(100, 100, 100 + width, 100 + width);

    /* Korytnačky */
    Turtle turtle(window, (300 - width) / 2, 300 - 1, 0);
    for (int i = 0; i < n; i++) {
        turtle.forward(length);
        turtle.turnLeft(360.0 / n);
    }

    /* Ulož obrázok do súboru s príponou png. */
    window.savePng("obrazok.png");

    /* Zobraz na obrazovke a čakaj, kým užívateľ stlačí Exit,
       potom zavri okno. */
    window.showAndClose();
}

• Polia, stringy (char[])

int A[4]={3, 6, 8, 10}; //spravne
int B[4];               //spravne
B[4]={3, 6, 8, 10};     //nespravne
B[0]=3; B[1]=6; B[2]=8; B[3]=10;
char C[100] = "Edo";
char ch = 'l';
char D[100] = "pes";
char E[100];
D[0] = ch;     // priradíme do jedného prvku reťazca premmennú typu char. Výsledkom je 'les'.
D[0] = 'v';    // priradíme do jedného prvku reťazca konštantný znak. Výsledkom je 'ves'. 
D[0] = C[1];   // priradíme do jedného prvku reťazca prvok iného reťazca. Výsledkom je 'des'. 
E[0]='a'; E[1]='h'; E[2]='o'; E[3]='j; E[4]=0; //alebo E[4]='\0'; reťazec musí končiť 0.

• Vstup, výstup (spracovanie vstupu)
• Smerníky - dynamicky alokovaná pamäť, 2rozmerné polia

int i    // „klasická“ celočíselná premenná
int *p_i // ukazovateľ na celočíselnú premennú

p_i=&i;         // spravne
p_i = &(i + 3); // zle i+3 nie je premenna
p_i=&15;        //zle konstanta nema adresu
i=*p_i;         // spravne ak p_i bol inicializovany

int * cislo = new int;
*cislo = 50;
..
delete cislo;

int a[4];
int *b = a;  /* a,b su teraz takmer rovnocenne premenne */
int *A;
A = new int[n];
..
delete[] A

int **a;
a = new int *[n];
for (int i = 0; i < n; i++) a[i] = new int[m];
..
for (int i = 0; i < n; i++) delete[] a[i];
delete[] a;

Dátové štruktúry

• Abstraktná dátová štruktúra slovník
  • utriedené, neutriedené pole
  • hashovacia tabuľka
  • spájané zoznamy

struct node {
    int data;
    item* next;
};

node* p=new node;
p->data=NEJAKE_DATA;
p->next=NEJAKY_SMERNIK_NIEKAM;

• • stromy - binárne, lexikografické, vyhľadávacie

struct node {
    /* vrchol stromu  */
    dataType data;
    node * left;  /* lavy podvyraz */
    node * right; /* pravy podvyraz */
};

node * createNode(dataType data, node *left, node *right) {
    node *v = new node;
    v->data = data;
    v->left = left;
    v->right = right;
    return v;
}

struct node {    /* vrchol stromu  */
    char data;
    int use_count;
    node** next; 
};
struct trie {
    node* root;
};

• Fronta, zásobník

/* Rad - fronta - queue */
void init(queue &q);
bool isEmpty(queue &q);
void enqueue(queue &q, dataType data); 
dataType dequeue(queue &q);
dataType peek(queue &q);

/* Stack - zásobník */
void init(stack &s);
bool isEmpty(stack &s);
void push(stack &s, dataType data); 
dataType pop(stack &q);
dataType top(stack &q);

• • uloženie v poli a v spájanom zozname

struct stack {
    int top;  /* pozicia vrchného prvku zásobníka */
    dataType *items; /* pole prvkov */
};
struct queue {
    int first;  /* prvý prvok v rade */
    int count;  /* počet prvkov v rade */
    dataType *items; /* pole prvkov */
};
struct queue {
    int first;  /* prvý prvok v rade */
    int count;  /* počet prvkov v rade */
    dataType *items; /* pole prvkov */
};

struct node {  /* prvok spájaného zoznamu */
    dataType data;
    node* next;
};
struct stack {
    node *top; /* vrchný prvok zásobníka */
};
struct queue {
    node *last; /* posledný prvok v rade */
};

• • využitie zásobníka - aritmetické výrazy (postfix, infix, prefix, vyhodnocovanie výrazov, výraz vo forme stromu)
  • vyfarbovanie pomocou rekurzie, zásobníka, fronty

Algoritmy

• Rekurzia
  • Rekurzívné funkcie
  • Grafická rekurzia
  • Backtracking
• Triedenia
  • nerekurzívne: Bubblesort, Selectionsort, Insertsort
  • rekurzívne: Mergesort, Quicksort
• Iné algoritmy
  • Euklidov algoritmus, Eratostenovo sito

Záverečná písomka

• Termín: 19.12.2011 o 10:00 v B
• Opravný/náhradný termín: 9.1. o 10:00 v F1/328
• 90 minút
• Dobre si rozvrhnite čas, niektoré úlohy sú ťažšie, iné ľahšie.
• Aby ste mali šancu úspešne ukončiť predmet, musíte získať aspoň polovicu bodov.

Čo musíte, môžete a nemôžete

• Musíte
  • Index/ISIC
  • Perá (pre istotu aj viac)
• Môžete
  • Ťahák veľkosti A4
• Nemôžete
  • Žiadne elektronické pomôcky (vypnúť mobily)
  • Opisovať
  • Iné materiály na stole (čisté papiere dostanete od nás)

Príklady

• Bude zhruba 5 príkladov, niektoré ľahšie iné ťažšie
  • Príklad môže mať niekoľko podpríkladov, ktoré sú zároveň odporúčaným postupom krokov
• Náročnosť zhruba ako rozcvičky

Skúška pri počítači

• Termíny vypísané v AIS
• Prineste si čisté papiere a písacie potreby na písanie pracovných poznámok a ťahák v rozsahu jedného listu A4. Žiadne ďalšie pomôcky nie sú povolené, nebude k dispozícii ani internet.
• Stretávame sa vždy pred 8:50 v H3, kde sa dozviete pokyny a rozsadenie do miestností
• Doobeda: 2 hodiny práca pri počítačoch. Prostredie ako na cvičeniach (Linux, Netbeans)
  • Budete používať špeciálne skúškové konto, takže nebudete mať k dispozícii žiadne svoje súbory alebo nastavenia.
• Poobede: vyhodnotenie na rovnakom prostredí u prednášajúcich
• Prihlasovanie/odhlasovanie na skúšku do 14:00 deň pred skúškou
• Aby ste mali šancu úspešne ukončiť predmet, musíte získať aspoň polovicu bodov.

Príklady

• Na skúške budete riešiť dva príklady.
• V prvom príklade budete mať za úlohu samostatne napísať celý program, ktorý rieši zadanú úlohu. Typicky bude treba načítať dáta zo súboru, spracovať ich a vypísať výsledok alebo vykresliť dáta graficky pomocou knižnice SimpleDraw.
  • V tomto príklade môžete použiť ľubovoľný postup a ľubovoľné príkazy a štandardné knižnice jazyka C resp. C++.
• V druhom príklade dostanete kostru programu, pričom vašou úlohou bude doprogramovať niektoré funkcie.
  • V tomto príklade môžete mať v zadaní predpísaný spôsob, ako máte niektoré časti naprogramovať.
  • Môžu sa vyžadovať aj zložitejšie časti učiva, ako napríklad zoznamy, stromy a rekurzia.

Hodnotenie

• V prvom rade budeme hodnotiť správnosť myšlienky vášho programu. Predtým, ako začnete programovať, si dobre rozmyslite, ako budete úlohu riešiť.
• Ďalej je dôležité, aby sa program dal skompilovať (v štandardnom prostredí Netbeans) a aby správne fungoval na všetkých vstupoch spĺňajúcich podmienky v zadaní. Za nefunkčné programy môžete získať najviac polovicu bodov, aj keď ich myšlienka je správna.
• V druhej úlohe budeme jednotlivé funkcie hodnotiť zvlášť, takže môžete získať čiastočné body, ak ste niekoľko funkcií správne napísali.
• Hodnotiť budeme aj úpravu a štýl programu (komentáre, mená premenných, odsadzovanie, členenie dlhšieho programu na funkcie,...)
• Na tejto skúške nezáleží na rýchlosti vášho programu. Radšej napíšte jednoduchý, prehľadný a hlavne správny pomalší program, než rýchlejší, ale zbytočne zložitý, či nesprávny.

Prednáška 25

Na tejto prednáške si stručne ukážeme niektoré črty jazykov C a C++, ktoré sme počas semestra nepreberali. Nebudeme preberať väčšie detaily; cieľom je, aby ste neboli príliš prekvapení pri štúdiu existujúcich programov, resp. poskytnúť inšpiráciu pre ďalšie samoštúdium.

Tento materiál nebude vyžadovaný na skúške a ani Vám neodporúčame tieto črty jazyka používať, ak ste sa s nimi dostatočne pred skúškou neoboznámili. Z dnešného prehľadu vynecháme objektovo-orientované programovanie v jazyku C++. Objektovo-orientovanému programovaniu (v jazyku Java) sa budeme venovať budúci semester.

Jazyk C

• Jazyk C existuje v rôznych verziách.
• V starších verziách nefungujú mnohé veci z jazya C++, ktoré sme bežne používali, napr. komentáre vo forme //, všetky deklarácie premenných musia byť na začiatku funkcie a pod.

Ďalšie typy premenných

• Celé čísla: short int, long int, unsigned int, ...
  • Veľkosť jednotlivých typov závisí od kompilátora platformy
• Desatinné čísla: float (menej presný ako double)
• V staršom C-čku nie je bool, používa sa int, ktorý ma hodnotu 0 pre false a nenulovú (napr. 1) pre true.
• Zložený typ union: v tom istom mieste v pamäti môže byť jedna z alternívnych premenných, napr. pri artimetickom strome by sme mohli uložiť buď smerníky na deti, alebo hodnotu v liste a ušetriť tak trochu pamäti
• Typ enum: vymenujeme možné hodnoty, tie sa stanú celočíselnými konštantami: enum farby {biela, cierna, cervena};

Operátory

Okrem operátorov, ktoré sme bežne používali, existuje niekoľko ďalších, napríklad:

• Bitové operátory pracujú s celým číslom ako s poľom bitov (vhodnejšie sú unsigned typy):
  • << a >> cyklicky posúvajú bity doľava a doprava, zodpovedajú násobeniu a deleniu mocninami dvojky
  • & (and po bitoch), | (or po bitoch), ^ (xor po bitoch), ~ (negácia po bitoch)
• Ternárny operátor ?: má tvar (podmienka)?(hodnota pre true):(hodnota pre false), napr.

 cout << x << " je " << ((x%2==0) ? "parne" : "neparne") << endl;

• Pozor na rozdiel medzi a[i++]=0 a a[++i]=0, prehľadnejšie použiť dva príkazy: a[i]=0; i++ alebo i++; a[i] = 0;

Príkaz do-while

Nasledujúce dva spôsoby písania cyklu sú viac-menej ekvivalentné:

do { 
  prikazy;
} while(podmienka)

while(true) {
  prikazy;
  if(!podmienka) break;
}

Makrá a konštanty

• V C-čku nie sú klasické konštanty, robia sa pomocou makier. Nasledujúce dva riadky majú podobný význam:

#define MAXN 100
const int MAXN=100;

• Okrem konštánt môžeme definovať aj zložitejšie makrá s parametrami:

/* definicia makra: */
#define MIN(X,Y) ((X) < (Y) ? (X) : (Y))

/* priklad pouzitia: */
cout << MIN(a*a, b+5);
/* preprocesor dosadi, dostane: */
cout << ((a*a) < (b+5) ? (a*a) : (b+5));

• Treba dať kopu zátvoriek, aby nedošlo k interakcii s okolím použitia príkazu max

Delenie programu na súbory

• Väčší program chceme rozdeliť na viac súborov
• Chceme vytvárať a používať vlastné knižnice - skupiny funkcií s podobným účelom
  • Napríklad knižnica implementujúca funkcie pracujúce so zásobníkom
• Knižnicu rozdelíme na dva súbory, napr. stack.h a stack.c resp. stack.cpp
• V hlavičkovom súbore (header file) zadeklarujeme funkcie, ale neuvádzame ich kód, napr.:

typedef int dataType;
struct stack {
    int top;  /* pozicia vrchného prvku zásobníka */
    dataType *items; /* pole prvkov */
};
void init(stack &s);
bool isEmpty(stack &s);
void push(stack &s, dataType data); 
dataType pop(stack &q);

• Programy, ktoré chcú použiť stack, použijú include na tento súbor

#include "stack.h"

• V súbore stack.cpp uvedieme kód funkcií, napr.

#include "stack.h"
const int maxN = 100;
void init(stack &s) {
    s.top = -1;
    s.items = new dataType[maxN];
}
...

• Všimnite si, že v include dávame meno štandardných knižníc v <>, našich vlastných v ""
• Pri štandardných knižniciach sa v C-čku používa prípona h, v C++ sa namiesto toho väčšinou pridá c na začiatok (že je to knižnica z čistého C)
  • Napr. <cmath> vs. <math.h>

C nemá posielanie parametrov referenciou

• ... používame teda smerníky

void swap(int &a, int &b) {
  int tmp = a;
  a = b;
  b = tmp;
}

void swap(int *a, int *b) {
  int tmp;
  tmp = *a;
  *a = *b;
  *b = tmp;
}

Zopár užitočných funkcií

Hľadanie v reťazcoch

• strstr(text, vzorka) vracia smerník na char
  • NULL ak sa vzorka nenachádza v texte, smerník na začiatok prvého výskytu inak
  • pozíciu výskytu zistíme smerníkovou aritmetikou:

char *text, *vzorka;
char *where = strstr(text, vzorka);
if(where != NULL) {
  int position = where - text;
}

• Ako by ste spočítali počet výskytov vzorky v texte?
• Podobne strchr hľadá prvý výskyt znaku v texte

Alokácia pamäte

• V C-čku sa nepoužíva new a delete, resp. new[] a delete[]
• Pamäť sa alokuje funkciou malloc, ktorá alokuje kus pamäte s daným počtom bajtov
  • Ak sa nepodarilo, vráti NULL
  • Inak vrati pointer na void, treba pretypovať
  • Veľkosť spočítame operátorom sizeof

#include <stdlib.h>

/* vytvorime pole 100 int-ov */
int *a = (int *)malloc(sizeof(int) * 100);
/* odalokujeme pole a */
free(a);

Triedenie

• Funkcia qsort z knižnice stdlib.h
• Dostane pole, počet jeho prvkov, veľkosť každého prvku a funkciu, ktorá porovná dva prvky
  • Funkciu teda posielame ako parameter
  • Táto porovnávacia funkcia dostane smerníky na dva prvky v type void *
  • Vráti záporné číslo, ak prvý prvok je menší, nulu, ak sú rovnaké a kladné číslo, ak prvý je väčší
• Ak si napíšeme porovnávaciu funkciu, môžeme triediť prvky hocijakého typu

int compare (const void * a, const void * b) {
  return (*(int*)a - *(int*)b);
}
int a[] = {5, 3, 2, 4, 1};
qsort (a, 5, sizeof(int), compare);

• Podobne je aj funkcia bsearch na binárne vyhľadávanie v striedenom poli

Jazyk C++

Generické funkcie

• Často chceme napísať algoritmus, ktorý by mohol fungovať veľa rôznych typoch
• Napr. triediť môžeme celé alebo desatinné čísla, reťazce, zložitejšie štruktúry s určitým kľúčom a pod.
• Funkcia qsort nám to umožňuje, ale musíme sa zapodievať veľkosťami a pretypovaním, kde sa dajú ľahko narobiť chyby.
• V C++ sa dajú písať funkcie, ktoré majú typ ako parameter:

template <class T>
T max (T a, T b) {
  return (a>b)? a : b;
}

int i=3;
int j=5;
int k=max<int>(i,j);

• Už sme stretli aj jednu generickú dátovú štruktúru, vector:

  vector<int> A;
  for (int i=0; i<10; i++){
    A.push_back(i);
  }

Preťaženie operátorov

• Pre naše typy si vieme zadefinovať nové operátory
• Napr. dve mená porovnávame najskôr podľa priezviska, pri zhode podľa krstného mena

struct meno {
    char *krstne, *priezvisko;
};

bool operator < (meno x, meno y) {
    return strcmp(x.priezvisko, y.priezvisko)<0
            || strcmp(x.priezvisko, y.priezvisko)==0
            && strcmp(x.krstne, y.krstne)<0;
}

• Podobne môžeme zadefinovať napr. operátor + a * pre náš struct reprezentujúci trebárs polynómy alebo komplexné čísla...
• cin << "Hello" používa preťažený operátor << ak na ľavej strane je stream a na pravej reťazec

Niektoré užitočné štruktúry

STL (standard template library)

• Veľká knižnica rôznych dátových štruktúr
• Manuál napr. tu: http://www.sgi.com/tech/stl/
• Videli sme vector, string, iostream
  • Aj tieto štruktúry majú veľa ďalších užitočných funkcií, pozrite si v dokumentácii

• Štruktúra map implementuje slovník

  map <string, string> zoznam;
  zoznam["Jozko Mrkvicka"] = "02/12345678";
  if(zoznam.count("Jozko Mrkvicka") > 0) {
    cout << zoznam["Jozko Mrkvicka"] << endl;
  }

• Štruktúra deque implementuje zásobník aj rad naraz (double-ended queue)

  deque <int> a;
  a.push_back(0);
  a.push_front(1);
  cout << a.back() << endl;
  cout << a.front() << endl;
  a.pop_back();
  a.pop_front();

• Triedenie v knižnici <algorithm>

//triedime normalne pole
int A[6] = {1, 4, 2, 8, 5, 7};
sort(A, A + 6);

//triedime vektor
vector <int> A;
sort(A.begin(), A.end());

//triedime podla nasej porovnavacej funkcie, napr. podla absolutnej hodnoty
struct cmp {
    bool operator()(int x, int y) { return abs(x) < abs(y); }
};
cmp c;
sort(A.begin(), A.end(), c);

Cvičenia 12

• Nakreslite binárny vyhľadávací strom, ktorý dostaneme, ak do prázdneho slovníka postupne vkladáme záznamy s kľúčami 3, 4, 1, 2, 5, 6 (v tomto poradí).

• Nakreslite lexikografický strom s abecedou {a,b}, do ktorého sme vložili reťazce aba, aaab, baa, bab, ba. Vrcholy, ktoré zodpovedajú niektorému reťazcu zo vstupu zvýraznite dvojitým krúžkom.

• Nižšie na tejto stránke nájdete binárny vyhľadávací strom, ktorý meníme iba pomocou funkcie insert. Pridajte do štruktúry node položku count, ktorá bude obsahovať počet vrcholov v podstrome zakorenenom v danom vrchole. Napríklad pre list by mal byť tento počet 1, pre vrchol s dvoma synmi, ktorí sú obaja listami, by hodnota mala byť 3. Zmeňte funkcie createLeaf a insert tak, aby správne túto položku udržiavali vo všetkých vrcholoch stromu.

• Napíšte funkciu int rank(dictionary &d, keyType key), ktorá nájde prvok key v strome a vráti, koľký v utriedenom poradí spomedzi iných prvkov v strome je. Napríklad ak máme v strome čísla 1, 4, 7, funkcia rank(d, 4) by mala vrátiť 2, lebo prvok 4 je druhý najmenší. Môžete predpokladať, že hľadaný kľúč sa v strome určite nachádza. V tejto funkcii využite položku count, ktorú ste naprogramovali v predchádzajúcej úlohe. Ak totiž pokračujeme v hľadaní v pravom podstrome určitého vrcholu v, tak vrchol v aj všetky vrcholy v jeho ľavom podstrome sú pred hľadaným prvkom.

• Nižšie máte ukážkový program pre lexikografický strom, v ktorom sme namiesto useCount použili položku isWord, ktorá určuje, či aktuálny vrchol je koncom nejakého vloženého reťazca (slova). Strom predpokladá, že reťazce obsahujú iba malé písmená anglickej abecedy. Zmeňte program tak, aby najskôr načítal zo súboru dict.txt zoznam anglických slov a uložil ich do stromu. Potom načíta od užívateľa nejaký reťazec a vypíše všetky slová, ktoré na tento reťazec začínajú. Napríklad pre reťazec all vypíše all allah allegiance allen alley alliance allied allow allowance allowed allowing allude allusion ally. Skúste pozmeniť alebo využiť funkcie printTrie a searchTrie.

• Napíšte funkciu keyType select(dictionary &d, int k), ktorá vráti k-ty najmenší prvok vo vyhľadávacom strome. Aj v tejto funkcii využite položku count. Ak je totiž k najviac rovné počtu vrcholov v ľavom podstrome, k-ty najmenší prvok musí byť niekde v tomto podstrome. Ak je naopak k veľké, hľadaný prvok musí byť v pravom podstrome a vieme spočítať aj to, koľký najmenší v rámci tohto podstromu je.

Ukážkový program pre binárny vyhľadávací strom

#include <iostream>
#include <cassert>
using namespace std;

typedef int keyType;
typedef int dataType;

struct node {
    /* vrchol binarneho vyhladavacieho stromu  */
    keyType key;    /* kluc podla ktoreho vyhladavame */
    dataType data;  /* data spojene s klucom */
    node * parent;  /* otec vrchola */
    node * left;    /* lavy syn */
    node * right;   /* pravy syn */
};

struct dictionary {
    node *root;
};

void init(dictionary &d) {
    /* inicializuje prazdny slovnik */
    d.root = NULL;
}

node * createLeaf(keyType key, dataType data, node * parent) {
    /* vytvor novy vrchol s danymi hodnotami, obe deti nastav na NULL */
    node *v = new node;
    v->key = key;
    v->data = data;
    v->left = NULL;
    v->right = NULL;
    v->parent = parent;
    return v;
}

node * findNode(node *root, keyType key) {
    /* V binarnom vyhladavacom strom s korenom root najdi a vrat
     * vrchol s klucom a ak neexistuje, vrat NULL. */
    node * v = root;
    while (v != NULL && v->key != key) {
        if (key < v->key) {
            v = v->left;
        } else {
            v = v->right;
        }
    }
    return v;
}

void findNode(node *root, keyType key, node *&v, node *&parent) {
    /* Do v uloz smernik na vrchol s klucom key alebo NULL ak neexistuje.
     * Do parent uloz otca v, NULL ak neexistuje a ak key nie je v strome
     * tak smernik na vrchol, ktory by mal byt otcom pre vrchol
     * s hodnotou key.*/
    parent = NULL;
    v = root;
    while (v != NULL && v->key != key) {
        parent = v;
        if (key < v->key) {
            v = v->left;
        } else {
            v = v->right;
        }
    }
}

bool find(dictionary &d, keyType key, dataType &data) {
    /* V slovniku s najde kluc key a do data ulozi data s nim
     * spojene. Ak tam nie je, vrati false, inak vrati true. */
    node *v = findNode(d.root, key);
    if (v != NULL) {
        assert(v->key == key);
        data = v->data;
        return true;
    } else {
        return false;
    }
}

void insert(dictionary &d, keyType key, dataType data) {
    /* Do slovnika d vlozi kluc key a jeho data.
     * Predpokladame, ze takyto kluc este v slovniku nie je. */
    if (d.root == NULL) {
        /* prazdny strom - treba vytvorit koren */
        d.root = createLeaf(key, data, NULL);
    } else {
        node *v;
        node *parent;
        findNode(d.root, key, v, parent);
        /* parent je teraz vrchol, ktoreho syn ma byt novy vrchol */
        assert(v == NULL && parent != NULL);
        /* zisti, ci mame byt lave alebo prave dieta otca */
        if (key < parent->key) {
            assert(parent->left == NULL);
            parent->left = createLeaf(key, data, parent);
        } else {
            assert(parent->right == NULL);
            parent->right = createLeaf(key, data, parent);
        }
    }
}

int main() {
    dictionary d;
    init(d);

    insert(d, 3, 0);
    insert(d, 4, 0);
    insert(d, 1, 0);
    insert(d, 2, 0);
    insert(d, 5, 0);
    insert(d, 6, 0);
}

Ukážkový program pre lexikografický strom

#include <iostream>
#include <cassert>
using namespace std;

const int Abeceda = 26;

struct node {
    /* vrchol stromu  */
    char data;   /* znak vo vrchole */
    bool isWord; /* zodpoveda tento vrchol celemu slovu? */
    node **next;
};

struct trie {
    node* root;
};

node* initNode(){
    node* v=new node;
    node** w=new node*[Abeceda];
    for (int i=0; i<Abeceda; i++) w[i]=NULL;
    v->next=w;
    v->isWord = false;
    v->data='x';
    return v;
}

trie* initTrie(){
    node* root = initNode();
    trie* t=new trie;
    t->root=root;
    return t;
}

void insertTrie(trie* t, char* key) {
    node **r; // opäť budeme používať smerník na smerník, aby sme mohli ukazovať priamo na hranu a nemali problém s NULL na konci
    node *v;
    char *p;
    int c;

    r = &t->root;
    p = key;

    while (true) {
        v = *r;
        if (v == NULL) {
            v = initNode(); /* vrchol neexistuje, vytvor ho */
            (v->data)=c;
            *r = v;     /* smernik na smernik do trie */
        }

        c = *p;                /* Aktualny znak: */
        if (c == '\0') { /* ak je tu koniec vkladaneho slova */
            v->isWord = true;  /* poznacime si to*/
            break;             /* a ukoncime cyklus */
        }
        assert(c>='a' && c-'a'<Abeceda);
        r = &v->next[c - 'a']; /* inac pokracujeme dalsim znakom */

        p++;
    }
}


bool searchTrie(trie* t, char* s){
    node *v = t->root;
    while(*s != '\0'){
        int c = *s - 'a';
        assert(c>=0 && c<Abeceda);
        if (v->next[c] == NULL) return false;
        else v = v->next[c];
        *s++;
    }
    if(v->isWord) return true;
    else return false;
}


void printTrie(int depth, node *p, char* prefix) {
    if (p->isWord) { /* ak treba, vyspieme toto slovo */
        cout << prefix << endl;
    }
    for (int i = 0; i < Abeceda; i++) {
        if (p->next[i] != NULL) {
            prefix[depth] = (p->next[i])->data; // pridám si ďalšie písmeno
            prefix[depth + 1] = '\0'; // a zaň koniec slova
            printTrie(depth + 1, p->next[i], prefix); // zavolám sa rekurzívne
        }
    }
}

int main() {
    trie *t = initTrie();
    char a[] = "abcd";
    char b[] = "ab";
    char c[] = "abc";
    insertTrie(t, a);
    insertTrie(t, b);
    cout << searchTrie(t, a) << endl;
    cout << searchTrie(t, c) << endl;
    char word[100];
    word[0] = 0;
    printTrie(0, t->root, word);
}