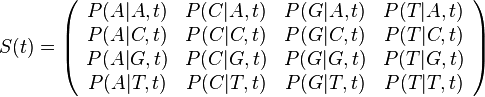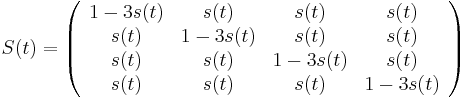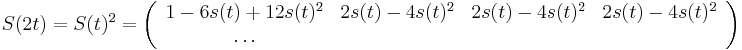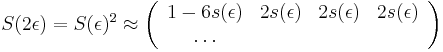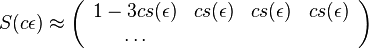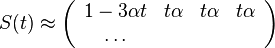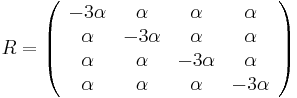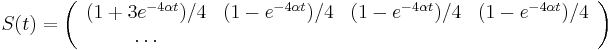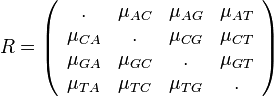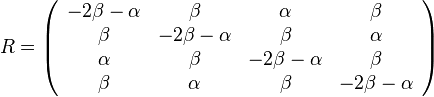CI07
Z MBI
Obsah
Substitučné modely - odvodenie
- Nech
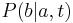 je pravdepodobnosť, že ak začneme s bázou a, tak po čase t budeme mať bázu b.
je pravdepodobnosť, že ak začneme s bázou a, tak po čase t budeme mať bázu b.
- Pre dané t môžeme také pravdepodobnosti usporiadať do matice 4x4 (ak študujeme DNA):
- Riadky zodpovedaju povodnej baze a, stlpce novej baze b
- Sucet kazdeho riadku je 1
Požiadavky na S(t)
- Intuitivne cim vacsie t, tym vacsia pravdepodobnost zmeny, pre nulovy cas este ziadna zmena nemala kedy nastat, mame teda
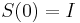 (jednotkova matica)
(jednotkova matica)
- Naopak ked t ide do nekonecna, kazda baza velakrat zmutovala a teda uz prilis nezalezi, co to bolo na zaciatku. S(t) ma teda v limite pre velke t vsetky riadky rovnake.
-
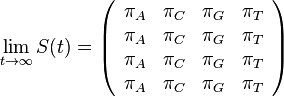
- Rozdelenie pravdepodobnosti
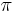 nazyvame limitne (equilibrium)
nazyvame limitne (equilibrium)
- Predpokladame tiez, ze pravdepodobnost mutacie zavisi len od aktualnej bazy, nie od minulych stavov a ze charakter procesu mutacii sa v case nemeni. Teda ak mame matice pre casy
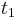 a
a 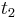 , vieme spocitat maticu pre cas
, vieme spocitat maticu pre cas 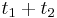 :
: 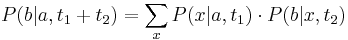 a teda v maticovej notacii
a teda v maticovej notacii 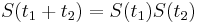 . Preto takyto model nazyvame multiplikativny.
. Preto takyto model nazyvame multiplikativny.
- Ak by sme uvazovali iba diskretne (celociselne) casy, stacilo by nam urcit iba
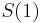 a vsetky ostatne casy dostaneme umocnenim tejto matice. Je vsak elegantnejsie mat
a vsetky ostatne casy dostaneme umocnenim tejto matice. Je vsak elegantnejsie mat 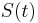 definovane aj pre realne t.
definovane aj pre realne t.
- Tento typ modelu sa nazyva Markovov retazec so spojitym casom (continuous-time Markov chain)
Jukes-Cantorov substitučný model
- Tento model predpoklada, ze vsetky substitucie su rovnako pravdepodobne, matica teda musí vyzerať nejako takto:
Matica rýchlostí pre J-C model
- Pre velmi maly cas t je s(t) velmi male cislo (blizke 0) a pre velmi male s(t) su kvadraticke cleny
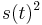 ovela mensie ako linearne cleny s(t) a teda
ovela mensie ako linearne cleny s(t) a teda
- Aj pre ine rozumne male nasobky
- Tento vztah dava zmysel: pre velmi male t mozeme zanedbat moznost, ze baza zmutovala viackrat a pravdepodobnost jednej mutacie linearne rastie s dlzkou casu.
- Ak oznacime
 a
a  dostaneme pre velmi male t
dostaneme pre velmi male t
- Vytvorme si teraz maticu rychlosti (intenzit) (transition rate matrix, substitution rate matrix)
- Dostavame, ze pre velmi male casy plati
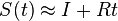
-
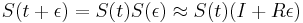 a teda
a teda 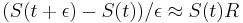
- V limite dostaneme
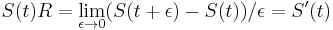
- Dostali sme diferencialnu rovnicu S(t)R = S'(t), pociatocny stav
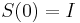 ).
).
- Nasobenim matic S(t) a R dostavame, ze diagonalny prvok
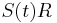 je
je 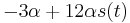 a nediagonalny
a nediagonalny  . Takze dostavame diferencialnu rovnicu
. Takze dostavame diferencialnu rovnicu 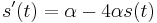 z rovnosti nediagonalnych prvkov (z rovnosti diagonalnych prvkov dostavame tu istu rovnicu len prenasobenu konstantou -3).
z rovnosti nediagonalnych prvkov (z rovnosti diagonalnych prvkov dostavame tu istu rovnicu len prenasobenu konstantou -3).
Poriadnejšie odvodenie diferenciálnej rovnice
-
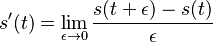 z definicie limity
z definicie limity
-
 podla multiplikativnosti S(t)
podla multiplikativnosti S(t)
- po úprave
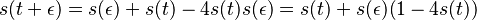
-
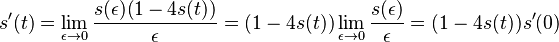
- oznacme
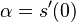 (alfa je konstanta, nezavisi od epsilon ani t)
(alfa je konstanta, nezavisi od epsilon ani t)
-
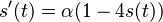 (finalna diferencialna rovnica, rovnaka ako predtym pre matice)
(finalna diferencialna rovnica, rovnaka ako predtym pre matice)
- Riesenie diferencialnej rovnice
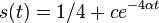 pre kazdu konstantu c
pre kazdu konstantu c
- Mozeme overit dosadenim do rovnice, pricom
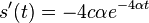
- c=-1/4 dopocitame z pociatocnej podmienky s(0)=0
- overime tiez, ze
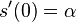
Vlastnosti riešenia
- Takže máme maticu:
- Ked
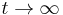 , dostávame všetky prvky matice rovné 1/4, t.j.
, dostávame všetky prvky matice rovné 1/4, t.j. 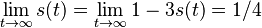 .
.
-
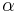 je teda pravdepodobnosť konkrétnej zmeny za jednotku času, ak uvažujeme veľmi krátke časy alebo presnejšie derivácia prvku s(t) vzhľadom na t v bode 0
je teda pravdepodobnosť konkrétnej zmeny za jednotku času, ak uvažujeme veľmi krátke časy alebo presnejšie derivácia prvku s(t) vzhľadom na t v bode 0
- Aby sme nemali naraz aj
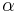 aj
aj 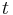 , zvykneme maticu R normalizovat tak, aby priemerný počet substitúcii za jednotku času bol 1. V prípade Jukes-Cantorovho modelu je to keď
, zvykneme maticu R normalizovat tak, aby priemerný počet substitúcii za jednotku času bol 1. V prípade Jukes-Cantorovho modelu je to keď 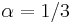 .
.
Substitučné matice, zhrnutie
- S(t): matica 4x4, kde políčko
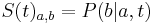 je pravdepodobnosť, že ak začneme s bázou a, tak po čase t budeme mať bázu b.
je pravdepodobnosť, že ak začneme s bázou a, tak po čase t budeme mať bázu b.
- Jukes-Cantorov model predpokladá, že táto pravdepodobnosť je rovnaká pre každé dve bázy

- Pre daný čas t máme teda všade mimo diagonály s(t) a na diagonále 1-3s(t)
- Matica rýchlostí R: pre Jukes-Cantorov model všade mimo diagonály
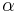 , na diagonále
, na diagonále 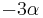
- Pre veľmi malý čas t je S(t) zhruba I-Rt
- Rýchlost alpha je teda pravdepodobnosť zmeny za jednotku casu, ak uvažujeme veľmi krátke časy, resp. derivácia s(t) vzhľadom na t v bode 0
- Riešením diferenciálnych rovníc pre Jukes-Cantorov model dostávame
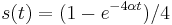
- Matica rýchlostí sa zvykne normalizovať tak, aby na jednotku času pripadla v priemere jedna substitúcia, čo dosiahneme ak
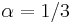
Použitie na odhad evolučnej vzdialenosti
- V case
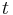 je pravdepodobnost, ze uvidime zmenenu bazu
je pravdepodobnost, ze uvidime zmenenu bazu 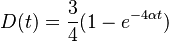
- V realnom pouziti (vypocet matice vzdialenosti pre metodu spajania susedov) mame dve zarovnane sekvencie, medzi ktorymi vidime
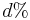 zmenenych baz, chceme odhadnut t
zmenenych baz, chceme odhadnut t
- Spatne teda zratame t, ktore by hodnote
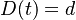 prinalezalo.
prinalezalo.
- Spatne teda zratame t, ktore by hodnote
- Dostavame teda vzorec pre vzdialenost, ktory sme videli na prednaske
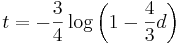
- Ak
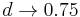 , dostavame
, dostavame 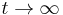
- Preco sme ten vzorec odvodili takto? V skutocnosti chceme najst najvierohodnejsiu hodnotu t, t.j. taku, pre ktore hodnota P(data|t) bude najvacsia. Zhodou okolnosti vyjde takto.
Zložitejšie modely
V praxi sa používajú komplikovanejsie substitučné modely, ktoré majú všeobecnejšiu maticu rýchlostí R
Hodnoty na diagonále matice sa dopočítavajú aby súčet každého riadku bol 0.
- Hodnota
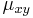 v tejto matici vyjadruje rýchlosť, akou sa určitá báza x mení na inú bázu y.
v tejto matici vyjadruje rýchlosť, akou sa určitá báza x mení na inú bázu y.
- Presnejšie
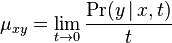 .
.
Kimurov model napr. zachytáva, ze puríny sa častejšie menia na iné puríny (A a G) a pyrimidíny na ine pyrimidíny (C a T).
- Má dva parametre: rýchlosť tranzícií alfa, transverzií beta
- HKY model (Hasegawa, Kishino & Yano) tiež umožnuje rôzne pravdepodobnosti A, C, G a T v ekvilibriu.
- Ak nastavíme čas v evolučnom modeli na nekonečno, nezáleží na tom, z ktorej bázy sme začali, frekvencia výskytu jednotlivých báz sa ustáli v tzv. ekvilibriu.
- V Jukes-Cantorovom modeli je pravdepodobnosť ľubovoľnej bázy v ekvilibriu 1/4.
- V HKY si zvolime aj frekvencie jednotlivých nukleotidov v ekvilibriu
 so súčtom 1
so súčtom 1
- Parameter kapa: pomer tranzícií a transverzií (alfa/beta)
- Matica rýchlostí:
-
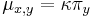 ak mutácia x->y je tranzícia,
ak mutácia x->y je tranzícia,
-
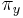 ak mutácia x->y je transverzia
ak mutácia x->y je transverzia
-
- Pre zložité modely nevieme odvodiť explicitný vzorec na výpočet S(t), ako sme mali pri Jukes-Cantorovom modeli
- Ale vo všeobecnosti pre maticu rýchlostí
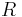 dostávame
dostávame 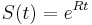 .
.
- Exponenciálna funkcia matice A sa definuje ako
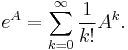
- Ak maticu rychlosti R diagonalizujeme (určite sa dá pre symetrické R)
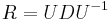 , kde D je diagonálna matica (na jej diagonále budu vlastné hodnoty R), tak
, kde D je diagonálna matica (na jej diagonále budu vlastné hodnoty R), tak 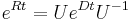 , t.j. exponenciálnu funkciu uplatníme iba na prvky na uhlopriečke matice D.
, t.j. exponenciálnu funkciu uplatníme iba na prvky na uhlopriečke matice D.
- Exponenciálna funkcia matice A sa definuje ako