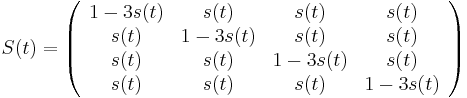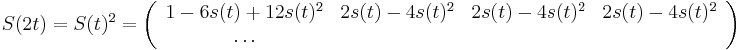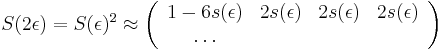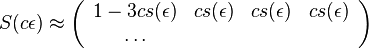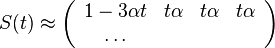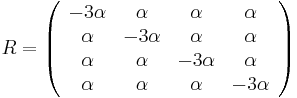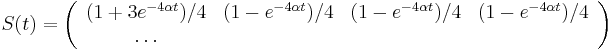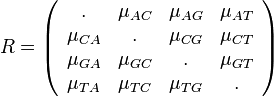MBI 2023/2024
Literature:
- BV: Brejová, Vinař: Metódy v bioinformatike. (preliminary version of lecture notes in Slovak, only several lectures)
- DEKM: Durbin, Eddy, Krogh, Mitchison: Biological sequence analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press 1998. Can be studied in the FMFI library under code I-INF-D-21
- ZB: Zvelebil, Baum: Understanding Bioinformatics. Taylor & Francis 2008. Can be studied in the FMFI library under code I-INF-Z-2
For each lecture, we list book chapters best corresponding to the covered material. However, the lecture may differ substantially from the listed chapters which serve as the source of additional information.
Recordings of lectures in Slovak from 2018/19
Presentations
Notes
L: lecture (everybody), TI: tutorial for computer science/informatics students, TB: tutorial for biology/chemistry/physics students
Week 1, Week 2, Week 3, Week 4, Week 5, Week 6, Week 7, Week 8, Week 9, Week 10, Week 11, Week 12, Week 13
| Sept. 21 | |||
| L: | Introduction, course rules, sequencing and genome assembly | ||
| BV chapter 1, video 1 video 2 | |||
| TI: | Introduction to biology | notes | |
| ZB chapter 1, video | |||
| TB: | Introduction to computer science, UCSC genome browser | notes | |
| Sept. 28 | |||
| L: | Genome assembly 2 | ||
| video | |||
| TI: | Introduction to probability, genome coverage by sequencing reads | notes | |
| Python simulations and approximations colab | |||
| TB: | Introduction to dynamic programming, introduction to probability | notes | |
| Oct. 5 | |||
| L: | Sequence alignment: Smith-Waterman, Needleman-Wunsch, scoring | ||
| BV chapter 2, DEKM chapter 2.1-2.4, 2.8, ZB chapter 4.1-4.4, 5.1-5.2, video | |||
| TI: | Introduction to dynamic programming, proteomics | notes | |
| Python implementation of DP and visualisations colab | |||
| TB: | Dynamic programming for sequence alignment, dotplots | notes | |
| Oct. 12 | |||
| L: | Sequence alignment: heuristic alignment (BLAST), statistical significance of alignments, whole genome alignments, multiple alignments | ||
| BV chapter 2, DEKM chapter 2.5, 2.7, 6.1-6.3; ZB chapter 4.5-4.7, 5.3-5.5, video | |||
| TI: | Advanced algorithms for sequence alignment | notes | |
| TB: | Programs for sequence alignment, scoring schemes | notes | |
| Oct. 19 | |||
| L: | Gene finding, hidden Markov models | ||
| BV chapter 4, DEKM chapter 3; ZB chapter 9.3, 10.4-10.7, video | |||
| TI: | Fast similarity search, BLAST, MinHash | ||
| TB: | Hidden Markov models, E-value | notes | |
| Oct. 26 | |||
| L: | Phylogenetic tree reconstruction (parsimony, neighbor joining, models of evolution) | ||
| BV chapter 3, DEKM chapter 7,8; ZB chapter 7, 8.1-8.2, video | |||
| TI: | Algorithms for HMM | notes | |
| TB: | Substitution models, bootstrap, tree rooting | notes | |
| Nov. 2 No lecture, no tutorials | |||
| Nov. 9 | |||
| L: | Comparative genomics, detection of positive and purification selection, comparative gene finding, phylogenetic HMMs | ||
| BV chapter 5, ZB chapter 9.8, 10.8, video | |||
| TI: | Substitution models | notes | |
| TB: | Practical phylogenetic trees | notes | |
| Nov. 16 | |||
| L: | Protein structure and function | ||
| DEKM chapter 5; ZB chapter 4.8-4.10, 6.1-6.2, 13.1-13.2, SK video | |||
| TI: | Felsenstein algorithm, algorithms for HMM and phyloHMM | ||
| TB: | Pfam, PSI-blast, Example of command-line tools | notes1, notes2 | |
| Nov. 23 | |||
| L: | Gene expression, clustering, classification, regulatory networks, transcription factors, sequence motifs | ||
| DEKM chapter 5.1, 11.5, ZB chapter 6.6,15.1,16.1-16.5,17.1, SK video | |||
| TI: | Examples of biological databases, introduction to context-free grammars | notes | |
| TB: | Introduction to context-free grammars | notes | |
| Nov. 30 | |||
| L: | RNA, secondary structure, Nussinov algorithm, stochastic context-free grammars, RNA family profiles | ||
| DEKM chapter 10, ZB chapter 11.9, SK video | |||
| TI: | Motif finding by EM and Gibbs sampling | ||
| TB: | K-means clustering, enrichment, multiple testing correction | notes | |
| Dec. 7 | |||
| L: | Population genetics | ||
| SK video | |||
| TI: | RNA structure | ||
| TB: | Course summary, graphs, microarray data, RNA structure, MEME, transcription factors in SGD, population genetics | notes | |
| Dec. 14 | |||
| L: | Optional journal club presentations | ||
| TI: | Protein threading via integer linear programming, course summary | ||
| TB: | Project consultations | ||
Obsah
- 1 CI01
- 2 CB01
- 3 CI02
- 4 CB02
- 5 CI03
- 6 CB03
- 7 CI04
- 8 CB04
- 9 CB05
- 10 CI06
- 11 CB06
- 12 CI07
- 13 CB07
- 14 CB10
- 15 Budeme robiť na neskoršom cvičení
- 16 CB11
- 17 CI10
- 18 CB09
- 19 CB08
- 20 CB12
CI01
Úvod do biológie pre informatikov
Užitočné linky
Pesničky z YouTube:
CB01
Používanie počítačov v M 217
- V textovom menu pri štarte zvoľte Linux, v prihlasovacom menu zadajte užívatela bioinf, heslo dostanete
- Na dolnom okraji obrazovky je lišta s často používanými nástrojmi, napr. internetový prehliadač Firefox
- Vo Firefoxe si otvorte stránku predmetu http://compbio.fmph.uniba.sk/vyuka/mbi/ čast Prednášky a poznámky, nalistujte materiály k dnešnému cvičeniu
UCSC genome browser
- On-line grafický nástroj na prezeranie genómov
- Konfigurovateľný, veľa možností, ale pomerne málo organizmov
- V programe Firefox choďte na stránku UCSC genome browser http://genome-euro.ucsc.edu/ (európsky mirror stránky http://genome.ucsc.edu/ )
- Hore v modrom menu zvoľte Genomes, potom zvoľte ľudský genóm verzia hg38. Do okienka search term zadajte HOXA2. Vo výsledkoch hľadania (Gencode genes) zvoľte gén homeobox A2 na chromozóme 7.
- Pozrime si spolu túto stránku
- V hornej časti sú ovládacie prvky na pohyb vľavo, vpravo, približovanie, vzďaľovanie
- Pod tým schéma chromozómu, červeným vyznačená zobrazená oblasť
- Pod tým obrázok vybranej oblasti, rôzne tracky
- Pod tým zoznam všetkých trackov, dajú sa zapínať, vypínať a konfigurovať
- Po kliknutí na obrázok sa často zobrazí ďalšia informácia o danom géne alebo inom zdroji dát
- V génoch exony hrubé, UTR tenšie, intróny vodorovné čiary
- Koľko má HOXA2 exónov? Na ktorom chromozóme a pozícii je? Pozor, je na opačnom vlákne. Ako je táto skutočnosť naznačená na obrázku?
- V tracku GENCODE kliknite na gén, mali by ste sa dostať na stránku popisujúcu jeho rôzne vlastnosti. Čo ste sa dozvedeli o jeho funkcii?
- Na tejto stránke nájdite linku na stiahnutie proteínovej sekvencie. Aké sú prvé štyri aminokyseliny?
Sekvenovanie v UCSC genome browseri
- Vráťte sa na UCSC genome browser http://genome-euro.ucsc.edu/
- Pozrieme si niekoľko vecí týkajúcich sa sekvenovania a skladania genómov
- Hore v modrom menu zvoľte Genomes, časť Other
- Na ďalšej stránke zvoľte človeka a pomocou menu Human Assembly zistite, kedy boli pridané posledné tri verzie ľudského genómu (hg19, hg38, hs1)
- Na tej istej stránke dole nájdete stručný popis zvolenej verzie genómu. Pre ktoré oblasti genómu máme v hg38 najviac alternatívnych verzií?
- Prejdite na región chr21:31,250,000-31,300,000 v hg19 touto linkou: [1]
- Zapnite si tracky Mapability a RepeatMasker na "full"
- Mapability: nakoľko sa daný úsek opakuje v genóme a či teda vieme jednoznačne jeho čítania namapovať pri použití Next generation sequencing
- Ako a prečo sa pri rôznych dĺžkach čítaní líšia? (Keď kliknete na linku "Mapability", môžete si prečítať bližšie detaily.)
- Približne v strede zobrazeného regiónu je pokles mapovateľnosti. Akému typu opakovania zodpovedá? (pozrite track RepeatMasker)
- Zapnite si tracky "Assembly" a "Gaps" a pozrite si región chr2:110,000,000-110,300,000 v hg19: [2] Aká dlhá je neosekvenovaná medzera (gap) v strede tohto regiónu? Približnú veľkosť môžete odčítať z obrázku, presnejší údaj zistíte kliknutím na čierny obdĺžnik zodpovedajúci tejto medzere (úplne presná dĺžka aj tak nebola známa, nakoľko nebola osekvenovaná).
- Cez menu položku View, In other genomes si pozrite, ako zobrazený úsek vyzerá vo verzii hg38 and hs1. Ako sa zmenila dĺžka z pôvodných 300kb?
QUAST: program na štatistiky o kvalite poskladania genómu (nerobili sme)
- Čítania technológie Illumina MiSeq z 500kbp oblasti genómu E.coli
- Boli poskladané programom SPAdes [3]
- Vzniknuté kontigy sú tu: [4]
- Pozrime si štatistiky tohto poskladania v nástroji Quast,
- Teraz si tento výpočet spustíme v systéme Galaxy
Prehľad systému Galaxy (nerobili sme)
- https://usegalaxy.eu/
- Obsahuje veľa bioinformatických nástrojov, ktoré môžete spúšťať
- Ale na výsledky treba niekedy dlho čakať
- V ľavom stĺpci hľadanie nástroja alebo nahrávanie dát
- V pravom stĺpci zoznam nahratých dát, bežiacich programov a hotových výsledkov (výsledky si pozriete ikonou oka alebo stiahnete ikonou diskety)
- V strede nastavenia nástroja alebo prezeranie výsledkov
- Pri serióznom používaní odporúčam vytvoriť si konto a prihlásiť sa
- Stiahnite si kontigy [5], uložte ako súbor
- V ľavom menu zvolíme Upload Data a nahráme stiahnutý súbor
- V časti Tools v ľavom menu zadáme do vyhľadávania Quast, zvolíme Quast
- Ako Contigs/scaffolds file zadáme nahratý súbor, ostatné položky necháme predvolené, stlačíme Execute
- Predpočítané výsledky [6]
- Druhá analýza: porovnanie poskladaných kontigov so správnou odpoveďou (ak je známa)
- Skutočná E.coli sekvencia, ktorú sme chceli dostať
- Dá sa zadať do nástroja Quast, ak zvolíte Yes v Use a reference genome a tento súbor nahráte ako Reference genome
Ďalšie dáta pre záujemcov:
- Použité čítania: prvé čítania z páru, druhé čítania z páru
- Galaxy obsahuje aj program SPAdes na skladanie
CI02
Úvod do pravdepodobnosti
- Myšlienkový experiment, v ktorom vystupuje náhoda, napr. hod ideálnou kockou/mincou
- Výsledkom experimentu je nejaká hodnota (napr. číslo, alebo aj niekoľko čísel, reťazec)
- Túto neznámu hodnotu budeme volať náhodná premenná
- Zaujíma nás pravdepodobnosť, s akou náhodná premenná nadobúda jednotlivé možné hodnoty
- T.j. ak experiment opakujeme veľa krát, ako často uvidíme nejaký výsledok
Príklad 1: hodíme idealizovanou kockou, premenná X bude hodnota, ktorú dostaneme
- Možné hodnoty 1,2,..,6, každá rovnako pravdepodobná
- Pišeme napr. Pr(X=2)=1/6
Príklad 2: hodíme 2x kockou, náhodná premenná X bude súčet hodnôt, ktoré dostaneme
- Možné hodnoty: 2,3,...,12
- Každá dvojica hodnôt (1,1), (1,2),...,(6,6) na kocke rovnako pravdepodobná, t.j. pravdepodobnosť 1/36
- Súčet 5 môžeme dostať 1+4,2+3,3+2,4+1 - t.j. P(X=5) = 4/36
- Súčet 11 môžeme dostať 5+6 alebo 6+5, t.j. P(X=11) = 2/36
- Rozdelenie pravdepodobnosti: (tabuľka udávajúca pravdepodobnosť pre každú možnú hodnotu)
hodnota i: 2 3 4 5 6 7 8 9 10 11 12 Pr(X=i): 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36
- Overte, ze súčet pravdepodobností je 1
Stredná hodnota E(X):
- priemer z možných hodnôt váhovaných ich pravdepodobnosťami
- v našom príklade
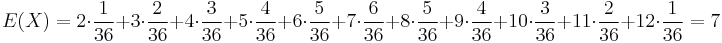
- Ak by sme experiment opakovali veľa krát a zrátali priemer hodnôt X, ktoré nám vyšli, dostali by sme číslo blízke E(X)
- Iný výpočet strednej hodnoty:
- X=X1+X2, kde X1 je hodnota na prvej kocke a X2 je hodnota na druhej kocke
-
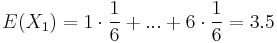 , podobne aj E(X2) = 3.5
, podobne aj E(X2) = 3.5
- Platí, že E(X1+X2)=E(X1) + E(X2) a teda E(X) = 3.5 + 3.5 = 7
- Pozor, pre súčin a iné funkcie takéto vzťahy platiť nemusia, napr.
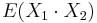 nie je vždy
nie je vždy 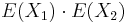
Počítanie pokrytia genómov
- Pozrite tiež grafy k pravdepodobnosti: pdf
- Náš problém: spočítanie pokrytia
- G = dĺžka genómu, napr. 1 000 000 (predpokladajme, že je cirkulárny)
- N = počet čítaní (readov), napr. 10 000
- L = dlzka čítania, napr. 1000
- Celková dĺžka čítaní NL, pokrytie (coverage) NL/G, v nasom pripade 10x
- V priemere každá báza pokrytá 10x
- Niektoré sú ale pokryté viackrát, iné menej.
- Zaujímajú nás otázky typu: koľko báz očakávame, že bude pokrytých menej ako 3x?
- Dôležité pri plánovaní experimentov (aké veľké pokrytie potrebujem na dosiahnutie určitej kvality)
- Pokrytie genómu: predpokladáme, že každé čítanie začína na náhodnej pozícii zo všetkých možných G
- Takže ak premenná Y_i bude začiatok i-tého čítania, jej rozdelenie bude rovnomerné
- P(Y_i=1) = P(Y_i=2) = ... = P(Y_i=G) = 1/G
- Aká je pravdepodobnosť že nejaké konkrétne i-te čítanie pokrýva konkrétnu pozíciu j?
- P(Y_i>=j-L+1 and Y_i<=j) = P(Y_i=j-L+1)+...+P(Y_i=j) = L/G, označme túto hodnotu p, v našom príklade p=0.001 (1 promile)
- Uvazujme premennu X_j, ktora udava pocet čítaní pokryvajucich poziciu j
- mozne hodnoty 0..N
- i-te čítanie pretina poziciu j s pravdepodobnostou p=L/G
- to iste ako keby sme N krat hodili mincou, na ktorej spadne hlava s pravd. p a znak 1-p a oznacili ako X_j pocet hlav
- Priklad: majme mincu, ktora ma hlavu s pr. 1/4 a hodime ju 3x.
HHH 1/64 HHT 3/64 HTH 3/64 HTT 9/64 THH 3/64 THT 9/64 TTH 9/64 TTT 27/64
- P(X_j=3) = 1/64, P(X_j=2)=9/64, P(X_j=1)=27/64, P(X_j=0)=27/64
- taketo rozdelenie pravdepodobnosti sa vola binomicke
- P(X_j = k) = (N choose k) p^k (1-p)^(N-k), kde
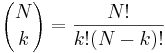 a n! = 1*2*...*n
a n! = 1*2*...*n
- napr pre priklad s troma hodmi kockou P(X_j=2) = 3!/(2!*1!) * (1/4)^2 * (3/4)^1 = 9/64
- Zle sa pocita pre velke N, preto sa niekedy pouziva aproximacia Poissonovym rozdelenim s parametrom lambda = Np, ktore ma
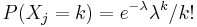
- Spat k sekvenovaniu: vieme spocitat rozdelenie pravdepodobnosti a tiez napr. P(X_i<3) = P(X_i=0)+P(X_i=1)+P(X_i=2) = 0.000045+0.00045+0.0023=0.0028
- Stredna hodnota poctu baz v celom genome s pokrytim k je G*P(X_i=k)
- V priemere teda ocakavame 45 baz nepokrytych, 2800 pokrytých menej ako 3 krát a pod.
- Takyto graf, odhad, vieme lahko spravit pre rozne pocty čítaní a tak naplanovat, kolko čítaní potrebujeme
Chceme tiež odhadnúť počet kontigov (podľa článku E.S. Lander and M.S. Waterman. "Genomic mapping by fingerprinting random clones: a mathematical analysis." Genomics 2.3 (1988): 231-239 [7])
- Ak niekoľko báz vôbec nie je pokrytých čítaniami, preruší sa kontig
- Vieme, koľko báz je v priemere nepokrytých, ale niektoré môžu byť vedľa seba
- Nový kontig vznikne aj ak sa susedné čítania málo prekrývajú
- Predpokladajme, že na spojenie dvoch čítaní potrebujeme prekryv aspoň T=50
- Nech p je pravdepodobnosť, ze dané čítanie i bude posledné v kontigu
- Aby sa to stalo, žiadne čítanie j!=i nesmie začínať v prvých L-T bázach kontigu i
- Každé čítanie tam začína s pravdepodobnosťou q=(L-T)/G
- Ak X je počet čítaní, ktoré zacinaju v tomto useku, tak p = Pr(X=0) = (1-q)^(N-1) podla binomickeho rozdelenia
- v priemere ich tam zacne E(X) = (N-1)(L-T)/G co je zhruba N(L-T)/G
- Jednoduchší vzorec pre p dostaneme ak binomické rozdelenie premennej X aproximujeme Poissonovým s parametrom
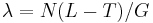 (t.j. aby mali rovnakú strednú hodnotu)
(t.j. aby mali rovnakú strednú hodnotu)
- V Poissonovom rozdelení p = Pr(X=0) = exp(-lambda) = exp(-N(L-T)/G)
- Presnosť aproximácie: pre parametre N,L,G,T uvedené vyššie dostaneme z binomického rozdelenia p=7.459e-5, z Poissonovho 7.485e-5
- Pre N čítaní dostaneme priemerný počet kontigov N*p = N*exp(-N(L-T)/G)
- NL/G je pokrytie, N(L-T)/G je pokrytie, ak by sme dĺžku každého čítania skrátili o dĺžku prekryvu
- Pre T=50 dostaneme priemerný počet koncov kontigov 0.75 (ak pokryjeme celý kruh, máme nula koncov, preto je hodnota menšia ako 1). Ak znížime N na 5000 (5x pokrytie) dostaneme 43 kontigov
- Môže sa zdať zvláštne, ze pri priemernom pocte nepokrytych baz 45 mame pocet koncov v priemere menej ako jedna. Situacia je vsak taka, ze pri opakovaniach tohto experimentu casto dostavame jeden suvisly kontig, ale ak je uz aspon jeden koniec kontigu, byva tam pomerne velka medzera. Tu je napriklad 50 opakovani expertimentu s T=0, priemerny pocet koncov je 0.55, priemerny pocet nepokrytych baz je 49.
nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 274 koncov: 2 nepokr: 282 koncov: 1 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 8 koncov: 1 nepokr: 0 koncov: 0 nepokr: 12 koncov: 1 nepokr: 0 koncov: 0 nepokr: 122 koncov: 1 nepokr: 135 koncov: 1 nepokr: 111 koncov: 1 nepokr: 13 koncov: 1 nepokr: 1 koncov: 1 nepokr: 56 koncov: 1 nepokr: 265 koncov: 1 nepokr: 0 koncov: 0 nepokr: 10 koncov: 1 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 130 koncov: 1 nepokr: 217 koncov: 1 nepokr: 3 koncov: 1 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 86 koncov: 1 nepokr: 139 koncov: 2 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 76 koncov: 1 nepokr: 221 koncov: 1 nepokr: 26 koncov: 1 nepokr: 0 koncov: 0 nepokr: 1 koncov: 1 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 0 koncov: 0 nepokr: 12 koncov: 1 nepokr: 103 koncov: 2 nepokr: 0 koncov: 0 nepokr: 71 koncov: 1 nepokr: 69 koncov: 1 nepokr: 0 koncov: 0
- Tento jednoduchy model nepokryva vsetky faktory:
- čítania nemaju rovnaku dlzku
- Problemy v zostavovani kvoli chybam, opakovaniam a pod.
- čítania nie su rozlozene rovnomerne (cloning bias a pod.)
- Vplyv koncov chromozomov pri linearnych chromozomoch
- Uzitocny ako hruby odhad
- Na spresnenie mozeme skusat spravit zlozitejsie modely, alebo simulovat data
- Poznamka: pravdepodobnosti z binomickeho rozdelenia mozeme lahko spocitat napr. statistickym softverom R. Tu su prikazy, ktore sa na to hodia, pre pripad, ze by vas to zaujimalo:
dbinom(10,1e4,0.001); #(12.5% miest ma pokrytie presne 10) pbinom(10,1e4,0.001,lower.tail=TRUE); #(58% miest ma pokrytie najviac 10) dbinom(0:30,1e4,0.001); #tabulka pravdepodobnosti [1] 4.517335e-05 4.521856e-04 2.262965e-03 7.549258e-03 1.888637e-02 [6] 3.779542e-02 6.302390e-02 9.007019e-02 1.126216e-01 1.251601e-01 [11] 1.251726e-01 1.137933e-01 9.481826e-02 7.292252e-02 5.207187e-02 [16] 3.470068e-02 2.167707e-02 1.274356e-02 7.074795e-03 3.720595e-03 [21] 1.858621e-03 8.841718e-04 4.014538e-04 1.743354e-04 7.254524e-05 [26] 2.897743e-05 1.112843e-05 4.115040e-06 1.467156e-06 5.050044e-07 [31] 1.680146e-07
Zhrnutie
- Pravdepobnostny model: myslienkovy experiment, v ktorom vystupuje nahoda, napr. hod idealizovanou kockou
- Vysledok je hodnota, ktoru budeme volat nahodna premenna
- Tabulka, ktora pre kazdu moznu hodnotu nahodnej premennej urci jej pravdepodobnost, sa vola rozdelenie pravdepodobnosti, sucet hodnot v tabulke je 1
- Znacenie typu P(X=7)=0.1
- Priklad: mame genom dlzky G=1mil., nahodne umiestnime N=10000 čítaní dlzky L=1000
- Nahodna premenna X_i je pocet čítaní pokryvajucich urcitu poziciu i
- Podobne, ako keby sme N krat hodili kocku, ktora ma cca 1 promile sancu padnu ako hlava a 99.9% ako znak a pytame sa, kolko krat padne znak (1 promile sme dostali po zaukruhleni z L/(G-L+1))
- Rozdelenie pravdepobnosti sa v tomto pripade vola binomicke a existuje vzorec, ako ho spocitat
- Takyto model nam moze pomoct urcit, kolko čítaní potrebujeme osekvenovat, aby napr. aspon 95% pozicii bolo pokrytych aspon 4 čítaniami
CB02
Úvod do pravdepodobnosti
- Myšlienkový experiment, v ktorom vystupuje náhoda, napr. hod ideálnou kockou/korunou
- Výsledkom experimentu je nejaká hodnota (napr. číslo, alebo aj niekoľko čísel, reťazec)
- Túto neznámu hodnotu budeme volať náhodná premenná
- Zaujíma nás pravdepodobnosť, s akou náhodná premenná nadobúda jednotlivé možné hodnoty
- T.j. ak experiment opakujeme veľa krát, ako často uvidíme nejaký výsledok
Príklad 1: hodíme idealizovanou kockou, premenná X bude hodnota, ktorú dostaneme
- Možné hodnoty 1,2,..,6, každá rovnako pravdepodobná
- Píšeme napr. Pr(X=2)=1/6
Príklad 2: hodíme 2x kockou, náhodná premenná X bude súčet hodnôt, ktoré dostaneme
- Možné hodnoty: 2,3,...,12
- Každá dvojica hodnôt (1,1), (1,2),...,(6,6) na kocke rovnako pravdepodobná, t.j. pravdepodobnosť 1/36
- Súčet 5 môžeme dostať 1+4,2+3,3+2,4+1 - t.j. P(X=5) = 4/36
- Súčet 11 môžeme dostať 5+6 alebo 6+5, t.j. P(X=11) = 2/36
- Rozdelenie pravdepodobnosti: (tabuľka udávajúca pravdepodobnosť pre každú možnú hodnotu)
hodnota i: 2 3 4 5 6 7 8 9 10 11 12 Pr(X=i): 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36
- Overte, ze súčet pravdepodobností je 1
Stredná hodnota E(X):
- priemer z možných hodnôt váhovaných ich pravdepodobnosťami
- v našom príklade
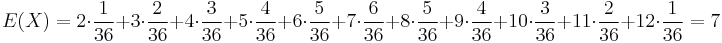
- Ak by sme experiment opakovali veľa krát a zrátali priemer hodnôt X, ktoré nám vyšli, dostali by sme číslo blízke E(X)
- Iný výpočet strednej hodnoty:
- X=X1+X2, kde X1 je hodnota na prvej kocke a X2 je hodnota na druhej kocke
-
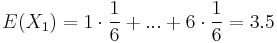 , podobne aj E(X2) = 3.5
, podobne aj E(X2) = 3.5
- Platí, že E(X1+X2)=E(X1) + E(X2) a teda E(X) = 3.5 + 3.5 = 7
- Pozor, pre súčin a iné funkcie takéto vzťahy platiť nemusia, napr.
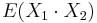 nie je vždy
nie je vždy 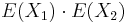
Pravdepodobnostný model náhodnej sekvencie
- Napríklad chceme modelovať náhodnú DNA sekvenciu dĺžky n s obsahom GC 40%
- Máme vrece s guľôčkami označenými A,C,G,T, pričom guľôčok označených A je 30%, C 20%, G 20% a T 30%.
- Vytiahneme guľôčku, zapíšeme si písmeno, hodíme ju naspäť, zamiešame a opakujeme s ďalším písmenom atď, až kým nevygenerujeme n písmen
- Vytiahnime z mechu 2x guľôčku. Prvé písmeno, ktoré nám vyjde, označme X1 a druhé X2
- Pr(X1=A) = 0.3, Pr(X2=C)=0.2
- Pr(X1=A a X2=C) = Pr(X1=A)*Pr(X2=C) = 0.3*0.2 = 0.06
- T.j. šanca, že dostaneme sekvenciu AC po dvoch ťahoch je 6%
- Ak rátame pravdepodobnosť, že sa dve nezávislé udalosti stanú súčasne, ich pravdepodobnosti násobíme. V tomto prípade to, či X1=A je nezávislé od toho, či X2=C
- Pr(X1 je A alebo C) = Pr(X1=A)+Pr(X1=C) = 0.3+0.2 = 0.5
- Pravdepodobnosť, že prvé písmeno bude A alebo C je 50%
- Pravdepodobnosti navzájom sa vylučujúcich udalostí (X1=A a X1=C) sa môžu sčítať, čím dostaneme pravdepodobnosť, že aspoň jedna z nich nastane
- Pr(v sekvencii je aspoň jedno A) = Pr(X1=A alebo X2=A) nemôžeme počítať ako Pr(X1=A)+Pr(X2=A), lebo sa navzájom nevylučujú a prípad, že X1=A a X2=A by sme započítali dvakrát
- Správne je Pr(X1 je A alebo X2 je A) = Pr(X1=A) + Pr(X1 <> A a X2=A) = Pr(X1=A) + Pr(X1 <> A) * Pr(X2=A) = 0.3+0.7*0.3 = 0.51
- Pr(X1=X2) = Pr(X1=X2=A) + Pr(X1=X2=C) + Pr(X1=X2=G) + Pr(X1=X2=T) = 0.3*0.3+0.2*0.2+0.2*0.2+0.3*0.3 = 0.26.
- Ak u označíme pravdepodobnosť u = Pr(X1=A)=Pr(X1=T)=Pr(X2=A)=Pr(X2=T) a v=Pr(X1=C)=Pr(X1=G)=Pr(X2=C)=Pr(X2=G), aký bude vzorec pre Pr(X1=X2)?
Príklad použitia modelu: Máme krátky primer AACAT. Koľko bude mať v priemere výskytov v sekvencii dĺžky 1000 v našom modeli?
- Pravdepodobnosť, ze AACAT je v náhodnej sekvencii hneď na začiatku je Pr(X1=A a X2=A a X3=C a X4=A a X5=A) = 0.3*0.3*0.2*0.3*0.3 = 0.00162
- Rovnaká pravdepodobnosť aj na pozícii 2,3,...996
- Nech V je počet výskytov v celej sekvencii (náhodná premenná s možnými hodnotami 0,1,...,996, aj keď napr. 996 to určite nemôže byť)
- Ideálne by sme chceli spočítať celú tabuľku pravdepodobností pre V, ale uspokojíme sa aj so strednou hodnotou E(V)
- Nech Vi je počet výskytov na pozícii i (co je vzdy 0 alebo 1)
-
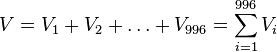
-
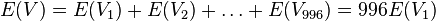
-
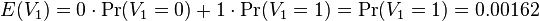
- E(V) = 996*0.00162 = 1.61352
- Takze primer AACAT sa v priemere bude v náhodnej sekvencii dĺžky 1000 s 40% obsahom GC vyskytovať v priemere cca 1,6 krát
- Primery byvaju dlhsie, takze sanca nahodnych vyskytov je ovela mensia, co je to co vacsinou chceme (chceme primer cielit na konkretnu poziciu, nie na vela nahodnych zhod)
Použitie pravdepodobnosti na analýzu potrebného pokrytia pri sekvenovaní
Pozri cvičenia pre informatikov
Dynamické programovanie
- Túto techniku uvidíme na ďalšej prednáške na hľadanie zarovnaní (alignments)
- Uvažujme problém platenia pomocou najmenšieho počtu mincí
- Napr. máme mince hodnoty 1,2,5 centov, z každej dostatok kusov
- Ako môžeme zaplatiť určitú sumu, napr. 13 centov, s čo najmenším počtom mincí?
- Aké je riešenie? 5+5+2+1 (4 mince)
- Všeobecná formulácia:
- Vstup: hodnoty k mincí m_1,m_2,...,m_k a cieľová suma X (všetko kladné celé čísla)
- Výstup: najmenší počet mincí, ktoré potrebujeme na zaplatenie X
- V našom príklade k=3, m_1 = 1, m_2 = 2, m_3 = 5, X=13
- Jednoduchý spôsob riešenia: použi najväčšiu mincu, ktorá je najviac X, odčítaj od X, opakuj
- Príklad: najprv použijeme mincu 5, zostane X=8, použijeme opäť mincu 5, zostane X=3, použijeme mincu 2, zostane X=1, použijeme mincu 1.
- Nefunguje vždy: zoberme mince hodnôt 1,3,4. Pre X=6 najlepšie riešenie je 2 mince: 3+3, ale náš postup (algoritmus) nájde 3 mince 4+1+1
- Ukážeme si algoritmus na základe dyn. programovania, ktorý pre každý vstup nájde najlepšie riešenie
- Zrátame najlepší počet mincí nielen pre X, ale pre všetky možné cieľové sumy 1,2,3,...,X-1,X
- To sa zdá byť ťažšia úloha, ale ukáže sa, že z riešenia pre menšie sumy vieme zostaviť riešenie pre väčšie sumy, takže nám to vlastne pomôže
- Spravíme si tabuľku, kde si pre každú sumu i=0,1,2,...X pamätáme A[i]=najmenší počet mincí, ktoré treba na vyplatenie sumy i
- Ukážme si to na príklade s mincami 1,3,4
i 0 1 2 3 4 5 6 7 8 9 A[i] 0 1 2 1 1 2 2 2 2 3
- Nevypĺňali sme ju žiadnym konkrétnym postupom, nejde o algoritmus
- Ale predstavme si, ze teraz chceme vyplniť A[10].
- V najlepšom riešení je prvá minca, ktorú použijeme 1,3, alebo 4
- ak je prvá minca 1, máme ešte zaplatiť sumu 10-1=9, tú podľa tabuľky vieme najlepšie zaplatiť na 3 mince, takže potrebujeme 4 mince na zaplatenie 10
- ak je prvá minca 3, máme ešte zaplatiť 10-3 = 7, na čo potrebujeme podla tabuľky 2 mince, takže spolu 3 mince na zaplatenie 10
- ak je prvá minca 4, máme ešte zaplatiť 10-4 = 6, na čo treba 2 mince, t.j. 3 mince na 10
- Nevieme, ktorá z týchto možností je naozaj v najlepšom riešení, ale pre druhé dva prípady dostávame menej mincí, takže výsledok budu 3 mince (napr. 3+3+4)
- Zovšeobecníme: A[i] = min { A[i-1]+1, A[i-3]+1, A[i-4]+1 }
- A[11] = min { 3+1, 2+1, 2+1} = min {4, 3, 3 } = 3
- Pre sústavu mincí 1,2,5, máme A[i] = 1+ min { A[i-1], A[i-2], A[i-5] }
- Vo všeobecnosti A[i] = 1+ min { A[i-m_1], A[i-m_2], ..., A[i-m_k] }
- Vzorec treba modifikovať pre malé hodnoty i, ktoré sú menšie ako najväčšia minca, lebo A[-1] a pod. nie je definované
- Pre zaujímavosť, program v Pythone, stačí meniť hodnoty m a X:
m = [1,3,4]
X = 11
k = len(m)
nekonecno = math.inf
A = [0]
for i in range(1, X + 1):
min = nekonecno
for j in range(k):
if i >= m[j] and A[i - m[j]] < min:
min = A[i - m[j]]
A.append(1 + min)
print(A)
- Ako nájsť, ktoré mince použiť?
- Pridáme druhú tabuľku B, kde v B[i] si pamätáme, ktorá bola najlepšia prvá minca, keď sme počítali A[i] (ak je viac možností, zoberieme ľubovoľnú, napr. najväčšiu)
i 0 1 2 3 4 5 6 7 8 9 10 A[i] 0 1 2 1 1 2 2 2 2 3 3 B[i] - 1 1 3 4 4 3 4 4 4 4
- Potom ak chceme nájsť napr. mince pre 10, vidíme, že prvá bola B[10]=4. Zvyšok je 6 a prvá minca na vyplatenie 6 je B[6]=3. Zostáva nám 3 a B[3]=3. Potom nám už zostáva 0, takže sme hotoví. Takže najlepšie vyplatenie je 4+3+3
- Celý program v Pythone:
m = [1,3,4]
X = 11
k = len(m)
nekonecno = math.inf
A = [0]
B = [-1]
for i in range(1, X + 1):
min = nekonecno
min_minca = -1
for j in range(k):
if i >= m[j] and A[i - m[j]] < min:
min = A[i - m[j]]
min_minca = m[j]
A.append(1 + min)
B.append(min_minca)
while X > 0:
print(B[X])
X = X - B[X]
Dynamické programovanie vo všeobecnosti
- Okrem riešenia celého problému vyriešime aj veľa menších podproblémov
- Riešenia podproblémov ukladáme do tabuľky
- Pri riešení väčšieho podproblému používame už vypočítané hodnoty pre menšie podproblémy
Aká je časová zložitosť tohto algoritmu?
- Dva parametre: X a k
- Tabuľka veľkosti O(X), každé políčko čas O(k). Celkovo O(Xk)
CI03
Dynamické programovanie
- Pozri Cvičenia pre biológov
Uvod do proteomiky
- Viac informacii: [8], Bafna, Reinert 2004
- Pozri tiež prezentáciu k cvičeniu
Gélová elektroforéza (gel electrophoresis) - uvedene pre zaujimavost, nerobili sme
- Izolovanie jednotlivých proteínov, porovnávanie ich množstva.
- Negatívne nabité proteíny migrujú v géli v elektrickom poli. Väčšie proteíny migrujú pomalšie, dochádza v oddeleniu do pruhov. Táto metóda sa používa aj na DNA a RNA. Pre proteíny možno tiež robiť 2D gél (podľa hmotnosti a náboja).
- Bioinformatický problém: zisti, ktoré fliačiky na dvoch 2D géloch zodpovedajú tým istým proteínom.
- Automatizovanejšia technológia: kvapalinová chromatografia (liquid chromatography) - separácia proteínov v tenkom stĺpci
Hmotnostná spektrometria (mass spectrometry)
- Hmotnostná spektrometria meria pomer hmostnosť/náboj molekúl vo vzorke.
- Používa sa na identifikáciu proteínov, napr. z 2D gélu.
- Proteín nasekáme enzýmom trypsín (seká na [KR]{P}) na peptidy
- Meriame hmostnosť kúskov, porovnáme s databázou proteínov.
- Tandemová hmotnostná spektrometria (MS/MS) ďalej fragmentuje každý kúsok a dosiahne podrobnejšie spektrum, ktoré obsahuje viac informácie
- v niektorých prípadoch vieme sekvenciu proteínu určiť priamo z MS/MS, bez databázy proteínov
Sekvenovanie proteinov pomocou MS/MS
Vsetky hmotnosti budeme povazovat za cele cisla
Vstup:
- celková hmotnosť peptidu M,
- hmotnosti aminokyselín a[1],...,a[20],
- spektrum ako tabuľka f[0],...,f[M], ktorá hmotnosti m určí skóre f[m] podľa signálu v okolí príslušného bodu grafu
Označenie:
- Uvažujme postupnosť aminokyselín
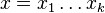
- Nech
![m(x)=\sum _{{j=1}}^{k}a[x_{j}]](/vyuka/mbi/images/math/5/1/e/51e47d7db5cc3125eee0a57b9e19c12c.png) je hmotnosť x
je hmotnosť x
- Nech
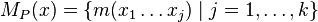 sú hmotnosti prefixov x
sú hmotnosti prefixov x
- Nech
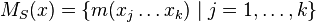 sú hmotnosti sufixov x
sú hmotnosti sufixov x
Problém 1
Berme do uvahy len b-iony, ktore zodpovedaju hmotnosti prefixu
Výstup:
- postupnosť aminokyselín x taká, že
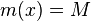 a
a ![\sum _{{m\in M_{P}(x)}}f[m]](/vyuka/mbi/images/math/e/f/c/efca77d5389ed7769b65877ff30a2c69.png) je maximálna možná
je maximálna možná
- Chceme teda najst peptid, ktory maximalizuje sucet skore svojich prefixov
Riešenie
- Dynamicke programovanie s podproblemom S[m] je skore najlepsieho prefixu s hmotnostou m
- Rekurencia? Zlozitost? Je to polynomialny algoritmus? (Aky velky je vlastne vstup?)
Problém 2
Berme do uvahy aj y-iony, ktore meraju hmotnost sufixu, scitame skore prefixov a sufixov
Výstup:
- postupnosť aminokyselín x taká, že
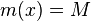 a
a ![\sum _{{m\in M_{P}(x)}}f[m]+\sum _{{m\in M_{S}(x)}}f[m]](/vyuka/mbi/images/math/6/9/9/699ef640d8249b3456c1241580179964.png) je maximálna možná
je maximálna možná
Riešenie
- pouzijeme upravenu skorovaciu tabulku g[m]=f[m]+f[M-m] a algoritmus pre problem 1
Problem tejto formulacie:
- jeden signal sa moze ratat dvakrat, raz ako b-ion, raz ako y-ion, algoritmus ma tendenciu pridavat taketo artefakty
Problém 3
Ak hmotnost nejakeho prefixu a nejakeho sufixu su rovnake, zarataj ich skore iba raz (skore peptidu je skore mnoziny hmotnosti jeho prefixov a sufixov)
Výstup:
- postupnosť aminokyselín x taká, že
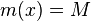 a
a ![\sum _{{m\in M_{P}(x)\cup M_{S}(x)}}f[m]](/vyuka/mbi/images/math/6/6/5/665a026ed145fe16ec6b27b6044972b8.png) je maximálna možná
je maximálna možná
Riesenie:
- Ina formulacia: maximalizujeme
![\sum _{{m\in M_{p}(x)\cup M_{S}(x),m\leq M/2}}h[m]](/vyuka/mbi/images/math/d/2/0/d20e9653e2a74d027573395f12f2f0f1.png)
-
![h[m]=\left\{{\begin{array}{ll}f[m]+f[M-m]&{\mbox{ak }}m<M/2\\f[m]&{\mbox{ak }}m=M/2\end{array}}\right.](/vyuka/mbi/images/math/6/b/9/6b9baa42bbaae35399de43cab3712d19.png)
- Definuj novy podproblem: S[p,s] je najlepsie skore, ktore moze dosiahnut prefix s hmotnostou p a sufix s hmotnostou s, kde 0<=p,s<=M/2,
- Rekurencia
![S[p,s]=\left\{{\begin{array}{ll}\max _{{i=1\dots 20}}S[p,s-a[i]]+h[s]&{\mbox{ak }}p<s\\\max _{{i=1\dots 20}}S[p-a[i],s]+h[p]&{\mbox{ak }}p>s\\\max _{{i=1\dots 20}}S[p-a[i],s]&{\mbox{ak }}p=s\\\end{array}}\right.](/vyuka/mbi/images/math/f/b/1/fb198e39be6b286cd92f4e0a8c0bbddf.png)
- Ako ukoncime dynamicke programovanie? Zlozitost?
- Zrychlenie: staci uvazovat s od p-w po p+w kde w je maximalna hmotnost aminokyseliny
Detekcia znamych proteinov pomocou MS (nerobili sme)
- Predikcia spektra pre dany peptid, porovnanie s realnym spektrom, zlozite skorovacie schemy
- Filtrovanie kandidatov na proteiny, ktore obsahuju peptidy s pozorovanou hmotnostou
- Problem: mame danu databazu proteinov a cielovu hmotnost peptidu M, pozname hmotnost kazdej aminokyseliny. Najdite vsetky podretazce s hmotnostou M.
- Databazu proteinov si vieme predstavit aj ako postupnost cisel - hmotnosti aminokyselin, hladame intervaly so suctom M.
- Trivialny algoritmus: zacni na kazdej pozicii, pricitavaj kym nedosiahnes hmotnost>=M. Zlozitost? Vieme zlepsit?
- Predspracovanie: pocitajme hmotnosti vsetkych podretazcov, potom vyhladajme binarne. Zlozitost?
- Zlozitejsi alg. s predspracovanim pomocou FFT (Fast Fourier Transform) Bansal, Cieliebak, Liptak 2004
CB03
Zarovnávanie sekvencií, opakovanie
- Uvažujme skórovanie zhoda +3, nezhoda -1, medzera -2
- Reťazce TAACGG a CACACT
Globálne zarovnanie
- Rekurencia: A[i,j] = max {A[i-1,j]-2, A[i,j-1]-2, A[i-1,j-1]+s(x_i, y_j) }, pričom A[0,i]=-2i, A[i,0]=-2i
C A C A C T
0 -2 -4 -6 -8 -10 -12
T -2
A -4
A -6
C -8
G -10
G -12
Lokálne zarovnanie
- Rekurencia: A[i,j] = max {0, A[i-1,j]-2, A[i,j-1]-2, A[i-1,j-1]+s(x_i, y_j) }, pričom A[0,i]=0, A[i,0]=0
C A C A C T
0 0 0 0 0 0 0
T 0
A 0
A 0
C 0
G 0
G 0
Dotploty
- Dotplot je graf, ktory ma na kazdej osi jednu sekvenciu a ciarky zobrazuju lokalne zarovnania (cesty v matici)
- Niekoľko príkladov dotplotov: pdf
- Prvé príklady dotplotov porovnávajú rôzne mitochondriálne genomy
- Tieto boli vytvorene pomocou nastroja YASS http://bioinfo.lifl.fr/yass/yass.php
- Dalsi priklad je zarovnanie genu Oaz Drosophila zinc finger s genomickym usekom chr2R:10,346,241-10,352,965
- Trochu iny dotplot, ktory funguje pre proteiny a nerobi lokalne zarovnania, iba spocita skore bez medzier v kazdom okne danej vysky a nakresli ciaru ak prekroci urcenu hodnotu
- http://emboss.bioinformatics.nl/cgi-bin/emboss/dotmatcher
- Vyskusame protein escargot voci sebe s hodnotami http://pfam.xfam.org/protein/ESCA_DROME window 8 threshold 24
- Pomocou YASSu vyskusame kluster zhlukov PRAME z ludskeho genomu
Dynamické programovanie v Exceli
Práca so vzorcami v tabuľkovom procesore (Excel, LibreOffice, ...)
- Okrem konkrétnych hodnôt, napr. 0.3, môžu byť aj vzorce, ktoré začínajú =, napr =0.3*0.3 dá do políčka 0.09 (* znamená násobenie)
- Vo vzorcoch môžeme používať aj hodnoty z iných políčok, napr. =A2+B2 dáme do políčka C2, zobrazí sa tam súčet
- Ak políčko so vzorcom skopírujeme do iného políčka, Excel sa snaží uhádnuť, ako zmeniť vzorec
- Ak sme v C2 mali =A2+B2 a skopírovali sme to do C3, vzorec sa zmení na =A3+B3
- Ak niektoré adresy políčok majú zostávať rovnaké aj pri kopírovaní, dáme pred písmeno aj číslo $,
- Ak v C2 máme =A2+$B$2 a skopírujeme to do C3, dostaneme =A3+B2
- Dolár môžeme dať aj pred iba jednu súradnicu (stĺpec alebo riadok), tá sa potom nebude pri kopírovaní meniť
Späť k rozmieňaniu mincí
- Vráťme sa k príkladu s rozmieňaním mincí a skúsme si ho "naprogramovať" v Exceli, resp. spreadsheet aplikácii v OpenOffice
- Vseobecna formulacia:
- Vstup: hodnoty k minci m_1,m_2,...,m_k a cielova suma X (vsetko kladne cele cisla)
- Vystup: najmensi pocet minci, ktore potrebujeme na zaplatenie X
- My pouzijeme mince hodnot 1,3,4
- Spravime si tabulku, kde si pre kazdu sumu i=0,1,2,...X pamatame A[i]=najmensi pocet minci, ktore treba na vyplatenie sumy i
i 0 1 2 3 4 5 6 7 8 9 A[i] 0 1 2 1 1 2 2 2 2 3
- vzorec A[i] = min { A[i-1]+1, A[i-3]+1, A[i-4]+1 }
- aby sme nemuseli zvlast uvazovat hodnoty mensie ako 4, (kde sa neda A[i-4]), urcime si A[-1], A[-2] atd ako nejake velke cislo (napr 100), takze vzorec plati pre vsetky i>0
i -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 A[i] 100 100 100 100 0 1 2 1 1 2 2 2 2 3
- v exceli si najskor spravime horny riadok tabulky
- do nejakeho policka (napr, B4) zapiseme prvu hodnotu (-4)
- do susedneho C4 zapiseme vzorec =B4+1, dostaneme hodnotu -3
- vzorce zacinaju znamienkom =
- B4 je suradnica policka o jedno vlavo, k nej pripocitame 1
- policko C4 nakopirujeme do riadku kolkokrat chceme, dostaneme hodnoty -2, -1, 0, 1,...
- kopirovat sa da tahanim laveho dolneho rohu okienka
- vzorec sa automaticky posuva na =C4+1, =D4+1, atd
- o riadok nizsie do B5..E5 napiseme hodnotu 100 (okienka A[-4]..A[-1])
- do F5 dame 0 (okienko A[0] nasej tabulky)
- do G5 napiseme vzorec =MIN(F5+1,D5+1,C5+1), t.j. A[1] = min(A[1-1]+1,A[1-3]+1,A[1-4]+1)
- tento vzorec potom nakopirujeme do riadku tabulky
- F5 sa bude posuvat na G5, H5,... a podobne ostatne dva cleny
Cvičenie:
- Ako by sme zmenili na inu mincovu sustavu, napr. 1,2,5?
- Stiahnite si subor zo stranky predmetu a skuste si tuto zmenu urobit [9]
Zarovnávanie sekvencií v Exceli
- skusme si dynamicke programovanie pre globalne zarovnanie naprogramovat v Exceli
- budeme postupovat podobne ako pri minciach, ale potrebujeme dve specialne funkcie: MID(text,od,dlzka) z textu vyberie urcitu cast. Pomocou toho si vstupny text rozdelime na jednotlive pismena, ktore si napiseme do zahlavia tabulky
- vsimnite si pouzivanie dolarov v nazvoch policok: ak je pred menom stlpca alebo riadku $, tento sa neposuva ked vzorec kopirujem do inych policok
- IF(podmienka,hodnota1,hodnota2) vyberie bud hodnotu 1 ak je podmienka splnena alebo hodnotu2 ak nie je. Napr IF(F$8=$B12 ,1,-1) zvoli skore +1 ak sa hodnota v F8 rovna hodnote v B12 a skore -1 ak sa nerovnaju.
Cvičenie:
- Zmente tabulku tak, aby skore pre zhody, nezhody a medzery bolo dane bunkami B1, B2 a B3 tabulky. Staci zmenit vzorce a policka D9, C10 a D10 a nakopirovat do zvysku tabulky. Ake bude skore najlepsieho zarovnania sekvencii AACGTA a ACACCTA ak skore nezhody je -2 a medzery -3?
- Ako treba zmenit vzorce, aby sme pocitali lokalne zarovnanie?
- Subor najdete tu
CI04
Opakovanie dynamického programovania pre globálne zarovnanie
Uvažujme napríklad skórovanie zhoda +1, nezhoda -1, medzera -1 a vstupné sekvencie 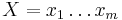 a
a 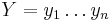 . Nech s(x,y) je skóre písmen x a y, t.j. 1 ak sa zhodujú a -1 ak nie. Máme rekurenciu:
. Nech s(x,y) je skóre písmen x a y, t.j. 1 ak sa zhodujú a -1 ak nie. Máme rekurenciu:
- Ako presne by sme implementovali?
- Ako spočítame maticu spätných šípok B?
- Aká je časová a pamäťová zložitosť?
Reprezentácia pomocou grafu
Takéto dynamické programovanie vieme reprezentovať vo forme acyklického orientovaného grafu:
- vrchol (i,j) pre každé
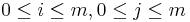 , t.j. pre každé políčko dyn. prog. tabuľky
, t.j. pre každé políčko dyn. prog. tabuľky
- hrana z (i-1,j-1) do (i,j) s cenou
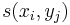
- hrana z (i-1,j) do (i,j) s cenou -1
- hrana z (i,j-1) do (i,j) s cenou -1
- súčet súradníc na každej hrane rastie, graf teda nemôže obsahovať cyklus, je acyklický
- každá cesta z (0,0) do (m,n) zodpovedá zarovnaniu, jej cena je cenou zarovnania (každá hrana jeden stĺpec)
- optimálne zarovnanie teda zodpovedá ceste s maximálnou cenou
Krátka vsuvka o acyklických orientovaných grafoch
- Mame dany acyklicky orientovany graf s ohodnotenymi hranami a startovaci vrchol s, koncovi vrchol t a chceme najst cestu s max. cenou z s do t.
- Hladanie cesty s maximalnou cenou je vo vseobecnosti NP-tazke (podobne na Hamiltonovsku cestu)
- V acyklickom grafe to vsak vieme riesit efektivne
- Najskor si graf zotriedime topologicky, t.j. usporiadame vrcholy tak, aby kazda hrana isla z vrcholu z mensim cislom do vrcholu s vacsim cislom. To sa da modifikaciou prehladavania do hlbky v case O(|V|+|E|)
- Potom pocitame dynamickym programovanim, kde A[u] je dlzka najdlhsej cesty z s do u:
![A[u]=\max _{{v:v\rightarrow u\in E}}A[v]+c(v\rightarrow u)](/vyuka/mbi/images/math/6/d/9/6d90a7118031848ff55c4204bc8b4552.png) pricom na zaciatku nastavime A[s]=0 a na konci mame cenu cesty v A[t].
pricom na zaciatku nastavime A[s]=0 a na konci mame cenu cesty v A[t].
- Cas vypoctu je O(|V|+|E|)
- Vsimnime si, ze tiez dostaneme najdlhsie cesty z s do vsetkych vrcholov.
Ak tento algoritmus nasadime na graf pre globalne zarovnanie, dostavame presne nasu rekurenciu (topologicke triedenie mozno vynechat - poradie zhora dole a zlava doprava je topologicky utriedene). Vyhoda je, ze mozeme modifikaciou grafu ziskavat riesenia roznych pribuznych problemov bez toho, aby sme vzdy vymyslali novu rekurenciu.
Lokálne zarovnanie
- Zarovnanie moze zacat a skoncit hocikde v matici
- Pridaj startovaci vrchol s, koncovy vrchol t
- Pridaj hrany s->(i,j) a (i,j)->t s cenou 0 pre kazde (i,j)
- Opat ekvivalentne s rekurenciou z prednasky
Variant: chceme zarovnat cely retazec X k nejakej casti retazca Y (napr. mapovanie sekvenovacich readov na genom)
- Iba zmenime hrany z s a hrany do t (ako?)
Afínne skóre medzier
- Napr. otvorenie medzery o=-3, pokracovanie medzery e=-1
A - - - T C G A C G C T C C 1 -3 -1 -1 1 1 -1
Nesprávne riešenie pomocou dynamického programovania
Pouzijeme bezne dynamicke programovanie pre globalne zarovnanie, ale v rekurencii zmenime vypocet penalty za medzeru:
- c(i,j,s) = o, ak v policku A[i,j] mame sipku s
- c(i,j,s) = e, ak v policku A[i,j] mame inu sipku
Preco toto riesenie nefunguje?
- Co ak pre policko (i,j) je viac rovnako dobrych rieseni s roznymi sipkami?
- Co ak pre policko (i,j) je najlepsie riesenie so sipkou napr. sikmo, ale druhe najlepsie je len 1 horsie a ma sipku hore?
Toto je obvykla chyba pri dynamickom programovani:
- aby bolo dynamicke programovanie spravne, musi platit, ze optimalne riesenie vacsieho podproblemu musi obsahovat optimalne riesenie mensieho podproblemu
Správne riešenie pomocou dynamického programovanania
Riesenie 1:
- Pridame hrany pre cele suvisle useky medzier so spravnou cenou
- (i,j)->(i,k) s cenou o+(k-j)e
- (i,j)->(k,j) s cenou o+(k-i)e
- Cas O(mn(m+n)), t.j. kubicky
- pozor, mame aj cesty, ktore nezopodvedaju ziadnemu spravnemu skore, napr. (i.j)->(i+1,j)->(i+2,j) ma cenou 2o, ale ma mat o+e. Nastastie hrana (i,j)->(i+2,j) ma vyssiu cenu, takze ta dlhsia cesta sa nepouzije.
Riesenie 2:
- ztrojnasobime kazdy vrchol
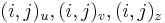
- v indexe si pamatame, odkial sme do (i,j) prisli (u=uhlopriecne, v=vodorovne, z=zvislo)
- ak ideme napr. z
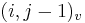 do
do 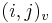 , pokracujeme v uz existujucej medzere, takze skore je e
, pokracujeme v uz existujucej medzere, takze skore je e
- ak ideme napr. z
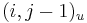 do
do 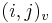 , zaciname novu medzeru, takze skore je o
, zaciname novu medzeru, takze skore je o
- ake vsetky hrany teda mozeme mat? Kolko je spolu v grafe hran a vrcholov a aka je zlozitost algoritmu?
Lineárna pamäť: Hirshbergov algoritmus 1975
- Klasicke dynamicke programovanie potrebuje cas O(nm)
- Trivialna implementacia tiez pouzije pamat O(mn) - uklada si celu maticu A, pripadne maticu B so sipkami naspat
- Na vypocet matice A nam z stacia dva riadky tejto matice: riadok i pocitam len pomocou riadku i-1, starsie viem zahodit
- Ale ak chcem aj vy[isat zarovnanie, stale potrebujem pamat O(mn) na maticu sipok B
- Hirschbergov algoritmus znizi pamat na O(m+n), zhruba zdvojnasobi cas (stale O(mn))
- Prejdeme celú maticu a spočítame maticu A. Zapamätáme si, kde moja cesta prejde cez stredný riadok matice
- Nech B_k[i,j] je najväčší index v riadku k, cez ktorý prechádza najkratšia cesta z (0,0) do (i,j)
- Ako vieme B_k[i,j] spočítať?
- ak A[i,j] = A[i-1,j-1]+w(S[i],T[j])$, potom B_k[i,j]=B_k[i-1,j-1].
- ak A[i,j]=A[i-1,j]+1, potom B_k[i,j]=B_k[i-1,j].
- ak A[i,j]=A[i,j-1]+1, potom B_k[i,j]=B_k[i,j-1]
- Toto platí, ak i > k. Pre i=k nastavíme B_k[i,j]=j
- Ak už poznáme A[i-1,*] a B_k[i-1,*], vieme spočítať A[i,*] a B_k[i,*].
- Stacia nam teda iba dva riadky matice A a B_k
- Nech k'=B_k[m,n]. Potom v optimálnom zarovnaní sa S[1..k] zarovná s T[1..k'] a S[k+1..m] s T[k'+1..n].
- Toto použijeme na rekurzívny algoritmus na výpočet zarovnania:
optA(l1, r1, l2, r2) { // align S[l1..r1] and T[l2..r2]
if(r1-l1 <= 1 || r2-l2 <=1)
solve using dynamic programming
else {
k=(r-l+1)/2;
for (i=0; i<=k; i++)
compute A[i,*] from A[i-1,*]
for (i=k+1; i<=r-l+1; i++)
compute A[i,*], B_k[i,*] from A[i-1,*], B_k[i-1,*]
k2=B_k[r1-l1-1,r2-l2-1];
optA(l1, l1+k-1, l2, l2+k2-1);
optA(l1+k, r2, l2+k2, r2);
}
}
Casova zlozitost:
- Označme si N=nm (súčin dĺžky dvoch daných reťazcov).
- Na hornej úrovni rekurzie spúšťame dynamické programovanie pre celú maticu -- čas bude $cN$.
- Na druhej urovni mame dva podproblemy, velkosti N1 a N2, pricom N1+N2<=0.5*N (z kazdeho stlpca matice A najviac polovica riadkov pocitana znova)
- Na tretej urovni mame 4 podproblemy N11, N12, N21, N22, pricom N11+N12 <= 0.5*N1 a N21+N22 <= 0.5*N2 a teda celkovy sucet podproblemov na druhej urvni je najviac N/4.
Na stvrtej urovni je sucet podproblemov najviac N/8 atd, Dostavame geometricky rad cN+cn/2+cN/4+... ktoreho sucet je 2cN
Vypísanie všetkých najlepších riešení
- Namiesto jednej spatnej sipky si pamatame vsetky, ktore v danom A[i,j] viedli k maximalnej cene
- Potom mozeme rekurzivne prehladavat a vypisovat vsetky cesty z (m,n) do (0,0) ktore pozostavaju iba zo zapamatanych hran
- Cas na vypisanie jednej cesty je polynomialny, ale ciest moze byt exponencialne vela!
- Mozno namiesto toho chceme len pocet takych ciest, alebo vsetky dvojice pismen, ktore mozu byt spolu zarovnane v niektorom optimalnom zarovnani
CB04
Skórovacie matice
Chceme určiť skórovaciu schému pre zarovnávanie dvoch DNA sekvencií (bez medzier). Máme dva modely, každý z nich vie vygenerovať 2 zarovnané sekvencie dĺžky n.
Model R (random) reprezentuje nezávislé náhodne sekvencie
- Použijeme naše vrece s guličkami označenými A,C,G,T, pričom guličiek označených A je 30%, C 20%, G 20% a T 30%.
- Vytiahneme guličku, zapíšeme si písmeno, hodíme ju naspäť, zamiešame a opakujeme s ďalším písmenom atď až kým nevygenerujeme n písmen pre jednu sekvenciu a n písmen pre druhú
- Máme jednu sekvenciu ACT a druhú ACC. Aká je pravdepodobnosť, že práve tieto sekvencie vygenerujeme v našom modeli R?
- Nezávislé udalosti pre jednotlivé písmená, t.j. Pr(X1=A)*Pr(X2=C)*Pr(X3=T)*Pr(Y1=A)*Pr(Y2=C)*Pr(Y3=C) = 0.3*0.2*0.3*0.3*0.2*0.2 = 0.000216
- Spolu máme v modeli
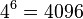 možností ako vygenerovať 2 DNA sekvencie dĺžky 3
možností ako vygenerovať 2 DNA sekvencie dĺžky 3
Model H (homolog) reprezentuje zarovnanie vzájomne súvisiacich sekvencií
- máme vrece, v ktorom je napr.
- po 21% guličiek označených AA, TT
- po 14% označených CC, GG
- po 2.4% označených AC, AG, CA, CT, GA, GT, TC, TG
- po 3.6% označených AT, TA
- po 1.6% označených CG, GC.
- Spolu máme 70% guličiek označených rovnakými písmenami, 30% rôznymi
- n krát z vreca vytiahneme guličku a písmená píšeme ako stĺpce zarovnania A1, A2,.., An.
- aká je pravdepodobnosť, ze dostaneme ACT zarovnané s ACC?
- Pr(A1=AA)*Pr(A2=CC)*Pr(A3=TC) = 0.21*0.14*0.024 = 0.0007056
Skóre zarovnania je log Pr(zarovnania v H)/Pr(zarovnania v R), t.j. log (0.0007056 / 0.000216) = 0.514105 (pre desiatkový logaritmus)
- kladné skóre znamená, že model H lepšie zodpovedá dátam (zarovnaniu) ako model R
- záporné skóre znamená, že model R lepšie zodpovedá dátam
Cvičenie pri počítači
- Stiahnite si súbor nižšie, uložte si ho a otvorte v Exceli / OpenOffice / LibreOffice
- V záložke Matica vyplňte do žltej oblasti vzorce na výpočet pravdepodobnosti krátkeho zarovnania, logaritmus pomeru pravdepodobnosti a súčet skóre, pričom vo vzorcoch použijete odkazy na políčka v riadkoch 9-13, stĺpcoch B a E
- Súčet skóre by mal byť zhruba rovný desaťnásobku logaritmu pomeru - prečo vidíme rozdiely?
- Potom skúšajte meniť %GC a %identity v horných riadkoch tabuľky a pozrite sa, ako to ovplyvní skórovanie. Výsledné skóre zo stĺpca E ručne prepíšte (bez formúl) do tabuľky v záložke Výsledky. Prečo nastávajú také zmeny ako vidíte?
Praktické cvičenie pri počítači: dotploty
Yass a dotploty
- Program Yass hlada lokalne zarovnania v DNA sekvenciach, zobrazuje vo forme dot plotov
- V novom okne/tabe si otvorte YASS server na adrese http://bioinfo.lifl.fr/yass/yass.php
- V dalsom okne si na stranke UCSC genome browseru si zobrazte oblast chr21:9,180,027-9,180,345 vo verzii hg38 ludskeho genomu [10]
- tento región obsahuje Alu repeat. Tieto opakovania tvoria cca 10% ľudského genómu, viac ako milión kópií
- zobrazte si DNA sekvenciu tohto useku takto: na hornej modrej liste zvolte View, potom v podmenu DNA, na dalsej obrazovke tlacidlo get DNA
- DNA sekvenciu Alu opakovania chceme zarovnat samu k sebe programom YASS
- DNA sekvenciu Alu opakovania skopirujte do okienka "Paste your sequences" v stranke Yass-u a dvakrat stlacte tlacidlo Select vedla okienka
- Nizsie v casti "Selected DNA sequence(s)" by sa Vam malo v oboch riadkoch objavit "Pasted file 1"
- Nizsie v casti "Parameters" zvolte "E-value threshold" 0.01 a stlacte "Run YASS"
- Vo vysledkoch si pozrite Dotplot, co z neho viete usudit o podobnosti jednotlivych casti Alu opakovania?
- Vo vysledkoch si pozrite Raw: blast, ake su suradnice opakujucej sa casti a kolko zarovnanie obsahuje zhod/nezhod/medzier? (Pozor, prve zarovnanie je cela sekvencia sama k sebe, druhe je asi to, co chcete)
- V genome browseri sa presunte na poziciu chr21:8,552,000-8,562,000 (10kb sekvencie na chromozome 21, s niekolkymi vyskytmi Alu) [11]
- Chceme teraz porovnat tento usek genomu so sekvenciou Alu pomocou YASSu
- Ako predtym si stiahnite DNA sekvenciu tohto useku
- V YASSe chodte sipkou spat na formular
- Skopirujte DNA sekvenciu do YASSoveho formulara, do okienka vpravo (vyznacit si ju mozete klavesovou kombinaciou Ctrl-A alebo Select All v menu Edit),
- V casti formulara Selected DNA sequence(s) stlacte Remove pri hornom riadku
- Pri pravom okienku, kam ste nakopirovali sekvenciu, stlacte Select
- Zase stlacte Run YASS
- Pozrite si vysledok ako Dotplot, kolko opakovani Alu ste nasli? Preco je jedno cervene?
- Pozrite si Raw: blast, na kolko percent sa podoba najpodobnejsia a na kolko druha najpodobnejsia kopia?
Dotplot celých kvasinových genómov
- Na stránke https://dgenies.toulouse.inra.fr/run (based on minimap2 program)
- Zadáme URL dvoch genómov z NCBI:
- Predpočítaný výsledok https://dgenies.toulouse.inra.fr/result/CL9nR_20231012150020
- Iná dvojica:
- Magnusiomyces ingens ftp://ftp.ebi.ac.uk/pub/databases/ena/wgs/public/uid/UIDE01.fasta.gz [12]
- Saprochaete ingens ftp://ftp.ebi.ac.uk/pub/databases/ena/wgs/public/cab/CABVLU01.fasta.gz [13]
Príklady praktických programov
Pozrime sa na niekolko nastrojov, vsimnime si, ake poskytuju nastavenia a co vypisuju na vystupe, dajme to do suvisu s prednaskami
- viacnasobne zarovnania neskor
Plné dynamické programovanie
- Balicek emboss, obsahuje programy na klasicke dynamicke programovanie (needle - globalne, water - lokalne), najdu sa na stranke EBI http://www.ebi.ac.uk/Tools/psa/
- porovnanie lokalneho a globalneho zarovnania
- Dva proteiny z rôznych kvasiniek zarovnáme lokálne, globálne a globálne s tým, že neplatíme za medzery na koncoch
- sekvencie a vysledne zarovnania: CB-aln-dp
- vo vysledku si vsimnime, kolko ma kazde z nich %identity, %gaps, a kam sa zarovna sekvencia IRESPLGG ktora je na pozicii 29 v prvom a 30 v druhom proteine
Lokalne zarovnanie Length: 588 Identity: 170/588 (28.9%) Similarity: 270/588 (45.9%) Gaps: 116/588 (19.7%) Score: 611.0 MCA_00027_1 29-568 (z 595) RKM3_YEAST 30-549 (z 552) Globalne zarovnanie Length: 650 Identity: 178/650 (27.4%) Similarity: 282/650 (43.4%) Gaps: 153/650 (23.5%) Score: 588.5 Globalne zarovnanie s nulovou penaltou za medzeru na koncoch Length: 651 Identity: 177/651 (27.2%) Similarity: 282/651 (43.3%) Gaps: 155/651 (23.8%) Score: 608.0
NCBI Blast
- NCBI BLAST http://blast.ncbi.nlm.nih.gov/ vela roznych nastrojov (porovnavanie DNA vs proteiny, pripadne translacia DNA na protein v 6 ramcoch)
- Heuristicky algoritmus, moze niektore zarovnania vynechat
- rozne nastavenia, vystup E-value
Low complexity masking: nepouzivat pri hladani jadier zarovnania regiony v ktorych sa velakrat opakuje ta ista aminokyselina
- Priklad (z ucebnice Zvelebil and Baum):
>sp|P04156|PRIO_HUMAN Major prion protein OS=Homo sapiens GN=PRNP PE=1 SV=1 MANLGCWMLVLFVATWSDLGLCKKRPKPGGWNTGGSRYPGQGSPGGNRYPPQGGGGWGQP HGGGWGQPHGGGWGQPHGGGWGQPHGGGWGQGGGTHSQWNKPSKPKTNMKHMAGAAAAGA VVGGLGGYMLGSAMSRPIIHFGSDYEDRYYRENMHRYPNQVYYRPMDEYSNQNNFVHDCV NITIKQHTVTTTTKGENFTETDVKMMERVVEQMCITQYERESQAYYQRGSSMVLFSSPPV ILLISFLIFLIVG
- Hladajme v databaze Reference sequence (Refseq), organizmus human
Bez maskovania vypise napr aj toto zarovnanie:
>ref|NP_065842.1| serine/threonine-protein kinase TAO1 isoform 1 [Homo sapiens]
Length=1001
Score = 45.1 bits (105), Expect = 1e-06, Method: Composition-based stats.
Identities = 26/61 (43%), Positives = 27/61 (44%), Gaps = 11/61 (18%)
Query 38 YPGQGSPGGNRYPPQGGGG--WGQPHGG---GWGQPHGGG---WGQPHGGGWGQPHGGGWG 90
YPG G + P GG G WG P GG WG P GG WG P G G P G G
Sbjct 904 YPGAS---GWSHNPTGGPGPHWGHPMGGPPQAWGHPMQGGPQPWGHPSGPMQGVPRGSSMG 961
Score = 40.0 bits (92), Expect = 4e-05, Method: Composition-based stats.
Identities = 25/62 (40%), Positives = 25/62 (40%), Gaps = 10/62 (16%)
Query 26 PKPGGW--NTGGSRYPGQGSPGGNRYPPQGGGGWGQPHGGG---WGQPHGGGWGQPHGGGWG 82
P GW N G P G P G PPQ WG P GG WG P G G P G
Sbjct 905 PGASGWSHNPTGGPGPHWGHPMGG--PPQA---WGHPMQGGPQPWGHPSGPMQGVPRGSSMG 961
Ak zapneme maskovanie, toto zarovnanie uz nenajde, v zarovnani sameho so sebou sa objavia male pismena alebo Xka:
>ref|NP_000302.1|major prion protein preproprotein [Homo sapiens]
Length=253
Score = 520 bits (1340), Expect = 0.0, Method: Compositional matrix adjust.
Identities = 253/253 (100%), Positives = 253/253 (100%), Gaps = 0/253 (0%)
Query 1 MANLGCWMLVLFVATWSDLGLCKKRPKPGGWNTGGSRYPGQGSPGGNRYppqggggwgqp 60
MANLGCWMLVLFVATWSDLGLCKKRPKPGGWNTGGSRYPGQGSPGGNRYPPQGGGGWGQP
Sbjct 1 MANLGCWMLVLFVATWSDLGLCKKRPKPGGWNTGGSRYPGQGSPGGNRYPPQGGGGWGQP 60
Query 61 hgggwgqphgggwgqphgggwgqphgggwgqgggTHSQWNKPSKPKTNMKHMagaaaaga 120
HGGGWGQPHGGGWGQPHGGGWGQPHGGGWGQGGGTHSQWNKPSKPKTNMKHMAGAAAAGA
Sbjct 61 HGGGWGQPHGGGWGQPHGGGWGQPHGGGWGQGGGTHSQWNKPSKPKTNMKHMAGAAAAGA 120
Query 121 vvgglggymlgsamsRPIIHFGSDYEDRYYRENMHRYPNQVYYRPMDEYSNQNNFVHDCV 180
VVGGLGGYMLGSAMSRPIIHFGSDYEDRYYRENMHRYPNQVYYRPMDEYSNQNNFVHDCV
Sbjct 121 VVGGLGGYMLGSAMSRPIIHFGSDYEDRYYRENMHRYPNQVYYRPMDEYSNQNNFVHDCV 180
Query 181 NITIKQHtvttttkgenftetDVKMMERVVEQMCITQYERESQAYYQRGSSMVLFSsppv 240
NITIKQHTVTTTTKGENFTETDVKMMERVVEQMCITQYERESQAYYQRGSSMVLFSSPPV
Sbjct 181 NITIKQHTVTTTTKGENFTETDVKMMERVVEQMCITQYERESQAYYQRGSSMVLFSSPPV 240
Query 241 illisfliflivG 253
ILLISFLIFLIVG
Sbjct 241 ILLISFLIFLIVG 253
Uniprot pre projekty
- Prehladny pohlad na proteiny, vela linkov na ine databazy, cast vytvarana rucne
- Pozrieme sa na známy koronavírusový proteín Spike
- Nájdime ho na stránke http://www.uniprot.org/ pod názvom SPIKE_SARS2
- Pozrime si podrobne jeho stránku, ktoré časti boli predpovedané bioinformatickými metódami z prednášky?
- Všimnime si niektorú Pfam doménu a pozrime si jej stránku
Praktické cvičenie pri počítači: BLAT vs BLAST
BLAT, chains, nets v UCSC browseri
- Program BLAT v UCSC browseri http://genome-euro.ucsc.edu/ rychlo vyhladava sekvencie v genome, ale nevie najst slabsie podobnosti
- Vhodne pouzitie: zarovnanie mRNA ku genomu, presne urcenie suradnic nejakej sekvencie, a pod.
- Net tracky v UCSC genome browseri nam umoznuju prechadzat medzi homologickymi oblastami roznych genomov
BLAT/BLAST
- Sekvencia uvedena nizsie vznikla pomocou RT-PCR na ľudských cDNA knižniciach
- Choďte na UCSC genome browser http://genome-euro.ucsc.edu/ , na modrej lište zvoľte BLAT, zadajte túto sekvenciu a hľadajte ju v ľudskom genóme. Akú podobnosť (IDENTITY) má najsilnejší nájdený výskyt? Aký dlhý úsek genómu zasahuje? (SPAN). Všimnite si, že ostatné výskyty sú oveľa kratšie.
- V stĺpci ACTIONS si pomocou Details môžete pozrieť detaily zarovnania a pomocou Browser si pozrieť príslušný úsek genómu.
- V tomto úseku genómu si zapnite track Vertebrate net na full a kliknutím na farebnú čiaru na obrázku pre tento track zistite, na ktorom chromozóme sliepky sa vyskytuje homologický úsek.
- Skusme tu istu sekvenciu zarovnat ku genomu sliepky programom Blat: stlacte najprv na hornej modrej liste Genomes, zvolte Vertebrates a Chicken a potom na hornej liste BLAT. Do okienka zadajte tu istu sekvenciu. Akú podobnosť a dĺžku má najsilnejší nájdený výskyt teraz? Na ktorom je chromozóme?
- Skúsme to isté v NCBI blaste: Choďte na http://blast.ncbi.nlm.nih.gov/ zvoľte nucleotide blast, database others a z menu reference genomic sequence, organism chicken (taxid:9031), program blastn
- Aká je dĺžka, identity a E-value najlepšieho zarovnania? Na ktorom je chromozóme?
RT PCR sekvencia z cvičenia vyššie
AACCATGGGTATATACGACTCACTATAGGGGGATATCAGCTGGGATGGCAAATAATGATTTTATTTTGAC TGATAGTGACCTGTTCGTTGCAACAAATTGATAAGCAATGCTTTCTTATAATGCCAACTTTGTACAAGAA AGTTGGGCAGGTGTGTTTTTTGTCCTTCAGGTAGCCGAAGAGCATCTCCAGGCCCCCCTCCACCAGCTCC GGCAGAGGCTTGGATAAAGGGTTGTGGGAAATGTGGAGCCCTTTGTCCATGGGATTCCAGGCGATCCTCA CCAGTCTACACAGCAGGTGGAGTTCGCTCGGGAGGGTCTGGATGTCATTGTTGTTGAGGTTCAGCAGCTC CAGGCTGGTGACCAGGCAAAGCGACCTCGGGAAGGAGTGGATGTTGTTGCCCTCTGCGATGAAGATCTGC AGGCTGGCCAGGTGCTGGATGCTCTCAGCGATGTTTTCCAGGCGATTCGAGCCCACGTGCAAGAAAATCA GTTCCTTCAGGGAGAACACACACATGGGGATGTGCGCGAAGAAGTTGTTGCTGAGGTTTAGCTTCCTCAG TCTAGAGAGGTCGGCGAAGCATGCAGGGAGCTGGGACAGGCAGTTGTGCGACAAGCTCAGGACCTCCAGC TTTCGGCACAAGCTCAGCTCGGCCGGCACCTCTGTCAGGCAGTTCATGTTGACAAACAGGACCTTGAGGC ACTGTAGGAGGCTCACTTCTCTGGGCAGGCTCTTCAGGCGGTTCCCGCACAAGTTCAGGACCACGATCCG GGTCAGTTTCCCCACCTCGGGGAGGGAGAACCCCGGAGCTGGTTGTGAGACAAATTGAGTTTCTGGACCC CCGAAAAGCCCCCACAAAAAGCCG
CB05
Príklady stavových automatov pre HMM
Uvazujme HMM so specialnym zaciatocnym stavom b a koncovym stavom e, ktore nic negeneruju.
- Nakreslite HMM (stavovy diagram), ktory generuje sekvencie, ktore zacinaju niekolkymi cervenymi pismenami a potom obsahuju niekolko modrych
- Ako treba zmenit HMM, aby dovoloval ako "niekolko" aj nula?
- Ako treba zmenit HMM, aby pocet cervenych aj modrych bol vzdy parne cislo?
- Ako zmenit HMM, aby sa striedali cervene a modre kusy parnej dlzky?
V dalsich prikladoch uvazujeme aj to, ktore pismena su v ktorom stave povolene (pravdepodobnost emisie > 0) a ktore su zakazane
- cervena sekvencia dlzky dva, ktora zacina na A
- cervena sekvencia dlzky dva, ktora je hocico okrem AA
- toto sa da rozsirit na HMM, ktory reprezentuje ORF, teda nieco, co zacina start kodonom, potom niekolko beznych kodonov, ktore nie su stop kodonom a na koniec stop kodon
Dalsi biologicky priklad HMM: topologia transmembranovych proteinov.
E-hodnota (E-value) zarovnania
- Priklady k tejto casti v prezentacii pdf
- Mame dotaz dlzky m, databazu dlzky n, skore najlepsieho lokálneho zarovnania S
- E-value je ocakavany pocet zarovnani so skore aspon S ak dotaz aj databaza su nahodne
- Hrackarsky priklad: dotaz dlzky m=10, databaza dlzky n=300, S=6
- Zoberme nas nahodny model s obsahom GC 50%
- Mame vrece s gulockami oznacenymi A,C,G,T, z kazdej 25%
- Vytiahneme gulicku, zapiseme si pismeno, hodime ju naspat, zamiesame a opakujeme s dalsim pismenom atd az kym nevygenerujeme m pismen pre dotaz a n pismen pre databazu
- Pre nase vygenerovane sekvencie spocitame, kolkokrat sa dotaz vyskytuje v databaze
- Cely experiment opakujeme vela krat a spocitame priemerny pocet vyskytov, co bude odhad E-value
Vypocet strednej hodnoty vzorcom namiesto simulacie (rychlejsie)
- zlozita matematicka teoria [14]
- E-value sa priblizne da odhadnut vzorcom:
- n a m su dlzky porovnavanych sekvencii, S je skore, K a lambda su parametre, ktore zavisia od skorovacej schemy a od frekvencii vyskytu jednotlivych baz v nasom modeli nahodnej sekvencie.
- Napr blastn pre skorovaci system zhoda 1, nezhoda -1, medzera -2 používa lambda=0.800, K=0.0640
-
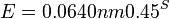 .
.
- Zdvojnásobenie dĺžky databázy alebo dĺžky dotazu zdvojnásobí E-value
- Zníženie skóre o 1 tiež zhruba zdvojnásobí E-value (delenie 0.45, t.j. nasobenie 2.2)
- Cislo, ktorym nasobime, zalezi od lambda a teda od skorovacej schemy a frekvencii vyskytu baz
Dynamické programovanie v Exceli
Použitie stránky Galaxy
- https://usegalaxy.eu/
- Obsahuje veľa bioinformatických nástrojov, ktoré môžete spúšťať
- Ale na výsledky treba niekedy dlho čakať
- V ľavom stĺpci hľadanie nástroja alebo nahrávanie dát
- V pravom stĺpci zoznam nahratých dát, bežiacich programov a hotových výsledkov (výsledky si pozriete ikonou oka alebo stiahnete ikonou diskety)
- V strede nastavenia nástroja alebo prezeranie výsledkov
- Pri serióznom používaní odporúčam vytvoriť si konto a prihlásiť sa
- Programy napr. Alphafold 2, SignalP, TMHMM, WoLF
CI06
HMM opakovanie
Parametre HMM:
-
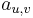 : prechodová pravdepodobnosť zo stavu
: prechodová pravdepodobnosť zo stavu 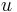 do stavu
do stavu 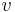
-
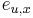 : pravdepodobnosť emisie
: pravdepodobnosť emisie 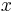 v stave
v stave 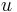
-
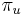 : pravdepodobnosť, že začneme v stave
: pravdepodobnosť, že začneme v stave 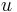
- Sekvencia
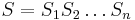
- Anotácia
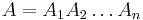
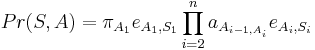
Trénovanie
- Proces, pri ktorom sa snažíme čo najlepšie odhadnúť pravdepodobnosti
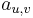 a
a 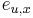 v modeli podľa trénovacích dát
v modeli podľa trénovacích dát
Usudzovanie (inferencia)
- Proces, pri ktorom sa snažíme pre sekvenciu
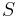 nájsť anotáciu
nájsť anotáciu 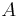 , ktorá sekvenciu
, ktorá sekvenciu 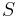 emituje s veľkou pravdepodobnosťou.
emituje s veľkou pravdepodobnosťou.
Inferencia pomocou najpravdepodobnejšej cesty, Viterbiho algoritmus
Hľadáme najpravdepodobnejšiu postupnosť stavov 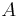 , teda
, teda 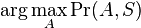 . Úlohu budeme riešiť dynamickým programovaním.
. Úlohu budeme riešiť dynamickým programovaním.
- Podproblém
![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) : Pravdepodobnosť najpravdepodobnejšej cesty končiacej po
: Pravdepodobnosť najpravdepodobnejšej cesty končiacej po 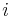 krokoch v stave
krokoch v stave 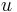 , pričom vygeneruje
, pričom vygeneruje 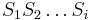 .
.
- Rekurencia:
-
![V[1,u]=\pi _{u}e_{{u,S_{1}}}](/vyuka/mbi/images/math/f/1/3/f13d26742a6a93123093e174c3fd90aa.png) (*)
(*)
-
![V[i,u]=\max _{w}V[i-1,w]a_{{w,u}}e_{{u,S_{i}}}](/vyuka/mbi/images/math/e/3/b/e3bf534bb50c39843ed166123ecc374b.png) (**)
(**)
-
Algoritmus:
- Nainicializuj
![V[1,*]](/vyuka/mbi/images/math/5/d/9/5d9f1d4ebd3080a0804a6501977b5dae.png) podľa (*)
podľa (*)
- for i=2 to n=dĺžka reťazca
- for u=1 to m=počet stavov
- vypočítaj
![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) pomocou (**)
pomocou (**)
- vypočítaj
- for u=1 to m=počet stavov
- Maximálne
![V[n,j]](/vyuka/mbi/images/math/1/2/9/12924883f1d662364326a1d3f0fed497.png) je pravdepodobnosť najpravdepodobnejšej cesty
je pravdepodobnosť najpravdepodobnejšej cesty
Aby sme vypísali anotáciu, pamätáme si pre každé ![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) stav
stav 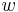 , ktorý viedol k maximálnej hodnote vo vzorci (**).
, ktorý viedol k maximálnej hodnote vo vzorci (**).
Zložitosť: 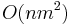
Poznámka: pre dlhé sekvencie budú čísla ![V[i,u]](/vyuka/mbi/images/math/8/2/b/82b63b00ee9d341b172ed7a0c7c44f7b.png) veľmi malé a môže dôjsť k podtečeniu. V praxi teda používame zlogaritmované hodnoty, namiesto násobenia súčet.
veľmi malé a môže dôjsť k podtečeniu. V praxi teda používame zlogaritmované hodnoty, namiesto násobenia súčet.
Inferencia - dopredný algoritmus
Aká je celková pravdepodobnosť, že vygenerujeme sekvenciu 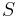 , t.j.
, t.j. 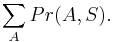 Podobný algoritmus ako Viterbiho.
Podobný algoritmus ako Viterbiho.
Podproblém ![F[i,u]](/vyuka/mbi/images/math/4/e/6/4e6962ec814d01e4ca0d1f2aa085a831.png) : pravdepodobnosť, že po
: pravdepodobnosť, že po 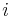 krokoch vygenerujeme
krokoch vygenerujeme 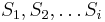 a dostaneme sa do stavu
a dostaneme sa do stavu 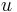 .
.
![F[i,u]=\Pr(A_{i}=u\wedge S_{1},S_{2},\dots ,S_{i})=\sum _{{A_{1},A_{2},\dots ,A_{i}=u}}\Pr(A_{1},A_{2},...,A_{i}\wedge S_{1},S_{2},...,S_{i})](/vyuka/mbi/images/math/9/c/5/9c51082607764a6c99095ebaa1ba26f4.png)
![F[1,u]=\pi _{u}e_{{u,S_{1}}}](/vyuka/mbi/images/math/f/e/a/fead9f93f8bf3927b34f49597d884996.png)
![F[i,u]=\sum _{v}F[i-1,v]a_{{v,u}}e_{{u,S_{i}}}](/vyuka/mbi/images/math/d/1/c/d1c9473aeb8cc364771bc9c575c7a73f.png)
Celková pravdepodobnosť ![\sum _{u}F[n,u]](/vyuka/mbi/images/math/1/b/2/1b2108be9d84620e173cb861e49c6b35.png)
Inferencia - posterior decoding
Aposteriórna pravdepodobnosť stavu u na pozícii i: 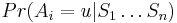
Pre každý index i chceme nájsť stav u s najväčšiou aposteriórnou pravdepodobnosťou, dostaneme tak inú možnú anotáciu.
Spustíme dopredný algoritmus a jeho symetrickú verziu, spätný algoritmus, ktorý počíta hodnoty
![B[i,u]=\Pr(A_{i}=u\wedge S_{{i+1}}\dots S_{n})](/vyuka/mbi/images/math/6/e/8/6e82648bde89df23b004629c06c05c23.png)
Aposteriórna pravdepodobnosť stavu u na pozícii i: ![Pr(A_{i}=u|S_{1}\dots S_{n})=F[i,u]B[i,u]/\sum _{u}F[n,u].](/vyuka/mbi/images/math/2/7/c/27cea5da3d3a25dfb8a677a41dc9e9b1.png)
Posterior decoding uvažuje všetky anotácie, nielen jednu s najvyššou pravdepodobnosťou. Môže však vypísať anotáciu, ktorá má sama o sebe nulovú pravdepodobnosť (napr. počet kódujúcich báz v géne nie je deliteľný 3).
Trénovanie HMM
- Stavový priestor + povolené prechody väčšinou ručne
- Parametre (pravdepodobnosti prechodu, emisie a počiatočné) automaticky z trénovacích sekvencií
- Ak máme anotované trénovacie sekvencie, jednoducho počítame frekvencie
- Ak máme iba neanotované sekvencie, snažíme sa maximalizovať vierohodnosť trénovacích dát v modeli. Používajú sa heuristické iteratívne algoritmy, napr. Baum-Welchov, ktorý je verziou všeobecnejšieho algoritmu EM (expectation maximization).
- Čím zložitejší model a viac parametrov máme, tým potrebujeme viac trénovacích dát, aby nedošlo k preučeniu, t.j. k situácii, keď model dobre zodpovedá nejakým zvláštnostiam trénovacích dát, nie však ďalším dátam.
- Presnosť modelu testujeme na zvláštnych testovacích dátach, ktoré sme nepoužili na trénovanie.
Tvorba stavového priestoru modelu
- Promótor + niekoľko prokaryotických génov
- Repeaty v intrónoch: multiple path problem
- Intrón má dĺžku aspoň 10
Zovšeobecnené HMM
- Predstavme si HMM s dvoma stavmi, napr. gén / negén, pričom každý stav má prechod do seba aj do druhého stavu
- Úloha: Nech p je pravdepodobnosť, že zostaneme v tom istom stave, (1-p), že prejdeme do druhého stavu. Aká je pravdepodobnosť, že v stave zostaneme presne k krokov (k>=1)?
- Riešenie:
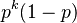
- Toto rozdelenie sa nazýva geometrické a pravdepodbnosť exponenciálne rýchlo klesá s rastúcim k
- Riešenie:
- Keď sa pozrieme na histogram reálny dĺžkov génov / exónov a iných oblastí, väčšinou sa enpodobá na geometrické rozdelnie, môže priponínať napr. normálne rozdelenie s určitou priemenrou dĺžkou a rozptylom okolo
- Jednoduché HMM teda dobre nemodeluje tento fenomén
- Zovšeobecnené HMM (semi-Markov) pracuje tak, že v stave má ľubovoľné rozdelenie pravdepodobnosti dĺžok. Model vôjde do stavu, vygeneruje dĺžku k z tohto rozdelenia, potom vygeneruje k znakov z príslušnej emisnej tabuľky a na záver sa rozhodne, ktorým prechodom opustí stav
- Úloha: ako spočítame pravdepodobnosť konkrétnej sekvencie a konkrétnej postupnosti stavov aj s dĺžkami? (zaveďme si aj nejaké vhodné označenie)
- Úloha: ako treba upraviť Viterbiho algoritmus pre tento model? Aká bude jeho zložitosť?
- Zložitosť bude kvadraticky rásť od dĺžky sekvencie, predtým rástla lineárne
- Predstavme si teraz, že rozdelenie dĺžok má hornú hranicu D takú, že všetky dĺžky väčšie ako D majú nulovú pravdepodobnosť.
- Úloha: ako sa toto obmedzenie prejaví v zložitosti Viterbiho algoritmu?
- Uloha: navrhnite, ako modelovať zovšeobecnený HMM s rozdelením dĺžok ohraničeným D pomocou normálneho stavu, kde sa jedne zovšeobecnený stav nahradí vhodnou postupnosťou D obyčajných stavov.
Párové HMM (pair HMM)
Nebrali sme, uvedene pre zaujimavost
- Emituje dve sekvencie
- V jednom kroku moze emitovat:
- pismenka v oboch sekvenciach naraz
- pismenko v jednej skevencii
- pismenko v druhej sekvencii
Priklad: HMM s jednym stavom v, takym, ze
-
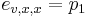
-
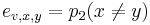 ,
,
-
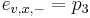 ,
,
-
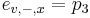
- tak, aby sucet emisnych pravdepodobnosti bol 1
- Co reprezentuje najpravdepodobnejsia cesta v tomto HMM?
Zlozitejsi HMM: tri stavy M, X, Y, uplne navzajom poprepajane
-
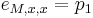
-
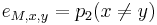 ,
,
-
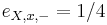 ,
,
-
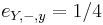 ,
,
- Co reprezentuje najpravdepodobnejsia cesta v tomto HMM?
Viterbiho algoritmus pre parove HMM
- V[i,j,u] = pravdepodobnost najpravdepodobnejsej postupnosti stavov, ktora vygeneruje x1..xi a y1..yj a skonci v stave u
-
![V[i,j,u]=\max _{w}\left\{{\begin{array}{l}V[i-1,j-1,w]\cdot a_{{w,u}}\cdot e_{{u,x_{i},y_{j}}}\\V[i-1,j,w]\cdot a_{{w,u}}\cdot e_{{u,x_{i},-}}\\V[i,j-1,w]\cdot a_{{w,u}}\cdot e_{{u,-,y_{j}}}\\\end{array}}\right.](/vyuka/mbi/images/math/d/5/0/d5064f1dc674bec18ec3404260675e81.png)
- Casova zlozitost O(mnk^2) kde m a n su dlzky vstupnych sekvencii, k je pocet stavov
Ako by sme spravili parove HMM na hladanie genov v dvoch sekvenciach naraz?
- Predpokladajme rovnaky pocet exonov
- V exonoch medzery len cele kodony (oboje zjednodusuje)
- Inde hocijake medzery
CB06
Fylogenetické stromy
Terminológia:
- zakorenený strom, rooted tree
- nezakorenený strom, unrooted tree
- hrana, vetva, edge, branch
- vrchol, uzol, vertex, node
- list, leaf, leaf node, tip, terminal node
- vnútorný vrchol, internal node
- koreň, root
- podstrom, subtree, clade
Zopár faktov o stromoch
- Majme zakorenený strom s n listami, v ktorom má každý vnútorný vrchol 2 deti. Takýto strom vždy má n-1 vnútorných vrcholov a 2n-2 vetiev (prečo?)
- Majme nezakorenený strom s n listami, v ktorom má každý vnútorný vrchol 3 susedov. Takýto strom vždy má n-2 vnútorných vrcholov a 2n-3 vetiev
- Koľkými spôsobmi môžeme zakoreniť nezakorenený strom s n listami?
- koreň môže byť na hociktorej vetve stromu, teda je 2n-3 možností zakorenenia
- Ak nakreslíme zakorenený strom obvyklým spôsobom, listy sú usporiadané zhora nadol (alebo zľava doprava). Koľko rôznych poradí listov vieme dostať rôznym zakresľovaním toho istého stromu s n listami?
- máme n-1 vnutornych vrcholov, v kazdom mozeme vymenit lave a prave dieta. Pre kazdu konfiguraciu takychto vymen dostavame ine poradie, celkovy pocet poradi je 2n-1
- Čo vieme zistiť o príbuznosti organizmov z nezakoreneného stromu (napr. kvartet 4 organizmov)?
- skúsime zakoreniť všetkými spôsobmi a vidíme, že o žiadnych dvoch listoch nevieme povedať, že by boli sesterské (evolučne bližšie než ostatné), lebo koreň stromu môže byť zrovna na niektorej hrane vedúcej ku nim
- vieme však zistiť, že niektoré dvojice sesterské nebudú
Iné použitie stromov v informatike:
- uvidíme hierarchické zhlukovanie, bayesovské siete, ale tiež efektívne dátové štruktúry
Bootstrap
- Náhodne vyberieme niektoré stĺpce zarovnania, zostrojíme strom vybranou metódou
- Celé to opakujeme veľa krát
- Značíme si, koľkokrát sa ktorá vetva opakuje v stromoch, ktoré dostávame
- Pri nezakorenených stromoch je vetva rozdelenie listov na dve skupiny (bipartícia)
- Nakoniec zostavíme strom z celých dát a pozrieme sa ako často sa ktorá jeho vetva vyskytovala
- Môžeme zostaviť aj strom z často sa vyskytujúcich hrán (napr. tých, ktoré sú vo viac ako 50% stromov)
- Bootstrap hodnoty nám dajú určitý odhad spoľahlivosti, hlavne ak máme celkovo málo dát (krátke zarovnanie)
- Ak však dáta nezodpovedajú vybranej metóde/modelu, tak aj pre zlý strom môžeme dostať vysoký bootstrap
Detail: pri náhodnom výbere stĺpcov pre bootstrap väčšinou používame rovnaký počet stĺpcov ako pôvodné zarovnanie, pričom vzorkujeme z pôvodného zarovnania s povolením opakovania stĺpca.
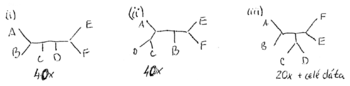
Príklad
- Robili sme 100x bootstrap, 40x sme dostali strom (i) na obrázku, 40x sme dostali strom (ii) a 20x sme dostali strom (iii)
- Strom (iii) sme dostali aj spustením metody na celých dátach
- Zistite úroveň bootstrap podpory pre jednotlivé vetvy stromu (iii)
- Ktoré ďalšie vetvy majú podporu aspoň 20%?
- Aký strom by sme dostali, ak by sme chceli nechať iba vetvy s podporou aspoň 80%?
Opakovanie pravdepodobnostných modelov
Keď počítame pravdepodobnosť, rozmýšľame o myšlienkovom experimente, v ktorom hádžeme kockou, ťaháme gulôčky z vreca a pod.
- Dôležité je vždy si poriadne uvedomiť, ako tento experiment prebieha
- Tieto myšlienkové experimenty však nastavujeme tak, aby odzrkadľovali nejaké aspekty reality, napr. skutočných DNA sekvencií, ich evolúcie a pod.
- Takže pravdepodobnosti, ktoré spočítame v idealizovanom svete nám možno niečo povedia o reálnom svete
- Slávny citát štatistika Georga Boxa "All models are wrong, but some are useful."
Aké sme doteraz videli modely
- Skórovacie matice: porovnávame model náhodných sekvencií a model náhodných zarovnaní
- E-value v BLASTe: náhodne vygenerujeme databázu a dotaz (query), koľko bude v priemere medzi nimi lokálnych zarovnaní so skóre aspoň S?
- Hľadanie génov: model generujúci sekvenciu+anotáciu naraz (parametre nastavené na známych génoch). Pre danú sekvenciu, ktorá anotácia je najpravdepodobnejšia?
- Evolúcia, Jukes-Cantorov model: model generujúci stĺpec zarovnania. Neznáme parametre: strom, dĺžky hrán. Pre danú sadu stĺpcov zarovnania, ktoré parametre povedú k najväčšej pravdepodobnosti?
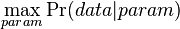
- Trochu detailov: pravdepodobnosť zmeny/nezmeny na hrane dĺžky t:
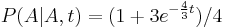 ,
, 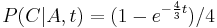
- Ak poznáme ancestrálne sekvencie, vieme spočítať pravdepodobnosť dát
- Ancestrálne sekvencie sú náhodné premenné, ktoré nás nezaujímajú: marginalizujeme ich (uvažujeme všetky ich možné hodnoty)
- Trochu detailov: pravdepodobnosť zmeny/nezmeny na hrane dĺžky t:
Zložitejšie evolučné modely
- Jukes-Cantorov model uvažuje len dĺžku hrany udanú ako priemerný počet substitúcií (vrátane tých, ktore nevidíme, kvôli tomu, že boli dve na tom istom mieste)
- Nie všetky substitúcie sa dejú rovnako často: tranzície (v rámci pyrimidínov T<->C, v rámci purínov A<->G) sú pravdepodobnejšie ako tranzverzie (A,G)<->(C,T)
- Nie všetky nukleotidy sa v danom genóme vyskytujú rovnako často (napr. mitochondriálne genómy majú nízky obsah GC)
- Tieto javy zachytáva HKY model (Hasegawa, Kishino & Yano)
- Matica rýchlostí zmeny (substitution rate matrix)
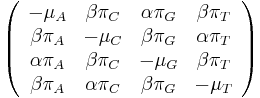
-
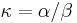 je pomer rýchlostí, ktorými sa deju tranzície vs. transverzie
je pomer rýchlostí, ktorými sa deju tranzície vs. transverzie
-
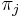 je frekvencia bazy
je frekvencia bazy 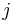 v sekvencii
v sekvencii
- Rýchlosť, ako sa deje substitúcia z X do Y je súčin pravdepodobnosti Y a faktoru, ktorý zavisí od toho, či ide o tranzíciu alebo transverziu
- Súčet každého riadku matice má byť 0, t.j.
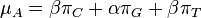
- Matica sa znormalizuje tak, aby priemerný počet substitúcii za jednotku času bol 1
- Matica ma styri parametre:
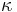 a tri frekvencie (stvrta musi doplnit do 1) plus dlzka hrany
a tri frekvencie (stvrta musi doplnit do 1) plus dlzka hrany
- Zlozitejsi model lepsie zodpoveda skutocnym procesom, ale na odhad viac parametrov potrebujeme viacej dat.
- Existuju metody, ktore pre dany cas t z matice rychlosti spocitaju pravdepodobnost, ze baza X zmutuje na bazu Y Pr(Y|X,t)
- Napr. pre velmi maly cas
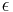 mame
mame 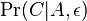 je zhruba
je zhruba 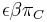
- Pre rozumne dlhe casy toto neplati, preto sa pouzivaju algebraicke metódy, ktoré berú do úvahy možnosť viacerých substitúcií na tom istom mieste
- Je aj vela inych modelov s mensim alebo vacsim poctom parametrov
Fitchov algoritmus
Nerobili sme, uvedene pre zaujimavost
- Parsimony/uspornost
- Vstup: fylogeneticky strom, 1 stlpec zarovnania (jedna baza v kazdom liste stromu)
- Vystup: priradenie baz predkom minimalizujuce pocet substitucii
- Priklad - obr 1
- Uvazujme, co vieme povedat o strome s dvoma susednymi listami vo vacsom strome (oznacenie: obr. 2, listy v1 a v2, hrany do listov e1, e2, ich predok v3, hrana z v3 vyssie e3).
- Ak oba listy maju bazu rovnaku bazu, napr. A, predok v3 v optimalnom rieseni bude urcite mat bazu A
- Dokaz sporom: nech to tak nie je, nech optimalne riesenie ma nejaku inu bazu, napr. C. Vymenme v tomto rieseni toto C za A. Moze nam pribudnut jedna mutacia na hrane e3, ale ubudnu dve na hranach e1 a e2. Tym celkova cena riesenia klesne o 1, takze nebolo optimalne.
- Ak tieto dva listy maju rozne bazy, napr. A a C, tak existuje optimalne riesenie, ktore ma v predkovi v3 bazu A alebo C.
- Dokaz: vezmime optimalne riesenie. Ak ma v3 bazu A alebo C, tvrdenie plati. Ak ma v3 nejaku inu bazu, napr T, mozeme ju vymenit napr. za A, ci mozno pribudne jedna mutacia na e3 ale urcite ubudne mutacia na e1. Teda celkovy pocet mutacii sa nezvysi a nase nove riesenie je stale optimalne. Pozor, vo vseobecnosti nevieme povedat, ci ma v3 mat bazu A alebo C. V niektorych pripadoch su optimalne obe, v niektorych len jedna z nich.
- Fitchov algoritmus 1971
- Kazdemu vrcholu v priradime mnozinu baz M(v)
- M(v) pocitame od listov smerom ku korenu
- Pre list v bude M(v) obsahovat bazu v tomto liste
- Uvazujme vnutorny vrchol v s detmi x a y. Mame uz spocitane M(x) a M(y), chceme M(v)
- Ak M(x) a M(y) maju nejake spolocne bazy, vsetky tieto spolocne bazy dame do M(v), t.j.
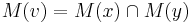
- Ak M(x) a M(y) nemaju spolocne bazy, do M(v) dame vsetky bazy z M(x) aj M(v), t.j.
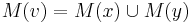
- V tomto pripade pocet mutacii vzrastie o jedna
- Ked mame M(v) spocitane pre vsetky vrcholy, ideme od korena smerom k listom a vyberieme vzdy jednu bazu z M(v).
- Ak sme vybrali pre rodica bazu x a x je v M(v), zvolime x aj pre v, inak zvolime lubovolnu bazu z M(v).
- Priklad algoritmu na obr 3
CI07
Substitučné modely - odvodenie
- Nech
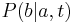 je pravdepodobnosť, že ak začneme s bázou a, tak po čase t budeme mať bázu b.
je pravdepodobnosť, že ak začneme s bázou a, tak po čase t budeme mať bázu b.
- Pre dané t môžeme také pravdepodobnosti usporiadať do matice 4x4 (ak študujeme DNA):
- Riadky zodpovedaju povodnej baze a, stlpce novej baze b
- Sucet kazdeho riadku je 1
Požiadavky na S(t)
- Intuitivne cim vacsie t, tym vacsia pravdepodobnost zmeny, pre nulovy cas este ziadna zmena nemala kedy nastat, mame teda
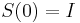 (jednotkova matica)
(jednotkova matica)
- Naopak ked t ide do nekonecna, kazda baza velakrat zmutovala a teda uz prilis nezalezi, co to bolo na zaciatku. S(t) ma teda v limite pre velke t vsetky riadky rovnake.
-
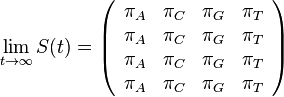
- Rozdelenie pravdepodobnosti
 nazyvame limitne (equilibrium)
nazyvame limitne (equilibrium)
- Predpokladame tiez, ze pravdepodobnost mutacie zavisi len od aktualnej bazy, nie od minulych stavov a ze charakter procesu mutacii sa v case nemeni. Teda ak mame matice pre casy
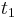 a
a 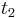 , vieme spocitat maticu pre cas
, vieme spocitat maticu pre cas 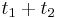 :
: 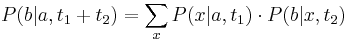 a teda v maticovej notacii
a teda v maticovej notacii 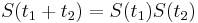 . Preto takyto model nazyvame multiplikativny.
. Preto takyto model nazyvame multiplikativny.
- Ak by sme uvazovali iba diskretne (celociselne) casy, stacilo by nam urcit iba
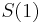 a vsetky ostatne casy dostaneme umocnenim tejto matice. Je vsak elegantnejsie mat
a vsetky ostatne casy dostaneme umocnenim tejto matice. Je vsak elegantnejsie mat 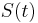 definovane aj pre realne t.
definovane aj pre realne t.
- Tento typ modelu sa nazyva Markovov retazec so spojitym casom (continuous-time Markov chain)
Jukes-Cantorov substitučný model
- Tento model predpoklada, ze vsetky substitucie su rovnako pravdepodobne, matica teda musí vyzerať nejako takto:
Matica rýchlostí pre J-C model
- Pre velmi maly cas t je s(t) velmi male cislo (blizke 0) a pre velmi male s(t) su kvadraticke cleny
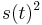 ovela mensie ako linearne cleny s(t) a teda
ovela mensie ako linearne cleny s(t) a teda
- Aj pre ine rozumne male nasobky
- Tento vztah dava zmysel: pre velmi male t mozeme zanedbat moznost, ze baza zmutovala viackrat a pravdepodobnost jednej mutacie linearne rastie s dlzkou casu.
- Ak oznacime
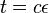 a
a 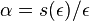 dostaneme pre velmi male t
dostaneme pre velmi male t
- Vytvorme si teraz maticu rychlosti (intenzit) (transition rate matrix, substitution rate matrix)
- Dostavame, ze pre velmi male casy plati
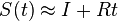
-
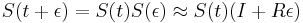 a teda
a teda 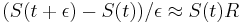
- V limite dostaneme
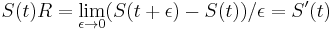
- Dostali sme diferencialnu rovnicu S(t)R = S'(t), pociatocny stav
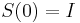 ).
).
- Nasobenim matic S(t) a R dostavame, ze diagonalny prvok
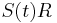 je
je 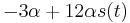 a nediagonalny
a nediagonalny 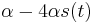 . Takze dostavame diferencialnu rovnicu
. Takze dostavame diferencialnu rovnicu 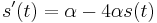 z rovnosti nediagonalnych prvkov (z rovnosti diagonalnych prvkov dostavame tu istu rovnicu len prenasobenu konstantou -3).
z rovnosti nediagonalnych prvkov (z rovnosti diagonalnych prvkov dostavame tu istu rovnicu len prenasobenu konstantou -3).
Poriadnejšie odvodenie diferenciálnej rovnice
-
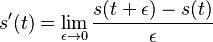 z definicie limity
z definicie limity
-
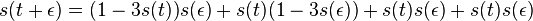 podla multiplikativnosti S(t)
podla multiplikativnosti S(t)
- po úprave
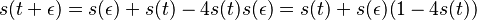
-
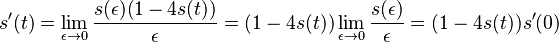
- oznacme
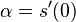 (alfa je konstanta, nezavisi od epsilon ani t)
(alfa je konstanta, nezavisi od epsilon ani t)
-
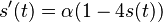 (finalna diferencialna rovnica, rovnaka ako predtym pre matice)
(finalna diferencialna rovnica, rovnaka ako predtym pre matice)
- Riesenie diferencialnej rovnice
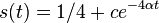 pre kazdu konstantu c
pre kazdu konstantu c
- Mozeme overit dosadenim do rovnice, pricom
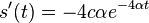
- c=-1/4 dopocitame z pociatocnej podmienky s(0)=0
- overime tiez, ze
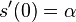
Vlastnosti riešenia
- Takže máme maticu:
- Ked
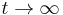 , dostávame všetky prvky matice rovné 1/4, t.j.
, dostávame všetky prvky matice rovné 1/4, t.j. 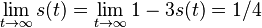 .
.
-
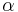 je teda pravdepodobnosť konkrétnej zmeny za jednotku času, ak uvažujeme veľmi krátke časy alebo presnejšie derivácia prvku s(t) vzhľadom na t v bode 0
je teda pravdepodobnosť konkrétnej zmeny za jednotku času, ak uvažujeme veľmi krátke časy alebo presnejšie derivácia prvku s(t) vzhľadom na t v bode 0
- Aby sme nemali naraz aj
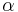 aj
aj 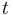 , zvykneme maticu R normalizovat tak, aby priemerný počet substitúcii za jednotku času bol 1. V prípade Jukes-Cantorovho modelu je to keď
, zvykneme maticu R normalizovat tak, aby priemerný počet substitúcii za jednotku času bol 1. V prípade Jukes-Cantorovho modelu je to keď 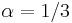 .
.
Substitučné matice, zhrnutie
- S(t): matica 4x4, kde políčko
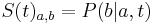 je pravdepodobnosť, že ak začneme s bázou a, tak po čase t budeme mať bázu b.
je pravdepodobnosť, že ak začneme s bázou a, tak po čase t budeme mať bázu b.
- Jukes-Cantorov model predpokladá, že táto pravdepodobnosť je rovnaká pre každé dve bázy
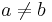
- Pre daný čas t máme teda všade mimo diagonály s(t) a na diagonále 1-3s(t)
- Matica rýchlostí R: pre Jukes-Cantorov model všade mimo diagonály
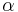 , na diagonále
, na diagonále 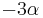
- Pre veľmi malý čas t je S(t) zhruba I-Rt
- Rýchlost alpha je teda pravdepodobnosť zmeny za jednotku casu, ak uvažujeme veľmi krátke časy, resp. derivácia s(t) vzhľadom na t v bode 0
- Riešením diferenciálnych rovníc pre Jukes-Cantorov model dostávame
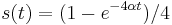
- Matica rýchlostí sa zvykne normalizovať tak, aby na jednotku času pripadla v priemere jedna substitúcia, čo dosiahneme ak
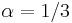
Použitie na odhad evolučnej vzdialenosti
- V case
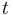 je pravdepodobnost, ze uvidime zmenenu bazu
je pravdepodobnost, ze uvidime zmenenu bazu 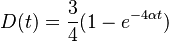
- V realnom pouziti (vypocet matice vzdialenosti pre metodu spajania susedov) mame dve zarovnane sekvencie, medzi ktorymi vidime
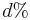 zmenenych baz, chceme odhadnut t
zmenenych baz, chceme odhadnut t
- Spatne teda zratame t, ktore by hodnote
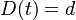 prinalezalo.
prinalezalo.
- Spatne teda zratame t, ktore by hodnote
- Dostavame teda vzorec pre vzdialenost, ktory sme videli na prednaske
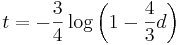
- Ak
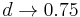 , dostavame
, dostavame 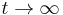
- Preco sme ten vzorec odvodili takto? V skutocnosti chceme najst najvierohodnejsiu hodnotu t, t.j. taku, pre ktore hodnota P(data|t) bude najvacsia. Zhodou okolnosti vyjde takto.
Zložitejšie modely
V praxi sa používajú komplikovanejsie substitučné modely, ktoré majú všeobecnejšiu maticu rýchlostí R
Hodnoty na diagonále matice sa dopočítavajú aby súčet každého riadku bol 0.
- Hodnota
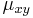 v tejto matici vyjadruje rýchlosť, akou sa určitá báza x mení na inú bázu y.
v tejto matici vyjadruje rýchlosť, akou sa určitá báza x mení na inú bázu y.
- Presnejšie
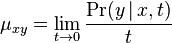 .
.
Kimurov model napr. zachytáva, ze puríny sa častejšie menia na iné puríny (A a G) a pyrimidíny na ine pyrimidíny (C a T).
- Má dva parametre: rýchlosť tranzícií alfa, transverzií beta
- HKY model (Hasegawa, Kishino & Yano) tiež umožnuje rôzne pravdepodobnosti A, C, G a T v ekvilibriu.
- Ak nastavíme čas v evolučnom modeli na nekonečno, nezáleží na tom, z ktorej bázy sme začali, frekvencia výskytu jednotlivých báz sa ustáli v tzv. ekvilibriu.
- V Jukes-Cantorovom modeli je pravdepodobnosť ľubovoľnej bázy v ekvilibriu 1/4.
- V HKY si zvolime aj frekvencie jednotlivých nukleotidov v ekvilibriu
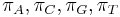 so súčtom 1
so súčtom 1
- Parameter kapa: pomer tranzícií a transverzií (alfa/beta)
- Matica rýchlostí:
-
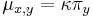 ak mutácia x->y je tranzícia,
ak mutácia x->y je tranzícia,
-
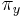 ak mutácia x->y je transverzia
ak mutácia x->y je transverzia
-
- Pre zložité modely nevieme odvodiť explicitný vzorec na výpočet S(t), ako sme mali pri Jukes-Cantorovom modeli
- Ale vo všeobecnosti pre maticu rýchlostí
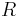 dostávame
dostávame 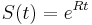 .
.
- Exponenciálna funkcia matice A sa definuje ako
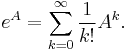
- Ak maticu rychlosti R diagonalizujeme (určite sa dá pre symetrické R)
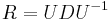 , kde D je diagonálna matica (na jej diagonále budu vlastné hodnoty R), tak
, kde D je diagonálna matica (na jej diagonále budu vlastné hodnoty R), tak 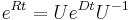 , t.j. exponenciálnu funkciu uplatníme iba na prvky na uhlopriečke matice D.
, t.j. exponenciálnu funkciu uplatníme iba na prvky na uhlopriečke matice D.
- Exponenciálna funkcia matice A sa definuje ako
CB07
Praktická ukážka tvorby stromov
Viacnásobné zarovania z UCSC browsera
- V UCSC browseri mozeme ziskavat viacnasobne zarovnania jednotlivych genov (nukleotidy alebo proteiny). Nasledujuci postup nemusite robit, subor si stiahnite tu: http://compbio.fmph.uniba.sk/vyuka/mbi-data/cb06/cb06-aln.fa
- UCSC browseri si pozrieme usek ludskeho genomu (verzia hg38) chr6:135,851,998-136,191,840 s genom PDE7B (phosphodiesterase 7B) [15]
- Na modrej liste zvolime Tools, Table browser. V nastaveniach tabuliek Group: Genes and Gene Predictions, Track: GENCODE v 32., zaklikneme Region: position, a Output fomat: CDS FASTA alignment a stlacime Get output
- Na dalsej obrazovke zaklikneme show nucleotides, zvolime MAF table multiz100way a vyberieme si, ktore organizmy chceme. V nasom pripade z primatov zvolime chimp, rhesus, bushbaby, z inych cicavcov mouse, rat, rabbit, pig, cow, dog, elephant a z dalsich organizmov opposum, platypus, chicken, stlacime Get output.
- Vystup ulozime do suboru, nechame si iba prvu formu genu (ENST00000308191.11_hg38), z mien sekvencii zmazeme spolocny zaciatok (ENST00000308191.11_hg38), pripadne celkovo prepiseme mena na anglicke nazvy
Strom metódou spájania susedov
- Skusme zostavit strom na stranke http://www.ebi.ac.uk/Tools/phylogeny/clustalw2_phylogeny/
- Distance correction: ako na prednáške, z počtu pozorovaných mutácií na evolučný čas
- Exclude gaps: vynechať všetky stĺpce s pomlčkami
- Clustering method: UPGMA predpokladá molekulárne hodiny, spájanie susedov nie
- P.I.M. vypíš aj maticu vzdialeností (% identity, pred korekciou)
- Vo vyslednom strome by sme mali zmenit zakorenenie, aby sme mali sliepku (chicken) ako outgroup
- Výsledky z programu http://www.phylogeny.fr/alacarte.cgi , ktorý podporuje aj bootstrap:
- Vysledok s povodnym zakorenenim
- Vysledok so spravnym zakorenenim (chicken = outgroup)
- "Spravny strom" [16] v nastaveniach Conservation track-u v UCSC browseri (podla clanku Murphy WJ et al Resolution of the early placental mammal radiation using Bayesian phylogenetics. Science 2001 [17])
- Nas strom ma dost zlych hran: zle postavenie hlodavcov, ale aj slona a psa. Zle postavenie hlodavcov môže byť spôsobené long branch attraction.
- Ak chcete skusit zostavit aj zarovnania, treba zacat z nezarovnanych sekvencii: [18]
Stromy na Galaxy
Webstránka s veľa nástrojmi https://usegalaxy.eu/
- na tvorbu stromov sa dá použiť IQ-TREE
- modely vid tu: https://github.com/Cibiv/IQ-TREE/wiki/Substitution-Models
- vysledok CB:phylo
- viewer napr. http://phylotree.hyphy.org/
Pre dalsie pokusy: nezarovnane sekvencie proteinov z roznych organizmov:
- Sekvencie
- Nájdené pomocou BLAST v Uniprote ako homology proteínu YCF1 z S. cerevisiae uniprot
- Zarovnáme na Galaxy pomocou muscle, strom spravíme cez rapidnj alebo IQ-tree
- Zobrazíme kliknutím na ikonku visualize alebo cez phylotree viewer
Gény, evolúcia a komparatívna genomika v UCSC genome browseri (cvičenie pri počítači)
- Zobrazme si gén CLCA4 [19]
- Zapnite si štandardnú sadu track-ov (Tlačidlo Configure pod obrázkom, potom tlačidlo Default v druhej sekcii stránky)
- Po kliknutí na gén si môžete prečítať o jeho funkcii, po kliknutí na ľavú lištu alebo na názov tracku v zozname na spodku stránky si môžete prečítať viac o tracku a meniť nastavenia
- V tracku RefSeq genes si všimnite, že v tejto databáze má tento gén dve formy zostrihu, jedna z nich sa považuje za nekódujúcu, pretína sa aj s necharakterizovanou nekódujúcou RNA na opačnom vlákne
- Track RefSeq a jeho subtrack RefSeq Curated treba zapnut na pack
- Nižšie vidíte track H3K27Ac Mark (Often Found Near Regulatory Elements) on 7 cell lines from ENCODE. Kde bola táto histónová modifikácia v okolí génu detegovaná?
- Všimnite si aj track ENCODE Candidate Cis-Regulatory Elements. Všimnite si jeho súvis s H3K27Ac trackom. Čo znamenajú farby v tomto tracku?
- Vsimnime si track Vertebrate Multiz Alignment & Conservation (100 Species)
- v spodnej casti tracku vidime zarovnania s roznymi inymi genomami
- v nastaveniach tracku zapnite Element Conservation (phastCons) na full a Conserved Elements na dense
- v tomto tracku vidíme PhyloP, co zobrazuje uroven konzerovanosti danej bazy len na zaklade jedneho stlpca zarovnania a dva vysledky z phyloHMM phastCons, ktory berie do uvahy aj okolite stlpce
- Konkretne cast Conserved elements zobrazuje konkretne useky, ktore su najvac konzervovane
- Ak chceme zistit, kolko percent genomu tieto useky pokryvaju, ideme na modrej liste do casti Tools->Table browser, zvolime group Comparative genomics, track Conservation, table 100 Vert. El, region zvolime genome (v celom genome) a stlacime tlacidlo Summary/statistics, dostaneme nieco taketo:
| item count | 10,350,729 |
| item bases | 162,179,256 (5.32%) |
| item total | 162,179,256 (5.32%) |
| smallest item | 1 |
| average item | 16 |
| biggest item | 3,732 |
| smallest score | 186 |
| average score | 333 |
| biggest score | 1,000 |
- Ak by nas zaujimali iba velmi dlhe "conserved elements", v Table browser stlacime tlacidlo Filter a na dalsej obrazovke do policka Free-form query dame chromEnd-chromStart>=1500
- Potom mozeme skusit Summary/Statistics alebo vystup typu Hyperlinks to genome browser a Get output - dostaneme zoznam tychto elementov a kazdy si mozeme jednym klikom pozriet v browseri, napr. taketo
- Pozrime si teraz ten isty gen CLCA4 v starsej verzii genomu hg18 [20]
- V casti Genes and Gene Prediction Tracks zapnite track Pos Sel Genes, ktory obsahuje geny s pozitivnym vyberom (cervenou, pripadne slabsie fialovou a modrou)
- Ked kliknete na cerveny obdlznik pre tento gen, uvidite, v ktorych castiach fylogenetickeho stromu bol detegovany pozitivny vyber
- Po priblizeni do jedneho z exonov [21] vidite dosledky nesynonymnych mutacii
Poznamka: Existuju aj webservery na predikciu pozitivneho vyberu, napriklad tieto dva (v sucasnosti asi nefunguju):
- Selecton, clanok
- Data monkey clanok
- Skusili sme na Selecton poslat CLCA4 zo 7 cicavcov, subor tu: [22]
- Nastroj HyPhy
- vyber metody [25]
- niektore HyPhy nastroje sa nachadzaju v Galaxy
Objavenie génu HAR1 pomocou komparatívnej genomiky
- Pollard KS, Salama SR, Lambert N, et al. (September 2006). "An RNA gene expressed during cortical development evolved rapidly in humans". Nature 443 (7108): 167–72. doi:10.1038/nature05113. PMID 16915236. pdf
- Zobrali všetky regióny dĺžky aspoň 100bp s > 96% podobnosťou medzi šimpanzom a myšou/potkanom (35,000)
- Porovnali s ostatnými cicavcami, zistili, ktoré majú veľa mutáci v človeku, ale málo inde (pravdepodobnostný model)
- 49 štatisticky významných regiónov, 96% nekódujúcich oblastiach
- Najvýznamnejší HAR1: 118nt, 18 substitúcii u človeka, očakávali by sme 0.27. Iba 2 zmeny medzi šimpanzom a sliepkou (310 miliónov rokov), ale nebol nájdený v rybách a žabe.
- Nezdá sa byť polymorfný u človeka
- Prekrývajúce sa RNA gény HAR1A a HAR1B
- HAR1A je exprimovaný v neokortexe u 7 a 9 týždenných embrií, neskôr aj v iných častiach mozgu (u človeka aj iných primátov)
- Všetky substitúcie v človeku A/T->C/G, stabilnejšia RNA štruktúra (ale tiež sú blízko k telomére, kde je viacej takýchto mutácii kvôli rekombinácii a biased gene conversion)
Cvičenie pri počítači
- Môžete si pozrieť tento region v browseri: chr20:63102114-63102274 (hg38), pricom ak sa este priblizite, uvidite zarovnanie aj s bazami a mozete vidiet, ze vela zmien je specifickych pre cloveka
CB10
PSI BLAST a Pfam
- Budeme uvažovať tri vzdialene podobné enzýmy
- Bis(5'-adenosyl)-triphosphatase (FHIT) u človeka, accession P49789 (Uniprot)
- Adenosine 5'-monophosphoramidase HNT1 u kvasinky Saccharomyces cerevisiae, (Uniprot)
- Galactose-1-phosphate uridylyltransferase u baktérie Haemophilus influenzae (GAL-1-P) (Uniprot)
- FHIT a HNT1 majú doménu HIT (Pfam).
- GAL-1-P má domény GalP_UDP_tr_C a GalP_UDP_transf. Tieto domény patria v databáze Pfam do toho istého klanu ako HIT.
- Pozrime si doménu HIT na stránke databázy Interpro [26], hlavne časť Signature
- Skúsme nájsť podobnosť medzi týmito proteínmi v BLASTe: https://blast.ncbi.nlm.nih.gov/ v časti proteíny, zvoľme databázu Swissprot, ako Query zadajme Accession proteínu FHIT P49789, spustime program PSI-BLAST, E-value zvýšená na 0.1.
- V prvom kole PSI-BLAST spúšťa bežný BLASTP
- Vidíte medzi výsledkami HNT1 a GAL-1-P? S akou E-hodnotou?
- Spustíme teraz druhú iteráciu PSI-BLAST, ktorá zostaví profil z proteínov s nízkou E-hodnotou v prvej iterácii
- Ako sa zmenili výsledky pre HNT1 a GAL-1-P?
Budeme robiť na neskoršom cvičení
RNA štruktúra
- Znama databaza rodin RNA genov je Rfam: http://rfam.xfam.org/
- Najdite si v nej rodinu RF00015 (U4 spliceosomal RNA)
- V casti Secondary structure si mozete pozriet obrazky farebne kodovane podla roznych kriterii
- Skuste pochopit, co jednotlive obrazky a ich farby znamenaju
- Jedna z mnohych ludskych kopii je tato:
AGCTTTGCGCAGTGGCAGTATCGTAGCCAATGAGGTTTATCCGAGGCGCG ATTATTGCTAATTGAAAACTTTTCCCAATACCCCGCCATGACGACTTGAA ATATAGTCGGCATTGGCAATTTTTGACAGTCTCTACGGAGA
- Skuste ju najst v ludskom genome nastrojom BLAT v UCSC genome browseri
- Pozrite si tracky GENCODE genes, conservation, RepeatMasker v jej okoli
- Vo verzii hg19 (kam sa viete z inej verzii dostat cez horne menu View->In Other Genomes) je track "CSHL Sm RNA-seq" ktory obsahuje RNASeq kratkych RNA z roznych casti buniek, zapnite si v jeho nastaveniach aj zobrazenie RNA z jadra (nucleus)
- Zadajte sekvenciu na RNAfold serveri [27]
- Ak vypocet dlho trva, pozrite si vysledok tu
- Podoba sa na strukturu zobrazenu v Rfame? v com sa lisi?
- RNA dizajn: mozete sa skusit zahrat na stranke http://www.eternagame.org/web/
Objavenie génu HAR1 pomocou komparatívnej genomiky
- Pollard KS, Salama SR, Lambert N, et al. (September 2006). "An RNA gene expressed during cortical development evolved rapidly in humans". Nature 443 (7108): 167–72. doi:10.1038/nature05113. PMID 16915236. pdf
- Zobrali všetky regióny dĺžky aspoň 100bp s > 96% podobnosťou medzi šimpanzom a myšou/potkanom (35,000)
- Porovnali s ostatnými cicavcami, zistili, ktoré majú veľa mutáci v človeku, ale málo inde (pravdepodobnostný model)
- 49 štatisticky významných regiónov, 96% nekódujúcich oblastiach
- Najvýznamnejší HAR1: 118nt, 18 substitúcii u človeka, očakávali by sme 0.27. Iba 2 zmeny medzi šimpanzom a sliepkou (310 miliónov rokov), ale nebol nájdený v rybách a žabe.
- Nezdá sa byť polymorfný u človeka
- Prekrývajúce sa RNA gény HAR1A a HAR1B
- HAR1A je exprimovaný v neokortexe u 7 a 9 týždenných embrií, neskôr aj v iných častiach mozgu (u človeka aj iných primátov)
- Všetky substitúcie v človeku A/T->C/G, stabilnejšia RNA štruktúra (ale tiež sú blízko k telomére, kde je viacej takýchto mutácii kvôli rekombinácii a biased gene conversion)
Cvičenie pri počítači
- Môžete si pozrieť tento region v browseri: chr20:63102114-63102274 (hg38), pricom ak sa este priblizite, uvidite zarovnanie aj s bazami a mozete vidiet, ze vela zmien je specifickych pre cloveka
Expresia génov
NCBI Gene Expression Omnibus http://www.ncbi.nlm.nih.gov/geo/
- Databaza gene expression dat na NCBI
- Do Search okienka zadajme GDS2925
- Mali by sme dostat dataset Various weak organic acids effect on anaerobic yeast chemostat cultures
- Mozeme si pozriet zakladne udaje, napr. citation, platform
- Link "Expression profiles" nam zobrazi grafy pre rozne geny
- Pri kazdom profile mozeme kliknut na profile neighbors, aby sme videli geny s podobnym profilom
- Data analysis tools, cast Cluster heatmaps, K-means, skuste rozne pocty clustrov
Sekvenčné motívy, program MEME
- Vazobne miesta transkripcnych faktorov sa casto reprezentuju ako sekvencne motivy
- Ak mame skupinu sekvencii, mozeme hladat motiv, ktory maju spolocny
- Znamy program na tento problem je MEME
- Chodte na stranku http://meme-suite.org/
- Zvolte nastroj MEME a v casti Input the primary sequences zvolte Type in sequences a zadajte tieto sekvencie
- Pozrite si ostatne nastavenia. Co asi robia?
- Ak server pocita dlho, mozete si pozriet vysledky tu
Nussinovovej algoritmus (nerobili sme)
Z cvičných príkladov na skúšku
- Vyplňte maticu dynamického programovania (Nussinovovej algoritmus) pre nájdenie najväčšieho počtu dobre uzátvorkovaných spárovaných báz v RNA sekvencii GAACUUCACUGA (dovoľujeme len komplementárne páry A-U, C-G) a nakreslite sekundárnu štruktúru, ktorú algoritmus našiel.
G A A C U U C A C U G A
0 0 0 1 1 2 3 3 3 4 4 4 G
0 0 0 1 2 2 2 2 3 4 4 A
0 0 1 1 1 2 2 2 3 4 A
0 0 0 0 1 1 1 2 3 C
0 0 0 1 1 1 2 3 U
0 0 1 1 1 2 3 U
0 0 0 1 2 2 C
0 0 1 1 1 A
0 0 1 1 C
0 0 1 U
0 0 G
0 A
- Ako by sme algoritmus upravili, aby dlzka slucky na konci helixu bola vzdy aspon 3?
CB11
Ukážka práce v Linuxe
Prvá časť - príprava
- Prihláste sa na server podľa pokynov.
- Potom spúšťajte jednotlivé príkazy podľa pokynov nižšie.
- Odporúčame príkazy kopírovať myšou (v internetovom prehliadači vysvietiť, stlačiť Ctrl-C, v konzole Ctrl-Shift-V)
# riadky začínajúce mrežou # sú komentáre, netreba ich spúšťať # Dôležité: v príkazoch nižšie xx nahraďte vašimi iniciálkami, napr. bb mkdir xx cd xx # príkaz mkdir (make directory) vytvoril priečinok # príkaz cd (change directory) zmenil váš aktuálny priečinok na tento nový # v konzole by ste mali mať user@server:~/xx$ # kde xx je číslo vašej skupiny, napr. 01 # stiahneme si súbor s dátami zo stránky wget http://compbio.fmph.uniba.sk/vyuka/mbi-data/cb12.zip # rozzipujeme ho unzip cb12.zip
Druhá časť - skladanie genómov, mapovanie čítaní, zarovnanie
# prejdeme na priečinok s prvou časťou ohľadom sekvenovania cd 1-seq # ls vypíše zoznam súborov v priečinku ls # ls -l vypíše dlhšiu informáciu (long) ls -l # ls -lSh usporiada súbory podľa veľkosti (Size) a veľkosti vypíše priateľskejšie pre ľudí (human) ls -lSh # mali by sme vidieť kúsok sekvencie z E.coli (prípona .fasta) # a 2 súbory zo sekvenovania prístrojom Illumina Miseq (prípona .fastaq.gz) # tieto súbory obsahujú čítania z vyššie uvedeného kúsku genómu # ideme skladať genóm, bude to trvať dlho, preto to chceme spustiť na pozadí # aby sme mohli medzitým robiť niečo iné screen # stlačte Enter # spustite skladanie programom spades spades.py -t 1 -m 1 --pe1-1 miseq_R1.fastq.gz --pe1-2 miseq_R2.fastq.gz -o spades > spades.log # stlačte naraz Ctrl-a potom d # spades teraz beží na pozadí # príkaz top zobrazí bežiace procesy # ukončíte ho stlačením q (quit) top # príkaz less umožňuje prezerať si obsah textového súboru # aj príkaz less ukončíte stlačením q, šípkami sa pohybujete po súbore less ref.fasta # čítania sú komprimované, preto namiesto less použijeme zless zless miseq_R1.fastq.gz # tieto príkazy spočítajú počet riadkov - ako z toho zistíme počet čítaní? zcat miseq_R1.fastq.gz | wc -l zcat miseq_R2.fastq.gz | wc -l # keď spades skončí, vrátime sa do screen a ukončíme ho screen -r # exit ukončí screen exit # spades dal výstup do podpriečinku spades, pozrime si ho ls spades # skopírujeme si hlavný výsledok do nášho priečinka (cp = copy) cp -ip spades/contigs.fasta spades.fasta less spades.fasta # pozrime si hlavičky jednotlivých sekvencií vo fasta súbore grep '>' spades.fasta # programom last si spravíme dotplot referencia vs. naše skladanie # 1) vytvorenie indexu pre referenciu lastdb ref.fasta ref.fasta # 2) samotné zarovnanie lastal -f TAB ref.fasta spades.fasta > aln.tab # 3) vytvorenie obrázku s dotplotom last-dotplot aln.tab aln.png # a ešte dotplot referencia vs. referencia # 2) samotné zarovnanie (index už máme) lastal -f TAB ref.fasta ref.fasta > aln2.tab # 3) vytvorenie obrázku s dotplotom last-dotplot aln2.tab aln2.png # pozrieme si dotploty programom eog eog aln.png & eog aln2.png & # zarovnajme čítania k referenčnému genómu v 4 krokoch # 1) indexovanie fasta súboru bwa index ref.fasta # 2) samotné zarovnávanie čítaní programom bwa bwa mem ref.fasta miseq_R1.fastq.gz miseq_R2.fastq.gz > ref-miseq.sam # 3) zmeníme textový sam formát na binárny bam formát samtools view -S -b ref-miseq.sam | samtools sort - -o ref-miseq.bam # 4) vytvoríme index bam súboru samtools index ref-miseq.bam # pozrime sa na zoznam súborov od najnovšieho po najstarší ls -lth # sam súbor so zarovnaniami sa dá pozrieť, ale nie je veľmi prehľadný less ref-miseq.sam # vytvoríme aj zarovnanie nášho poskladaného genómu k referencii vo formáte bam samtools faidx ref.fasta lastal ref.fasta spades.fasta -E1e-20 | maf-convert sam > ref-spades.sam samtools view -S -b -t ref.fasta.fai ref-spades.sam | samtools sort - -o ref-spades.bam samtools index ref-spades.bam # výsledky si zobrazíme v grafickom prehliadači igv # obdoba genome browsera, ktorú si môžete nainštalovať na vašom počítači # POZOR: POTREBUJE VEĽA PAMÄTE, SPUSTÍME IBA JEDEN NARAZ igv -g ref.fasta # pomocou Menu->File->Load from File otvorte ref-spades.bam a ref-miseq.bam # pozrime si región ecoli-frag:224,000-244,000 # Vidíte jednotlivé kontigy? Sedí tento pohľad s dotplotom? # a potom bližšie ecoli-frag:227,300-227,600 # Všimnite si sekvenačné chyby rozdiely medzi referenciou a kontigmi
Tretia časť - hľadanie génov, RNA-seq
# v druhom cvičení si vyskúšame hľadanie génov # najskôr sa presuňme do druhého priečinku cd ../2-genes # pozrime si, aké máme súbory ls -lSh # mali by sme mať kúsok referenčného genómu huby Aspergillus nidulans # fastq súbor s čítaniami z RNA-seq pre tento kúsok referencie # gff súbor s anotáciou génov z databázy # spustíme hľadač génov Augustus 2x: # raz s parametrami priamo pre A.nidulans a raz s parametrami pre ľudský genóm augustus --species=anidulans ref2.fasta > augustus-anidulans.gtf augustus --species=human ref2.fasta > augustus-human.gtf # RNA-seq zarovnáme k sekvencii nástrojom tophat2 (podporuje intróny) bowtie2-build ref2.fasta ref2.fasta tophat2 -i 10 -I 10000 --max-multihits 1 --output-dir rnaseq ref2.fasta rnaseq.fastq samtools sort rnaseq/accepted_hits.bam rnaseq samtools index rnaseq.bam # predikcie génov a RNA-seq si pozrieme v igv igv -g ref2.fasta # v igv si otvorte annot.gff, augustus-anidulans.gtf, augustus-human.gtf, rnaseq.bam # - ktoré parametre Augustusu dali presnejšie predpovede (za predpokladu, že anotácia je správna) # - pozrite si zblízka niektorý gén s vysokou expresiou (napr. druhy gen sprava), # mali by ste vidieť čítania podporujúce intróny
CI10
Úvod do bioinformatických databáz a on-line nástrojov
NCBI, Genbank, Pubmed, blast
- National Center for Biotechnology Information http://www.ncbi.nlm.nih.gov/
- Zhromazduje verejne pristupne data z molekularnej biologie
- Mozeme hladat klucove slova v roznych databazach
- Pubmed: databaza clankov, napr. najdime phastcons
- Gene: najdime DNA polymerase
- BLAST: najdime nasledujucu sekvenciu v genome kurata (zvoľme nucleotide blast, database others a z menu reference genomic sequence, organism chicken (taxid:9031), program blastn)
- Ide o osekvenovany kusok ludskej mRNA, kde v kuracom genome sme nasli homolog, ake ma dlzku, skore, E-value, % zhodnych baz?
AACCATGGGTATATACGACTCACTATAGGGGGATATCAGCTGGGATGGCAAATAATGATTTTATTTTGAC TGATAGTGACCTGTTCGTTGCAACAAATTGATAAGCAATGCTTTCTTATAATGCCAACTTTGTACAAGAA AGTTGGGCAGGTGTGTTTTTTGTCCTTCAGGTAGCCGAAGAGCATCTCCAGGCCCCCCTCCACCAGCTCC GGCAGAGGCTTGGATAAAGGGTTGTGGGAAATGTGGAGCCCTTTGTCCATGGGATTCCAGGCGATCCTCA CCAGTCTACACAGCAGGTGGAGTTCGCTCGGGAGGGTCTGGATGTCATTGTTGTTGAGGTTCAGCAGCTC CAGGCTGGTGACCAGGCAAAGCGACCTCGGGAAGGAGTGGATGTTGTTGCCCTCTGCGATGAAGATCTGC AGGCTGGCCAGGTGCTGGATGCTCTCAGCGATGTTTTCCAGGCGATTCGAGCCCACGTGCAAGAAAATCA GTTCCTTCAGGGAGAACACACACATGGGGATGTGCGCGAAGAAGTTGTTGCTGAGGTTTAGCTTCCTCAG TCTAGAGAGGTCGGCGAAGCATGCAGGGAGCTGGGACAGGCAGTTGTGCGACAAGCTCAGGACCTCCAGC TTTCGGCACAAGCTCAGCTCGGCCGGCACCTCTGTCAGGCAGTTCATGTTGACAAACAGGACCTTGAGGC ACTGTAGGAGGCTCACTTCTCTGGGCAGGCTCTTCAGGCGGTTCCCGCACAAGTTCAGGACCACGATCCG GGTCAGTTTCCCCACCTCGGGGAGGGAGAACCCCGGAGCTGGTTGTGAGACAAATTGAGTTTCTGGACCC CCGAAAAGCCCCCACAAAAAGCCG
Uniprot
- Prehladnejsi pohlad na proteiny, vela linkov na ine databazy, cast vytvarana rucne
- Pozrieme sa na známy koronavírusový proteín Spike
- Nájdime ho na stránke http://www.uniprot.org/ pod názvom SPIKE_SARS2
- Pozrime si podrobne jeho stránku, ktoré časti boli predpovedané bioinformatickými metódami z prednášky?
- Všimnime si niektorú Pfam doménu a pozrime si jej stránku
UCSC genome browser
- http://genome-euro.ucsc.edu/
- On-line grafický nástroj na prezeranie genómov
- Konfigurovateľný, veľa možností, prijemne pouzivatelske rozhranie
- Moznost stiahnut data vhodne na dalsie spracovanie alebo zobrazit vlastne data
- Pomerne málo organizmov
- doraz hlavne na ludsky genom
Základy
- Adresa http://genome-euro.ucsc.edu/
- Hore v modrom menu zvoľte Genomes, potom zvoľte ľudský genóm. Do okienka search term zadajte HOXA2. Vo výsledkoch hľadania (UCSC genes) zvoľte gén homeobox A2 na chromozóme 7.
- Pozrime si spolu túto stránku
- V hornej časti sú ovládacie prvky na pohyb vľavo, vpravo, približovanie, vzďaľovanie
- Pod tým schéma chromozómu, červeným vyznačená zobrazená oblasť
- Pod tým obrázok vybranej oblasti, rôzne tracky
- Pod tým zoznam všetkých trackov, dajú sa zapínať, vypínať a konfigurovať
- Po kliknutí na obrázok sa často zobrazí ďalšia informácia o danom géne alebo inom zdroji dát
- V génoch exony hrubé, UTR tenšie, intróny vodorovné čiary
- Po kliknutí na gén alebo inú časť nejakého tracku väčšinou o ňom dostaneme viac informácií. Kliknutim na listu ku tracku (lavy okraj obazku) sa dozviete viac o tracku a mozete nastavovat parametre zobrazenia
Sekvenovanie
- Hore v modrom menu zvoľte Genomes
- Na ďalšej stránke zvoľte človeka a v menu Assembly zistite, kedy boli pridané posledné dve verzie ľudského genómu (hg19 a hg38)
- Na tej istej stránke dole nájdete stručný popis zvolenej verzie genómu. Pre ktoré oblasti genómu máme v hg38 najviac alternatívnych verzií?
- Zadajte región chr21:31,250,000-31,300,000 v hg19 [28]
- Zapnite si tracky Mapability a RepeatMasker na "full"
- Mapability: nakoľko sa daný úsek opakuje v genóme a či teda vieme jednoznačne jeho ready namapovať pri použití Next generation sequencing
- Ako a prečo sa pri rôznych dĺžkach readov líšia? (Keď kliknete na linku "Mapability", môžete si prečítať bližšie detaily.)
- Približne v strede zobrazeného regiónu je pokles mapovateľnosti. Akému typu opakovania zodpovedá? (pozrite track RepeatMasker)
- Zapnite si tracky "Assembly" a "Gaps" a pozrite si región chr2:110,000,000-110,300,000 v hg19. [29] Aká dlhá je neosekvenovaná medzera (gap) v strede tohto regiónu? Približnú veľkosť môžete odčítať z obrázku, presnejší údaj zistíte kliknutím na čierny obdĺžnik zodpovedajúci tejto medzere (úplne presná dĺžka aj tak nebola známa, nakoľko nebola osekvenovaná).
- Cez menu položku View, In other genomes si pozrite, ako zobrazený úsek vyzerá vo verzii hg38. Ako sa zmenila dĺžka z pôvodných 300kb?
- Prejdite na genóm Rhesus, verzia rheMac2, región chr7:59,022,000-59,024,000 [30], zapnite si tracky Contigs, Gaps, Quality scores
- Aké typy problémov v kvalite sekvencie v tomto regióne vidíte?
Komparativna genomika
- V casti multiz alignments vidite zarovnania k roznym inym genomom (da sa zapinat, ze ku ktorym). Mozete si pozriet, ako sa uroven zarovnania zmeni ked sa priblizujeme a vzdalujeme (zoom in/zoom out).
- Ked sa priblizite na uroven "base", t.j. zobrazenych cca 100bp, v obdlzniku multiz alignment uvidite zarovnanie s homologickym usekom v inych genomoch.
- V casti conservation by PhyloP vidime graf toho, ako silne su zachovane jednotlive stlpce zarovnania
- Da sa zapnut track Placental Chain/Net a pozriet sa na ktorych chromozomoch je ortologicky usek v inych genomoch
Blat
- Choďte na UCSC genome browser (http//genome.ucsc.edu/), na modrej lište zvoľte BLAT, zadajte DNA sekvenciu vyssie a hľadajte ju v ľudskom genóme. Akú podobnosť (IDENTITY) má najsilnejší nájdený výskyt? Aký dlhý úsek genómu zasahuje? (SPAN). Všimnite si, že ostatné výskyty sú oveľa kratšie.
- V stĺpci ACTIONS si pomocou Details môžete pozrieť detaily zarovnania a pomocou Browser si pozrieť príslušný úsek genómu.
- V tomto úseku genómu si zapnite track Vertebrate net na full a kliknutím na farebnú čiaru na obrázku pre tento track zistite, na ktorom chromozóme kuraťa sa vyskytuje homologický úsek.
- Skusme tu istu sekvenciu namapovat do genomu sliepky: stlacte najprv na hornej modrej liste Genomes, zvolte Vertebrates a Chicken a potom na hornej liste BLAT. Do okienka zadajte tu istu sekvenciu. Akú podobnosť a dĺžku má najsilnejší nájdený výskyt teraz? Na ktorom je chromozóme?
- Ako sa to porovna s hodnotami, ktore sme dostali pomocou BLASTu na NCBI?
Práca s tabuľkami, sťahovanie anotácií
- Položka Tables na hornej lište umožnuje robiť rafinované veci s tabuľkami, ktoré obsahujú súradnice génov a pod.
- Základná vec: vyexportovať napr. všetky gény v zobrazenom výseku v niektorom formáte:
- sequence: fasta súbor proteínov, génov alebo mRNA s rôznymi nastaveniami
- GTF: súradnice
- Hyperlinks to genome browser: klikacia stránka
- Namiesto exportu si môžeme pozrieť rôzne štatistiky
- Zložitejšie: prienik dvoch tabuliek, napr. gény, ktoré sú viac než 50% pokryté simple repeats
- V intersection zvolíme group: Variation and repeats, track: RepeatMasker, nastavíme records that have at least 50% overlap with RepeatMasker
- V summary/statistics zistíme, kolko ich je v genóme, môžeme si ich preklikať cez Hyperlinks to genome browser
- Filter na tabuľku, napr. gény, ktoré majú v názve ribosomal (postup pre drozofilu):
- V casti hg19.kgXref based filters políčko description dáme *ribosomal*
Úvod do bezkontextových gramatík
- Na modelovanie štruktúry RNA sa používajú stochastické bezkontextové gramatiky (bude na ďalšej prednáške)
- Tie sú založené na bezkontextových gramatikách, ktoré mnohí poznáte z bakalárskeho štúdia
Gramatika
- Príklad: S->aSb, S->epsilon (píšeme aj skrátene S->aSb|epsilon)
- Dva typy symbolov: terminály (malé písmená), neterminály (veľké písmená)
- Pravidlá prepisujúce neterminál na reťazec terminálov a neterminálov (môže byť aj prázdny reťazec, ktorý označujeme epsilon)
- Neterminál S je "štartovací"
Použitie gramatiky na generovanie reťazcov
- Začneme so štartovacím neterminálom S
- V každom kroku prepíšeme najľavejší neterminál podľa niektorého pravidla
- Skončíme, keď nezostanú žiadne neterminály
- Príklad: S->aSb->aaSbb->aaaSbbb->epsilon
- Aké všetky slová vie táto gramatika generovať?
- V tvare aa...abb...b s rovnakým počtom á-čok a b-čiek (informatici píšu
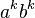 )
)
- V tvare aa...abb...b s rovnakým počtom á-čok a b-čiek (informatici píšu
Cvičenia
- Zostavte gramatiku na slova typu aa..abb..b kde acok je rovnako alebo viac ako bcok,
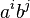 pre
pre 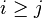
- S->aSb|aS|epsilon
- Zostavte gramatiku pre slova toho isteho typu, kde acok je viac ako bcok, t.j. i>j
- S->aSb|aT T->aT|epsilon (alebo S->aSb|aS|a)
- Zostavte gramatiku pre dobre uzatvorkovane vyrazy zo zatvoriek (,),[,]. Napr. [()()([])] je dobre uzatvorkovany, ale [(]) nie je.
- S->SS|(S)|[S]|epsilon
- priklad odvedenia v tejto gramatike: S->[S]->[SS]->[SSS]->[(S)SS]->[()SS]->[()(S)S]->[()()S]->[()()(S)]->[()()([S])]->[()()([])]
Parsovanie retazca pomocou gramatiky: urcit, ako mohol byt retazec vygenerovany pomocou pravidiel
- Gramatika pre dobre uzatvrokovane vyrazy nam pomoze urcit, ktora zatvorka patri ku ktorej: tie, ktore boli vygenerovane v jednom kroku
Dalsie cvicenia
- Zostavte gramatiku na DNA palindromy, t.j. sekvencie, ktore zozadu po skomplementovani baz daju to iste, ako napr. GATC
- S->gSc|cSg|aSt|tSa|epsilon
- Vlasenky RNA s lubovolne dlhou sparovanou castou a 3 nesparovanymi nukleotidmi v strede
- S->gSc|cSg|aSu|uSa|aaa|aac|aag|aau|...|uuu
- Tazsi priklad: Zostavte gramatiku na slova s rovnakym poctom acok a bcok v lubovolnom poradi
- S->epsilon|aSbS|bSaS
- ako bude generovat aababbba?
- preco vie vygenerovat vsetky take retazce?
CB09
Bezkontextové gramatiky
- Na modelovanie štruktúry RNA sa používajú stochastické bezkontextové gramatiky (bude na ďalšej prednáške)
- My si teraz ukážeme bezkontextové gramatiky, ktoré nemajú pravdepodobnosti
- Zaviedol Noam Chomsky v lingvistike 50-te roky 20. storočia, tiež dôležité v informatike
Gramatika
- Príklad: S->aSb, S->epsilon (píšeme aj skrátene S->aSb|epsilon)
- Dva typy symbolov: terminály (malé písmená), neterminály (veľké písmená)
- Pravidlá prepisujúce neterminál na reťazec terminálov a neterminálov (môže byť aj prázdny reťazec, ktorý označujeme epsilon)
- Neterminál S je "štartovací"
Použitie gramatiky na generovanie reťazcov
- Začneme so štartovacím neterminálom S
- V každom kroku prepíšeme najľavejší neterminál podľa niektorého pravidla
- Skončíme, keď nezostanú žiadne neterminály
- Príklad: S->aSb->aaSbb->aaaSbbb->epsilon
- Aké všetky slová vie táto gramatika generovať?
- V tvare aa...abb...b s rovnakým počtom á-čok a b-čiek (informatici píšu
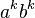 )
)
- V tvare aa...abb...b s rovnakým počtom á-čok a b-čiek (informatici píšu
Cvičenia
- Zostavte gramatiku na slová typu aa..abb..b kde á-čok je rovnako alebo viac ako b-čok,
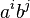 pre
pre 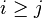
- S->aSb|aS|epsilon
- Zostavte gramatiku pre slová toho istého typu, kde á-čok je viac ako b-čok, t.j. i>j
- S->aSb|aT T->aT|epsilon (alebo S->aSb|aS|a)
- Zostavte gramatiku pre dobre uzátvorkované výrazy zo zátvoriek (,),[,]. Napr. [()()([])] je dobre uzátvorkovaný, ale [(]) nie je.
- S->SS|(S)|[S]|epsilon
- príklad odvodenia v tejto gramatike: S->[S]->[SS]->[SSS]->[(S)SS]->[()SS]->[()(S)S]->[()()S]->[()()(S)]->[()()([S])]->[()()([])]
Parsovanie reťazca pomocou gramatiky: určiť, ako mohol byt reťazec vygenerovaný pomocou pravidiel
- Gramatika pre dobre uzátvorkované výrazy nám pomôže určiť, ktorá zátvorka patrí ku ktorej: tie, ktoré boli vygenerované v jednom kroku
Ďalšie cvičenia
- Zostavte gramatiku na DNA palindromy, t.j. sekvencie, ktore zozadu po skomplementovani baz daju to iste, ako napr. GATC
- S->gSc|cSg|aSt|tSa|epsilon
- Vlasenky RNA s lubovolne dlhou sparovanou castou a 3 nesparovanymi nukleotidmi v strede
- S->gSc|cSg|aSu|uSa|aaa|aac|aag|aau|...|uuu
- Tazsi priklad: Zostavte gramatiku na slova s rovnakym poctom acok a bcok v lubovolnom poradi
- S->epsilon|aSbS|bSaS
- ako bude generovat aababbba?
- preco vie vygenerovat vsetky take retazce?
CB08
Na týchto cvičeniach sa budeme venovať trom štatistickým témam súvisiacim s komparatívnou genomikou a s analýzou expresie génov. Tieto techniky sa však využívajú aj v iných oblastiach a môžete sa s nimi často stretnúť v genomických článkoch.
Zhlukovanie
- Máme vstupné dáta, väčšinou ako vektory dĺžky n
- Snažíme sa ich rozdeliť do skupín tak, aby dáta v rámci skupiny boli podobné a medzi skupinami rôzne
Využitie:
- hľadanie génov s podobným profilom expresie
- hľadanie skupín pacientov s podobným profilom expresie génov (objavovanie podtypov nejakej choroby)
- hľadanie rodín podobných proteínov
- automatická segmentácia obrázkov (napríklad rozlíšiť jednotlivé políčka microarray alebo gelu od pozadia)
Na prednáške sme videli hierarchické zhlukovanie, ktoré z dát vytvorilo strom. Teraz si ukážeme zhlukovanie, ktoré sa snaží dáta rozdeliť na k skupín, kde k je vopred daný parameter.
K-Means
- pozri tiež prezentáciu pdf
- Vstup: n-rozmerné vektory
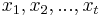 a počet zhlukov k
a počet zhlukov k
- Výstup: Rozdelenie vektorov do k zhlukov takéto:
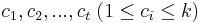 - priradenie vektoru k zhluku
- priradenie vektoru k zhluku
- n-rozmerné vektory
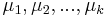 - centrá každého zhluku
- centrá každého zhluku
- Úloha: minimalizovať súčet štvorcov vzdialeností od každého vektoru k centru jeho zhluku:
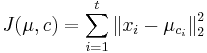
-
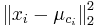 je druhá mocnina vzdialenosti vektora xi od centra jeho zhluku
je druhá mocnina vzdialenosti vektora xi od centra jeho zhluku
-
Algoritmus
Heuristika, ktorá nenájde vždy najlepšie zhlukovanie. Začne z nejakého zhlukovania a postupne ho zlepšuje. Pozri aj clanok na Wikipedii
- inicializácia: náhodne vyber k centier
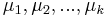
- opakuj kým sa niečo mení:
- priraď každý bod najbližšiemu centru:
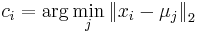
- vypočítaj nové centroidy:
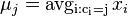 (spriemerujeme všetky body v jednom zhluku)
(spriemerujeme všetky body v jednom zhluku)
- priraď každý bod najbližšiemu centru:
Nadreprezentacia, obohatenie (enrichment)
- Mnohe celogenomove analyzy nam daju zoznam genov, ktore sa v nejakom ukazovateli vyrazne lisia od priemeru.
- Napriklad geny s pozitivnym vyberom v komparativnej genomike, geny vyrazne nadexprimovane alebo podexprimovane v microrarray experimentoch, geny regulovane urcitym transkripcnym faktorom a pod.
- Niektore z nich budu preskumanejsie (znama funkcia a pod.), niektore mozu mat nejake udaje o funkcii prenesene z homologov a dalsie mozu byt uplne nezname
- Co s takym zoznamom "zaujimavych genov"?
- moznost 1: vybrat si z neho niekolko malo zaujimavych kandidatov a preskumat ich podrobnejsie (experimentalne alebo informaticky)
- moznost 2: zistit, ci tato cela skupina je obohatena o geny urcitych skupin
- napr. v pripade pozitivneho vyberu nam casto vychadzaju geny suvisiace s imunitou, lebo su pod velkym evolucnym tlakom od patogenov
- takato analyza nam teda da informaciu o suvislostiach medzi roznymi procesmi
- Priklad (Kosiol et al)
- 16529 genov celkovo, 70 genov v GO kategorii innate immune response (0.4% zo vsetkych genov)
- 400 genov s pozivnym vyberom, mame 8 genov s innate immune response (2% zo vsetky genov s poz. vyb.)
- Celkovy pocet genov n, imunitnych ni, pozitivny vyber np, imunitnych s poz. vyb. nip.
- Kontingencna tabulka
| Pozitivny vyber | Bez poz. vyberu | Sucet | |
|---|---|---|---|
| Imunitne | 8 (nip) | 62 | 70 (ni) |
| Ostatne | 392 | 16067 | 16459 |
| Sucet | 400 (np) | 16129 | 16529 (n) |
- Nulova hypoteza: geny v nasom zozname boli nahodne vybrane z celeho genomu, t.j. ak v celom genome je frekvencia imunitnych genov ni/n (cca 0.4%), vo vzorke velkosti np (geny s pozitivnym vyberom) ocakavame cca np * (ni / n) imunitnych genov.
- aj v nulovej hypoteze vsak vzorka velkosti ni cisto nahodou moze obsahovat viac alebo menej takych genov.
- presnejsie mame urnu so ni (70) bielymi a n-ni (16459) ciernymi gulickami, vytiahneme nahodne np (400) guliciek, kolko bude medzi nimi bielych, nazvime tuto nahodnu premennu Xip
- v nasom priklade by sme ocakavali 1.7 genu s innate immune response, ale mame 8 (4.7xviac)
- Rozdelenie pravdepodobnosti Xip je hypergeometricke, t.j.
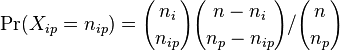
- Aka je pravdepodobnost, ze v nulovej hypoteze bude Xip tolko, kolko sme namerali alebo viac? (Chvost rozdelenia). V nasom pripade p-value 2.8e-4.
- Hypergeometric or Fisher's exact test, pripadne ich aproximacie pre velke hodnoty v tabulke (chi^2 test) zisti, ci sa nasa tabulka velmi lisi od toho, co by sme ocakavali v nulovej hypoteze
- Suvisiace clanky
- Rivals I, Personnaz L, Taing L, Potier MC (February 2007). "Enrichment or depletion of a GO category within a class of genes: which test?". Bioinformatics (Oxford, England) 23 (4): 401–7. doi:10.1093/bioinformatics/btl633. PMID 17182697.
- Huang da W, Sherman BT, Lempicki RA (January 2009). "Bioinformatics enrichment tools: paths toward the comprehensive functional analysis of large gene lists". Nucleic Acids Research 37 (1): 1–13. doi:10.1093/nar/gkn923. PMID 19033363.
- Reimand, Jüri, et al. "Pathway enrichment analysis and visualization of omics data using g: Profiler, GSEA, Cytoscape and EnrichmentMap." Nature protocols 14.2 (2019): 482. [31]
- Existuju web servery, napr. GOrilla pre ludske geny: http://cbl-gorilla.cs.technion.ac.il/, DAVID (http://david.niaid.nih.gov), g:Profiler http://biit.cs.ut.ee/gprofiler/
- Treba dat pozor, ci pocitaju to co chceme
- Kod v statistickom systeme R na pocitanie hypergeometrickeho rozdelenia
> dhyper(0:70, 70, 16529-70, 400); [1] 1.793421e-01 3.126761e-01 2.679872e-01 1.505169e-01 6.231088e-02 [6] 2.027586e-02 5.400796e-03 1.210955e-03 2.332580e-04 3.920215e-05 [11] 5.818723e-06 7.702558e-07 9.166688e-08 9.873221e-09 9.678760e-10 [16] 8.677204e-11 7.143849e-12 5.420388e-13 3.802134e-14 2.472342e-15 [21] 1.493876e-16 8.405488e-18 4.412274e-19 2.164351e-20 9.935473e-22 [26] 4.273662e-23 1.724446e-24 6.533742e-26 2.326517e-27 7.791092e-29 [31] 2.455307e-30 7.285339e-32 2.036140e-33 5.361856e-35 1.330660e-36 [36] 3.112566e-38 6.862558e-40 1.426089e-41 2.792792e-43 5.153006e-45 [41] 8.955105e-47 1.465159e-48 2.255667e-50 3.265636e-52 4.442631e-54 [46] 5.674366e-56 6.797781e-58 7.629501e-60 8.012033e-62 7.860866e-64 [51] 7.193798e-66 6.129013e-68 4.851139e-70 3.558526e-72 2.412561e-74 [56] 1.506983e-76 8.641725e-79 4.530590e-81 2.161126e-83 9.326620e-86 [61] 3.617279e-88 1.250737e-90 3.817900e-93 1.016417e-95 2.323667e-98 [66] 4.469699e-101 7.034762e-104 8.698702e-107 7.924236e-110 4.728201e-113 [71] 1.386176e-116 phyper(7, 70, 16529-70, 400, lower.tail=FALSE); # pr pocet bielych>7 (t.j. >=8) ak taham 400 z vreca so 70 bielymi a 16529-70 ciernymi # sucet cisiel z tabulky od 2.332580e-04 az po koniec d = dhyper(0:15, 70, 16529-70, 400); plot(0:15,d) # test pre danu tabulku a=matrix(c(8,62,392,16067),nrow=2, ncol=2) fisher.test(a,alternative = "greater")
Multiple testing correction
- V mnohych situaciach robime vela testov toho isteho typu, kazdy ma urcitu p-value
- Napr. testujeme 1000 genov v genome na pozitivny vyber, zvolime tie, kde p-value <= 0.05
- Alebo testujeme obohatenie 1000 funkcnych kategorii v nejakej vzorke genov, zvolime tie, kde p-value <= 0.05
- Problem: ak kazda z 1000 kategorii ma 5% sancu tam byt len nahodou, ocakavali by sme 50 cisto nahodnych pozitivnych vysledkov. Ak sme napr. nasli 100 pozitivnych vysledkov (obohatenych kategorii), cca polovica z nich je zle
- Preto potrebujeme pri velkom mnozstve testov umelo znizit prah na p-value tak, aby nahodny sum netvoril velke percento nasich vysledkov
- Toto sa vola multiple testing correction, je viac technik, napr. FDR (false discovery rate)
Nadreprezentácia (cvičenie pri počítači)
Data o expresii ludskych genov v roznych tkanivach a podobne v UCSC genome browseri
- Chodte na genome browser http://genome-euro.ucsc.edu/
- Zvolte Tools->Gene Sorter, 'assembly na hg38, sort by na Expression (GTEx), a do okienka search zadajme identifikator genu PTPRZ1
- Dostane tabulku genov s podobnym profilom expresie ako PTPRZ1 (červená je vysoká expresia, zelená nízka)
- Zoznam tychto genov v textovom formate najdete tu
- http://biit.cs.ut.ee/gprofiler/ mena genov skopirujme do policka Query, stlacte g:Profile!
- Ak by výpočet dlho trval, nájdete ho aj tu
- Vo výslednej tabuľke je každý riadok jedna funkcna kategoria, v ktorej su geny s tymto profilom expresie nadreprezentovane, kazdy stlpec jeden gen.
- V spodnej casti tabuly su aj asociacie k chorobam a k transkripcnym faktorom, ktore by mohli prislusne geny regulovat
- Co by sme na zaklade nadreprezentovanych kategorii usudzovali o gene PTPRZ1?
- Najdite tento gen v Uniprote (http://www.uniprot.org/), potvrdzuje nase domnienky?
- Vratme sa do genome browsera, najdime si PTPRZ1 gen v genome [32]
- V browseri su rozne tracky tykajuce sa expresie, napr. GTEx. Precitajte si, co je v tomto tracku zobrazene, zapnite si ho a pozrite si expresiu okolitych genov okolo PTPRZ1
CB12
Zhrnutie semestra a úvod do teórie grafov
- vid prezentacie k cviceniu
Populacna genomika v UCSC genome browseri
Zopar zaujimavych polymorfizmov v ludskom genome
- SNP rs1815739 CC: SNPedia, genome browser
- SNP rs12255372 GT: SNPedia, genome browser
- SNP rs2472297 TT: SNPedia, genome browser
- Ďalšie zaujímavé SNPy: rs10427255 CC, rs671 GG, rs713598 GG, rs17822931 CT, rs4988235 CC, rs1042725 CC, rs7495174 AA, rs1426654 AA, rs4481887 AG
- V browseri si vsimnite tracky (specificke pre verziu genomu hg19):
- HGDP Allele Freq s mapou sveta s distribuciou alel
- Genome Variants obsahuje genomy niekolkych ludi, napr Jima Watsona
- Takisto sa da pozriet genom ludi z jaskyne Denisova a Neandertalcov
UCSC genome browser ma aj dalsie tracky tykajuce sa populacnej genomiky a polymorfizmov
- Pozrime si napriklad region chr2:46,570,000-46,630,000 v hg38
- V casti Phenotype and Disease Associations
- napr. OMIM Alleles obsahuju asociacie variantov k chorobam
- GWAS Catalog sú výsledky GWAS štúdií
V starsej verzii ludskeho genomu hg18 je aj trojuholnikovy graf vazbovej nerovnovahy
- region chr2:164,862-426,468 v hg18
- zapnite "HapMap LD Phased" na Full (cast Variation and Repeats)
- vsimnite si, ze miery LD sa medzi ludskymi podpopulaciami lisia (YRI: Nigeria; CEU: Europa; JPT+CHB: Japonsko, Cina)
Sekvenčné motívy, program MEME
- Vazobne miesta transkripcnych faktorov sa casto reprezentuju ako sekvencne motivy
- Ak mame skupinu sekvencii, mozeme hladat motiv, ktory maju spolocny
- Znamy program na tento problem je MEME
- Chodte na stranku http://meme-suite.org/
- Zvolte nastroj MEME a v casti Input the primary sequences zvolte Type in sequences a zadajte tieto sekvencie
- Pozrite si ostatne nastavenia. Co asi robia?
- Ak server pocita dlho, mozete si pozriet vysledky tu
Kvasinkové transkripčné faktory v SGD
- Yeast genome database SGD obsahuje pomerne podrobne stranky pre jednotlive transkripcne faktory
- Pozrime si stranku pre transkripcny faktor GAL4 [33]
Staršie cvičenia
- Nadreprezentácia link
![A[i,j]=\max \left\{A[i-1,j-1]+s(x_{i},y_{j}),A[i-1,j]-1,A[i,j-1]-1\right\}](/vyuka/mbi/images/math/5/7/a/57aa12313311ee6d3565ad23b8a04a77.png)
![A[i,j]=\max \left\{A[i-1,j-1]+s(x_{i},y_{j}),A[i-1,j]+c(i-1,j,hore),A[i,j-1]+c(i,j-1,vlavo)\right\}](/vyuka/mbi/images/math/8/c/c/8cc47a0f26c209544027bcd2bbe77818.png)