Programovanie (1) v C/C++
1-INF-127, ZS 2024/25
Letný semester, prednáška č. 8: Rozdiel medzi revíziami
| Riadok 372: | Riadok 372: | ||
=== Existencia cesty medzi dvojicou vrcholov === | === Existencia cesty medzi dvojicou vrcholov === | ||
| − | Riešme teraz nasledujúci problém: pre danú dvojicu vrcholov ''u'' a ''v'' nejakého (orientovaného alebo neorientovaného) grafu potrebujeme zistiť, či sú spojené ''sledom'' – t.j. postupnosťou postupne na seba nadväzujúcich hrán (táto postupnosť môže byť aj prázdna, takže z každého vrcholu triviálne vedie sled do seba samého). Existencia sledu medzi dvoma vrcholmi je očividne ekvivalentná existencii ''cesty'' (t.j. sledu, v ktorom sa žiaden vrchol nezopakuje). V nasledujúcom preto budeme hovoriť o cestách. | + | Riešme teraz nasledujúci problém: pre danú dvojicu vrcholov ''u'' a ''v'' nejakého (orientovaného alebo neorientovaného) grafu potrebujeme zistiť, či sú spojené ''sledom'' – t. j. postupnosťou postupne na seba nadväzujúcich hrán (táto postupnosť môže byť aj prázdna, takže z každého vrcholu triviálne vedie sled do seba samého). Existencia sledu medzi dvoma vrcholmi je očividne ekvivalentná existencii ''cesty'' (t. j. sledu, v ktorom sa žiaden vrchol nezopakuje). V nasledujúcom preto budeme hovoriť o cestách. |
Pre ''neorientované'' grafy možno tento problém chápať aj ako úlohu zistiť, či sú tieto dva vrcholy v rovnakom ''komponente súvislosti'' grafu. Komponent súvislosti neorientovaného grafu je každý jeho (vzhľadom na inklúziu) maximálny podgraf, ktorý je súvislý – komponent súvislosti grafu teda pozostáva z nejakej podmnožiny jeho vrcholov, všetkých hrán pôvodného grafu spájajúcich vrcholy z tejto podmnožiny, pričom ľubovoľné dva vrcholy komponentu sú spojené cestou a pridaním ľubovoľného ďalšieho vrcholu grafu sa táto vlastnosť poruší. (Pri tejto „definícii” využívame fakt, že existencia cesty v ''neorientovanom'' grafe je zjavne reláciou ekvivalencie na množine jeho vrcholov.) | Pre ''neorientované'' grafy možno tento problém chápať aj ako úlohu zistiť, či sú tieto dva vrcholy v rovnakom ''komponente súvislosti'' grafu. Komponent súvislosti neorientovaného grafu je každý jeho (vzhľadom na inklúziu) maximálny podgraf, ktorý je súvislý – komponent súvislosti grafu teda pozostáva z nejakej podmnožiny jeho vrcholov, všetkých hrán pôvodného grafu spájajúcich vrcholy z tejto podmnožiny, pričom ľubovoľné dva vrcholy komponentu sú spojené cestou a pridaním ľubovoľného ďalšieho vrcholu grafu sa táto vlastnosť poruší. (Pri tejto „definícii” využívame fakt, že existencia cesty v ''neorientovanom'' grafe je zjavne reláciou ekvivalencie na množine jeho vrcholov.) | ||
| Riadok 468: | Riadok 468: | ||
''Cestou'' v grafe rozumieme postupnosť vrcholov ''v<sub>0</sub>, v<sub>1</sub>, ..., v<sub>n</sub>'' takú, že žiaden z vrcholov sa v nej nevyskytuje viac ako raz a pre ''i = 1,...,n'' existuje v grafe hrana z ''v<sub>i-1</sub>'' do ''v<sub>i</sub>''. | ''Cestou'' v grafe rozumieme postupnosť vrcholov ''v<sub>0</sub>, v<sub>1</sub>, ..., v<sub>n</sub>'' takú, že žiaden z vrcholov sa v nej nevyskytuje viac ako raz a pre ''i = 1,...,n'' existuje v grafe hrana z ''v<sub>i-1</sub>'' do ''v<sub>i</sub>''. | ||
| − | * ''Dĺžkou cesty'' rozumieme počet hrán na nej – t.j. číslo ''n''. | + | * ''Dĺžkou cesty'' rozumieme počet hrán na nej – t. j. číslo ''n''. |
Hľadanie najkratších ciest v danom (vo všeobecnosti aj orientovanom) grafe realizuje trieda <tt>ShortestPathsFromVertex</tt>: | Hľadanie najkratších ciest v danom (vo všeobecnosti aj orientovanom) grafe realizuje trieda <tt>ShortestPathsFromVertex</tt>: | ||
Verzia zo dňa a času 10:00, 24. marec 2021
Obsah
Oznamy
- Dnes po prednáške bude zverejnené zadanie tretej domácej úlohy, ktorú bude potrebné odovzdať do pondelka 12. apríla, 9:00 (čiže do začiatku budúcej prednášky).
- V stredu na cvičeniach bude zverejnených niekoľko nebodovaných úloh zameraných na grafy a grafové algoritmy.
- Počas cvičení v stredu 7. apríla bude prebiehať tretí test zameraný na látku z prvých siedmich prednášok (časť úloh bude zameraná na grafy, časť ešte na skoršiu látku).
Triedy pre grafy z minulej prednášky
package graphs;
/**
* Rozhranie pre reprezentacie grafov o vrcholoch 0, 1, ..., n-1 pre nejake
* prirodzene cislo n.
*/
public interface Graph {
/**
* Metoda, ktora vrati pocet vrcholov reprezentovaneho grafu.
*
* @return Pocet vrcholov grafu.
*/
int getNumberOfVertices();
/**
* Metoda, ktora vrati pocet hran reprezentovaneho grafu.
*
* @return Pocet hran grafu.
*/
int getNumberOfEdges();
/**
* Metoda, ktora zisti, ci v grafe existuje hrana medzi danou dvojicou vrcholov.
*
* @param from Pociatocny vrchol.
* @param to Koncovy vrchol.
* @return Vrati true prave vtedy, ked v grafe existuje hrana z vrcholu from do vrcholu to.
*/
boolean existsEdge(int from, int to);
/**
* Metoda, ktora vrati vsetkych naslednikov daneho vrcholu -- cize vsetky vrcholy, do ktorych vedie z daneho vrcholu
* orientovana hrana. Pre neorientovane grafy tak tato metoda vzdy vrati vsetkych susedov daneho vrcholu.
*
* @param vertex Lubovolny vrchol grafu.
* @return Naslednici vrcholu vertex ako instancia typu Iterable<Integer>.
*/
Iterable<Integer> outgoingEdgesDestinations(int vertex);
}
package graphs;
public class Edge {
private int from, to;
public Edge(int from, int to) {
this.from = from;
this.to = to;
}
public int getFrom() {
return from;
}
public int getTo() {
return to;
}
@Override
public boolean equals(Object o) {
if (o == null) {
return false;
}
return this.getClass() == o.getClass() && from == ((Edge) o).from && to == ((Edge) o).to;
}
@Override
public int hashCode() {
return Integer.valueOf(from).hashCode() + 31 * Integer.valueOf(to).hashCode();
}
}
package graphs;
import java.util.*;
/**
* Trieda reprezentujuca orientovany graf pomocou zoznamov naslednikov jednotlivych jeho vrcholov.
*/
public class SuccessorListsGraph implements Graph {
/**
* Pre kazdy vrchol zoznam jeho naslednikov.
*/
private ArrayList<ArrayList<Integer>> successorLists;
/**
* Pocet hran v grafe (velkost grafu).
*/
private int edgeCount;
/**
* Konstruktor, ktory dostane ako argumenty pocet vrcholov grafu (t. j. jeho rad), ako aj vsetky hrany grafu.
*
* @param vertexCount Rad grafu, cize pocet jeho vrcholov.
* @param edges Zoskupenie pozostavajuce zo vsetkych hran grafu.
*/
public SuccessorListsGraph(int vertexCount, Collection<Edge> edges) {
successorLists = new ArrayList<>();
for (int i = 0; i <= vertexCount - 1; i++) {
successorLists.add(new ArrayList<>());
}
edgeCount = 0;
for (Edge e : edges) {
if (!existsEdge(e.getFrom(), e.getTo())) {
successorLists.get(e.getFrom()).add(e.getTo());
edgeCount++;
}
}
}
@Override
public int getNumberOfVertices() {
return successorLists.size();
}
@Override
public int getNumberOfEdges() {
return edgeCount;
}
@Override
public boolean existsEdge(int from, int to) {
return successorLists.get(from).contains(to);
}
@Override
public Iterable<Integer> outgoingEdgesDestinations(int from) {
return Collections.unmodifiableList(successorLists.get(from)); // Vratime nemodifikovatelnu kopiu zoznamu.
}
}
package graphs;
import java.util.*;
/**
* Trieda reprezentujuca orientovany graf pomocou matice susednosti.
*/
public class AdjacencyMatrixGraph implements Graph {
/**
* Matica susednosti.
*/
private boolean adjacencyMatrix[][];
/**
* Pocet hran v grafe (velkost grafu).
*/
private int edgeCount;
/**
* Konstruktor, ktory dostane ako argumenty pocet vrcholov grafu (t. j. jeho rad), ako aj vsetky hrany grafu.
*
* @param vertexCount Rad grafu, cize pocet jeho vrcholov.
* @param edges Zoskupenie pozostavajuce zo vsetkych hran grafu.
*/
public AdjacencyMatrixGraph(int vertexCount, Collection<Edge> edges) {
adjacencyMatrix = new boolean[vertexCount][vertexCount];
edgeCount = 0;
for (Edge e : edges) {
if (!existsEdge(e.getFrom(), e.getTo())) {
adjacencyMatrix[e.getFrom()][e.getTo()] = true;
edgeCount++;
}
}
}
@Override
public int getNumberOfVertices() {
return adjacencyMatrix.length;
}
@Override
public int getNumberOfEdges() {
return edgeCount;
}
@Override
public boolean existsEdge(int from, int to) {
return adjacencyMatrix[from][to];
}
@Override
public Iterable<Integer> outgoingEdgesDestinations(int vertex) {
List<Integer> a = new ArrayList<>();
for (int i = 0; i <= getNumberOfVertices() - 1; i++) {
if (adjacencyMatrix[vertex][i]) {
a.add(i);
}
}
return Collections.unmodifiableList(a);
}
}
package graphs;
public interface UndirectedGraph extends Graph {
}
package graphs;
import java.util.*;
/**
* Pomocne metody na pracu so zoskupeniami hran.
*/
public class Edges {
public static Collection<Edge> symmetricClosure(Collection<Edge> edges) {
List<Edge> result = new ArrayList<>();
for (Edge e : edges) {
result.add(e);
if (e.getFrom() != e.getTo()) {
result.add(new Edge(e.getTo(), e.getFrom()));
}
}
return result;
}
public static int distinctUndirectedEdges(Collection<Edge> edges) {
HashSet<Edge> set = new HashSet<>();
for (Edge e : edges) {
if (!set.contains(e) && !set.contains(new Edge(e.getTo(), e.getFrom()))) {
set.add(e);
}
}
return set.size();
}
}
package graphs;
import java.util.*;
/**
* Trieda reprezentujuca neorientovany graf pomocou zoznamov susedov jednotlivych jeho vrcholov.
*/
public class AdjacencyListsUndirectedGraph extends SuccessorListsGraph implements UndirectedGraph {
private int undirectedEdgeCount;
public AdjacencyListsUndirectedGraph(int vertexCount, Collection<Edge> edges) {
super(vertexCount, Edges.symmetricClosure(edges));
undirectedEdgeCount = Edges.distinctUndirectedEdges(edges);
}
@Override
public int getNumberOfEdges() {
return undirectedEdgeCount;
}
}
package graphs;
import java.util.*;
/**
* Trieda reprezentujuca neorientovany graf pomocou matice susednosti.
*/
public class AdjacencyMatrixUndirectedGraph extends AdjacencyMatrixGraph implements UndirectedGraph {
private int undirectedEdgeCount;
public AdjacencyMatrixUndirectedGraph(int vertexCount, Collection<Edge> edges) {
super(vertexCount, Edges.symmetricClosure(edges));
undirectedEdgeCount = Edges.distinctUndirectedEdges(edges);
}
@Override
public int getNumberOfEdges() {
return undirectedEdgeCount;
}
}
Pokračovanie úvodu do grafov
Vytvorenie grafu
Metóda readGraph triedy Trieda uvedenej nižšie prečíta pomocou danej inštancie triedy Scanner reprezentáciu grafu a vytvorí z nej graf typu určeného jej druhým parametrom. Argument pre typ grafu je pritom vymenovaného typu GraphType (o vymenovaných typoch sa možno dočítať viac tu).
package graphs;
public enum GraphType {
DIRECTED_SUCCESSOR_LISTS, DIRECTED_ADJACENCY_MATRIX, UNDIRECTED_ADJACENCY_LISTS, UNDIRECTED_ADJACENCY_MATRIX
}
package graphs;
import java.util.*;
public class Trieda {
/**
* Metoda, ktora precita textovu reprezentaciu grafu pozostavajucu z poctu vrcholov n, poctu hran m a z m dvojic
* vrcholov udavajucich jednotlive hrany a vytvori z nej graf urceneho typu.
*
* @param scanner Scanner, z ktoreho sa reprezentacia grafu cita.
* @param graphType Typ vytvaraneho grafu.
* @return Vytvoreny graf.
*/
public static Graph readGraph(Scanner scanner, GraphType graphType) {
int n = scanner.nextInt();
int m = scanner.nextInt();
List<Edge> edges = new ArrayList<>();
for (int i = 1; i <= m; i++) {
edges.add(new Edge(scanner.nextInt(), scanner.nextInt()));
}
Graph g = null;
switch (graphType) {
case DIRECTED_SUCCESSOR_LISTS:
g = new SuccessorListsGraph(n, edges);
break;
case DIRECTED_ADJACENCY_MATRIX:
g = new AdjacencyMatrixGraph(n, edges);
break;
case UNDIRECTED_ADJACENCY_LISTS:
g = new AdjacencyListsUndirectedGraph(n, edges);
break;
case UNDIRECTED_ADJACENCY_MATRIX:
g = new AdjacencyMatrixUndirectedGraph(n, edges);
break;
}
return g;
}
}
Volanie metódy readGraph potom môže vyzerať napríklad nasledovne:
Graph g = readGraph(scanner, GraphType.DIRECTED_SUCCESSOR_LISTS);
Porovnanie reprezentácií grafov
Majme orientovaný graf s n vrcholmi a m hranami – počet hrán m teda môže byť od 0 po n2. V závislosti od použitej reprezentácie grafu sa líši ako časová zložitosť jednotlivých operácií na grafoch, tak aj pamäťová zložitosť samotnej tejto reprezentácie. Napríklad:
- Pamäť potrebná na uloženie matice susednosti grafu je vždy rádovo veľkosti n2. Pri reprezentácii pomocou zoznamov následníkov resp. susedov je veľkosť reprezentácie grafu rádovo n+m. Hlavne pre riedke grafy (s menším počtom hrán) je teda reprezentácia pomocou zoznamov pamäťovo efektívnejšia.
- Operácia existsEdge sa pre grafy reprezentované maticou susednosti vykoná v konštantnom čase. Pre grafy reprezentované zoznamami následníkov resp. susedov môže byť zložitosť tejto operácie až lineárna v závislosti od počtu vrcholov grafu (je potrebné prejsť celý zoznam susedov jedného vrchola, ktorý môže obsahovať až n rôznych vrcholov).
- Naopak vytvorenie zoznamu následníkov resp. susedov grafu v metóde outgoingEdgesDestinations je efektívnejšie pri reprezentácii pomocou zoznamov.
Ďalšie varianty grafov
Grafy na tejto prednáške chápeme v relatívne obmedzenom slova zmysle. V praxi sa často zídu aj rôzne rozšírenia definície grafu:
- Grafy s násobnými hranami (niekde tiež multigrafy) umožňujú viesť medzi danou dvojicou vrcholov viacero paralelných hrán. To možno v pamäti počítača realizovať napríklad nahradením booleovskej matice maticou prirodzených čísel udávajúcich násobnosti jendotlivých hrán, prípadne pridaním informácie o multiplicite do zoznamov následníkov resp. susedov.
- Ohodnotené grafy obsahujú na hranách nejakú ďalšiu prídavnú informáciu (napríklad pri cestnej sieti si môžeme pamätať dĺžku jednotlivých úsekov, prípadne ich možno využiť aj na reprezentáciu multigrafov). Možno ich reprezentovať nahradením booleovskej matice maticou ohodnotení, prípadne zakomponovaním informácie o ohodnotení hrán do zoznamov následníkov resp. susedov. S ohodnotenými grafmi sa okrajovo stretneme aj tento semester.
- Dynamické grafy podporujú aj pridávanie a mazanie vrcholov a/alebo hrán.
Prehľadávanie (orientovaného alebo neorientovaného) grafu do hĺbky
Existencia cesty medzi dvojicou vrcholov
Riešme teraz nasledujúci problém: pre danú dvojicu vrcholov u a v nejakého (orientovaného alebo neorientovaného) grafu potrebujeme zistiť, či sú spojené sledom – t. j. postupnosťou postupne na seba nadväzujúcich hrán (táto postupnosť môže byť aj prázdna, takže z každého vrcholu triviálne vedie sled do seba samého). Existencia sledu medzi dvoma vrcholmi je očividne ekvivalentná existencii cesty (t. j. sledu, v ktorom sa žiaden vrchol nezopakuje). V nasledujúcom preto budeme hovoriť o cestách.
Pre neorientované grafy možno tento problém chápať aj ako úlohu zistiť, či sú tieto dva vrcholy v rovnakom komponente súvislosti grafu. Komponent súvislosti neorientovaného grafu je každý jeho (vzhľadom na inklúziu) maximálny podgraf, ktorý je súvislý – komponent súvislosti grafu teda pozostáva z nejakej podmnožiny jeho vrcholov, všetkých hrán pôvodného grafu spájajúcich vrcholy z tejto podmnožiny, pričom ľubovoľné dva vrcholy komponentu sú spojené cestou a pridaním ľubovoľného ďalšieho vrcholu grafu sa táto vlastnosť poruší. (Pri tejto „definícii” využívame fakt, že existencia cesty v neorientovanom grafe je zjavne reláciou ekvivalencie na množine jeho vrcholov.)
Na riešenie problému existencie cesty pritom použijeme prehľadávanie do hĺbky – podobné, ako sme už používali minulý semester pri vyfarbovaní súvislých oblastí v obdĺžnikovej mriežke. Procedúra na grafoch však bude všeobecnejšia:
- Mriežku môžeme reprezentovať neorientovaným grafom, v ktorom vrcholy zodpovedajú políčkam mriežky. Dvojica vrcholov je navyše spojená hranou práve vtedy, keď zodpovedajúce políčka spolu susedia a súčasne majú rovnakú farbu.
- Ostrovy rovnakej farby v mriežke potom zodpovedajú komponentom súvislosti výsledného neorientovaného grafu.
Na riešenie uvedeného problému napíšeme rekurzívnu metódu search, ktorá bude prehľadávať všetkých ešte nenavštívených susedov daného vrcholu. Informáciu o navštívení jednotlivých vrcholov si budeme uchovávať v zozname visited. Metóda existsPath bude metódu search využívať na riešenie horeuvedeného problému.
/* Pomocna metoda pre metodu existsPath.
Dostane (orientovany alebo neorientovany) graf g, vrchol vertex a zoznam visited
s informaciou o navstiveni jednotlivych vrcholov.
Pri volani by malo platit visited.get(vertex) == false.
Metoda rekurzivne prehlada vsetky doposial nenavstivene vrcholy dosiahnutelne z vrcholu vertex. */
static void search(Graph g, int vertex, List<Boolean> visited) {
visited.set(vertex, true);
for (int neighbour : g.adjVertices(vertex)) {
if (!visited.get(neighbour)) {
search(g, neighbour, visited);
}
}
}
/* Metoda, ktora zisti, ci su vrcholy from a to v grafe g spojene cestou. */
static boolean existsPath(Graph g, int from, int to) {
ArrayList<Boolean> visited = new ArrayList<>();
for (int i = 0; i <= g.getNumberOfVertices() - 1; i++) {
visited.add(false);
}
search(g, from, visited);
return visited.get(to);
}
Hľadanie komponentov súvislosti neorientovaného grafu
V prípade, že pracujeme s neorientovaným grafom a existenciu cesty medzi dvojicami vrcholov by sme chceli testovať veľakrát, oplatí sa nájsť všetky komponenty súvislosti v danom grafe. Komponenty môžeme očíslovať od nuly až po nejaké k - 1, pričom pre každý vrchol si môžeme pamätať číslo jeho komponentu. Túto úlohu realizuje nasledujúca trieda:
/* Trieda reprezentujuca rozdelenie neorientovaneho grafu na komponenty suvislosti: */
class Components {
private UndirectedGraph g; // Neorientovany graf
private ArrayList<Integer> componentId; // Pre kazdy vrchol si budeme v tomto zozname pamatat cislo jeho komponentu
private int numComponents; // Celkovy pocet komponentov
/* Konstruktor, ktory dostane graf a prehladavanim do hlbky najde jeho komponenty suvislosti: */
public Components(UndirectedGraph g) {
this.g = g;
numComponents = 0; // Pocet komponentov inicializujeme na 0
int n = g.getNumberOfVertices(); // Pocet vrcholov grafu
componentId = new ArrayList<>();
for (int i = 0; i <= n - 1; i++) { // Komponenty jednotlivych vrcholov inicializujeme na -1 (nezmyselna hodnota)
componentId.add(-1);
}
for (int i = 0; i <= n - 1; i++) { // Prejdeme vsetky vrcholy ...
if (componentId.get(i) == -1) { // ... a ak najdeme nespracovany ...
search(i, numComponents); // ... vyrobime novy komponent suvislosti
numComponents++;
}
}
}
/* Pomocna rekurzivna metoda pouzivana v konstruktore na oznacenie jedneho komponentu suvislosti cislom id: */
private void search(int vertex, int id) {
componentId.set(vertex, id);
for (int neighbour : g.adjVertices(vertex)) {
if (componentId.get(neighbour) == -1) {
search(neighbour, id);
}
}
}
/* Metoda, ktora vrati true prave vtedy, ked su vrcholy from a to v rovnakom komponente: */
public boolean existsPath(int from, int to) {
return componentId.get(from).equals(componentId.get(to));
}
/* Metoda, ktora vrati pocet komponentov grafu: */
public int getNumberOfComponents() {
return numComponents;
}
}
Prehľadávanie (orientovaného alebo neorientovaného) grafu do šírky
- Jednou z tém minulej prednášky bolo prehľadávanie grafu do hĺbky (angl. depth-first search). Pri neorientovaných grafoch sme ho použili aj ako nástroj na hľadanie komponentov súvislosti.
- Teraz si ukážeme prehľadávanie grafu do šírky (angl. breadth-first search) – to sa bude dať použiť na hľadanie najkratších ciest medzi dvojicami vrcholov orientovaného (a teda aj neorientovaného) grafu.
- Opäť pôjde o zovšeobecnenie algoritmu, ktorý sme videli už minulý semester v súvislosti s vyfarbovaním súvislých oblastí mriežky.
Hľadanie najkratšej cesty
Cestou v grafe rozumieme postupnosť vrcholov v0, v1, ..., vn takú, že žiaden z vrcholov sa v nej nevyskytuje viac ako raz a pre i = 1,...,n existuje v grafe hrana z vi-1 do vi.
- Dĺžkou cesty rozumieme počet hrán na nej – t. j. číslo n.
Hľadanie najkratších ciest v danom (vo všeobecnosti aj orientovanom) grafe realizuje trieda ShortestPathsFromVertex:
- Jej konštruktor dostane ako parameter graf g a nejaký jeho význačný „štartovací” vrchol start. Následne spustí na grafe g prehľadávanie do šírky z vrcholu start.
- Takto sa postupne prehľadajú vrcholy vo vzdialenosti 1 od start, potom vrcholy vo vzdialenosti 2 od start, atď. Na zabezpečenie takéhoto poradia sa použije rad, podobne ako pri algoritme na mriežke minulý semester. V každom momente vykonávania algoritmu môže tento rad obsahovať vrcholy najviac dvoch rôznych vzdialeností od start.
- Pre každý vrchol v sa počas prehľadávania do ArrayList-u dist uloží jeho vzdialenosť od start a do ArrayList-u prev sa uloží vrchol u, z ktorého bol vrchol v objavený (to je nutne predposledný vrchol na najkratšej ceste zo start do v).
- Metóda distanceFromStart bude pre daný vrchol vertex vracať jeho vzdialenosť od vrcholu start. Tu sa jednoducho využije hodnota uložená v ArrayList-e dist.
- Metóda shortestPathFromStart bude pre daný vrchol vertex vracať najkratšiu cestu z vrcholu start do vrcholu vertex reprezentovanú zoznamom vrcholov. Tú bude konštruovať od konca: začne vo vrchole vertex a postupne bude hľadať predchodcov pomocou hodnôt uložených v ArrayList-e prev.
/* Trieda, ktora reprezentuje najkratsie cesty a vzdialenosti
z jedneho vrcholu orientovaneho grafu do vsetkych ostatnych vrcholov. */
class ShortestPathsFromVertex {
private final Graph g; // Orientovany (alebo neorientovany) graf, v ktorom budeme cesty hladat.
private final int start; // Vrchol grafu g, v ktorom maju cesty zacinat.
private final ArrayList<Integer> dist; // i-ty prvok zoznamu bude vzdialenost zo start do i
private final ArrayList<Integer> prev; // i-ty prvok zoznamu bude predchodca i na najkratsej ceste zo start do i
/* Konstruktor dostane graf g a startovaci vrchol start a prehladavanim do sirky
vypocita najkratsie cesty z vrcholu start do ostatnych vrcholov. */
public ShortestPathsFromVertex(Graph g, int start) {
this.g = g;
this.start = start;
/* Incializacia zoznamov dist a prev: */
dist = new ArrayList<>();
prev = new ArrayList<>();
for (int i = 0; i <= g.getNumberOfVertices() - 1; i++) {
dist.add(-1); // i-ty prvok zoznamu dist bude -1, ak sa zo start neda dostat do i
prev.add(-1); // i-ty prvok zoznamu prev bude -1, ak sa zo start neda dostat do i alebo ak i == start
}
/* Prehladavanim do sirky vypocitame vzdialenosti a najkratsie cesty zo start: */
LinkedList<Integer> queue = new LinkedList<>();
dist.set(start, 0);
queue.addLast(start); // Vzdialenost zo start do start je 0
while (!queue.isEmpty()) {
int vertex = queue.removeFirst(); // Vyberieme vrchol z radu
/* Prejdeme vsetkych susedov vrcholu vertex; ak este neboli navstiveni,
nastavime im vzdialenost a predchodcu a vlozime ich do radu:*/
for (int neighbour : g.adjVertices(vertex)) {
if (dist.get(neighbour) == -1) {
dist.set(neighbour, dist.get(vertex) + 1);
prev.set(neighbour, vertex);
queue.addLast(neighbour);
}
}
}
}
/* Metoda, ktora vrati vzdialenost vrcholu vertex od vrcholu start: */
public int distanceFromStart(int vertex) {
return dist.get(vertex);
}
/* Metoda, ktora vrati najkratsiu cestu z vrcholu start do vrcholu vertex.
Reprezentaciou cesty je zoznam vrcholov na nej.
V pripade, ze neexistuje ziadna cesta zo start do vertex, vrati null. */
public List<Integer> shortestPathFromStart(int vertex) {
if (dist.get(vertex) == -1) { // Ak neexistuje cesta, vrat null
return null;
}
LinkedList<Integer> path = new LinkedList<>();
int v = vertex;
while (v != start) { // Postupne pridavaj vrcholy od konca cesty
path.addFirst(v);
v = prev.get(v);
}
path.addFirst(start);
return path;
}
}
Nasledujúci kód načíta graf a dvojicu jeho vrcholov; vypíše najkratšiu cestu medzi danými vrcholmi.
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Zadaj graf:");
Graph g = readGraph(scanner, false, false);
// PRE NEORIENTOVANY GRAF: Graph g = readGraph(scanner, true, false);
System.out.println("Zadaj pociatocny a koncovy vrchol:");
int from = scanner.nextInt();
int to = scanner.nextInt();
ShortestPathsFromVertex spfv = new ShortestPathsFromVertex(g, from);
System.out.println("Najkratsia cesta ma dlzku " + spfv.distanceFromStart(to));
List<Integer> shortest = spfv.shortestPathFromStart(to);
if (shortest != null) {
System.out.println(shortest);
}
}
Špeciálny prípad neorientovaných grafov
Inštanciu triedy ShortestPathsFromVertex možno vytvoriť ako pre orientované, tak aj pre neorientované grafy (neorientované grafy sme implementovali ako špeciálny prípad orientovaných a všetky grafy implementujú spoločné rozhranie Graph).
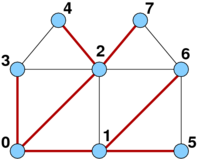
Pre neorientované grafy si v súvislosti s prehľadávaním do šírky možno všimnúť nasledujúce:
- Hrany medzi vrcholmi a ich predchodcami tvoria strom (ak je graf súvislý, je tento strom jeho kostrou) – to je znázornené na obrázku vpravo.
- Najkratšia cesta zo start do v je potom (ak existuje) jediná cesta zo start do v v tomto strome.
(V orientovaných grafoch je situácia podobná; stromy najkratších ciest však navyše majú hrany orientované smerom od start.)
Prehľadávanie s návratom na grafoch
Pre veľa úloh na grafoch nie sú známe (a v prípade platnosti niektorých hypotéz z teoretickej informatiky často ani neexistujú) efektívne algoritmy. Backtrackingom však vieme spočítať odpoveď aspoň pre malé vstupy.
Hľadanie ciest dĺžky k
Nasledujúca trieda FixedLengthPaths pre daný graf g, danú dvojicu vrcholov from, to a dané prirodzené číslo length vypisuje všetky cesty dĺžky presne length vedúce v g z vrcholu from do vrcholu to. Tento proces sa spustí hneď v konštruktore (nebude teda mať veľký význam vytvárať inštancie triedy FixedLengthPaths).
Prehľadávaním s návratom budeme v LinkedList-e path postupne generovať všetky takéto cesty. Pre každý vrchol budeme mať navyše v ArrayList-e visited poznačené, či sme ho už v generovanej ceste použili. Akonáhle nájdeme cestu požadovanej dĺžky končiacu vo vrchole to, vypíšeme ju na výstup.
/* Trieda, pomocou ktorej mozno najst vsetky cesty danej dlzky medzi danou dvojicou vrcholov. */
class FixedLengthPaths {
private Graph g; // Orientovany (alebo neorientovany) graf
private int from, to; // Pociatocny a koncovy vrchol
private int length; // Pozadovana dlzka cesty
private LinkedList<Integer> path; // Zoznam, v ktorom budeme postupne generovat cesty
private ArrayList<Boolean> visited; // i-ty prvok zoznamu visited bude true, ak sa vrchol i nachadza v path
/* Konstruktor dostane graf, pociatocny a koncovy vrchol a pozadovanu dlzku cesty.
Spusti prehladavanie s navratom, ktore hlada vsetky cesty danej dlzky medzi
danymi vrcholmi a rovno aj vypisuje vysledky. */
public FixedLengthPaths(Graph g, int from, int to, int length) {
this.g = g;
this.from = from;
this.to = to;
this.length = length;
visited = new ArrayList<>();
for (int i = 0; i <= g.getNumberOfVertices() - 1; i++) {
visited.add(false);
}
path = new LinkedList<>();
path.add(from); // Kazda cesta z from bude zacinat vo from
visited.set(from, true);
search(); // Spusti generovanie ciest
}
/* Hlavna rekurzivna metoda prehladavania s navratom.
Ak je vygenerovana cesta kratsia ako length, postupne vyskusa vsetky
moznosti jej predlzenia.
Ak sa vygeneruje cesta dlzky length, overi sa, ci tato cesta vedie do
vrcholu to; ak ano, vypise sa.
*/
private void search() {
if (path.size() == length + 1) { // Ak uz mame cestu pozadovanej dlzky ...
if (path.getLast() == to) { // ... a konci v pozadovanom stave ...
System.out.println(path); // ... vypis ju
}
} else {
/* Ak este nemame cestu pozadovanej dlzky, vyskusaj vsetky moznosti
jej predlzenia: */
for (int neighbour : g.adjVertices(path.getLast())) {
if (!visited.get(neighbour)) {
visited.set(neighbour, true);
path.addLast(neighbour);
search();
path.removeLast();
visited.set(neighbour, false);
}
}
}
}
}
Nasledujúci kód načíta graf, dvojicu vrcholov from, to a prirodzené číslo length a vypíše všetky cesty dĺžky length z vrcholu from do vrcholu to.
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Zadaj graf:");
Graph g = readGraph(scanner, true, false);
// PRE ORIENTOVANY GRAF: Graph g = readGraph(scanner, false, false);
System.out.println("Zadaj pociatocny a koncovy vrchol:");
int from = scanner.nextInt();
int to = scanner.nextInt();
System.out.println("Zadaj dlzku cesty:");
int length = scanner.nextInt();
System.out.println("Cesty dlzky " + length + ":");
new FixedLengthPaths(g, from, to, length);
Príklad: pre neorientovaný graf s vrcholmi {0,...,4} a hranami {{0,1},{0,2},{0,3},{1,2},{2,3},{2,4},{3,4}}, počiatočný vrchol 0 a koncový vrchol 3 dostávame nasledujúce výstupy
Cesty dlzky 1: 0 3 Cesty dlzky 2: 0 2 3 Cesty dlzky 3: 0 1 2 3 0 2 4 3 Cesty dlzky 4: 0 1 2 4 3
Cvičenia:
- Upravte triedu FixedLengthPaths tak, aby namiesto vypisovania ciest iba počítala, koľko ich je.
- Upravte triedu FixedLengthPaths tak, aby iba zisťovala, či existuje cesta danej dĺžky (po prvej nájdenej ceste je teda možné prehľadávanie ukončiť).
- Navrhnite spôsoby, ako v niektorých prípadoch zistiť, že aktuálne rozrobenú cestu už nie je možné požadovaným spôsobom rozšíriť.
Hľadanie najdlhšej cesty
Uvažujme teraz problém nájdenia nejakej z najdlhších ciest z u do v (ak existuje aspoň jedna). Túto úlohu bude realizovať trieda LongestPath; oproti predchádzajúcemu programu sa ten nasledujúci bude líšiť iba málo:
- Budeme si pamätať najdlhšiu nájdenú cestu.
- Vždy, keď prídeme do cieľového vrcholu, porovnáme dĺžku aktuálnej cesty s najdlhšou cestou nájdenou doteraz.
/* Trieda, pomocou ktorej mozno najst jednu z najdlhsich ciest medzi danou dvojicou vrcholov. */
class LongestPath {
private Graph g; // Orientovany (alebo neorientovany) graf
private int from, to; // Pociatocny a koncovy vrchol
private int maxLength; // Dlzka doposial najdlhsej najdenej cesty z from do to
private LinkedList<Integer> path; // Zoznam, v ktorom budeme postupne generovat cesty
private LinkedList<Integer> longestPath; // Okrem toho si budeme pamatat najdlhsiu doposial vygenerovanu cestu
private ArrayList<Boolean> visited; // i-ty prvok zoznamu visited bude true, ak sa vrchol i nachadza v path
/* Konstruktor dostane graf, pociatocny a koncovy vrchol. Spusti prehladavanie
s navratom, ktore hlada najdlhsiu cestu medzi danymi vrcholmi. */
public LongestPath(Graph g, int from, int to) {
this.g = g;
this.from = from;
this.to = to;
visited = new ArrayList<>();
for (int i = 0; i <= g.getNumberOfVertices() - 1; i++) {
visited.add(false);
}
maxLength = -1; // Doposial nemame ziadnu cestu
path = new LinkedList<>();
path.add(from); // Kazda cesta z from bude zacinat vo from
visited.set(from, true);
search(); // Spusti generovanie ciest
}
/* Hlavna rekurzivna metoda prehladavania s navratom.
Ak cesta dorazila do vrchola to, jej dlzka sa porovna s najdlhsou doposial
najdenou cestou a ak je dlhsia, ulozi sa ako nova doposial najdlhsia cesta.
Ak este nedorazila do vrchola to, vyskusaju sa vsetky moznosti na jej
predlzenie.
*/
private void search() {
if (path.getLast() == to) { // Ak sme dorazili do cieloveho vrchola, ukonci prehladavanie
if (path.size() - 1 > maxLength) {
maxLength = path.size() - 1;
longestPath = new LinkedList<>(path);
}
} else { // Inak vyskusaj vsetky moznosti predlzenia cesty
for (int neighbour : g.adjVertices(path.getLast())) {
if (!visited.get(neighbour)) {
visited.set(neighbour, true);
path.addLast(neighbour);
search();
path.removeLast();
visited.set(neighbour, false);
}
}
}
}
/* Metoda, ktora vrati najdenu najdlhsiu cestu: */
public List<Integer> longestPath() {
if (longestPath != null) {
return Collections.unmodifiableList(longestPath);
} else {
return null;
}
}
}
Použitie triedy:
LongestPath lp = new LongestPath(g, from, to);
List<Integer> longest = lp.longestPath();
if (longest != null) {
System.out.println("Najdlhsia cesta: " + longest);
}
Príklad výstupu na rovnakom grafe ako vyššie:
Najdlhsia cesta: [0, 1, 2, 4, 3]