Programovanie (1) v C/C++
1-INF-127, ZS 2024/25
Letný semester, prednáška č. 9: Rozdiel medzi revíziami
Skočit na navigaci
Skočit na vyhledávání
(Vytvorená stránka „== Oznamy == * Dnes po prednáške bude zverejnené zadanie štvrtej domácej úlohy, ktorú bude potrebné odovzdať ''do pondelka 26. apríla, 9:00'' (čiže do zači…“) |
|||
| Riadok 113: | Riadok 113: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Použitie triedy: | + | Použitie triedy: |
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
| − | LongestPath longestPath = new LongestPath(g, from, to); | + | public static void main(String[] args) { |
| − | List<Integer> longest = longestPath.getLongestPath(); | + | Scanner scanner = new Scanner(System.in); |
| − | if (longest != null) { | + | System.out.println("Zadaj graf:"); |
| − | + | Graph g = readGraph(scanner, GraphType.DIRECTED_SUCCESSOR_LISTS); | |
| + | System.out.println("Zadaj pociatocny a koncovy vrchol:"); | ||
| + | int from = scanner.nextInt(); | ||
| + | int to = scanner.nextInt(); | ||
| + | |||
| + | LongestPath longestPath = new LongestPath(g, from, to); | ||
| + | List<Integer> longest = longestPath.getLongestPath(); | ||
| + | if (longest != null) { | ||
| + | System.out.println("Najdlhsia cesta: " + longest); | ||
| + | } else { | ||
| + | System.out.println("Ziadna cesta neexistuje."); | ||
| + | } | ||
} | } | ||
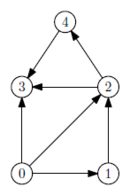
| − | </syntaxhighlight> | + | </syntaxhighlight> [[Image:Graf5.png|thumb|130px|right]] |
| − | Príklad výstupu na | + | Príklad výstupu pre graf na obrázku vpravo, počiatočný vrchol ''0'' a koncový vrchol ''3'': |
<pre> | <pre> | ||
Najdlhsia cesta: [0, 1, 2, 4, 3] | Najdlhsia cesta: [0, 1, 2, 4, 3] | ||
Verzia zo dňa a času 11:54, 4. apríl 2021
Obsah
Oznamy
- Dnes po prednáške bude zverejnené zadanie štvrtej domácej úlohy, ktorú bude potrebné odovzdať do pondelka 26. apríla, 9:00 (čiže do začiatku jedenástej prednášky).
- Počas stredajších cvičení bude prebiehať štvrtý test zameraný predovšetkým na grafy a grafové algoritmy.
- V rámci stredajších cvičení tiež bude zverejnené zadanie tretej bonusovej úlohy s termínom odovzdania do stredy 21. apríla, 11:30.
Prehľadávanie s návratom na grafoch: pokračovanie
Hľadanie najdlhšej cesty
Uvažujme problém nájdenia niektorej z najdlhších ciest z vrcholu u do vrcholu v daného orientovaného grafu (ak existuje aspoň jedna). Je dokázané, že za predpokladu platnosti určitých hypotéz z teoretickej informatiky pre túto úlohu neexistuje žiaden efektívny algoritmus. Použijeme teda prehľadávanie s návratom. To bude realizovať trieda LongestPath, ktorú získame drobnou úpravou triedy FixedLengthPaths z minulej prednášky.
- Počas prehľadávania si budeme pamätať najdlhšiu doposiaľ nájdenú cestu.
- Vždy, keď prídeme do cieľového vrcholu, porovnáme dĺžku práve nájdenej cesty s najdlhšou doposiaľ nájdenou cestou.
package graphs;
import java.util.*;
/**
* Trieda realizujuca najdenie najdlhsej cesty medzi danou dvojicou vrcholov grafu.
*/
public class LongestPath {
/**
* Graf, v ktorom sa hladanie ciest realizuje.
*/
private Graph g;
/**
* Pociatocny vrchol hladanych ciest.
*/
private int from;
/**
* Koncovy vrchol hladanych ciest.
*/
private int to;
/**
* Pomocny zoznam, v ktorom sa budu pomocou prehladavania s navratom postupne generovat jednotlive cesty.
*/
private LinkedList<Integer> path;
/**
* Pomocny zoznam, v ktorom si budeme pocas generovania ciest pre kazdy vrchol pamatat, ci sa nachadza alebo
* nenachadza v doposial vygenerovanej casti cesty.
*/
private ArrayList<Boolean> visited;
/**
* Zoznam, v ktorom bude ulozena najdlhsia cesta medzi danou dvojicou vrcholov (pocas prehladavania pojde
* o najdlhsiu doposial najdenu cestu).
*/
private List<Integer> longestPath;
/**
* Konstruktor, ktory rovno aj spusti prehladavanie s navratom a do zoznamu longestPath ulozi niektoru spomedzi
* najdlhsich ciest medzi danou dvojicou vrcholov grafu.
* @param g Graf, v ktorom sa hladanie ciest realizuje.
* @param from Pociatocny vrchol hladanych ciest.
* @param to Koncovy vrchol hladanych ciest.
*/
public LongestPath(Graph g, int from, int to) {
this.g = g;
this.from = from;
this.to = to;
visited = new ArrayList<>();
for (int i = 0; i <= g.getNumberOfVertices() - 1; i++) {
visited.add(false);
}
path = new LinkedList<>();
path.add(from);
visited.set(from, true);
search();
}
/**
* Metoda realizujuca samotne rekurzivne prehladavanie s navratom. V pripade, ze sa vygenerovala cesta konciaca
* vo vrchole to, porovna sa jej dlzka s dlzkou doposial najdlhsej najdenej cesty a ak je dlhsia, ulozi sa ako nova
* doposial najdlhsia cesta. V opacnom pripade sa vyskusaju vsetky moznosti predlzenia cesty.
*/
private void search() {
if (path.getLast() == to) {
if (longestPath == null || path.size() > longestPath.size()) {
longestPath = new LinkedList<>(path);
}
} else {
for (int successor : g.outgoingEdgesDestinations(path.getLast())) {
if (!visited.get(successor)) {
visited.set(successor, true);
path.add(successor);
search();
path.removeLast();
visited.set(successor, false);
}
}
}
}
/**
* Metoda, ktora vrati najdenu najdlhsiu cestu medzi danou dvojicou vrcholov.
* @return Nemodifikovatelny pohlad na zoznam vrcholov na najdlhsej ceste z vrcholu from do vrcholu to.
*/
public List<Integer> getLongestPath() {
if (longestPath != null) {
return Collections.unmodifiableList(longestPath);
} else {
return null;
}
}
}
Použitie triedy:
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Zadaj graf:");
Graph g = readGraph(scanner, GraphType.DIRECTED_SUCCESSOR_LISTS);
System.out.println("Zadaj pociatocny a koncovy vrchol:");
int from = scanner.nextInt();
int to = scanner.nextInt();
LongestPath longestPath = new LongestPath(g, from, to);
List<Integer> longest = longestPath.getLongestPath();
if (longest != null) {
System.out.println("Najdlhsia cesta: " + longest);
} else {
System.out.println("Ziadna cesta neexistuje.");
}
}
Príklad výstupu pre graf na obrázku vpravo, počiatočný vrchol 0 a koncový vrchol 3:
Najdlhsia cesta: [0, 1, 2, 4, 3]