Prednáška 10

Oznamy

• Dnes 22:00 termín odovzdania DÚ1
• Dnes po prednáške sa objaví zadanie DÚ2
• Zajtrajšia rozcvička bude z dnešnej prednášky
• Tento týždeň neplánujeme na piatok bonusovú rozcvičku, cvičenia sa však budú konať
• Budúci pondelok je sviatok, prednáška nebude
• Budúci utorok prvú polovicu cvičení bude rozcvička na papieri (krátky test podobne ako na prednáške 4.10.).
  • Bude zahŕňať učivo po dnešnú prednášku
  • Môžete si priniesť ťahák 1 list A4. Používanie počítača nebude povolené.
  • Po odovzdaní testu môžete riešiť zadané úlohy na počítači (bude ich menej)

Opakovanie rekurzie

• Rekurzívna definícia: určitý objekt definujeme pomocou menších objektov toho istého typu
  • Napr. Fibonacciho čísla F(n) = F(n-1) + F(n-2)
  • Nezabudnime na triviálne prípady, napr. F(0)=0, F(1)=1

• Rekurzívne definície vieme často priamočiaro zapísať do rekurzívnych funkcií

int fib(int n){
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        return fib(n - 1) + fib(n - 2);
    }
}

• V rekurzívnej funkcii riešime problém pomocou menších podproblémov toho istého typu
  • Napríklad aby sme našli číslo x v utriedenom poli medzi indexami left a right, potrebujeme ho porovnať so stredným prvkom tohoto intervalu a potom riešiť tú istú úlohu pre menší interval
  • Aj keď sme pôvodne chceli hľadať prvok v celom poli, úlohu rozšírime o parametre left a right, aby sa dala spraviť rekurzia

int find(int a[], int left, int right, int x) {
    if (left > right) {
        return -1;
    }
    int index = (left + right) / 2;
    if (a[index] == x) {
        return index;
    }
    else if (a[index] < x) {
        return find(a, index+1, right, x);
    }
    else {
        return find(a, left, index - 1, x);
    }
}

Zásobník volaní

Druhý pohľad na rekurziu je dynamický: môžeme simulovať, čo sa v programe deje so zásobníkom volaní (call stack)

• Skúsme napríklad odsimulovať, čo sa deje ak vo funkcii main zavoláme fib(3)
• Kvôli prehľadnosti si fib rozpíšeme na viac riadkov:

#include <iostream>
using namespace std;

int fib(int n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        int a = fib(n - 1); // riadok (A)
        int b = fib(n - 2); // riadok (B)
        return a+b;
    }
}

int main() {
    int x = fib(3);    // riadok (C)
    cout << x << endl; 
}

Tu je priebeh programu (obsah zásobníka)

(1)          (2)                      (3)

                                       fib n=2
              fib n=3                  fib n=3, a=?, b=?, riadok A
main, x=?     main, x=?, riadok C      main, x=?, riadok C

(4)                             (5)
 
fib n=1                         
fib n=2, a=?, b=?, riadok A     fib n=2, a=1, b=?, riadok A
fib n=3, a=?, b=?, riadok A     fib n=3, a=?, b=?, riadok A
main, x=?, riadok C             main, x=?, riadok C             


(6)                             (7)
 
fib n=0                         
fib n=2, a=1, b=?, riadok B     fib n=2, a=1, b=0, riadok B
fib n=3, a=?, b=?, riadok A     fib n=3, a=?, b=?, riadok A
main, x=?, riadok C             main, x=?, riadok C             


(8)                             (9)

                                fib n=1
fib n=3, a=1, b=?, riadok A     fib n=3, a=1, b=?, riadok B 
main, x=?, riadok C             main, x=?, riadok C                 


(10)                            (11)

fib n=3, a=1, b=1, riadok B     
main, x=?, riadok C             main, x=2, riadok C 

Postupnosť volaní počas výpočtu vieme znázorniť aj stromovým diagramom:

Pozor, priamočiary rekurzívny zápis výpočtu Fibonacciho čísel je neefektívny, lebo výpočet Fibonacciho čísel sa opakuje

• Napr. pre n=5 počítame fib(2) trikrát, pre n=6 päťkrát a pre n=20 až 4181-krát

Vypisovanie variácií s opakovaním

Vypíšte všetky trojice cifier, pričom každá cifra je z množiny {0..n-1} a cifry sa môžu opakovať (variácie 3-tej triedy z n prvkov). Napr. pre n=2:

000
001
010
011
100
101
110
111

Veľmi jednoduchý program s troma cyklami:

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n;
    for(int i=0; i<n; i++) {
        for(int j=0; j<n; j++) {
            for(int k=0; k<n; k++) {
                cout << i << j << k << endl;
            }
        }
    }
}

Rekurzívne riešenie pre všeobecné k

Čo ak chceme k-tice pre všeobecné k? Využijeme rekurziu.

• Variácie k-tej triedy vieme rozdeliť na n skupín podľa prvého prvku:
  • tie čo začínajú na 0, tie čo začínajú na 1, ..., tie čo začínajú na n-1.
• V každej skupine ak odoberieme prvý prvok, dostaneme variácie triedy k-1

#include <iostream>
using namespace std;

void vypis(int a[], int k) {
    for (int i = 0; i < k; i++) {
        cout << a[i];
    }
    cout << endl;
}

void generuj(int a[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        vypis(a, k);
    } else {
        for (int x = 0; x < n; x++) {
            a[i] = x;
            generuj(a, i + 1, k, n);
        }
    }
}

int main() {
    const int maxK = 100;
    int a[maxK];
    int k, n;
    cout << "Zadajte k a n: ";
    cin >> k >> n;
    generuj(a, 0, k, n);
}

Strom rekurzívnych volaní pre k=3, n=2 (generuj je skrátené na gen, červenou je zobrazený obsah poľa a):

Ďalšie rozšírenia

• Čo ak chceme všetky k-tice písmen A-Z?
• Čo ak chceme všetky DNA reťazce dĺžky k (DNA pozostáva z "písmen" A,C,G,T)?

// pouzi n=26
void vypis(int a[], int k) {
    for (int i = 0; i < k; i++) {
        char c = 'A'+a[i];
        cout << c;
    }
    cout << endl;
}

// pouzi n=4
void vypis(int a[], int k) {
    char abeceda[5] = "ACGT";
    for (int i = 0; i < k; i++) {
        cout << abeceda[a[i]];
    }
    cout << endl;
}

Cvičenia

• Ako by sme vypisovali všetky k-ciferné hexadecimálne čísla (šestnástková sústava), kde používame cifry 0-9 a písmená A-F?
• Ako by sme vypisovali všetky k-tice písmen v opačnom poradí, od ZZZ po AAA?

Variácie bez opakovania

Teraz chceme vypísať všetky k-tice cifier z množiny {0, ..., n-1}, v ktorých sa žiaden prvok neopakuje (pre k=n dostávame permutácie)

Príklad pre k=3, n=3

012
021
102
120
201
210

Skúšanie všetkých možností

• Jednoduchá možnosť: použijeme predchádzajúci program a pred výpisom skontrolujeme, či je riešenie správne

Prvý pokus:

bool spravne(int a[], int k, int n) {
    /* je v poli a dlzky k kazde cislo od 0 po n-1 najviac raz? */
    bool bolo[maxN];
    for (int i = 0; i < n; i++) {
        bolo[i] = false;
    }
    for (int i = 0; i < k; i++) {
        if (bolo[a[i]]) return false;
        bolo[a[i]] = true;
    }
    return true;
}

void generuj(int a[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        if (spravne(a, k, n)) {
            vypis(a, k);
        }
    } else {
        for (int x = 0; x < n; x++) {
            a[i] = x;
            generuj(a, i + 1, k, n);
        }
    }
}

Cvičenie: ako by sme napísali funkciu spravne, ak by nedostala ako parameter hodnotu n?

Prehľadávanie s návratom, backtracking

• Predchádzajúce riešenie je neefektívne, lebo prechádza cez všetky variácie s opakovaním a veľa z nich zahodí.
  • Napríklad pre k=7 a n=10 pozeráme 10⁷ variácií s opakovaním, ale iba 604800 z nich je správnych, čo je asi 6%
• Len čo sa v poli a vyskytne opakujúca sa cifra, chceme túto vetvu prehľadávania ukončiť, lebo doplnením ďalších cifier problém neodstránime
• Spravíme funkciu moze(a,i,x), ktorá určí, či je možné na miesto i v poli a dať cifru x
• Testovanie správnosti vo funkcii generuj sa dá vynechať

bool moze(int a[], int i, int x) {
    /* Mozeme dat hodnotu x na poziciu i v poli a?
     * Mozeme, ak sa nevyskytuje v a[0..i-1] */
    for (int j = 0; j < i; j++) {
        if (a[j] == x) return false;
    }
    return true;
}

void generuj(int a[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        vypis(a, k);
    } else {
        for (int x = 0; x < n; x++) {
            if (moze(a, i, x)) {
                a[i] = x;
                generuj(a, i + 1, k, n);
            }
        }
    }
}

Možné zrýchlenie: vytvoríme trvalé pole bolo, v ktorom bude zaznamené, ktoré cifry sa už vyskytli a to použijeme namiesto funkcie moze.

• Po návrate z rekurzie nesmieme zabudúť príslušnú hodnotu odznačiť!

void generuj(int a[], bool bolo[], int i, int k, int n) {
    /* v poli a dlzky k mame prvych i cifier,
     * v poli bolo mame zaznamenane, ktore cifry su uz pouzite,
     * chceme vygenerovat vsetky moznosti
     * poslednych k-i cifier */
    if (i == k) {
        vypis(a, k);
    } else {
        for (int x = 0; x < n; x++) {
            if (!bolo[x]) {
                a[i] = x;
                bolo[x] = true;
                generuj(a, bolo, i + 1, k, n);
                bolo[x] = false;
            }
        }
    }
}

int main() {
    const int maxK = 100;
    const int maxN = 100;
    int a[maxK];
    bool bolo[maxN];
    int k, n;
    cout << "Zadajte k a n (k<=n): ";
    cin >> k >> n;
    for (int i = 0; i < n; i++) {
        bolo[i] = false;
    }
    generuj(a, bolo, 0, k, n);
}

Cvičenie: ako potrebujeme zmeniť program, aby sme generovali všetky postupnosti k cifier z množiny {0,..,n-1}, také, že z každej cifry sú v postupnosti najviac 2 výskyty?

Technika rekurzívneho prehľadávania všetkých možností s orezávaním beznádejných vetiev sa nazýva prehľadávanie s návratom alebo backtracking.

• Hľadáme všetky postupnosti, ktoré spĺňajú nejaké podmienky
  • Vo všeobecnosti nemusia byť rovnako dlhé
• Ak máme celú postupnosť, vieme otestovať, či spĺňa podmienku (funkcia spravne)
• Ak máme časť postupnosti a nový prvok, vieme otestovať, či po pridaní tohto prvku má ešte šancu tvoriť časť riešenia (funkcia moze)
  • Funkcia moze nesmie vrátiť false, ak ešte je možné riešenie
  • Môže vrátiť true, ak už nie je možné riešenie, ale nevie to ešte odhaliť
  • Snažíme sa však odhaliť problém čím skôr

Všeobecná schéma

void generuj(int a[], int i) {
    /* v poli a dlzky k mame prvych i cisel z riesenia */
    if (spravne(a, i)) { 
        /* ak uz mame cele riesenie, vypiseme ho */
        vypis(a, i);
    } else {
        pre vsetky hodnoty x {
            if (moze(a,i,x)) {
                a[i] = x;
                generuj(a, i + 1);
            }
        }
    }
}

Prehľadávanie s návratom môže byť vo všeobecnosti veľmi pomalé, čas výpočtu exponenciálne rastie.

Generovanie všetkých podmnožín

Chceme vypísať všetky podmnožiny množiny {0,..,m-1}. Na rozdiel od variácií nám v podmnožine nezáleží na poradí (napr. {0,1} = {1,0}), prvky teda budeme vždy vypisovať od najmenšieho po najväčší. Napr. pre m=2 máme podmnožiny

{}
{0}
{1}
{0,1}

Podmnožinu vieme vyjadriť ako binárne pole dĺžky m,

• a[i]=0 znamená, že i nepatrí do množiny a a[i]=1 znamená, že patrí.
• Napríklad podmnožinu {0,2,3} množiny {0,1,2,3,4} sa zapíše ako pole 1,0,1,1,0.

Teda môžeme použiť predchádzajúci program pre n=2, k=m a zmeniť iba výpis:

void vypis(int a[], int m) {
    cout << "{";
    bool prve = true;
    for (int i = 0; i < m; i++) {
        if (a[i] == 1) {
            if (prve) {
                cout << "" << i;
                prve=false;
            } else {
                cout << "," << i;
            }
        }
    }
    cout << "}" << endl;
}

• V premennej prve si pamätáme, či máme oddeliť ďalšie vypisované číslo od predchádzajúceho.
  • Ak ešte žiadne nebolo, oddeľovač je prázdny reťazec.
  • Ak už sme niečo vypísali, oddeľovač je čiarka.

Namiesto poľa intov môžeme použiť pole boolovských hodnôt a celý program trochu prispôsobiť tomu, že generujeme podmnožiny:

#include <iostream>
#include <cstring>
using namespace std;

void vypis(bool a[], int m) {
    cout << "{";
    bool prve = true;
    for (int i = 0; i < m; i++) {
        if (a[i]) {
            if (prve) {
                cout << "" << i;
                prve=false;
            } else {
                cout << "," << i;
            }
        }
    }
    cout << "}" << endl;
}

void generuj(bool a[], int i, int m) {
    /* v poli a dlzky k mame rozhodnutie o prvych i
     * prvkoch, chceme vygenerovat vsetky podmnoziny
     * prvkov {i..m-1} */
    if (i == m) {
        vypis(a, m);
    } else {
        a[i] = true;
        generuj(a, i + 1, m);
        a[i] = false;
        generuj(a, i + 1, m);
    }
}

int main() {
    const int maxM = 100;
    int m;
    cin >> m;
    bool a[maxM];
    generuj(a, 0, m);
}

Pre n=3 program vypíše:

{0,1,2}
{0,1}
{0,2}
{0}
{1,2}
{1}
{2}
{}

Cvičenie: Čo by program vypísal, ak by sme prehodili true a false v rekurzii?

Problém batoha (Knapsack problem)

Metódu prehľadávania s návratom využijeme na riešenie problému batoha. Ide o dôležitý problém, s ktorým sa ešte počas štúdia stretnete. Predstaviť si ho môžeme napríklad takto:

• Zlodej sa vlúpal do obchodu, v ktorom našiel niekoľko predmetov.
• Pozná cenu aj hmotnosť predmetov.
• Z obchodu dokáže odniesť iba lup nepresahujúci nosnosť svojho batoha.
• Ktoré predmety má zlodej odcudziť, aby ich celková hmotnosť nepresahovala nosnosť batoha a aby odišiel s čo najcennejším lupom?

Vstup nášho programu bude vyzerať napríklad nejako takto:

Zadaj pocet predmetov v obchode: 3
Zadaj hmotnost a cenu predmetu cislo 1: 5 9
Zadaj hmotnost a cenu predmetu cislo 2: 4 6
Zadaj hmotnost a cenu predmetu cislo 3: 4 4
Zadaj nosnost batoha: 8

Výstup programu na horeuvedenom vstupe potom bude takýto:

Zober nasledujuce predmety: 2 3
Celkova hodnota lupu: 10

Pri reálnom použití nosnosť batoha môže reprezentovať dostupné zdroje, napr. výpočtový čas na serveri, dostupných pracovníkov, veľkosť rozpočtu a pod, a predmety sú potenciálne úlohy, z ktorých si chceme vybrať podmnožinu, ktorú by sme s danými zdrojmi vedeli vykonať a dosiahnuť čo najvyšší zisk alebo iný ukazovateľ.

Prvé riešenie: preskúmanie všetkých možných výberov

• Preskúmame všetky podmnožiny množiny predmetov v obchode, čiže všetky potenciálne lupy.
• Na to upravíme program generujúci všetky podmnožiny danej množiny.
• Pre každú podmnožinu namiesto výpisu spravíme nasledovné:
  • Spočítame celkovú hmotnosť a cenu nájdeného potenciálneho lupu.
  • Ak hmotnosť tohto lupu nepresahuje nosnosť batoha, porovnáme jeho cenu s najlepším doposiaľ nájdeným lupom.
  • Ak je cennejší, ako doposiaľ najlepší lup, ide o nového kandidáta na optimálny lup a zapamätáme si ho.

• Pre jednoduchosť použijeme v programe globálne premenné, lebo potrebujeme veľa údajov
  • Globálne premenné spôsobujú problémy vo väčších programoch: mená premenných sa môžu "biť", môžeme si omylom prepísať číslo dôležité v inej časti programu
  • Mohli by sme si tiež spraviť struct obsahujúci všetky premenné potrebné v rekurzii a odovzdávať si ten

Podmnožiny budeme reprezentovať poľom typu bool, v ktorom si pre každý predmet pamätáme, či do danej podmnožiny patrí.

#include <iostream>
using namespace std;

const int maxN = 100;

/* Struktura reprezentujuca jeden predmet */
struct predmet {
    int hmotnost;
    int cena;
}; 

/* Globalne premenne pouzivane v rekurzii: */

// pocet predmetov v obchode
int N;                         
// pole s udajmi o jednotlivych predmetoch
predmet a[maxN];                 
// nosnost batoha
int nosnost;                     

// najcennejsi doposial najdeny potencialny lup (na uvod neinicializovany)
bool najlepsiLup[maxN];          
// jeho cena (kazdy lup bude urcite cennejsi ako -1)
int cenaNajlepsiehoLupu = -1;    

int spocitajHmotnostLupu(bool lup[]) {
    int hmotnost = 0;
    for (int i = 0; i < N; i++) {
        if (lup[i]) {
            hmotnost += a[i].hmotnost;
        }
    }
    return hmotnost;
}

int spocitajCenuLupu(bool lup[]) {
    int cena = 0;
    for (int i = 0; i < N; i++) {
        if (lup[i]) {
            cena += a[i].cena;
        }
    }
    return cena;
}

void vypisLup(bool lup[]) {
    cout << "Zober nasledujuce predmety:";
    for (int i = 0; i < N; i++) {
        if (lup[i]) {
             cout << " " << i + 1;
        }            
    }
    cout << endl;
}

/* Generovanie vsetkych moznych lupov (podmnozin predmetov) */
void generujLupy(bool lup[], int index) {
    /* V poli lup[] dlzky N postupne generujeme podmnoziny predmetov.
       O hodnotach prvkov lup[0],...,lup[index-1] uz je rozhodnute.
       Postupne vygenerujeme vsetky moznosti pre lup[index],...,lup[N-1].
       Kazdy vysledny lup porovname s doposial najlepsim 
       a v pripade potreby optimum aktualizujeme.    
    */
    if (index == N) {                                
        // Lup je vygenerovany; zisti, ci ho batoh unesie.                               
        if (spocitajHmotnostLupu(lup) <= nosnost) {  
            // Ak ano, porovnaj cenu lupu s doposial najlepsim.
            int cenaLupu = spocitajCenuLupu(lup);
            if (cenaLupu > cenaNajlepsiehoLupu) {    
                // Ak je najdeny lup drahsi, uloz ho
                cenaNajlepsiehoLupu = cenaLupu;
                for (int i = 0; i < N; i++) {
                    najlepsiLup[i] = lup[i];
                } 
            }
        }
    } else {                                         
        // Lup este nie je vygenerovany,
        // skus obe moznosti pre lup[index]. 
        lup[index] = false;
        generujLupy(lup, index+1);
        lup[index] = true;
        generujLupy(lup, index+1);
    }
} 

int main() {
    cout << "Zadaj pocet predmetov v obchode: ";
    cin >> N;
    for (int i = 0; i < N; i++) {
        cout << "Zadaj hmotnost a cenu predmetu cislo " << (i+1) << ": ";
        cin >> a[i].hmotnost >> a[i].cena;
    }
    cout << "Zadaj nosnost batoha: ";
    cin >> nosnost;
    
    bool lup[maxN];
    generujLupy(lup, 0);
    
    cout << endl;
    vypisLup(najlepsiLup);
    cout << "Celkova hodnota lupu: " << cenaNajlepsiehoLupu << endl;
}

Cvičenie: čo sa stane, keď každý predmet má hmotnosť väčšiu ako nosnosť batoha?

Optimalizácia č. 1: ukončenie prehľadávania vždy, keď je prekročená nosnosť

Keď je už po vygenerovaní nejakej podmnožiny (čiže prvých niekoľko hodnôt poľa lup) jasné, že hmotnosť lupu bude presahovať nosnosť batoha, možno túto vetvu prehľadávania ukončiť.

Okrem samotnej funkcie generujLupy je potrebné prispôsobiť aj funkciu spocitajHmotnostLupu tak, aby ju bolo možné aplikovať aj na neúplne vygenerované podmnožiny.

/* Potrebujeme vediet spocitat hmotnost len pre cast predmetov: */

int spocitajHmotnostLupu(bool lup[], int pokial) {
    int hmotnost = 0;
    for (int i = 0; i <= pokial; i++) {
        if (lup[i]) {
            hmotnost += a[i].hmotnost;
        }
    }
    return hmotnost;
}

void generujLupy(bool lup[], int index) {
    if (spocitajHmotnostLupu(lup, index-1) > nosnost) {
        // Ak dosial vygenerovana cast lupu presahuje nosnost batoha, 
        // mozno prehladavanie ukoncit
        return;  
    }
    if (index == N) {
        int cenaLupu = spocitajCenuLupu(lup);
        if (cenaLupu > cenaNajlepsiehoLupu) {
            cenaNajlepsiehoLupu = cenaLupu;
            for (int i = 0; i < N; i++) {
                najlepsiLup[i] = lup[i];
            } 
        }
    } else {
        lup[index] = false;
        generujLupy(lup, index+1);
        lup[index] = true;
        generujLupy(lup, index+1);
    }
}

Optimalizácia č. 2: hmotnosť a cenu lupu netreba zakaždým počítať odznova

Predchádzajúci program vždy znovu a znovu prepočítava hmotnosť a cenu lupu, aj keď sa zoznam vybraných predmetov zmení iba trochu. Namiesto toho môžeme cenu a hmotnosť doposiaľ vygenerovanej časti lupu predávať funkcii generuj ako parameter.

#include <iostream>
using namespace std;

const int maxN = 100;

struct predmet {
    int hmotnost;
    int cena;
}; 

int N;
predmet a[maxN];
int nosnost;

bool najlepsiLup[maxN];
int cenaNajlepsiehoLupu = -1;

void vypisLup(bool lup[]) {
    cout << "Zober nasledujuce predmety:";
    for (int i = 0; i < N; i++) {
        if (lup[i]) {
            cout << " " << i + 1;
        }    
    }
    cout << endl;
}

void generujLupy(bool lup[], int index, int hmotnostLupu, int cenaLupu) {
    if (hmotnostLupu > nosnost) {
        return;
    }
    if (index == N) {
        if (cenaLupu > cenaNajlepsiehoLupu) {
            cenaNajlepsiehoLupu = cenaLupu;
            for (int i = 0; i < N; i++) {
                najlepsiLup[i] = lup[i];
            } 
        }
    } else {
        lup[index] = false;
        generujLupy(lup, index+1, hmotnostLupu, cenaLupu);
        lup[index] = true;
        generujLupy(lup, index+1, hmotnostLupu + a[index].hmotnost, 
                    cenaLupu + a[index].cena);
    }
} 

int main() {
    cout << "Zadaj pocet predmetov v obchode: ";
    cin >> N;
    for (int i = 0; i < N; i++) {
        cout << "Zadaj hmotnost a cenu predmetu cislo " << (i+1) << ": ";
        cin >> a[i].hmotnost >> a[i].cena;
    }
    cout << "Zadaj nosnost batoha: ";
    cin >> nosnost;
    
    bool lup[maxN];
    // Doposial nie je nic vygenerovane; hmotnost aj cena lupu su zatial nulove
    generujLupy(lup, 0, 0, 0); 
    
    cout << endl;
    vypisLup(najlepsiLup);
    cout << "Celkova hodnota lupu: " << cenaNajlepsiehoLupu << endl;
}

Problém 8 dám

Prehľadávanie s návratom sa dá využiť aj na riešenie rôznych hlavolamov. Tu si ukážeme jeden z nich.

Cieľom je rozmiestniť n dám na šachovnici nxn tak, aby sa žiadne dve navzájom neohrozovali, tj. aby žiadne dve neboli v rovnakom riadku, stĺpci, ani na rovnakej uhlopriečke.

Príklad pre n=4:

 . * . .
 . . . *
 * . . .
 . . * .

• V každom riadku bude práve jedna dáma, teda riešenie môžeme reprezentovať ako pole damy dĺžky n, kde damy[i] je stĺpec, v ktorom je dáma na riadku i
  • Príklad vyššie by v poli damy mal čísla 1,3,0,2
• Podobne ako pri generovaní variácií bez opakovania chceme do poľa dať čísla od 1 po n, aby spĺňali ďalšie podmienky (v každom stĺpci a na každej uhlopriečke najviac 1 dáma)
• Vytvoríme polia, kde si pre každý stĺpec a uhlopriečku pamätáme, či už je obsadená
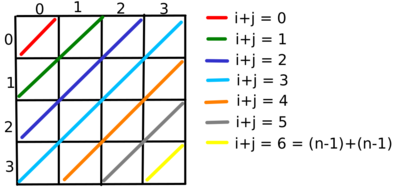
• Uhlopriečky v oboch smeroch očíslujeme číslami od 0 po 2n-2
  • V jednom smere majú miesta na uhlopriečke rovnaký súčet, ten teda bude číslom uhlopriečky
  • V druhom smere majú rovnaký rozdiel, ten však môže byť aj záporný, pričítame n-1

#include <iostream>
using namespace std;

/* globalne premenne */
const int maxN = 100;
int n;
int damy[maxN];       /* damy[i] je stlpec s damou v riadku i*/
bool bolStlpec[maxN]; /* bolStlpec[i] je true ak stlpec i obsadeny */

/* polia ktore obsahuju true ak uhlopriecky obsadene */
bool bolaUhl1[2 * maxN - 1];  
bool bolaUhl2[2 * maxN - 1];
int pocet;       /* pocet najdenych rieseni */

int uhl1(int i, int j) {
    /* na ktorej uhlopriecke je riadok i, stlpec j v smere 1? */
    return i + j;
}

int uhl2(int i, int j) {
    /* na ktorej uhlopriecke je riadok i, stlpec j v smere 2? */
    return n - 1 + i - j;
}

void vypis() {
    /* vypis sachovnicu textovo a zvys pocitadlo rieseni */
    pocet++;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (damy[i] == j) cout << " *";
            else cout << " .";
        }
        cout << endl;
    }
    cout << endl;
}

void generuj(int i) {
    /* v poli damy mame prvych i dam, dopln dalsie */
    if (i == n) {
        vypis();
    } else {
        for (int j = 0; j < n; j++) {
            /* skus dat damu na riadok i, stlpec j */
            if (!bolStlpec[j]
                && !bolaUhl1[uhl1(i, j)] 
                && !bolaUhl2[uhl2(i, j)]) {
                damy[i] = j;
                bolStlpec[j] = true;
                bolaUhl1[uhl1(i, j)] = true;
                bolaUhl2[uhl2(i, j)] = true;
                generuj(i + 1);
                bolStlpec[j] = false;
                bolaUhl1[uhl1(i, j)] = false;
                bolaUhl2[uhl2(i, j)] = false;
            }
        }
    }
}

int main() {
    cout << "Zadajte velkost sachovnice: ";
    cin >> n;
    for (int i = 0; i < n; i++) {
        bolStlpec[i] = false;
    }
    for (int i = 0; i < 2 * n + 1; i++) {
        bolaUhl1[i] = false;
        bolaUhl2[i] = false;
    }

    /* rekuzia */
    pocet = 0;
    generuj(0);
    cout << "Pocet rieseni: " << pocet << endl;
}

Zhrnutie

• Videli sme ako rekurzívne generovať všetky postupnosti spĺňajúce určité požiadavky
• Ak máme špeciálne požiadavky, napr. že žiadne číslo sa neopakuje, môžeme buď generovať všetky k-tice a testovať to pred výpisom, alebo už počas generovania urezávať neperspektívne vetvy výpočtu, čo je rýchlejšie
• Táto technika sa volá prehľadávanie s návratom (backtracking)
• Pozor, čas výpočtu prudko (exponenciálne) rastie s dĺžkou postupností, takže vhodné len pre malé vstupy.
• Dve ukážky: problém batoha, problém 8 dám.