Programovanie (1) v C/C++
1-INF-127, ZS 2024/25
Prednáška 22: Rozdiel medzi revíziami
| Riadok 299: | Riadok 299: | ||
} | } | ||
for (int i = 0; word[i] != 0; i++) { | for (int i = 0; word[i] != 0; i++) { | ||
| − | + | int c = word[i] - 'a'; | |
| + | assert(c >= 0 && c < alphSize); | ||
| + | v = v->children[c]; | ||
if (v == NULL) { | if (v == NULL) { | ||
return false; | return false; | ||
Verzia zo dňa a času 21:55, 11. december 2021
Obsah
Oznamy
Plán prednášok a cvičení na zvyšok semestra:
- Dnes pokračujeme stromy.
- V utorok 14.12. v rámci cvičení tréning na skúšku.
- Na testovači už sú tréningové príklady na skúšku. Za niektoré budete môcť získať bonusový bod, ak ich vyriešite do 12.1. (ako tréning sa dajú riešiť aj neskôr). V utorok na cvičeniach pribudne ešte jeden tréningový príklad za 4 body. Ak prídete na cvičenia a odovzdáte na konci aspoň rozumne rozrobenú verziu programu, získate jeden bonusový bod, aj keď ho nestihnete dokončiť.
- V stredu 15.12. ak treba dokončíme stromy, potom nepovinná prednáška o nepreberaných črtách jazykov C a C++ (táto nepovinná časť učiva nebude vyžadovaná na skúške, ale môžete ju použiť).
- V piatok 17.12. od 12:00 predtermín skúšky, doplnkové cvičenia nebudú
Binárne vyhľadávacie stromy
Opakovanie
Binárny vyhľadávací strom (binary search tree) je dátová štruktúra určená na ukladanie dynamickej množiny prvkov.
- V binárnom vyhľadávacom strome má každý vrchol 0, 1 alebo 2 deti
- V každom vrchole máme položku s dátami (pre jednoduchosť typu int)
- Pre každý vrchol v stromu platí:
- Každý vrchol v ľavom podstrome v má hodnotu data menšiu ako vrchol v
- Každý vrchol v pravom podstrome v má hodnotu data väčšiu ako vrchol v
struct node {
/* vrchol binárneho vyhľadávacieho stromu */
int data; /* hodnota */
node * parent; /* rodič vrchola, NULL v koreni */
node * left; /* ľavé dieťa, NULL ak neexistuje */
node * right; /* pravé dieťa, NULL ak neexistuje */
};
/* Samotná štruktúra binárneho vyhľadávacieho stromu (obal pre používateľa). */
struct binarySearchTree {
node *root; /* koreň stromu, NULL pre prázdny strom */
};
Videli sme vyhľadávanie prvku v binárnom vyhľadávacom strome. Čas výpočtu je v najhoršom prípade úmerný výške stromu.
Vkladanie do binárneho vyhľadávacieho stromu
Nasledujúca funkcia insertNode vloží uzol *v na správne miesto podstromu zakoreneného v *root ako jeho list.
- Predpokladáme, že prvok v strome nie je.
- Putujeme po strome podobne ako pri vyhľadávaní prvku, až kým nenarazíme na nulový smerník.
- Na tomto mieste by mal byť nový prvok, takže ho tam pridáme ako nový list
- Uvádzame rekurzívnu verziu, dá sa aj cyklom, podobne ako pri hľadaní
- Funkcia bstInsert vytvorí uzol s daným kľúčom key a pomocou funkcie insertNode ho vloží do binárneho vyhľadávacieho stromu t.
/* Vloží uzol v na správne miesto podstromu zakoreneného v root */
void insertNode(node *root, node *v) {
assert(root != NULL && v != NULL);
if (v->data < root->data) {
if (root->left == NULL) {
root->left = v;
v->parent = root;
} else {
insertNode(root->left, v);
}
} else {
if (root->right == NULL) {
root->right = v;
v->parent = root;
} else {
insertNode(root->right, v);
}
}
}
/* Vloží do stromu t nový uzol s kľúčom key. */
void bstInsert(binarySearchTree &t, int key) {
node *v = new node;
v->data = key;
v->left = NULL;
v->right = NULL;
v->parent = NULL;
if (t.root == NULL) {
t.root = v;
} else {
insertNode(t.root, v);
}
}
Čas vkladania je tiež v najhoršom prípade úmerný hĺbke stromu.
Cvičenia
- Napíšte nerekurzívny variant funkcie insertNode.
- Napíšte funkciu treeSort, ktorá z poľa celých čísel a pomocou volaní funkcie bstInsert vytvorí binárny vyhľadávací strom a následne pomocou prehľadávania tohto stromu v poradí inorder pole a utriedi.
- Ako bude vyzerať strom po nasledujúcej postupnosti operácií?
binarySearchTree t;
bstInit(t);
bstInsert(t, 2);
bstInsert(t, 5);
bstInsert(t, 3);
bstInsert(t, 10);
bstInsert(t, 7);
Minimum a následník
Uvedieme teraz dve funkcie, ktoré sa zídu pri mazaní prvku zo stromu, ale môžu sa zísť aj inokedy.
Prvá funkcia minNode nájde vo vyhľadávacom strome uzol, v ktorom je uložená najmenšia hodnota.
- Všetky prvky menšie ako koreň sú v ľavom podstrome, bude tam zrejme aj minimum.
- Tá istá úvaha platí pre koreň ľavého podstromu.
- Ideme teda doľava kým sa dá, posledný vrchol vrátime (list alebo vrchol, ktorý má iba pravé dieťa).
- Nie je treba teda prechádzať celý strom a nemusíme sa ani pozerať na položku data v uzloch.
- Dá sa napísať cyklom aj rekurzívne.
- Obalom pre používateľa bude funkcia bstMin, ktorá pomocou funkcie minNode nájde minimálny kľúč v danom binárnom vyhľadávacom strome t.
/* Vrati uzol s minimalnou hodnotou data v podstrome s korenom v. */
node *minNode(node *v) {
assert(v != NULL);
while (v->left != NULL) {
v = v->left;
}
return v;
}
/* Vrati minimalny kluc uzla v strome t. */
int bstMin(binarySearchTree &t) {
assert(t.root != NULL);
return minNode(t.root)->data;
}
Cvičenia:
- Napíšte rekurzívny variant funkcie minNode.
- Ako by bolo treba funkciu zmeniť, aby hľadala maximum?
Funkcia successorNode nájde pre daný uzol v jeho následníka (angl. successor) v binárnom vyhľadávacom strome, čiže uzol, ktorý vo vzostupnom poradí podľa kľúčov nasleduje bezprostredne za uzlom v.
- Ak má uzol v pravé dieťa, následník uzla v bude vrchol s minimálnou hodnotou data v pravom podstrome
- V opačnom prípade môže byť následníkom uzla v jeho rodič, ak v je jeho ľavé dieťa.
- Ak je v pravým dieťaťom svojho rodiča, môže to byť jeho prarodič (ak je rodič uzla v ľavým dieťaťom tohto prarodiča), atď.
- Vo všeobecnosti teda ide o najbližšieho predka uzla v takého, že v patrí do jeho ľavého podstromu.
- V strome existuje práve jeden uzol bez následníka (najväčší prvok).
- Ako presne sa bude funkcia nižšie pre tento prvok správať?
/* Vrati uzol, ktory vo vzostupnom poradi uzlov podla klucov nasleduje za v. Ak taky uzol neexistuje, vrati NULL. */
node *successorNode(node *v) {
assert(v != NULL);
if (v->right != NULL) {
return minNode(v->right);
}
while (v->parent != NULL && v == v->parent->right) {
v = v->parent;
}
return v->parent;
}
Mazanie z binárneho vyhľadávacieho stromu
Nasledujúca funkcia bstRemove zmaže z binárneho vyhľadávacieho stromu t uzol s kľúčom key (ak sa taký uzol v strome vyskytuje).
- Najprv pomocou funkcie findNode nájde uzol v s kľúčom key.
- Ak je v list, jednoducho ho zmažeme.
- Ak má v jedno dieťa, toto dieťa prevesíme priamo pod otca v a v zmažeme.
- Ak má v dve deti, nájdeme nasledovníka v, t.j. minimum v pravom podstrome v.
- Tento nasledovník nemá ľavé dieťa, vieme ho teda zmazať.
- Jeho údaje presunieme do vrcholu v.
- Tiež treba dať pozor na mazanie koreňa.
/* Zmaze zo stromu t uzol s klucom key, ak tam taky je. */
void bstRemove(binarySearchTree &t, int key) {
// Najde uzol v s hodnotou, ktoru treba vymazat.
node *v = findNode(t.root, key);
if (v == NULL) {
return;
}
// Najde uzol *rm stromu t, ktory sa napokon realne zmaze.
node *rm;
if (v->left == NULL || v->right == NULL) {
rm = v;
} else {
rm = successorNode(v);
}
// Ak rm != v, presunie kluc uzla *rm do uzla *v.
if (rm != v) {
v->data = rm->data;
}
// ak ma uzol rm dieta, jeho rodicom bude rodic rm
node *child;
if (rm->left != NULL) {
child = rm->left;
} else {
child = rm->right;
}
if (child != NULL) {
child->parent = rm->parent;
}
if (rm->parent == NULL) {
t.root = child;
} else if (rm == rm->parent->left) {
rm->parent->left = child;
} else if (rm == rm->parent->right) {
rm->parent->right = child;
}
// rm uz nie je v strome, uvolnime jeho pamat
delete rm;
}
Zložitosť jednotlivých operácií
- Časová zložitosť operácií bstFind(t), bstInsert(t) aj bstRemove(t) je úmerná výške stromu t, ktorú označíme h.
- Predminule sme ukázali, že pre strom s n uzlami máme log2(n+1)-1 ≤ h ≤ n-1.
- Zložitosť uvedených operácií je teda v najhoršom prípade lineárna od počtu uzlov stromu (tento prípad nastane, ak prvky vkladáme od najmenšieho po najväčší alebo naopak).
- Dá sa však ukázať, že ak sa prvky vkladajú v náhodnom poradí, výška stromu bude v priemere logaritmická od počtu uzlov.
- Na predmete Algoritmy a dátové štruktúry (druhý ročník) sa tieto tvrdenia dokazujú poriadne a preberajú sa tam aj varianty vyhľadávacích stromov, pre ktoré je zložitosť uvedených operácií logaritmická aj v najhoršom prípade.
Lexikografické stromy
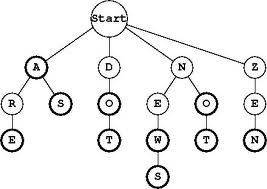
Lexikografické stromy (niekde tiež prefixové stromy; angl. trie zo slova retrieval) sú dátová štruktúra na uchovávanie množiny reťazcov. Ide o stromy, ktoré nemusia byť binárne:
- Uzol lexikografického stromu má najviac toľko detí, koľko je znakov v uvažovanej abecede. Každé dieťa je označené iným znakom abecedy. Graficky si môžeme predstaviť tento znak prislúchajúci k hrane spájajúcej ridiča a dieťa.
- Koreň lexikografického stromu zodpovedá prázdnemu reťazcu.
- Uzol v hĺbke k zodpovedá reťazcu dĺžky k, ktorý dostaneme prečítaním písmen na ceste z koreňa do daného uzla.
- Každý uzol lexikografického stromu obsahuje logickú hodnotu vyjadrujúcu, či k nemu prislúchajúci reťazec patrí do množiny reprezentovanej týmto lexikografickým stromom.
- V korektnom lexikografickom strome všetky listy zodpovedajú reťazcom z reprezentovanej množiny.
- Vnútorné vrcholy môžu zodpovedať reťazcu z množiny alebo iba prefixu jedného alebo viacerých takých reťazcov.
Uzly lexikografickéeho stromu budeme reprezentovať šruktúrou node
- Uzol obsahuje obsahuje booleovskú premennú isWord, v ktorej je uložená informácia o tom, či reťazec prislúchajúci k danému uzlu patrí alebo nepatrí do reprezentovanej množiny a pole children smerníkov na jednotlivé deti daného uzla.
- Veľkosť alphSize tohto poľa je rovná veľkosti uvažovanej abecedy.
- V ukážkovom programe uvažujeme abecedu 'a'..'z'.
const int alphSize = 'z' - 'a' + 1;
struct node {
// pole smernikov na deti
node *children[alphSize];
// udava, ci uzol prislucha k slovu z reprezentovanej mnoziny
bool isWord;
};
Samotný lexikografický strom je potom daný iba smerníkom na svoj koreň:
struct trie {
node *root;
};
Inicializácia a likvidácia lexikografického stromu
Nasledujúca funkcia inicializuje prázdny lexikografický strom t:
void trieInit(trie &t) {
t.root = NULL;
}
Uvoľnenie pamäte alokovanej pre podstrom zakorenený v uzle root realizujeme obdobne ako pri binárnych vyhľadávacích stromoch. Jediný rozdiel spočíva v potenciálne väčšom počte detí uzla root.
void destroySubtree(node *root) {
if (root != NULL) {
for (int i = 0; i < alphSize; i++) {
destroySubtree(root->children[i]);
}
delete root;
}
}
Nasledujúca funkcia potom zlikviduje celý lexikografický strom t:
void trieDestroy(trie &t) {
destroySubtree(t.root);
}
Hľadanie v lexikografickom strome
Funkcia trieFind pre daný lexikografický strom t a reťazec word zistí, či slovo word patrí do množiny reprezentovanej stromom t.
- Postupuje po písmenách reťazca word. Kým nedôjde na koniec slova, snaží sa ísť po hranách, ktoré zodpovedajú jednotlivým písmenám.
- V prípade, že v niektorom bode narazí na NULL, slovo word sa v strome nenachádza.
- V opačnom prípade toto slovo dočíta v nejakom uzle v. V takom prípade slovo word patrí do reprezentovanej množiny práve vtedy, keď v->isWord má hodnotu true.
bool trieFind(trie &t, const char *word) {
node *v = t.root;
if (v == NULL) {
return false;
}
for (int i = 0; word[i] != 0; i++) {
int c = word[i] - 'a';
assert(c >= 0 && c < alphSize);
v = v->children[c];
if (v == NULL) {
return false;
}
}
return v->isWord;
}
Vkladanie do lexikografického stromu
Pri vkladaní reťazca do množiny realizovanej lexikografickým stromom často vznikne potreba vytvárať nové uzly tohto stromu. Túto podúlohu realizuje funkcia createNode, ktorá vytvorí nový uzol s hodnotou isWord danou jej argumentom a so všetkými smerníkmi na deti nastavenými na NULL.
node *createNode(bool isWord) {
node *v = new node;
for (int i = 0; i < alphSize; i++) {
v->children[i] = NULL;
}
v->isWord = isWord;
return v;
}
Vloženie reťazca word do lexikografického stromu t potom realizuje funkcia trieInsert, ktorá pracuje nasledovne:
- Začne v koreni stromu, odkiaľ postupuje nižšie smerom k listom.
- V každom uzle sa pozrie na ďalšie písmeno slova word. Ak danému uzlu chýba dieťa pre toto písmeno, vytvorí ho pomocou funkcie createNode. Následne sa presunie do tohto dieťaťa.
- Ak v nejakom uzle v príde na koniec slova word, nastaví hodnotu v->isWord na true.
void trieInsert(trie &t, const char *word) {
if (t.root == NULL) {
t.root = createNode(false);
}
node *v = t.root;
for (int i = 0; word[i] != 0; i++) {
int c = word[i] - 'a';
if (v->children[c] == NULL) {
v->children[c] = createNode(false);
}
v = v->children[c];
}
v->isWord = true;
}
Vymazávanie z lexikografického stromu
Vymazávanie slov z množiny reprezentovanej lexikografickým stromom budeme realizovať prostredníctvom pomocnej rekurzívnej funkcie removeFromSubtree.
- Funkcia z podstromu zakorenenom v uzle root vymaže sufix reťazca word začínajúci na pozícii index.
- Funkcia vráti booleovskú hodnotu podľa toho, či sa pri tomto vymazaní sufixu z daného podstromu vymazal jeho koreň root.
- Ak sa slovo word v reprezentovanej množine nenachádza, funkcia removeFromSubtree vyhlási chybu pomocou funkcie assert.
Funkcia removeFromSubtree pracuje nasledovne:
- Ak je sufix reťazca word začínajúci na indexe index prázdny, nastaví hodnotu root->isWord na false.
- V opačnom prípade funkcia removeFromSubtree zavolá rekurzívne samú seba pre dieťa zodpovedajúce písmenu na pozícii index reťazca word. Ak toto volanie dané dieťa zmaže, prestaví smerník na toto dieťa na NULL.
- V prípade, že po vykonaní jednej z predchádzajúcich dvoch operácií nemá uzol root žiadne dieťa a súčasne má root->isWord hodnotu false, uvoľní pamäť alokovanú pre uzol root a informáciu o jeho zmazaní vráti na výstupe.
bool removeFromSubtree(node *root, const char *word, int index) {
assert(root != NULL);
if (word[index] == 0) {
assert(root->isWord);
root->isWord = false;
} else {
int c = word[index] - 'a';
bool deleted = removeFromSubtree(root->children[c], word, index + 1);
if (deleted) {
root->children[c] = NULL;
}
}
int numChildren = 0;
for (int i = 0; i < alphSize; i++) {
if (root->children[i] != NULL) {
numChildren++;
}
}
if (numChildren == 0 && !root->isWord) {
delete root;
return true;
} else {
return false;
}
}
Samotné odstránenie reťazca word z množiny reprezentovanej stromom t potom realizuje funkcia trieRemove.
void trieRemove(trie &t, const char *word) {
// zavolame rekurziu pre koren stromu
bool rootRemoved = removeFromSubtree(t.root, word, 0);
// ak bol koren odstraneny, nastavime t.root na NULL
if (rootRemoved) {
t.root = NULL;
}
}
Výška lexikografického stromu
Nasledujúca funkcia vypočíta výšku podstromu zakoreneného v uzle root:
int subtreeHeight(node *root) {
if (root == NULL) {
return -1;
}
int maxHeight = -1;
for (int i = 0; i < alphSize; i++) {
int height = subtreeHeight(root->children[i]);
if (height > maxHeight) {
maxHeight = height;
}
}
return maxHeight + 1;
}
Výšku samotného lexikografického stromu t potom spočíta nasledujúca funkcia:
int trieHeight(trie &t) {
return subtreeHeight(t.root);
}
Vypisovanie slov reprezentovaných lexikografickým stromom
Nasledujúca funkcia printSubtree prehľadáva podstrom zakorenený v uzle root a v reťazci s postupne generuje všetky slová z reprezentovanej množiny, ktoré zároveň vypisuje na konzolu. V parametri index dostane hĺbku aktuálneho vrcholu, t.j. pozíciu, v reťazci, na ktorú pridáme ďalší znak.
void printSubtree(node *root, char *s, int index) {
if (root == NULL) {
return;
}
if (root->isWord) {
s[index] = 0; // ukoncenie retazca pred vypisom
printf("%s\n", s);
}
for (int i = 0; i < alphSize; i++) {
s[index] = 'a' + i;
printSubtree(root->children[i], s, index + 1);
}
}
Funkcia triePrint vypisujúca všetky slová v množine reprezentovanej lexikografickým stromom t najprv spočíta výšku stromu t, ktorá je rovná dĺžke najdlšieho reťazca tejto množiny. Následne dynamicky alokuje reťazec dostatočnej dĺžky na uchovanie každého slova množiny a zavolá funkciu printSubtree pre koreň stromu t.
void triePrint(trie &t) {
int height = trieHeight(t);
if (height >= 0) {
char *s = new char[height + 1];
printSubtree(t.root, s, 0);
delete[] s;
}
}
Abstraktný dátový typ slovník
- ADT dynamická množina reprezentoval dynamickú množinu prvkov s operáciami add, remove a contains.
- Často chceme k jednotlivým kľúčom ukladať aj ďalšie údaje a tieto údaje pre daný kľúč vrátiť.
- Príkladom môže byť zoznam kontaktov, kde kľúčom je meno osoby a pre dané meno chceme vrátiť kontaktné údaje danej osoby (emailová adresa, telefón a pod.)
- ADT s touto funkcionalitou sa nazýva slovník.
- Všetky implementácie množiny vieme priamočiaro rozšíriť na ukladanie takých ďalších údajov.
- Ukážkový program nižšie spočíta výskyty slov v texte. Jednotlivé slová sú kľúčami v slovníku implementovanom pomocou lexikografického stromu a v každom uzle si pamätáme namiesto hodnoty isWord počítadlo, ktoré udáva, koľkokrát sme príslušné slovo videli na vstupe.
Sylaby predmetu
Základy
Konštrukcie jazyka C
- premenné typov int, double, char, bool, konverzie medzi nimi
- podmienky (if, else, switch), cykly (for, while)
- funkcie (a parametre funkcií - odovzdávanie hodnotou, referenciou, smerníkom)
void f1(int x){} //hodnotou
void f2(int &x){} //referenciou
void f3(int* x){} //smerníkom
void f(int a[], int n){} //polia bez & (ostanú zmeny)
void kresli(Turtle &t){} //korytnačky, SVGdraw a pod. s &
Polia, reťazce (char[])
int A[4]={3, 6, 8, 10};
int B[4];
B[0]=3; B[1]=6; B[2]=8; B[3]=10;
char C[100] = "pes";
char D[100] = {'p', 'e', 's', 0};
- funkcie strlen, strcpy, strcmp, strcat
Súbory, spracovanie vstupu
- cin, cout alebo printf, scanf
- fopen, fclose, feof
- fprintf, fscanf
- getc, putc, ungetc, fgets, fputs
- spracovanie súboru po znakoch, po riadkoch, po číslach alebo slovách
Smerníky, dynamicky alokovaná pamäť, dvojrozmerné polia
int i; // „klasická“ celočíselná premenná
int *p; // ukazovateľ na celočíselnú premennú
p = &i; // spravne
p = &(i + 3); // zle i+3 nie je premenna
p = &15; // zle konstanta nema adresu
i = *p; // spravne ak p bol inicializovany
int * cislo = new int; // alokovanie jednej premennej
*cislo = 50;
..
delete cislo;
int a[4];
int *b = a; // a,b su teraz takmer rovnocenne premenne
int *A = new int[n]; // alokovanie 1D pola danej dlzky
..
delete[] A;
int **a; // alokovanie 2D matice
a = new int *[n];
for (int i = 0; i < n; i++) a[i] = new int[m];
..
for (int i = 0; i < n; i++) delete[] a[i];
delete[] a;
Abstraktné dátové typy
Abstraktný dátový typ dynamické pole (rastúce pole)
- operácie init, add, get, set, length
Abstraktný dátový typ dynamická množina (set)
- operácie init, find, insert, remove
- implementácie pomocou
- neutriedeného poľa
- utriedeného poľa
- spájaných zoznamov
- binárnych vyhľadávacích stromov
- hašovacej tabuľky
- lexikografického stromu (ak kľúč je reťazec)
Abstraktné dátové typy rad a zásobník
- operácie pre rad (frontu, queue): init, isEmpty, enqueue, dequeue, peek
- operácie pre zásobník (stack): init, isEmpty, push, pop
- implementácie: v poli alebo v spájanom zozname
- využitie: ukladanie dát na spracovanie, odstránenie rekurzie
- kontrola zátvoriek a vyhodnocovanie výrazov pomocou zásobníka
Dátové štruktúry
Spájané zoznamy
struct node {
int data;
item* next;
};
struct linkedList {
item* first;
};
void insertFirst(linkedList &z, int d){
/* do zoznamu z vlozi na zaciatok novy prvok s datami d */
item* p = new item; // vytvoríme nový prvok
p->data = d; // naplníme dáta
p->next = z.first; // prvok bude prvým prvkom zoznamu (ukazuje na doterajší začiatok)
z.first = p; // tento prvok je novým začiatkom
}
Binárne stromy
struct node {
/* vrchol stromu */
dataType data;
node * left; /* lavy syn */
node * right; /* pravy syn */
};
node * createNode(dataType data, node *left, node *right) {
node *v = new node;
v->data = data;
v->left = left;
v->right = right;
return v;
}
- prehľadávanie inorder, preorder, postorder
- použitie na uloženie aritmetických výrazov
Binárne vyhľadávacie stromy
- vrcholy vľavo od koreňa menší kľúč, vpravo od koreňa väčší
- insert, find, remove v čase závisiacom od hĺbky stromu
Lexikografické stromy
- ukladajú množinu reťazcov
- nie sú binárne: vrchol môže mať veľa synov
- insert, find, remove v čase závisiacom od dĺžky kľúča, ale nie od počtu kľúčov, ktoré už sú v strome
struct node {
/* vrchol lexikografickeho stromu */
char data; // pismeno ulozene v tomto vrchole
bool isWord; // je tento vrchol koncom slova?
node* next[Abeceda]; // pole smernikov na deti
};
Hašovanie
- hašovacia tabuľka veľkosti m
- kľúč k premietneme nejakou funkciou na index v poli (0,...,m-1}
- každé políčko hašovacej tabuľky spájaný zoznam prvkov, ktoré sa tam zahašovali
- v ideálnom prípade sa prvky rozhodia pomerne rovnomerne, zoznamy krátke, rýchle hľadanie, vkladenie, mazanie
- v najhoršom prípade všetky prvky v jednom zozname, pomalé hľadanie a mazanie
int hash(int k, int m){ // veľmi jednoduchá hašovacia funkcia, v praxi väčšinou zložitejšie
return abs(k) % m;
}
struct node {
int item;
node* next;
};
struct set {
node** data;
int m;
};
Algoritmy
Rekurzia
- Rekurzívne funkcie
- Vykresľovanie fraktálov
- Prehľadávanie s návratom (backtracking)
- Vyfarbovanie
- Prehľadávanie stromov
Triedenia
- nerekurzívne: Bubblesort, Selectionsort, Insertsort
- rekurzívne: Mergesort, Quicksort
- súvisiace algoritmy: binárne vyhľadávanie
Matematické úlohy
- Euklidov algoritmus, Eratostenovo sito
- Práca s aritmetickými výrazmi: vyhodnocovanie postfixovej formy, prevod z infixovej do postfixovej, reprezentácia vo forme stromu