Programovanie (2) v Jave
1-INF-166, letný semester 2023/24
Prednáška 14: Rozdiel medzi revíziami
| (43 medziľahlých úprav od 2 ďalších používateľov nie je zobrazených) | |||
| Riadok 1: | Riadok 1: | ||
== Oznamy == | == Oznamy == | ||
| − | * | + | * V stredu je dekanské voľno, prednáška nebude. |
| − | * | + | * Piatkové cvičenia sú povinné pre tých, ktorí na cvičeniach v utorok nezískajú aspoň 4 body. Informácia bude na testovači. |
| − | + | ** Väčšina príkladov bude na dvojrozmerné polia, vyskytnú sa aj spájané zoznamy z dnešnej prednášky. | |
| − | * | + | * DÚ2 odovzdávajte do utorka 19.11. 22:00. |
| − | + | * Pripomíname, že semestrálny test bude v stredu 11.12. o 18:10. Opravný termín v januári. | |
| − | + | ** Ak sa vyskytne konflikt s iným predmetom, hláste to vyučujúcim čo najskôr. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Dynamická množina== | ==Dynamická množina== | ||
=== Motivačný príklad === | === Motivačný príklad === | ||
| − | * Na fakulte sa dvere do niektorých miestností otvárajú priložením čipovej karty k čítačke | + | * Na fakulte sa dvere do niektorých miestností otvárajú priložením čipovej karty k čítačke. |
| − | * Každá karta má v sebe uložené identifikačné číslo | + | * Každá karta má v sebe uložené identifikačné číslo. |
| − | * Čítačka má v pamäti zoznam identifikačných čísel oprávnených osôb (študenti, vyučujúci a pod.) | + | * Čítačka má v pamäti zoznam identifikačných čísel oprávnených osôb (študenti, vyučujúci a pod.). |
| − | * Po priložení karty z nej prečíta číslo a zisťuje, či ho má vo svojom zozname | + | * Po priložení karty z nej prečíta číslo a zisťuje, či ho má vo svojom zozname. |
| − | * Administrátor tiež potrebuje vedieť pridávať a uberať oprávnené osoby | + | * Administrátor tiež potrebuje vedieť pridávať a uberať oprávnené osoby. |
* Ako asi môže byť systém pracujúci so zoznamom identifikačných čísel naprogramovaný? | * Ako asi môže byť systém pracujúci so zoznamom identifikačných čísel naprogramovaný? | ||
===Dynamická množina=== | ===Dynamická množina=== | ||
| − | Chceli by sme vytvoriť dátovú štruktúru s nasledujúcou špecifikáciou | + | Chceli by sme vytvoriť dátovú štruktúru s nasledujúcou špecifikáciou. |
| − | * Máme množinu ''A'', ktorá sa bude postupne meniť, preto ju nazývame dynamická množina | + | * Máme množinu ''A'', ktorá sa bude postupne meniť, preto ju nazývame dynamická množina. |
| − | * Funkcia <tt>contains</tt> dostane množinu ''A'' a hodnotu ''x'' a zistí, či ''x'' patrí do ''A'' | + | * Funkcia <tt>contains</tt> dostane množinu ''A'' a hodnotu ''x'' a zistí, či ''x'' patrí do ''A''. |
| − | * Funkcia <tt>add</tt> dostane množinu ''A'' a hodnotu ''x'' a pridá ''x'' do ''A'' | + | * Funkcia <tt>add</tt> dostane množinu ''A'' a hodnotu ''x'' a pridá ''x'' do ''A''. |
| − | * Funkcia <tt>remove</tt> dostane množinu ''A'' a prvok ''x'' a odoberie ''x'' z ''A'' | + | * Funkcia <tt>remove</tt> dostane množinu ''A'' a prvok ''x'' a odoberie ''x'' z ''A''. |
| − | * Pre jednoduchosť funkciu <tt>remove</tt> nebudeme dnes uvažovať | + | * Pre jednoduchosť funkciu <tt>remove</tt> nebudeme dnes uvažovať. |
* Niekedy sa môžu zísť aj iné operácie. | * Niekedy sa môžu zísť aj iné operácie. | ||
| Riadok 75: | Riadok 40: | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | /* | + | /* Štruktúra reprezentujúca dynamickú množinu. */ |
struct set { | struct set { | ||
// ... | // ... | ||
}; | }; | ||
| − | /* Funkcia | + | /* Funkcia vytvorí prázdnu dynamickú množinu. */ |
void init(set &s) { | void init(set &s) { | ||
// ... | // ... | ||
} | } | ||
| − | /* Funkcia, | + | /* Funkcia zistí, či prvok x patrí do množiny s. */ |
bool contains(set &s, int x) { | bool contains(set &s, int x) { | ||
// ... | // ... | ||
} | } | ||
| − | /* Funkcia | + | /* Funkcia pridá prvok x do množiny s. */ |
void add(set &s, int x) { | void add(set &s, int x) { | ||
// ... | // ... | ||
} | } | ||
| − | /* Funkcia | + | /* Funkcia uvoľní množinu s z pamäte. */ |
void destroy(set &s) { | void destroy(set &s) { | ||
// ... | // ... | ||
| Riadok 137: | Riadok 102: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Ukážeme si teraz niekoľko rôznych implementácii dynamickej množiny; začneme s dvoma, ktoré sú nám už | + | Ukážeme si teraz niekoľko rôznych implementácii dynamickej množiny; začneme s dvoma, ktoré sú nám už známe. |
=== Dynamická množina ako pole === | === Dynamická množina ako pole === | ||
| Riadok 154: | Riadok 119: | ||
struct set { | struct set { | ||
| − | int * | + | int *items; // Smerník na nultý prvok poľa |
| − | int length; // | + | int length; // Počet prvkov v poli |
}; | }; | ||
void init(set &s) { | void init(set &s) { | ||
| − | s. | + | s.items = new int[maxN]; |
s.length = 0; | s.length = 0; | ||
} | } | ||
| Riadok 165: | Riadok 130: | ||
bool contains(set &s, int x) { | bool contains(set &s, int x) { | ||
for (int i = 0; i < s.length; i++) { | for (int i = 0; i < s.length; i++) { | ||
| − | if (s. | + | if (s.items[i] == x) { |
return true; | return true; | ||
} | } | ||
| Riadok 174: | Riadok 139: | ||
void add(set &s, int x) { | void add(set &s, int x) { | ||
assert(s.length < maxN); | assert(s.length < maxN); | ||
| − | s. | + | s.items[s.length] = x; |
s.length++; | s.length++; | ||
} | } | ||
void destroy(set &s) { | void destroy(set &s) { | ||
| − | delete[] s. | + | delete[] s.items; |
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 185: | Riadok 150: | ||
===Dynamická množina ako utriedené pole === | ===Dynamická množina ako utriedené pole === | ||
Prvky množiny môžeme v poli uchovávať aj utriedené od najmenšieho po najväčšie. | Prvky množiny môžeme v poli uchovávať aj utriedené od najmenšieho po najväčšie. | ||
| − | * Funkcia <tt>contains</tt> potom môže použiť binárne vyhľadávanie. Je teda rýchlejšia, ako v predchádzajúcom prípade (v poli veľkosti ''n'' sa pozrie len na približne log ''n'' pozícií; napríklad pre miliónprvkové pole sa pozrieme asi na 20 prvkov poľa). | + | * Funkcia <tt>contains</tt> potom môže použiť binárne vyhľadávanie. Je teda rýchlejšia, ako v predchádzajúcom prípade (v poli veľkosti ''n'' sa pozrie len na približne log<sub>2</sub> ''n'' pozícií; napríklad pre miliónprvkové pole sa pozrieme asi na 20 prvkov poľa). |
* Funkcia <tt>add</tt> ale musí vložiť prvok na správne miesto v utriedenom poli; je teda o dosť pomalšia. | * Funkcia <tt>add</tt> ale musí vložiť prvok na správne miesto v utriedenom poli; je teda o dosť pomalšia. | ||
| + | * Tento spôsob by teda bol vhodný, ak sa množina mení zriedkavo. | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 196: | Riadok 162: | ||
struct set { | struct set { | ||
| − | int * | + | int *items; // smerník na nultý prvok poľa |
| − | int length; // | + | int length; // počet prvkov v poli |
}; | }; | ||
void init(set &s) { | void init(set &s) { | ||
| − | s. | + | s.items = new int[maxN]; |
s.length = 0; | s.length = 0; | ||
} | } | ||
| Riadok 210: | Riadok 176: | ||
while (left <= right) { | while (left <= right) { | ||
int index = (left + right) / 2; | int index = (left + right) / 2; | ||
| − | if (s. | + | if (s.items[index] == x) { |
return true; | return true; | ||
| − | } else if (s. | + | } else if (s.items[index] > x) { |
right = index - 1; | right = index - 1; | ||
} else { | } else { | ||
| Riadok 224: | Riadok 190: | ||
assert(s.length < maxN); | assert(s.length < maxN); | ||
int kam = s.length; | int kam = s.length; | ||
| − | while (kam > 0 && s. | + | while (kam > 0 && s.items[kam - 1] > x) { |
| − | s. | + | s.items[kam] = s.items[kam - 1]; |
kam--; | kam--; | ||
} | } | ||
| − | s. | + | s.items[kam] = x; |
s.length++; | s.length++; | ||
} | } | ||
void destroy(set &s) { | void destroy(set &s) { | ||
| − | delete[] s. | + | delete[] s.items; |
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 241: | Riadok 207: | ||
Dnes uvidíme ďalšie dva spôsoby implementácie dynamickej množiny: | Dnes uvidíme ďalšie dva spôsoby implementácie dynamickej množiny: | ||
| − | * Množina ako ''' | + | * Množina ako '''spájaný zoznam''': |
** Ľahko pridáme nové prvky, nepotrebujeme vopred vedieť veľkosť. | ** Ľahko pridáme nové prvky, nepotrebujeme vopred vedieť veľkosť. | ||
** Nedá sa rýchlo binárne vyhľadávať. | ** Nedá sa rýchlo binárne vyhľadávať. | ||
| Riadok 248: | Riadok 214: | ||
** Často veľmi rýchle vyhľadávanie. | ** Často veľmi rýchle vyhľadávanie. | ||
** Použijeme polia aj spájané zoznamy. | ** Použijeme polia aj spájané zoznamy. | ||
| + | |||
| + | == Odbočka: smerníky a <tt>struct</tt> == | ||
| + | |||
| + | === Opakovanie základnej práce so smerníkmi === | ||
| + | |||
| + | <syntaxhighlight lang="C++"> | ||
| + | int n = 7; // premenná typu int | ||
| + | int * p = &n; // smerník na int | ||
| + | // n, *p teraz znamenajú to isté | ||
| + | |||
| + | int * p2 = new int; // p2 ukazuje na alokovanú pamäť | ||
| + | *p2 = 7; // cez *p2 pracujeme s touto pamäťou | ||
| + | delete p2; // uvoľníme pamäť | ||
| + | p2 = p; // meníme samotný smerník | ||
| + | p = NULL; // NULL "nikam neukazuje" | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | === Smerníky a <tt>struct</tt> === | ||
| + | |||
| + | Smerník môže ukazovať aj na <tt>struct</tt>. Operátory <tt>.</tt> (prístup k prvku štruktúry) a <tt>[]</tt> (prístup k prvku poľa) majú vyššiu prioritu ako operátory <tt>*</tt> (dereferencia smerníka) a <tt>&</tt> (adresa). Preto napríklad: | ||
| + | * Zápis <tt>*s.cokolvek</tt> je to isté ako <tt>*(s.cokolvek)</tt> a vyjadruje dereferenciu smerníka <tt>s.cokolvek</tt>. | ||
| + | * Zápis <tt>(*p).cokolvek</tt> vyjadruje prvok <tt>cokolvek</tt> štruktúry získanej dereferenciou smerníka <tt>p</tt>. | ||
| + | * Zvyčajne je potrebnejší zápis <tt>(*p).cokolvek</tt>; existuje preň preto skratka <tt>p->cokolvek</tt>. | ||
| + | |||
| + | <syntaxhighlight lang="C++"> | ||
| + | struct bod { | ||
| + | int x, y; | ||
| + | }; | ||
| + | |||
| + | // ... | ||
| + | |||
| + | bod b; | ||
| + | b.x = 0; | ||
| + | b.y = 0; | ||
| + | bod *p = &b; // p ukazuje na bod b | ||
| + | |||
| + | bod *p2 = new bod; // alokovanie nového bodu | ||
| + | (*p2).x = 20; // bod, na ktorý ukazuje p2, bude mať x 20 | ||
| + | p2->y = 10; // bod, na ktorý ukazuje p2, bude mať y 10 | ||
| + | delete p2; // uvoľnenie pamäte | ||
| + | </syntaxhighlight> | ||
| + | |||
==Spájané zoznamy== | ==Spájané zoznamy== | ||
| − | ''Spájaný zoznam'' (angl. ''linked list'') je postupnosť uzlov rovnakého typu usporiadaných za sebou. Každý uzol pritom pozostáva z dvoch častí: | + | '''Spájaný zoznam''' (angl. ''linked list'') je postupnosť uzlov rovnakého typu usporiadaných za sebou. Každý uzol pritom pozostáva z dvoch častí: |
* Samotné dáta; v našom prípade jedno číslo typu <tt>int</tt>. | * Samotné dáta; v našom prípade jedno číslo typu <tt>int</tt>. | ||
| − | * Smerník, ktorý ukazuje na nasledujúci prvok zoznamu | + | * Smerník <tt>next</tt>, ktorý ukazuje na nasledujúci prvok zoznamu. |
| − | + | ** Tieto smerníky umožňujú pohybovať sa po zozname zľava doprava. | |
| − | Posledný uzol zoznamu nemá následníka | + | ** Posledný uzol zoznamu nemá následníka, smerník <tt>next</tt> bude mať hodnotu <tt>NULL</tt>. |
Štruktúra spájaného zoznamu je znázornená na nasledujúcom obrázku: | Štruktúra spájaného zoznamu je znázornená na nasledujúcom obrázku: | ||
[[Image:PROG-list.png|300px]] | [[Image:PROG-list.png|300px]] | ||
| − | |||
| − | |||
Uzol jednosmerne spájaného zoznamu budeme reprezentovať pomocou <tt>struct</tt>-u <tt>node</tt>: | Uzol jednosmerne spájaného zoznamu budeme reprezentovať pomocou <tt>struct</tt>-u <tt>node</tt>: | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | /* | + | /* Štruktúra reprezentujúca uzol jednosmerne spájaného zoznamu: */ |
struct node { | struct node { | ||
| − | int data; // Hodnota | + | int data; // Hodnota uložená v danom uzle |
| − | node *next; // | + | node *next; // Smerník na nasledujúci uzol |
}; | }; | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Vo vnútri definície typu <tt>node</tt> teda používame smerník na samotný typ <tt>node</tt>. | Vo vnútri definície typu <tt>node</tt> teda používame smerník na samotný typ <tt>node</tt>. | ||
| − | + | Samotná množina reprezentovaná spájaným zoznamom je potom štruktúra <tt>set</tt> obsahujúca iba smerník na prvý prvok zoznamu. Ak je zoznam prázdny, bude tento smerník <tt>NULL</tt>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | /* | + | /* Štruktúra implementujúca množinu ako spájaný zoznam: */ |
struct set { | struct set { | ||
| − | node *first; // | + | node *first; // Smerník na prvý uzol zoznamu |
}; | }; | ||
| Riadok 293: | Riadok 294: | ||
===Vkladanie na začiatok zoznamu=== | ===Vkladanie na začiatok zoznamu=== | ||
| − | Nasledujúca funkcia na začiatok zoznamu vloží nový uzol s dátami x: | + | Nasledujúca funkcia na začiatok zoznamu vloží nový uzol s dátami ''x'': |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
void add(set &s, int x) { | void add(set &s, int x) { | ||
| − | node *p = new node; | + | // Vytvoríme nový uzol, uložíme doňho x |
| − | p->data = x; | + | node * p = new node; |
| − | p->next = s.first; | + | p->data = x; |
| − | s.first = p; | + | // uzol p bude novým prvým prvkom zoznamu |
| + | p->next = s.first; | ||
| + | s.first = p; | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 319: | Riadok 322: | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | Funkcia by sa dala napísať aj pomocou for cyklu | ||
| + | <syntaxhighlight lang="C++"> | ||
| + | bool contains(set &s, int x) { | ||
| + | for(node *p = s.first; p != NULL; p = p->next) { | ||
| + | if (p->data == x) { | ||
| + | return true; | ||
| + | } | ||
| + | } | ||
| + | return false; | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | V tejto forme sa viac podobá na funkciu pre polia: | ||
| + | <syntaxhighlight lang="C++"> | ||
| + | bool contains(set &s, int x) { | ||
| + | for (int i = 0; i < s.length; i++) { | ||
| + | if (s.items[i] == x) { | ||
| + | return true; | ||
| + | } | ||
| + | } | ||
| + | return false; | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | * Smerník <tt>p</tt> je teda v zoznamoch ekvivalentom indexu <tt>i</tt> | ||
| + | * Inicializácia je <tt>p = s.first</tt> namiesto <tt>i = 0</tt> | ||
| + | * Posun na ďalší prvok je <tt>p = p->next</tt> namiesto <tt>i++</tt> | ||
| + | * Podmienka na pokračovanie je <tt>p != NULL</tt> namiesto <tt>i < s.length</tt> | ||
=== Uvoľnenie zoznamu === | === Uvoľnenie zoznamu === | ||
| − | Funkcia | + | Funkcia, ktorá uvoľní zoznam z pamäti, pracuje podobne: prechádza postupne zoznam od začiatku až po jeho koniec a uvoľňuje z pamäte jednotlivé uzly. Treba si však dať pozor na to, aby sme smerník na nasledujúci uzol získali ešte predtým, než z pamäti uvoľníme ten predošlý. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 348: | Riadok 380: | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | === Varianty spájaných zoznamov === | ||
| + | * V našom zozname si v každom uzle pamätáme iba smerník na následníka, hovoríme o ''jednosmerne spájanom zozname''. | ||
| + | * Často sú užitočné aj ''obojsmerne spájané zoznamy'', kde sa v každom uzle uchováva aj smerník na predchodcu; takéto zoznamy sú ale o niečo náročnejšie na údržbu. | ||
| + | * Používajú sa dokonca aj cyklické zoznamy, kde posledný prvok ukazuje späť na prvý prvok zoznamu. | ||
== Hašovanie == | == Hašovanie == | ||
| Riadok 353: | Riadok 390: | ||
Úplne odlišným spôsobom implementácie dynamickej množiny je tzv. ''priame adresovanie'' (angl. ''direct addressing''). | Úplne odlišným spôsobom implementácie dynamickej množiny je tzv. ''priame adresovanie'' (angl. ''direct addressing''). | ||
| − | * Množinu všetkých možných hodnôt, ktoré v danej implementácii môžeme chcieť do množiny pridať, nazveme univerzum ''U'' | + | * Množinu všetkých možných hodnôt, ktoré v danej implementácii môžeme chcieť do množiny pridať, nazveme univerzum ''U''. |
| − | * Predchádzajúce implementácie sa ľahko dali upraviť na rôzne univerzá (celé čísla, desatinné čísla, smerníky na zložitejšie štruktúry, napr. struct, pole, reťazec) | + | * Predchádzajúce implementácie sa ľahko dali upraviť na rôzne univerzá (celé čísla, desatinné čísla, smerníky na zložitejšie štruktúry, napr. struct, pole, reťazec). |
| − | * Na rozdiel od toho sa priame adresovanie dá použiť iba ak univerzum je ''U'' = {0,1,...,''m''-1} pre nejaké rozumne malé prirodzené číslo ''m'' | + | * Na rozdiel od toho sa priame adresovanie dá použiť iba ak univerzum je ''U'' = {0,1,...,''m''-1} pre nejaké rozumne malé prirodzené číslo ''m''. |
* Podmnožinu ''A'' univerza ''U'' potom môžeme reprezentovať ako pole booleovských hodnôt dĺžky ''m'', kde ''i''-ty prvok poľa bude <tt>true</tt> práve vtedy, keď ''i'' patrí do ''A''. | * Podmnožinu ''A'' univerza ''U'' potom môžeme reprezentovať ako pole booleovských hodnôt dĺžky ''m'', kde ''i''-ty prvok poľa bude <tt>true</tt> práve vtedy, keď ''i'' patrí do ''A''. | ||
* Túto reprezentáciu sme používali napríklad v poli <tt>bolo</tt> pri prehľadávaní s návratom. | * Túto reprezentáciu sme používali napríklad v poli <tt>bolo</tt> pri prehľadávaní s návratom. | ||
| Riadok 361: | Riadok 398: | ||
* Funkcie <tt>contains</tt> aj <tt>add</tt> sú potom veľmi jednoduché a rýchle. | * Funkcie <tt>contains</tt> aj <tt>add</tt> sú potom veľmi jednoduché a rýchle. | ||
* Problémom tohto prístupu je ale vysoká pamäťová zložitosť, ak je číslo ''m'' veľké. | * Problémom tohto prístupu je ale vysoká pamäťová zložitosť, ak je číslo ''m'' veľké. | ||
| − | * Veľmi efektívne pre malé univerzá (napr. cifry | + | * Veľmi efektívne pre malé univerzá (napr. cifry 0,...,9, všetky znaky anglickej abecedy, všetky znaky s ASCII hodnotami od 0 po 255, a pod.). |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
#include <cassert> | #include <cassert> | ||
| + | /* Maximálne povolené číslo v množine */ | ||
const int m = 1000; | const int m = 1000; | ||
| − | /* | + | /* Štruktúra implementujúca množinu priamym adresovaním: */ |
struct set { | struct set { | ||
| − | bool * | + | bool *isin; |
}; | }; | ||
void init(set &s) { | void init(set &s) { | ||
| − | s. | + | s.isin = new bool[m]; |
for (int i = 0; i < m; i++) { | for (int i = 0; i < m; i++) { | ||
| − | s. | + | s.isin[i] = false; |
} | } | ||
} | } | ||
bool contains(set &s, int x) { | bool contains(set &s, int x) { | ||
| − | assert(x >= 0 && x < | + | assert(x >= 0 && x < m); |
| − | return s. | + | return s.isin[x]; |
} | } | ||
void add(set &s, int x) { | void add(set &s, int x) { | ||
| − | assert(x >= 0 && x < | + | assert(x >= 0 && x < m); |
| − | s. | + | s.isin[x] = true; |
} | } | ||
void destroy(set &s) { | void destroy(set &s) { | ||
| − | delete[] s. | + | delete[] s.isin; |
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 404: | Riadok 442: | ||
* Naprogramujeme ''hašovaciu funkciu'', ktorá transformuje prvky univerza ''U'' na indexy hašovacej tabuľky; pôjde teda o funkciu ''h'': ''U'' -> {0, 1, ... , ''m''−1}. | * Naprogramujeme ''hašovaciu funkciu'', ktorá transformuje prvky univerza ''U'' na indexy hašovacej tabuľky; pôjde teda o funkciu ''h'': ''U'' -> {0, 1, ... , ''m''−1}. | ||
* Najjednoduchšia hašovacia funkcia pre celočíselné prvky je ''h''(''x'') = |''x''| mod ''m''. | * Najjednoduchšia hašovacia funkcia pre celočíselné prvky je ''h''(''x'') = |''x''| mod ''m''. | ||
| − | ** |''x''| spočítame funkciou <tt>abs</tt> z knižnice <tt>cstdlib</tt> | + | ** |''x''| spočítame funkciou <tt>abs</tt> z knižnice <tt>cstdlib</tt>. |
| − | ** Absolútnu hodnotu používame, lebo napríklad <tt>-10 % 3</tt> je -1, čo mimo rozsahu indexov tabuľky | + | ** Absolútnu hodnotu používame, lebo napríklad <tt>-10 % 3</tt> je -1, čo mimo rozsahu indexov tabuľky. |
| − | ** V praxi sa používajú zložitejšie hašovacie funkcie. Ideálne je hašovacia funkcia jednoduchá a rýchla, ale pritom hodnoty do tabuľky distribuuje rovnomerne, aby sa príliš často nestávalo, že dva prvky sa namapujú na to isté políčko | + | ** V praxi sa používajú zložitejšie hašovacie funkcie. Ideálne je hašovacia funkcia jednoduchá a rýchla, ale pritom hodnoty do tabuľky distribuuje rovnomerne, aby sa príliš často nestávalo, že dva prvky sa namapujú na to isté políčko. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 414: | Riadok 452: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | + | Napríklad pre ''m = 5'': hash(12, 5) je 2, hash(-6, 5) je 1. | |
| − | |||
| − | |||
Prvý pokus o prácu hašovacou tabuľkou by teda mohol vyzerať takto: | Prvý pokus o prácu hašovacou tabuľkou by teda mohol vyzerať takto: | ||
'''Vkladanie''' prvku ''x'': | '''Vkladanie''' prvku ''x'': | ||
| − | * Spočítame <tt>index = hash(x, m)</tt> a prvok vložíme na pozíciu <tt> | + | * Spočítame <tt>index = hash(x, m)</tt> a prvok vložíme na pozíciu <tt>table[index]</tt>. |
'''Vyhľadávanie''' prvku ''x'': | '''Vyhľadávanie''' prvku ''x'': | ||
| Riadok 428: | Riadok 464: | ||
'''Problémy''': | '''Problémy''': | ||
| − | * Na akú hodnotu inicializovať prvky poľa <tt> | + | * Na akú hodnotu inicializovať prvky poľa <tt>table</tt>? |
* Čo ak budeme potrebovať vložiť prvok na miesto, kde je už niečo uložené? | * Čo ak budeme potrebovať vložiť prvok na miesto, kde je už niečo uložené? | ||
| Riadok 434: | Riadok 470: | ||
* Pri vkladaní prvku sme narazili na problém, ak na už obsadené miesto chceme vložiť iný prvok. | * Pri vkladaní prvku sme narazili na problém, ak na už obsadené miesto chceme vložiť iný prvok. | ||
| − | * Ak sa dva prvky ''x'' a ''y'' sa zahašujú na rovnakú pozíciu ''h''(''x'') = ''h''(''y''), hovoríme, že nastala '''kolízia''' | + | * Ak sa dva prvky ''x'' a ''y'' sa zahašujú na rovnakú pozíciu ''h''(''x'') = ''h''(''y''), hovoríme, že nastala '''kolízia'''. |
| − | |||
* Existujú rôzne prístupy na riešenie kolízií, môžeme napríklad hľadať iné voľné miesto v tabuľke. | * Existujú rôzne prístupy na riešenie kolízií, môžeme napríklad hľadať iné voľné miesto v tabuľke. | ||
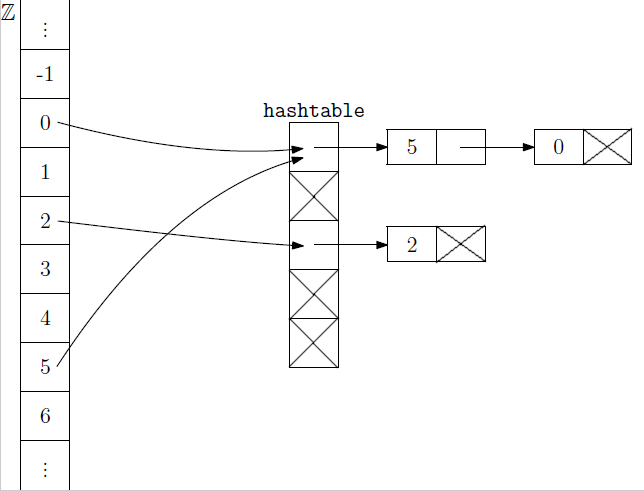
* V našom programe kolízie vyriešime tak, že v každom políčku tabuľky uložíme spájaný zoznam všetkých prvkov, ktoré sa tam zahašovali. | * V našom programe kolízie vyriešime tak, že v každom políčku tabuľky uložíme spájaný zoznam všetkých prvkov, ktoré sa tam zahašovali. | ||
| − | ** Táto situácia je znázornená na nasledujúcom obrázku, v ktorom | + | ** Táto situácia je znázornená na nasledujúcom obrázku, v ktorom sme do hašovacej tabuľky pre m=5 pridali prvky 0,2,5. |
[[Súbor:Hash2.png]] | [[Súbor:Hash2.png]] | ||
| Riadok 445: | Riadok 480: | ||
#include <cstdlib> | #include <cstdlib> | ||
| − | /* | + | /* hašovacia funkcia: */ |
int h(int x, int m) { | int h(int x, int m) { | ||
return abs(x) % m; | return abs(x) % m; | ||
} | } | ||
| − | /* | + | /* štruktúra reprezentujúca jeden prvok spájaného zoznamu: */ |
struct node { | struct node { | ||
int data; | int data; | ||
| Riadok 456: | Riadok 491: | ||
}; | }; | ||
| − | /* | + | /* štruktúra implementujúca dynamickú množinu hašovaním: */ |
struct set { | struct set { | ||
| − | node ** | + | node **table; // pole smerníkov na začiatky zoznamov |
| − | int m; | + | int m; // veľkost hašovacej tabuľky |
}; | }; | ||
| − | void init(set &s, int m) { // | + | void init(set &s, int m) { |
| + | // veľkosť tabuľky je parametrom funkcie init | ||
s.m = m; | s.m = m; | ||
| − | s. | + | s.table = new node *[m]; |
for (int i = 0; i < m; i++) { | for (int i = 0; i < m; i++) { | ||
| − | s. | + | s.table[i] = NULL; |
} | } | ||
} | } | ||
bool contains(set &s, int x) { | bool contains(set &s, int x) { | ||
| − | int index = h(x, s.m); | + | // spočítame políčko tabuľky |
| − | node *p = s. | + | int index = h(x, s.m); |
| − | + | node *p = s.table[index]; | |
| − | while (p != NULL) { | + | // p ukazuje na začiatok zoznamu |
| + | while (p != NULL) { | ||
| + | // prechádzame zoznam, hľadáme x | ||
if (p->data == x) { | if (p->data == x) { | ||
return true; | return true; | ||
| Riadok 484: | Riadok 522: | ||
void add(set &s, int x) { | void add(set &s, int x) { | ||
| − | int index = h(x, s.m); | + | // spočítame políčko tabuľky |
| − | node * | + | int index = h(x, s.m); |
| − | + | // vytvoríme nový uzol | |
| − | + | node *p = new node; | |
| − | s. | + | p->data = x; |
| + | // uzol vložíme na začiatok zoznamu | ||
| + | p->next = s.table[index]; | ||
| + | s.table[index] = p; | ||
} | } | ||
void destroy(set &s) { | void destroy(set &s) { | ||
for (int i = 0; i < s.m; i++) { | for (int i = 0; i < s.m; i++) { | ||
| − | node *p = s. | + | // uvoľníme zoznam s.table[i] |
| + | node *p = s.table[i]; | ||
while (p != NULL) { | while (p != NULL) { | ||
node *p2 = p->next; | node *p2 = p->next; | ||
| Riadok 500: | Riadok 542: | ||
} | } | ||
} | } | ||
| − | delete[] s. | + | delete[] s.table; |
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 513: | Riadok 555: | ||
** Ak je tabuľka dosť veľká a hašovacia funkcia vhodne zvolená, tento prípad je pomerne obvyklý. | ** Ak je tabuľka dosť veľká a hašovacia funkcia vhodne zvolená, tento prípad je pomerne obvyklý. | ||
** Hašovacie tabuľky sa často používajú v praxi. | ** Hašovacie tabuľky sa často používajú v praxi. | ||
| − | * Viac budúci rok na predmete | + | * Viac budúci rok na predmete Algoritmy a dátové štruktúry. |
| + | |||
| + | == Zhrnutie == | ||
| + | |||
| + | * Videli sme abstraktný dátový typ dynamická množina. | ||
| + | * Implementovali sme ho pomocou neutriedených a utriedených polí, spájaných zoznamov, priamym adresovaním (ak prvky sú napr. malé celé čísla) a hašovaním. | ||
| + | * Ďalšie dve implementácie uvidíme na konci semestra. | ||
| + | * Spájané zoznamy sú ďalším príkladom využitia smerníkov. Ich výhodou je možnosť rýchlo pridávať a uberať uzly na začiatku zoznamu, alebo aj na ľubovoľnom mieste zoznamu, pokiaľ máme smerník na predchodcu. Nevieme však rýchlo pristupovať k prvku na danej pozícii. Prácu so zoznamami si precvičíme na cvičeniach tento a budúci týždeň. | ||
| + | * Na zamyslenie: pri jednoduchej implementácii množiny v poli sme skúsili dve možnosti: utriedenú a neutriedenú. Malo by zmysel uvažovať aj utriedený spájaný zoznam? | ||
Aktuálna revízia z 19:43, 10. november 2024
Obsah
Oznamy
- V stredu je dekanské voľno, prednáška nebude.
- Piatkové cvičenia sú povinné pre tých, ktorí na cvičeniach v utorok nezískajú aspoň 4 body. Informácia bude na testovači.
- Väčšina príkladov bude na dvojrozmerné polia, vyskytnú sa aj spájané zoznamy z dnešnej prednášky.
- DÚ2 odovzdávajte do utorka 19.11. 22:00.
- Pripomíname, že semestrálny test bude v stredu 11.12. o 18:10. Opravný termín v januári.
- Ak sa vyskytne konflikt s iným predmetom, hláste to vyučujúcim čo najskôr.
Dynamická množina
Motivačný príklad
- Na fakulte sa dvere do niektorých miestností otvárajú priložením čipovej karty k čítačke.
- Každá karta má v sebe uložené identifikačné číslo.
- Čítačka má v pamäti zoznam identifikačných čísel oprávnených osôb (študenti, vyučujúci a pod.).
- Po priložení karty z nej prečíta číslo a zisťuje, či ho má vo svojom zozname.
- Administrátor tiež potrebuje vedieť pridávať a uberať oprávnené osoby.
- Ako asi môže byť systém pracujúci so zoznamom identifikačných čísel naprogramovaný?
Dynamická množina
Chceli by sme vytvoriť dátovú štruktúru s nasledujúcou špecifikáciou.
- Máme množinu A, ktorá sa bude postupne meniť, preto ju nazývame dynamická množina.
- Funkcia contains dostane množinu A a hodnotu x a zistí, či x patrí do A.
- Funkcia add dostane množinu A a hodnotu x a pridá x do A.
- Funkcia remove dostane množinu A a prvok x a odoberie x z A.
- Pre jednoduchosť funkciu remove nebudeme dnes uvažovať.
- Niekedy sa môžu zísť aj iné operácie.
Problém príslušnosti k množine sa vyskytuje aj v mnohých iných situáciách.
- Ako dnes uvidíme, dynamickú množinu môžeme implementovať rôznymi spôsobmi.
- Hovoríme, že dynamická množina je abstraktný dátový typ, špecifikuje totiž iba rozhranie, ktoré má dátová štruktúra poskytovať používateľovi, nie jeho implementáciu.
- Ak by sme zmenili implementáciu z jednej na inú, nemusíme nutne meniť programy, ktoré dynamickú množinu využívajú, pokiaľ k nej pristupujú iba pomocou uvedených funkcií.
Implementácie dynamických množín
- Pre jednoduchosť budeme uvažovať iba dynamickú množinu celých čísel.
- Dynamickú množinu budeme uchovávať v štruktúre set.
- Navyše budeme mať implementovaných niekoľko funkcií, ktoré s dynamickými množinami pracujú.
- Kostra programu teda bude vyzerať pre ľubovoľnú implementáciu dynamickej množiny takto:
/* Štruktúra reprezentujúca dynamickú množinu. */
struct set {
// ...
};
/* Funkcia vytvorí prázdnu dynamickú množinu. */
void init(set &s) {
// ...
}
/* Funkcia zistí, či prvok x patrí do množiny s. */
bool contains(set &s, int x) {
// ...
}
/* Funkcia pridá prvok x do množiny s. */
void add(set &s, int x) {
// ...
}
/* Funkcia uvoľní množinu s z pamäte. */
void destroy(set &s) {
// ...
}
Bez ohľadu na implementáciu štruktúry set a uvedených funkcií už teraz môžeme napísať program, ktorý ich využíva. Z konzoly číta príkazy a postupne ich vykonáva.
#include <iostream>
#include <cstring>
using namespace std;
// ...
const int maxlength = 100;
int main(void) {
set A;
init(A);
while (true) {
char prikaz[maxlength];
cin.width(maxlength);
cin >> prikaz;
if (strcmp(prikaz, "contains") == 0) {
int x;
cin >> x;
cout << contains(A, x) << endl;
} else if (strcmp(prikaz, "add") == 0) {
int x;
cin >> x;
add(A, x);
} else if (strcmp(prikaz, "end") == 0) {
break;
}
}
destroy(A);
}
Ukážeme si teraz niekoľko rôznych implementácii dynamickej množiny; začneme s dvoma, ktoré sú nám už známe.
Dynamická množina ako pole
Dynamickú množinu môžeme implementovať tak, že jej prvky budeme ukladať do poľa v ľubovoľnom poradí.
- Funkcia contains musí zakaždým prejsť celé pole lineárnym prehľadávaním (nie je teda zrovna rýchla).
- Funkcia add je naopak veľmi rýchla: stačí pridať prvok na koniec poľa.
- Je ale potrebné dávať pozor na prekročenie kapacity poľa (mohli by sme použiť dynamické pole).
#include <cassert>
// ...
const int maxN = 1000;
struct set {
int *items; // Smerník na nultý prvok poľa
int length; // Počet prvkov v poli
};
void init(set &s) {
s.items = new int[maxN];
s.length = 0;
}
bool contains(set &s, int x) {
for (int i = 0; i < s.length; i++) {
if (s.items[i] == x) {
return true;
}
}
return false;
}
void add(set &s, int x) {
assert(s.length < maxN);
s.items[s.length] = x;
s.length++;
}
void destroy(set &s) {
delete[] s.items;
}
Dynamická množina ako utriedené pole
Prvky množiny môžeme v poli uchovávať aj utriedené od najmenšieho po najväčšie.
- Funkcia contains potom môže použiť binárne vyhľadávanie. Je teda rýchlejšia, ako v predchádzajúcom prípade (v poli veľkosti n sa pozrie len na približne log2 n pozícií; napríklad pre miliónprvkové pole sa pozrieme asi na 20 prvkov poľa).
- Funkcia add ale musí vložiť prvok na správne miesto v utriedenom poli; je teda o dosť pomalšia.
- Tento spôsob by teda bol vhodný, ak sa množina mení zriedkavo.
#include <cassert>
// ...
const int maxN = 1000;
struct set {
int *items; // smerník na nultý prvok poľa
int length; // počet prvkov v poli
};
void init(set &s) {
s.items = new int[maxN];
s.length = 0;
}
bool contains(set &s, int x) {
int left = 0;
int right = s.length - 1;
while (left <= right) {
int index = (left + right) / 2;
if (s.items[index] == x) {
return true;
} else if (s.items[index] > x) {
right = index - 1;
} else {
left = index + 1;
}
}
return false;
}
void add(set &s, int x) {
assert(s.length < maxN);
int kam = s.length;
while (kam > 0 && s.items[kam - 1] > x) {
s.items[kam] = s.items[kam - 1];
kam--;
}
s.items[kam] = x;
s.length++;
}
void destroy(set &s) {
delete[] s.items;
}
Ďalšie možnosti implementácie dynamickej množiny (plán na dnes)
Dnes uvidíme ďalšie dva spôsoby implementácie dynamickej množiny:
- Množina ako spájaný zoznam:
- Ľahko pridáme nové prvky, nepotrebujeme vopred vedieť veľkosť.
- Nedá sa rýchlo binárne vyhľadávať.
- Založené na smerníkoch.
- Množina pomocou hašovania:
- Často veľmi rýchle vyhľadávanie.
- Použijeme polia aj spájané zoznamy.
Odbočka: smerníky a struct
Opakovanie základnej práce so smerníkmi
int n = 7; // premenná typu int
int * p = &n; // smerník na int
// n, *p teraz znamenajú to isté
int * p2 = new int; // p2 ukazuje na alokovanú pamäť
*p2 = 7; // cez *p2 pracujeme s touto pamäťou
delete p2; // uvoľníme pamäť
p2 = p; // meníme samotný smerník
p = NULL; // NULL "nikam neukazuje"
Smerníky a struct
Smerník môže ukazovať aj na struct. Operátory . (prístup k prvku štruktúry) a [] (prístup k prvku poľa) majú vyššiu prioritu ako operátory * (dereferencia smerníka) a & (adresa). Preto napríklad:
- Zápis *s.cokolvek je to isté ako *(s.cokolvek) a vyjadruje dereferenciu smerníka s.cokolvek.
- Zápis (*p).cokolvek vyjadruje prvok cokolvek štruktúry získanej dereferenciou smerníka p.
- Zvyčajne je potrebnejší zápis (*p).cokolvek; existuje preň preto skratka p->cokolvek.
struct bod {
int x, y;
};
// ...
bod b;
b.x = 0;
b.y = 0;
bod *p = &b; // p ukazuje na bod b
bod *p2 = new bod; // alokovanie nového bodu
(*p2).x = 20; // bod, na ktorý ukazuje p2, bude mať x 20
p2->y = 10; // bod, na ktorý ukazuje p2, bude mať y 10
delete p2; // uvoľnenie pamäte
Spájané zoznamy
Spájaný zoznam (angl. linked list) je postupnosť uzlov rovnakého typu usporiadaných za sebou. Každý uzol pritom pozostáva z dvoch častí:
- Samotné dáta; v našom prípade jedno číslo typu int.
- Smerník next, ktorý ukazuje na nasledujúci prvok zoznamu.
- Tieto smerníky umožňujú pohybovať sa po zozname zľava doprava.
- Posledný uzol zoznamu nemá následníka, smerník next bude mať hodnotu NULL.
Štruktúra spájaného zoznamu je znázornená na nasledujúcom obrázku:
Uzol jednosmerne spájaného zoznamu budeme reprezentovať pomocou struct-u node:
/* Štruktúra reprezentujúca uzol jednosmerne spájaného zoznamu: */
struct node {
int data; // Hodnota uložená v danom uzle
node *next; // Smerník na nasledujúci uzol
};
Vo vnútri definície typu node teda používame smerník na samotný typ node.
Samotná množina reprezentovaná spájaným zoznamom je potom štruktúra set obsahujúca iba smerník na prvý prvok zoznamu. Ak je zoznam prázdny, bude tento smerník NULL.
/* Štruktúra implementujúca množinu ako spájaný zoznam: */
struct set {
node *first; // Smerník na prvý uzol zoznamu
};
void init(set &s) {
s.first = NULL;
}
Vkladanie na začiatok zoznamu
Nasledujúca funkcia na začiatok zoznamu vloží nový uzol s dátami x:
void add(set &s, int x) {
// Vytvoríme nový uzol, uložíme doňho x
node * p = new node;
p->data = x;
// uzol p bude novým prvým prvkom zoznamu
p->next = s.first;
s.first = p;
}
Vyhľadávanie v zozname
Funkcia vyhľadávajúca číslo x v zozname bude pracovať tak, že postupne prehľadáva zoznam od jeho začiatku, s využitím smerníkov na nasledujúce prvky:
bool contains(set &s, int x) {
node *p = s.first;
while (p != NULL) {
if (p->data == x) {
return true;
}
p = p->next;
}
return false;
}
Funkcia by sa dala napísať aj pomocou for cyklu
bool contains(set &s, int x) {
for(node *p = s.first; p != NULL; p = p->next) {
if (p->data == x) {
return true;
}
}
return false;
}
V tejto forme sa viac podobá na funkciu pre polia:
bool contains(set &s, int x) {
for (int i = 0; i < s.length; i++) {
if (s.items[i] == x) {
return true;
}
}
return false;
}
- Smerník p je teda v zoznamoch ekvivalentom indexu i
- Inicializácia je p = s.first namiesto i = 0
- Posun na ďalší prvok je p = p->next namiesto i++
- Podmienka na pokračovanie je p != NULL namiesto i < s.length
Uvoľnenie zoznamu
Funkcia, ktorá uvoľní zoznam z pamäti, pracuje podobne: prechádza postupne zoznam od začiatku až po jeho koniec a uvoľňuje z pamäte jednotlivé uzly. Treba si však dať pozor na to, aby sme smerník na nasledujúci uzol získali ešte predtým, než z pamäti uvoľníme ten predošlý.
void destroy(set &s) {
node *p = s.first;
while (p != NULL) {
node *p2 = p->next;
delete p;
p = p2;
}
}
Výpis zoznamu
Môžeme napísať aj nasledujúcu funkciu, ktorá po zavolaní vypíše obsah celého zoznamu:
void print(set &s) {
node *p = s.first;
while (p != NULL) {
cout << p->data << " ";
p = p->next;
}
cout << endl;
}
Varianty spájaných zoznamov
- V našom zozname si v každom uzle pamätáme iba smerník na následníka, hovoríme o jednosmerne spájanom zozname.
- Často sú užitočné aj obojsmerne spájané zoznamy, kde sa v každom uzle uchováva aj smerník na predchodcu; takéto zoznamy sú ale o niečo náročnejšie na údržbu.
- Používajú sa dokonca aj cyklické zoznamy, kde posledný prvok ukazuje späť na prvý prvok zoznamu.
Hašovanie
Implementácia množiny priamym adresovaním
Úplne odlišným spôsobom implementácie dynamickej množiny je tzv. priame adresovanie (angl. direct addressing).
- Množinu všetkých možných hodnôt, ktoré v danej implementácii môžeme chcieť do množiny pridať, nazveme univerzum U.
- Predchádzajúce implementácie sa ľahko dali upraviť na rôzne univerzá (celé čísla, desatinné čísla, smerníky na zložitejšie štruktúry, napr. struct, pole, reťazec).
- Na rozdiel od toho sa priame adresovanie dá použiť iba ak univerzum je U = {0,1,...,m-1} pre nejaké rozumne malé prirodzené číslo m.
- Podmnožinu A univerza U potom môžeme reprezentovať ako pole booleovských hodnôt dĺžky m, kde i-ty prvok poľa bude true práve vtedy, keď i patrí do A.
- Túto reprezentáciu sme používali napríklad v poli bolo pri prehľadávaní s návratom.
- Funkcie contains aj add sú potom veľmi jednoduché a rýchle.
- Problémom tohto prístupu je ale vysoká pamäťová zložitosť, ak je číslo m veľké.
- Veľmi efektívne pre malé univerzá (napr. cifry 0,...,9, všetky znaky anglickej abecedy, všetky znaky s ASCII hodnotami od 0 po 255, a pod.).
#include <cassert>
/* Maximálne povolené číslo v množine */
const int m = 1000;
/* Štruktúra implementujúca množinu priamym adresovaním: */
struct set {
bool *isin;
};
void init(set &s) {
s.isin = new bool[m];
for (int i = 0; i < m; i++) {
s.isin[i] = false;
}
}
bool contains(set &s, int x) {
assert(x >= 0 && x < m);
return s.isin[x];
}
void add(set &s, int x) {
assert(x >= 0 && x < m);
s.isin[x] = true;
}
void destroy(set &s) {
delete[] s.isin;
}
Jednoduché hašovanie
Priame adresovanie sa nehodí pre veľké univerzá, lebo by vyžadovalo veľa pamäte.
Hašovanie (angl. hashing) je jednoduchá finta, ktorá funguje nasledovne:
- Nech U je univerzum všetkých možných prvkov množiny.
- Vytvoríme hašovaciu tabuľku (angl. hash table), čo je pole nejakej rozumnej veľkosti m.
- Naprogramujeme hašovaciu funkciu, ktorá transformuje prvky univerza U na indexy hašovacej tabuľky; pôjde teda o funkciu h: U -> {0, 1, ... , m−1}.
- Najjednoduchšia hašovacia funkcia pre celočíselné prvky je h(x) = |x| mod m.
- |x| spočítame funkciou abs z knižnice cstdlib.
- Absolútnu hodnotu používame, lebo napríklad -10 % 3 je -1, čo mimo rozsahu indexov tabuľky.
- V praxi sa používajú zložitejšie hašovacie funkcie. Ideálne je hašovacia funkcia jednoduchá a rýchla, ale pritom hodnoty do tabuľky distribuuje rovnomerne, aby sa príliš často nestávalo, že dva prvky sa namapujú na to isté políčko.
int hash(int x, int m) {
return abs(x) % m;
}
Napríklad pre m = 5: hash(12, 5) je 2, hash(-6, 5) je 1.
Prvý pokus o prácu hašovacou tabuľkou by teda mohol vyzerať takto:
Vkladanie prvku x:
- Spočítame index = hash(x, m) a prvok vložíme na pozíciu table[index].
Vyhľadávanie prvku x:
- Ak je prvok s kľúčom x v tabuľke, musí byť na indexe hash(x, m).
- Skontrolujeme túto pozíciu a ak tam je niečo iné ako x, prvok x sa v tabuľke nenachádza.
Problémy:
- Na akú hodnotu inicializovať prvky poľa table?
- Čo ak budeme potrebovať vložiť prvok na miesto, kde je už niečo uložené?
Kolízie
- Pri vkladaní prvku sme narazili na problém, ak na už obsadené miesto chceme vložiť iný prvok.
- Ak sa dva prvky x a y sa zahašujú na rovnakú pozíciu h(x) = h(y), hovoríme, že nastala kolízia.
- Existujú rôzne prístupy na riešenie kolízií, môžeme napríklad hľadať iné voľné miesto v tabuľke.
- V našom programe kolízie vyriešime tak, že v každom políčku tabuľky uložíme spájaný zoznam všetkých prvkov, ktoré sa tam zahašovali.
- Táto situácia je znázornená na nasledujúcom obrázku, v ktorom sme do hašovacej tabuľky pre m=5 pridali prvky 0,2,5.
#include <cstdlib>
/* hašovacia funkcia: */
int h(int x, int m) {
return abs(x) % m;
}
/* štruktúra reprezentujúca jeden prvok spájaného zoznamu: */
struct node {
int data;
node *next;
};
/* štruktúra implementujúca dynamickú množinu hašovaním: */
struct set {
node **table; // pole smerníkov na začiatky zoznamov
int m; // veľkost hašovacej tabuľky
};
void init(set &s, int m) {
// veľkosť tabuľky je parametrom funkcie init
s.m = m;
s.table = new node *[m];
for (int i = 0; i < m; i++) {
s.table[i] = NULL;
}
}
bool contains(set &s, int x) {
// spočítame políčko tabuľky
int index = h(x, s.m);
node *p = s.table[index];
// p ukazuje na začiatok zoznamu
while (p != NULL) {
// prechádzame zoznam, hľadáme x
if (p->data == x) {
return true;
}
p = p->next;
}
return false;
}
void add(set &s, int x) {
// spočítame políčko tabuľky
int index = h(x, s.m);
// vytvoríme nový uzol
node *p = new node;
p->data = x;
// uzol vložíme na začiatok zoznamu
p->next = s.table[index];
s.table[index] = p;
}
void destroy(set &s) {
for (int i = 0; i < s.m; i++) {
// uvoľníme zoznam s.table[i]
node *p = s.table[i];
while (p != NULL) {
node *p2 = p->next;
delete p;
p = p2;
}
}
delete[] s.table;
}
Cvičenie: Ako bude vyzerať hašovacia tabuľka pri riešení kolízií pomocou spájaných zoznamov, ak hašovacia funkcia je |x| mod 5 a vkladáme prvky 13, -2, 0, 8, 10, 17?
Zložitosť
- Rýchlosť závisí od veľkosti tabuľky m, hašovacej funkcie a počtu kolízií.
- V najhoršom prípade sa všetky prvky zahašujú do toho istého políčka, a teda musíme pri hľadaní prejsť všetky prvky množiny.
- Ak máme šťastie a v každom políčku máme len málo prvkov, bude aj vyhľadávanie rýchle.
- Ak je tabuľka dosť veľká a hašovacia funkcia vhodne zvolená, tento prípad je pomerne obvyklý.
- Hašovacie tabuľky sa často používajú v praxi.
- Viac budúci rok na predmete Algoritmy a dátové štruktúry.
Zhrnutie
- Videli sme abstraktný dátový typ dynamická množina.
- Implementovali sme ho pomocou neutriedených a utriedených polí, spájaných zoznamov, priamym adresovaním (ak prvky sú napr. malé celé čísla) a hašovaním.
- Ďalšie dve implementácie uvidíme na konci semestra.
- Spájané zoznamy sú ďalším príkladom využitia smerníkov. Ich výhodou je možnosť rýchlo pridávať a uberať uzly na začiatku zoznamu, alebo aj na ľubovoľnom mieste zoznamu, pokiaľ máme smerník na predchodcu. Nevieme však rýchlo pristupovať k prvku na danej pozícii. Prácu so zoznamami si precvičíme na cvičeniach tento a budúci týždeň.
- Na zamyslenie: pri jednoduchej implementácii množiny v poli sme skúsili dve možnosti: utriedenú a neutriedenú. Malo by zmysel uvažovať aj utriedený spájaný zoznam?