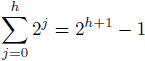Programovanie (1) v C/C++
1-INF-127, ZS 2024/25
Prednáška 20: Rozdiel medzi revíziami
(→Oznamy) |
|||
| (45 medziľahlých úprav od 2 ďalších používateľov nie je zobrazených) | |||
| Riadok 1: | Riadok 1: | ||
== Oznamy == | == Oznamy == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == Aritmetické | + | * Na testovači dnes pribudnú nejaké úlohy z budúcich cvičení, ktoré vám pomôžu s prípravou na test. |
| + | * V piatok sú cvičenia nepovinné, budú na nich vzorové riešenia testu. Môžeme vám tiež poradiť s riešením úloh z cvičení alebo domácej úlohy, prípadne ak máte otázky k ukážkovým príkladom na test. | ||
| + | * Termín DÚ3 je v piatok večer. | ||
| + | * Takisto do piatka je potrebné hlásiť záujem o prípadný preklad zadaní, viď [[Zimný semester, semestrálny test|informácie k testu]] | ||
| + | |||
| + | ==Opakovanie z minulej prednášky== | ||
| + | Aritmetické výrazy | ||
| + | * Bežná infixová notácia, napr. (65 – 3*5)/(2 + 3) | ||
| + | * Postfixová notácia 65 3 5 * - 2 3 + / | ||
| + | * Prefixová notácia / - 65 * 3 5 + 2 3 | ||
| + | * Prefixová a postfixová notácia nepotrebujú zátvorky | ||
| + | * Prevod z infixovej notácie na postfixovú pomocou zásobníka | ||
| + | ** Čo si ukladáme do zásobníka? | ||
| + | * Vyhodnocovanie postfixovej notácie pomocou zásobníka | ||
| + | ** Čo si ukladáme do zásobníka? | ||
| + | |||
| + | == Aritmetický výraz ako strom == | ||
[[Image:PROG-P21-aritm.png|thumb|right|Strom pre výraz <tt>(65 – 3 * 5)/(2 + 3)</tt>]] | [[Image:PROG-P21-aritm.png|thumb|right|Strom pre výraz <tt>(65 – 3 * 5)/(2 + 3)</tt>]] | ||
| − | Aritmetické výrazy | + | Aritmetické výrazy môžeme veľmi prirodzene reprezentovať vo forme ''stromu'' |
| − | * Operátory a čísla tvoria tzv. ''uzly'' stromu. | + | * Operátory a čísla tvoria tzv. ''uzly'' (alebo ''vrcholy'') stromu. |
| − | * Operátory tvoria tzv. ''vnútorné uzly'' stromu | + | * Operátory tvoria tzv. ''vnútorné uzly'' stromu, každý z nich má dve ''deti'' zodpovedajúce podvýrazom pre jednotlivé operandy. |
| − | * Čísla tvoria tzv. ''listy'' | + | ** Pre jednoduchosť na dnešnej prednáške neuvažujeme unárne mínus, dalo by sa však ľahko dorobiť. |
| − | * Strom obsahuje jediný uzol, ktorý | + | * Čísla tvoria tzv. ''listy'' stromu, tie už nemajú žiadne deti. |
| + | * Strom obsahuje jediný uzol, ktorý nemá rodiča. Tento sa nazýva ''koreň'' stromu a reprezentuje celý aritmetický výraz. | ||
* Informatici stromy väčšinou kreslia „hore nohami”, s koreňom na vrchu. | * Informatici stromy väčšinou kreslia „hore nohami”, s koreňom na vrchu. | ||
| − | Uzol | + | Uzol takéhoto stromu tak môžeme reprezentovať napríklad nasledujúcou štruktúrou: |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
struct treeNode { | struct treeNode { | ||
| − | + | // číselná hodnota (len v listoch) | |
| − | + | double val; | |
| − | + | ||
| − | treeNode *right; | + | // operátor vo vnútorných uzloch, pre listy medzera |
| + | char op; | ||
| + | |||
| + | // smerníky na podstromy | ||
| + | treeNode * left, * right; | ||
}; | }; | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 40: | Riadok 56: | ||
Celý strom pritom budeme reprezentovať jeho koreňom. | Celý strom pritom budeme reprezentovať jeho koreňom. | ||
| − | + | V tejto reprezentácii sú niektoré položky štruktúry <tt>treeNode</tt> nevyužité (napr. <tt>val</tt> vo vnútorných vrcholoch). S využitím objektového programovania (letný semester) budeme vedieť stromy pre aritmetické výrazy reprezentovať elegantnejšie. | |
| − | === Vytvorenie uzlu | + | === Vytvorenie uzlu === |
Nasledujúce funkcie vytvoria nový vnútorný uzol (pre operátor) resp. nový list (pre číslo): | Nasledujúce funkcie vytvoria nový vnútorný uzol (pre operátor) resp. nový list (pre číslo): | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | treeNode *createOp(char op, treeNode *left, treeNode *right) { | + | treeNode * createOp(char op, treeNode * left, treeNode * right) { |
| − | treeNode *v = new treeNode; | + | treeNode * v = new treeNode; |
v->left = left; | v->left = left; | ||
v->right = right; | v->right = right; | ||
| Riadok 55: | Riadok 71: | ||
} | } | ||
| − | treeNode *createNum(double val) { | + | treeNode * createNum(double val) { |
| − | treeNode *v = new treeNode; | + | treeNode * v = new treeNode; |
v->left = NULL; | v->left = NULL; | ||
v->right = NULL; | v->right = NULL; | ||
| Riadok 67: | Riadok 83: | ||
„Ručne” teraz môžeme vytvoriť strom pre výraz <tt>(65 – 3 * 5)/(2 + 3)</tt>: | „Ručne” teraz môžeme vytvoriť strom pre výraz <tt>(65 – 3 * 5)/(2 + 3)</tt>: | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | treeNode *root = createOp('/', | + | treeNode * root = createOp('/', |
| − | + | createOp('-', | |
| − | + | createNum(65), | |
| − | + | createOp('*', createNum(3), createNum(5))), | |
| − | + | createOp('+', createNum(2), createNum(3))); | |
</syntaxhighlight> | </syntaxhighlight> | ||
Alebo po častiach: | Alebo po častiach: | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | treeNode *v65 = createNum(65); | + | treeNode * v65 = createNum(65); |
| − | treeNode *v3 = createNum(3); | + | treeNode * v3 = createNum(3); |
| − | treeNode *v5 = createNum(5); | + | treeNode * v5 = createNum(5); |
| − | treeNode *v2 = createNum(2); | + | treeNode * v2 = createNum(2); |
| − | treeNode *v3b = createNum(3); | + | treeNode * v3b = createNum(3); |
| − | treeNode *vKrat = createOp('*', v3, v5); | + | treeNode * vKrat = createOp('*', v3, v5); |
| − | treeNode *vMinus = createOp('-', v65, vKrat); | + | treeNode * vMinus = createOp('-', v65, vKrat); |
| − | treeNode *vPlus = createOp('+', v2, v3b); | + | treeNode * vPlus = createOp('+', v2, v3b); |
| − | treeNode *vDeleno = createOp('/', vMinus, vPlus); | + | treeNode * vDeleno = createOp('/', vMinus, vPlus); |
</syntaxhighlight> | </syntaxhighlight> | ||
| − | === | + | === Ďalší plán === |
| + | Ďalej uvidíme: | ||
| + | * jednoduchú rekurzívnu funkciu na vyhodnotenie výrazu uloženého ako strom, | ||
| + | * ďalšie rekurzívne funkcie na uvoľnenie pamäte stromu a výpis výrazu, | ||
| + | * funkciu na vytvorenie stromu z postfixového výrazu. | ||
| − | + | Stromy majú v informatike veľa využití, nielen na aritmetické výrazy. Ďalej sa teda budeme venovať práci so stromami všeobecne. | |
| − | + | === Vyhodnotenie výrazu reprezentovaného stromom === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Nasledujúca rekurzívna funkcia vypočíta hodnotu aritmetického výrazu reprezentovaného stromom s koreňom <tt>root</tt>. | |
| + | * Ak je zadaný vrchol listom, vrátime hodnotu uloženú v položke <tt>val</tt>. | ||
| + | * V opačnom prípade rekurzívne spočítame hodnoty pre obidva podvýrazy a skombinujeme ich podľa typu znamienka. | ||
| + | * Celkovo veľmi jednoduchý a prirodzený výpočet, nie je potrebný explicitný zásobník. | ||
| + | * Funkcia nižšie nefunguje pre unárne mínus, nebolo by však ťažké ho dorobiť. | ||
| − | + | Rekurziu budeme používať vždy, keď potrebujeme prejsť všetky uzly stromu. Cyklom sa to programuje ťažko, lebo z uzla potrebujeme ísť doľava aj doprava. | |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | double evaluateTree(treeNode *root) { | + | double evaluateTree(treeNode * root) { |
assert(root != NULL); | assert(root != NULL); | ||
if (root->op == ' ') { | if (root->op == ' ') { | ||
| Riadok 131: | Riadok 147: | ||
} | } | ||
return 0; // realne nedosiahnutelny prikaz | return 0; // realne nedosiahnutelny prikaz | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | === Uvoľnenie pamäte === | ||
| + | |||
| + | Nasledujúca funkcia uvoľní z pamäte celý strom s koreňom <tt>root</tt>. | ||
| + | * Opäť používa rekurziu na prejdenie celého stromu. | ||
| + | * Pozor na poradie príkazov, treba najskôr uvoľniť podstromy až potom zavolať delete na root, inak by sme stratili prístup k deťom. | ||
| + | * Všimnite si, ako sú riešené triviálne prípady, funkcia ani nezisťuje, s akým typom uzla pracuje. | ||
| + | |||
| + | <syntaxhighlight lang="C++"> | ||
| + | void destroyTree(treeNode * root) { | ||
| + | if (root != NULL) { | ||
| + | destroyTree(root->left); | ||
| + | destroyTree(root->right); | ||
| + | delete root; | ||
| + | } | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 136: | Riadok 169: | ||
=== Vypísanie výrazu reprezentovaného stromom v rôznych notáciách === | === Vypísanie výrazu reprezentovaného stromom v rôznych notáciách === | ||
| − | Infixovú, prefixovú, resp. postfixovú reprezentáciu aritmetického výrazu reprezentovaného stromom s koreňom <tt>root</tt> možno získať pomocou nasledujúcich funkcií | + | Infixovú, prefixovú, resp. postfixovú reprezentáciu aritmetického výrazu reprezentovaného stromom s koreňom <tt>root</tt> možno získať pomocou nasledujúcich funkcií. |
| + | * Opäť používajú rekurziu na prejdenie celého stromu. | ||
| + | * Líšia sa hlavne umiestnením príkazu na vypísanie operátora (pred, medzi alebo za rekurzívnym vypísaním podvýrazov). | ||
| + | * Infixová notácia potrebuje aj zátvorky. Táto funkcia ich pre istotu dáva všade. Rozmyslite si, ako by sme ich vedeli vypísať iba tam, kde treba. | ||
| + | * Ako by sme funkcie rozšírili pre unárne mínus? | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | void printInorder( | + | /** Funkcia vypíše aritmetický výraz v inorder poradí */ |
| + | void printInorder(treeNode * root) { | ||
if (root->op == ' ') { | if (root->op == ' ') { | ||
| − | + | printf("%g", root->val); | |
} else { | } else { | ||
| − | + | printf("("); | |
| − | printInorder( | + | printInorder(root->left); |
| − | + | printf(" %c ", root->op); | |
| − | printInorder( | + | printInorder(root->right); |
| − | + | printf(")"); | |
} | } | ||
} | } | ||
| − | |||
| − | + | /** Funkcia vypíše aritmetický výraz v preorder poradí */ | |
| − | void printPreorder( | + | void printPreorder(treeNode * root) { |
if (root->op == ' ') { | if (root->op == ' ') { | ||
| − | + | printf("%g ", root->val); | |
} else { | } else { | ||
| − | + | printf("%c ", root->op); | |
| − | printPreorder( | + | printPreorder(root->left); |
| − | printPreorder( | + | printPreorder(root->right); |
} | } | ||
} | } | ||
| − | |||
| − | + | /** Funkcia vypíše aritmetický výraz v postorder poradí */ | |
| − | void printPostorder( | + | void printPostorder(treeNode * root) { |
if (root->op == ' ') { | if (root->op == ' ') { | ||
| − | + | printf("%g ", root->val); | |
} else { | } else { | ||
| − | printPostorder( | + | printPostorder(root->left); |
| − | printPostorder( | + | printPostorder(root->right); |
| − | + | printf("%c ", root->op); | |
} | } | ||
} | } | ||
| Riadok 178: | Riadok 214: | ||
=== Vytvorenie stromu z postfixového výrazu === | === Vytvorenie stromu z postfixového výrazu === | ||
| − | Pripomeňme si z [[ | + | Pripomeňme si z [[Prednáška 19|minulej prednášky]] funkciu na vyhodnocovanie postfixového výrazu: |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | + | /** Funkcia vyhodnotí a vráti hodnotou výrazu v postfixovom tvare. */ | |
| + | double evaluatePostfix(tokenSequence & tokens) { | ||
| + | // zásobník, do ktorého ukladáme čísla | ||
| + | stack numberStack; | ||
| + | init(numberStack); | ||
| − | + | for (int i = 0; i < tokens.length; i++) { | |
| − | + | // aktuálny token zo vstupu | |
| − | + | token curToken = tokens.items[i]; | |
| − | + | if (curToken.op == ' ') { | |
| − | + | // čísla rovno ukladáme na zásobník | |
| − | + | push(numberStack, curToken); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | if ( | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | push( | ||
| − | |||
| − | |||
| − | |||
} else { | } else { | ||
| − | + | // spracovanie operátora | |
| − | + | token num1, num2, result; | |
| − | + | // najskôr vyberieme 1 alebo 2 čísla zo zásobníka | |
| − | + | if (curToken.op == '~') { | |
| − | + | num1 = pop(numberStack); | |
| − | + | } else { | |
| − | + | num2 = pop(numberStack); | |
| − | + | num1 = pop(numberStack); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
| − | + | // na operandy aplikujeme operátor | |
| + | applyOp(curToken, num1, num2, result); | ||
| + | // výsledné číslo uložíme na zásobník | ||
| + | push(numberStack, result); | ||
} | } | ||
} | } | ||
| − | + | // zo zásobníka vyberieme výsledné číslo | |
| − | assert(isEmpty( | + | token result = pop(numberStack); |
| − | destroy( | + | // skontrolujeme, že zásobník je prázdny a výsledok je číslo |
| − | + | assert(isEmpty(numberStack) && result.op == ' '); | |
| − | return result; | + | // uvoľníme pamäť zásobníka |
| + | destroy(numberStack); | ||
| + | return result.val; | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Túto funkciu možno jednoducho prepísať tak, aby namiesto vyhodnocovania výrazu konštruovala zodpovedajúci aritmetický strom. Namiesto hodnôt jednotlivých podvýrazov stačí na zásobníku uchovávať korene stromov, ktoré tieto podvýrazy reprezentujú. Aplikácii aritmetickej operácie | + | |
| + | * Túto funkciu možno jednoducho prepísať tak, aby namiesto vyhodnocovania výrazu konštruovala zodpovedajúci aritmetický strom. | ||
| + | * Namiesto hodnôt jednotlivých podvýrazov stačí na zásobníku uchovávať korene stromov, ktoré tieto podvýrazy reprezentujú. | ||
| + | * Aplikácii aritmetickej operácie bude zodpovedať spojenie dvoch podstromov do jedného stromu. | ||
| + | * V tomto prípade nepoužívame postupnosť symbolov (tokenov), ale priamo spracovávame postfixový výraz vo forme reťazca. | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 238: | Riadok 264: | ||
| − | /* Sem | + | /* Sem príde definícia štruktúry pre zásobník a všetkých funkcií poskytovaných zásobníkom. */ |
| + | treeNode * postfixToTree(char * str) { | ||
| + | // zásobník, do ktorého ukladáme korene podstromov | ||
| + | stack treeStack; | ||
| + | init(treeStack); | ||
| + | int strPos = 0; // pozícia v rámci reťazca | ||
| + | while (str[strPos] != 0) { // kým nie sme na konci str | ||
| + | if (isspace(str[strPos])) { // preskakujeme biele znaky | ||
| + | strPos++; | ||
| + | } else if (isdigit(str[strPos]) || str[strPos] == '.') { | ||
| + | // keď nájdeme cifru alebo bodku (začiatok čísla) | ||
| + | double val; | ||
| + | int skip; | ||
| + | // načítame toto číslo pomocou sscanf, | ||
| + | // do skip uložíme počet znakov čísla | ||
| + | sscanf(&(str[strPos]), "%lf%n", &val, &skip); | ||
| + | // preskočíme všetky znaky čísla | ||
| + | strPos += skip; | ||
| − | + | // vytvoríme list a uložíme na zásobník | |
| − | + | push(treeStack, createNum(val)); | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | push( | ||
| − | |||
| − | |||
| − | |||
} else { | } else { | ||
| − | treeNode *right = pop( | + | // spracovanie operátora |
| − | + | assert(strchr("+-/*", str[strPos]) != NULL); | |
| − | push( | + | treeNode * left, * right; |
| − | + | // najskôr vyberieme 2 podstromy zo zásobníka | |
| + | // vytvoríme nový koreň, | ||
| + | // ktorý bude ich rodičom a vložíme na zásobník | ||
| + | right = pop(treeStack); | ||
| + | left = pop(treeStack); | ||
| + | push(treeStack, createOp(str[strPos], left, right)); | ||
| + | strPos++; | ||
} | } | ||
} | } | ||
| − | treeNode *result = pop( | + | // zo zásobníka vyberieme výsledný strom |
| − | assert(isEmpty( | + | treeNode * result = pop(treeStack); |
| − | destroy( | + | // skontrolujeme, že zásobník je prázdny |
| − | + | assert(isEmpty(treeStack)); | |
| + | // uvoľníme pamäť zásobníka | ||
| + | destroy(treeStack); | ||
return result; | return result; | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | === Ukážkový program pracujúci | + | === Ukážkový program pracujúci so stromami pre aritmetické výrazy === |
| − | Nasledujúci program prečíta z konzoly aritmetický výraz v postfixovom tvare, skonštruuje jeho aritmetický strom a následne preň zavolá funkcie na výpočet hodnoty výrazu a jeho výpis v rôznych notáciách | + | Nasledujúci program prečíta z konzoly aritmetický výraz v postfixovom tvare, skonštruuje jeho aritmetický strom a následne preň zavolá funkcie na výpočet hodnoty výrazu a jeho výpis v rôznych notáciách. Celý program je [[#Program_pre_aritmetick.C3.A9_v.C3.BDrazy_ako_stromy|na konci prednášky]]. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | int main( | + | int main() { |
| − | char | + | // načítame postfixový výraz do reťazca |
| − | fgets( | + | const int maxLine = 100; |
| − | treeNode *root = | + | char postfix[maxLine]; |
| − | + | fgets(postfix, maxLine, stdin); | |
| − | printf(" | + | // výraz konvertujeme na strom |
| − | printf(" | + | treeNode * root = postfixToTree(postfix); |
| + | // spočítame hodnotu výrazu | ||
| + | double value = evaluateTree(root); | ||
| + | printf(" value: %g\n", value); | ||
| + | // vypíšeme vo všetkých troch notáciách | ||
| + | printf(" inorder: "); | ||
printInorder(stdout, root); | printInorder(stdout, root); | ||
| − | printf("\n | + | printf("\n predorder: "); |
| − | |||
printPreorder(stdout, root); | printPreorder(stdout, root); | ||
| − | printf("\n | + | printf("\n postdorder: "); |
| − | |||
printPostorder(stdout, root); | printPostorder(stdout, root); | ||
printf("\n"); | printf("\n"); | ||
| − | + | // uvoľníme pamäť | |
| − | destroyTree(root) | + | destroyTree(root); |
| − | |||
| − | |||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 303: | Riadok 339: | ||
== Binárne stromy == | == Binárne stromy == | ||
| − | + | Stromy pre aritmetické výrazy sú špeciálnym prípadom ''binárnych stromov''. V informatike majú binárne stromy množstvo rozličných uplatnení. Ukážeme si teda všeobecnú dátovú štruktúru binárneho stromu. | |
=== Terminológia stromov === | === Terminológia stromov === | ||
| − | + | * Strom obsahuje množinu ''uzlov'' alebo ''vrcholov'' prepojených hranami. (uzol angl. node, vrchol vertex, hrana edge). | |
| + | * Ak je strom neprázdny, jeden jeho vrchol nazývame ''koreň'' (angl. root) | ||
| + | * Každý uzol ''u'' okrem koreňa je spojený hranou s práve jedným ''rodičom'' (angl. ''parent''), ktorým je nejaký uzol ''v''. Naopak uzol ''u'' je ''dieťaťom'' (angl. ''child'') uzla ''v''. | ||
| + | * Vo všeobecnom strome môže mať každý uzol ľubovoľný počet detí (aj nula). | ||
| + | * Strom je ''binárny'', ak má každý uzol ''najviac'' dve deti. Budeme pritom rozlišovať medzi pravým a ľavým dieťaťom. | ||
| + | * Uzly zakoreneného stromu, ktoré nemajú žiadne dieťa, nazývame ''listami''; zvyšné uzly nazývame ''vnútornými uzlami''. | ||
| + | * ''Predkom'' uzla ''u'' nazveme ľubovoľný uzol ''v'' ležiaci na ceste z ''u'' do koreňa stromu (vrátane ''u'' a koreňa). Naopak potom hovoríme, že ''u'' je ''potomkom'' uzla ''v''. | ||
| + | * ''Podstromom'' stromu ''T'' zakoreneným v nejakom uzle ''v'' stromu ''T'' budeme rozumieť strom s koreňom ''v'' pozostávajúci zo všetkých jeho potomkov a všetkých hrán stromu ''T'' vedúcich medzi týmito uzlami. | ||
| − | + | Každý binárny strom je teda buď prázdny, alebo je tvorený jeho koreňom a dvoma podstromami – ľavým a pravým. | |
| − | |||
| − | Každý | ||
| − | |||
| − | |||
| − | |||
| − | '' | + | Takéto stromy sa nazývajú zakorenené. Presnejšiu matematickú definíciu zakorenených aj nezakorenených stromov uvidíte na predmete ''Úvod do kombinatoriky a teórie grafov'' (letný semester). |
| − | |||
| − | |||
=== Štruktúra pre uzol binárneho stromu === | === Štruktúra pre uzol binárneho stromu === | ||
| − | V nasledujúcom budeme pracovať výhradne s ''binárnymi stromami''. Štruktúra pre uzol všeobecného binárneho stromu je podobná, ako pri | + | V nasledujúcom budeme pracovať výhradne s ''binárnymi stromami''. Štruktúra pre uzol všeobecného binárneho stromu je podobná, ako pri stromoch pre aritmetické výrazy, namiesto operátora alebo hodnoty si však v každom uzle budeme pamätať hodnotu ľubovoľného typu <tt>dataType</tt>, napríklad <tt>int</tt>. |
| − | |||
| − | |||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | + | /* Typ prvkov ukladaných v uzloch binárneho stromu */ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | /* Typ prvkov | ||
typedef int dataType; | typedef int dataType; | ||
| − | /* | + | /* Uzol binárneho stromu */ |
| − | + | struct node { | |
| − | + | // hodnota uložená v uzle | |
| − | + | dataType data; | |
| − | + | // smerníky na podstromy | |
| − | + | node * left, * right; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | node *left | ||
| − | |||
}; | }; | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Riadok 357: | Riadok 377: | ||
=== Vytvorenie binárneho stromu === | === Vytvorenie binárneho stromu === | ||
| − | Nasledujúca funkcia vytvorí uzol binárneho stromu s dátami <tt>data</tt>, ľavým podstromom zakoreneným v uzle <tt>*left</tt> a pravým podstromom zakoreneným v uzle <tt>*right</tt> (parametre <tt>left</tt> a <tt>right</tt> sú teda smerníkmi na uzly). Ako výstup funkcia vráti smerník na novovytvorený uzol. | + | Nasledujúca funkcia vytvorí uzol binárneho stromu s dátami <tt>data</tt>, ľavým podstromom zakoreneným v uzle <tt>* left</tt> a pravým podstromom zakoreneným v uzle <tt>* right</tt> (parametre <tt>left</tt> a <tt>right</tt> sú teda smerníkmi na uzly). Ako výstup funkcia vráti smerník na novovytvorený uzol. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
/* Vytvori uzol binarneho stromu */ | /* Vytvori uzol binarneho stromu */ | ||
| − | node *createNode(dataType data, node *left, node *right) { | + | node * createNode(dataType data, node * left, node * right) { |
| − | node *v = new node; | + | node * v = new node; |
v->data = data; | v->data = data; | ||
v->left = left; | v->left = left; | ||
| Riadok 370: | Riadok 390: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Nasledujúca volanie tak napríklad vytvorí binárny strom so šiestimi uzlami zakorenený v uzle <tt>*root</tt>. | + | Nasledujúca volanie tak napríklad vytvorí binárny strom so šiestimi uzlami zakorenený v uzle <tt>* root</tt>. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | node *root = createNode(1, | + | node * root = createNode(1, |
| − | + | createNode(2, | |
| − | + | createNode(3, NULL, NULL), | |
| − | + | createNode(4, NULL, NULL)), | |
| − | + | createNode(5, | |
| − | + | NULL, | |
| − | + | createNode(6, NULL, NULL))); | |
</syntaxhighlight> | </syntaxhighlight> | ||
''Cvičenie'': nakreslite binárny strom vytvorený predchádzajúcim volaním. | ''Cvičenie'': nakreslite binárny strom vytvorený predchádzajúcim volaním. | ||
| + | |||
| + | === Prehľadávanie stromov a vypisovanie ich uzlov === | ||
| + | |||
| + | Často je potrebné prejsť celý strom a spracovať (napríklad vypísať) hodnoty vo všetkých uzloch. Toto prehľadávanie možno, podobne ako pri stromoch pre výrazy, realizovať v troch základných poradiach: ''preorder'', ''inorder'' a ''postorder''. | ||
| + | |||
| + | Pri vypisovaní predpokladáme, že pre hodnoty typu <tt>dataType</tt> máme k dispozícii funkciu <tt>printDataType</tt>, ktorá ich v nejakom vhodnom formáte vypisuje. | ||
| + | |||
| + | |||
| + | <syntaxhighlight lang="C++"> | ||
| + | /* Funkcia pre výpis hodnoty typu dataType */ | ||
| + | void printDataType(dataType data) { | ||
| + | printf("%d ", data); // pre int | ||
| + | } | ||
| + | |||
| + | /* Vypíše podstrom s koreňom * root v poradí preorder */ | ||
| + | void printPreorder(node * root) { | ||
| + | if (root != NULL) { | ||
| + | printDataType(root->data); | ||
| + | printPreorder(root->left); | ||
| + | printPreorder(root->right); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | /* Vypíše podstrom s koreňom * root v poradí inorder */ | ||
| + | void printInorder(node * root) { | ||
| + | if (root != NULL) { | ||
| + | printInorder(root->left); | ||
| + | printDataType(root->data); | ||
| + | printInorder(root->right); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | /* Vypíše podstrom s koreňom * root v poradí postorder */ | ||
| + | void printPostorder(node * root) { | ||
| + | if (root != NULL) { | ||
| + | printPostorder(root->left); | ||
| + | printPostorder(root->right); | ||
| + | printDataType(root->data); | ||
| + | } | ||
| + | } | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Cvičenie: ako by sme spočítali súčet hodnôt uložených v uzloch stromu? | ||
=== Likvidácia binárneho stromu === | === Likvidácia binárneho stromu === | ||
| − | Nasledujúca rekurzívna funkcia zlikviduje celý podstrom zakorenený v uzle <tt>*root</tt> (t. j. | + | Nasledujúca rekurzívna funkcia zlikviduje celý podstrom zakorenený v uzle <tt>* root</tt> (t. j. uvoľní pamäť pre všetky jeho uzly). Veľmi sa podobá na funkciu pre strom reprezentujúci aritmetický výraz. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | /* Zlikviduje podstrom s korenom *root ( | + | /* Zlikviduje podstrom s korenom * root (uvolni pamat) */ |
| − | void destroyTree(node *root) { | + | void destroyTree(node * root) { |
if (root != NULL) { | if (root != NULL) { | ||
destroyTree(root->left); | destroyTree(root->left); | ||
| Riadok 401: | Riadok 464: | ||
=== Výška binárneho stromu === | === Výška binárneho stromu === | ||
| − | ''Hĺbkou uzla'' binárneho stromu nazveme jeho vzdialenosť od koreňa. Koreň má teda hĺbku ''0'', jeho | + | * ''Hĺbkou uzla'' binárneho stromu nazveme jeho vzdialenosť od koreňa. |
| + | ** Koreň má teda hĺbku ''0'', jeho deti majú hĺbku ''1'', atď. | ||
| + | * ''Výškou binárneho stromu'' potom nazveme maximálnu hĺbku niektorého z jeho vrcholov. | ||
| + | ** Strom s jediným vrcholom má teda výšku ''0''; pre ostatné stromy je ich výška daná ako 1 plus maximum z výšok ľavého a pravého podstromu. | ||
Nasledujúca funkcia počíta výšku stromu (kvôli elegancii zápisu pritom pracuje s rozšírením definície výšky stromu na prázdne stromy, za ktorých výšku sa považuje číslo ''-1''). | Nasledujúca funkcia počíta výšku stromu (kvôli elegancii zápisu pritom pracuje s rozšírením definície výšky stromu na prázdne stromy, za ktorých výšku sa považuje číslo ''-1''). | ||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| − | /* | + | /* Spočíta výšku podstromu s koreňom * root. |
| − | int height(node *root) { | + | * Pre root == NULL vráti -1. */ |
| + | int height(node * root) { | ||
if (root == NULL) { | if (root == NULL) { | ||
return -1; | return -1; | ||
} | } | ||
| − | int hLeft = height(root->left); | + | // rekurzívne spočíta výšku ľavého a pravého podstromu |
| − | int hRight = height(root->right); // | + | int hLeft = height(root->left); |
| − | if (hLeft >= hRight) { | + | int hRight = height(root->right); |
| + | // vráti max(hLeft, hRight) + 1 | ||
| + | if (hLeft >= hRight) { | ||
return hLeft + 1; | return hLeft + 1; | ||
} else { | } else { | ||
| Riadok 421: | Riadok 490: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Pre výšku ''h'' stromu s ''n'' uzlami | + | Cvičenie: prepíšte funkciu tak, aby triviálnym prípadom bol list, nie prázdny strom. Funkcia teda vždy dostane smerník na neprázdny strom a nebude volať rekurziu na prázdne podstromy. Ktorá verzia je jednoduchšia? Ktorá sa vám zdá jednoduchšia na pochopenie? |
| + | |||
| + | === Aká môže byť výška binárneho stromu? === | ||
| + | |||
| + | Pre výšku ''h'' binárneho stromu s ''n'' uzlami platia nasledujúce vzťahy: | ||
* Určite ''h ≤ n-1''. Tento prípad nastáva, ak sú všetky uzly „navešané jeden pod druhý”. | * Určite ''h ≤ n-1''. Tento prípad nastáva, ak sú všetky uzly „navešané jeden pod druhý”. | ||
* Strom s výškou ''h'' má najviac | * Strom s výškou ''h'' má najviac | ||
| Riadok 429: | Riadok 502: | ||
* Dostávame teda log<sub>2</sub>''(n+1)-1 ≤ h ≤ n-1''. | * Dostávame teda log<sub>2</sub>''(n+1)-1 ≤ h ≤ n-1''. | ||
* Napríklad strom s milión vrcholmi má teda hĺbku medzi ''19'' a ''999999''. | * Napríklad strom s milión vrcholmi má teda hĺbku medzi ''19'' a ''999999''. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Príklad: plné binárne stromy === | === Príklad: plné binárne stromy === | ||
| − | Binárny strom výšky ''h'' s maximálnym počtom vrcholov ''2<sup>h+1</sup>-1'' sa nazýva ''plný binárny strom''. Nasledujúca funkcia <tt>createFullTree</tt> vytvorí takýto strom a vráti smerník na jeho koreň. Jeho | + | Binárny strom výšky ''h'' s maximálnym počtom vrcholov ''2<sup>h+1</sup>-1'' sa nazýva ''plný binárny strom''. Nasledujúca funkcia <tt>createFullTree</tt> vytvorí takýto strom a vráti smerník na jeho koreň. Jeho uzly pritom očísľuje 1, 2, 3,... (predpokladáme, že <tt>dataType</tt> je <tt>int</tt>) pomocou globálnej premennej <tt>count</tt>. |
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 476: | Riadok 513: | ||
/* Vytvori plny binarny strom vysky height s datami uzlov count, count + 1, ... */ | /* Vytvori plny binarny strom vysky height s datami uzlov count, count + 1, ... */ | ||
| − | node *createFullTree(int height) { | + | node * createFullTree(int height) { |
if (height == -1) { | if (height == -1) { | ||
return NULL; | return NULL; | ||
} | } | ||
| − | node *v = createNode(count | + | node * v = createNode(count, NULL, NULL); |
| + | count++; | ||
v->left = createFullTree(height - 1); | v->left = createFullTree(height - 1); | ||
v->right = createFullTree(height - 1); | v->right = createFullTree(height - 1); | ||
| Riadok 486: | Riadok 524: | ||
} | } | ||
| − | int main( | + | int main() { |
count = 1; | count = 1; | ||
| − | node *root = createFullTree(3); | + | node * root = createFullTree(3); |
printf("Vyska: %d\n", height(root)); | printf("Vyska: %d\n", height(root)); | ||
| Riadok 501: | Riadok 539: | ||
printf("\n"); | printf("\n"); | ||
| − | destroyTree(root) | + | destroyTree(root); |
| − | |||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | ''Cvičenie'': opíšte poradie, v ktorom sa v uvedenom programe jednotlivým uzlom priraďujú ich hodnoty. | + | ''Cvičenie'': |
| + | * Nakreslite strom aj s hodnotami v uzloch, ktorý vznikne pre výšku 2. | ||
| + | * Vo všeobecnosti opíšte poradie, v ktorom sa v uvedenom programe jednotlivým uzlom priraďujú ich hodnoty. | ||
| + | * Ako by ste v programe odstránili globálnu premennú <tt>count</tt>? | ||
| + | |||
| + | |||
| + | == Program pre aritmetické výrazy ako stromy== | ||
| + | |||
| + | <syntaxhighlight lang="C++"> | ||
| + | #include <cstdio> | ||
| + | #include <cctype> | ||
| + | #include <cassert> | ||
| + | #include <cstring> | ||
| + | using namespace std; | ||
| + | |||
| + | struct treeNode { | ||
| + | // číselná hodnota (len v listoch) | ||
| + | double val; | ||
| + | |||
| + | // operátor vo vnútorných uzloch, pre listy medzera | ||
| + | char op; | ||
| + | |||
| + | // smerníky na podstromy | ||
| + | treeNode * left, * right; | ||
| + | }; | ||
| + | |||
| + | /** Funkcia vráti nový uzol pre operátor */ | ||
| + | treeNode * createOp(char op, treeNode * left, treeNode * right) { | ||
| + | treeNode * v = new treeNode; | ||
| + | v->left = left; | ||
| + | v->right = right; | ||
| + | v->op = op; | ||
| + | return v; | ||
| + | } | ||
| + | |||
| + | /** Funkcia vráti nový uzol pre číslo */ | ||
| + | treeNode * createNum(double val) { | ||
| + | treeNode * v = new treeNode; | ||
| + | v->left = NULL; | ||
| + | v->right = NULL; | ||
| + | v->op = ' '; | ||
| + | v->val = val; | ||
| + | return v; | ||
| + | } | ||
| + | |||
| + | |||
| + | // Nasleduje kód pre zásobník uzlov stromu | ||
| + | typedef treeNode * dataType; | ||
| + | |||
| + | /** Uzol spájaného zoznamu pre zásobník */ | ||
| + | struct node { | ||
| + | dataType data; // dáta uložené v uzle | ||
| + | node * next; // smerník na ďalší uzol zoznamu | ||
| + | }; | ||
| + | |||
| + | /** Štruktúra pre zásobník implementovaný pomocou zoznamu*/ | ||
| + | struct stack { | ||
| + | node * top; // Smernik na vrch zasobníka alebo NULL | ||
| + | }; | ||
| + | |||
| + | /** Funkcia inicializuje prázdny zásobník */ | ||
| + | void init(stack & s) { | ||
| + | s.top = NULL; | ||
| + | } | ||
| + | |||
| + | /** Funkcia zistí, či je zásobník prázdny */ | ||
| + | bool isEmpty(stack & s) { | ||
| + | return s.top == NULL; | ||
| + | } | ||
| + | |||
| + | /** Funkcia pridá prvok item na vrch zásobníka */ | ||
| + | void push(stack & s, dataType item) { | ||
| + | node * tmp = new node; | ||
| + | tmp->data = item; | ||
| + | tmp->next = s.top; | ||
| + | s.top = tmp; | ||
| + | } | ||
| + | |||
| + | /** Funkcia odoberie prvok z vrchu zasobnika a vráti ho */ | ||
| + | dataType pop(stack & s) { | ||
| + | assert(!isEmpty(s)); | ||
| + | dataType result = s.top->data; | ||
| + | node * tmp = s.top->next; | ||
| + | delete s.top; | ||
| + | s.top = tmp; | ||
| + | return result; | ||
| + | } | ||
| + | |||
| + | /** Funkcia vráti prvok na vrchu zásobníka, ale nechá ho v zásobníku */ | ||
| + | dataType peek(stack & s) { | ||
| + | assert(!isEmpty(s)); | ||
| + | return s.top->data; | ||
| + | } | ||
| + | |||
| + | /** Funkcia uvoľní pamäť zásobníka */ | ||
| + | void destroy(stack & s) { | ||
| + | while (!isEmpty(s)) { | ||
| + | pop(s); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | /** Funkcia konvertuje výraz v postfixovom tvare na strom */ | ||
| + | treeNode * postfixToTree(char * str) { | ||
| + | // zásobník, do ktorého ukladáme korene podstromov | ||
| + | stack treeStack; | ||
| + | init(treeStack); | ||
| + | |||
| + | int strPos = 0; // pozícia v rámci reťazca | ||
| + | while (str[strPos] != 0) { // kým nie sme na konci str | ||
| + | if (isspace(str[strPos])) { // preskakujeme biele znaky | ||
| + | strPos++; | ||
| + | } else if (isdigit(str[strPos]) || str[strPos] == '.') { | ||
| + | // keď nájdeme cifru alebo bodku (začiatok čísla) | ||
| + | double val; | ||
| + | int skip; | ||
| + | // načítame toto číslo pomocou sscanf, | ||
| + | // do skip uložíme počet znakov čísla | ||
| + | sscanf(&(str[strPos]), "%lf%n", &val, &skip); | ||
| + | // preskočíme všetky znaky čísla | ||
| + | strPos += skip; | ||
| + | |||
| + | // vytvoríme list a uložíme na zásobník | ||
| + | push(treeStack, createNum(val)); | ||
| + | } else { | ||
| + | // spracovanie operátora | ||
| + | assert(strchr("+-/*", str[strPos]) != NULL); | ||
| + | treeNode * left, * right; | ||
| + | // najskôr vyberieme 2 podstromy zo zásobníka | ||
| + | // vytvoríme nový koreň, | ||
| + | // ktorý bude ich rodičom a vložíme na zásobník | ||
| + | right = pop(treeStack); | ||
| + | left = pop(treeStack); | ||
| + | push(treeStack, createOp(str[strPos], left, right)); | ||
| + | strPos++; | ||
| + | } | ||
| + | } | ||
| + | // zo zásobníka vyberieme výsledný strom | ||
| + | treeNode * result = pop(treeStack); | ||
| + | // skontrolujeme, že zásobník je prázdny | ||
| + | assert(isEmpty(treeStack)); | ||
| + | // uvoľníme pamäť zásobníka | ||
| + | destroy(treeStack); | ||
| + | return result; | ||
| + | } | ||
| + | |||
| + | /** Funkcia spočíta hodnotu výrazu reprezentovaného stromom */ | ||
| + | double evaluateTree(treeNode * root) { | ||
| + | assert(root != NULL); | ||
| + | if (root->op == ' ') { | ||
| + | return root->val; | ||
| + | } else { | ||
| + | double valLeft = evaluateTree(root->left); | ||
| + | double valRight = evaluateTree(root->right); | ||
| + | switch (root->op) { | ||
| + | case '+': | ||
| + | return valLeft + valRight; | ||
| + | break; | ||
| + | case '-': | ||
| + | return valLeft - valRight; | ||
| + | break; | ||
| + | case '*': | ||
| + | return valLeft * valRight; | ||
| + | break; | ||
| + | case '/': | ||
| + | return valLeft / valRight; | ||
| + | break; | ||
| + | default: | ||
| + | assert(false); | ||
| + | break; | ||
| + | } | ||
| + | } | ||
| + | return 0; // realne nedosiahnutelny prikaz | ||
| + | } | ||
| + | |||
| + | /** Funkcia uvoľní pamäť daného stromu */ | ||
| + | void destroyTree(treeNode * root) { | ||
| + | if (root != NULL) { | ||
| + | destroyTree(root->left); | ||
| + | destroyTree(root->right); | ||
| + | delete root; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | /** Funkcia vypíše aritmetický výraz v inorder poradí */ | ||
| + | void printInorder(treeNode * root) { | ||
| + | if (root->op == ' ') { | ||
| + | printf("%g", root->val); | ||
| + | } else { | ||
| + | printf("("); | ||
| + | printInorder(root->left); | ||
| + | printf(" %c ", root->op); | ||
| + | printInorder(root->right); | ||
| + | printf(")"); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | /** Funkcia vypíše aritmetický výraz v preorder poradí */ | ||
| + | void printPreorder(treeNode * root) { | ||
| + | if (root->op == ' ') { | ||
| + | printf("%g ", root->val); | ||
| + | } else { | ||
| + | printf("%c ", root->op); | ||
| + | printPreorder(root->left); | ||
| + | printPreorder(root->right); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | /** Funkcia vypíše aritmetický výraz v postorder poradí */ | ||
| + | void printPostorder(treeNode * root) { | ||
| + | if (root->op == ' ') { | ||
| + | printf("%g ", root->val); | ||
| + | } else { | ||
| + | printPostorder(root->left); | ||
| + | printPostorder(root->right); | ||
| + | printf("%c ", root->op); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | |||
| + | int main() { | ||
| + | // načítame postfixový výraz do reťazca | ||
| + | const int maxLine = 100; | ||
| + | char postfix[maxLine]; | ||
| + | fgets(postfix, maxLine, stdin); | ||
| + | // výraz konvertujeme na strom | ||
| + | treeNode * root = postfixToTree(postfix); | ||
| + | // spočítame hodnotu výrazu | ||
| + | double value = evaluateTree(root); | ||
| + | printf(" value: %g\n", value); | ||
| + | // vypíšeme vo všetkých troch notáciách | ||
| + | printf(" inorder: "); | ||
| + | printInorder(root); | ||
| + | printf("\n predorder: "); | ||
| + | printPreorder(root); | ||
| + | printf("\n postdorder: "); | ||
| + | printPostorder(root); | ||
| + | printf("\n"); | ||
| + | // uvoľníme pamäť | ||
| + | destroyTree(root); | ||
| + | } | ||
| + | </syntaxhighlight> | ||
Aktuálna revízia z 19:56, 3. december 2024
Obsah
Oznamy
- Na testovači dnes pribudnú nejaké úlohy z budúcich cvičení, ktoré vám pomôžu s prípravou na test.
- V piatok sú cvičenia nepovinné, budú na nich vzorové riešenia testu. Môžeme vám tiež poradiť s riešením úloh z cvičení alebo domácej úlohy, prípadne ak máte otázky k ukážkovým príkladom na test.
- Termín DÚ3 je v piatok večer.
- Takisto do piatka je potrebné hlásiť záujem o prípadný preklad zadaní, viď informácie k testu
Opakovanie z minulej prednášky
Aritmetické výrazy
- Bežná infixová notácia, napr. (65 – 3*5)/(2 + 3)
- Postfixová notácia 65 3 5 * - 2 3 + /
- Prefixová notácia / - 65 * 3 5 + 2 3
- Prefixová a postfixová notácia nepotrebujú zátvorky
- Prevod z infixovej notácie na postfixovú pomocou zásobníka
- Čo si ukladáme do zásobníka?
- Vyhodnocovanie postfixovej notácie pomocou zásobníka
- Čo si ukladáme do zásobníka?
Aritmetický výraz ako strom
Aritmetické výrazy môžeme veľmi prirodzene reprezentovať vo forme stromu
- Operátory a čísla tvoria tzv. uzly (alebo vrcholy) stromu.
- Operátory tvoria tzv. vnútorné uzly stromu, každý z nich má dve deti zodpovedajúce podvýrazom pre jednotlivé operandy.
- Pre jednoduchosť na dnešnej prednáške neuvažujeme unárne mínus, dalo by sa však ľahko dorobiť.
- Čísla tvoria tzv. listy stromu, tie už nemajú žiadne deti.
- Strom obsahuje jediný uzol, ktorý nemá rodiča. Tento sa nazýva koreň stromu a reprezentuje celý aritmetický výraz.
- Informatici stromy väčšinou kreslia „hore nohami”, s koreňom na vrchu.
Uzol takéhoto stromu tak môžeme reprezentovať napríklad nasledujúcou štruktúrou:
struct treeNode {
// číselná hodnota (len v listoch)
double val;
// operátor vo vnútorných uzloch, pre listy medzera
char op;
// smerníky na podstromy
treeNode * left, * right;
};
Pre vnútorné uzly stromu (zodpovedajúce operátorom) pritom:
- Smerníky left a right budú ukazovať na korene podstromov reprezentujúcich ľavý resp. pravý podvýraz.
- Znak op bude zodpovedať danému operátoru (napríklad '+').
- Hodnota val ostane nevyužitá.
Pre listy (zodpovedajúce číselným hodnotám) naopak:
- Smerníky left a right budú mať hodnotu NULL.
- Znak op bude medzera ' ' (podľa op teda môžeme rozlišovať, či ide o číslo alebo o operátor).
- Vo val bude uložená hodnota daného čísla.
Celý strom pritom budeme reprezentovať jeho koreňom.
V tejto reprezentácii sú niektoré položky štruktúry treeNode nevyužité (napr. val vo vnútorných vrcholoch). S využitím objektového programovania (letný semester) budeme vedieť stromy pre aritmetické výrazy reprezentovať elegantnejšie.
Vytvorenie uzlu
Nasledujúce funkcie vytvoria nový vnútorný uzol (pre operátor) resp. nový list (pre číslo):
treeNode * createOp(char op, treeNode * left, treeNode * right) {
treeNode * v = new treeNode;
v->left = left;
v->right = right;
v->op = op;
return v;
}
treeNode * createNum(double val) {
treeNode * v = new treeNode;
v->left = NULL;
v->right = NULL;
v->op = ' ';
v->val = val;
return v;
}
„Ručne” teraz môžeme vytvoriť strom pre výraz (65 – 3 * 5)/(2 + 3):
treeNode * root = createOp('/',
createOp('-',
createNum(65),
createOp('*', createNum(3), createNum(5))),
createOp('+', createNum(2), createNum(3)));
Alebo po častiach:
treeNode * v65 = createNum(65);
treeNode * v3 = createNum(3);
treeNode * v5 = createNum(5);
treeNode * v2 = createNum(2);
treeNode * v3b = createNum(3);
treeNode * vKrat = createOp('*', v3, v5);
treeNode * vMinus = createOp('-', v65, vKrat);
treeNode * vPlus = createOp('+', v2, v3b);
treeNode * vDeleno = createOp('/', vMinus, vPlus);
Ďalší plán
Ďalej uvidíme:
- jednoduchú rekurzívnu funkciu na vyhodnotenie výrazu uloženého ako strom,
- ďalšie rekurzívne funkcie na uvoľnenie pamäte stromu a výpis výrazu,
- funkciu na vytvorenie stromu z postfixového výrazu.
Stromy majú v informatike veľa využití, nielen na aritmetické výrazy. Ďalej sa teda budeme venovať práci so stromami všeobecne.
Vyhodnotenie výrazu reprezentovaného stromom
Nasledujúca rekurzívna funkcia vypočíta hodnotu aritmetického výrazu reprezentovaného stromom s koreňom root.
- Ak je zadaný vrchol listom, vrátime hodnotu uloženú v položke val.
- V opačnom prípade rekurzívne spočítame hodnoty pre obidva podvýrazy a skombinujeme ich podľa typu znamienka.
- Celkovo veľmi jednoduchý a prirodzený výpočet, nie je potrebný explicitný zásobník.
- Funkcia nižšie nefunguje pre unárne mínus, nebolo by však ťažké ho dorobiť.
Rekurziu budeme používať vždy, keď potrebujeme prejsť všetky uzly stromu. Cyklom sa to programuje ťažko, lebo z uzla potrebujeme ísť doľava aj doprava.
double evaluateTree(treeNode * root) {
assert(root != NULL);
if (root->op == ' ') {
return root->val;
} else {
double valLeft = evaluateTree(root->left);
double valRight = evaluateTree(root->right);
switch (root->op) {
case '+':
return valLeft + valRight;
break;
case '-':
return valLeft - valRight;
break;
case '*':
return valLeft * valRight;
break;
case '/':
return valLeft / valRight;
break;
default:
assert(false);
break;
}
}
return 0; // realne nedosiahnutelny prikaz
}
Uvoľnenie pamäte
Nasledujúca funkcia uvoľní z pamäte celý strom s koreňom root.
- Opäť používa rekurziu na prejdenie celého stromu.
- Pozor na poradie príkazov, treba najskôr uvoľniť podstromy až potom zavolať delete na root, inak by sme stratili prístup k deťom.
- Všimnite si, ako sú riešené triviálne prípady, funkcia ani nezisťuje, s akým typom uzla pracuje.
void destroyTree(treeNode * root) {
if (root != NULL) {
destroyTree(root->left);
destroyTree(root->right);
delete root;
}
}
Vypísanie výrazu reprezentovaného stromom v rôznych notáciách
Infixovú, prefixovú, resp. postfixovú reprezentáciu aritmetického výrazu reprezentovaného stromom s koreňom root možno získať pomocou nasledujúcich funkcií.
- Opäť používajú rekurziu na prejdenie celého stromu.
- Líšia sa hlavne umiestnením príkazu na vypísanie operátora (pred, medzi alebo za rekurzívnym vypísaním podvýrazov).
- Infixová notácia potrebuje aj zátvorky. Táto funkcia ich pre istotu dáva všade. Rozmyslite si, ako by sme ich vedeli vypísať iba tam, kde treba.
- Ako by sme funkcie rozšírili pre unárne mínus?
/** Funkcia vypíše aritmetický výraz v inorder poradí */
void printInorder(treeNode * root) {
if (root->op == ' ') {
printf("%g", root->val);
} else {
printf("(");
printInorder(root->left);
printf(" %c ", root->op);
printInorder(root->right);
printf(")");
}
}
/** Funkcia vypíše aritmetický výraz v preorder poradí */
void printPreorder(treeNode * root) {
if (root->op == ' ') {
printf("%g ", root->val);
} else {
printf("%c ", root->op);
printPreorder(root->left);
printPreorder(root->right);
}
}
/** Funkcia vypíše aritmetický výraz v postorder poradí */
void printPostorder(treeNode * root) {
if (root->op == ' ') {
printf("%g ", root->val);
} else {
printPostorder(root->left);
printPostorder(root->right);
printf("%c ", root->op);
}
}
Vytvorenie stromu z postfixového výrazu
Pripomeňme si z minulej prednášky funkciu na vyhodnocovanie postfixového výrazu:
/** Funkcia vyhodnotí a vráti hodnotou výrazu v postfixovom tvare. */
double evaluatePostfix(tokenSequence & tokens) {
// zásobník, do ktorého ukladáme čísla
stack numberStack;
init(numberStack);
for (int i = 0; i < tokens.length; i++) {
// aktuálny token zo vstupu
token curToken = tokens.items[i];
if (curToken.op == ' ') {
// čísla rovno ukladáme na zásobník
push(numberStack, curToken);
} else {
// spracovanie operátora
token num1, num2, result;
// najskôr vyberieme 1 alebo 2 čísla zo zásobníka
if (curToken.op == '~') {
num1 = pop(numberStack);
} else {
num2 = pop(numberStack);
num1 = pop(numberStack);
}
// na operandy aplikujeme operátor
applyOp(curToken, num1, num2, result);
// výsledné číslo uložíme na zásobník
push(numberStack, result);
}
}
// zo zásobníka vyberieme výsledné číslo
token result = pop(numberStack);
// skontrolujeme, že zásobník je prázdny a výsledok je číslo
assert(isEmpty(numberStack) && result.op == ' ');
// uvoľníme pamäť zásobníka
destroy(numberStack);
return result.val;
}
- Túto funkciu možno jednoducho prepísať tak, aby namiesto vyhodnocovania výrazu konštruovala zodpovedajúci aritmetický strom.
- Namiesto hodnôt jednotlivých podvýrazov stačí na zásobníku uchovávať korene stromov, ktoré tieto podvýrazy reprezentujú.
- Aplikácii aritmetickej operácie bude zodpovedať spojenie dvoch podstromov do jedného stromu.
- V tomto prípade nepoužívame postupnosť symbolov (tokenov), ale priamo spracovávame postfixový výraz vo forme reťazca.
typedef treeNode *dataType;
/* Sem príde definícia štruktúry pre zásobník a všetkých funkcií poskytovaných zásobníkom. */
treeNode * postfixToTree(char * str) {
// zásobník, do ktorého ukladáme korene podstromov
stack treeStack;
init(treeStack);
int strPos = 0; // pozícia v rámci reťazca
while (str[strPos] != 0) { // kým nie sme na konci str
if (isspace(str[strPos])) { // preskakujeme biele znaky
strPos++;
} else if (isdigit(str[strPos]) || str[strPos] == '.') {
// keď nájdeme cifru alebo bodku (začiatok čísla)
double val;
int skip;
// načítame toto číslo pomocou sscanf,
// do skip uložíme počet znakov čísla
sscanf(&(str[strPos]), "%lf%n", &val, &skip);
// preskočíme všetky znaky čísla
strPos += skip;
// vytvoríme list a uložíme na zásobník
push(treeStack, createNum(val));
} else {
// spracovanie operátora
assert(strchr("+-/*", str[strPos]) != NULL);
treeNode * left, * right;
// najskôr vyberieme 2 podstromy zo zásobníka
// vytvoríme nový koreň,
// ktorý bude ich rodičom a vložíme na zásobník
right = pop(treeStack);
left = pop(treeStack);
push(treeStack, createOp(str[strPos], left, right));
strPos++;
}
}
// zo zásobníka vyberieme výsledný strom
treeNode * result = pop(treeStack);
// skontrolujeme, že zásobník je prázdny
assert(isEmpty(treeStack));
// uvoľníme pamäť zásobníka
destroy(treeStack);
return result;
}
Ukážkový program pracujúci so stromami pre aritmetické výrazy
Nasledujúci program prečíta z konzoly aritmetický výraz v postfixovom tvare, skonštruuje jeho aritmetický strom a následne preň zavolá funkcie na výpočet hodnoty výrazu a jeho výpis v rôznych notáciách. Celý program je na konci prednášky.
int main() {
// načítame postfixový výraz do reťazca
const int maxLine = 100;
char postfix[maxLine];
fgets(postfix, maxLine, stdin);
// výraz konvertujeme na strom
treeNode * root = postfixToTree(postfix);
// spočítame hodnotu výrazu
double value = evaluateTree(root);
printf(" value: %g\n", value);
// vypíšeme vo všetkých troch notáciách
printf(" inorder: ");
printInorder(stdout, root);
printf("\n predorder: ");
printPreorder(stdout, root);
printf("\n postdorder: ");
printPostorder(stdout, root);
printf("\n");
// uvoľníme pamäť
destroyTree(root);
}
Binárne stromy
Stromy pre aritmetické výrazy sú špeciálnym prípadom binárnych stromov. V informatike majú binárne stromy množstvo rozličných uplatnení. Ukážeme si teda všeobecnú dátovú štruktúru binárneho stromu.
Terminológia stromov
- Strom obsahuje množinu uzlov alebo vrcholov prepojených hranami. (uzol angl. node, vrchol vertex, hrana edge).
- Ak je strom neprázdny, jeden jeho vrchol nazývame koreň (angl. root)
- Každý uzol u okrem koreňa je spojený hranou s práve jedným rodičom (angl. parent), ktorým je nejaký uzol v. Naopak uzol u je dieťaťom (angl. child) uzla v.
- Vo všeobecnom strome môže mať každý uzol ľubovoľný počet detí (aj nula).
- Strom je binárny, ak má každý uzol najviac dve deti. Budeme pritom rozlišovať medzi pravým a ľavým dieťaťom.
- Uzly zakoreneného stromu, ktoré nemajú žiadne dieťa, nazývame listami; zvyšné uzly nazývame vnútornými uzlami.
- Predkom uzla u nazveme ľubovoľný uzol v ležiaci na ceste z u do koreňa stromu (vrátane u a koreňa). Naopak potom hovoríme, že u je potomkom uzla v.
- Podstromom stromu T zakoreneným v nejakom uzle v stromu T budeme rozumieť strom s koreňom v pozostávajúci zo všetkých jeho potomkov a všetkých hrán stromu T vedúcich medzi týmito uzlami.
Každý binárny strom je teda buď prázdny, alebo je tvorený jeho koreňom a dvoma podstromami – ľavým a pravým.
Takéto stromy sa nazývajú zakorenené. Presnejšiu matematickú definíciu zakorenených aj nezakorenených stromov uvidíte na predmete Úvod do kombinatoriky a teórie grafov (letný semester).
Štruktúra pre uzol binárneho stromu
V nasledujúcom budeme pracovať výhradne s binárnymi stromami. Štruktúra pre uzol všeobecného binárneho stromu je podobná, ako pri stromoch pre aritmetické výrazy, namiesto operátora alebo hodnoty si však v každom uzle budeme pamätať hodnotu ľubovoľného typu dataType, napríklad int.
/* Typ prvkov ukladaných v uzloch binárneho stromu */
typedef int dataType;
/* Uzol binárneho stromu */
struct node {
// hodnota uložená v uzle
dataType data;
// smerníky na podstromy
node * left, * right;
};
Vytvorenie binárneho stromu
Nasledujúca funkcia vytvorí uzol binárneho stromu s dátami data, ľavým podstromom zakoreneným v uzle * left a pravým podstromom zakoreneným v uzle * right (parametre left a right sú teda smerníkmi na uzly). Ako výstup funkcia vráti smerník na novovytvorený uzol.
/* Vytvori uzol binarneho stromu */
node * createNode(dataType data, node * left, node * right) {
node * v = new node;
v->data = data;
v->left = left;
v->right = right;
return v;
}
Nasledujúca volanie tak napríklad vytvorí binárny strom so šiestimi uzlami zakorenený v uzle * root.
node * root = createNode(1,
createNode(2,
createNode(3, NULL, NULL),
createNode(4, NULL, NULL)),
createNode(5,
NULL,
createNode(6, NULL, NULL)));
Cvičenie: nakreslite binárny strom vytvorený predchádzajúcim volaním.
Prehľadávanie stromov a vypisovanie ich uzlov
Často je potrebné prejsť celý strom a spracovať (napríklad vypísať) hodnoty vo všetkých uzloch. Toto prehľadávanie možno, podobne ako pri stromoch pre výrazy, realizovať v troch základných poradiach: preorder, inorder a postorder.
Pri vypisovaní predpokladáme, že pre hodnoty typu dataType máme k dispozícii funkciu printDataType, ktorá ich v nejakom vhodnom formáte vypisuje.
/* Funkcia pre výpis hodnoty typu dataType */
void printDataType(dataType data) {
printf("%d ", data); // pre int
}
/* Vypíše podstrom s koreňom * root v poradí preorder */
void printPreorder(node * root) {
if (root != NULL) {
printDataType(root->data);
printPreorder(root->left);
printPreorder(root->right);
}
}
/* Vypíše podstrom s koreňom * root v poradí inorder */
void printInorder(node * root) {
if (root != NULL) {
printInorder(root->left);
printDataType(root->data);
printInorder(root->right);
}
}
/* Vypíše podstrom s koreňom * root v poradí postorder */
void printPostorder(node * root) {
if (root != NULL) {
printPostorder(root->left);
printPostorder(root->right);
printDataType(root->data);
}
}
Cvičenie: ako by sme spočítali súčet hodnôt uložených v uzloch stromu?
Likvidácia binárneho stromu
Nasledujúca rekurzívna funkcia zlikviduje celý podstrom zakorenený v uzle * root (t. j. uvoľní pamäť pre všetky jeho uzly). Veľmi sa podobá na funkciu pre strom reprezentujúci aritmetický výraz.
/* Zlikviduje podstrom s korenom * root (uvolni pamat) */
void destroyTree(node * root) {
if (root != NULL) {
destroyTree(root->left);
destroyTree(root->right);
delete root;
}
}
Výška binárneho stromu
- Hĺbkou uzla binárneho stromu nazveme jeho vzdialenosť od koreňa.
- Koreň má teda hĺbku 0, jeho deti majú hĺbku 1, atď.
- Výškou binárneho stromu potom nazveme maximálnu hĺbku niektorého z jeho vrcholov.
- Strom s jediným vrcholom má teda výšku 0; pre ostatné stromy je ich výška daná ako 1 plus maximum z výšok ľavého a pravého podstromu.
Nasledujúca funkcia počíta výšku stromu (kvôli elegancii zápisu pritom pracuje s rozšírením definície výšky stromu na prázdne stromy, za ktorých výšku sa považuje číslo -1).
/* Spočíta výšku podstromu s koreňom * root.
* Pre root == NULL vráti -1. */
int height(node * root) {
if (root == NULL) {
return -1;
}
// rekurzívne spočíta výšku ľavého a pravého podstromu
int hLeft = height(root->left);
int hRight = height(root->right);
// vráti max(hLeft, hRight) + 1
if (hLeft >= hRight) {
return hLeft + 1;
} else {
return hRight + 1;
}
}
Cvičenie: prepíšte funkciu tak, aby triviálnym prípadom bol list, nie prázdny strom. Funkcia teda vždy dostane smerník na neprázdny strom a nebude volať rekurziu na prázdne podstromy. Ktorá verzia je jednoduchšia? Ktorá sa vám zdá jednoduchšia na pochopenie?
Aká môže byť výška binárneho stromu?
Pre výšku h binárneho stromu s n uzlami platia nasledujúce vzťahy:
- Určite h ≤ n-1. Tento prípad nastáva, ak sú všetky uzly „navešané jeden pod druhý”.
- Strom s výškou h má najviac
- Z toho h ≥ log2(n+1)-1.
- Dostávame teda log2(n+1)-1 ≤ h ≤ n-1.
- Napríklad strom s milión vrcholmi má teda hĺbku medzi 19 a 999999.
Príklad: plné binárne stromy
Binárny strom výšky h s maximálnym počtom vrcholov 2h+1-1 sa nazýva plný binárny strom. Nasledujúca funkcia createFullTree vytvorí takýto strom a vráti smerník na jeho koreň. Jeho uzly pritom očísľuje 1, 2, 3,... (predpokladáme, že dataType je int) pomocou globálnej premennej count.
// ...
int count;
/* Vytvori plny binarny strom vysky height s datami uzlov count, count + 1, ... */
node * createFullTree(int height) {
if (height == -1) {
return NULL;
}
node * v = createNode(count, NULL, NULL);
count++;
v->left = createFullTree(height - 1);
v->right = createFullTree(height - 1);
return v;
}
int main() {
count = 1;
node * root = createFullTree(3);
printf("Vyska: %d\n", height(root));
printf("Inorder: ");
printInorder(root);
printf("\n");
printf("Preorder: ");
printPreorder(root);
printf("\n");
printf("Postorder: ");
printPostorder(root);
printf("\n");
destroyTree(root);
}
Cvičenie:
- Nakreslite strom aj s hodnotami v uzloch, ktorý vznikne pre výšku 2.
- Vo všeobecnosti opíšte poradie, v ktorom sa v uvedenom programe jednotlivým uzlom priraďujú ich hodnoty.
- Ako by ste v programe odstránili globálnu premennú count?
Program pre aritmetické výrazy ako stromy
#include <cstdio>
#include <cctype>
#include <cassert>
#include <cstring>
using namespace std;
struct treeNode {
// číselná hodnota (len v listoch)
double val;
// operátor vo vnútorných uzloch, pre listy medzera
char op;
// smerníky na podstromy
treeNode * left, * right;
};
/** Funkcia vráti nový uzol pre operátor */
treeNode * createOp(char op, treeNode * left, treeNode * right) {
treeNode * v = new treeNode;
v->left = left;
v->right = right;
v->op = op;
return v;
}
/** Funkcia vráti nový uzol pre číslo */
treeNode * createNum(double val) {
treeNode * v = new treeNode;
v->left = NULL;
v->right = NULL;
v->op = ' ';
v->val = val;
return v;
}
// Nasleduje kód pre zásobník uzlov stromu
typedef treeNode * dataType;
/** Uzol spájaného zoznamu pre zásobník */
struct node {
dataType data; // dáta uložené v uzle
node * next; // smerník na ďalší uzol zoznamu
};
/** Štruktúra pre zásobník implementovaný pomocou zoznamu*/
struct stack {
node * top; // Smernik na vrch zasobníka alebo NULL
};
/** Funkcia inicializuje prázdny zásobník */
void init(stack & s) {
s.top = NULL;
}
/** Funkcia zistí, či je zásobník prázdny */
bool isEmpty(stack & s) {
return s.top == NULL;
}
/** Funkcia pridá prvok item na vrch zásobníka */
void push(stack & s, dataType item) {
node * tmp = new node;
tmp->data = item;
tmp->next = s.top;
s.top = tmp;
}
/** Funkcia odoberie prvok z vrchu zasobnika a vráti ho */
dataType pop(stack & s) {
assert(!isEmpty(s));
dataType result = s.top->data;
node * tmp = s.top->next;
delete s.top;
s.top = tmp;
return result;
}
/** Funkcia vráti prvok na vrchu zásobníka, ale nechá ho v zásobníku */
dataType peek(stack & s) {
assert(!isEmpty(s));
return s.top->data;
}
/** Funkcia uvoľní pamäť zásobníka */
void destroy(stack & s) {
while (!isEmpty(s)) {
pop(s);
}
}
/** Funkcia konvertuje výraz v postfixovom tvare na strom */
treeNode * postfixToTree(char * str) {
// zásobník, do ktorého ukladáme korene podstromov
stack treeStack;
init(treeStack);
int strPos = 0; // pozícia v rámci reťazca
while (str[strPos] != 0) { // kým nie sme na konci str
if (isspace(str[strPos])) { // preskakujeme biele znaky
strPos++;
} else if (isdigit(str[strPos]) || str[strPos] == '.') {
// keď nájdeme cifru alebo bodku (začiatok čísla)
double val;
int skip;
// načítame toto číslo pomocou sscanf,
// do skip uložíme počet znakov čísla
sscanf(&(str[strPos]), "%lf%n", &val, &skip);
// preskočíme všetky znaky čísla
strPos += skip;
// vytvoríme list a uložíme na zásobník
push(treeStack, createNum(val));
} else {
// spracovanie operátora
assert(strchr("+-/*", str[strPos]) != NULL);
treeNode * left, * right;
// najskôr vyberieme 2 podstromy zo zásobníka
// vytvoríme nový koreň,
// ktorý bude ich rodičom a vložíme na zásobník
right = pop(treeStack);
left = pop(treeStack);
push(treeStack, createOp(str[strPos], left, right));
strPos++;
}
}
// zo zásobníka vyberieme výsledný strom
treeNode * result = pop(treeStack);
// skontrolujeme, že zásobník je prázdny
assert(isEmpty(treeStack));
// uvoľníme pamäť zásobníka
destroy(treeStack);
return result;
}
/** Funkcia spočíta hodnotu výrazu reprezentovaného stromom */
double evaluateTree(treeNode * root) {
assert(root != NULL);
if (root->op == ' ') {
return root->val;
} else {
double valLeft = evaluateTree(root->left);
double valRight = evaluateTree(root->right);
switch (root->op) {
case '+':
return valLeft + valRight;
break;
case '-':
return valLeft - valRight;
break;
case '*':
return valLeft * valRight;
break;
case '/':
return valLeft / valRight;
break;
default:
assert(false);
break;
}
}
return 0; // realne nedosiahnutelny prikaz
}
/** Funkcia uvoľní pamäť daného stromu */
void destroyTree(treeNode * root) {
if (root != NULL) {
destroyTree(root->left);
destroyTree(root->right);
delete root;
}
}
/** Funkcia vypíše aritmetický výraz v inorder poradí */
void printInorder(treeNode * root) {
if (root->op == ' ') {
printf("%g", root->val);
} else {
printf("(");
printInorder(root->left);
printf(" %c ", root->op);
printInorder(root->right);
printf(")");
}
}
/** Funkcia vypíše aritmetický výraz v preorder poradí */
void printPreorder(treeNode * root) {
if (root->op == ' ') {
printf("%g ", root->val);
} else {
printf("%c ", root->op);
printPreorder(root->left);
printPreorder(root->right);
}
}
/** Funkcia vypíše aritmetický výraz v postorder poradí */
void printPostorder(treeNode * root) {
if (root->op == ' ') {
printf("%g ", root->val);
} else {
printPostorder(root->left);
printPostorder(root->right);
printf("%c ", root->op);
}
}
int main() {
// načítame postfixový výraz do reťazca
const int maxLine = 100;
char postfix[maxLine];
fgets(postfix, maxLine, stdin);
// výraz konvertujeme na strom
treeNode * root = postfixToTree(postfix);
// spočítame hodnotu výrazu
double value = evaluateTree(root);
printf(" value: %g\n", value);
// vypíšeme vo všetkých troch notáciách
printf(" inorder: ");
printInorder(root);
printf("\n predorder: ");
printPreorder(root);
printf("\n postdorder: ");
printPostorder(root);
printf("\n");
// uvoľníme pamäť
destroyTree(root);
}