Programovanie (1) v C/C++
1-INF-127, ZS 2024/25
Letný semester, prednáška č. 8: Rozdiel medzi revíziami
(→Oznamy) |
|||
| (16 medziľahlých úprav od rovnakého používateľa nie je zobrazených.) | |||
| Riadok 1: | Riadok 1: | ||
== Oznamy == | == Oznamy == | ||
| − | * | + | * Na začiatku zajtrajších cvičení bude okrem niekoľkých bežných úloh k cvičeniam zverejnená aj druhá bonusová domáca úloha, za ktorú bude možné získať 2 body navyše. Odovzdať ju bude možné ''do 16. apríla 2024, 9:50'' – čiže do začiatku deviatych cvičení. |
| − | * | + | * Budúci týždeň počas cvičení – čiže ''v utorok 16. apríla od 9:50 do 11:20'' – bude prebiehať tretí test zameraný na látku z prvých ôsmich týždňov. Body z testu bude možné získať iba v prípade prítomnosti na cvičeniach v miestnosti I-H6. |
== Triedy pre grafy z minulej prednášky == | == Triedy pre grafy z minulej prednášky == | ||
| Riadok 474: | Riadok 474: | ||
Hovoríme, že ''neorientovaný'' graf je ''súvislý'', ak je ľubovoľná dvojica vrcholov tohto grafu spojená cestou. | Hovoríme, že ''neorientovaný'' graf je ''súvislý'', ak je ľubovoľná dvojica vrcholov tohto grafu spojená cestou. | ||
| − | Pre ''neorientované'' grafy možno problém existencie cesty medzi dvoma vrcholmi chápať aj ako úlohu zistiť, či sú tieto dva vrcholy v rovnakom ''komponente súvislosti'' grafu. Komponent súvislosti neorientovaného grafu je každý jeho (vzhľadom na inklúziu) maximálny podgraf, ktorý je súvislý – komponent súvislosti grafu teda pozostáva z nejakej podmnožiny vrcholov grafu a všetkých hrán pôvodného grafu spájajúcich vrcholy z tejto podmnožiny, pričom ľubovoľné dva vrcholy komponentu sú spojené cestou a žiaden vrchol komponentu nie je v pôvodnom grafe spojený cestou s vrcholom mimo komponentu. Stručnejšie to možno vyjadriť s využitím pozorovania, že existencia cesty v ''neorientovanom'' grafe je zjavne reláciou ekvivalencie na množine jeho vrcholov – komponenty súvislosti potom zodpovedajú triedam ekvivalencie tejto relácie. Napríklad neorientovaný graf na nasledujúcom obrázku pozostáva z troch komponentov súvislosti. | + | Pre ''neorientované'' grafy možno problém existencie cesty medzi dvoma vrcholmi chápať aj ako úlohu zistiť, či sú tieto dva vrcholy v rovnakom ''komponente súvislosti'' grafu. Komponent súvislosti neorientovaného grafu je každý jeho (vzhľadom na inklúziu) maximálny podgraf s nenulovým počtom vrcholov, ktorý je súvislý – komponent súvislosti grafu teda pozostáva z nejakej neprázdnej podmnožiny vrcholov grafu a všetkých hrán pôvodného grafu spájajúcich vrcholy z tejto podmnožiny, pričom ľubovoľné dva vrcholy komponentu sú spojené cestou a žiaden vrchol komponentu nie je v pôvodnom grafe spojený cestou s vrcholom mimo komponentu. Stručnejšie to možno vyjadriť s využitím pozorovania, že existencia cesty v ''neorientovanom'' grafe je zjavne reláciou ekvivalencie na množine jeho vrcholov – komponenty súvislosti potom zodpovedajú triedam ekvivalencie tejto relácie. Napríklad neorientovaný graf na nasledujúcom obrázku pozostáva z troch komponentov súvislosti. |
[[Súbor:Graf3.png|center]] | [[Súbor:Graf3.png|center]] | ||
| Riadok 482: | Riadok 482: | ||
* Ostrovy rovnakej farby v mriežke potom zodpovedajú komponentom súvislosti výsledného neorientovaného grafu. | * Ostrovy rovnakej farby v mriežke potom zodpovedajú komponentom súvislosti výsledného neorientovaného grafu. | ||
| − | + | Prehľadávanie (orientovaného alebo neorientovaného) grafu do hĺbky budeme realizovať rekurzívnou metódou <tt>search</tt>, ktorá prehľadá všetkých ešte nenavštívených následníkov daného vrcholu. Informáciu o navštívení jednotlivých vrcholov si pritom budeme uchovávať v zozname <tt>visited</tt>. Metóda <tt>existsPath</tt> bude metódu <tt>search</tt> využívať na riešenie problému existencie cesty medzi danými dvoma vrcholmi. | |
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
| Riadok 650: | Riadok 650: | ||
public class ShortestPathsFromVertex { | public class ShortestPathsFromVertex { | ||
/** | /** | ||
| − | + | * Zoznam obsahujuci pre kazdy vrchol grafu jeho vzdialenost zo "startovacieho" vrcholu z argumentu konstruktora. | |
| − | + | * Ak zo "startovacieho" vrcholu do nejakeho vrcholu nevedie ziadna cesta, bude namiesto jeho vzdialenosti v zozname | |
| − | + | * ulozena hodnota -1. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * Zoznam obsahujuci pre kazdy vrchol grafu jeho vzdialenost zo startovacieho vrcholu | ||
| − | |||
*/ | */ | ||
private List<Integer> distances; | private List<Integer> distances; | ||
/** | /** | ||
| − | * Zoznam obsahujuci pre kazdy vrchol v grafu g jeho predchodcu na najkratsej ceste | + | * Zoznam obsahujuci pre kazdy vrchol v grafu g jeho predchodcu na najkratsej ceste zo "startovacieho" vrcholu |
| − | + | * do vrcholu v. Pre "startovaci" vrchol a vrcholy, do ktorych z neho nevedie cesta, bude v zozname ulozena | |
| + | * hodnota -1. | ||
*/ | */ | ||
private List<Integer> predecessors; | private List<Integer> predecessors; | ||
| Riadok 679: | Riadok 670: | ||
*/ | */ | ||
public ShortestPathsFromVertex(DirectedGraph g, int start) { | public ShortestPathsFromVertex(DirectedGraph g, int start) { | ||
| − | |||
| − | |||
| − | |||
/* Inicializacia zoznamov distances a predecessors: */ | /* Inicializacia zoznamov distances a predecessors: */ | ||
distances = new ArrayList<>(); | distances = new ArrayList<>(); | ||
| Riadok 763: | Riadok 751: | ||
* Hovoríme teda o ''stromoch prehľadávania do hĺbky'' resp. ''do šírky'' (angl. ''DFS Tree'' resp. ''BFS Tree''). | * Hovoríme teda o ''stromoch prehľadávania do hĺbky'' resp. ''do šírky'' (angl. ''DFS Tree'' resp. ''BFS Tree''). | ||
* V prípade, že je graf neorientovaný a súvislý, ide v obidvoch prípadoch o jeho ''kostru'' (t. j. strom zložený zo ''všetkých'' vrcholov grafu a jeho vybraných hrán). | * V prípade, že je graf neorientovaný a súvislý, ide v obidvoch prípadoch o jeho ''kostru'' (t. j. strom zložený zo ''všetkých'' vrcholov grafu a jeho vybraných hrán). | ||
| − | * | + | * Pri stromoch prehľadávania ''do šírky'' reprezentujú cesty od koreňa k nejakému inému vrcholu vždy niektorú z najkratších ciest medzi príslušnými vrcholmi grafu. |
''Príklad.'' Nižšie je znázornený diagram orientovaného grafu a jeho stromy prehľadávania do hĺbky a do šírky v prípade, že prehľadávanie začne vo vrchole 0 a pri spracúvaní následníkov sa postupuje vzostupne podľa čísel vrcholov (čo nemusí byť vždy tak). | ''Príklad.'' Nižšie je znázornený diagram orientovaného grafu a jeho stromy prehľadávania do hĺbky a do šírky v prípade, že prehľadávanie začne vo vrchole 0 a pri spracúvaní následníkov sa postupuje vzostupne podľa čísel vrcholov (čo nemusí byť vždy tak). | ||
| Riadok 781: | Riadok 769: | ||
Pre veľa úloh na grafoch nie sú známe – a v prípade platnosti niektorých hypotéz z teoretickej informatiky často ani neexistujú – žiadne efektívne algoritmy. Prehľadávaním s návratom však vieme spočítať odpoveď aspoň pre malé vstupy. | Pre veľa úloh na grafoch nie sú známe – a v prípade platnosti niektorých hypotéz z teoretickej informatiky často ani neexistujú – žiadne efektívne algoritmy. Prehľadávaním s návratom však vieme spočítať odpoveď aspoň pre malé vstupy. | ||
| − | === Hľadanie ciest dĺžky | + | === Hľadanie ciest danej dĺžky === |
| − | Nasledujúca trieda <tt>FixedLengthPaths</tt> pre daný graf <tt>g</tt>, danú dvojicu vrcholov <tt>from, to</tt> a dané prirodzené číslo <tt>length</tt> nájde všetky cesty dĺžky ''presne'' <tt>length</tt> vedúce v <tt>g</tt> z vrcholu <tt>from</tt> do vrcholu <tt>to</tt>. Prehľadávanie s návratom sa spustí hneď v konštruktore a nájdené cesty sa uložia do zoznamu <tt>paths</tt>. | + | Nasledujúca trieda <tt>FixedLengthPaths</tt> pre daný graf <tt>g</tt>, danú dvojicu vrcholov <tt>from, to</tt> a dané prirodzené číslo <tt>length</tt> nájde všetky cesty dĺžky ''presne'' <tt>length</tt> vedúce v grafe <tt>g</tt> z vrcholu <tt>from</tt> do vrcholu <tt>to</tt>; takéto cesty môžu evidentne existovať iba v prípade, že je prirodzené číslo <tt>length</tt> menšie, než počet vrcholov grafu. Prehľadávanie s návratom sa spustí hneď v konštruktore a nájdené cesty sa uložia do zoznamu <tt>paths</tt>. |
Pri prehľadávaní sa v spájanom zozname <tt>path</tt> budú postupne generovať všetky cesty hľadaného typu. Pre každý vrchol budeme mať navyše v zozname <tt>visited</tt> poznačené, či sme ho už v generovanej ceste použili. Akonáhle nájdeme cestu požadovanej dĺžky končiacu vo vrchole <tt>to</tt>, uložíme ju do zoznamu <tt>paths</tt>. | Pri prehľadávaní sa v spájanom zozname <tt>path</tt> budú postupne generovať všetky cesty hľadaného typu. Pre každý vrchol budeme mať navyše v zozname <tt>visited</tt> poznačené, či sme ho už v generovanej ceste použili. Akonáhle nájdeme cestu požadovanej dĺžky končiacu vo vrchole <tt>to</tt>, uložíme ju do zoznamu <tt>paths</tt>. | ||
| Riadok 800: | Riadok 788: | ||
*/ | */ | ||
private DirectedGraph g; | private DirectedGraph g; | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
/** | /** | ||
| Riadok 842: | Riadok 825: | ||
public FixedLengthPaths(DirectedGraph g, int from, int to, int length) { | public FixedLengthPaths(DirectedGraph g, int from, int to, int length) { | ||
this.g = g; | this.g = g; | ||
| − | |||
this.to = to; | this.to = to; | ||
this.length = length; | this.length = length; | ||
| Riadok 927: | Riadok 909: | ||
* Upravte triedu <tt>FixedLengthPaths</tt> tak, aby namiesto hľadania a ukladania všetkých ciest danej dĺžky iba počítala, koľko ich je. | * Upravte triedu <tt>FixedLengthPaths</tt> tak, aby namiesto hľadania a ukladania všetkých ciest danej dĺžky iba počítala, koľko ich je. | ||
* Upravte triedu <tt>FixedLengthPaths</tt> tak, aby iba zisťovala, či existuje cesta danej dĺžky (po prvej nájdenej ceste je teda možné prehľadávanie ukončiť). | * Upravte triedu <tt>FixedLengthPaths</tt> tak, aby iba zisťovala, či existuje cesta danej dĺžky (po prvej nájdenej ceste je teda možné prehľadávanie ukončiť). | ||
| − | * Navrhnite spôsoby, ako v niektorých prípadoch zistiť, že | + | * Navrhnite spôsoby, ako v niektorých prípadoch zistiť, že rozrobenú cestu už nie je možné požadovaným spôsobom predĺžiť a danú vetvu prehľadávania s návratom tak možno ukončiť. |
===Hľadanie najdlhšej cesty=== | ===Hľadanie najdlhšej cesty=== | ||
| Riadok 948: | Riadok 930: | ||
*/ | */ | ||
private DirectedGraph g; | private DirectedGraph g; | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
/** | /** | ||
| Riadok 985: | Riadok 962: | ||
public LongestPath(DirectedGraph g, int from, int to) { | public LongestPath(DirectedGraph g, int from, int to) { | ||
this.g = g; | this.g = g; | ||
| − | |||
this.to = to; | this.to = to; | ||
Aktuálna revízia z 16:52, 2. apríl 2024
Obsah
Oznamy
- Na začiatku zajtrajších cvičení bude okrem niekoľkých bežných úloh k cvičeniam zverejnená aj druhá bonusová domáca úloha, za ktorú bude možné získať 2 body navyše. Odovzdať ju bude možné do 16. apríla 2024, 9:50 – čiže do začiatku deviatych cvičení.
- Budúci týždeň počas cvičení – čiže v utorok 16. apríla od 9:50 do 11:20 – bude prebiehať tretí test zameraný na látku z prvých ôsmich týždňov. Body z testu bude možné získať iba v prípade prítomnosti na cvičeniach v miestnosti I-H6.
Triedy pre grafy z minulej prednášky
package graphs;
/**
* Rozhranie implementovane reprezentaciami orientovanych grafov o vrcholoch 0, 1, ..., n-1 pre nejake prirodzene n.
* Aj neorientovane grafy budu povazovane za specialny pripad orientovanych grafov; toto rozhranie tak bude
* implementovane vsetkymi triedami reprezentujucimi grafy.
*/
public interface DirectedGraph {
/**
* Metoda, ktora vrati pocet vrcholov reprezentovaneho grafu.
*
* @return Pocet vrcholov grafu.
*/
int getVertexCount();
/**
* Metoda, ktora zisti, ci graf obsahuje vrchol s cislom vertex.
* @param vertex Vrchol, ktoreho existencia sa ma zistit.
* @return Vrati true prave vtedy, ked graf obsahuje vrchol s cislom vertex.
*/
boolean hasVertex(int vertex);
/**
* Metoda, ktora vrati pocet orientovanych hran reprezentovaneho grafu.
*
* @return Pocet orientovanych hran grafu.
*/
int getDirectedEdgeCount();
/**
* Metoda, ktora zisti, ci v grafe existuje hrana medzi danou dvojicou vrcholov.
*
* @param from Pociatocny vrchol.
* @param to Koncovy vrchol.
* @return Vrati true prave vtedy, ked v grafe existuje hrana z vrcholu from do vrcholu to.
*/
boolean hasEdge(int from, int to);
/**
* Metoda, ktora vrati vsetkych naslednikov daneho vrcholu -- cize vsetky vrcholy, do ktorych vedie z daneho vrcholu
* orientovana hrana. Pre neorientovane grafy tak tato metoda vzdy vrati vsetkych susedov daneho vrcholu.
*
* @param vertex Lubovolny vrchol grafu.
* @return Naslednici vrcholu vertex ako instancia typu Iterable<Integer>.
*/
Iterable<Integer> outgoingEdgesDestinations(int vertex);
}
package graphs;
public class DirectedEdge {
private int from, to;
public DirectedEdge(int from, int to) {
this.from = from;
this.to = to;
}
public int getFrom() {
return from;
}
public int getTo() {
return to;
}
@Override
public boolean equals(Object o) {
if (o == null) {
return false;
}
return this.getClass() == o.getClass() && from == ((DirectedEdge) o).from && to == ((DirectedEdge) o).to;
}
@Override
public int hashCode() {
return Integer.valueOf(from).hashCode() + 31 * Integer.valueOf(to).hashCode();
}
}
package graphs;
import java.util.*;
/**
* Trieda reprezentujuca orientovany graf pomocou zoznamov naslednikov jednotlivych jeho vrcholov.
*/
public class SuccessorListsDirectedGraph implements DirectedGraph {
/**
* Pre kazdy vrchol si pamatame zoznam jeho naslednikov.
*/
private ArrayList<ArrayList<Integer>> successorLists;
/**
* Pocet orientovanych hran v grafe (velkost grafu).
*/
private int directedEdgeCount;
/**
* Konstruktor, ktory dostane ako argumenty pocet vrcholov grafu (t. j. jeho rad), ako aj vsetky hrany grafu.
*
* @param vertexCount Rad grafu, cize pocet jeho vrcholov.
* @param directedEdges Zoskupenie pozostavajuce zo vsetkych orientovanych hran grafu.
*/
public SuccessorListsDirectedGraph(int vertexCount, Collection<? extends DirectedEdge> directedEdges) {
if (vertexCount <= 0) {
throw new IllegalArgumentException("Nonpositive vertex count.");
}
successorLists = new ArrayList<>();
for (int i = 0; i <= vertexCount - 1; i++) {
successorLists.add(new ArrayList<>());
}
directedEdgeCount = 0;
for (DirectedEdge e : directedEdges) {
if (!hasVertex(e.getFrom()) || !hasVertex(e.getTo())) {
throw new IllegalArgumentException("Edge incident to a nonexistent vertex.");
}
if (!hasEdge(e.getFrom(), e.getTo())) {
successorLists.get(e.getFrom()).add(e.getTo());
directedEdgeCount++;
} else {
throw new IllegalArgumentException("Multiple edges connecting the same pair of vertices.");
}
}
}
@Override
public int getVertexCount() {
return successorLists.size();
}
@Override
public boolean hasVertex(int v) {
return v >= 0 && v <= getVertexCount() - 1;
}
@Override
public int getDirectedEdgeCount() {
return directedEdgeCount;
}
@Override
public boolean hasEdge(int from, int to) {
if (!hasVertex(from) || !hasVertex(to)) {
throw new IllegalArgumentException("Nonexistent vertex.");
}
return successorLists.get(from).contains(to);
}
@Override
public Iterable<Integer> outgoingEdgesDestinations(int vertex) {
if (!hasVertex(vertex)) {
throw new IllegalArgumentException("Nonexistent vertex.");
}
// Nasledujucim prikazom vratime nemodifikovatelny pohlad na zoznam naslednikov vrcholu vertex
return Collections.unmodifiableList(successorLists.get(vertex));
}
}
package graphs;
import java.util.*;
/**
* Trieda reprezentujuca orientovany graf pomocou matice susednosti.
*/
public class AdjacencyMatrixDirectedGraph implements DirectedGraph {
/**
* Matica susednosti.
*/
private boolean[][] adjacencyMatrix;
/**
* Pocet orientovanych hran v grafe (velkost grafu).
*/
private int directedEdgeCount;
/**
* Konstruktor, ktory dostane ako argumenty pocet vrcholov grafu (t. j. jeho rad), ako aj vsetky hrany grafu.
*
* @param vertexCount Rad grafu, cize pocet jeho vrcholov.
* @param directedEdges Zoskupenie pozostavajuce zo vsetkych orientovanych hran grafu.
*/
public AdjacencyMatrixDirectedGraph(int vertexCount, Collection<? extends DirectedEdge> directedEdges) {
if (vertexCount <= 0) {
throw new IllegalArgumentException("Nonpositive vertex count.");
}
adjacencyMatrix = new boolean[vertexCount][vertexCount];
directedEdgeCount = 0;
for (DirectedEdge e : directedEdges) {
if (!hasVertex(e.getFrom()) || !hasVertex(e.getTo())) {
throw new IllegalArgumentException("Edge incident to a nonexistent vertex.");
}
if (!hasEdge(e.getFrom(), e.getTo())) {
adjacencyMatrix[e.getFrom()][e.getTo()] = true;
directedEdgeCount++;
} else {
throw new IllegalArgumentException("Multiple edges connecting the same pair of vertices.");
}
}
}
@Override
public int getVertexCount() {
return adjacencyMatrix.length;
}
@Override
public boolean hasVertex(int v) {
return v >= 0 && v <= getVertexCount() - 1;
}
@Override
public int getDirectedEdgeCount() {
return directedEdgeCount;
}
@Override
public boolean hasEdge(int from, int to) {
if (!hasVertex(from) || !hasVertex(to)) {
throw new IllegalArgumentException("Nonexistent vertex.");
}
return adjacencyMatrix[from][to];
}
@Override
public Iterable<Integer> outgoingEdgesDestinations(int vertex) {
if (!hasVertex(vertex)) {
throw new IllegalArgumentException("Nonexistent vertex.");
}
List<Integer> a = new ArrayList<>();
for (int i = 0; i <= getVertexCount() - 1; i++) {
if (adjacencyMatrix[vertex][i]) {
a.add(i);
}
}
return Collections.unmodifiableList(a);
}
}
package graphs;
/**
* Rozhranie implementovane reprezentaciami neorientovanych grafov o vrcholoch 0, 1, ..., n-1 pre nejake prirodzene n.
*/
public interface UndirectedGraph extends DirectedGraph {
/**
* Metoda, ktora vrati pocet neorientovanych hran reprezentovaneho grafu.
*
* @return Pocet neorientovanych hran grafu.
*/
int getUndirectedEdgeCount();
}
package graphs;
import java.util.*;
public class UndirectedEdge {
private Set<Integer> incidentVertices;
public UndirectedEdge(int u, int v) {
incidentVertices = new HashSet<>();
incidentVertices.add(u);
incidentVertices.add(v);
}
public Set<Integer> getIncidentVertices() {
return Collections.unmodifiableSet(incidentVertices);
}
@Override
public boolean equals(Object o) {
if (o == null) {
return false;
}
return this.getClass() == o.getClass() && incidentVertices.equals(((UndirectedEdge) o).getIncidentVertices());
}
@Override
public int hashCode() {
return incidentVertices.hashCode();
}
}
package graphs;
import java.util.*;
public class Edges {
/**
* Metoda, ktora prerobi zoskupenie neorientovanych hran na prislusny zoznam orientovanych hran.
* @param undirectedEdges Zoznam neorientovanych hran.
* @return Prislusny zoznam orientovanych hran.
*/
public static List<DirectedEdge> undirectedToDirectedEdges(Collection<? extends UndirectedEdge> undirectedEdges) {
ArrayList<DirectedEdge> result = new ArrayList<>();
for (UndirectedEdge e : undirectedEdges) {
ArrayList<Integer> vertices = new ArrayList<>(e.getIncidentVertices());
if (vertices.size() == 1) {
result.add(new DirectedEdge(vertices.get(0), vertices.get(0)));
} else {
result.add(new DirectedEdge(vertices.get(0), vertices.get(1)));
result.add(new DirectedEdge(vertices.get(1), vertices.get(0)));
}
}
return Collections.unmodifiableList(result);
}
}
package graphs;
import java.util.*;
/**
* Trieda reprezentujuca neorientovany graf pomocou zoznamov susedov jednotlivych jeho vrcholov.
*/
public class AdjacencyListsUndirectedGraph extends SuccessorListsDirectedGraph implements UndirectedGraph {
private int undirectedEdgeCount;
public AdjacencyListsUndirectedGraph(int vertexCount, Collection<? extends UndirectedEdge> undirectedEdges) {
super(vertexCount, Edges.undirectedToDirectedEdges(undirectedEdges));
undirectedEdgeCount = undirectedEdges.size();
}
@Override
public int getUndirectedEdgeCount() {
return undirectedEdgeCount;
}
}
package graphs;
import java.util.*;
/**
* Trieda reprezentujuca neorientovany graf pomocou matice susednosti.
*/
public class AdjacencyMatrixUndirectedGraph extends AdjacencyMatrixDirectedGraph implements UndirectedGraph {
private int undirectedEdgeCount;
public AdjacencyMatrixUndirectedGraph(int vertexCount, Collection<? extends UndirectedEdge> undirectedEdges) {
super(vertexCount, Edges.undirectedToDirectedEdges(undirectedEdges));
undirectedEdgeCount = undirectedEdges.size();
}
@Override
public int getUndirectedEdgeCount() {
return undirectedEdgeCount;
}
}
package graphs;
import java.io.*;
import java.util.*;
public class Trieda {
/**
* Metoda vypise do daneho vystupneho prudu pocet vrcholov a hran orientovaneho grafu, ako aj vsetky dvojice
* vrcholov tvoriace orientovane hrany grafu.
*
* @param g Graf, pre ktory sa vypis realizuje.
* @param out Vystupny prud, do ktoreho sa vypis realizuje.
*/
public static void printDirectedGraph(DirectedGraph g, PrintStream out) {
int n = g.getVertexCount();
out.println(n + " " + g.getDirectedEdgeCount());
for (int u = 0; u <= n - 1; u++) {
for (int v : g.outgoingEdgesDestinations(u)) {
out.println(u + " " + v);
}
}
}
/**
* Metoda, ktora precita textovu reprezentaciu orientovaneho grafu pozostavajucu z poctu vrcholov n, poctu hran m
* a z m dvojic vrcholov udavajucich jednotlive orientovane hrany a vytvori podla nej graf urcenej implementacie.
*
* @param scanner Skener, z ktoreho sa reprezentacia grafu cita.
* @param implementation Implementacia vytvaraneho grafu (zoznamy naslednikov, alebo matica susednosti).
* @return Vytvoreny graf.
*/
public static DirectedGraph readDirectedGraph(Scanner scanner, GraphImplementation implementation) {
int n = scanner.nextInt();
int m = scanner.nextInt();
List<DirectedEdge> edges = new ArrayList<>();
for (int i = 1; i <= m; i++) {
edges.add(new DirectedEdge(scanner.nextInt(), scanner.nextInt()));
}
DirectedGraph g = null;
switch (implementation) {
case LISTS:
g = new SuccessorListsDirectedGraph(n, edges);
break;
case MATRIX:
g = new AdjacencyMatrixDirectedGraph(n, edges);
break;
}
return g;
}
/**
* Metoda, ktora precita textovu reprezentaciu neorientovaneho grafu pozostavajucu z poctu vrcholov n, poctu hran m
* a z m dvojic vrcholov udavajucich jednotlive neorientovane hrany a vytvori podla nej graf urcenej implementacie.
*
* @param scanner Skener, z ktoreho sa reprezentacia grafu cita.
* @param implementation Implementacia vytvaraneho grafu (zoznamy naslednikov, alebo matica susednosti).
* @return Vytvoreny graf.
*/
public static UndirectedGraph readUndirectedGraph(Scanner scanner, GraphImplementation implementation) {
int n = scanner.nextInt();
int m = scanner.nextInt();
List<UndirectedEdge> edges = new ArrayList<>();
for (int i = 1; i <= m; i++) {
edges.add(new UndirectedEdge(scanner.nextInt(), scanner.nextInt()));
}
UndirectedGraph g = null;
switch (implementation) {
case LISTS:
g = new AdjacencyListsUndirectedGraph(n, edges);
break;
case MATRIX:
g = new AdjacencyMatrixUndirectedGraph(n, edges);
break;
}
return g;
}
}
Prehľadávanie (orientovaného alebo neorientovaného) grafu do hĺbky
Existencia cesty medzi dvojicou vrcholov
Riešme teraz nasledujúci problém: pre danú dvojicu vrcholov u a v nejakého (orientovaného alebo neorientovaného) grafu potrebujeme zistiť, či sú spojené sledom – t. j. či sa dá medzi nimi prejsť pomocou postupne na seba nadväzujúcich hrán (počet týchto hrán môže byť aj nulový, takže z každého vrcholu triviálne vedie sled do seba samého). Existencia sledu medzi dvoma vrcholmi je očividne ekvivalentná existencii cesty – čiže sledu, v ktorom sa žiaden vrchol neopakuje. Keby totiž najkratší sled medzi danými dvoma vrcholmi nebol súčasne aj cestou, dal by sa skrátiť tak, ako je to znázornené na nasledujúcom obrázku – a tým by sme dostali spor.
V nasledujúcom preto budeme hovoriť o existencii ciest.
Pojmy sledu a cesty o niečo presnejšie:
- Sledom v grafe rozumieme postupnosť vrcholov v0, v1, ..., vn takú, že n je prirodzené číslo (aj nula) a pre i = 1,...,n existuje v danom grafe hrana z vi-1 do vi.
- Cestou rozumieme sled v0, v1, ..., vn taký, že vrcholy v0, v1, ..., vn sú po dvoch rôzne.
- Dĺžkou sledu (alebo cesty) v0, v1, ..., vn nazveme číslo n, čiže počet hrán tento sled tvoriacich.
Z každého vrcholu v tak vedie do v sled dĺžky nula, ktorý je súčasne aj cestou; žiadne ďalšie sledy nulovej dĺžky v grafe existovať nemôžu. Sledy dĺžky jedna zodpovedajú hranám grafu a cesty dĺžky jedna zodpovedajú hranám, ktoré nie sú slučkami.
Hovoríme, že neorientovaný graf je súvislý, ak je ľubovoľná dvojica vrcholov tohto grafu spojená cestou.
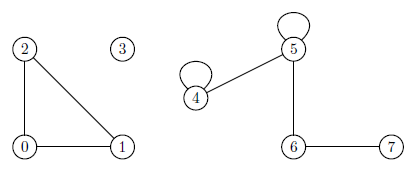
Pre neorientované grafy možno problém existencie cesty medzi dvoma vrcholmi chápať aj ako úlohu zistiť, či sú tieto dva vrcholy v rovnakom komponente súvislosti grafu. Komponent súvislosti neorientovaného grafu je každý jeho (vzhľadom na inklúziu) maximálny podgraf s nenulovým počtom vrcholov, ktorý je súvislý – komponent súvislosti grafu teda pozostáva z nejakej neprázdnej podmnožiny vrcholov grafu a všetkých hrán pôvodného grafu spájajúcich vrcholy z tejto podmnožiny, pričom ľubovoľné dva vrcholy komponentu sú spojené cestou a žiaden vrchol komponentu nie je v pôvodnom grafe spojený cestou s vrcholom mimo komponentu. Stručnejšie to možno vyjadriť s využitím pozorovania, že existencia cesty v neorientovanom grafe je zjavne reláciou ekvivalencie na množine jeho vrcholov – komponenty súvislosti potom zodpovedajú triedam ekvivalencie tejto relácie. Napríklad neorientovaný graf na nasledujúcom obrázku pozostáva z troch komponentov súvislosti.
Na riešenie problému existencie cesty použijeme prehľadávanie do hĺbky (angl. depth-first search) – podobné, ako ste už používali minulý semester pri vyfarbovaní súvislých oblastí v obdĺžnikovej mriežke. Procedúra na grafoch však bude všeobecnejšia:
- Mriežku môžeme reprezentovať neorientovaným grafom, v ktorom vrcholy zodpovedajú políčkam mriežky. Dvojica vrcholov je navyše spojená hranou práve vtedy, keď zodpovedajúce políčka spolu susedia a súčasne majú rovnakú farbu.
- Ostrovy rovnakej farby v mriežke potom zodpovedajú komponentom súvislosti výsledného neorientovaného grafu.
Prehľadávanie (orientovaného alebo neorientovaného) grafu do hĺbky budeme realizovať rekurzívnou metódou search, ktorá prehľadá všetkých ešte nenavštívených následníkov daného vrcholu. Informáciu o navštívení jednotlivých vrcholov si pritom budeme uchovávať v zozname visited. Metóda existsPath bude metódu search využívať na riešenie problému existencie cesty medzi danými dvoma vrcholmi.
/**
* Pomocna metoda pre metodu existsPath, ktora rekurzivne prehlada vsetky doposial nenavstivene vrcholy
* dosiahnutelne z daneho vrcholu.
* @param g Orientovany alebo neorientovany graf, v ktorom sa prehladavanie realizuje.
* @param vertex Vrchol grafu g, v ktorom sa prehladavanie zacina.
* @param visited Zoznam obsahujuci informacie o navstiveni jednotlivych vrcholov grafu. Pri volani metody by malo
* platit visited.get(vertex) == false.
*/
private static void search(DirectedGraph g, int vertex, List<Boolean> visited) {
visited.set(vertex, true);
for (int successor : g.outgoingEdgesDestinations(vertex)) {
if (!visited.get(successor)) {
search(g, successor, visited);
}
}
}
/**
* Metoda, ktora zisti, ci je dvojica vrcholov grafu spojena cestou.
* @param g Graf, v ktorom sa uloha realizuje.
* @param from Pociatocny vrchol.
* @param to Koncovy vrchol.
* @return Vystup je true prave vtedy, ked v grafe g existuje cesta z vrcholu from do vrcholu to.
*/
public static boolean existsPath(DirectedGraph g, int from, int to) {
ArrayList<Boolean> visited = new ArrayList<>();
for (int i = 0; i <= g.getVertexCount() - 1; i++) {
visited.add(false);
}
search(g, from, visited);
return visited.get(to);
}
Cvičenie. Vytvorte abstraktnú triedu AbstractDirectedGraph implementujúcu rozhranie DirectedGraph a upravte triedy SuccessorListsDirectedGraph a AdjacencyMatrixDirectedGraph tak, aby dedili od triedy AbstractDirectedGraph. Prepíšte metódy existsPath a search uvedené vyššie ako metódy inštancie triedy AbstractDirectedGraph. Aký bude mať táto zmena vplyv na argumenty týchto metód?
Hľadanie komponentov súvislosti neorientovaného grafu
V prípade, že pracujeme s neorientovaným grafom a existenciu cesty medzi dvojicami vrcholov by sme chceli testovať veľakrát, oplatí sa nájsť všetky komponenty súvislosti v danom grafe. Komponenty môžeme očíslovať od nuly až po nejaké k - 1, pričom pre každý vrchol si môžeme pamätať číslo jeho komponentu. Túto úlohu realizuje nasledujúca trieda:
package graphs;
import java.util.*;
/**
* Trieda reprezentujuca rozdelenie neorientovaneho grafu na komponenty suvislosti.
*/
public class Components {
/**
* Neorientovany graf, ktoreho komponenty suvislosti su instanciou tejto triedy reprezentovane.
*/
private UndirectedGraph g;
/**
* Zoznam, v ktorom si pre kazdy vrchol grafu g budeme pamatat cislo jeho komponentu.
*/
private ArrayList<Integer> componentId;
/**
* Celkovy pocet komponentov suvislosti grafu g.
*/
private int componentCount;
/**
* Konstruktor, ktory dostane ako argument neorientovany graf, najde komponenty suvislosti tohto grafu a informacie
* o nich ulozi do premennych instancie.
* @param g Neorientovany graf, ktoreho komponenty su reprezentovane instanciou tejto triedy.
*/
public Components(UndirectedGraph g) {
this.g = g;
componentCount = 0;
int n = g.getVertexCount();
componentId = new ArrayList<>();
for (int i = 0; i <= n - 1; i++) {
componentId.add(-1);
}
for (int i = 0; i <= n - 1; i++) {
if (componentId.get(i) == -1) {
search(i, componentCount);
componentCount++;
}
}
}
/**
* Pomocna metoda pre konstruktor, ktora oznaci vrcholy jedneho komponentom suvislosti identifikatorom tohto
* komponentu. Pracuje na baze prehladavania do hlbky.
* @param vertex Vrchol, z ktoreho sa zacina prehladavanie vrcholov komponentu.
* @param id Identifikator komponentu suvislosti.
*/
private void search(int vertex, int id) {
componentId.set(vertex, id);
for (int neighbour : g.outgoingEdgesDestinations(vertex)) {
if (componentId.get(neighbour) == -1) {
search(neighbour, id);
}
}
}
/**
* Metoda, ktora zisti, ci v grafe, ktoreho komponenty reprezentuje instancia tejto triedy, existuje cesta spajajuca
* danu dvojicu vrcholov.
* @param from Pociatocny vrchol.
* @param to Koncovy vrchol.
* @return Metoda vrati true prave vtedy, ked v grafe existuje cesta z vrcholu from do vrcholu to.
*/
public boolean existsPath(int from, int to) {
return componentId.get(from).equals(componentId.get(to));
}
/**
* Metoda, ktora vrati celkovy pocet komponentov grafu.
* @return Pocet komponentov.
*/
public int getComponentCount() {
return componentCount;
}
}
Nasledujúci kód načíta neorientovaný graf a dvojicu jeho vrcholov. Na konzolu následne vypíše, či sú tieto dva vrcholy v danom grafe spojené cestou.
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Zadaj neorientovany graf:");
UndirectedGraph g = readUndirectedGraph(scanner, GraphImplementation.LISTS);
System.out.println("Zadaj dvojicu vrcholov grafu:");
int from = scanner.nextInt();
int to = scanner.nextInt();
Components components = new Components(g);
if (components.existsPath(from, to)) {
System.out.println("Vrcholy su spojene cestou.");
} else {
System.out.println("Vrcholy nie su spojene cestou.");
}
}
Prehľadávanie (orientovaného alebo neorientovaného) grafu do šírky
Podobne ako prehľadávanie do hĺbky možno vo všeobecnejšom kontexte grafov aplikovať aj prehľadávanie do šírky (angl. breadth-first search), ktorého variant pre obdĺžnikovú mriežku poznáte z minulého semestra. Prehľadávanie grafu do šírky bude možné použiť na hľadanie najkratších ciest medzi dvojicami vrcholov orientovaného (a teda aj neorientovaného) grafu, kde dĺžka cesty je meraná počtom hrán.
Hľadanie najkratšej cesty
Hľadanie najkratších ciest v grafe – či už orientovanom alebo neorientovanom – možno realizovať napríklad nasledujúcou triedou ShortestPathsFromVertex:
- Jej konštruktor dostane ako parameter graf g a nejaký jeho význačný „štartovací” vrchol start. Následne spustí na grafe g prehľadávanie do šírky z vrcholu start.
- Takto sa postupne prehľadajú vrcholy vo vzdialenosti 1 od start, potom vrcholy vo vzdialenosti 2 od start, atď. Na zabezpečenie takéhoto poradia sa použije rad, podobne ako pri algoritme na mriežke minulý semester. V každom momente vykonávania algoritmu môže tento rad obsahovať vrcholy najviac dvoch rôznych vzdialeností od start.
- Pre každý vrchol v sa počas prehľadávania do zoznamu distances uloží jeho vzdialenosť od vrcholu start a do zoznamu predecessors sa uloží vrchol u, z ktorého bol vrchol v objavený – musí pritom vždy ísť o predposledný vrchol na jednej z najkratších ciest zo start do v.
- Metóda distanceFromStart bude pre daný vrchol vertex vracať jeho vzdialenosť od vrcholu start. Tu sa jednoducho využije hodnota uložená v zozname distances.
- Metóda shortestPathFromStart bude pre daný vrchol vertex vracať najkratšiu cestu z vrcholu start do vrcholu vertex reprezentovanú zoznamom vrcholov. Tú bude konštruovať od konca: začne vo vrchole vertex a postupne bude hľadať predchodcov pomocou hodnôt uložených v zozname predecessors.
package graphs;
import java.util.*;
/**
* Trieda reprezentujuca najkratsie cesty z pevne daneho pociatocneho vrcholu do vsetkych ostatnych vrcholov grafu.
*/
public class ShortestPathsFromVertex {
/**
* Zoznam obsahujuci pre kazdy vrchol grafu jeho vzdialenost zo "startovacieho" vrcholu z argumentu konstruktora.
* Ak zo "startovacieho" vrcholu do nejakeho vrcholu nevedie ziadna cesta, bude namiesto jeho vzdialenosti v zozname
* ulozena hodnota -1.
*/
private List<Integer> distances;
/**
* Zoznam obsahujuci pre kazdy vrchol v grafu g jeho predchodcu na najkratsej ceste zo "startovacieho" vrcholu
* do vrcholu v. Pre "startovaci" vrchol a vrcholy, do ktorych z neho nevedie cesta, bude v zozname ulozena
* hodnota -1.
*/
private List<Integer> predecessors;
/**
* Konstruktor, ktory pre dany graf a "startovaci" vrchol rovno aj najde najkratsie cesty zo startovacieho vrcholu
* do vsetkych ostatnych vrcholov grafu.
* @param g Graf, v ktorom sa hladanie ciest realizuje.
* @param start "Startovaci" vrchol.
*/
public ShortestPathsFromVertex(DirectedGraph g, int start) {
/* Inicializacia zoznamov distances a predecessors: */
distances = new ArrayList<>();
predecessors = new ArrayList<>();
for (int i = 0; i <= g.getVertexCount() - 1; i++) {
distances.add(-1);
predecessors.add(-1);
}
/* Samotne prehladavanie do sirky: */
Queue<Integer> queue = new LinkedList<>();
distances.set(start, 0);
queue.add(start);
while (!queue.isEmpty()) {
// Vyberieme vrchol z radu, prejdeme vsetkych jeho naslednikov, nenavstivenych spracujeme a vlozime do radu:
int vertex = queue.remove();
for (int successor : g.outgoingEdgesDestinations(vertex)) {
if (distances.get(successor) == -1) {
distances.set(successor, distances.get(vertex) + 1);
predecessors.set(successor, vertex);
queue.add(successor);
}
}
}
}
/**
* Metoda, ktora vrati dlzku najkratsej cesty z vrcholu start do daneho vrcholu.
* @param vertex Vrchol, vzdialenost ktoreho z vrcholu start sa pocita.
* @return Dlzka najkratsej cesty z vrcholu start do vrcholu vertex. Ak ziadna neexistuje, vrati sa -1.
*/
public int distanceFromStart(int vertex) {
return distances.get(vertex);
}
/**
* Metoda, ktora vrati najkratsiu cestu z vrcholu start do daneho vrcholu, reprezentovanu ako zoznam vrcholov.
* @param vertex Vrchol, najkratsia cesta do ktoreho z vrcholu start sa pocita.
* @return Nemodifikovatelny zoznam obsahujuci postupne vsetky vrcholy najkratsej cesty zo start do vertex.
* Ak ziadna cesta zo start do vertex neexistuje, vrati metoda referenciu null.
*/
public List<Integer> shortestPathFromStart(int vertex) {
if (distances.get(vertex) == -1) {
return null;
}
LinkedList<Integer> path = new LinkedList<>();
int v = vertex;
while (v != -1) {
path.addFirst(v);
v = predecessors.get(v);
}
return path;
}
}
Nasledujúci kód načíta graf a dvojicu jeho vrcholov; vypíše najkratšiu cestu medzi danými vrcholmi.
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Zadaj graf:");
DirectedGraph g = readDirectedGraph(scanner, GraphImplementation.LISTS);
System.out.println("Zadaj pociatocny a koncovy vrchol:");
int from = scanner.nextInt();
int to = scanner.nextInt();
ShortestPathsFromVertex shortestPathsFromVertex = new ShortestPathsFromVertex(g, from);
System.out.println("Najkratsia cesta ma dlzku " + shortestPathsFromVertex.distanceFromStart(to) + ".");
List<Integer> shortestPath = shortestPathsFromVertex.shortestPathFromStart(to);
if (shortestPath != null) {
System.out.println(shortestPath);
}
}
Stromy prehľadávania do hĺbky a do šírky
Označme pri prehľadávaní do hĺbky aj do šírky tie hrany, ktoré boli použité pri objavovaní nových vrcholov – to znamená: pri prehľadávaní do hĺbky hrany (u,v) také, že vo volaní metódy search pre vrchol u sa táto metóda zavolala rekurzívne aj pre vrchol v a pri prehľadávaní do šírky hrany (u,v) také, že sa v rámci prehľadávania následníkov vrcholu u do radu pridal vrchol v.
- V oboch prípadoch potom takéto hrany tvoria strom zakorenený vo vrchole, v ktorom prehľadávanie začalo (pri orientovaných grafoch sú všetky hrany orientované smerom od koreňa k listom).
- Hovoríme teda o stromoch prehľadávania do hĺbky resp. do šírky (angl. DFS Tree resp. BFS Tree).
- V prípade, že je graf neorientovaný a súvislý, ide v obidvoch prípadoch o jeho kostru (t. j. strom zložený zo všetkých vrcholov grafu a jeho vybraných hrán).
- Pri stromoch prehľadávania do šírky reprezentujú cesty od koreňa k nejakému inému vrcholu vždy niektorú z najkratších ciest medzi príslušnými vrcholmi grafu.
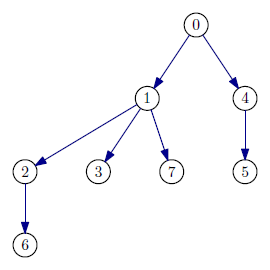
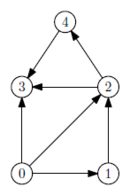
Príklad. Nižšie je znázornený diagram orientovaného grafu a jeho stromy prehľadávania do hĺbky a do šírky v prípade, že prehľadávanie začne vo vrchole 0 a pri spracúvaní následníkov sa postupuje vzostupne podľa čísel vrcholov (čo nemusí byť vždy tak).
Strom prehľadávania do hĺbky:
Strom prehľadávania do šírky:
Prehľadávanie s návratom na grafoch
Pre veľa úloh na grafoch nie sú známe – a v prípade platnosti niektorých hypotéz z teoretickej informatiky často ani neexistujú – žiadne efektívne algoritmy. Prehľadávaním s návratom však vieme spočítať odpoveď aspoň pre malé vstupy.
Hľadanie ciest danej dĺžky
Nasledujúca trieda FixedLengthPaths pre daný graf g, danú dvojicu vrcholov from, to a dané prirodzené číslo length nájde všetky cesty dĺžky presne length vedúce v grafe g z vrcholu from do vrcholu to; takéto cesty môžu evidentne existovať iba v prípade, že je prirodzené číslo length menšie, než počet vrcholov grafu. Prehľadávanie s návratom sa spustí hneď v konštruktore a nájdené cesty sa uložia do zoznamu paths.
Pri prehľadávaní sa v spájanom zozname path budú postupne generovať všetky cesty hľadaného typu. Pre každý vrchol budeme mať navyše v zozname visited poznačené, či sme ho už v generovanej ceste použili. Akonáhle nájdeme cestu požadovanej dĺžky končiacu vo vrchole to, uložíme ju do zoznamu paths.
package graphs;
import java.util.*;
/**
* Trieda realizujuca najdenie vsetkych ciest danej fixnej dlzky medzi danou dvojicou vrcholov daneho grafu.
*/
public class FixedLengthPaths {
/**
* Graf, v ktorom sa hladanie ciest realizuje.
*/
private DirectedGraph g;
/**
* Koncovy vrchol hladanych ciest.
*/
private int to;
/**
* Pozadovana dlzka hladanych ciest.
*/
private int length;
/**
* Pomocny zoznam, v ktorom sa budu pomocou prehladavania s navratom postupne generovat jednotlive cesty.
*/
private LinkedList<Integer> path;
/**
* Pomocny zoznam, v ktorom si budeme pocas generovania ciest pre kazdy vrchol pamatat, ci sa nachadza alebo
* nenachadza v doposial vygenerovanej casti cesty.
*/
private ArrayList<Boolean> visited;
/**
* Zoznam, v ktorom budu ulozene vsetky vygenerovane cesty.
*/
private List<List<Integer>> paths;
/**
* Konstruktor, ktory rovno aj spusti prehladavanie s navratom a do zoznamu paths postupne ulozi vsetky cesty danej
* dlzky medzi danou dvojicou vrcholov daneho grafu.
* @param g Graf, v ktorom sa hladanie ciest realizuje.
* @param from Pociatocny vrchol hladanych ciest.
* @param to Koncovy vrchol hladanych ciest.
* @param length Pozadovana dlzka hladanych ciest.
*/
public FixedLengthPaths(DirectedGraph g, int from, int to, int length) {
this.g = g;
this.to = to;
this.length = length;
paths = new LinkedList<>();
visited = new ArrayList<>();
for (int i = 0; i <= g.getVertexCount() - 1; i++) {
visited.add(false);
}
path = new LinkedList<>();
path.add(from);
visited.set(from, true);
search();
}
/**
* Metoda realizujuca samotne rekurzivne prehladavanie s navratom. Ak je dosial vygenerovana cast cesty kratsia nez
* length, postupne sa vyskusaju vsetky moznosti jej predlzenia. V pripade, ze uz ide o cestu dlzky length, overi
* sa, ci cesta konci vo vrchole to a ak ano, prida sa kopia tejto cesty do zoznamu paths.
*/
private void search() {
if (path.size() == length + 1) { // Dlzka zoznamu je vzdy o jedna vacsia, nez dlzka nim reprezentovanej cesty.
if (path.getLast() == to) {
paths.add(Collections.unmodifiableList(new LinkedList<>(path)));
}
} else {
for (int successor : g.outgoingEdgesDestinations(path.getLast())) {
if (!visited.get(successor)) {
visited.set(successor, true);
path.add(successor);
search();
path.removeLast();
visited.set(successor, false);
}
}
}
}
/**
* Metoda, ktora vrati nemodifikovatelny pohlad na zoznam vsetkych vygenerovanych ciest.
* @return Nemodifikovatelny zoznam vsetkych ciest dlzky length veducich v grafe g z vrcholu from do vrcholu to.
*/
public List<List<Integer>> getPaths() {
return Collections.unmodifiableList(paths);
}
}
Nasledujúci kód načíta graf, dvojicu vrcholov from, to a prirodzené číslo length a vypíše všetky cesty dĺžky length z vrcholu from do vrcholu to.
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Zadaj graf:");
DirectedGraph g = readDirectedGraph(scanner, GraphImplementation.LISTS);
System.out.println("Zadaj pociatocny a koncovy vrchol:");
int from = scanner.nextInt();
int to = scanner.nextInt();
System.out.println("Zadaj dlzku generovanych ciest:");
int length = scanner.nextInt();
FixedLengthPaths fixedLengthPaths = new FixedLengthPaths(g, from, to, length);
System.out.println("Cesty dlzky " + length + ":");
for (List<Integer> path : fixedLengthPaths.getPaths()) {
System.out.println(path);
}
}
Príklad. Pre orientovaný graf s vrcholmi {0,...,4} a hranami {(0,1),(0,2),(0,3),(1,2),(2,3),(2,4),(4,3)}, počiatočný vrchol 0 a koncový vrchol 3 dostávame nasledujúce výstupy
Cesty dlzky 1: [0, 3] Cesty dlzky 2: [0, 2, 3] Cesty dlzky 3: [0, 1, 2, 3] [0, 2, 4, 3] Cesty dlzky 4: [0, 1, 2, 4, 3]
Cvičenia:
- Upravte triedu FixedLengthPaths tak, aby namiesto hľadania a ukladania všetkých ciest danej dĺžky iba počítala, koľko ich je.
- Upravte triedu FixedLengthPaths tak, aby iba zisťovala, či existuje cesta danej dĺžky (po prvej nájdenej ceste je teda možné prehľadávanie ukončiť).
- Navrhnite spôsoby, ako v niektorých prípadoch zistiť, že rozrobenú cestu už nie je možné požadovaným spôsobom predĺžiť a danú vetvu prehľadávania s návratom tak možno ukončiť.
Hľadanie najdlhšej cesty
Uvažujme teraz problém nájdenia nejakej z najdlhších ciest z u do v (ak existuje aspoň jedna). Túto úlohu bude realizovať trieda LongestPath, ktorá sa oproti triede FixedLengthPaths bude líšiť len málo.
- Počas prehľadávania si budeme pamätať najdlhšiu doposiaľ nájdenú cestu.
- Vždy, keď prídeme do cieľového vrcholu, porovnáme dĺžku práve nájdenej cesty s najdlhšou doposiaľ nájdenou cestou.
package graphs;
import java.util.*;
/**
* Trieda realizujuca najdenie najdlhsej cesty medzi danou dvojicou vrcholov grafu.
*/
public class LongestPath {
/**
* Graf, v ktorom sa hladanie ciest realizuje.
*/
private DirectedGraph g;
/**
* Koncovy vrchol hladanych ciest.
*/
private int to;
/**
* Pomocny zoznam, v ktorom sa budu pomocou prehladavania s navratom postupne generovat jednotlive cesty.
*/
private LinkedList<Integer> path;
/**
* Pomocny zoznam, v ktorom si budeme pocas generovania ciest pre kazdy vrchol pamatat, ci sa nachadza alebo
* nenachadza v doposial vygenerovanej casti cesty.
*/
private ArrayList<Boolean> visited;
/**
* Zoznam, v ktorom bude ulozena najdlhsia cesta medzi danou dvojicou vrcholov (pocas prehladavania pojde
* o najdlhsiu doposial najdenu cestu).
*/
private List<Integer> longestPath;
/**
* Konstruktor, ktory rovno aj spusti prehladavanie s navratom a do zoznamu longestPath ulozi niektoru spomedzi
* najdlhsich ciest medzi danou dvojicou vrcholov grafu.
* @param g Graf, v ktorom sa hladanie ciest realizuje.
* @param from Pociatocny vrchol hladanych ciest.
* @param to Koncovy vrchol hladanych ciest.
*/
public LongestPath(DirectedGraph g, int from, int to) {
this.g = g;
this.to = to;
visited = new ArrayList<>();
for (int i = 0; i <= g.getVertexCount() - 1; i++) {
visited.add(false);
}
path = new LinkedList<>();
path.add(from);
visited.set(from, true);
search();
}
/**
* Metoda realizujuca samotne rekurzivne prehladavanie s navratom. V pripade, ze sa vygenerovala cesta konciaca
* vo vrchole to, porovna sa jej dlzka s dlzkou doposial najdlhsej najdenej cesty a ak je dlhsia, ulozi sa ako nova
* doposial najdlhsia cesta. V opacnom pripade sa vyskusaju vsetky moznosti predlzenia cesty.
*/
private void search() {
if (path.getLast() == to) {
if (longestPath == null || path.size() > longestPath.size()) {
longestPath = new LinkedList<>(path);
}
} else {
for (int successor : g.outgoingEdgesDestinations(path.getLast())) {
if (!visited.get(successor)) {
visited.set(successor, true);
path.add(successor);
search();
path.removeLast();
visited.set(successor, false);
}
}
}
}
/**
* Metoda, ktora vrati najdenu najdlhsiu cestu medzi danou dvojicou vrcholov.
* @return Nemodifikovatelny pohlad na zoznam vrcholov na najdlhsej ceste z vrcholu from do vrcholu to.
*/
public List<Integer> getLongestPath() {
if (longestPath != null) {
return Collections.unmodifiableList(longestPath);
} else {
return null;
}
}
}
Použitie triedy:
LongestPath longestPath = new LongestPath(g, from, to);
List<Integer> longest = longestPath.getLongestPath();
if (longest != null) {
System.out.println("Najdlhsia cesta: " + longest);
}
Príklad výstupu na rovnakom grafe ako vyššie pre počiatočný vrchol 0 a koncový vrchol 3:
Najdlhsia cesta: [0, 1, 2, 4, 3]