Programovanie (1) v C/C++
1-INF-127, ZS 2024/25
Letný semester, prednáška č. 9: Rozdiel medzi revíziami
| Riadok 332: | Riadok 332: | ||
== Orientované acyklické grafy a topologické triedenie == | == Orientované acyklické grafy a topologické triedenie == | ||
| + | |||
| + | Budeme teraz pracovať s ''orientovanými acyklickými grafmi'' – čiže orientovanými grafmi neobsahujúcimi žiaden cyklus. Takéto grafy sa zídu pri rôznych praktických úlohách, kde môžu reprezentovať napríklad časové závislosti – alebo ''prerekvizity'' – medzi vykonávanými činnosťami (celý proces je očividne vykonateľný práve vtedy, keď je tento orientovaný graf acyklický). | ||
| + | |||
| + | ''Príklad orientovaného acyklického grafu:'' | ||
| + | |||
| + | :::[[Súbor:Graf7.png]] | ||
| + | |||
| + | Pod ''topologickým usporiadaním'' orientovaného acyklického grafu o vrcholoch ''0,1,...,n-1'' budeme rozumieť permutáciu ''π'': {''0,1,...,n-1''} → {''0,1,...,n-1''} takú, že pre všetky hrany ''(u,v)'' grafu platí ''π''(''u'') ≤ ''π''(''v''). V princípe teda ide o úplné usporiadanie na množine vrcholov grafu (vrchol ''v'' vždy ide ako ''π''(''v'')-ty v poradí) také, že všetky hrany v grafe idú „v smere tohto usporiadania”. Topologické usporiadanie teda napríklad môže určovať poradie, v ktorom možno vykonať jednotlivé činnosti tak, aby boli splnené všetky ich prerekvizity. | ||
| + | Väčšinou budeme pod topologickým usporiadaním chápať priamo postupnosť vrcholov v poradí určenom príslušnou permutáciou, t. j. ''π<sup>-1</sup>''(''0''), ''π<sup>-1</sup>''(''1''), ..., ''π<sup>-1</sup>''(''n - 1''). Pod ''topologickým triedením'' budeme rozumieť proces hľadania topologického usporiadania. | ||
| + | |||
| + | Jeden orientovaný acyklický graf môže mať aj viacero topologických usporiadaní. Napríklad graf na obrázku vyššie má presne štyri topologické usporiadania: | ||
| + | <pre> | ||
| + | [5, 6, 4, 3, 1, 2, 0] | ||
| + | [6, 5, 4, 3, 1, 2, 0] | ||
| + | [5, 6, 4, 3, 2, 1, 0] | ||
| + | [6, 5, 4, 3, 2, 1, 0] | ||
| + | </pre> | ||
| + | |||
| + | ''Poznámka'': matematicky o niečo výstižnejšia ekvivalentná definícia topologického usporiadania využíva fakt, že orientované acyklické grafy sú práve tie orientované grafy, ktorých reflexívno-tranzitívny uzáver možno chápať ako čiastočné usporiadanie na množine vrcholov (neexistencia cyklu zodpovedá antisymetrii). V tomto zmysle teda každý orientovaný acyklický graf jednoznačne určuje čiastočné usporiadanie ⪯ na množine vrcholov grafu. Topologické usporiadanie je potom ľubovoľné úplné usporiadanie ≤ na tej istej množine vrcholov také, že ⪯ ⊆ ≤. | ||
| + | |||
| + | ''Veta'': Každý orientovaný acyklický graf má aspoň jedno topologické usporiadanie. | ||
| + | |||
| + | ''Dôkaz''. Indukciou vzhľadom na počet vrcholov. Graf o jednom vrchole ''v'' má evidentne topologické usporiadanie ''v''. Predpokladajme teraz, že tvrdenie platí pre všetky grafy veľkosti ''n'' a uvažujme orientovaný acyklický graf veľkosti ''n+1''. Ten musí obsahovať najmenej jeden vrchol, z ktorého nevychádza žiadna hrana – v opačnom prípade by totiž každý sled bolo možné predĺžiť na dlhší, pričom sled dĺžky ''n+1'' nutne musí obsahovať cyklus. Nech má túto vlastnosť vrchol ''u''. Podľa indukčného predpokladu potom existuje topologické usporiadanie grafu, ktorý z uvažovaného grafu získame odstránením vrcholu ''u'' a všetkých do neho vedúcich hrán (ten má totiž ''n'' vrcholov). Ak je týmto usporiadaním ''v<sub>1</sub>'',...,''v<sub>n</sub>'', je ''v<sub>1</sub>'',...,''v<sub>n</sub>'',''u'' topologickým usporiadaním uvažovaného grafu. | ||
== Úlohy na ohodnotených grafoch == | == Úlohy na ohodnotených grafoch == | ||
Verzia zo dňa a času 15:57, 4. apríl 2021
Obsah
Oznamy
- Dnes po prednáške bude zverejnené zadanie štvrtej domácej úlohy, ktorú bude potrebné odovzdať do pondelka 26. apríla, 9:00 (čiže do začiatku jedenástej prednášky).
- Počas stredajších cvičení bude prebiehať štvrtý test zameraný predovšetkým na grafy a grafové algoritmy.
- V rámci stredajších cvičení tiež bude zverejnené zadanie tretej bonusovej úlohy s termínom odovzdania do stredy 21. apríla, 11:30.
Prehľadávanie s návratom na grafoch: pokračovanie
Hľadanie najdlhšej cesty
Uvažujme problém nájdenia niektorej z najdlhších ciest z vrcholu u do vrcholu v daného orientovaného grafu (ak existuje aspoň jedna). Je dokázané, že za predpokladu platnosti určitých hypotéz z teoretickej informatiky pre túto úlohu neexistuje žiaden efektívny algoritmus. Použijeme teda prehľadávanie s návratom. To bude realizovať trieda LongestPath, ktorú získame drobnou úpravou triedy FixedLengthPaths z minulej prednášky.
- Počas prehľadávania si budeme pamätať najdlhšiu doposiaľ nájdenú cestu.
- Vždy, keď prídeme do cieľového vrcholu, porovnáme dĺžku práve nájdenej cesty s najdlhšou doposiaľ nájdenou cestou.
package graphs;
import java.util.*;
/**
* Trieda realizujuca najdenie najdlhsej cesty medzi danou dvojicou vrcholov grafu.
*/
public class LongestPath {
/**
* Graf, v ktorom sa hladanie ciest realizuje.
*/
private Graph g;
/**
* Pociatocny vrchol hladanych ciest.
*/
private int from;
/**
* Koncovy vrchol hladanych ciest.
*/
private int to;
/**
* Pomocny zoznam, v ktorom sa budu pomocou prehladavania s navratom postupne generovat jednotlive cesty.
*/
private LinkedList<Integer> path;
/**
* Pomocny zoznam, v ktorom si budeme pocas generovania ciest pre kazdy vrchol pamatat, ci sa nachadza alebo
* nenachadza v doposial vygenerovanej casti cesty.
*/
private ArrayList<Boolean> visited;
/**
* Zoznam, v ktorom bude ulozena najdlhsia cesta medzi danou dvojicou vrcholov (pocas prehladavania pojde
* o najdlhsiu doposial najdenu cestu).
*/
private List<Integer> longestPath;
/**
* Konstruktor, ktory rovno aj spusti prehladavanie s navratom a do zoznamu longestPath ulozi niektoru spomedzi
* najdlhsich ciest medzi danou dvojicou vrcholov grafu.
* @param g Graf, v ktorom sa hladanie ciest realizuje.
* @param from Pociatocny vrchol hladanych ciest.
* @param to Koncovy vrchol hladanych ciest.
*/
public LongestPath(Graph g, int from, int to) {
this.g = g;
this.from = from;
this.to = to;
visited = new ArrayList<>();
for (int i = 0; i <= g.getNumberOfVertices() - 1; i++) {
visited.add(false);
}
path = new LinkedList<>();
path.add(from);
visited.set(from, true);
search();
}
/**
* Metoda realizujuca samotne rekurzivne prehladavanie s navratom. V pripade, ze sa vygenerovala cesta konciaca
* vo vrchole to, porovna sa jej dlzka s dlzkou doposial najdlhsej najdenej cesty a ak je dlhsia, ulozi sa ako nova
* doposial najdlhsia cesta. V opacnom pripade sa vyskusaju vsetky moznosti predlzenia cesty.
*/
private void search() {
if (path.getLast() == to) {
if (longestPath == null || path.size() > longestPath.size()) {
longestPath = new LinkedList<>(path);
}
} else {
for (int successor : g.outgoingEdgesDestinations(path.getLast())) {
if (!visited.get(successor)) {
visited.set(successor, true);
path.add(successor);
search();
path.removeLast();
visited.set(successor, false);
}
}
}
}
/**
* Metoda, ktora vrati najdenu najdlhsiu cestu medzi danou dvojicou vrcholov.
* @return Nemodifikovatelny pohlad na zoznam vrcholov na najdlhsej ceste z vrcholu from do vrcholu to.
*/
public List<Integer> getLongestPath() {
if (longestPath != null) {
return Collections.unmodifiableList(longestPath);
} else {
return null;
}
}
}
Použitie triedy:
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Zadaj graf:");
Graph g = readGraph(scanner, GraphType.DIRECTED_SUCCESSOR_LISTS);
System.out.println("Zadaj pociatocny a koncovy vrchol:");
int from = scanner.nextInt();
int to = scanner.nextInt();
LongestPath longestPath = new LongestPath(g, from, to);
List<Integer> longest = longestPath.getLongestPath();
if (longest != null) {
System.out.println("Najdlhsia cesta: " + longest);
} else {
System.out.println("Ziadna cesta neexistuje.");
}
}
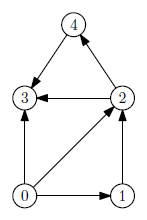
Príklad výstupu pre graf na obrázku vyššie, počiatočný vrchol 0 a koncový vrchol 3:
Najdlhsia cesta: [0, 1, 2, 4, 3]
Hľadanie najväčšej kliky v neorientovanom grafe
Uvažujme teraz neorientované grafy bez slučiek (slučky síce nebudeme zakazovať, ale v našich nasledujúcich úvahách ich budeme ignorovať; najvhodnejšia predstava teda je, že pracujeme s grafmi, ktoré žiadne slučky neobsahujú).
- Klikou (angl. clique) v neorientovanom grafe rozumieme jeho úplný podgraf, čiže podmnožinu K množiny vrcholov grafu takú, že každé dva rôzne vrcholy z K sú navzájom spojené hranou. Veľkosťou kliky rozumieme počet vrcholov kliku tvoriacich. Špeciálne každý vrchol sám o sebe tvorí kliku veľkosti jedna a ľubovoľné dva vrcholy spojené hranou tvoria kliku veľkosti dva.
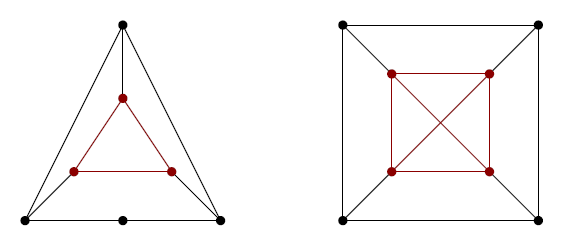
- V grafoch na nasledujúcom obrázku sú vyznačené kliky veľkosti tri a štyri.
Budeme sa teraz zaoberať problémom nájdenia najväčšej kliky (angl. maximum clique) v neorientovanom grafe.
- Ide o nájdenie kliky s najväčšou veľkosťou spomedzi všetkých klík daného grafu.
- Pozor na terminológiu: maximálna klika (angl. maximal clique) je ľubovoľná klika, ktorú nemožno pridaním ďalšieho vrcholu rozšíriť na väčšiu kliku. Nie každá maximálna klika ale musí byť aj najväčšia. My sa budeme zaoberať prakticky užitočnejším problémom hľadania najväčších klík.
- Aj pre problém najväčšej kliky je dokázané, že v prípade platnosti určitých hypotéz z teoretickej informatiky preň neexistuje žiaden efektívny algoritmus. Použijeme teda prehľadávanie s návratom – nebudeme ním však teraz konštruovať cesty, ale množiny vrcholov grafu.
- Postupne budeme generovať všetky množiny vrcholov daného grafu ako utriedené spájané zoznamy. Zakaždým sa pokúsime daný vrchol do množiny pridať a rekurzívne pokračovať na ďalší vrchol, následne sa ho pokúsime vynechať a tiež rekurzívne pokračovať na ďalší vrchol. Po vygenerovaní kompletnej množiny zistíme, či ide o kliku; ak áno, porovnáme jej veľkosť s najväčšou doposiaľ nájdenou klikou, ktorú v prípade potreby aktualizujeme.
Trieda MaximumClique realizujúca nájdenie najväčšej kliky v neorientovanom grafe:
package graphs;
import java.util.*;
/**
* Trieda realizujuca najdenie niektorej spomedzi najvacsich klik v danom neorientovanom grafe.
*/
public class MaximumClique {
/**
* Neorientovany graf, v ktorom sa hladanie najvacsej kliky realizuje.
*/
private UndirectedGraph g;
/**
* Zoznam vrcholov najvacsej kliky neorientovaneho grafu g, resp. pocas prehladavania s navratom doposial najvacsej
* najdenej kliky.
*/
private LinkedList<Integer> maximumClique;
/**
* Zoznam, v ktorom sa pocas prehladavania s navratom budu postupne generovat vsetky (utriedene) mnoziny vrcholov
* grafu g.
*/
private LinkedList<Integer> currentVertices;
/**
* Konstruktor, ktory pomocou prehladavania s navratom najde najvacsiu kliku v danom neorientovanom grafe.
* @param g Neorientovany graf, v ktorom sa hladanie najvacsej kliky realizuje.
*/
public MaximumClique(UndirectedGraph g) {
this.g = g;
maximumClique = new LinkedList<>();
currentVertices = new LinkedList<>();
search(0);
}
/**
* Rekurzivna metoda realizujuca samotne prehladavnie s navratom a v zozname currentVertices postupne generujuca
* vsetky (utriedene) mnoziny vrcholov grafu g. Predpoklada sa, ze pred volanim metody reprezentuje zoznam
* currentVertices nejaku utriedenu podmnozinu mnoziny vrcholov {0,...,vertex-1}. Metoda search
* sa najprv pokusi pridat do zoznamu vrchol vertex a vygenerovat vsetky mnoziny obsahujuce vrcholy z tohto zoznamu;
* nasledne sa pokusi vrchol vertex do zoznamu nepridat a taktiez vygeneruje vsetky taketo mnoziny.
* Volanie metody pre vertex == 0 teda postupne vygeneruje vsetky utriedene mnoziny vrcholov grafu g. V pripade, ze
* vertex == g.getNumberOfVertices(), povazuje sa mnozina vrcholov za vygenerovanu a zisti sa, ci ide o najvacsiu
* doposial najdenu kliku v grafe g.
* @param vertex Vrchol neorientovaneho grafu g alebo hodnota g.getNumberOfVertices().
*/
private void search(int vertex) {
if (vertex == g.getNumberOfVertices()) {
if (isClique(currentVertices) && currentVertices.size() > maximumClique.size()) {
maximumClique = new LinkedList<>(currentVertices);
}
} else {
currentVertices.addLast(vertex);
search(vertex + 1);
currentVertices.removeLast();
search(vertex + 1);
}
}
/**
* Pomocna metoda, ktora zisti, ci dane zoskupenie vrcholov zodpoveda klike v neorientovanom grafe g.
* @param vertices Zoskupenie vrcholov grafu g.
* @return Metoda vrati true prave vtedy, ked vrcholy zoskupenia vertices tvoria kliku v grafe g.
*/
private boolean isClique(Collection<Integer> vertices) {
for (int u : vertices) {
for (int v : vertices) {
if (u != v && !g.existsEdge(u, v)) {
return false;
}
}
}
return true;
}
/**
* Metoda, ktora vrati najdenu najvacsiu kliku v neorientovanom grafe g ako utriedeny zoznam jej vrcholov.
* @return Nemodifikovatelny zoznam obsahujuci vo vzostupnom poradi vsetky vrcholy najdenej najvacsej kliky.
*/
public List<Integer> getMaximumClique() {
return Collections.unmodifiableList(maximumClique);
}
}
Použitie triedy MaximumClique:
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Zadaj graf:");
UndirectedGraph g = (UndirectedGraph) readGraph(scanner, GraphType.UNDIRECTED_ADJACENCY_LISTS);
MaximumClique maximumClique = new MaximumClique(g);
System.out.println("Najvacsia klika v zadanom grafe: " + maximumClique.getMaximumClique());
}
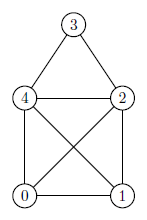
Uvažujme napríklad graf na nasledujúcom obrázku.
Vyššie uvedený program preň vypíše nasledujúci výstup:
Najvacsia klika v zadanom grafe: [0, 1, 2, 4]
Mierne zrýchlenie hľadania najväčšej kliky
Pri hľadaní najväčšej kliky v neorientovanom grafe sme zakaždým prešli cez všetkých 2n podmnožín n-prvkovej množiny vrcholov grafu. Často je ale možné už behom prehľadávania rozoznať, že rozpracovanú množinu vrcholov nebude možné rozšíriť na najväčšiu kliku. Zapracujeme teda do prehľadávania s návratom v triede MaximumClique dve vylepšenia, ktoré síce nijak nezmenia časovú zložitosť algoritmu v najhoršom prípade, ale pre veľké množstvo grafov jeho vykonávanie podstatne urýchlia:
- Vrchol budeme pridávať do rozpracovanej množiny iba v prípade, že je spojený hranou so všetkými vrcholmi v tejto množine – v opačnom prípade už totiž z tejto množiny, ani po prípadnom pridaní ďalších vrcholov, kliku nikdy nevytvoríme. V takom prípade bude po vygenerovaní kompletnej množiny garantované, že ide o kliku a kontrolu metódou isClique môžeme vypustiť.
- Vrchol tiež budeme pridávať iba v prípade, že je počet jeho susedov – čo je jedna z možných definícií stupňa vrcholu – väčší alebo rovný počtu vrcholov v doposiaľ najväčšej objavenej klike. Ak má totiž najväčšia doposiaľ objavená klika veľkosť k, má pridanie vrcholu do rozpracovanej množiny zmysel iba v prípade, že bude môcť byť súčasťou kliky veľkosti aspoň k+1; každý vrchol, ktorý je súčasťou takejto kliky, má evidentne aspoň k susedov.
Upravená trieda MaximumClique:
package graphs;
import java.util.*;
public class MaximumClique {
private UndirectedGraph g;
private LinkedList<Integer> maximumClique;
private LinkedList<Integer> currentVertices;
public MaximumClique(UndirectedGraph g) {
this.g = g;
maximumClique = new LinkedList<>();
currentVertices = new LinkedList<>();
search(0);
}
private void search(int vertex) {
if (vertex == g.getNumberOfVertices()) {
if (currentVertices.size() > maximumClique.size()) {
maximumClique = new LinkedList<>(currentVertices);
}
} else {
if (connectedWithEach(vertex, currentVertices) && neighbourCount(vertex) >= maximumClique.size()) {
currentVertices.addLast(vertex);
search(vertex + 1);
currentVertices.removeLast();
}
search(vertex + 1);
}
}
private boolean connectedWithEach(int vertex, Collection<Integer> vertices) {
for (int v : vertices) {
if (!g.existsEdge(vertex, v)) {
return false;
}
}
return true;
}
private int neighbourCount(int vertex) {
int result = 0;
for (int v : g.outgoingEdgesDestinations(vertex)) {
result++;
}
return result;
}
public List<Integer> getMaximumClique() {
return Collections.unmodifiableList(maximumClique);
}
}
Cvičenia:
- Opíšte beh uvedeného programu na grafe obsahujúcom niekoľko vrcholov a žiadnu hranu.
- Urýchlite uvedený algoritmus vhodnou implementáciou metódy neighbourCount už v triedach pre grafy (keďže bude potrebná implementácia aj pre orientované grafy, bude asi vhodnejšie premenovať metódu na successorCount a implementovať ju tak, aby pre každý vrchol vrátila počet jeho následníkov v orientovanom grafe).
Orientované acyklické grafy a topologické triedenie
Budeme teraz pracovať s orientovanými acyklickými grafmi – čiže orientovanými grafmi neobsahujúcimi žiaden cyklus. Takéto grafy sa zídu pri rôznych praktických úlohách, kde môžu reprezentovať napríklad časové závislosti – alebo prerekvizity – medzi vykonávanými činnosťami (celý proces je očividne vykonateľný práve vtedy, keď je tento orientovaný graf acyklický).
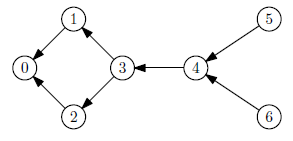
Príklad orientovaného acyklického grafu:
Pod topologickým usporiadaním orientovaného acyklického grafu o vrcholoch 0,1,...,n-1 budeme rozumieť permutáciu π: {0,1,...,n-1} → {0,1,...,n-1} takú, že pre všetky hrany (u,v) grafu platí π(u) ≤ π(v). V princípe teda ide o úplné usporiadanie na množine vrcholov grafu (vrchol v vždy ide ako π(v)-ty v poradí) také, že všetky hrany v grafe idú „v smere tohto usporiadania”. Topologické usporiadanie teda napríklad môže určovať poradie, v ktorom možno vykonať jednotlivé činnosti tak, aby boli splnené všetky ich prerekvizity. Väčšinou budeme pod topologickým usporiadaním chápať priamo postupnosť vrcholov v poradí určenom príslušnou permutáciou, t. j. π-1(0), π-1(1), ..., π-1(n - 1). Pod topologickým triedením budeme rozumieť proces hľadania topologického usporiadania.
Jeden orientovaný acyklický graf môže mať aj viacero topologických usporiadaní. Napríklad graf na obrázku vyššie má presne štyri topologické usporiadania:
[5, 6, 4, 3, 1, 2, 0] [6, 5, 4, 3, 1, 2, 0] [5, 6, 4, 3, 2, 1, 0] [6, 5, 4, 3, 2, 1, 0]
Poznámka: matematicky o niečo výstižnejšia ekvivalentná definícia topologického usporiadania využíva fakt, že orientované acyklické grafy sú práve tie orientované grafy, ktorých reflexívno-tranzitívny uzáver možno chápať ako čiastočné usporiadanie na množine vrcholov (neexistencia cyklu zodpovedá antisymetrii). V tomto zmysle teda každý orientovaný acyklický graf jednoznačne určuje čiastočné usporiadanie ⪯ na množine vrcholov grafu. Topologické usporiadanie je potom ľubovoľné úplné usporiadanie ≤ na tej istej množine vrcholov také, že ⪯ ⊆ ≤.
Veta: Každý orientovaný acyklický graf má aspoň jedno topologické usporiadanie.
Dôkaz. Indukciou vzhľadom na počet vrcholov. Graf o jednom vrchole v má evidentne topologické usporiadanie v. Predpokladajme teraz, že tvrdenie platí pre všetky grafy veľkosti n a uvažujme orientovaný acyklický graf veľkosti n+1. Ten musí obsahovať najmenej jeden vrchol, z ktorého nevychádza žiadna hrana – v opačnom prípade by totiž každý sled bolo možné predĺžiť na dlhší, pričom sled dĺžky n+1 nutne musí obsahovať cyklus. Nech má túto vlastnosť vrchol u. Podľa indukčného predpokladu potom existuje topologické usporiadanie grafu, ktorý z uvažovaného grafu získame odstránením vrcholu u a všetkých do neho vedúcich hrán (ten má totiž n vrcholov). Ak je týmto usporiadaním v1,...,vn, je v1,...,vn,u topologickým usporiadaním uvažovaného grafu.