Programovanie (2) v Jave
1-INF-166, letný semester 2023/24
Prednáška 14: Rozdiel medzi revíziami
| Riadok 23: | Riadok 23: | ||
* Zápis <tt>(*p).cokolvek</tt> vyjadruje prvok <tt>cokolvek</tt> štruktúry získanej dereferenciou smerníka <tt>p</tt>. | * Zápis <tt>(*p).cokolvek</tt> vyjadruje prvok <tt>cokolvek</tt> štruktúry získanej dereferenciou smerníka <tt>p</tt>. | ||
* Zvyčajne je potrebnejší zápis <tt>(*p).cokolvek</tt>; existuje preň preto skratka <tt>p->cokolvek</tt>. | * Zvyčajne je potrebnejší zápis <tt>(*p).cokolvek</tt>; existuje preň preto skratka <tt>p->cokolvek</tt>. | ||
| − | |||
| − | |||
| − | |||
<syntaxhighlight lang="C++"> | <syntaxhighlight lang="C++"> | ||
| Riadok 37: | Riadok 34: | ||
b.x = 0; | b.x = 0; | ||
b.y = 0; | b.y = 0; | ||
| + | bod *p = &b; // p ukazuje na bod b | ||
| − | |||
| − | |||
| − | |||
| − | |||
bod *p2 = new bod; // alokovanie noveho bodu | bod *p2 = new bod; // alokovanie noveho bodu | ||
| − | (*p2).x = 20; // bod, na ktory ukazuje p2, bude mat x | + | (*p2).x = 20; // bod, na ktory ukazuje p2, bude mat x 20 |
| − | p2->y = 10; // bod, na ktory ukazuje p2, bude mat y | + | p2->y = 10; // bod, na ktory ukazuje p2, bude mat y 10 |
delete p2; // uvolnenie pamate | delete p2; // uvolnenie pamate | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Verzia zo dňa a času 21:28, 30. október 2021
Obsah
Oznamy
- Tento týždeň bude okrem bežnej rozcvičky na utorňajších cvičeniach aj bonusová rozcvička počas piatkových doplnkových cvičení (za 1 bonusový bod). Termín odovzdania zvyšných úloh z týchto cvičení bude streda 18. novembra, 22:00.
- Druhú domácu úlohu treba odovzdať do piatku 13. novembra, 22:00.
- Budúci týždeň budú kvôli štátnemu sviatku iba piatkové cvičenia. V pondelok 16. novembra bude zverejnených niekoľko úloh na cvičenia č. 9 (menej, než obvykle).
- V piatok 20. novembra bude na začiatku doplnkových cvičení krátky test, body za ktorý budú riadnou súčasťou hodnotenia z cvičení č. 9. Pokyny ohľadom technickej realizácie testu budú upresnené neskôr.
Ešte k smerníkom
Opakovanie základnej práce so smerníkmi
int a = 7; // premenna typu int
int *b = NULL; // smernik na int
b = &a; // b obsahuje adresu premennej a
*b = 8; // v premennej a je teraz 8
a = (*b)+1; // v premennej a je teraz 9
Smerníky a struct
Smerník môže ukazovať aj na struct. Operátory . (prístup k prvku štruktúry) a [] (prístup k prvku poľa) majú vyššiu prioritu ako operátory * (dereferencia smerníka) a & (adresa). Preto napríklad:
- Zápis *s.cokolvek je to isté ako *(s.cokolvek) a vyjadruje dereferenciu smerníka s.cokolvek.
- Zápis (*p).cokolvek vyjadruje prvok cokolvek štruktúry získanej dereferenciou smerníka p.
- Zvyčajne je potrebnejší zápis (*p).cokolvek; existuje preň preto skratka p->cokolvek.
struct bod {
int x, y;
};
// ...
bod b;
b.x = 0;
b.y = 0;
bod *p = &b; // p ukazuje na bod b
bod *p2 = new bod; // alokovanie noveho bodu
(*p2).x = 20; // bod, na ktory ukazuje p2, bude mat x 20
p2->y = 10; // bod, na ktory ukazuje p2, bude mat y 10
delete p2; // uvolnenie pamate
Dynamické množiny: úvod
Uvažujme nasledujúce dva „motivačné” príklady:
Príklad č. 1
Na fakulte sa dvere do niektorých miestností otvárajú priložením čipovej karty k čítačke. Jeden (asi nie úplne optimálny) prístup k implementácii takéhoto systému by mohol byť nasledovný:
- Každá karta má v sebe uložené identifikačné číslo.
- Čítačka má v pamäti zoznam identifikačných čísel oprávnených osôb (študenti, niektorí vyučujúci a pod.).
- Po priložení karty z nej čítačka prečíta číslo a zisťuje, či ho má vo svojom zozname.
Ako môže byť takýto prístupový systém naprogramovaný?
Príklad č. 2
Dispečing prepravnej spoločnosti s veľkým množstvom vozidiel má systém pracujúci nasledujúcim spôsobom:
- Pre každé vozidlo si pamätá, či je momentálne k dispozícii alebo nie.
- Vozidlá neustále menia svoj stav podľa toho, ako prichádzajú do resp. odchádzajú z vozovne.
- V prípade požiadavky na vozidlo sa vyberie niektoré, ktoré je momentálne k dispozícii.
- Výnimočne je potrebné pozvať niektorého vodiča k šéfovi na koberec; v takom prípade je potrebné pre konkrétne vozidlo zistiť, či je akurát k dispozícii.
Ako môže byť takýto systém implementovaný?
Dynamické množiny
V obidvoch horeuvedených príkladoch sa vyskytuje nejaká množina A. V prvom príklade môže ísť napríklad o osoby s oprávnením vstupu do miestnosti a v druhom príklade môže ísť o vozidlá, ktoré sú momentálne k dispozícii. Tieto množiny sa v čase menia – hovoríme preto o dynamických množinách. V obidvoch príkladoch pritom potrebujeme nasledujúce funkcie:
- Funkciu contains, ktorá pre daný prvok x zistí, či patrí do množiny A.
- Funkciu add, ktorá do množiny pridá nový prvok x.
- Funkciu remove, ktorá z množiny odoberie prvok x (ňou sa ale dnes zaoberať nebudeme).
- Niekedy sa môžu zísť aj iné operácie.
Ako dnes uvidíme, dynamickú množinu môžeme implementovať množstvom rôznych spôsobov. Program s dynamickými množinami pracujúci si ale vystačí s operáciami popísanými vyššie, bez ohľadu na ich implementáciu. Hovoríme, že dynamické množiny sú abstraktný dátový typ – hovorí totiž iba o „rozhraní”, ktoré má dátová štruktúra poskytovať používateľovi, nie o jej implementácii.
Obidva uvedené príklady sa líšia „kritickosťou” jednotlivých operácií:
- Pri prístupovom systéme často potrebujeme predovšetkým operáciu contains, ktorá sa vykoná pri každom priložení karty k čítačke. Operácie add a remove sa vykonávajú zriedkavejšie, pri aktualizácii zoznamu oprávnených osôb.
- V druhom príklade naopak často voláme operácie add a remove (a prípadne ešte nejakú ďalšiu operáciu, ktorá vráti ľubovoľný prvok množiny). Operáciu contains používame zriedkavejšie (pri volaní konkrétneho vodiča na koberec).
Dynamické množiny sa používajú aj v mnohých iných situáciách a – ako uvidíme – dajú sa implementovať rozličnými spôsobmi. Tieto implementácie sú typicky zamerané na jednu alebo niekoľko z poskytovaných operácií, ktoré sú pri nej vykonávané efektívne. Pri rozličných aplikáciách je teda často potrebné zvoliť rozličné implementácie.
Implementácie dynamických množín
Pre jednoduchosť sa zaoberajme iba dynamickými množinami celých čísel. Bez ohľadu na konkrétnu implementáciu budeme takúto dynamickú množinu vždy uchovávať v štruktúre set. Navyše budeme mať implementovaných niekoľko funkcií, ktoré s dynamickými množinami pracujú. Kostra programu teda bude vyzerať pre ľubovoľnú implementáciu dynamickej množiny takto:
/* Struktura reprezentujuca dynamicku mnozinu. */
struct set {
// ...
};
/* Funkcia, ktora vytvori prazdnu dynamicku mnozinu. */
void init(set &s) {
// ...
}
/* Funkcia, ktora zisti, ci prvok x patri do mnoziny s. */
bool contains(set &s, int x) {
// ...
}
/* Funkcia, ktora prida prvok x do mnoziny s. */
void add(set &s, int x) {
// ...
}
/* Funkcia, ktora uvolni mnozinu s z pamate. */
void destroy(set &s) {
// ...
}
Bez ohľadu na implementáciu štruktúry set a uvedených funkcií už teraz môžeme napísať program, ktorý ich využíva – bude postupne z konzoly čítať príkazy a postupne tieto príkazy vykonávať.
#include <iostream>
#include <cstring>
using namespace std;
// ...
const int maxlength = 100;
int main(void) {
set A;
init(A);
while (true) {
char prikaz[maxlength];
cin.width(maxlength);
cin >> prikaz;
if (strcmp(prikaz, "contains") == 0) {
int x;
cin >> x;
cout << contains(A, x) << endl;
} else if (strcmp(prikaz, "add") == 0) {
int x;
cin >> x;
add(A, x);
} else if (strcmp(prikaz, "end") == 0) {
break;
}
}
destroy(A);
return 0;
}
Ukážeme si teraz niekoľko rôznych implementácii dynamickej množiny; začneme s dvoma, ktoré sú nám už v princípe známe.
Dynamická množina ako pole
Dynamickú množinu môžeme implementovať tak, že jej prvky budeme ukladať do poľa v ľubovoľnom poradí.
- Funkcia contains musí zakaždým prejsť celé pole lineárnym prehľadávaním (nie je teda zrovna rýchla).
- Funkcia add je naopak veľmi rýchla: stačí pridať prvok na koniec poľa.
- Je ale potrebné dávať pozor na prekročenie kapacity poľa (mohli by sme použiť dynamické pole).
#include <cassert>
// ...
const int maxN = 1000;
struct set {
int *p; // Smernik na nulty prvok pola.
int length; // Momentalna dlzka pola.
};
void init(set &s) {
s.p = new int[maxN];
s.length = 0;
}
bool contains(set &s, int x) {
for (int i = 0; i <= s.length - 1; i++) {
if (s.p[i] == x) {
return true;
}
}
return false;
}
void add(set &s, int x) {
assert(s.length < maxN);
s.p[s.length] = x;
s.length++;
}
void destroy(set &s) {
delete[] s.p;
}
Dynamická množina ako utriedené pole
Prvky množiny môžeme v poli uchovávať aj utriedené od najmenšieho po najväčšie.
- Funkcia contains potom môže použiť binárne vyhľadávanie. Je teda rýchlejšia, ako v predchádzajúcom prípade (v poli veľkosti n sa pozrie len na približne log n pozícií; napríklad pre miliónprvkové pole sa pozrieme asi na 20 prvkov poľa).
- Funkcia add ale musí vložiť prvok na správne miesto v utriedenom poli; je teda o dosť pomalšia.
#include <cassert>
// ...
const int maxN = 1000;
struct set {
int *p; // Smernik na nulty prvok pola.
int length; // Momentalna dlzka pola.
};
void init(set &s) {
s.p = new int[maxN];
s.length = 0;
}
bool contains(set &s, int x) {
int left = 0;
int right = s.length - 1;
while (left <= right) {
int index = (left + right) / 2;
if (s.p[index] == x) {
return true;
} else if (s.p[index] > x) {
right = index - 1;
} else {
left = index + 1;
}
}
return false;
}
void add(set &s, int x) {
assert(s.length < maxN);
int kam = s.length;
while (kam > 0 && s.p[kam - 1] > x) {
s.p[kam] = s.p[kam - 1];
kam--;
}
s.p[kam] = x;
s.length++;
}
void destroy(set &s) {
delete[] s.p;
}
Ďalšie možnosti implementácie dynamickej množiny (plán na dnes)
Dnes uvidíme ďalšie dva spôsoby implementácie dynamickej množiny:
- Množina ako jednosmerne spájaný zoznam:
- Ľahko pridáme nové prvky, nepotrebujeme vopred vedieť veľkosť.
- Nedá sa rýchlo binárne vyhľadávať.
- Založené na smerníkoch.
- Množina pomocou hešovania:
- Často veľmi rýchle vyhľadávanie.
- Použijeme polia aj spájané zoznamy.
Spájané zoznamy
Spájaný zoznam (angl. linked list) je postupnosť uzlov rovnakého typu usporiadaných za sebou. Každý uzol pritom pozostáva z dvoch častí:
- Samotné dáta; v našom prípade jedno číslo typu int.
- Smerník, ktorý ukazuje na nasledujúci prvok zoznamu – ten umožňuje „pohybovať sa” po zozname zľava doprava.
Posledný uzol zoznamu nemá následníka – jeho smerník na následníka teda bude mať hodnotu NULL.
Štruktúra spájaného zoznamu je znázornená na nasledujúcom obrázku:
Keďže si v každom uzle pamätáme iba smerník na následníka (t.j. uzol „napravo” od daného uzla), hovoríme tiež o jednosmerne spájanom zozname. Často sú užitočné aj obojsmerne spájané zoznamy, kde sa v každom uzle uchováva aj smerník na predchodcu; takéto zoznamy sú ale o niečo náročnejšie na „údržbu”.
Uzol jednosmerne spájaného zoznamu budeme reprezentovať pomocou struct-u node:
/* Struktura reprezentujuca uzol jednosmerne spajaneho zoznamu: */
struct node {
int data; // Hodnota ulozena v danom uzle
node *next; // Smernik na nasledujuci uzol
};
Vo vnútri definície typu node teda používame smerník na samotný typ node.
Na rozdiel od poľa, v ktorom je poradie stanovené indexmi, je poradie v spájanom zozname určované ukazovateľmi next. Ak x je uzol zoznamu, tak x.next je:
- Smerník na nasledujúci uzol zoznamu, ak takýto uzol existuje.
- NULL v opačnom prípade.
Samotný spájaný zoznam – resp. množina ním reprezentovaná – je potom iba štruktúra set obsahujúca smerník na prvý prvok zoznamu. Ak je zoznam prázdny, bude tento smerník NULL. V štruktúre set by sme v prípade potreby mohli uchovávať aj iné údaje, ako napríklad počet prvkov v zozname a podobne.
/* Struktura realizujuca mnozinu prostrednictvom spajaneho zoznamu: */
struct set {
node *first; // Smernik na prvy uzol zoznamu
};
void init(set &s) {
s.first = NULL;
}
Vkladanie na začiatok zoznamu
Nasledujúca funkcia na začiatok zoznamu vloží nový uzol s dátami x:
void add(set &s, int x) {
node *p = new node; // Vytvorime novy uzol ...
p->data = x; // ... a jeho data nastavime na x.
p->next = s.first; // Naslednikom noveho uzla p v zozname bude doposial prvy prvok zoznamu ...
s.first = p; // ... a uzol p bude odteraz novym prvym prvkom v zozname.
}
Vyhľadávanie v zozname
Funkcia vyhľadávajúca číslo x v zozname bude pracovať tak, že postupne prehľadáva zoznam od jeho začiatku, s využitím smerníkov na nasledujúce prvky:
bool contains(set &s, int x) {
node *p = s.first;
while (p != NULL) {
if (p->data == x) {
return true;
}
p = p->next;
}
return false;
}
Uvoľnenie zoznamu
Funkcia realizujúca uvoľnenie zoznamu z pamäti pracuje podobne – prechádza postupne zoznam od začiatku až po jeho koniec a uvoľňuje z pamäte jednotlivé uzly. Treba si tu však dať pozor na to, aby sme smerník na nasledujúci uzol získali ešte predtým, než z pamäti uvoľníme ten predošlý.
void destroy(set &s) {
node *p = s.first;
while (p != NULL) {
node *nxt = p->next;
delete p;
p = nxt;
}
}
Výpis zoznamu
Môžeme napísať aj nasledujúcu funkciu, ktorá po zavolaní vypíše obsah celého zoznamu:
void print(set &s) {
node *p = s.first;
while (p != NULL) {
cout << p->data << " ";
p = p->next;
}
cout << endl;
}
Hešovanie
Implementácia množiny priamym adresovaním
Úplne odlišným spôsobom realizácie dynamickej množiny je tzv. priame adresovanie (angl. direct addressing). Predpokladajme, že je univerzum všetkých hodnôt konečné – napríklad U = {0,1,...,m-1} pre nejaké prirodzené číslo m; v praxi je skôr potrebný predpoklad, že U je dostatočne „malé” na to, aby sme mohli rozumne definovať pole o m prvkoch. V takom prípade môžeme množinu A prvkov U reprezentovať ako pole booleovských hodnôt dĺžky m zodpovedajúce tzv. charakteristickej funkcii množiny A. To znamená, že i-ty prvok tohto poľa bude true práve vtedy, keď i patrí do A.
- Funkcie contains aj add sú veľmi rýchle.
- Problémom tohto prístupu je ale vysoká pamäťová zložitosť v prípade, že je číslo m veľké.
- Veľmi efektívne pre malé univerzá (napr. cifry 0,...,9, všetky znaky anglickej abecedy, všetky znaky s ASCII hodnotami od 0 po 255, a pod.).
#include <cassert>
// ...
const int m = 1000;
/* Struktura realizujuca mnozinu prostrednictvom priameho adresovania: */
struct set {
bool *p;
};
void init(set &s) {
s.p = new bool[m];
for (int i = 0; i <= m - 1; i++) {
s.p[i] = false;
}
}
bool contains(set &s, int x) {
assert(x >= 0 && x <= m - 1);
return s.p[x];
}
void add(set &s, int x) {
assert(x >= 0 && x <= m - 1);
s.p[x] = true;
}
void destroy(set &s) {
delete[] s.p;
}
Jednoduché hešovanie
Priame adresovanie sa príliš nehodí pre veľmi veľké univerzá – v takom prípade je totiž potrebné veľké množstvo pamäte.
Hešovanie je jednoduchá finta, ktorá funguje nasledovne:
- Nech U je univerzum všetkých možných prvkov množiny (kľúčov). V nasledujúcom budeme pre jednoduchosť predpokladať, že ide o nejakú podmnožinu množiny celých čísel (prípadne priamo o množinu všetkých celých čísel).
- Vytvoríme tzv. hešovaciu tabuľku hashtable – pole nejakej rozumnej veľkosti m, pozostávajúce z prvkov rovnakého typu ako prvky univerza (v našom prípade teda int).
- Naprogramujeme hešovaciu funkciu, ktorá transformuje prvky univerza U na indexy hešovacej tabuľky; pôjde teda o funkciu h: U -> {0, 1, ... , m−1}.
- Hešovacia funkcia by mala byť jednoduchá a rýchla, ale pritom by nemala „často prideľovať rovnaké indexy” (mala by kľúče do tabuľky distribuovať rovnomerne).
- Najjednoduchšia hešovacia funkcia je h(x) = x mod m pre m ≥ 3.
- Pozor: napríklad -10 % 3 je -1, takže radšej použijeme absolútnu hodnotu z x (funkcia abs z knižnice cstdlib).
int hash(int x, int m) {
return abs(x) % m;
}
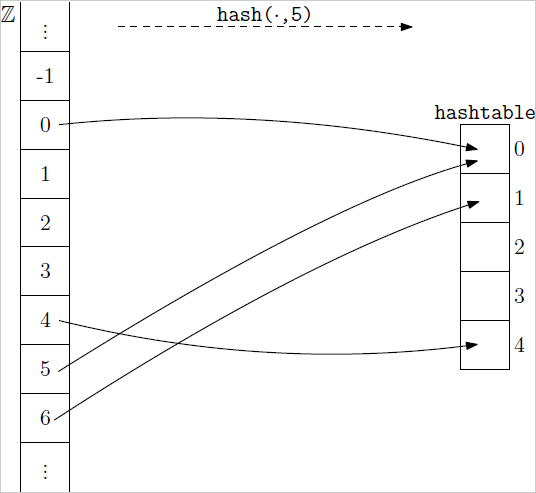
Pre m = 5 je táto funkcia znázornená na nasledujúcom obrázku.
S hešovacou tabuľkou teraz môžeme pracovať nasledovne:
Vkladanie prvku x:
- Spočítame index = hash(x, m) a prvok vložíme na pozíciu hashtable[index].
Vyhľadávanie prvku x:
- Ak je prvok s kľúčom x v tabuľke, musí byť na indexe hash(x, m).
- Skontrolujeme túto pozíciu a ak tam je niečo iné ako x, prvok x sa v tabuľke nenachádza.
Problémy:
- Na akú hodnotu inicializovať prvky poľa hashtable?
- Čo ak budeme potrebovať vložiť prvok na miesto, kde je už niečo uložené?
Kolízie
Pri vkladaní prvku sme narazili na problém, ak na už obsadané miesto chceme vložiť iný prvok. Môže sa stať, že dva prvky x a y sa zahešujú na rovnakú pozíciu h(x) = h(y). Takémuto javu hovoríme kolízia a existuje viacero spôsobov, ako sa s ním vysporiadať. Naše riešenie bude spočívať v nasledujúcej myšlienke:
- Kolidujúci prvok aj tak vložíme na vypočítané miesto v tabuľke, na ktorom už teda bude môcť byť uložený viac ako jeden prvok.
- Prvky na danej pozícii hešovacej tabuľky budeme uchovávať v spájanom zozname.
Existujú však aj iné prístupy – môžeme napríklad hľadať iné voľné miesto v tabuľke a podobne (viac budúci rok na predmete Algoritmy a dátové štruktúry).
Riešenie kolízií pomocou spájaných zoznamov
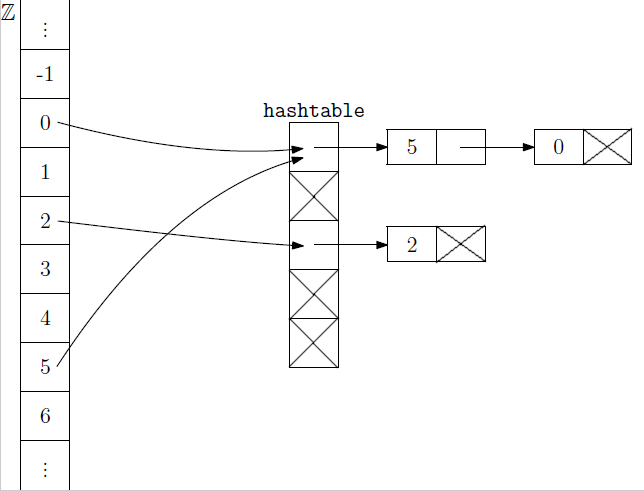
V každom políčku hešovacej tabuľky teda budeme uchovávať spájaný zoznam so všetkými prvkami množiny, ktoré hešovacia funkcia priradila na toto políčko. Táto situácia je znázornená na nasledujúcom obrázku, v ktorom šípky zodpovedajú vkladaniam prvkov (celých čísel) do množiny reprezentovanej hešovacou tabuľkou.
#include <cstdlib>
// ...
/* Hesovacia funkcia: */
int h(int x, int m) {
return abs(x) % m;
}
/* Struktura reprezentujuca jeden prvok spajaneho zoznamu: */
struct node {
int data;
node *next;
};
/* Struktura realizujuca dynamicku mnozinu pomocou hesovania: */
struct set {
node **hashtable; // Pole smernikov na zaciatky jednotlivych zoznamov
int m; // Velkost hesovacej tabulky
};
void init(set &s, int m) { // Velkost tabulky bude parametrom funkcie init
s.m = m;
s.hashtable = new node *[m];
for (int i = 0; i <= m - 1; i++) {
s.hashtable[i] = NULL;
}
}
bool contains(set &s, int x) {
int index = h(x, s.m); // Spocitame spravne policko hesovacej tabulky
node *p = s.hashtable[index]; // Smernik p ukazuje na prvy prvok spajaneho
// zoznamu na danom policku
while (p != NULL) { // Prechadzame zoznam, hladame x
if (p->data == x) {
return true;
}
p = p->next;
}
return false;
}
void add(set &s, int x) {
int index = h(x, s.m); // Spocitame spravne policko hesovacej tabulky
node *temp = new node; // Vytvorime novy uzol do spajaneho zoznamu
temp->data = x;
temp->next = s.hashtable[index]; // Vlozime uzol temp na zaciatok zoznamu.
s.hashtable[index] = temp;
}
void destroy(set &s) {
for (int i = 0; i <= s.m - 1; i++) {
node *p = s.hashtable[i]; // Uvolni zoznam s.hashtable[i]
while (p != NULL) {
node *nxt = p->next;
delete p;
p = nxt;
}
}
delete[] s.hashtable;
}
Cvičenie: Ako bude vyzerať hešovacia tabuľka pri riešení kolízií pomocou spájaných zoznamov, ak hešovacia funkcia je |x| mod 5 a vkladáme prvky 13, -2, 0, 8, 10, 17?
Zložitosť
- Rýchlosť závisí od toho, akú máme veľkosť tabuľky m, hešovaciu funkciu a koľko prvkov sa zahešuje do jedného políčka.
- V najhoršom prípade sa všetky prvky zahešujú do toho istého políčka, a teda musíme pri hľadaní prejsť všetky prvky množiny.
- Ak máme šťastie a v každom políčku máme len málo prvkov, bude aj vyhľadávanie rýchle.
- Ak je tabuľka dosť veľká a hešovacia funkcia vhodne zvolená, tento prípad je pomerne obvyklý.
- Hešovacie tabuľky sa často používajú v praxi.
- Viac budúci rok na predmete Algoritmy a dátové štruktúry.