Letný semester, prednáška č. 9

Oznamy

• Dnes po prednáške bude zverejnené zadanie štvrtej domácej úlohy, ktorú bude potrebné odovzdať do pondelka 26. apríla, 9:00 (čiže do začiatku jedenástej prednášky).
• Počas stredajších cvičení bude prebiehať štvrtý test zameraný predovšetkým na grafy a grafové algoritmy.
• V rámci stredajších cvičení tiež bude zverejnené zadanie tretej bonusovej úlohy s termínom odovzdania do stredy 28. apríla, 11:30.
• Cvičenia v stredu 21. apríla budú aj napriek dekanskému voľnu (účasť je samozrejme dobrovoľná, rovnako ako aj na ostatných cvičeniach, na ktorých sa nepíše test).
• Boli vypísané predbežné termíny skúšok:
  • Predtermín v piatok 14. mája, 11:30 (ústne skúšky po 15:30). Maximálne 12 prihlásených študentov.
  • Ďalšie termíny vo štvrtky 20. mája, 3. júna, 17. júna a 24. júna, vždy o 9:00 (ústne skúšky po 14:00). Maximálne 18 prihlásených študentov na každý z termínov.
  • Každý z termínov možno využiť ako riadny aj ako opravný; žiadne ďalšie termíny ale nebudú.
  • Prípadné námietky voči týmto termínom dajte vedieť najneskôr na prednáške 26. apríla. Po tejto prednáške bude otvorené prihlasovanie na skúšky v AIS.
  • Na každý z termínov bude potrebné prihlásiť sa cez AIS najneskôr 24 hodín vopred.

Prehľadávanie s návratom na grafoch: pokračovanie

Hľadanie najdlhšej cesty

Uvažujme problém nájdenia niektorej z najdlhších ciest z vrcholu u do vrcholu v daného orientovaného grafu (ak existuje aspoň jedna). Je dokázané, že za predpokladu platnosti určitých hypotéz z teoretickej informatiky pre túto úlohu neexistuje žiaden efektívny algoritmus. Použijeme teda prehľadávanie s návratom. To bude realizovať trieda LongestPath, ktorú získame drobnou úpravou triedy FixedLengthPaths z minulej prednášky.

• Počas prehľadávania si budeme pamätať najdlhšiu doposiaľ nájdenú cestu.
• Vždy, keď prídeme do cieľového vrcholu, porovnáme dĺžku práve nájdenej cesty s najdlhšou doposiaľ nájdenou cestou.

package graphs;

import java.util.*;

/**
 * Trieda realizujuca najdenie najdlhsej cesty medzi danou dvojicou vrcholov grafu.
 */
public class LongestPath {
    /**
     * Graf, v ktorom sa hladanie ciest realizuje.
     */
    private Graph g;

    /**
     * Pociatocny vrchol hladanych ciest.
     */
    private int from;

    /**
     * Koncovy vrchol hladanych ciest.
     */
    private int to;

    /**
     * Pomocny zoznam, v ktorom sa budu pomocou prehladavania s navratom postupne generovat jednotlive cesty.
     */
    private LinkedList<Integer> path;

    /**
     * Pomocny zoznam, v ktorom si budeme pocas generovania ciest pre kazdy vrchol pamatat, ci sa nachadza alebo
     * nenachadza v doposial vygenerovanej casti cesty.
     */
    private ArrayList<Boolean> visited;

    /**
     * Zoznam, v ktorom bude ulozena najdlhsia cesta medzi danou dvojicou vrcholov (pocas prehladavania pojde
     * o najdlhsiu doposial najdenu cestu).
     */
    private List<Integer> longestPath;

    /**
     * Konstruktor, ktory rovno aj spusti prehladavanie s navratom a do zoznamu longestPath ulozi niektoru spomedzi
     * najdlhsich ciest medzi danou dvojicou vrcholov grafu.
     * @param g      Graf, v ktorom sa hladanie ciest realizuje.
     * @param from   Pociatocny vrchol hladanych ciest.
     * @param to     Koncovy vrchol hladanych ciest.
     */
    public LongestPath(Graph g, int from, int to) {
        this.g = g;
        this.from = from;
        this.to = to;

        visited = new ArrayList<>();
        for (int i = 0; i <= g.getNumberOfVertices() - 1; i++) {
            visited.add(false);
        }
        path = new LinkedList<>();
        path.add(from);
        visited.set(from, true);
        search();
    }

    /**
     * Metoda realizujuca samotne rekurzivne prehladavanie s navratom. V pripade, ze sa vygenerovala cesta konciaca
     * vo vrchole to, porovna sa jej dlzka s dlzkou doposial najdlhsej najdenej cesty a ak je dlhsia, ulozi sa ako nova
     * doposial najdlhsia cesta. V opacnom pripade sa vyskusaju vsetky moznosti predlzenia cesty.
     */
    private void search() {
        if (path.getLast() == to) {
            if (longestPath == null || path.size() > longestPath.size()) {
                longestPath = new LinkedList<>(path);
            }
        } else {
            for (int successor : g.outgoingEdgesDestinations(path.getLast())) {
                if (!visited.get(successor)) {
                    visited.set(successor, true);
                    path.add(successor);
                    search();
                    path.removeLast();
                    visited.set(successor, false);
                }
            }
        }
    }

    /**
     * Metoda, ktora vrati najdenu najdlhsiu cestu medzi danou dvojicou vrcholov.
     * @return Nemodifikovatelny pohlad na zoznam vrcholov na najdlhsej ceste z vrcholu from do vrcholu to.
     */
    public List<Integer> getLongestPath() {
        if (longestPath != null) {
            return Collections.unmodifiableList(longestPath);
        } else {
            return null;
        }
    }
}

Použitie triedy:

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    System.out.println("Zadaj graf:");
    Graph g = readGraph(scanner, GraphType.DIRECTED_SUCCESSOR_LISTS);
    System.out.println("Zadaj pociatocny a koncovy vrchol:");
    int from = scanner.nextInt();
    int to = scanner.nextInt();

    LongestPath longestPath = new LongestPath(g, from, to); 
    List<Integer> longest = longestPath.getLongestPath();
    if (longest != null) {
        System.out.println("Najdlhsia cesta: " + longest);
    } else {
        System.out.println("Ziadna cesta neexistuje.");
    }
}

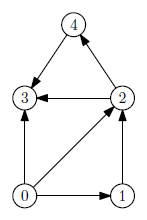
Príklad výstupu pre graf na obrázku vyššie, počiatočný vrchol 0 a koncový vrchol 3:

Najdlhsia cesta: [0, 1, 2, 4, 3]

Hľadanie najväčšej kliky v neorientovanom grafe

Uvažujme teraz neorientované grafy bez slučiek (slučky síce nebudeme zakazovať, ale v našich nasledujúcich úvahách ich budeme ignorovať; najvhodnejšia predstava teda je, že pracujeme s grafmi, ktoré žiadne slučky neobsahujú).

• Klikou (angl. clique) v neorientovanom grafe rozumieme jeho úplný podgraf, čiže podmnožinu K množiny vrcholov grafu takú, že každé dva rôzne vrcholy z K sú navzájom spojené hranou. Veľkosťou kliky rozumieme počet vrcholov kliku tvoriacich. Špeciálne každý vrchol sám o sebe tvorí kliku veľkosti jedna a ľubovoľné dva vrcholy spojené hranou tvoria kliku veľkosti dva.
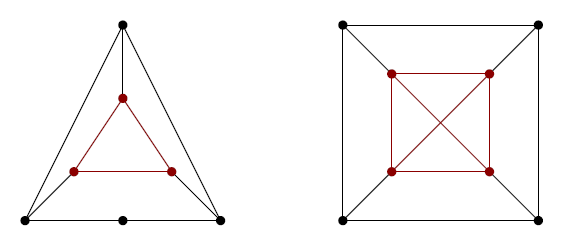
• V grafoch na nasledujúcom obrázku sú vyznačené kliky veľkosti tri a štyri.

Budeme sa teraz zaoberať problémom nájdenia najväčšej kliky (angl. maximum clique) v neorientovanom grafe.

• Ide o nájdenie kliky s najväčšou veľkosťou spomedzi všetkých klík daného grafu.
• Pozor na terminológiu: maximálna klika (angl. maximal clique) je ľubovoľná klika, ktorú nemožno pridaním ďalšieho vrcholu rozšíriť na väčšiu kliku. Nie každá maximálna klika ale musí byť aj najväčšia. My sa budeme zaoberať prakticky užitočnejším problémom hľadania najväčších klík.
• Aj pre problém najväčšej kliky je dokázané, že v prípade platnosti určitých hypotéz z teoretickej informatiky preň neexistuje žiaden efektívny algoritmus. Použijeme teda prehľadávanie s návratom – nebudeme ním však teraz konštruovať cesty, ale množiny vrcholov grafu.
• Postupne budeme generovať všetky množiny vrcholov daného grafu ako utriedené spájané zoznamy. Zakaždým sa pokúsime daný vrchol do množiny pridať a rekurzívne pokračovať na ďalší vrchol, následne sa ho pokúsime vynechať a tiež rekurzívne pokračovať na ďalší vrchol. Po vygenerovaní kompletnej množiny zistíme, či ide o kliku; ak áno, porovnáme jej veľkosť s najväčšou doposiaľ nájdenou klikou, ktorú v prípade potreby aktualizujeme.

Trieda MaximumClique realizujúca nájdenie najväčšej kliky v neorientovanom grafe:

package graphs;

import java.util.*;

/**
 * Trieda realizujuca najdenie niektorej spomedzi najvacsich klik v danom neorientovanom grafe.
 */
public class MaximumClique {
    /**
     * Neorientovany graf, v ktorom sa hladanie najvacsej kliky realizuje.
     */
    private UndirectedGraph g;

    /**
     * Zoznam vrcholov najvacsej kliky neorientovaneho grafu g, resp. pocas prehladavania s navratom doposial najvacsej
     * najdenej kliky.
     */
    private LinkedList<Integer> maximumClique;

    /**
     * Zoznam, v ktorom sa pocas prehladavania s navratom budu postupne generovat vsetky (utriedene) mnoziny vrcholov
     * grafu g.
     */
    private LinkedList<Integer> currentVertices;

    /**
     * Konstruktor, ktory pomocou prehladavania s navratom najde najvacsiu kliku v danom neorientovanom grafe.
     * @param g Neorientovany graf, v ktorom sa hladanie najvacsej kliky realizuje.
     */
    public MaximumClique(UndirectedGraph g) {
        this.g = g;
        maximumClique = new LinkedList<>();
        currentVertices = new LinkedList<>();
        search(0);
    }

    /**
     * Rekurzivna metoda realizujuca samotne prehladavnie s navratom a v zozname currentVertices postupne generujuca
     * vsetky (utriedene) mnoziny vrcholov grafu g. Predpoklada sa, ze pred volanim metody reprezentuje zoznam
     * currentVertices nejaku utriedenu podmnozinu mnoziny vrcholov &lbrace;0,...,vertex-1&rbrace;. Metoda search
     * sa najprv pokusi pridat do zoznamu vrchol vertex a vygenerovat vsetky mnoziny obsahujuce vrcholy z tohto zoznamu;
     * nasledne sa pokusi vrchol vertex do zoznamu nepridat a taktiez vygeneruje vsetky taketo mnoziny.
     * Volanie metody pre vertex == 0 teda postupne vygeneruje vsetky utriedene mnoziny vrcholov grafu g. V pripade, ze
     * vertex == g.getNumberOfVertices(), povazuje sa mnozina vrcholov za vygenerovanu a zisti sa, ci ide o najvacsiu
     * doposial najdenu kliku v grafe g.
     * @param vertex Vrchol neorientovaneho grafu g alebo hodnota g.getNumberOfVertices().
     */
    private void search(int vertex) {
        if (vertex == g.getNumberOfVertices()) {
            if (isClique(currentVertices) && currentVertices.size() > maximumClique.size()) {
                maximumClique = new LinkedList<>(currentVertices);
            }
        } else {
            currentVertices.addLast(vertex);
            search(vertex + 1);
            currentVertices.removeLast();
            search(vertex + 1);
        }
    }

    /**
     * Pomocna metoda, ktora zisti, ci dane zoskupenie vrcholov zodpoveda klike v neorientovanom grafe g.
     * @param vertices Zoskupenie vrcholov grafu g.
     * @return         Metoda vrati true prave vtedy, ked vrcholy zoskupenia vertices tvoria kliku v grafe g.
     */
    private boolean isClique(Collection<Integer> vertices) {
        for (int u : vertices) {
            for (int v : vertices) {
                if (u != v && !g.existsEdge(u, v)) {
                    return false;
                }
            }
        }
        return true;
    }

    /**
     * Metoda, ktora vrati najdenu najvacsiu kliku v neorientovanom grafe g ako utriedeny zoznam jej vrcholov.
     * @return Nemodifikovatelny zoznam obsahujuci vo vzostupnom poradi vsetky vrcholy najdenej najvacsej kliky.
     */
    public List<Integer> getMaximumClique() {
        return Collections.unmodifiableList(maximumClique);
    }
}

Použitie triedy MaximumClique:

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    System.out.println("Zadaj graf:");
    UndirectedGraph g = (UndirectedGraph) readGraph(scanner, GraphType.UNDIRECTED_ADJACENCY_LISTS);
  
    MaximumClique maximumClique = new MaximumClique(g);
    System.out.println("Najvacsia klika v zadanom grafe: " + maximumClique.getMaximumClique());
}

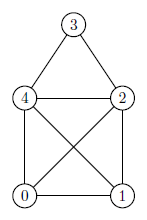
Uvažujme napríklad graf na nasledujúcom obrázku.

Vyššie uvedený program preň vypíše nasledujúci výstup:

Najvacsia klika v zadanom grafe: [0, 1, 2, 4]

Mierne zrýchlenie hľadania najväčšej kliky

Pri hľadaní najväčšej kliky v neorientovanom grafe sme zakaždým prešli cez všetkých 2ⁿ podmnožín n-prvkovej množiny vrcholov grafu. Často je ale možné už behom prehľadávania rozoznať, že rozpracovanú množinu vrcholov nebude možné rozšíriť na najväčšiu kliku. Zapracujeme teda do prehľadávania s návratom v triede MaximumClique dve vylepšenia, ktoré síce nijak nezmenia časovú zložitosť algoritmu v najhoršom prípade, ale pre veľké množstvo grafov jeho vykonávanie podstatne urýchlia:

• Vrchol budeme pridávať do rozpracovanej množiny iba v prípade, že je spojený hranou so všetkými vrcholmi v tejto množine – v opačnom prípade už totiž z tejto množiny, ani po prípadnom pridaní ďalších vrcholov, kliku nikdy nevytvoríme. V takom prípade bude po vygenerovaní kompletnej množiny garantované, že ide o kliku a kontrolu metódou isClique môžeme vypustiť.
• Vrchol tiež budeme pridávať iba v prípade, že je počet jeho susedov – ktorý pre neorientované grafy bez slučiek možno nazvať aj stupňom vrcholu – väčší alebo rovný počtu vrcholov v doposiaľ najväčšej objavenej klike. Ak má totiž najväčšia doposiaľ objavená klika veľkosť k, má pridanie vrcholu do rozpracovanej množiny zmysel iba v prípade, že bude môcť byť súčasťou kliky veľkosti aspoň k+1; každý vrchol, ktorý je súčasťou takejto kliky, má evidentne aspoň k susedov.

Upravená trieda MaximumClique:

package graphs;

import java.util.*;

public class MaximumClique {
    private UndirectedGraph g;
    private LinkedList<Integer> maximumClique;
    private LinkedList<Integer> currentVertices;

    public MaximumClique(UndirectedGraph g) {
        this.g = g;
        maximumClique = new LinkedList<>();
        currentVertices = new LinkedList<>();
        search(0);
    }

    private void search(int vertex) {
        if (vertex == g.getNumberOfVertices()) {
            if (currentVertices.size() > maximumClique.size()) {
                maximumClique = new LinkedList<>(currentVertices);
            }
        } else {
            if (hasEdgeToEach(vertex, currentVertices) && neighbourCount(vertex) >= maximumClique.size()) {
                currentVertices.addLast(vertex);
                search(vertex + 1);
                currentVertices.removeLast();
            }
            search(vertex + 1);
        }
    }

    private boolean hasEdgeToEach(int vertex, Collection<Integer> vertices) {
        for (int v : vertices) {
            if (!g.existsEdge(vertex, v)) {
                return false;
            }
        }
        return true;
    }

    private int neighbourCount(int vertex) {
        int result = 0;
        for (int v : g.outgoingEdgesDestinations(vertex)) {
            result++;
        }
        return result;
    }

    public List<Integer> getMaximumClique() {
        return Collections.unmodifiableList(maximumClique);
    }
}

Cvičenia:

• Opíšte beh uvedeného programu na grafe obsahujúcom niekoľko vrcholov a žiadnu hranu.
• Urýchlite uvedený algoritmus vhodnou implementáciou metódy neighbourCount už v triedach pre grafy (keďže bude potrebná implementácia aj pre orientované grafy, bude asi vhodnejšie premenovať metódu na successorCount a implementovať ju tak, aby pre každý vrchol vrátila počet jeho následníkov v orientovanom grafe).

Orientované acyklické grafy a topologické usporiadanie

Budeme teraz pracovať s orientovanými acyklickými grafmi – čiže orientovanými grafmi neobsahujúcimi žiaden cyklus. Takéto grafy sa zídu pri rôznych praktických úlohách, kde môžu reprezentovať napríklad časové závislosti – alebo prerekvizity – medzi vykonávanými činnosťami (celý proces je očividne vykonateľný práve vtedy, keď je tento orientovaný graf acyklický).

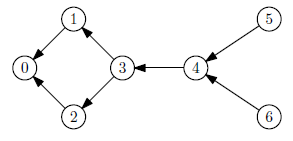
Príklad orientovaného acyklického grafu:

Pod topologickým usporiadaním orientovaného acyklického grafu o vrcholoch 0,1,...,n-1 budeme rozumieť permutáciu π: {0,1,...,n-1} → {0,1,...,n-1} takú, že pre všetky hrany (u,v) grafu platí π(u) ≤ π(v). V princípe teda ide o úplné usporiadanie na množine vrcholov grafu (vrchol v vždy ide ako π(v)-ty v poradí) také, že všetky hrany v grafe idú „v smere tohto usporiadania”. Topologické usporiadanie teda napríklad môže určovať poradie, v ktorom možno vykonať jednotlivé činnosti tak, aby boli splnené všetky ich prerekvizity. Väčšinou budeme pod topologickým usporiadaním chápať priamo postupnosť vrcholov v poradí určenom príslušnou permutáciou, t. j. π^-1(0), π^-1(1), ..., π^-1(n - 1). Pod topologickým triedením budeme rozumieť proces hľadania topologického usporiadania.

Jeden orientovaný acyklický graf môže mať aj viacero topologických usporiadaní. Napríklad graf na obrázku vyššie má presne štyri topologické usporiadania:

[5, 6, 4, 3, 1, 2, 0]
[6, 5, 4, 3, 1, 2, 0]
[5, 6, 4, 3, 2, 1, 0]
[6, 5, 4, 3, 2, 1, 0]

Poznámka: matematicky o niečo výstižnejšia ekvivalentná definícia topologického usporiadania využíva fakt, že orientované acyklické grafy sú práve tie orientované grafy, ktorých reflexívno-tranzitívny uzáver možno chápať ako čiastočné usporiadanie na množine vrcholov (neexistencia cyklu zodpovedá antisymetrii). V tomto zmysle teda každý orientovaný acyklický graf jednoznačne určuje čiastočné usporiadanie ⪯ na množine vrcholov grafu. Topologické usporiadanie je potom ľubovoľné úplné usporiadanie ≤ na tej istej množine vrcholov také, že ⪯ ⊆ ≤.

Veta: Každý orientovaný acyklický graf má aspoň jedno topologické usporiadanie.

Dôkaz. Indukciou vzhľadom na počet vrcholov. Graf o jednom vrchole v má evidentne topologické usporiadanie v. Predpokladajme teraz, že tvrdenie platí pre všetky grafy veľkosti n a uvažujme orientovaný acyklický graf veľkosti n+1. Ten musí obsahovať najmenej jeden vrchol, z ktorého nevychádza žiadna hrana – v opačnom prípade by totiž každý sled bolo možné predĺžiť na dlhší, pričom sled dĺžky n+1 nutne musí obsahovať cyklus. Nech má túto vlastnosť vrchol u. Podľa indukčného predpokladu potom existuje topologické usporiadanie grafu, ktorý z uvažovaného grafu získame odstránením vrcholu u a všetkých do neho vedúcich hrán (ten má totiž n vrcholov). Ak je týmto usporiadaním v₁,...,v_n, je v₁,...,v_n,u topologickým usporiadaním uvažovaného grafu. □

Naopak je zrejmé, že orientovaný graf obsahujúci cyklus nemôže mať žiadne topologické usporiadanie (napríklad žiaden vrchol cyklu nemôže byť spomedzi týchto vrcholov v usporiadaní prvý).

Topologické triedenie grafu

Napíšeme teraz statickú metódu topologicalSort, ktorá realizuje topologické triedenie daného orientovaného acyklického grafu.

• Vstupom metódy je orientovaný graf.
• V prípade, že je tento graf acyklický, vráti metóda na výstupe zoznam vrcholov zodpovedajúci nejakému jeho topologickému usporiadaniu.
• V opačnom prípade metóda vráti na výstupe referenciu null.

Samotný algoritmus si bude v zozname edgesFromUnprocessedVertices pre každý vrchol pamätať počet vrcholov, z ktorých do daného vrcholu vedie hrana a ktoré ešte neboli pridané do topologického usporiadania. Ak je tento počet pre nejaký vrchol nulový, možno ho pridať ako ďalší vrchol do topologického usporiadania. Vrcholy s touto vlastnosťou sa budú udržiavať v rade ready (rovnako dobre ako rad by sme mohli použiť aj inú dátovú štruktúru).

public static List<Integer> topologicalSort(Graph g) {
    /* Inicializacia: */
    int n = g.getNumberOfVertices();
    List<Integer> edgesFromUnprocessedVertices = new ArrayList<>();
    for (int v = 0; v <= n - 1; v++) {
        edgesFromUnprocessedVertices.add(0);
    }
    for (int v = 0; v <= n - 1; v++) {
        for (int successor : g.outgoingEdgesDestinations(v)) {
            edgesFromUnprocessedVertices.set(successor, edgesFromUnprocessedVertices.get(successor) + 1);
        }
    }
    Queue<Integer> ready = new LinkedList<>();
    for (int v = 0; v <= n - 1; v++) {
        if (edgesFromUnprocessedVertices.get(v) == 0) {
            ready.add(v);
        }
    }
    List<Integer> result = new LinkedList<>();
 
    /* Samotne topologicke triedenie: */
    while (!ready.isEmpty()) {
        int vertex = ready.remove();
        result.add(vertex);
        for (int successor : g.outgoingEdgesDestinations(vertex)) {
            edgesFromUnprocessedVertices.set(successor, edgesFromUnprocessedVertices.get(successor) - 1);
            if (edgesFromUnprocessedVertices.get(successor) == 0) {
                ready.add(successor);
            }
        }
    }

    if (result.size() == n) {
        return result;
    } else {
        return null;
    }
}

Topologické triedenie na báze prehľadávania do hĺbky

Ukážme si ešte alternatívnu metódu topologického triedenia grafu, založenú na nasledujúcej úprave prehľadávania do hĺbky:

• Okrem zoznamu visited si budeme udržiavať aj zoznam finished, v ktorom si pre každý vrchol grafu budeme pamätať, či prehľadávanie v ňom započaté už skončilo.
• Pri objavení vrcholu teda nastavíme na true príslušnú položku zoznamu visited a po vykonaní všetkých rekurzívnych volaní metódy search pre susedov daného vrcholu nastavíme na true aj príslušnú položku zoznamu finished.

V každom momente vykonávania takto upraveného prehľadávania do hĺbky teda existujú tri množiny vrcholov:

• Už spracované vrcholy, pre ktoré sú rovné true príslušné položky v zozname visited aj v zozname finished.
• „Rozrobené” vrcholy, pre ktoré je príslušná položka v zozname visited rovná true, ale príslušná položka v zozname finished je rovná false.
• Ešte nenavštívené vrcholy, pre ktoré sú príslušné položky v zozname visited aj v zozname finished rovné false.

Ľahko pritom vidieť, že graf obsahuje cyklus práve vtedy, keď počas prehľadávania grafu do hĺbky z niektorého vrcholu objavíme „rozrobený” vrchol.

Pre účely topologického triedenia je kľúčová nasledujúca vlastnosť:

• Kedykoľvek v orientovanom acyklickom grafe skončí prehľadávanie do hĺbky z niektorého vrcholu v skôr, než prehľadávanie do hĺbky z vrcholu u, nemôže v tomto grafe viesť žiadna cesta z vrcholu v do vrcholu u. Ak totiž takáto cesta existuje, sú iba nasledujúce možnosti:
  • Vrchol u je na začiatku prehľadávania z vrcholu v nenavštívený. V takom prípade ho musíme, ako ešte nenavštívený vrchol dosiahnuteľný z v, navštíviť v rámci prehľadávania z v. Potom však prehľadávanie z vrcholu u skončí skôr, než prehľadávanie z vrcholu v: spor s predpokladom.
  • Vrchol u je na začiatku prehľadávania z vrcholu v „rozrobený”. To znamená, že sme vrchol v objavili v rámci prehľadávania spusteného vo vrchole u a z u do v teda vedie orientovaná cesta. Spojením tejto cesty s orientovanou cestou z v do u potom dostávame cyklus: spor s predpokladom acyklickosti.
  • Vrchol u je na začiatku prehľadávania z vrcholu v už spracovaný: spor s predpokladom, že prehľadávanie z v skončí skôr, než prehľadávanie z u.
• To znamená, že kedykoľvek prehľadávanie z nejakého vrcholu ukončíme, môžeme ho pridať na začiatok topologicky usporiadanej postupnosti vrcholov grafu.

package graphs;

import java.util.*;

/**
 * Trieda realizujuca topologicke triedenie pomocou prehladavania do hlbky.
 */
public class TopologicalSort {
    /**
     * Graf, v ktorom sa topologicke triedenie realizuje.
     */
    private Graph g;

    /**
     * Vysledne topologicke usporiadanie alebo jeho cast.
     */
    private LinkedList<Integer> topologicalOrder;

    /**
     * Pole, v ktorom si pre kazdy vrchol pamatame, ci bol prehladavanim do hlbky navstiveny.
     */
    private ArrayList<Boolean> visited;

    /**
     * Pole, v ktorom si pre kazdy vrchol pamatame, ci bolo prehladavanie z neho ukoncene.
     */
    private ArrayList<Boolean> finished;

    /**
     * Po vykonani konstruktora bude true prave vtedy, ked je graf g acyklicky.
     */
    private boolean acyclic = true;

    /**
     * Konstruktor, ktory pomocou prehladavania do hlbky najde niektore z topologickych usporiadani daneho grafu, resp.
     * v pripade grafov obsahujuci cyklus nastavi premennu acyclic na false.
     * @param g Graf, v ktorom sa topologicke triedenie realizuje.
     */
    public TopologicalSort(Graph g) {
        this.g = g;
        int n = g.getNumberOfVertices();
        topologicalOrder = new LinkedList<>();
        visited = new ArrayList<>();
        finished = new ArrayList<>();

        for (int v = 0; v <= n - 1; v++) {
            visited.add(false);
            finished.add(false);
        }

        for (int v = 0; v <= n - 1; v++) {
            if (!visited.get(v)) {
                search(v);
            }
        }
    }

    /**
     * Metoda realizujuca samotne prehladavanie do hlbky z vrcholu vertex.
     * @param vertex Vrchol, z ktoreho sa prehladavanie do hlbky spusta.
     */
    private void search(int vertex) {
        visited.set(vertex, true);
        for (int successor : g.outgoingEdgesDestinations(vertex)) {
            if (visited.get(successor) && !finished.get(successor)) {
                acyclic = false;
            }
            if (!visited.get(successor)) {
                search(successor);
            }
        }
        finished.set(vertex, true);
        topologicalOrder.addFirst(vertex);
    }

    /**
     * Metoda, ktora vrati najdene topologicke usporiadanie grafu.
     * @return Topologicke usporiadanie grafu ako nemodifikovatelny zoznam vrcholov. V pripade, ze graf nie je
     *         acyklicky, vrati sa na vystupe referencia null.
     */
    public List<Integer> getTopologicalOrder() {
        if (acyclic) {
            return Collections.unmodifiableList(topologicalOrder);
        } else {
            return null;
        }
    }

    /**
     * Metoda, ktora vrati informaciu o tom, ci je graf g acyklicky.
     * @return Vrati booleovsku hodnotu true prave vtedy, ked je graf g acyklicky.
     */
    public boolean isAcyclic() {
        return acyclic;
    }
}

Úlohy na ohodnotených grafoch

Po zvyšok tejto prednášky sa budeme zaoberať ohodnotenými grafmi nad množinou reálnych čísel. Ide o rozšírenie grafov, pri ktorom má každá hrana priradené nejaké reálne ohodnotenie. Pre ohodnotené grafy napíšeme rozhranie WeightedGraph a triedu WeightedSuccessorListsGraph reprezentujúcu orientované ohodnotené grafy pomocou zoznamov následníkov (podobným spôsobom ako na minulých prednáškach by sme však mohli napísať aj triedy ako WeightedAdjacencyMatrixGraph, WeightedAdjacencyListsUndirectedGraph a podobne).

Rozhranie pre ohodnotené grafy (WeightedGraph)

package graphs;

/**
 * Trieda reprezentujuca ohodnotenu hranu.
 */
public class WeightedEdge extends Edge {
    private double weight;

    public WeightedEdge(int from, int to, double weight) {
        super(from, to);
        this.weight = weight;
    }

    public double getWeight() {
        return weight;
    }

    @Override
    public boolean equals(Object o) {
        return super.equals(o) && ((WeightedEdge) o).weight == weight;
    }

    @Override
    public int hashCode() {
        return Double.valueOf(weight).hashCode() + 31 * super.hashCode();
    }
}

package graphs;

import java.util.*;

public class WeightedEdges {

    public static Collection<Edge> unweightedEdgeCollection(Collection<WeightedEdge> weightedEdges) {
        ArrayList<Edge> result = new ArrayList<>();
        for (WeightedEdge we : weightedEdges) {
            result.add(new Edge(we.getFrom(), we.getTo()));
        }
        return result;
    }
}

package graphs;

/**
 * Rozhranie pre ohodnoteny (vo vseobecnosti orientovany) graf.
 */
public interface WeightedGraph extends Graph {
    /**
     * Metoda, ktora vrati vsetky ohodnotene hrany vychadzajuce z vrcholu vertex reprezentovaneho ohodnoteneho grafu.
     * @param vertex Vrchol ohodnoteneho grafu.
     * @return       Ohodnotene hrany vychadzajuce z vrcholu vertex ako instancia typu Iterable<WeightedEdge&rt;.
     */
    Iterable<WeightedEdge> outgoingWeightedEdges(int vertex);
}

Orientované ohodnotené grafy pomocou zoznamov následníkov (WeightedSuccessorListsGraph)

Triedu WeightedSuccessorListsGraph reprezentujúcu ohodnotený orientovaný graf pomocou zoznamov následníkov napíšeme jednoduchým rozšírením príslušnej triedy SuccessorListsGraph pre neohodnotené grafy. Navyše si len pre každý vrchol budeme pamätať zoznam z neho vychádzajúcich hrán.

package graphs;

import java.util.*;

/**
 * Trieda reprezentujuca ohodnoteny orientovany graf pomocou zoznamov naslednikov.
 */
public class WeightedSuccessorListsGraph extends SuccessorListsGraph implements WeightedGraph {
    /**
     * Zoznamy ohodnotenych hran vychadzajucich z jednotlivych vrcholov.
     */
    private ArrayList<ArrayList<WeightedEdge>> outgoingWeightedEdges;

    /**
     * Konstruktor, ktory vytvori ohodnoteny graf s danym poctom vrcholov a obsahujuci hrany podla daneho zoskupenia.
     * @param vertexCount   Pocet vrcholov vytvaraneho grafu.
     * @param weightedEdges Ohodnotene hrany vytvaraneho grafu. Zoskupenie nesmie obsahovat viacero hran s roznymi
     *                      ohodnoteniami veduce medzi rovnakymi dvojicami vrcholov.
     */
    public WeightedSuccessorListsGraph(int vertexCount, Collection<WeightedEdge> weightedEdges) {
        super(vertexCount, WeightedEdges.unweightedEdgeCollection(weightedEdges));
        outgoingWeightedEdges = new ArrayList<>();
        for (int i = 0; i <= vertexCount - 1; i++) {
            outgoingWeightedEdges.add(new ArrayList<>());
        }
        Set<WeightedEdge> processedWeightedEdges = new HashSet<>();
        Set<Edge> processedUnweightedEdges = new HashSet<>();
        for (WeightedEdge we : weightedEdges) {
            if (!processedUnweightedEdges.contains(new Edge(we.getFrom(), we.getTo()))) {
                outgoingWeightedEdges.get(we.getFrom()).add(we);
                processedWeightedEdges.add(we);
                processedUnweightedEdges.add(new Edge(we.getFrom(), we.getTo()));
            } else if (!processedWeightedEdges.contains(we)) {
                throw new IllegalArgumentException("Multiple edges with different weights connecting the same" +
                        " pair of vertices.");
            }
        }
    }

    @Override
    public Iterable<WeightedEdge> outgoingWeightedEdges(int vertex) {
        return Collections.unmodifiableList(outgoingWeightedEdges.get(vertex));
    }
}

Hľadanie najdlhšej cesty v ohodnotenom grafe

Pod dĺžkou cesty v ohodnotenom grafe teraz budeme rozumieť súčet ohodnotení jej hrán. Podobne ako pre neohodnotené grafy potom možno najdlhšiu cestu medzi dvoma vrcholmi nájsť pomocou prehľadávania s návratom.

package graphs;

import java.util.*;

/**
 * Trieda realizujuca najdenie najdlhsej ohodnotenej cesty v ohodnotenom grafe z daneho pociatocneho do daneho koncoveho
 * vrcholu.
 */
public class LongestWeightedPath {
    /**
     * Ohodnoteny graf, v ktorom sa hladanie najdlhsej cesty realizuje.
     */
    private WeightedGraph g;

    /**
     * Pociatocny vrchol hladanej najdlhsej cesty.
     */
    private int from;

    /**
     * Koncovy vrchol hladanej najdlhsej cesty.
     */
    private int to;

    /**
     * Dlzka vygenerovanej casti cesty.
     */
    private double length;

    /**
     * Dlzka doposial najdlhsej najdenej cesty z vrcholu from do vrcholu to.
     */
    private double maxLength;

    /**
     * Zoznam, v ktorom sa postupne budu cesty generovat.
     */
    private LinkedList<Integer> path;

    /**
     * Doposial najdlhsia najdena cesta z vrcholu from do vrcholu to.
     */
    private LinkedList<Integer> longestWeightedPath;

    /**
     * Informacie o navstiveni jednotlivych vrcholov pri prehladavani s navratom.
     */
    private ArrayList<Boolean> visited;

    /**
     * Konstruktor, ktory najde najdlhsiu ohodnotenu cestu medzi danymi dvoma vrcholmi daneho ohodnoteneho grafu.
     * @param g    Graf, v ktorom sa hladanie ciest realizuje.
     * @param from Pociatocny vrchol.
     * @param to   Koncovy vrchol.
     */
    public LongestWeightedPath(WeightedGraph g, int from, int to) {
        this.g = g;
        this.from = from;
        this.to = to;

        visited = new ArrayList<>();
        for (int i = 0; i <= g.getNumberOfVertices() - 1; i++) {
            visited.add(false);
        }

        maxLength = Integer.MIN_VALUE;
        length = 0;
        path = new LinkedList<>();
        path.add(from);
        visited.set(from, true);
        search();
    }

    /**
     * Metoda realizujuca samotne prehladavanie s navratom.
     */
    private void search() {
        if (path.getLast() == to) {
            if (length > maxLength) {
                maxLength = length;
                longestWeightedPath = new LinkedList<>(path);
            }
        } else {
            for (WeightedEdge we : g.outgoingWeightedEdges(path.getLast())) {
                int successor = we.getTo();
                double weight = we.getWeight();
                if (!visited.get(successor)) {
                    visited.set(successor, true);
                    path.addLast(successor);
                    length += weight;
                    search();
                    length -= weight;
                    path.removeLast();
                    visited.set(successor, false);
                }
            }
        }
    }

    /**
     * Metoda, ktora vrati najdenu najdlhsiu ohodnotenu cestu.
     * @return Jedna z najdlhsich ohodnotenych ciest z from do to ako nemodifikovatelny zoznam. V pripade, ze ziadna
     *         cesta medzi vrcholmi from a to neexistuje, vrati sa na vystupe referencia null.
     */
    public List<Integer> getLongestWeightedPath() {
        if (longestWeightedPath != null) {
            return Collections.unmodifiableList(longestWeightedPath);
        } else {
            return null;
        }
    }
}

Použitie tejto triedy:

public class Trieda {

    public static WeightedGraph readWeightedGraph(Scanner s) {
        int n = s.nextInt();
        int m = s.nextInt();
        ArrayList<WeightedEdge> weightedEdges = new ArrayList<>();
        for (int i = 1; i <= m; i++) {
            int u = s.nextInt();
            int v = s.nextInt();
            double weight = s.nextDouble();
            weightedEdges.add(new WeightedEdge(u, v, weight));
        }
        return new WeightedSuccessorListsGraph(n, weightedEdges);
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.println("Zadaj ohodnoteny graf:");
        WeightedGraph g = readWeightedGraph(scanner);
        System.out.println("Zadaj pociatocny a koncovy vrchol:");
        int from = scanner.nextInt();
        int to = scanner.nextInt();

        LongestWeightedPath longestWeightedPath = new LongestWeightedPath(g, from, to);
        List<Integer> longest = longestWeightedPath.getLongestWeightedPath();
        if (longest != null) {
            System.out.println("Najdlhsia cesta: " + longest);
        } else {
            System.out.println("Ziadna cesta neexistuje.");
        }
    }
}

Najkratšie cesty v ohodnotených grafoch

Poznamenajme, že najkratšia cesta v ohodnotenom grafe sa vo všeobecnosti nedá nájsť prehľadávaním do šírky:

• Ak sú ohodnoteniami prirodzené čísla, možno hranu ohodnotenú číslom k reprezentovať postupnosťou k nadväzujúcich hrán a aplikovať algoritmus pre neohodnotené grafy. Pokiaľ však nemáme zaručené, že sú ohodnotenia hrán malé, ide o extrémne neefektívny prístup.
• Najkratšiu cestu samozrejme možno hľadať aj prehľadávaním s návratom, podobne ako cestu najdlhšiu. To je však tiež veľmi neefektívne (pri najdlhšej ceste to až tak nevadí, keďže efektívny algoritmus s najväčšou pravdepodobnosťou neexistuje).
• „Rozumné” algoritmy na hľadanie najkratšej cesty v ohodnotenom grafe sa preberajú napríklad v rámci predmetu Tvorba efektívnych algoritmov. Tieto predpokladajú neexistenciu cyklov zápornej dĺžky (čo je v praxi zmysluplný predpoklad), a teda v skutočnosti hľadajú najkratšie sledy. V prípade možnej existencie cyklov zápornej dĺžky efektívny algoritmus, rovnako ako pri najdlhšej ceste, s najväčšou pravdepodobnosťou neexistuje.

Zhrnutie prebratých grafových algoritmov

Väčšina grafových algoritmov (s výnimkou prvého algoritmu pre topologické triedenie), s ktorými sme sa v rámci posledných niekoľkých prednášok stretli, bola založená na niektorej z nasledujúcich troch techník:

• Prehľadávanie do hĺbky (angl. depth-first search).
• Prehľadávanie do šírky (angl. breadth-first search).
• Prehľadávanie s návratom (angl. backtracking).

Prvé dve z týchto techník sú pomerne efektívne – je pri nich zaručené, že žiadna hrana nebude pri „objavovaní” nových vrcholov použitá viac, než raz. To znamená, že časová zložitosť týchto algoritmov je rádovo O(n + m), kde n je počet vrcholov a m je počet hrán grafu.

Prehľadávanie s návratom je naopak extrémne neefektívna technika prehľadávajúca všetky možnosti, ktorých vo všeobecnosti môže byť veľmi veľa. Dá sa teda aplikovať iba na malé vstupy, a to najmä vtedy, keď efektívny algoritmus pre danú úlohu neexistuje alebo nie je známy.