Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
Streaming model: Rozdiel medzi revíziami
Z VPDS
(→Count-Min sketch) |
(→Count-Min sketch) |
||
| Riadok 28: | Riadok 28: | ||
** for a fixed row i: <math>E[A[i,h_i(j)] = F[j]+ \sum_{k\ne j} F[k]/w</math>, because every other element k has probability 1/w to hash to column h_i(j) and thus it cntributes F[k]/w to | ** for a fixed row i: <math>E[A[i,h_i(j)] = F[j]+ \sum_{k\ne j} F[k]/w</math>, because every other element k has probability 1/w to hash to column h_i(j) and thus it cntributes F[k]/w to | ||
** <math>E[A[i,h_i(j)]\le F[j]+M\epsilon/e</math> | ** <math>E[A[i,h_i(j)]\le F[j]+M\epsilon/e</math> | ||
| − | ** By Markov inequality <math>\Pr(A[i,h_i(j)]-F[j]\ | + | ** By Markov inequality <math>\Pr(A[i,h_i(j)]-F[j]\ge M\epsilon) \le 1/e</math> |
** Probability that this happens in every row i is at most <math>e^{-d} \le \delta</math> | ** Probability that this happens in every row i is at most <math>e^{-d} \le \delta</math> | ||
* Memory does not depend on n | * Memory does not depend on n | ||
* Note: if we insert million elements and then delete all but 4 of them, in the final structure we are very likely to be able to identify the 4 remaining ones as M is only 4 | * Note: if we insert million elements and then delete all but 4 of them, in the final structure we are very likely to be able to identify the 4 remaining ones as M is only 4 | ||
Verzia zo dňa a času 18:31, 17. apríl 2017
Definition
- Input: stream of n elements
- Goal: do one pass through the stream (or only a few passes), use a small memory (e.g. O(1) or O(log n)) and answer a specific query about the stream
- Good for processing very fast streams, such as IP packets passing a router or measurements of a very low-powered device
- Not enough memory to store the whole stream, each item should be processed fast
- Strict turnstile model:
- underlying set {0,...,n-1}
- virtual vector F of length n initialized to zeroes
- stream consists of operations (j,x) meaning F[j]+=x
- At every point we have F[j]>=0 for each j
- Cash register model: all values x are positive
- Example: if all values x are +1, we are simply counting frequencies of elements from {0,...,n-1} on input
Count-Min sketch
- Strict turnstile model
- CM sketch with parameters epsilon and delta
- Array of counters A of depth
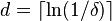 and width
and width 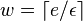
- Each row i of A has a hash function h_i from {0,...,n-1} to {0,...,w-1} (assume totally random, but a weaker assumption of pairwise independence sufficient for analysis)
- Update (j,x) does A[i,h_i(j)]+=x for all hash function i=0,...,n-1
- Query F[j]=? returns min_i A[i,h_i(j)]
- Let F be the correct answer, F' the answer returned
- Clearly F'>=F, because each A[i,k] may have contributions from other elements as well
- With probability at least 1-delta we have
![F'[j]\leq F[j]+\epsilon \sum _{i}F[i]](/vyuka/vpds/images/math/3/4/d/34dad0560ecc4efeb4be516b2898b0e4.png)
- Proof:
- Let
![M=\sum _{k}F[k]](/vyuka/vpds/images/math/0/8/0/080a114851fae348eafebcb7d3ecc93e.png)
- for a fixed row i:
![E[A[i,h_{i}(j)]=F[j]+\sum _{{k\neq j}}F[k]/w](/vyuka/vpds/images/math/c/d/f/cdfe94be7077d0d054d0194d8162c5fb.png) , because every other element k has probability 1/w to hash to column h_i(j) and thus it cntributes F[k]/w to
, because every other element k has probability 1/w to hash to column h_i(j) and thus it cntributes F[k]/w to
-
![E[A[i,h_{i}(j)]\leq F[j]+M\epsilon /e](/vyuka/vpds/images/math/e/8/9/e893e63da255a8c878db27a265864d42.png)
- By Markov inequality
![\Pr(A[i,h_{i}(j)]-F[j]\geq M\epsilon )\leq 1/e](/vyuka/vpds/images/math/6/9/6/696074ff2c3300ed9035ba634b71719a.png)
- Probability that this happens in every row i is at most
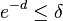
- Let
- Memory does not depend on n
- Note: if we insert million elements and then delete all but 4 of them, in the final structure we are very likely to be able to identify the 4 remaining ones as M is only 4