Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
Streaming model: Rozdiel medzi revíziami
Z VPDS
(→Majority element) |
(→Majority element) |
||
| Riadok 31: | Riadok 31: | ||
This algorithm can be generalized to find all elements with frequency greater than M/k by keeping k-1 counters (Misra and Gries 1982) | This algorithm can be generalized to find all elements with frequency greater than M/k by keeping k-1 counters (Misra and Gries 1982) | ||
| − | * If current element | + | * If current element has a counter, increase its counter |
| − | * Otherwise if some counter at 0, replace with current, start at 1 | + | * Otherwise if some counter at 0, replace with current element, start at 1 |
* Otherwise decrease all counters by 1 | * Otherwise decrease all counters by 1 | ||
* At the end the final set is guaranteed to contain all elements with frequency more than M/k (but we do not know which they are) | * At the end the final set is guaranteed to contain all elements with frequency more than M/k (but we do not know which they are) | ||
| − | ** Decreasing all counters is equivalent | + | ** Decreasing all counters is equivalent to removing k distinct elements from the input multiset (k-1 counters plus the current element) |
| − | ** The counters at the end correspond to up to k-1 items on which operation of removing k distinct elements cannot be applied - all elements with more than M/k occurrences must be among counters | + | ** The counters at the end correspond to up to k-1 distinct items on which operation of removing k distinct elements cannot be applied - all elements with more than M/k occurrences must be among counters |
==Count-Min sketch== | ==Count-Min sketch== | ||
Verzia zo dňa a času 21:22, 17. apríl 2017
Definition
- Input: stream of n elements
- Goal: do one pass through the stream (or only a few passes), use a small memory (e.g. O(1) or O(log n)) and answer a specific query about the stream
- Good for processing very fast streams, such as IP packets passing a router or measurements of a very low-powered device
- Not enough memory to store the whole stream, each item should be processed fast
- Strict turnstile model:
- underlying set {0,...,n-1}
- virtual vector F of length n initialized to zeroes
- stream consists of operations (j,x) meaning F[j]+=x
- At every point we have F[j]>=0 for each j
- Cash register model: all values x are positive
- Example: if all values x are +1, we are simply counting frequencies of elements from {0,...,n-1} on input
Majority element
Boyer–Moore majority vote algorithm 1981
- Consider the cash register model with x=1 in each update
- Assume that the stream contains a majority element j, i.e. F[j]>M/2 where M is the sum of all F[k]
- With this assumption j can be found by a simple algorithm with O(1) memory and O(1) time per element:
- Keep one candidate element j and a counter x
- Initialize j to fist element of the stream and x=1
- For each element k of the stream:
- if(j==k) x++;
- else if(x>0) x--;
- else { j=k; x=1; }
- Correctness:
- If j* is the majority element, at the of of the algorithm it is stored in j and x>0
- Any element other than j* can be paired with some occurrence of j*. Some occurrences of j* will remain
- If we are allowed a second pass, we can verify of found j is indeed majority
This algorithm can be generalized to find all elements with frequency greater than M/k by keeping k-1 counters (Misra and Gries 1982)
- If current element has a counter, increase its counter
- Otherwise if some counter at 0, replace with current element, start at 1
- Otherwise decrease all counters by 1
- At the end the final set is guaranteed to contain all elements with frequency more than M/k (but we do not know which they are)
- Decreasing all counters is equivalent to removing k distinct elements from the input multiset (k-1 counters plus the current element)
- The counters at the end correspond to up to k-1 distinct items on which operation of removing k distinct elements cannot be applied - all elements with more than M/k occurrences must be among counters
Count-Min sketch
- Strict turnstile model
- CM sketch with parameters epsilon and delta
- Array of counters A of depth
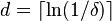 and width
and width 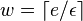
- Each row i of A has a hash function h_i from {0,...,n-1} to {0,...,w-1} (assume totally random, but a weaker assumption of pairwise independence sufficient for analysis)
- Update (j,x) does A[i,h_i(j)]+=x for all hash function i=0,...,n-1
- Query F[j]=? returns min_i A[i,h_i(j)]
- Let F be the correct answer, F' the answer returned
- Clearly F'>=F, because each A[i,k] may have contributions from other elements as well
- With probability at least 1-delta we have
![F'[j]\leq F[j]+\epsilon \sum _{i}F[i]](/vyuka/vpds/images/math/3/4/d/34dad0560ecc4efeb4be516b2898b0e4.png)
- Proof:
- Let
![M=\sum _{k}F[k]](/vyuka/vpds/images/math/0/8/0/080a114851fae348eafebcb7d3ecc93e.png)
- for a fixed row i:
![E[A[i,h_{i}(j)]=F[j]+\sum _{{k\neq j}}F[k]/w](/vyuka/vpds/images/math/c/d/f/cdfe94be7077d0d054d0194d8162c5fb.png) , because every other element k has probability 1/w to hash to column h_i(j) and thus it cntributes F[k]/w to
, because every other element k has probability 1/w to hash to column h_i(j) and thus it cntributes F[k]/w to
-
![E[A[i,h_{i}(j)]\leq F[j]+M\epsilon /e](/vyuka/vpds/images/math/e/8/9/e893e63da255a8c878db27a265864d42.png)
- By Markov inequality
![\Pr(A[i,h_{i}(j)]-F[j]\geq M\epsilon )\leq 1/e](/vyuka/vpds/images/math/6/9/6/696074ff2c3300ed9035ba634b71719a.png)
- Probability that this happens in every row i is at most
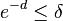
- Let
- Memory does not depend on n
- Note: if we insert million elements and then delete all but 4 of them, in the final structure we are very likely to be able to identify the 4 remaining ones as M is only 4
Heavy hitters
- Consider cash register model, for simplicity let all updates by simple increments by 1 (x=1)
- Let M = sum of values in F
- Given parameter phi, output all elements i from {0,...,n-1} such that F[i]>=phi*M (we will solve this problem with approximation)
- Keep current value of M plus a CM sketch with ln(n/delta) rows (instead of n, one could use an upper bound on M if F is very sparse)
- Also keep a hash table of elements j with current estimate F'[j]>=phi*M for current M and a min-priority queue (binary heap) of these elements with F'[j] as key (hash table keeps indexes within heap of individual elements)
- After each update (j,x), get estimated F'[j] and if it is at least phi*M, add/update j in priority queue and hash table
- Also check if minimum item k in the heap has its key large enough compared to current M, otherwise remove it
- At each moment at most 1/phi elements in the heap and hash table
- Memory O(ln(n/delta)/epsilon+1/phi), time for update O(ln(n/delta)+log(1/phi))
- Theorem: Every item which occurs with count more than phi * M is output, and with probability 1 − delta, no item whose count is less than (phi-epsilon)M is output.
- Threshold phi*M increases in each step; the only element which may become one of heavy hitters is the one just increased
- Since count-min sketch gives upper bounds, no heavy hitter is ommitted
- For each individual element j we have Pr(F'[j]-F[j]>=epsilon*M) <= delta/n
- By union bound Pr(exists j such that F'[j]-F[j]>=epsilon*M) <= delta
- So with prob >= 1-delta for every j such that F[j]<(phi-epsilon)*M, we have F'[j]<Phi*M
Sources
- Presentation at AK Data Science Summit - S. Muthu Muthukrishnan 2013 Count-Min Sketch 10 years later video, slides
- Cormode G, Muthukrishnan S. An improved data stream summary: the count-min sketch and its applications. Journal of Algorithms. 2005 Apr 1;55(1):58-75. [1]
- Journal article with count-min sketch
- Muthukrishnan S. Data streams: Algorithms and applications. Foundations and Trends in Theoretical Computer Science. 2005 Sep 27;1(2):117-236. [2]
- Survey of streaming model results, count-min sketch starts at page 26
- Cormode, Graham, and Marios Hadjieleftheriou. "Finding the frequent items in streams of data." Communications of the ACM 52.10 (2009): 97-105. [3]
- Survey and empirical comparison, include Boyer-Moore as well as count-min sketch
- Wikipedia Count-min sketch, Streaming algorithms, Boyer-Moore algorithm