OHW

Nepovinnú domácu úlohu môžete odovzdať písomne na hodine do termínu pre príslušný príklad a môžete za ňu dostať body za aktivitu. Všetky odpovede stručne zdôvodnite.

A (2 body) do 26.4.

Uvažujme Morissov-Prattov algoritmus pre vzorku P dĺžky m, ktorý bežíme na veľmi dlhom texte T. Koľko najviac bude trvať spracovanie úseku dĺžky k niekde uprostred textu T ako funkcia parametrov m a k? Hodnota k môže byť menšia alebo väčšia ako m. Uveďte asymptotický horný aj dolný odhad, t.j. aj príklad, kde to bude trvať čo najdlhšie (príklad by mal fungovať pre všeobecné m a k, ale môžete si zvoliť T a P a aj ktorý úsek T dĺžky k uvažujete).

B1 (1 bod) do 26.4.

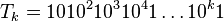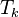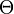V nasledujúcej sérii podpríkladov sa vrátime k binárnemu reťazcu, o ktorom sme sa bavili, že má veľký lexikografický strom všetkých sufixov. Postupne to podrobnejšie ukážeme. Uvažujme reťazec tvaru $T_{k}=1010^{2}10^{3}10^{4}1\dots 10^{k}1$. Aká je dĺžka $T_{k}$? (presný vzorec). Ak označíme $n=|T_{k}|$, vyjadrite k ako funkciu n, asymptoticky, t.j. v $\Theta$ notácii.

B2 (2 body) do 26.4.

Ak vezmeme dva sufixy reťazca 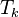$T_{k}$ a začneme ich porovnávať od začiatku, ako dlho bude v najhoršom prípade trvať, kým nájdeme prvý rozdiel? Vyjadrite asymptoticky ako funkciu n, horný aj dolný odhad.

Poznámka: pýtame sa na časovú zložitosť cyklu x=0; while(Tk[i+x]==Tk[j+x]} { x++; } kde i a j sú začiatky sufixov.

B3 (1 bod) do 26.4.

Dokážte, s využitím prechádzajúcich podúloh, že veľkosť lexikografického stromu (trie) všetkých sufixov 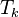$T_{k}$ je $\Theta (n^{2})$.

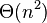B4 (? bodov) do 26.4.

Pokúste sa veľkosť lexikografického stromu reťazca 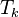$T_{k}$ určiť čo najpresnejšie ako funkciu k alebo n, t.j. zistiť niečo aj o konštante ukrytej v asymptotickej notácii, horné a dolné odhady, prípadne aj presný vzorec. Ak neviete riešiť analyticky, môžete aspoň spočítať pre nejaké konkrétne hodnoty k, napr. s využitím nejakej existujúcej implementácie lexikografických stromov. Počet bodov za túto úlohu záleží od náročnosti vášho riešenia.