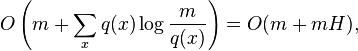Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
Amortizované vyhľadávacie stromy a link-cut stromy
Predbežná verzia poznámok, nebojte sa upravovať: pripojiť informácie z prezentácie, pridať viac vysvetľujúceho textu a pod.
Scapegoat trees
Introduction
- Lazy amortized binary search trees
- Relatively simple to implement
- Do not require balancing information stored in nodes (needs only left child, right child and key)
- Insert and delete O(log n) amortized
- Search O(log n) worst-case
- Height of tree always O(log n)
- For now let us consider only insert and search
- Store the total number of nodes n
- Invariant: keep the height of the tree at most
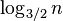
- Note: 3/2 can be changed to 1/alpha for alpha in (1/2,1)
- Let D(v) denotes the size (the number of nodes) of subtree rooted at v
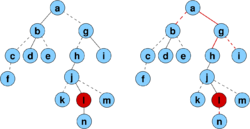
Insert
- Start with a usual insert, as in unbalanced BST
- If a node inserted at higher depth, restructure as follows
- Follow the path back from inserted node to the root
- Find the first node u on this path and its parent p for which D(u)/D(p) > 2/3
- This means that node p is very unbalanced - one of its children containing more than 2/3 of the total subtree size
- Node p will be called the scapegoat
- We will show later that a scapegoat always exists on the path to root (Lemma 1)
- Completely rebuild subtree rooted at p so that it contains the same values but is completely balanced
- This is done by traversing entire subtree in inorder, storing keys in an array (sorted)
- Root of the subtree will be the median of the array, left and right subtrees constructed recursively
- Running time O(D(p))
- This can be also done using linked lists built from right pointers in the node, with only O(log n) auxiliary memory for stack
- The height was before violated by 1, this improves it at least by 1, so the invariant is satisfied
- Why we always get improvement by at least 1:
- Let x be a sibling of u, if no sibling set D(x)=0
- D(u) > 2D(p)/3 > D(p)/3 >= D(p)-D(u), do D(p)-D(u)<=D(u)-1
- D(x) = D(p)-D(u)-1 <= D(u)-2
- so the sizes of left and right subtree of p differ by at least 2
- Let height of D(u) be h. The last level contains only the last inserted node, so D(u)-1 nodes can fit to h-1 levels
- In the rebuilt tree, the size of left and right subtree will differ by at most 1 and thus both will have at most D(u)-1 nodes and so they can fit into h-1 levels; the hight will thus decrease by at least 1
- Finding the scapegoat also takes O(D(p)) because we need to compute D(v) at every visited node
- Each computation in time O(D(v))
- But up to node u, child has always size at most 2/3 of parent
- Therefore sizes of subtrees for which we compute D(v) grow exponentially (geometric sum) and are dominated by the last 2 computations of D(u) and D(p)
Lemma 1: If a node v in a tree with n nodes is in depth greater than 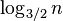 , then on the path from v to the root there is a node u and it parent p such that D(u)/D(p) > 2/3
, then on the path from v to the root there is a node u and it parent p such that D(u)/D(p) > 2/3
Proof:
- Assume that this is not the case, let nodes nodes on the path from v to root be v_k, v_{k-1},...v_0, where v_k=v and v_0 is the root and
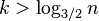
- D(v_0) = n.
- Since D(v_i)<=2/3 D(v_{i-1}), we have D(v_i) <= (2/3)^i n.
-
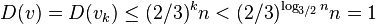
- Thus we have D(v)<1, which is a contradiction, because the subtree rooted at v contains at least one node
Amortized analysis of insert
- Potential of a node v with children x,y:
-
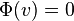 if |D(x)-D(y)| <= 1 (sizes of subtrees approximately the same)
if |D(x)-D(y)| <= 1 (sizes of subtrees approximately the same)
-
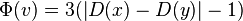
-
- Potential of tree: sum of potentials of subtrees
- Insert in depth d except rebuilding:
- real cost O(d)
- change of Phi at most 3d, because potential increases by at most 3 for nodes on the path to newly inserted vertex and does not change elsewhere
- amortized cost O(d) = O(log n)
- Rebuilding:
- real cost m = D(p) where p is the scapegoat
- let x and y be children of p before rebuilt, D(x)>D(y)
- m = D(p)=D(x)+D(y)+1, D(x)>2m/3, D(y)<m/3, D(x)-D(y)>1/3 m
- before rebuilt Phi(p) > m-3
- potential in all nodes in the rebuilt subtree is 0
- change of Phi <= -m +3
- amortized cost O(1)
Delete
- Very lazy version
- Do not delete nodes, only mark them as deleted
- Keep counter of deleted nodes
- When more than half nodes marked as deleted, completely rebuild the whole tree without them
- Each lazy delete pays a constant towards future rebuild. At least n/2 deleted before next rebuild.
- Variant: delete nodes as in unbalanced binary tree. This never increases height. Rebuild when many nodes deleted.
Uses of scapegoat trees
Scapegoat trees are useful if nodes of tree hold auxiliary information which is hard to rebuild after rotation
- we will see an example in range trees used in geometry
- another simple example from Morin's book Open Data Structures:
- we want to maintain a sequence of elements (conceptually something like a linked list)
- insert gets a pointer to one node of the list and inserts a new node before it, returns pointer to the new node
- compare gets pointers to two nodes from the same list and decided which is earlier in the list
- idea: store in a scapegoat tree, key is the position in the list. Each node holds the path from the root as a binary number stored in an int (height is logarithmic, so it should fit)
- Exercise: details?
Sources
- https://en.wikipedia.org/wiki/Scapegoat_tree
- https://people.ksp.sk/~kuko/gnarley-trees/?page_id=55
- I. Galperin, R.L.Rivest. Scapegoat trees. SODA 1993 [1]
- Similar idea also A.Andersson. Improving partial rebuilding by using simple balance criteria. WADS 1989. [2]
- Pat Morin. Open Data Structures, chapter 8 [3]
Splay trees
- intro on slides
Intuition and examples
- if height of tree is large, search is expensive, we use potential
- potential of path-like trees should be large, balanced trees smaller
- what happens if we apply splay on a leaf on a path?
- side benefit: if we search for some nodes more often, they tend to be near the root
Amortized analysis of splaying
- real cost: number of rotations
- D(x): number of descendants of node x, including x (size of a node)
- r(x): lg (D(x)) rank of a node (lg denotes log_2)
-
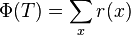
- Exercise: asymptotically estimate potential of a path and balanced tree with n nodes
Lemma1 (proof later): consider one step of splaying x (1 or 2 rotations)
- let r(x) be rank of x before splaying, r'(x) after splaying
- amortized cost of one step of splaying is at most
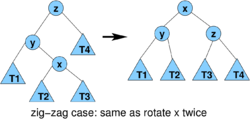
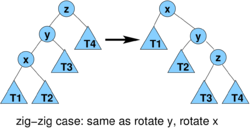
- 3(r'(x)-r(x)) for zig-zag and zig-zig
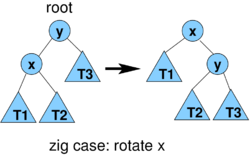
- 3(r'(x)-r(x))+1 for zig
Lemma2: Amortized cost of splaying x to the root in a tree with n nodes is O(log n)
- Let r_i be rank of x after i steps of splaying, let k be the number of steps
- amortized cost is at most
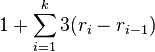
- (use Lemma 1, +1 is from the last step of splaying)
- telescopic sum, terms cancel, we get
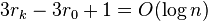
Theorem: Amortized cost of insert, search and delete in splay tree is O(log n)
- search:
- walk down to x, then splay x (if x not found, splay the last visited node)
- amortized cost is O(log n)
- insert:
- insert x as in normal binary search tree, then splay x.
- Inserting increase rank of all nodes on the path P from root r to x
- consider node v and its parent p on this path P
- D'(v) = 1 + D(v) <= D(p)
- r'(v) <= r(p)
- change in potential
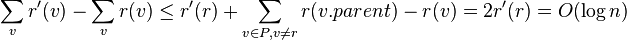
- amortized cost of insert + splaying is thus O(log n)
- delete:
- delete x as from binary search tree (may in fact delete node for predecessor or successor of x), then splay parent of deleted node
- deletion itself decreases potential, amortized cost of splaying is O(log n)
- amortized cost is O(log n)
- overall time in each operation proportional to the length of the path traversed and therefore to the number of rotations done in splaying
- therefore amortized time O(log n) for each operation.
Proof of Lemma 1:
- case zig: cost 1, r'(x) = r(y), all nodes except x and y keep their ranks
- amortized cost
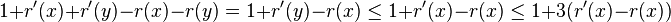
- amortized cost
- case zig-zig: cost 2,
- amortized cost
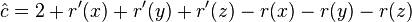
- we have r'(x) = r(z), r'(y)<=r'(x), r(y)>=r(x)
- therefore
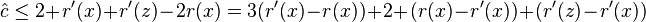
- therefore we need (r(x)-r'(x))+(r'(z)-r'(x))<=-2 or lg (D(x)/D'(x)) + lg (D'(z)/D'(x)) <= -2
- observe that D(x)+D'(z) <= D'(x)
- let a = D(x)/D'(x), b = D'(z)/D'(x), we have a+b<=1
- binary logarithm is concave, i.e. (lg(a)+lg(b))/2 <= lg((a+b)/2)
- and if a+b<=1, lg((a+b)/2) <= lg(1/2) = -1
- lg (D(x)/D'(x)) + lg (D'(z)/D'(x)) = lg a + lg b <= -2
- amortized cost
- case zig-zag is analogous
- amortized cost
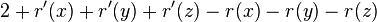
- r'(x) = r(z), r(x)<=r(y)
- therefore am. cost at most
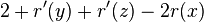
- we will prove that 2 <= 2r'(x)-r'(y)-r'(z) and this will imply amortized cost is at most 2(r'(x)-r(x))
- we have D'(y)+D'(z) <= D'(x), use the same logarithmic trick as before
- amortized cost
Adaptability of splay trees
If some element is accessed frequently, it tends to be located near the root, making access time shorter
Weighted potential function
- Each node x fixed weight w(x)>0
- D(x): the sum of weights in the subtree rooted at x
- r(x) = lg(D(x)) (rank of node x)
-
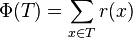
Weighted version of Lemma 2:
- Amortized cost of splaying x to the root is 1+3(r(t)-r(x)) = O(1+log (D(t)/D(x))), where t is the original root before splaying.
- Proof similar to Lemma 2
- By setting weight 1 for every node we get Lemma 2 as a corollary
Static optimality theorem:
- Starting with a tree with n nodes, execute a sequence of m find operations, where find(x) is done q(x)>=1 times.
- The total access time is
- where H is the entropy of the sequence of operations.
Proof:
- Set w(x)=q(x)/m. In weighted Lemma 2, w(T)<=1, D(x)>=w(x)=q(x)/m.
- Amortized cost of splaying x is thus O(1+log(m/q(x))); this is done q(x) times.
- After summing this expression for all operations we get the stated bound.
- However, we have to add a decrease of potential (using up money from the bank)
- with these weights, D(x)<=1, r(x)<=0 and thus Phi(x)<=0
- on the other hand, D(x)>w(x),
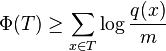
-
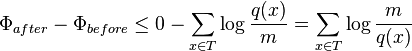
- Since q(x)>=1 and log(m/q(x))>=0, this is within stated upper bound
Note:
- Lower bound for a static tree is
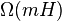 (see Melhorn 1975)
(see Melhorn 1975)
Sequential access theorem:
- Starting from any tree with n nodes, splaying each node to the root once in the increasing order of the keys has total time O(n).
- Proved by Tarjan 1985, improved proof Elmasry 2004 (proof not covered in the course)
- Trivial upper bound is O(n log n)
Collection of splay trees
Image now a collection of splay trees. The following operations can be done in O(log n) amortized time (each operation gets pointer to a node)
- findMin(v): find minumum element in a tree containing v and make it root of that tree
- splay v, follow left pointers to min m, splay m, return m
- join(v1, v2): all elements in tree of v1 must be smaller than all elements in tree of v2. Join these two trees into one
- m = findMin(v2), splay(v1), connect v1 as a left child of m, return m
- connecting increases rank of m by at most log n
- splitAfter(x) - split tree containing v into 2 trees, one containing keys <=x, one containing keys > x, return root of the second tree
- splay(v), then cut away its right child and return it
- decreases rank of v
- splitBefore(v) - split tree containing v into 2 trees, one containing keys <x, one containing keys >=x, return root of the first tree
- analogous, cut away left child
Sources
- Sleator, Daniel Dominic, and Robert Endre Tarjan. "Self-adjusting binary search trees." Journal of the ACM 32, no. 3 (1985): 652-686.
- Original publication of splay trees.
- Elmasry A. On the sequential access theorem and deque conjecture for splay trees. Theoretical Computer Science. 2004 Apr 10;314(3):459-66.
- Proof of an improved version of the sequential access theorem
- Mehlhorn K. Nearly optimal binary search trees. Acta Informatica. 1975 Dec 1;5(4):287-95.
- Proof of the lower bound on static optma binary search trees (theorem 2, page 292)
Link-cut trees
Union/find
Maintains a collection of disjoint sets, supports operations
- union(v, w): connects sets containing v and w
- find(v): returns representative element of set containing v (can be used to test of v and w are in the same set)
Can be used to maintain connected components if we add edges to the graph, also useful in Kruskal's algorithm for minimum spanning tree
Implementation
- each set a (non-binary) trees, in which each node v has a pointer to its parent v.p
- find(v) follows pointers to the root of the tree, return the root
- union calls find for v and w and joins one with the other
- if we keep track of tree height and always join shorter tree below higher tree plus do path compression, we get amortized time O(alpha(m+n,n)) where alpha is inverse ackermann function, extremely slowly growing (n = number of elements, m = number of queries)
Exercise: implement as a collection of splay trees
- hint: want to use join for union, but what about the keys?
- splay trees actually do not need to store key values if we do not search
Link/cut trees
Maintains a collection of disjoint rooted trees on n nodes
- findRoot(v) find root of tree containing v
- link(v,w) w a root, v not in tree of w, make w a child of v
- cut(v) cut edge connecting v to its parent (v not a root)
O(log n) amortized per operation. We will show O(log^2) amortized time. Can be also modified to support these operations in worst-case O(log n) time, add more operations e.g. with weights in nodes.
Similar as union-find, but adds cut plus we cannot rearrange trees as needed as in union-find
Simpler version for paths
Simpler version for paths (imagine them as going upwards):
- findPathHead(v) - highest element on path containing v
- linkPaths(v, w) - join paths containing v and w (head of v's path will remain head)
- splitPathAbove(v) - remove edge connecting v to its parent p, return some node in the path containing p
- splitPathBelow(v) - remove edge connecting v to its chold c, return some node in the path containing c
Can be done by splay trees
- keep each path in a splay tree, using position as a key (not stored anywhere)
- findPathHead(v): findMin(v)
- linkPaths(v, w): join(v, w)
- splitPathAbove(v): splitBefore(v)
- splitPathBelow(v): splitAfter(v)
Back to link/cut trees
- label each edge as dashed or solid; among children of each node at most one connected by a solid edge
- series of solid paths (some solid paths contain only a single vertex)
- each solid path represented as a splay tree as above
- each node remembers the dashed edge going to its parent (if any) - only in the head of a solid path
- expose(v): make v the lower end of a solid path to root (make all edges on the path to root solid and make other edges dashed as necessary)
- assume for now that this can be done in O(log^2 n) amortized time
- findRoot(v): findPathHead(expose(v))
- link(v,w):
- expose(v)
- linkPaths(v, w)
- cut(v):
- expose(v) note: v not a root and thus connected to its parent by a solid edge
- splitPathAbove(v)
expose(v)
- series of splices where each splice adds one solid edge on the path from v to root
y = cutPathBellow(v);
if(y!=NULL) findPathHead(y).dashed = v;
while(true) {
x = findPathHead(v);
w = x.dashed;
if(w == NULL) break;
x.dashed = NULL;
q = splitPathBelow(w);
if(q != NULL) {
findPathHead(q).dashed = w;
}
linkPaths(w, x); v = x;
}
- we will prove that m link-cut operations with n nodes cause O(m log n) splices which means O(log n) splices amortized per expose
- each splice O(log n) amortized time (from splay trees), therefore O(log^2 n) amortized time per link-cut operation
Heavy-light decomposition
edge from v to its parent p is called heavy if D(v)> D(p)/2, otherwise it is light. Observations:
- each path from v to root at most lg n light edges because with each light edge the size of the subtree goes down by at least 1/2
- each node has at most one child connected to it by a heavy edge
Proof that there are O(log n) splices amortized per expose
- potential function: number of heavy dashed edges
- real cost: number of splices (= number of iterations of the while loop in expose)
consider a single splice, there are two cases:
- case 1: new solid edge is heavy
- before it was dashed heavy edge, not it is solid heavy edge, so potential decreases by 1
- some edge might have been changes from solid to dashed, but this edge is for sure light, because its sibling is heavy
- overall change of potential is therefore -1, real cost 1, amortized cost 0
- case 2: new solid edge is light
- change of potential is at most 1, because we might have created one new dashed edge and it is possible that this edge is heavy
- real cost is 1, therefore amortized vost is at most 2
- amortized cost of the whole expose is therefore 2L+1, where L is the number of new light solid edges created in expose
- +1 comes from the child of v which was potentially changed from solid to dashed in the first step
- all new light solid edges are light edges on the path from v to root, therefore L=O(log n)
- the total amortized cost of expose is therefore O(log n)
some operations change the tree and create new heavy dashed edges from light dashed edges
- consider edge from u to its parent p
- it can become heavy if u becomes heavier by linking in its subtree
- this never happens because edge u->p would be solid before linking
- it can also become heavy if some other child x of p becomes lighter by cutting something in its subtree
- after cutting, x is connected to p by a light edge
- there are at most lg n vertices on the path exposed by cutting that are light after the cut and can play role of x
- each x has at most one sibling u that becomes heavy
- therefore there are at most lg n new heavy dashed edges, which adds O(log n) splices to amortized cost of cut
Fully dynamic connectivity
- insert delete edges, insert delete isolated vertices, test if there is a path from v to w O(log^2 n) amortized
- Holm, Jacob, Kristian De Lichtenberg, and Mikkel Thorup. "Poly-logarithmic deterministic fully-dynamic algorithms for connectivity, minimum spanning tree, 2-edge, and biconnectivity." Journal of the ACM (JACM) 48, no. 4 (2001): 723-760.
- uses link-cut trees as components
- good idea for presentation?
- if no delete, can use union-find
Applications
- At the time of publication improved best known running time of maximum flow problem from O(nm log^2 n) to O(nm log n). Since then some improvements.
- lca(u,v) least common ancestor:
- expose(u)
- expose(v)
- w = findPathHead(u)
- if w.dashed==null return u else return w.dashed
- we have seen O(1) lca after preprocessing a static tree, this would be O(log n) dynamic