Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
Amortizované vyhľadávacie stromy a link-cut stromy
Splay trees
- intro on slides
Intuition and examples
- if height of tree is large, search is expensive, we use potential
- potential of path-like trees should be large, balanced trees smaller
- what happens if we apply splay on a leaf on a path?
- side benefit: if we search for some nodes more often, they tend to be near the root
Amortized analysis of splaying
- real cost: number of rotations
- D(x): number of descendants of node x, including x (size of a node)
- r(x): log_2 (D(x)) rank of a node (we will denote log_2 by lg)
-
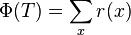
- Exercise: asymptotically estimate potential of a path and balanced tree with n nodes
Lemma1 (proof later): consider one step of splaying x (1 or 2 rotations)
- let r(x) be rank of x before splaying, r'(x) after splaying
- amortized cost of one step of splaying is at most
- 3(r'(x)-r(x)) for zig-zag and zig-zig
- 3(r'(x)-r(x))+1 for zig
Lemma2: Amortized cost of splaying x to the root in a tree with n nodes is O(log n)
- Let r_i be rank of x after i steps of splaying, let k be the number of steps
- amortized cost is at most
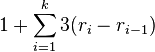
- (use Lemma 1, +1 is from the last step of splaying)
- telescopic sum, terms cancel, we get

Theorem: Amortized cost of insert, search and delete in splay tree is O(log n)
- search:
- walk down to x, then splay x (if x not found, splay the last visited node)
- amortized cost is O(log n)
- insert:
- insert x as in normal binary search tree, then splay x.
- Inserting increase rank of all nodes on the path P from root r to x
- consider node v and its parent p(v) on this path P
- D'(v) = 1 + D(v) <= D(p(v))
- r'(v) <= r(p(v))
- change in potential
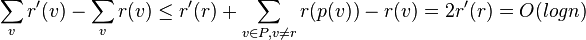
- amortized cost of insert + splaying is thus O(log n)
- delete:
- delete x as from binary search tree (may in fact delete node for predecessor or successor of x), then splay parent of deleted node
- deletion itself decreases potential, amortized cost of splaying is O(log n)
- amortized cost is O(log n)
- overall time in each operation proportional to the length of the path traversed and therefore to the number of rotations done in splaying
- therefore amortized time O(log n) for each operation.
Proof of Lemma 1:
- case zig: cost 1, r'(x) = r(y), all nodes except x and y keep their ranks
- amortized cost
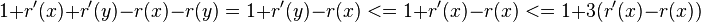
- amortized cost
- case zig-zig: cost 2,
- amortized cost

- we have r'(x) = r(z), r'(y)<=r'(x), r(y)>=r(x)
- therefore am. cost at most
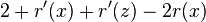
- want 3(r'(x)-r(x)) therefore we need 2 <= 2r'(x)-r(x)-r'(z) or (r(x)-r'(x))+(r'(z)-r'(x))<=-2 or lg (D(x)/D'(x)) + lg (D'(z)/D'(x)) <= -2
- observe that D(x)+D'(z) <= D'(x)
- if we have a,b>0 s.t. a+b<=1, then lg a + lg b has maximum -2 at a=b=1/2.
- how would you go about proving this?
- binary logarithm is concave, i.e. lg(ta+(1-t)b)>= t lg(a)+(1-t)lg(b) for every t in [0,1]
- set t = 1/2, (lg(x)+lg(y))/2 <= lg((x+y)/2) <= lg(1/2) = -1
- here x = D(x)/D'(x), y = D'(z)/D'(x)
- amortized cost
- case zig-zag is analogous
- amortized cost

- r'(x) = r(z), r(x)<=r(y)
- therefore am. cost at most
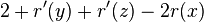
- we will prove that 2 <= 2r'(x)-r'(y)-r'(z) and this will imply amortized cost is at most 2(r'(x)-r(x))
- we have D'(y)+D'(z) <= D'(x), use the same logarithmic trick as before
- amortized cost
Link-cut trees
Splay trees
Image now a collection of splay trees. The following operations can be done in O(log n) amortized time (each operation gets pointer to a node)
- findMin(v): find minumum element in a tree containing v and make it root of that tree
- splay v, follow left pointers to min m, splay m, return m
- join(v1, v2): all elements in tree of v1 must be smaller than all elements in tree of v2. Join these two trees into one
- m = findMin(v2), splay(v1), connect v1 as a left child of m, return m
- connecting increases rank of m by at most log n
- splitAfter(x) - split tree containing v into 2 trees, one containing keys <=x, one containing keys > x, return root of the second tree
- splay(v), then cut away its right child and return it
- decreases rank of v
- splitBefore(v) - split tree containing v into 2 trees, one containing keys <x, one containing keys >=x, return root of the first tree
- analogous, cut away left child
Union/find
Maintains a collection of disjoint sets, supports operations
- union(v, w): connects sets containing v and w
- find(v): returns representative element of set containing v (can be used to test of v and w are in the same set)
Can be used to maintain connected components if we add edges to the graph, also useful in Kruskal's algorithm for minimum spanning tree
Implementation
- each set a (non-binary) trees, in which each node v has a pointer to its parent v.p
- find(v) follows pointers to the root of the tree, return the root
- union calls find for v and w and joins one with the other
- if we keep track of tree height and always join shorter tree below higher tree plus do path compression, we get amortized time O(alpha(m+n,n)) where alpha is inverse ackermann function, extremely slowly growing (n = number of elements, m = number of queries)
Link/cut trees
Maintains a collection of disjoint rooted trees on n nodes
- findRoot(v) find root of tree containing v
- link(v,w) v a root, w not in tree of v, make v a child of w
- cut(v) cut edge connecting v to its parent (v not a root)
O(log n) amortized per operation. We will show O(log^2) amortized time. Can be also modified to support these operations in worst-case O(log n) time, add more operations e.g. with weights in nodes.
Similar as union-find, but adds cut plus we cannot rearrange trees as needed as in union-find
Simpler version for paths
Simpler version for paths (imagine them as going upwards):
- findPathHead(v) - highest element on path containing v
- linkPaths(v, w) - join paths containing v and w (head of v's path will remain head)
- splitPathAbove(v) - remove edge connecting v to its parent p, return some node in the path containing p
- splitPathBelow(v) - remove edge connecting v to its chold c, return some node in the path containing c
Can be done by splay trees
- keep each path in a splay tree, using position as a key (not stored anywhere)
- findPathHead(v): findMin(v)
- linkPaths(v, w): join(v, w)
- splitPathAbove(v): splitBefore(v)
- splitPathBelow(v): splitAfter(v)
Back to link/cut trees
- separate edges in each tree into dashed and solid, each node has at most one solid edge coming from one of the children
- series of solid paths (some solid paths contain only a single vertex)
- each solid path represented as a splay tree as above
- each node remembers the dashed edge going from its top (if any) - only in the head of solid path
- expose(v): make v the lower end of a solid path to root (make all edges on the path to root solid and make other edges dashed as necessary)
- assume can be done in O(log^2 n) amortized time
- findRoot(v): findPathHead(expose(v))
- link(v,w):
- expose(v) v is now 1-node solid path
- expose(w)
- linkPaths(v, w)
- cut(v):
- expose(v)
- splitPathAbove(v)
expose(v)
- series of splices where we add one solid edge on the path from v to root
y=cutPathBellow(v);
findPathHead(y).dashed = v;
while(true) {
x = findHead(v)
w=x.dashed;
if(w==NULL) break;
x.dashed=NULL;
q = splitPathBelow(w)
if(q!=NULL) {
findPathHead(q).dashed = w;
}
linkPaths(w, x)
}
- m operations with n nodes cause O(m log n) splices which means O(log n) splices amortized per expose
- each slice O(log n) amortized time, therefore O(log^2 n) amortized time per each operation in link-cut tree
Heavy-light decomposition
edge from v to its parent p is called heavy if D(v)> D(p)/2, otherwise it is light. Observations:
- each path from v to root at most lg n light edges because with each light edge the size of the subtree goes down by at least 1/2
- each node has at most one child connected to it by a heavy edge
Proof that there are O(log n) splices amortized per expose
- potential function: number of heavy dashed edges
- cost: splice
- assume expose creates L new light solid edges and H new solid heavy edges.
- real cost L+H
- it creates at most L+1 new heavy dashed edges (only splices which create new light solid edge can create heavy dashed edge plus 1 from child of v)
- removes H heavy dashed edges (they become solid by splice)
- change of potential <= L+1-H
- amortized cost 2L+1 = O(log n) because all new light solid edges are light edge on a path from v to root
- some operations change the tree and create new heavy dashed edges from light dashed edges
- consider edge from v to its parent p
- it can become heavy if v becomes heavier by linking in its subtree
- this never happens because edge v->p would be solid before linking
- it can also become heavy if some other child x of p becomes lighter by cutting something in its subtree
- after cuting, x is connected to p by a light edge
- there are at most lg n vertices on the path exposed by cutting that are light after the cut and can play role of x
- each x has at most one sibling v that becomes heavy
- therefore there are at most lg new heavy dashed edges, which adds O(log n) splices to amortized cost of cuting
Fully dynamic connectivity
- insert delete edges, insert delete isolated vertices, test if there is a path from v to w O(log^2 n) amortized
- Holm, Jacob, Kristian De Lichtenberg, and Mikkel Thorup. "Poly-logarithmic deterministic fully-dynamic algorithms for connectivity, minimum spanning tree, 2-edge, and biconnectivity." Journal of the ACM (JACM) 48, no. 4 (2001): 723-760.
- uses link-cut trees as components
- good idea for presentation?
- if no delete, can use union-find
Applications
- lca least common ancestor: expose(v), expose(w), during expose w the last dasdes edge turned to solid leads to lca
- later will do O(1) lca after preprocessing a static tree
- At the time of publication improved best known running time of maximum flow problem from O(nm log^2 n) to O(nm log n). Since then some improvements.