Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
OHW: Rozdiel medzi revíziami
| Riadok 1: | Riadok 1: | ||
| − | Nepovinnú domácu úlohu môžete odovzdať písomne | + | =Nová sada= |
| + | Príklady C-F odovzdajte najneskôr do piatka 27.5. 10:00, ak máte skúšku 27.5., alebo do štvrtka 16.6. 10:00, ak máte skúšku 17.6. Nepovinnú domácu úlohu môžete odovzdať písomne v M163 alebo emailom v pdf formáte a môžete za ňu dostať body za aktivitu. Všetky odpovede stručne zdôvodnite. | ||
| − | ==C (2 body) | + | ==C (2 body)== |
Máme dané Bloom filtre pre množiny A a B, vytvorené s tou istou sadou hešovacích funkcií (a teda aj s tou istou veľkosťou tabuľky). | Máme dané Bloom filtre pre množiny A a B, vytvorené s tou istou sadou hešovacích funkcií (a teda aj s tou istou veľkosťou tabuľky). | ||
* Ako môžeme z týchto dvoch Bloom filterov zostrojiť Bloom filter pre zjednotenie A a B? Bude taký istý, ako keby sme priamo vkladali prvky zjednotenia do bežného Bloom filtera? | * Ako môžeme z týchto dvoch Bloom filterov zostrojiť Bloom filter pre zjednotenie A a B? Bude taký istý, ako keby sme priamo vkladali prvky zjednotenia do bežného Bloom filtera? | ||
* Ako môžeme zistrojiť Bloom filter pre prienik A a B? Bude taký istý, ako keby sme priamo vkladali prvky prieniku do bežného Bloom filtera? | * Ako môžeme zistrojiť Bloom filter pre prienik A a B? Bude taký istý, ako keby sme priamo vkladali prvky prieniku do bežného Bloom filtera? | ||
| − | ==D (3 body) | + | ==D (3 body) == |
Máme reťazce X a Y rovnakej dĺžky n, ktorých Hammingova vzdialenosť je 1. | Máme reťazce X a Y rovnakej dĺžky n, ktorých Hammingova vzdialenosť je 1. | ||
* Aká môže byť v najhoršom prípade Hammingova vzdialenosť reťazcov BWT(X$) a BWT(Y$)? Nájdite príklad, kde je táto vzdialenosť čo najväčšia (ako funkcia n). Naopak, snažte sa dokázať aj horný odhad. | * Aká môže byť v najhoršom prípade Hammingova vzdialenosť reťazcov BWT(X$) a BWT(Y$)? Nájdite príklad, kde je táto vzdialenosť čo najväčšia (ako funkcia n). Naopak, snažte sa dokázať aj horný odhad. | ||
* Pomôcka: abeceda môže byť veľká (môže mať aj veľkosť n) | * Pomôcka: abeceda môže byť veľká (môže mať aj veľkosť n) | ||
| − | ==E (? bodov, podľa náročnosti) | + | ==E (? bodov, podľa náročnosti)== |
Máme reťazce X a Y rovnakej dĺžky n, ktorých Hammingova vzdialenosť je 1. | Máme reťazce X a Y rovnakej dĺžky n, ktorých Hammingova vzdialenosť je 1. | ||
* Aká môže byť v najhoršom prípade '''editačná''' vzdialenosť reťazcov BWT(X$) a BWT(Y$)? Nájdite príklad, kde je táto vzdialenosť čo najväčšia (ako funkcia n). Naopak, snažte sa dokázať aj horný odhad. | * Aká môže byť v najhoršom prípade '''editačná''' vzdialenosť reťazcov BWT(X$) a BWT(Y$)? Nájdite príklad, kde je táto vzdialenosť čo najväčšia (ako funkcia n). Naopak, snažte sa dokázať aj horný odhad. | ||
| + | |||
| + | ==F (2 body)== | ||
| + | |||
| + | Bonus z DÚ: Segmentové stromy chceme rozšíriť tak, aby vedeli podporovať nasledovné operácie: | ||
| + | |||
| + | * RMQ(i,j) vráti pozíciu minima v a[i...j] v čase O(log^2 n), | ||
| + | * add(i,j,x) pripočíta hodnotu x (kladnú alebo zápornú) ku každému číslu v intervale a[i..j] v čase O(log^2 n), | ||
| + | * value(i) vráti hodnotu a[i] v čase O(log n). | ||
| + | |||
| + | Na to, aby operácia add fungovala v O(log^2 n) bez ohľadu na dĺžku intervalu, nebudeme hodnoty a[i] uschovávať priamo v poli. Namiesto toho budeme mať určitú hodnotu v každom vrchole segmentového stromu a a[i] bude súčtom hodnôt vo všetkých vrcholoch, ktorých intervaly obsahujú i. Pre jednoduchosť strom teraz rozšírime aj o intervaly dĺžky jedna. Vrcholy stromu taktiež budú obsahovať index minima pre operáciu RMQ. Tieto indexy treba pri operácii add | ||
| + | vhodne upraviť. Napíšte a stručne zdôvodnite pseudokód pre všetky tri operácie v tejto reprezentácii. Využite kanonickú dekompozíciu z prednášky. | ||
| + | |||
| + | Poznámka: mierna úprava dátovej štruktúry môže znížiť čas každej operácie na O(log n), za takúto verzou môžete dostať 4 body- | ||
| + | |||
=Predchádzajúce kolo= | =Predchádzajúce kolo= | ||
Verzia zo dňa a času 22:12, 23. máj 2016
Obsah
Nová sada
Príklady C-F odovzdajte najneskôr do piatka 27.5. 10:00, ak máte skúšku 27.5., alebo do štvrtka 16.6. 10:00, ak máte skúšku 17.6. Nepovinnú domácu úlohu môžete odovzdať písomne v M163 alebo emailom v pdf formáte a môžete za ňu dostať body za aktivitu. Všetky odpovede stručne zdôvodnite.
C (2 body)
Máme dané Bloom filtre pre množiny A a B, vytvorené s tou istou sadou hešovacích funkcií (a teda aj s tou istou veľkosťou tabuľky).
- Ako môžeme z týchto dvoch Bloom filterov zostrojiť Bloom filter pre zjednotenie A a B? Bude taký istý, ako keby sme priamo vkladali prvky zjednotenia do bežného Bloom filtera?
- Ako môžeme zistrojiť Bloom filter pre prienik A a B? Bude taký istý, ako keby sme priamo vkladali prvky prieniku do bežného Bloom filtera?
D (3 body)
Máme reťazce X a Y rovnakej dĺžky n, ktorých Hammingova vzdialenosť je 1.
- Aká môže byť v najhoršom prípade Hammingova vzdialenosť reťazcov BWT(X$) a BWT(Y$)? Nájdite príklad, kde je táto vzdialenosť čo najväčšia (ako funkcia n). Naopak, snažte sa dokázať aj horný odhad.
- Pomôcka: abeceda môže byť veľká (môže mať aj veľkosť n)
E (? bodov, podľa náročnosti)
Máme reťazce X a Y rovnakej dĺžky n, ktorých Hammingova vzdialenosť je 1.
- Aká môže byť v najhoršom prípade editačná vzdialenosť reťazcov BWT(X$) a BWT(Y$)? Nájdite príklad, kde je táto vzdialenosť čo najväčšia (ako funkcia n). Naopak, snažte sa dokázať aj horný odhad.
F (2 body)
Bonus z DÚ: Segmentové stromy chceme rozšíriť tak, aby vedeli podporovať nasledovné operácie:
- RMQ(i,j) vráti pozíciu minima v a[i...j] v čase O(log^2 n),
- add(i,j,x) pripočíta hodnotu x (kladnú alebo zápornú) ku každému číslu v intervale a[i..j] v čase O(log^2 n),
- value(i) vráti hodnotu a[i] v čase O(log n).
Na to, aby operácia add fungovala v O(log^2 n) bez ohľadu na dĺžku intervalu, nebudeme hodnoty a[i] uschovávať priamo v poli. Namiesto toho budeme mať určitú hodnotu v každom vrchole segmentového stromu a a[i] bude súčtom hodnôt vo všetkých vrcholoch, ktorých intervaly obsahujú i. Pre jednoduchosť strom teraz rozšírime aj o intervaly dĺžky jedna. Vrcholy stromu taktiež budú obsahovať index minima pre operáciu RMQ. Tieto indexy treba pri operácii add vhodne upraviť. Napíšte a stručne zdôvodnite pseudokód pre všetky tri operácie v tejto reprezentácii. Využite kanonickú dekompozíciu z prednášky.
Poznámka: mierna úprava dátovej štruktúry môže znížiť čas každej operácie na O(log n), za takúto verzou môžete dostať 4 body-
Predchádzajúce kolo
A (2 body) do 26.4.
Uvažujme Morissov-Prattov algoritmus pre vzorku P dĺžky m, ktorý bežíme na veľmi dlhom texte T. Koľko najviac bude trvať spracovanie úseku dĺžky k niekde uprostred textu T ako funkcia parametrov m a k? Hodnota k môže byť menšia alebo väčšia ako m. Uveďte asymptotický horný aj dolný odhad, t.j. aj príklad, kde to bude trvať čo najdlhšie (príklad by mal fungovať pre všeobecné m a k, ale môžete si zvoliť T a P a aj ktorý úsek T dĺžky k uvažujete).
B1 (1 bod) do 26.4.
V nasledujúcej sérii podpríkladov sa vrátime k binárnemu reťazcu, o ktorom sme sa bavili, že má veľký lexikografický strom všetkých sufixov. Postupne to podrobnejšie ukážeme. Uvažujme reťazec tvaru 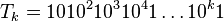 . Aká je dĺžka
. Aká je dĺžka 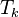 ? (presný vzorec). Ak označíme
? (presný vzorec). Ak označíme  , vyjadrite k ako funkciu n, asymptoticky, t.j. v
, vyjadrite k ako funkciu n, asymptoticky, t.j. v 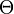 notácii.
notácii.
B2 (2 body) do 26.4.
Ak vezmeme dva sufixy reťazca 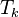 a začneme ich porovnávať od začiatku, ako dlho bude v najhoršom prípade trvať, kým nájdeme prvý rozdiel? Vyjadrite asymptoticky ako funkciu n, horný aj dolný odhad.
a začneme ich porovnávať od začiatku, ako dlho bude v najhoršom prípade trvať, kým nájdeme prvý rozdiel? Vyjadrite asymptoticky ako funkciu n, horný aj dolný odhad.
Poznámka: pýtame sa na časovú zložitosť cyklu x=0; while(Tk[i+x]==Tk[j+x]} { x++; } kde i a j sú začiatky sufixov.
B3 (1 bod) do 26.4.
Dokážte, s využitím prechádzajúcich podúloh, že veľkosť lexikografického stromu (trie) všetkých sufixov 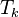 je
je 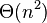 .
.
B4 (? bodov) do 26.4.
Pokúste sa veľkosť lexikografického stromu reťazca 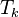 určiť čo najpresnejšie ako funkciu k alebo n, t.j. zistiť niečo aj o konštante ukrytej v asymptotickej notácii, horné a dolné odhady, prípadne aj presný vzorec. Ak neviete riešiť analyticky, môžete aspoň spočítať pre nejaké konkrétne hodnoty k, napr. s využitím nejakej existujúcej implementácie lexikografických stromov. Počet bodov za túto úlohu záleží od náročnosti vášho riešenia.
určiť čo najpresnejšie ako funkciu k alebo n, t.j. zistiť niečo aj o konštante ukrytej v asymptotickej notácii, horné a dolné odhady, prípadne aj presný vzorec. Ak neviete riešiť analyticky, môžete aspoň spočítať pre nejaké konkrétne hodnoty k, napr. s využitím nejakej existujúcej implementácie lexikografických stromov. Počet bodov za túto úlohu záleží od náročnosti vášho riešenia.