Prioritné rady

Nizsie su pracovne poznamky, ktore doplnuju informaciu z prezentacie, je mozne ich rozsirit, doplnit samotnou prezentaciou

Introduction to priority queues

Review

Operations        Bin. heap    Fib. heap 
                  worst case    amortized
MakeHeap()            O(1)       O(1)   
Insert(H, x)       O(log n)      O(1)   
Minimum(H)            O(1)       O(1)   
ExtractMin(H)      O(log n)    O(log n)   
Union(H1, H2)         O(n)       O(1)   
DecreaseKey(H, x, k)
                    O(log n)     O(1)   
Delete(H, x)        O(log n)   O(log n)   

Applications of priority queues

• job scheduling on a server (store jobs in a max-based priority queue, always select the one with highest priority - needs operations insert and extract_min, possibly also delete -needs a handle)
• event-driven simulation (store events, each with a time when it is supposed to happen. Always extract one event, process it and as a result potentially create new events - needs insert, extract_min Examples: queue in a bank or store: random customer arrival times, random service times per customer)
• finding intersections of line segments [1]
  • Bentley–Ottmann algorithm - sweepline: binary search tree of line intersections) plus a priority queue with events (start of segment, end of segment, crossing)
  • for n segments and k intersections do 2n+k inserts, 2n+k extractMin, overall O((n+k)log n) time

• heapsort (builds a heap from all elements or uses n time insert, then n times extract_min -implies a lower bound on time of insert+extract_min must be at least Omega(log n) in the comparison model)
• aside: partial sorting - given n elements, print k in sorted order - selection O(n), then sort in O(k log k), together O(n + k log k)
• incremental sorting: given n elements, build a data structure, then support extract_min called k times, k unknown in advance, running time a function of k and n
  • call selection each time O(kn)
  • heap (binary, Fibonacci etc) O(n + k log n) = O(n + k log k) because if k>= sqrt n, log n = Theta(log k) and of k < sqrt n, O(n) term dominates

• Kruskal's algorithm (can use sort, but instead we can use heap as well, builds heap, then calls extract_min up to m times, but possibly fewer, plus needs union-find set structure) O(m log n)
  • process edges from smallest weight upwards, if it connects 2 components, add it. Finosh when we have a tree.
• Prim's algorithm (build heap, n times extract-min, m times decrease_key - O(m log n) with binary heaps, O(m + n log n) with Fib heaps)
  • build a tree starting from one node. For each node outside tree keep the best cost to a node in a tree as a priority in a heap
• Dijkstra's algorithm for shortest paths (build heap, n times extract_min, m times decrease_key = the same as Prim's)
  • keep nodes in a heap which do not have final distance. Set the distance of minimum node to final, update distances of tis neighbors

Soft heap

• http://en.wikipedia.org/wiki/Soft_heap
• Chazelle, B. 2000. The soft heap: an approximate priority queue with optimal error rate. J. ACM 47, 6 (Nov. 2000), 1012-1027.
• Kaplan, H. and Zwick, U. 2009. A simpler implementation and analysis of Chazelle's soft heaps. In Proceedings of the Nineteenth Annual ACM -SIAM Symposium on Discrete Algorithms (New York, New York, January 4––6, 2009). Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics, Philadelphia, PA, 477-485. pdf

• provides constant amortized time for insert, union, findMin, delete
  • but corrupts (increases) keys of up to epsilon*n elements, where epsilon is a fixed parameter in (0,1/2) and n is the number of insertions so far
  • useful to obtain minimum spanning tree in O(m alpha(m,n)) where alpha is the inverse of Ackermann's function

Fibonacci heaps

Motivation

• To improve Dijkstra's shortes path algorithm from O(E*log V) to O(E + V*log V)

Structure of a Fibonacci heap

• Heap is collection of rooted trees, node degrees up to Deg(n) = O(log n)
• Min-heap property: Key in each non-root node ≥ key in its parent
• In each node store: key, other data, referrence for parent, first child, next and previous sibling, degree, binary mark
• In each heap: number of nodes n, pointers for: root with minimum key, first and last root
• Roots in a heap are connected by sibling pointers
• Non-root node is marked iff it lost a child since getting a parrent
• Potential function: number of roots + 2 * number of marked nodes

Example of Fibonacci heap

Operations analysis

• n number of nodes in heap
• Deg(n) - maximum degree of a node x in a heap of size n
• potential function Φ = number of roots + 2 * number of marked nodes
• Amortized cost = real cost + Φ_after- Φ_before

Lazy operations with O(1) amortized time:

MakeHeap()

• create empty heap
• cost O(1), Φ= 0
• initialize H.n = [], H.min = null

Insert(H,x)

• insert node with value x into heap H:
  • create new singleton node
  • add this node to left of minimum pointer - update H.n
  • update minimum pointer - H.min
• cost O(1), Φ= 1

Minimum(H)

• return minimum value from heap H - update H.min
• cost O(1), Φ= 0

Union(H1, H2)

• union two heaps
  • concatenate root lists - update H.n, H.min
• cost O(1), Φ = 0

Other operations

ExtractMin(H)

• from heap H remove node with minimum value
  • let x be root node with minimum key value, then it is in root list, and we have on him H.min pointer
  • if x is singleton node (with no children), we will just extract him, return H.min and run consolidate(H) to find new H.min
  • if x had children, before extracting x, we must add all children of x to root list, update their parent pointer, then return H.min and run then consolidate(H) to find new H.min
• what do consolite(H): changes structure of heap to achieve that no two nodes in root list have same degree, and finds H.min
  • during one iteration througth root list, for each node in root list it creates pointer to degree array, when it find two nodes with same degree, it will link them together (HeapLink), thus node with higher key value will be first left child of node with lower degree, also during this iteration it is finding H.min

Analysis:

• t1 original count of nodes in the root list, t2 new count
• actual cost: O(Deg(n) + t1)
  • O(Deg(n)) adding x's children into root list and updating H.min
  • O(Deg(n) + t1) consolidating trees - computating is proportional to size of root list, and number of roots decreases by one after each merging (HeapLink)
• Amortized cost: O(Deg(n))
  • t2 ≤ Deg(n) + 1, because each tree had different degree
  • Δ Φ ≤ Deg(n) + 1 - t1
  • let c be degree of z, c ≤ Deg(n) = O(log n)
  • ExtractMin: adding children to root list: cost c, Δ Φ = c
  • Consolidate: cost: t1 + Deg(n), Δ Φ = t2 - t1
  • amortized t2 + Deg(n), but t2 ≤ Deg(n), therefore O(log n)
  • Heaplink: cost 0, Φ = 0

• Pseudo code:

1 ExtractMin (H) {
2   z = H.min
3   Add each child of z to root list of H ( update its parent )
4   Remove z from root list of H
5   Consolidate (H)
6   return z
7 }

1 Consolidate (H) {
2   create array A [ 0..Deg(H.n ) ], initialize with null
3   for (each node x in the root listt of H) {
4     while (A[x.degree] != null ) {
5       y = A[x.degree] ;
6       A[x.degree] = null ;
7       x = HeapLink (H, x, y)
8     }
9   A[x.degree] = x
10  }
11  traverse A, create root list of H, find H.min
12 }

1 HeapLink (H, x, y) {
2   if (x.key > y.key) exchange x and y
3   remove y from root list of H
4   make y a child of x, update x.degree
5   y.mark = false ;
6   return x
7 }

DecreaseKey(H,x,k)

• target: for node x in heap H change key value to k (it is decrease operation, so new value k must be lower than old value)
• find x and change it's kye value to k, there are three scenarios:
  • 1. case: after changing key value for x, heap property is not changed = value of node will be still higher than value of it's parent, then update H.min
  • 2. case: new value of node x break min-heap property and parent y (for node x) is not marked (hasn't yet lost a child), then cut link between x and y, mark y (now he lost child) and tree x add to root list, update H.min
  • 3. case: new value of node x break min-heap property and parent y (for node x) is marked (in history of heap he lost child), then cut link between x and y, tree x add to root list (similar to previous 2. case, but...), cut link between y and its parent z, add tree y to root list, and continue recursively
    • unmark each marked node added into root list

Analysis:

• t1 original count of nodes in the root list, t2 count of nodes in new heap
• m1 original count of marks in H, m2 count of marks in new heap
• Actual cost: O(c)
  • O(1) for changing key value
  • O(1) for each c cascading cuts and adding into root list
• Change in potential: O(1) - c
  • t2 = t1 + c (adding c trees to root list)
  • m2 ≤ m1 -c + 2 (every marked node, that was cuted was unmarked in root list, but last cut could posibly mark a node)
  • Δ Φ ≤ c + 2*(-c + 2) = 4 - c
• Amortized cost: O(1)

• Pseudo code:

DecreaseKey (H, x, k) {
2   x.key = k
3   y = x.parent
4   if (y != NULL && x.key < y.key) {
5     Cut(H, x, y)
6     CascadingCut (H, y)
7   }
8   update H.min
9 }

1 CascadingCut (H, y) {
2   z = y.parent
3   if (z != null) {
4     if (y.mark==false) y.mark = true
5     else {
6       Cut(H, y, z) ;
7       CascadingCut(H, z)
8     }
9   }
10 }

Delete(H,x)

• remove node x from heap H
  • DecreaseKey(H,x, -infinity)
  • ExtractMin(H)
• O(log n) amortized

Maximum degree Deg(n)

Proof of Lemma 3:

• Linking done only in Consolidate for 2 roots of equal degree.
• When y_j was linked, y_1,...y_{j-1} were children, so at that time x.degree >= j-1.
• Therefore at that time y_j.degree>= j-1
• Since then y_j lost at most 1 child, so y_j.degree >= j=2.

Proof of Lemma 4:

• Let D(x) be the size of subtree rooted at x
• Let s_k be the minimum size of a node with degree k in any Fibonacci heap (we will prove $s_{k}>=F_{{k+2}}$)
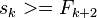• s_k<= s_{k+1}
  • If we have a subtree of degree k+1, we can cut it from its parent and then cut away one child to get a smaller tree of degree k
• Let x be a node of degree k and size s_k
• Let y_1,...y_k be its children from earliest
• D(x) = s_k = 1 + sum_{j=1}^k D(y_j) >= 1 + D(y_1) + sum_{j=2}^k s_{y_j.degree}
• >= 2 + sum_{j=2}^k s_{j-2} (lemma 3)
• by induction on k: s_k >= F_{k+2}
  • for k=0, s_0 = 1, F_2 = 1
  • for k=1, s_1 = 2, F_3 = 1
  • assume k>=2, s_i>=F_{i+2} for i<=k-1
  • s_k >= 2+ sum_{j=2}^k s_{j-2} >= 2 + sum_{j=2}^k F_j (IH)
  • = 1 + sum_{j=0}^k F_j = F_{k+2} (lemma 1)

Proof of Corollary:

• let x be a node of degree k in a Fibonacci heap with n nodes
• by lemma 4 n >= Φ^k
• therefore k<= log_Φ(n)

Exercise

• What sequence of operations will create a tree of depth n?
• Alternative delete (see slides)

Sources

• Michael L. Fredman, Robert E. Tarjan. "Fibonacci heaps and their uses in improved network optimization algorithms."Journal of the ACM 1987
• Cormen, Thomas H., Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms. MIT Press 2001

Pairing heaps

• Simple and fast in practice
• hard to analyze amortized time
• Fredman, Michael L.; Sedgewick, Robert; Sleator, Daniel D.; Tarjan, Robert E. (1986), "The pairing heap: a new form of self-adjusting heap", Algorithmica 1 (1): 111–129
• Stasko, John T.; Vitter, Jeffrey S. (1987), "Pairing heaps: experiments and analysis", Communications of the ACM 30 (3): 234–249
• Moret, Bernard M. E.; Shapiro, Henry D. (1991), "An empirical analysis of algorithms for constructing a minimum spanning tree", Proc. 2nd Workshop on Algorithms and Data Structures, Lecture Notes in Computer Science 519, Springer-Verlag, pp. 400–411
• Pettie, Seth (2005), "Towards a final analysis of pairing heaps", Proc. 46th Annual IEEE Symposium on Foundations of Computer Science, pp. 174–183 [2]

• a tree with arbitrary degrees
• each node pointer to the first child and next sibling (for delete and decreaseKey also pointer to previous sibling or parent if first child)
• each child has key >= key of parent
• linking two trees H1 and H2 s.t. H1 has smaller key:
  • make H2 the first child of H1 (original first child of H1 is sibling of H2)
  • subtrees thus ordered by age of linking from youngest to oldest

• extractMin is the most complex operation, the rest quite lazy
• insert: make a new tree of size 1, link with H
• union: link H1 and H2
• decreaseKey: cut x from its parent, decrease its key and link to H
• delete: cut x from parent, do extractMin on this tree, then link result to H

ExtractMin

• remove root, combine resulting trees to a new tree (actual cost up to n)
• start by linking pairs (1st and 2nd, 3rd and 4th,...), last may remain unpaired
• finally we link each remaining tree to the last one, starting from next-to-last back to the first (in the opposite order)
  • other variants of linking were studied as well

O(log n) amortized time can be proved by a similar analysis as in splay trees (not covered in the course)

• imagine as binary tree - rename first child to left and next sibling to right
• D(x): number of descendants of node x, including x (size of a node)
• r(x): lg (D(x)) rank of a node
• potential of a tree - sum of ranks of all nodes
• details in Fredman et al 1986
• Better bounds in Pettie 2005: amortized O(log n) ExtractMin; O(2^{2\sqrt{log log n}}) insert, union, decreaseKey; but decreaseKey not constant as in Fibonacci heaps)

Meldable heaps (not covered in the course)

• Advantages of Fibonacci compared to binary heap: faster decreaseKey (important for Prim's and Dijkstra's), faster union
• meldable heaps support O(log n) union, but all standard operations run in O(log n) time (except for build in O(n) and min in O(1))
• three versions: randomized, worst-case, amortized
• all of them use a binary tree similar to binary heap, but not always fully balanced
  • min-heap property: key of child >= key of parent
• key operation is union
  • insert: union of a single-node heap and original heap
  • extract_min: remove root, union of its two subtrees
• delete and decreaseKey more problematic, different for different versions, need pointer to parent
  • delete: cut away a node, union its two subtrees, hang back, may need some rebalancing
  • decrease_key: use delete and insert (or cut away a node, decrease its key, union with the original tree)

Random meldable heap

• http://opendatastructures.org/ Chapter 10.2 [3]
• Gambin1998-randomMeldableHeap.pdf

Union(H1, H2) {
    if (H1 == null) return H2;
    if (H2 == null) return H1;
    if (H1.key > H2.key) { exchange H1 and H2 }
    // now we know H1.key <= H2.key
    if (rand() % 2==1) {
       H1.left = merge(H1.left, H2);
    } else {
       H1.right = merge(H1.right, H2);
    }
    return H1;
}

Analysis:

• random walk in each tree from root to a null pointer (external node)
• in each recursive call choose H1 or H2 based on key values, choose direction left or right randomly
• running time proportional to the sum of lengths of these random walks

Lemma: The expected length of a random walk in a any binary tree with n nodes is at most lg(n+1).

• let W be the length of the walk, E[W] its expected value.
• Induction on n. For n=0 we have E[W] = 0 = lg(n+1). Assume the lemma holds for all n'<n
• Let n1 be the size of the left subtree, n2 the size of right subtree. n = n1 + n2 + 1
• By the induction hypothesis E[W] <= 1 + (1/2)lg(n1+1) + (1/2)lg(n2+1)
• lg is a concave function, meaning that (lg(x)+lg(y))/2 <= lg((x+y)/2)
• E[W] <= 1 + lg((n1+n2+2)/2) = lg(n1+n2+2) = lg(n+1)

Corollary: The expected time of Union is O(log n)

A different proof of the Lemma via entropy

• add so called external nodes instead of null pointers
• let di be the depth of ith external node
• binary tree with n nodes has n+1 external nodes
• probability of random walk reaching external node i is pi = 2^{-di}, and so di = lg(1/pi)
• E[W] = sum_{i=0}^n d_i p_i = sum_{i=0}^n p_i lg(1/pi)
• we have obtained entropy of a distribution over n+1 values which is at most lg(n+1)

Leftist heaps

• Mehta and Sahni Chap. 5
• Crane, Clark Allan. "Linear lists and priority queues as balanced binary trees." (1972) (TR and thesis)
• let s(x) be distance from x to nearest external node
  • s(x)=0 for external node x and s(x) = min(s(x.left), s(x.right))+1 for internal node x
• height-biased leftist tree is a binary tree in which for every internal node x we have s(x.left)>=s(x.right)
  • therefore in such a tree s(x) = s(x.right)+1

Union(H1, H2) {
    if (H1 == null) return H2;
    if (H2 == null) return H1;
    if (H1.key > H2.key) { exchange H1 and H2 }
    // now we know H1.key <= H2.key
    HN = Union(H1.right, H2);
    if(H1.left != null && HN.left.s <= H1.s) {
       return new node(H1.data, H1.left, HN) 
    } else {
       return new node(H1.data, HN, H1.left) 
    }
}

• note: s value kept in each node, recomputed in new node(...) using s(x) = s(x.right)+1
• recursion descends only along right edges

Lemma: (a) subtree with root x has at least 2^{s(x)}-1 nodes (b) if a subtree with root x has n nodes, s(x)<=lg(n+1) (c) the length of the path from node x using only edges to right child is s(x)

• (a) all levels up to s(x) are filled with nodes, therefore the number of nodes is at least 1+2+4+...+2^{s(x)-1} = 2^{s(x)}-1
• (b) an easy corollary of a (n>=2^s-1 => s<-lg(n+1))
• (c) implied by height-biased leftist tree property (in each step to the right, s(x) decreases by at least 1)

Corollary: Union takes O(log n) time

• recursive calls along right edges from both roots - at most s(x)<=lg(n+1) such edges in a tree of size n

Skew Heaps

• self-adjusting version of leftist heaps, no balancing values stored in nodes
• Mehta and Sahni Chap. 6

Union(H1, H2) {
    if (H1 == null) return H2;
    if (H2 == null) return H1;
    if (H1.key > H2.key) { exchange H1 and H2 }
    // now we know H1.root.key <= H2.root.key
    HN = Union(H1.right, H2);
    return new node(H1.data, HN, H1.left) 
}

Recall: Heavy-light decomposition from Link/cut trees

• D(x): number of descendants of node x, including x (size of a node)
• An edge from v to its parent p is called heavy if D(v)> D(p)/2, otherwise it is light.

Observations:

• each path from v to root at most lg n light edges because with each light edge the size of the subtree goes down by at least 1/2
• each node has at most one child connected to it by a heavy edge

Potential function: the number of heavy right edges (right edge is an edge to a right child)

Amortized analysis of union:

• Consider one recursive call. Let left child of H1 be A, right child B
• Imagine cutting edges from root of H1 to it children A and B before calling recursion and creating new edges to Union(B,H2) and A after recursive call
• Let real cost of one recursive call be 1
• If edge to H1.B was heavy
  • cutting edges has delta Phi = -1
  • adding edges back does not create a heavy right edge, therefore delta Phi = 0
  • amortized cost is 0
• If edge to H1.B was light
  • cutting edges has delta Phi = 0
  • adding edges creates at most one heavy right edge, therefore delta Phi <= 1
  • amortized cost is <= 2

All light edges we encounter in the algorithm are on the rightmost path in one of the two heaps, which means there are at most 2 lg n of them (lg n in each heap). This gives us amortized cost at most 4 lg n.