Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
RMQ a LCA
Z VPDS
Predbežná verzia poznámok, nebojte sa upravovať: pripojiť informácie z prezentácie, pridať viac vysvetľujúceho textu a pod.
Obsah
Introduction to LCA, RMQ
- v is ancestor of u if it is on the path from u to the root
- lca(u,v): node of greatest depth in the intersection of the set of ancestors of u and the set of ancestors of v
- note that a node is ancestor of itself and if u is ancestor of v, then lca(u,v)=u
Task: preprocess tree T in O(n), answer lca(u,v) in O(1)
History: Harel and Tarjan 1984, Schieber a Vishkin 1988 (Gusfield book), Bender and Farach-Colton 2000 (this lecture)
LCA via RMQ
- zname algoritmy a triv. algoritmy na slajde
- definicia poli V, D, R + ich vytvorenie slajdy
- V -- visited nodes
- D -- their depths
- R -- first occurrence of node in V
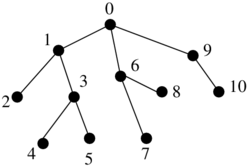
- assume that LCA(u,v) = x (fig.) and that R[u]<=R[v]
- tree traversal visits x, then subtree with u, then again x, then subtree with v, then again x, and only after that it can get above x
- D[x] = min D[R[u]..R[v]]
- this holds even if LCA(u,v)=u (LCA(u,v) cannot be v if R[u]<R[v])
- if we can quickly find k = arg min_k in {i..j} D[k], the result is V[k]
- we have trasformed LCA to a new problem
Range minimum query RMQ
- goal: preprocess array A so that we can any two indices i and j quickly find index of minimum in A[i..j]
- Alg 1: no preprocessing, O(n) query: find minimum in interval
- Alg 2: O(n^2) preprocessing, O(1) query: precompute for all (i,j) in a table
- Alg 3: O(n log n) preprocessing, O(1) query: store minimum only for intervals of length 2^k
- M[i,k]: index of minimum in A[i..i+2^k-1] for k=1,2,...,floor(log n)
i 0 1 2 3 4 5 6 7 8 9 10 11 12 A[i] 0 1 2 1 2 3 2 1 0 1 0 1 0 -------------------------------------------- k=1 0 1 3 3 4 6 7 8 0 10 10 12 - k=2 0 1 3 3 7 8 8 8 8 10 - - - k=3 0 8 8 8 8 8 - - - - - - -
- Preprocessing M[i,k]: if A[M[i,k-1]]<A[M[i+2^{k-1},k-1]] then M[i,k]=M[i,k-1], else M[i,k]=M[i+2^{k-1},k-1]
- RMQ(i,j):
- let k=floor(log_2(j-i+1)) (max size of a block inside A[i..j]), floor(log x) can be precomputed for i=1..n
- if A[M[i,k]]<A[M[j-2^k+1,k]] return M[i,k] else return M[j-2^k+1,k] (figure of overlapping intervals)
+-1RMQ
- Adjacent elements of array D in LCA differ by exactly 1, i.e. 1 D[i]-D[i+1] in {-1,1}
- We will show a better RMQ data structure for arrays with this property. This problem is called +-1RMQ
- Split A into blocks of size m = lg(n)/2
- Find minimum in each block, these minima store in array A'[0..n'-1] and position of these minima into array M'[0..n'-1] where n' = n/m = 2n/lg n
- Preprocess array A' using algorithm 3 in O(n'log n') = O(n) time
- RMQ(i,j) query considers two cases (figure):
- i and j are in different blocks bi and bj
- compute RMQ in A'[bi+1..bj-1] in O(1)
- compute minimum in block bi from i to end of block (see below)
- compute minimum in block bj from start to j (see below)
- find minimum of these three numbers
- i and j are in the same block
- compute minimum between two indices in the same block
- i and j are in different blocks bi and bj
- remains to show: how to compute +-1RMQ within blocksv ramci blokov
- representation of a block: the first element + differences between adjacent elements, e.g. 2,3,2,1 -> 2,+1,-1,-1
- na urcenie polohy minima nepotrebujeme vediet prvy prvok, staci iba m-1 rozdielov +1,-1,-1
- kazdy blok sa teda da zapisat ako binarne cislo s m-1 bitmi
- najviac 2^{m-1}<=sqrt(n) roznych typov blokov
- pre kazdy typ predpocitaj vsetky odpovede (alg. 2) v case O(m^2)
- spolu teda O(2^{m-1} m^2) = O(sqrt(n)*log(n)^2) = o(n)
+-1RMQ predpracovanie:
- spocitaj typ kazdeho bloku, uloz do pola O(n)
- pre kazdy typ spocitaj odpovede o(n) (v priemere sa jeden typ opakuje cca sqrt(n) krat, takze usetrime)
- spocitaj pole A' O(n)
- predspracuj pole A' O(n)
spolu O(n)
RMQ(i,j):
- 2x minimum v bloku O(1)
- 1x minimum v A' O(1)
spolu O(1)
LCA predspracovanie:
- prehladanie stromu a vytvorenie poli O(n)
- +-1 RMQ predspracovanie O(n)
LCA(u,v) 2 pristupy do pola R, +-1RMQ na poli D, pristup do pola V O(1)
RMQ via LCA
- vieme teda dobre riesit +-1RMQ a pomocou neho aj LCA
- vseobecne RMQ vieme riesit pomocou LCA
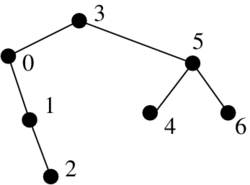
- z pola A vytvorime karteziansky strom:
- v koreni ma polohu i najmensieho cisla
- v lavom podstrome rekurzive definovany strom pre cast pola a[0..i-1]
- v pravom podstrome rekurzivne definovany strom pre cast pola a[i+1..n]
- RMQ(i,j) = LCA(i,j)
- vezmime si uplne minimum v poli na poz. k: pre ktore dvojice bude vyslekodm RMQ(i,j)?
- pre tie, kde i<=k, j>=k, pre tieto je k aj LCA
- ostatne dvojice su bude uplne nalavo od k alebo uplne napravo, tam je strom definovany rekurzivne a teda tiez funguje
- strom sa da vytvorit v O(n):
- ak uz mame strom pre a[0..i-1] a pridavame a[i], a[i] bude niekde na najpravejsej ceste
- ideme zo spodu po tejto ceste a najdeme prvy vrchol j, pre ktory a[j]<a[i]
- i dame ako prave dieta j, stare prave dieta j dame ako lave dieta i
- kazdy vrchol raz pridame do cesty a raz uberieme (vsetky vrcholy, ktore sme presli pri hladani j uz nie su na pravej ceste), teda celkovo O(n)
- potential function: number of vertices on the rightmost path
Segment trees
- root correspods to interval [0,n)
- leafs correspond to intervals of length 1, [i,i+1)
- if node corresponds to [i,j)
- left child corresponds to [i,k), right child to [k,j) where k = floor((i+j)/2)
- overall the number of nodes roughly 2n, height ceiling(lg n)
- each interval contains the result for its range (minimum, sum,...)
Decompose query interval [x,y) to a set of disjoint tree intervals (canonical decomposition):
- let current node has interval [i,j) and its left child interval [i,k)
- invariant: [i,j) overlaps with [x,y)
- if [i,j) is a subset of [x,y), include [i,j) in the decomposition and stop
- if [i,k) overlaps with [x,y), recurse on left child
- if [k,j) overlaps with [x,y), recurse on right child
Tree of recursive calls:
- sometimes recursion on only one child, sometimes both (split)
- first follow a single path from the root, each time moving to the left or right child
- last node before first split: smallest interval in the tree which contains whole [x,y), lca of leaves [x,x+1), [y,y+1)
- first split to both left and right: spliting point k inside [x,y)
- after that in the left branch [x,y) always covers right endpoint, therefore even if we split, right recursive calls will terminate in the next step with case 1
- similarly in the right branch [x,y) covers left endpoint, therefore left calls will terminate
- together at most 2 traversals from root to leaf plus a short call in each step, which means at most 4 ceil(lg n) vertices visited
Segment trees can also support dynamic case where we add operation set(i,x) which sets A[i] = x
- this would require large changes in prefix sum or O(n log n) RMQ data structures
- but here only O(log n) vertices on the path from the changed leaf to the root are affected
Print small
- mame pole cisel A, predspracovane pre RMQ
- chceme vypisat vsetky indexy k in {i..j} take ze A[i]<=x
void small(i,j,x) {
if(j<i) return;
k = rmq(i,j);
if(a[k]<=x) {
print k;
small(i,k-1);
small(k+1,j);
}
}
- analyzujte cas vypoctu vzhladom na p, kde p je pocet vypisanych indexov