Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
Úsporné dátové štruktúry: Rozdiel medzi revíziami
(→Wavelet tree: Rank nad vacsou abecedou) |
(→Wavelet tree: Rank nad vacsou abecedou) |
||
| Riadok 81: | Riadok 81: | ||
** nech j = B[i], i_2 = rank_j(i) v retazci B | ** nech j = B[i], i_2 = rank_j(i) v retazci B | ||
** pokracuj rekurzivne s hladanim S_j[i2] | ** pokracuj rekurzivne s hladanim S_j[i2] | ||
| + | |||
| + | ==Back to FM index== | ||
| + | * jednoducha finta na zlepsenie pamate pre rank: | ||
| + | ** ulozime si rank len pre niektore i, zvysne dopocitame na zaklade pocitania vyskytov v L (vydelime pamat k, vynasobime cas k) | ||
| + | * rank + L pomocou wavelet tree v n lg sigma + o(n log sigma) bitoch, hladanie vyskytov sa spomali na O(m log sigma) | ||
| + | * ako kompaktnejsie ulozit SA | ||
| + | * mozeme ulozit SA len pre niektore riadky, pre ine sa pomocou LF transformacie dostaneme k najblizsiemu riadku pre ktory mame SA | ||
| + | ** ako presne ulozit "niektore riadky" ked su nerovnomerne rozmiestnene v SA (rovnomerne v T)? | ||
| + | * samotne L mozeme ulozit aj komprimovanie s vhodnymi indexami, vid. clanok od F a M alebo ho mame reprezentovane implicitne vo wavelet tree | ||
===RRR=== | ===RRR=== | ||
Verzia zo dňa a času 23:07, 15. apríl 2015
Obsah
[skryť]Uvod do uspornych datovych struktur
- Retazec dlzky n nad abecedou velkosti sigma mozeme ulozit pomocou n lg sigma bitov (predpokladajme pre jednoduchost, ze sigma je mocnina 2)
- napr pre binarny retazec potrebuje n bitov
- Sufixove pole na umoznuje rychlo hladat vzorku, ale potrebuje n lg n bitov, pripadne 3 n lg n, co je rychlejsie rastuca funkcia ako n
- sufixove stromy maju tiez Theta(n log n) bitov s vacsou konstantou
- vedeli by sme rychlo vyhladavat vzorku aj s ovela mensim indexom?
- oblast uspornych datovych struktur
Uvod do rank/select
Chceme reprezentovat staticku mnozinu A subseteq {0..n-1}, nech m = |A|
- pole cisel v A v utriedenom poradi (m log n bitov)
- bitovy vektor dlzky n (n bitov)
Pole Bitovy vektor Pamat v bitoch m log n n Je x v A? O(log m) O(1) rank(x)>rank(x-1) max. y v A t.z. y<=x O(log m) O(n) select(rank(x)) i-ty najmensi prvok z A O(1) O(n) select(i) kolko je v A prvkov <=x O(log m) O(n) rank(x)
Ak m je pomerne velke (cca Omega(n/log n)), pamat mensia s vyuzitim bitoveho pola
Ak chcem rank v O(1)
- trivialne riesenie: pamatam si rank(x) pre kazde x, n log n bitov
- ukazeme si, ze staci o(n) bitov navyse k bitovemu vektoru s n bitmi
- prakticke riesenie:
- zvolim si hodnotu t
- pole R dlzky n/t, R[i] = rank(i*t)
- rank(x) = R[floor(x/t)]+pocet jedniciek v A[t*floor(x/t)+1..x]
- pamat n + (n/t)*lg(n) bitov, cas O(t)
- O(1) riesenie zalozene na tejto myslienke, trochu zlozitejsie detaily
Ak chcem select v O(1)
- trivialne riesenie je utriedene pole prvkov (pozri vyssie)
- da sa spravit usporne o(n) bitov navyse k bitovemu vektoru s n bitmi, ale zlozitejsie
- prakticky kompromis: binarne vyhladavanie, log n volani rank
Rank
- overview na slajde
- rank = rank of super-block + rank of block within superblock + rank of position within block
- block and superblock: integer division (or shifts of sizes power of 2)
- time O(1), memory n + O(n log log n / log n) bits
Select
- let t1 = lg n lglg n
- store select(t1 * i) for each i = 0..n/t1 memory O(n / t1 * lg n) = O(n/ lg lg n)
- divides bit vector into super-blocks of unequal size
- consider one such block of size r. Distinguish between small super-block of size r<t1^2 and big super-block of size >= t1^2
- large super-block: store array of indices of 1 bits
- at most n/(t1 ^2) large super-blocks, each has t1 1 bits, each 1 bit needs lg n bits, overall O(n/lg lg n) bits
- small super-block:
- repeat the same with t2 = (lg lg n)^2
- store select(t2*i) within super-block for each i = 0..n/t2 memory O(n/t2 * lg lg n) = O(n/lg lg n)
- divides super-block into blocks, split blocks into small (size less than t2^2) and large
- for large blocks store relative indices of 1 bits: n/(t2 ^2) large blocks, each has t2 1 bits, each 1 bit needs lg t1^2 = O(lg lg n) bits, overall O(n/log log n)
- for small blocks of size at most t2^2, store as (t2^2)-bit integer, lookup table of all answers. Size of table is O(2^(t2^2) * t2 * log(t1)); t2^2 < (1/2) log n for large enough n, so 2^(t2^2) is O(sqrt(n)), the rest is polylog
Wavelet tree: Rank nad vacsou abecedou
- nad binarnou abecedou vieme spravit rank_1(i): pocet vyskytov 1 v A[0..i]
- poznamka: ak chceme spocitat rank_0(i), pouzijeme i+1-rank_1(i)
- original paper: Grossi, Gupta and Vitter 2003 High-order entropy-compressed text indexes
- survey G. Navarro, Wavelet Trees for All, Proceedings of 23rd Annual Symposium on Combinatorial Pattern Matching (CPM), 2012
- http://alexbowe.com/wavelet-trees/
- namiesto bitoveho pola mame retazec S nad vacsou abecedou Sigma
- Chceme podporovat rank_a(i), co je pocet vyskytov pismena a v retazci S[0..i]
- OPT je n lg sigma
- Pouzijeme rank na binarnych retazcoch nasledovne:
- rozdelime abecedu na dve casti Sigma_0 a Sigma_1
- Vytvorime bin. retazec B dlzky n: B[i]=j iff S[i] je v Sigma_j
- Vytvorime retazce S_0 a S_1, kde S_j obsahuje pismena z S, ktore su v Sigma_j, sucet dlzok je n
- Rekurzivne pokracujeme v deleni abecedy a retazcov, az kym nedostaneme abecedy velkosti 2, kde pouzijeme binarny rank
- rank_a(i) v tejto strukture:
- ak a in Sigma_j, i_2=rank_j(i) v retazci B
- pokracuj rekurzivne s vypoctom rank_a(i_2) v lavom alebo pravom podstrome
- Velkost: binarne retazce n log_2 sigma + struktury pre rank nad bin. retazcami (mozem skonkatenovat na kazdej urovni a dostat o(n log_2 sigma)
- cas O(log sigma), robim jeden rank na kazdej urovni
- extrahovanie S[i] tiez v case O(log sigma)
- samotny retazec S teda nemusim ukladat
- nech j = B[i], i_2 = rank_j(i) v retazci B
- pokracuj rekurzivne s hladanim S_j[i2]
Back to FM index
- jednoducha finta na zlepsenie pamate pre rank:
- ulozime si rank len pre niektore i, zvysne dopocitame na zaklade pocitania vyskytov v L (vydelime pamat k, vynasobime cas k)
- rank + L pomocou wavelet tree v n lg sigma + o(n log sigma) bitoch, hladanie vyskytov sa spomali na O(m log sigma)
- ako kompaktnejsie ulozit SA
- mozeme ulozit SA len pre niektore riadky, pre ine sa pomocou LF transformacie dostaneme k najblizsiemu riadku pre ktory mame SA
- ako presne ulozit "niektore riadky" ked su nerovnomerne rozmiestnene v SA (rovnomerne v T)?
- samotne L mozeme ulozit aj komprimovanie s vhodnymi indexami, vid. clanok od F a M alebo ho mame reprezentovane implicitne vo wavelet tree
RRR
- Raman, Raman, Rao, from their 2002 paper Succinct indexable dictionaries with applications to encoding k-ary trees and multisets
- http://alexbowe.com/rrr/
class of a block: number of 1s
- R1: Array of ranks at superblock boundaries
- R2: Array of ranks at block boundaries within superblocks
- R3: precomputed table of ranks for each class, each signature within class and each position within block of size t2
- S1: Array of superblock starts in compressed bit array
- S2: Array of block offsets in compressed bit array
- C: class (the number of 1s) in each block
- L: size of signature for each class (ceil lg (t2 choose class))
- B: compressed bit array (concatenated signatures pf blocks)
rank(i):
- superblock = i/t1 (integer division)
- block = i/t2
- index = S1[superblock]+S2[block]
- class = C[block]
- length = L[class]
- signature = B[index..index+length-1]
- return R1[superblock]+R2[block]+R3[class, signature, i%t2]
Analysis of RRR:
- Let S be a string in which a occurs n_a times
- Its entropy is H(S) = sum_a \frac{n_a}{n} \log \frac{n}{n_a}
- let x_i be the number of 1s in block i, let n_1 be the overall number of 1s
-
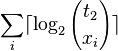
-
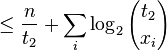
- <tex>= o(n)+\log_2 \prod_i {t_2 \choose x_{i}}</tex>
- <tex>\le o(n)+\log_2 {n \choose n_1}</tex> (choice of x_i in each block is subset of choice of n_1 overall)
- <tex>\log_2 {n \choose n_1} = [\ln(n!) - \ln(n_1!) - \ln(n_0!))]/\ln(2)</tex>
- <tex>= [n\ln(n)-n-n_1\ln(n_1)+n_1-n_0\ln n_0+n_0+O(\log n)]/\ln(2)</tex>
- <tex>= n_1\log_2 (n_1/n) + n_0\log_2 (n_0/n) + O(\log n)</tex> (linear terms cancel out, n\ln(n) divided into two parts: n_0\ln(n) and n_1\ln(n))
- <tex>= n H(B)+O(\log n)</tex>
Use in wavelet tree (see Navarro survey of wavelet trees):
- top level n0 zeroes, n1 ones, level 1: n00, n01, n10, n11
- top level entropy encoding uses n0 lg(n/n0) + n1 lg(n/n1) bits
- next level uses n00 lg(n0/n00) + n01 lg(n0/n01) + n10 lg(n1/n10) + n11 lg(n1/n11)
- add together n00 lg(n/n00) + n01 lg(n/n01) + n10 lg(n/n10) + n11 lg(n/n11)
- continue like this until you get sum_c n_c lg(n/n_c) which is nH(T)
Binarny strom
- pridame pomocne listy tak, aby kazdy povodny vrchol bol vnut vrchol s 2 detmi
- ak sme mali n vrcholov, teraz mame n vnut. vrcholov a n+1 listov, t.j. 2n+1 vrcholov
- ocislujeme ich v level-order (prehladavanie do sirky) cislami 1..2n+1
- vrchol je reprezentovany tymto cislom
- datova struktura: bitovy vektor dlzky 2n+1, ktory ma na pozicii i 1 prave vtedy ak vrchol i je vnutorny vrchol
- nad tymto vektorom vybudujeme rank/select struktury v o(n) pridavnej pamati
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1 1 1 1 1 0 1 0 0 1 1 0 0 0 0 0 0 A B C D E . F . . G H . . . . . .
Lemma: Pre i-ty vnutorny vrchol (i-ta jednotka vo vektore) su jeho deti na poziciach 2i a 2i+1
- indukcia na i
- pre i=1 (koren) ma deti na poziciach 2 a 3
- deti i-teho vnutorneho vrcholu su v poradi hned po detoch (i-1)-veho
- dva pripady podla toho, ci (i-1)-vy a i-ty su na tej istej alebo roznych urvniach, ale v oboch pripadoch medzi nimi len pomocne listy a teda medzi ich detmi nic (obrazok)
- kedze deti (i-1)-veho su na poziciach podla IH 2i-2 a 2i-1, deti i-teho budu na 2i a 2i+1.
Dosledok:
- left_child(i) = 2 rank(i)
- right_child(i) = 2 rank(i)+1
- parent(i) = select(floor(i/2))
Ak chceme pouzit ako lexikograficky strom nad binarnou abecedou: potrebujeme zistit, ci vnut. vrchol zodpoveda slovu v mnozine
- jednoduchu fix s n dalsimi bitmi: z cisla vrchola 1..2n+1 zistime rankom cislo vnut vrchola 0..n-1 a pre kazde si pamatame bit, ci je to slovo z mnoziny
- da sa asi aj lepsie
Catalanove cisla
Ekvivalentne problemy:
- kolko je binarnych stromov s n vrcholmi?
- kolko je usporiadanych zakorenenych stromov s n+1 vrcholmi?
- kolko je dobre uzatvorkovanych vyrazov z n parov zatvoriek?
- kolko je postupnosti, ktore obsahuju n krat +1 a n krat -1 a pre ktore su vsetky prefixove sucty nezaporne?
Chceme dokazat, ze odpoved je Catalanovo cislo <tex>C_n = {2n\choose n}/(n+1)</tex> (C_0 = 1, C_1=1, C_2 = 2, C_3 = 5,...)
- Rekurencia <tex>T(n) = \sum_{i=0}^{n-1} T(i)T(n-i-1)</tex> (nech najlavejsia zatvorka obsahuje vo vnutri i parov), riesime metodami kombinatorickej analyzy (generujuce funkcie)
- Iny dokaz [1]
- Nech X(n,m,k) je mnozina vsetkych postupnosti dlzky n+m obsahujucich n +1, m -1 a takych ze kazdy prefixovy sucet je aspon k.
- |X(n,m,-infty)| = n+m nad n
- my chceme |X(n,n,0)|
- nech Y = X(n,n,-infty)-X(n,n,0), t.j. vsetky zle postupnsti
- najdeme bijekciu medzi Y a X(n-1,n+1,-infty)
- vezmime postupnost z Y, najdime prvy zaporny prefixovy sucet (-1), od toho bodu napravo zmenme znamienka, dostavame postupnost z X(n-1,n+1,-infty) (obrazkovy dokaz so schodmi)
- naopak vezmime postupnost z X(n-1,n+1,-infty), najdeme prvy bod, kde je zaporny prefixovy sucet (-1), od toho bodu napravo zmenme znamienka, dostavame postupnost z Y
- tieto dve zobrazenia su navzajom inverzne, preto musi ist o bijekciu
- preto |X(n,n,0)| = |X(n,n,-infty)|-|X(n-1,n+1,-infty)|=(2n nad n) - (2n nad n-1) = (2n nad n)/(n+1)