Vybrané partie z dátových štruktúr
2-INF-237, LS 2016/17
Vyhľadávanie vzorky v texte: Rozdiel medzi revíziami
| Riadok 1: | Riadok 1: | ||
| + | ==Literatúra== | ||
| + | * Dan Gusfield (1997) [http://www.cambridge.org/uk/catalogue/catalogue.asp?isbn=0521585198 Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology.] Cambridge University Press. Prezenčne v knižnici so signatúrou I-INF-G-8. | ||
| + | * Poznámky z predmetu Vyhľadávanie v texte [http://compbio.fmph.uniba.sk/vyuka/vvt/poznamky/main-2013-05-20.pdf] (zčasti písané študentami a nedokončené) | ||
| + | |||
==Theoretical results for edit distance computation== | ==Theoretical results for edit distance computation== | ||
| Riadok 11: | Riadok 15: | ||
Source: Backurs A, Indyk P. Edit Distance Cannot Be Computed in Strongly Subquadratic Time (unless SETH is false). STOC2015, pp. 51-58 [http://arxiv.org/pdf/1412.0348v2.pdf] | Source: Backurs A, Indyk P. Edit Distance Cannot Be Computed in Strongly Subquadratic Time (unless SETH is false). STOC2015, pp. 51-58 [http://arxiv.org/pdf/1412.0348v2.pdf] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Aktuálna revízia z 12:49, 7. apríl 2016
Literatúra
- Dan Gusfield (1997) Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. Cambridge University Press. Prezenčne v knižnici so signatúrou I-INF-G-8.
- Poznámky z predmetu Vyhľadávanie v texte [1] (zčasti písané študentami a nedokončené)
Theoretical results for edit distance computation
Exact algorithm O(mn) or improved by logarithimc factor.
Approximation algorithm: For strings of length n and every fixed ε > 0 compute 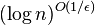 approximation in
approximation in 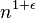 time
time
Source: Andoni A, Krauthgamer R, Onak K. Polylogarithmic approximation for edit distance and the asymmetric query complexity. FOCS2010, pp. 377-386 [2]
Conditional lower bound: If the edit distance can be computed in 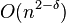 for some constant δ > 0, then the satisfiability of conjunctive normal form (CNF) formulas with N variables and M clauses can be solved in time
for some constant δ > 0, then the satisfiability of conjunctive normal form (CNF) formulas with N variables and M clauses can be solved in time 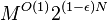 for a constant
for a constant 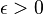 , which would violate Strong Exponential Time Hypothesis (SETH).
, which would violate Strong Exponential Time Hypothesis (SETH).
Source: Backurs A, Indyk P. Edit Distance Cannot Be Computed in Strongly Subquadratic Time (unless SETH is false). STOC2015, pp. 51-58 [3]